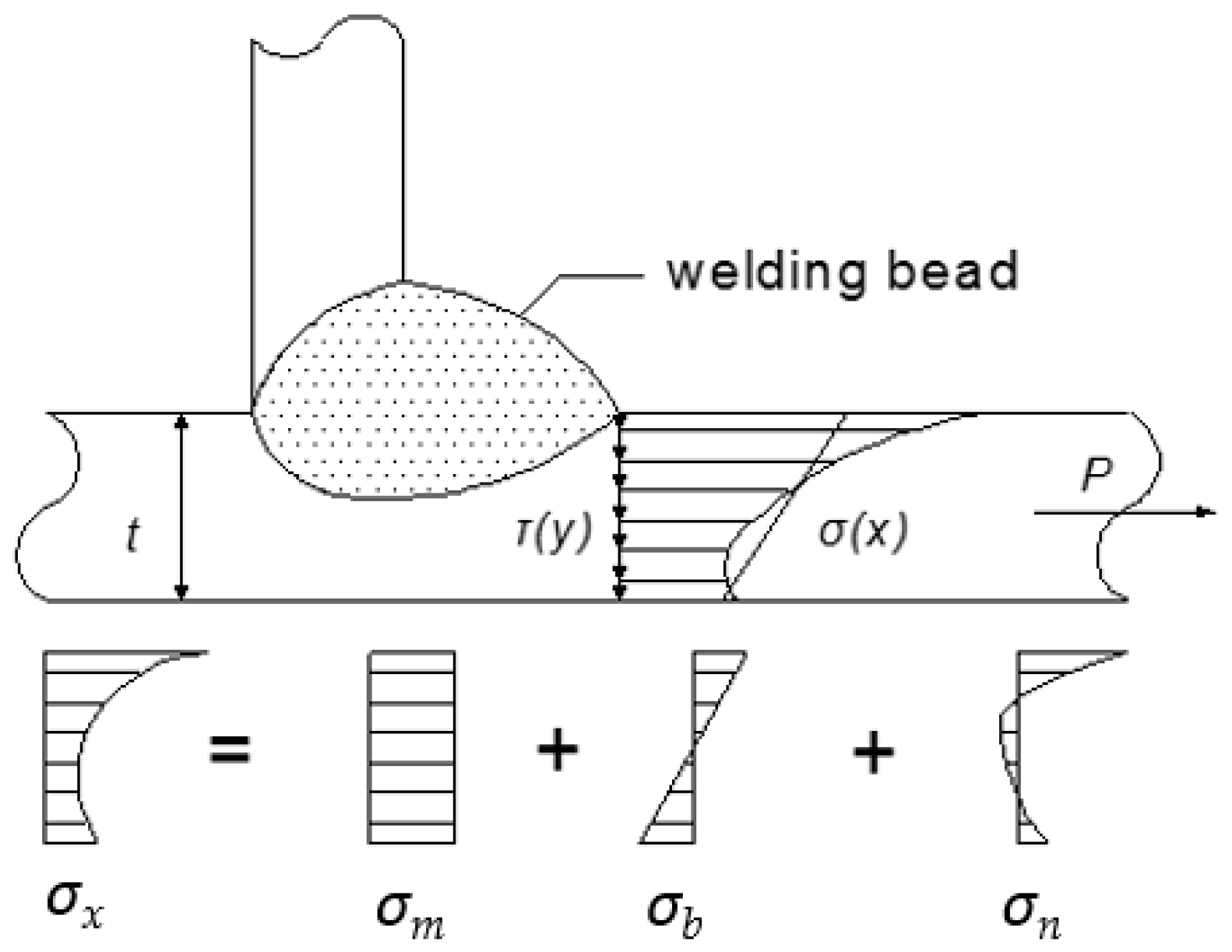
1. Introduction
At present, the widely-applied welding fatigue design and prediction are mainly based on nominal stress (
NS) approach, hot spot stress
(HSS) approach, and the master S-N curve approach [
1]. As is well-known, the nominal stress method was firstly proposed and used maturely for the fatigue analysis of welded structures [
2]. Due to the fact that it ignores the local stress effects of welded joints and is explicitly mathematically explained, many standard specifications have been established based on the nominal stress method using a large scale of experimental data from [
3,
4]. While some limitations have gradually come to light, the nominal stress of a complex structure is hard to determine and inconsistent stress calculation is caused by a singularity in the weld toe as well, which limit its universality in engineering applications [
5]. Afterwards, in order to obtain the accurate stress in the welding toe, the hot spot stress (
HSS) method that is extrapolated based on the nominal stress was first proposed by Niemi [
6]. It characterizes the stress condition in the weld toe by taking the effects of geometry structure into account so that hot spot stress can be extrapolated through an extrapolation formula indirectly in complex welded structures [
7]. Although this solves some problems existing in the nominal stress method, it is difficult to establish a uniform hot spot type and extrapolation formula for various welding types, which also limits its engineering applications.
As discussed in [
1], an innovative master S-N curve approach based on the equivalent structural stress (
ES) has been proposed by Dong via taking advantage of the new concept of structural stress (SS). The effectiveness of the master S-N curve approach is attributed to the fact that the structural stress calculated are mesh-insensitive and, therefore, intrinsic to a given joint geometry and loading mode from the perspective of fracture mechanics. Thus, an equivalent structural stress parameter in the context of a single master S-N curve has been established and proven to be effective in consolidating a large amount of weld S-N data obtained from drastically different joint geometries, plate thickness, and loading mode [
8].
Information entropy was defined by Shannon, “The father of information theory”, which can measure the uncertainty of random events. Originally, the concept of information entropy was used to measure the dispersion degree. Information entropy has been widely used in many field, such as engineering technology, economic decision-making, societal risk, etc. [
9,
10,
11,
12,
13,
14,
15].Currently, information entropy is gradually being used in the field of welding and fatigue research. Li et al. [
9] combined the theory of wavelet multi-resolution analysis with the information entropy together and proposed an algorithmic method of wavelet energy entropy based on wavelet multi-resolution analysis so that the wavelet energy entropy can be used to evaluate the stability of arc in square wave alternating current submerged arc welding. Kavrishvili et al. [
10] developed a method for the evaluation of the information content of the signals of welding current and arc voltage taking into account the statistical dependence of the appearance of the values in the given time range. Results show that these quantitative characteristics may be used for the evaluation of the quality of the characteristics of the components of the welding process. The concept of thermodynamic entropy generation was employed by Amiri et al. [
11] to assess degradation in processes involving metal fatigue. Conclusions were carried out that empirical fatigue models such as Miner’s rule, Coffin-Manson equation, and Paris law can be deduced from thermodynamic consideration. In addition, with the help of information entropy under multi-step independent communications from many sources, Skorobogatov [
12] described the disclosing indeterminacy in a pattern of cracks from the beginning and up to the end of loading for the first time. The curve of the parameter of serviceability coincides with the curve of the information entropy by the character of change which determines an assessment of expedience rehabilitation of a structure’s damage with unknown load. Incorporating all of the uncertainties, a maximum relative entropy (MRE) approach is proposed and developed by Guan et al. [
13] to update the statistical description of model parameters and narrow down the prognosis deviations. A detailed comparison between the proposed MRE approach and the classical Bayesian updating method is performed to illustrate advantages of the proposed prognosis framework. Additionally, a general method of probabilistic fatigue damage prognosis using limited and partial information is developed [
14]. The posterior distribution is formulated using the principle of maximum relative entropy (MRE) to perform probability updating is point measurements. Fatigue crack prognosis problems with experimental data are presented for demonstration and validation. The maximum entropy fracture model [
15] is a thermodynamically consistent and information theory inspired (non-empirical) damage accumulation theory for ductile solids, validated on both area array and peripheral array packages. Combining the authors’ knowledge of the constitutive behavior with the damage accumulation behavior, fatigue life predictions can be made for a wide variety of package types and mixed metallurgical conditions. A computational method based on the maximum entropy principle is proposed by Li et al. [
16] for identifying the probability distribution of fatigue life. The rationality and effectiveness of the proposed method are demonstrated by two groups of fatigue datasets available in the literature. Comparisons among the proposed method, the lognormal distribution and the three-parameter Weibull distribution are also carried out for the investigated groups of fatigue datasets.
In this paper information entropy was firstly employed to analyze the S-N data distribution of welding structure based on the equivalent structural stress. Probability distribution is analyzed by the proposed model, and importance level of the attributes governing the welding structure fatigue life is investigated for the first time by entropy ideology. Firstly, three S-N curves for aluminum alloy welded joints are established based on nominal stress, structural stress, and equivalent structural stress in the master S-N curve method. Then an evaluation of fatigue life data based on information entropy is established to study the correction of S-N distribution of the three kinds of approaches. There is consistency between the reducing trend of the weight based information entropy and the smaller and smaller standard deviation of the S-N curves. Especially, through calculating and analyzing the weighted information entropy of decision attributes, quantitative contribution of stress concentration, plate thickness and loading mode to the fatigue destruction are studied. Thus, the fatigue life evaluation method based on the information entropy can be a credible and effective method of the weld fatigue prediction.
3. Fatigue Data Evaluation Mode Based on Information Entropy
3.1. Establishment of the S-N Curve
As introduced before, information entropy was employed to analyze the S-N data distribution of welding structure based on the three types of stress in this paper. Firstly three S-N curves for aluminum alloy welded joints are established based on nominal stress, structural stress, and equivalent structural stress by means of the least square method. Then an evaluation mode of fatigue life data based on information entropy is established to study the correction of S-N distribution of the three types of approaches. Furthermore, the contrast between the weight based information entropy and the standard deviation of the S-N curves were carried out. Through calculating and analyzing the weighted information entropy of decision attributes, quantitative contribution of stress concentration, plate thickness and loading mode to the fatigue destruction are studied.
It is worth noting here that all of the S-N curves modeled and information entropy calculated in this paper are based on well-documented fatigue data. Aluminum alloy low cycle fatigue data for MIG [
19], GMAW [
20], TIG [
21], manual arc [
22], and in the as-welded conditions without stress-relief were cited. Forty-eight sets of welding fatigue data were arranged by welding factors including stress type (
T), plate thickness (
t), load ratio (
R), and stress ratio (
r), among which the parameters
R and
r are expressed as:
With respect to these data, the mean S-N curves based on
NS,
SS, and
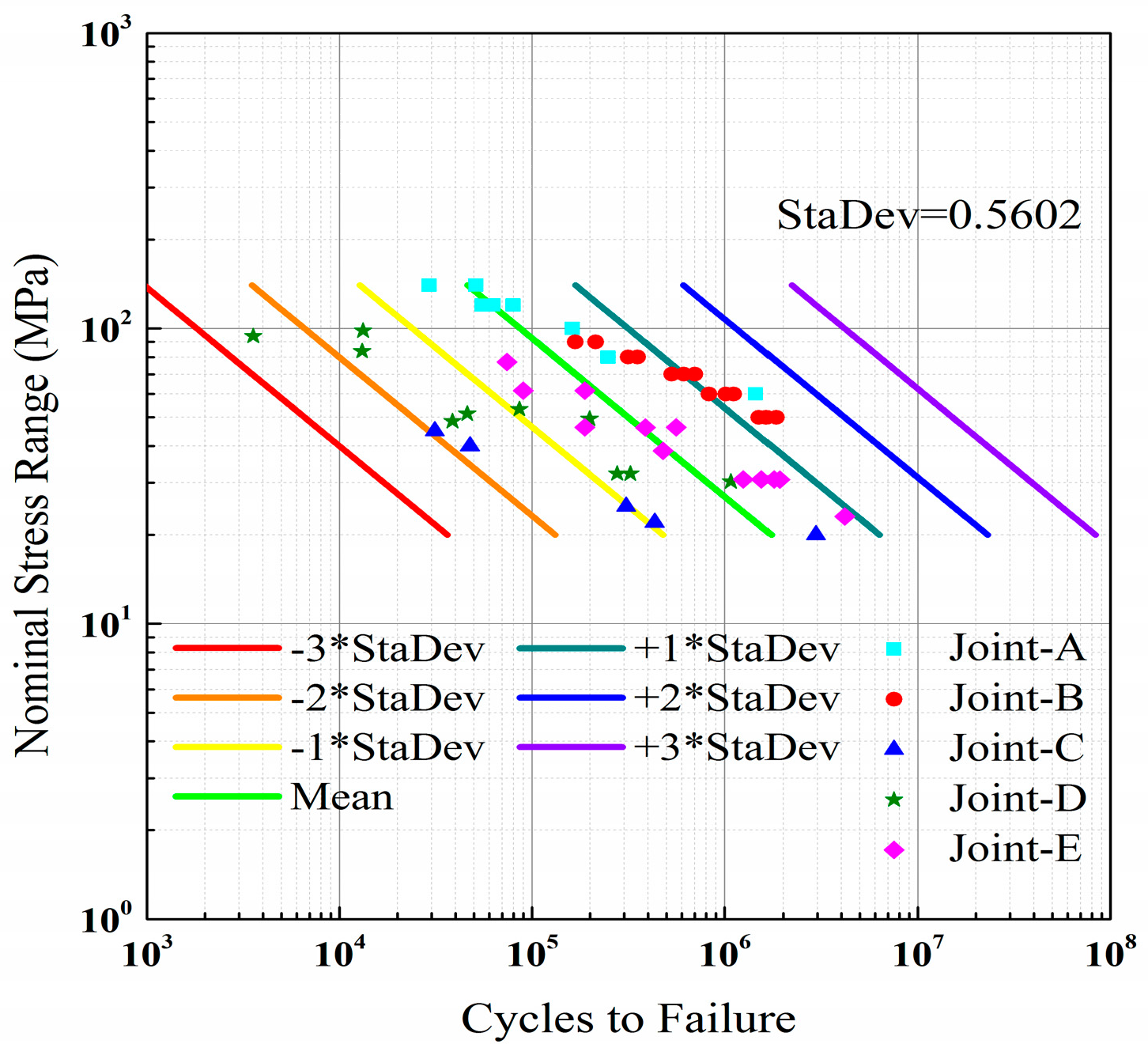
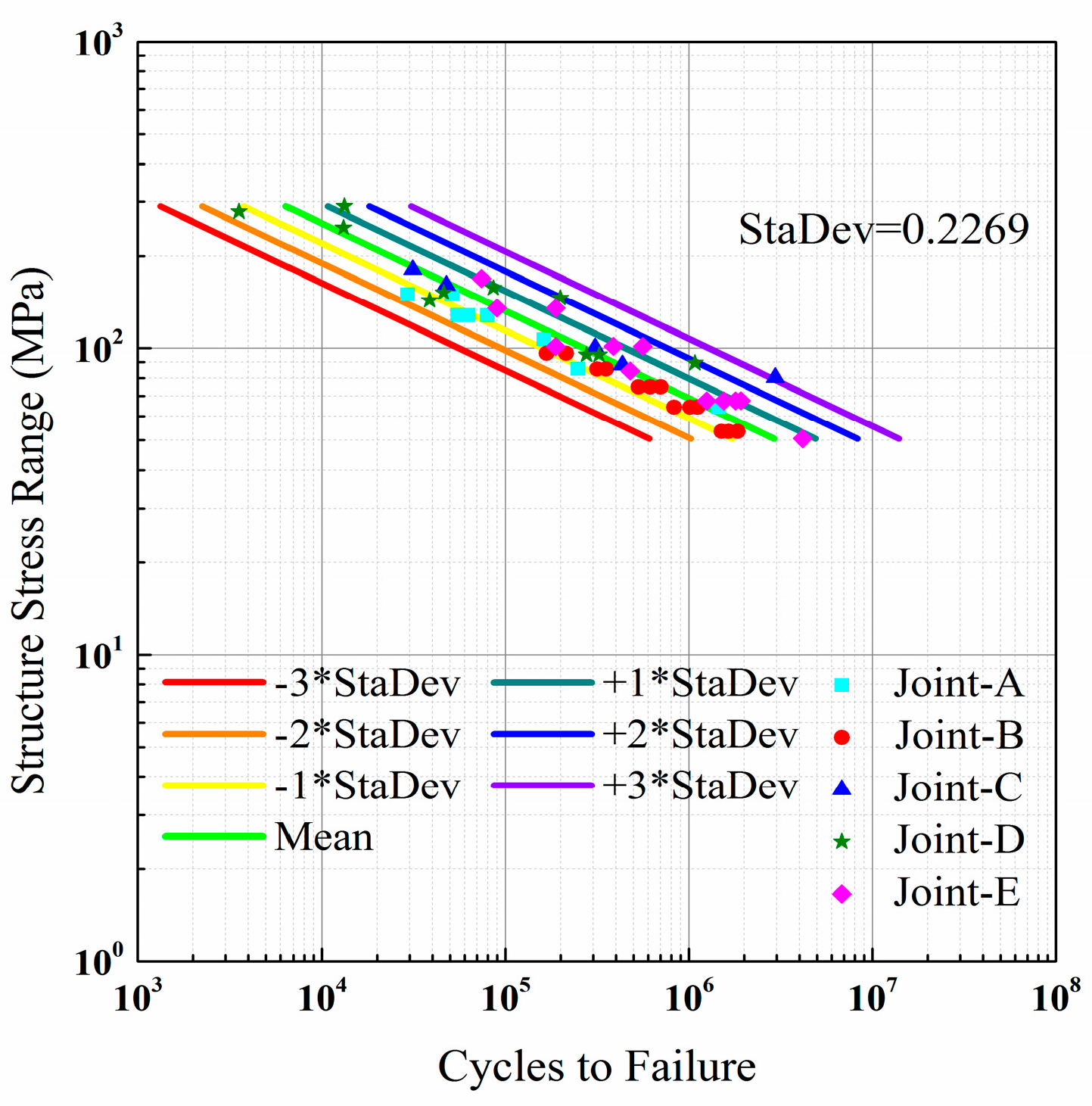
ES were fitted using the least square method and the standard deviations (StaDev) were calculated at the same time. The mean S-N curves and deviation curves with −3, −2, −1, +1, +2, and +3 magnifications were then carried out in respective coordinates, as shown in
Figure 2,
Figure 3 and
Figure 4 [
5]. According to the parameters above, the S-N data points based on
NS,
SS, and
ES, respectively, were discretized as shown in
Figure 2,
Figure 3 and
Figure 4. It is necessary to explain here that there are different experiment parameters as shown in
Table 1 from Joint-A to Joint-E.
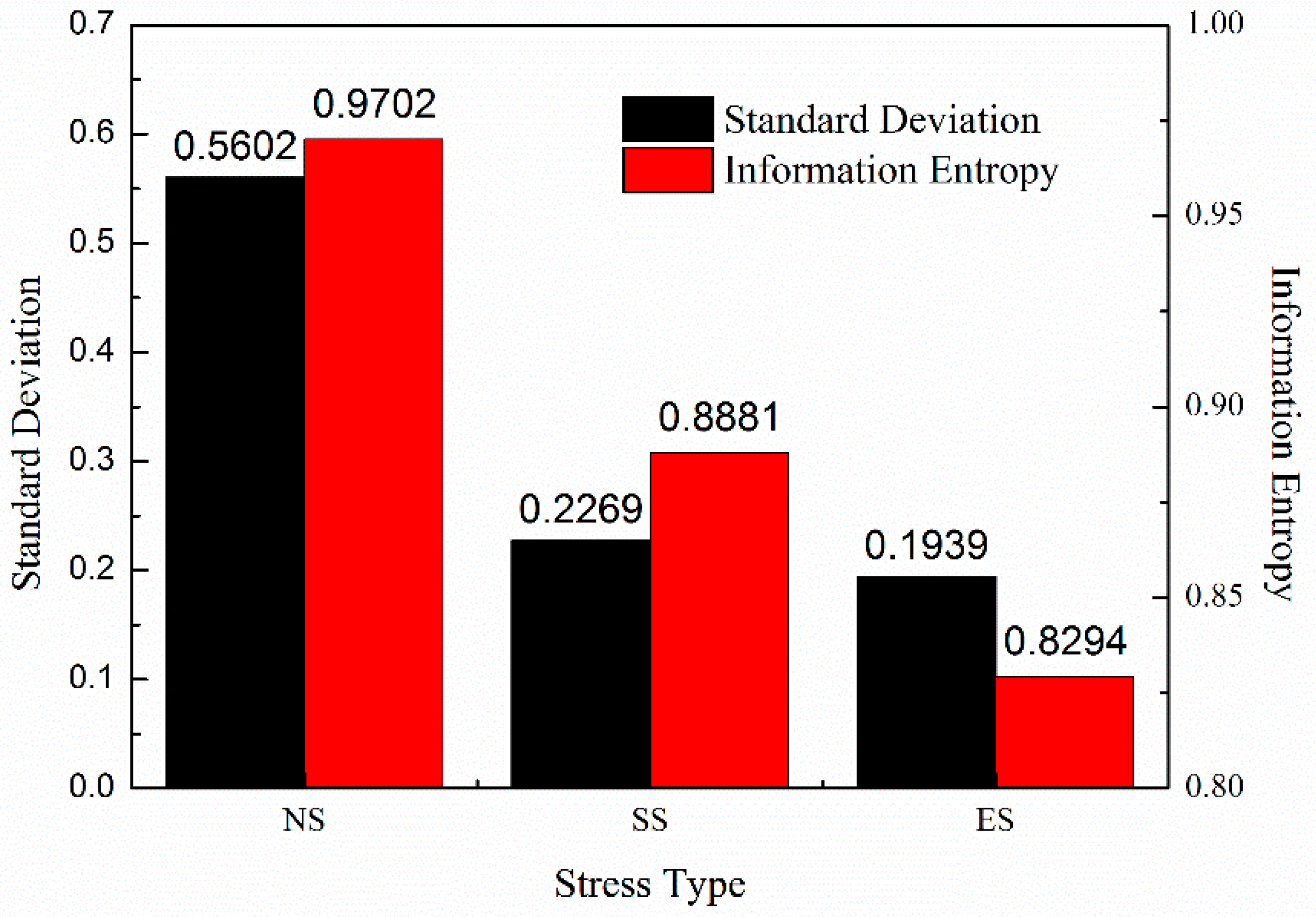
In order to analyze the distribution and dispersion of the fatigue data contrastively, for all of the S-N curves above, the scale of the horizontal axis is from 103 N to 108 N as well as the scale of the vertical axis is from 100 MPa to 103 MPa. The standard deviation of the three S-N curves is 0.5602, 0.2269, and 0.1939, respectively, and it is obvious that the width between the deviation curves is narrower, which is consistent with the smaller and smaller standard deviation. As illustrated above, the data points of the S-N curve based on the nominal stress scatter between the −3 and +2 magnifications deviation curves. The scale of the deviation curves is broad and the standard deviation is 0.5602, the largest of all. The structural stress rearranges the S-N discretized points, so that they are much more concentrated in the field nearby the mean S-N curve and the standard deviation becomes 0.2269 which is much smaller than the former. The equivalent structural stress translates them more uniform on both sides of the mean S-N curve and the smallest standard deviation 0.1939 is obtained. With the correction step the concentration and uniformity of S-N distribution were enhanced, which creates a Mmaster S-N curve with a single narrow brand curve.
3.2. Fatigue Data Evaluation Model Based on Information Entropy
In terms of decision-making, the concept of information entropy is usually introduced to determine the weight of attributes, according to which the greater the information entropy is, the more effects the attributes have on the dispersion degree. In addition, according to Dong [
8], all kinds of attributes have different level of effects on the concentration degree of the S-N distribution. Thus, from the weight point of view, the total information entropy of the attributes governing the welding fatigue was calculated and analyzed. Eventually, a brand-new evaluation procedure of welding fatigue was obtained.
In order to take advantage of information entropy to ascertain the weight of the attributes and then establish fatigue data evaluation model, information entropy calculation procedure of equivalent structural stress, for instance, is addressed according to the well-documented data [
16,
17,
18,
19], which is shown in
Table 2.
According to Equation (8), the value of ES is determined by the following four parameters and the effects of stress concentration factor (SCF) has been taken into account in the SS method. Thus, on the basis of Equations (9)–(12), information entropy of the four attributes structural stress (SS), stress ratio (R), plate thickness (t), and load ratio (r) is 0.9735, 0.7790, 0.9667, and 0.9819, respectively.
Next the distinction degree
Fj of
Xj is defined as:
Hence, distinction degree of the four attributes SS, R, t and r is 0.0265, 0.2210, 0.0333, and 0.0181 respectively.
Then weight calculation formula of the event is obtained:
According to Equation (16), weight based on the information entropy of the four attributes SS, R, t and r is 0.0887, 0.7393, 0.1113, and 0.0607.
Finally, the total information entropy
E that is an aggregative indicator to estimate the randomness and dispersion of an event is obtained:
Therefore, total information entropy
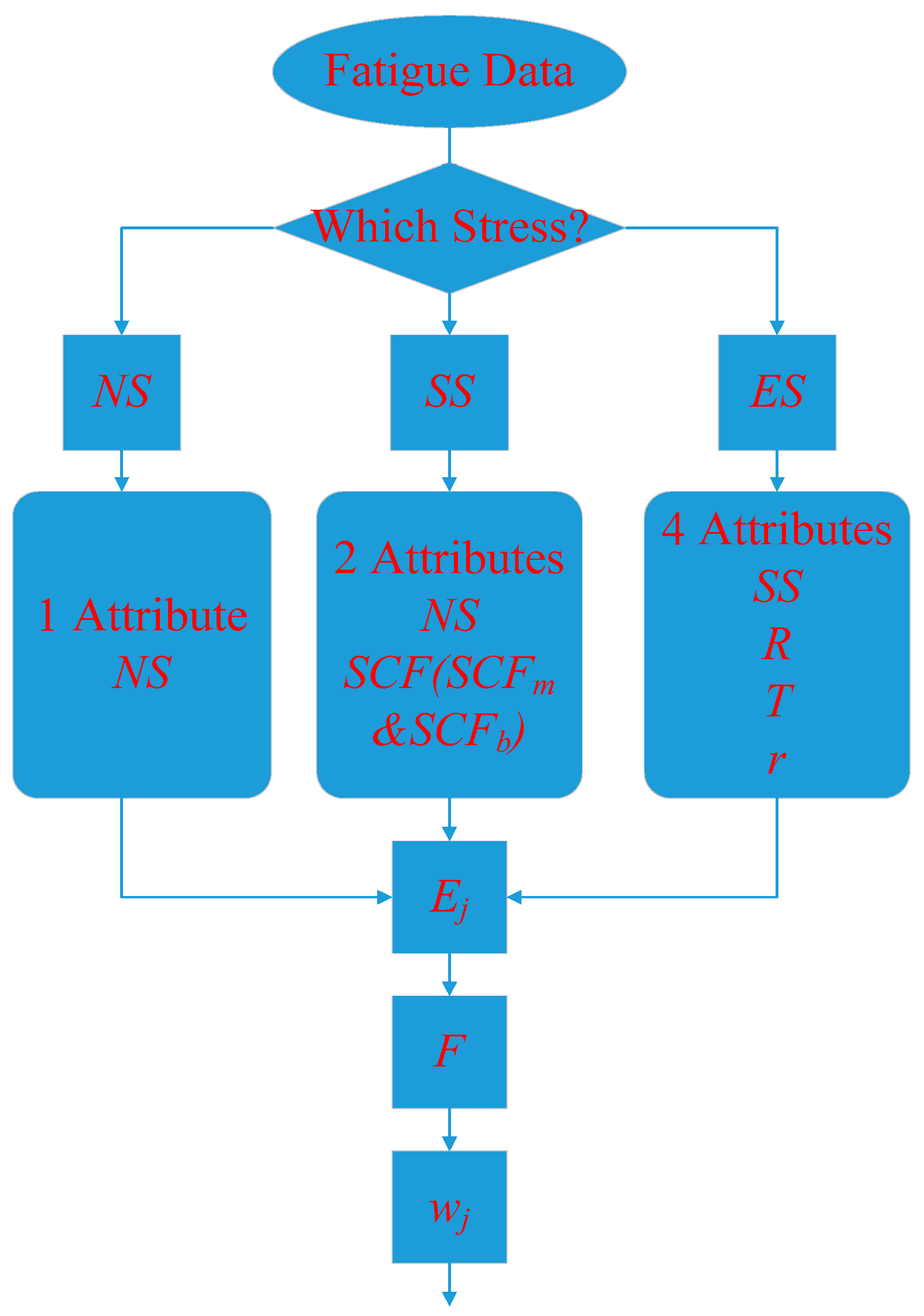
E of the equivalent structural stress is 0.8294. Up to this point, fatigue data analysis model based on the information entropy is set up. Fatigue data with all three types of stress based on this evaluation model will be analyzed in the following section. In order to show each step of the evaluation model clearly a flowchart, as shown in
Figure 5, is helpful to the following process.
4. Results and Discussion
On the basis of the evaluation model set up above, a comparison discussion between the standard deviation and total information entropy is carried out. In addition, quantitative contribution of various attributes on the distribution of the S-N curves will be analyzed and discussed in the following content from NS, SS, to ES, respectively. Then the key attribute which affects the S-N curves most can be explored, which is ought to be improved to optimize the master S-N method based on the equivalent structural stress. The results and discussion reveal that the fatigue life evaluation method based on the information entropy can be a credible and effective method of the weld fatigue prediction.
With respect to nominal stress (
NS), the property value of itself is the sole attribute to influence the S-N curve distribution of
Figure 2 without taking stress concentration, loading mode, and joint type, etc., into account. Therefore, the information entropy weight value of the nominal stress is 1 on the basis of Equation (16). Next, the total information entropy of nominal stress was calculated as 0.9702 that approaches 1, extremely, which indicates that the dispersion degree of the welding fatigue data is great, thus leading to the disorder and non-systematic points of the corresponding S-N curve to some extent. In
Figure 2, the total of 48 sets of welding fatigue data scatter out of order and locate mainly from −2 to +2 deviation curve magnifications, which is consistent with the large information entropy value of 0.9702.
With regard to structural stress (
SS), membrane and bending stress concentration factors are taken into consideration, defined as
SCFm and
SCFb. Firstly, the total stress concentration factor (
SCF) was obtained by the operation of
SCFm plus
SCFb so that structural stress can be calculated through multiplying nominal stress by the total stress concentration factor (
SCF). As a result, there are three attributes nominal stress,
SCFm and
SCFb corporately having effects on the distribution of S-N curve in
Figure 3. According to the equations from Equations (9)–(17), the information entropy of the
SCF were calculated as shown in
Table 3 as well as the information entropy of structural stress is shown in
Table 4. The total information entropy of structural stress was 0.8881, which is 8.46% smaller than that of nominal stress, resulting in that the distribution areas of the welding fatigue data are much narrower. By contrasting
Figure 2 and
Figure 3, much more of the welding fatigue data located between −1 and +1 deviation curve magnifications, which is in agreement with the 8.46% decrease of the information entropy.
When it comes to equivalent structural stress (
ES), structural stress (
SS), loading ratio (
R), plate thickness (
t), and bending ratio (
r) are taken into account and analyzed, respectively labeled as
SS,
R,
t, and
r in the context. As discussed before, there is no doubt that the above four attributes affect the stress calculation accuracy and S-N curve distribution to some degree. According to the equations from Equations (9)–(17), the information entropy appeared in
Table 5 of the equivalent structural stress is 0.8294, which is 6.61% smaller than that of structural stress and 14.51% smaller than that of nominal stress obviously. Subsequently, the equivalent structural stress rearranges the S-N points much more uniformly near the mean S-N curve, which demonstrates that fatigue data classification based S-N curves can be significantly reduced into possibly a single master S-N curve. The single master S-N curve phenomenon attributes to the smallest information entropy of the three types of stresses.
As mentioned in
Section 3.1, the standard deviation of the three S-N curves is 0.5602, 0.2269, and 0.1939, respectively, and it is obvious that the width between the deviation curves is narrower. On the other hand, the total weighted information entropy of fatigue data based on the three types of stress is 0.9702, 0.8881, and 0.8294 according to the Equations (9)–(17). The standard deviation of the nominal stress is 0.5602 and information entropy of the nominal stress is 0.9702, both of which are the largest of the three types of stresses. Meanwhile, the data points of
Figure 2 based on nominal stress are disordered and non-systematic. The standard deviation of the equivalent structural stress is 0.1939 and information entropy of the equivalent structural stress is 0.8294, both of which are the smallest of the three types of stresses. A single master S-N curve is obtained by the amendment of the several attributes. From nominal stress to equivalent structural stress, there is consistency between the reducing trend of the weighted information entropy and the smaller and smaller standard deviation of the S-N curves, which is shown in
Figure 6. Thus, from this perspective, the fatigue life evaluation method based on the information entropy can be a credible and effective method of the weld fatigue prediction.
Next, the attributes that have effects on the distribution of the S-N curves will be analyzed and discussed. There are two main attributes nominal stress and
SCF corporately having effects on the distribution of S-N curve based on structural stress. According to
Table 3 and
Table 4, the information entropy of nominal stress and
SCF is 0.9702 and 0.8694. As known from [
8], the fatigue property of welding structure are influenced by all kinds of attributes to different extent, thus, the attributes are supposed to assign in weight value of different levels. Based on the Equation (16), the attributes of nominal stress and
SCF possessed weight value of 0.1856 and 0.8144, respectively, then weighted information entropy of each attribute was obtained as 0.1801 and 0.7080 via multiplying information entropy by weight value. Similarly, weighted information entropy of
SCFm and
SCFb is 0.7118 and 0.1576. As a result, the three attributes nominal stress,
SCFm and
SCFb possessed 20.28%, 65.27%, and 14.45% of the total information entropy of structural stress as showed in
Figure 7. For the sector diagram depicting the weighted information entropy of nominal stress,
SCFm and
SCFb are carried out in
Figure 6, in which it is not hard to discover that weighted information entropy of nominal stress is about 20% so that nominal stress has a little effect on the distribution of structural stress S-N curve in
Figure 3. While the weighted information entropy of
SCF possesses 79.72% of the pie diagram, which illustrates that
SCF plays a decisive role in forming the S-N curve in
Figure 3, between the
SCFm and
SCFb,
SCFm possesses 81.87% of the
SCF and 65.27% of the total
SCF so that
SCFm plays an indispensable role in calculating structural stress.
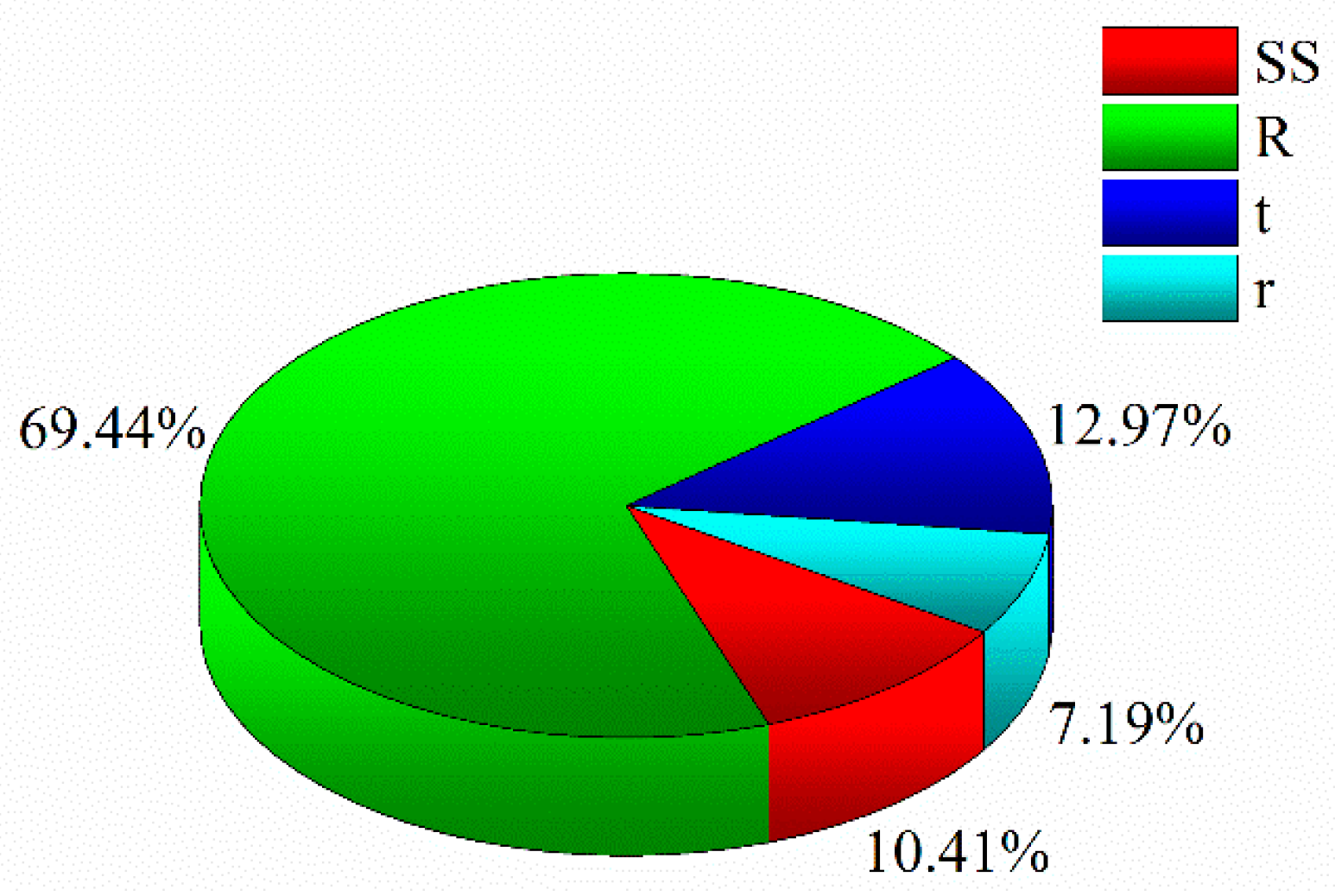
It is obvious that the weight-based information entropy of the four attributes of ES are respectively 0.0863, 0.5759, 0.1076, and 0.0596 via multiplying information entropy by weight value as expressed in Equation (17). The second sector diagram displaying the weight based information entropy of
SS,
R,
t, and
r is drew in
Figure 8, in which the value of
r is drastically small so that the attribute
r has finite effect on the process of establishing the S-N curve. When calculating the
SCF, some effect of
r has been taken into account in the total
SCF to consider the stress concentration, the decision-making degree of
r is weakened and harmonized in the equivalent structural stress. Additionally, another two important factors,
SS and
t, were then studied. Their weighted information entropy is 0.0863 and 0.1076, accounting for 10.41% and 12.97% of the final total entropy of the equivalent structural stress. Through considering the contribution of
SCF and
NS,
SS has been calculated precisely so that
SS just has a little effect on the value of the equivalent structural stress. According to [
1], changing of the plate thickness will lead to the stress distribution rule varying, thus plate thickness will affect the correction of the S-N curve to some degree. Finally, the vital attribute
R occupies 69.44% of the total information entropy due to the high weighted information entropy 0.7393, which proves that stress ratio is a key factor in leading to fatigue destruction.
It is worth noting that all S-N data considered in this paper reflect a broad stress ratio (
R) spectrum from 0 to 0.5. The effects of the
R on the S-N data distribution are seen as significant according to the large weight based information entropy. According to [
23,
24], it is demonstrated that the effects of
R become more pronounced as
R becomes small, particularly near the threshold regime. On the basis of the two stage crack growth mode, the
R effects on the stress intensity factor range can be included either in the first stage of the crack growth or the second stage of the crack growth. Especially, the effects of the stress ratio
R is more dominant when a crack is very small, or dominated by the first stage of the crack growth governed by exponent n in the present two-stage growth mode of Equation (5). It is important to point out that the stress ratio
R effects on crack growth rate are much stronger if
R is negative than the positive
R while there is no negative stress ratio
R in the well-documented data used in this paper, which remains to be investigated hereafter.