Face Detection Based on Skin Color Segmentation Using Fuzzy Entropy
Abstract
:1. Introduction
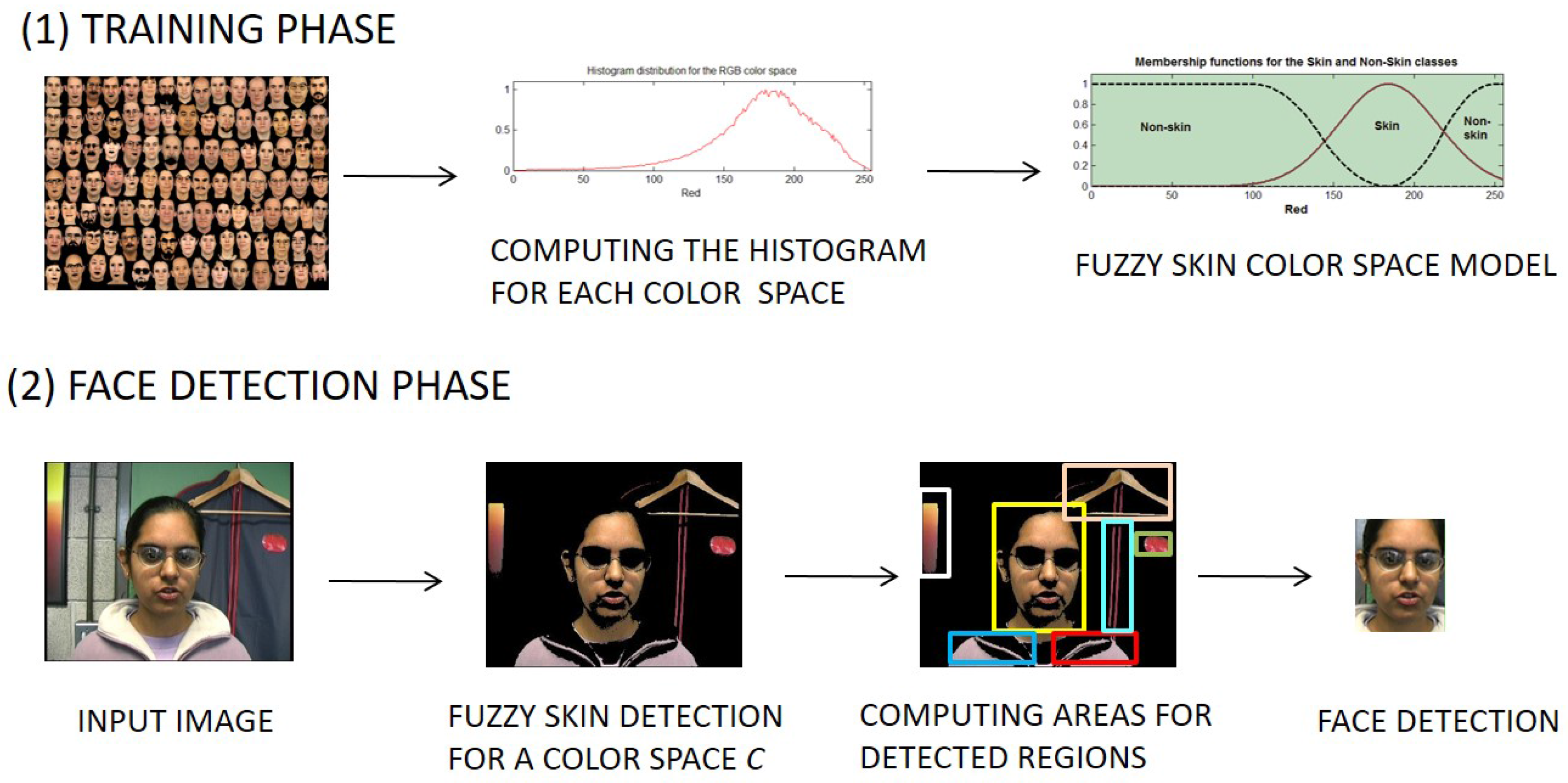
2. Development of a Fuzzy Face Detection System
2.1. Definitions
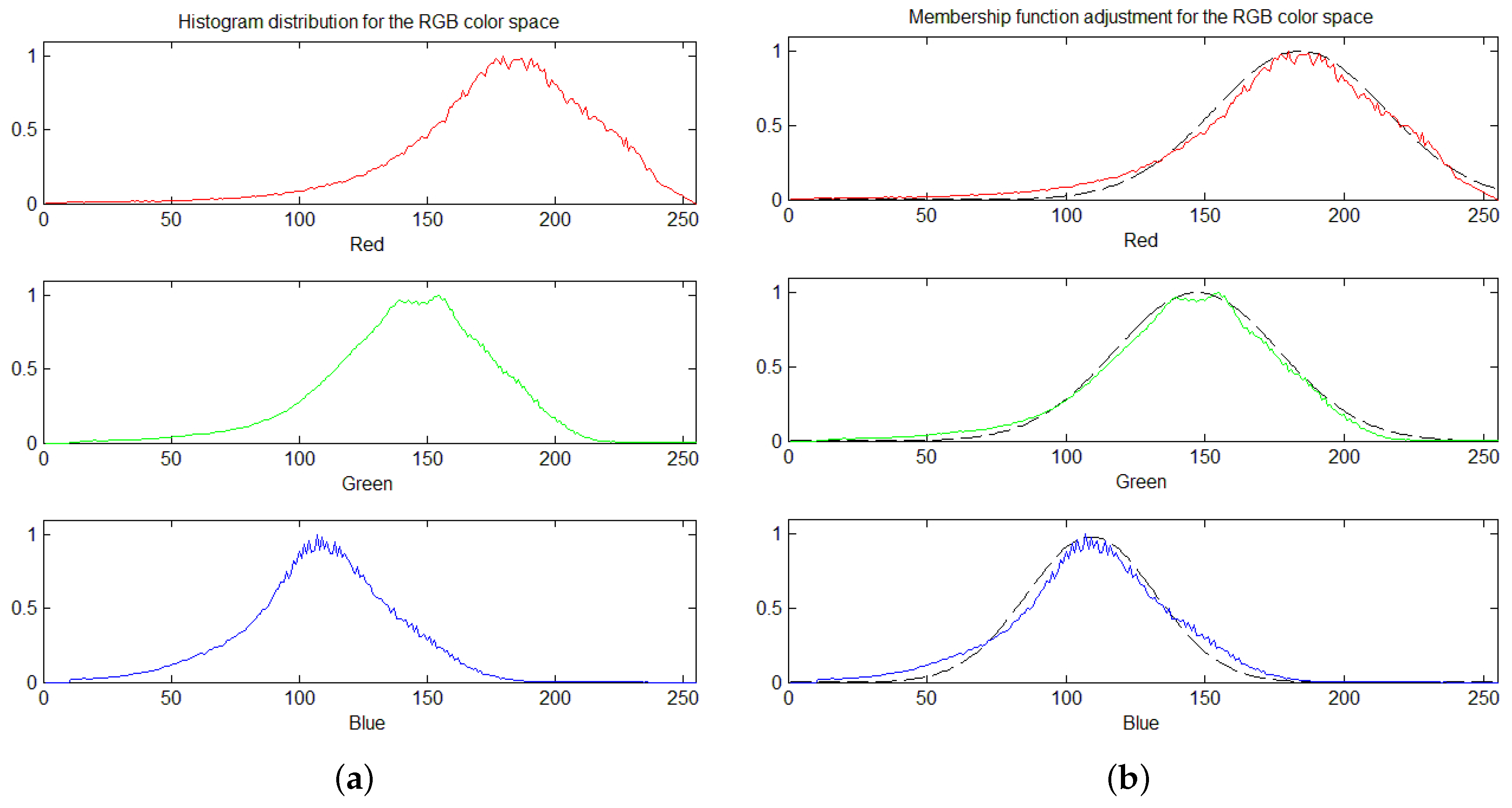
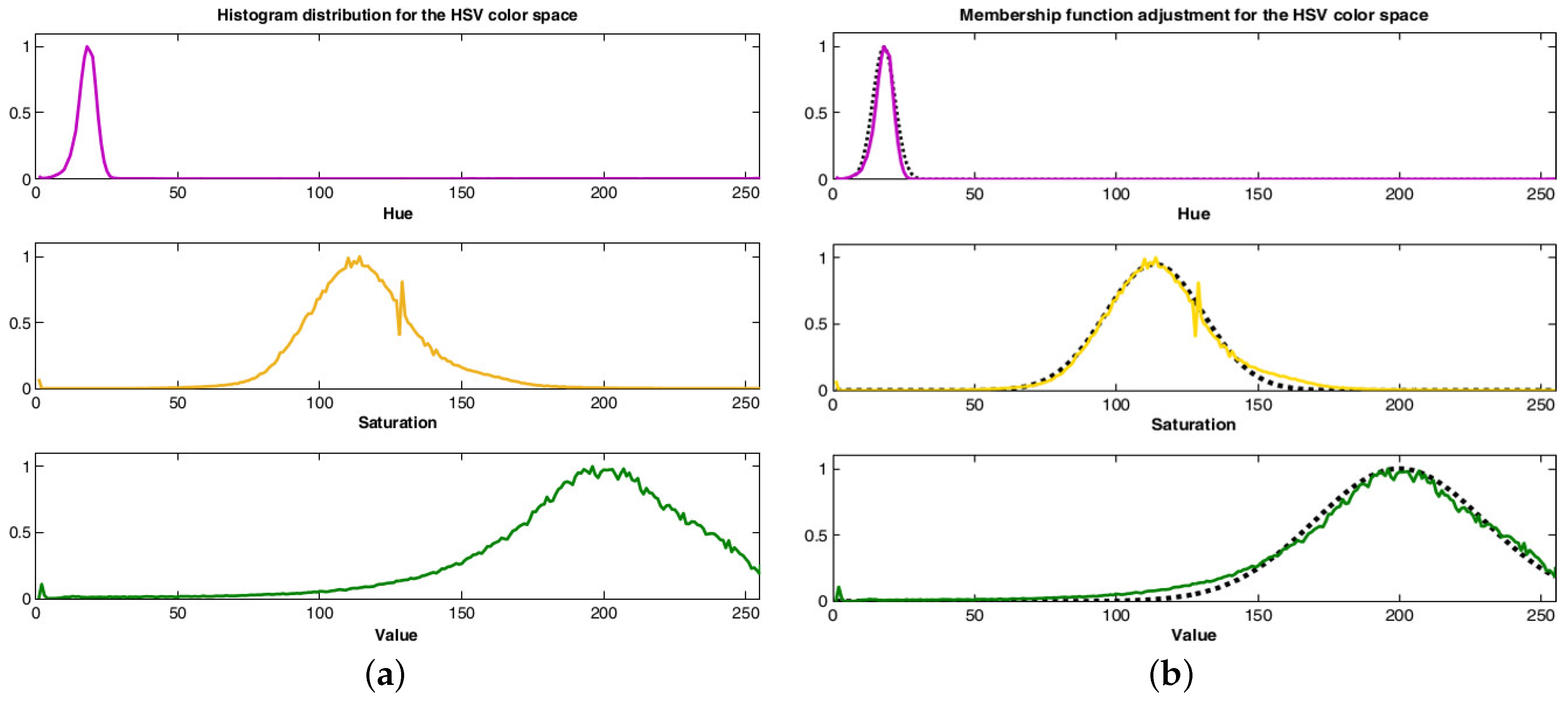
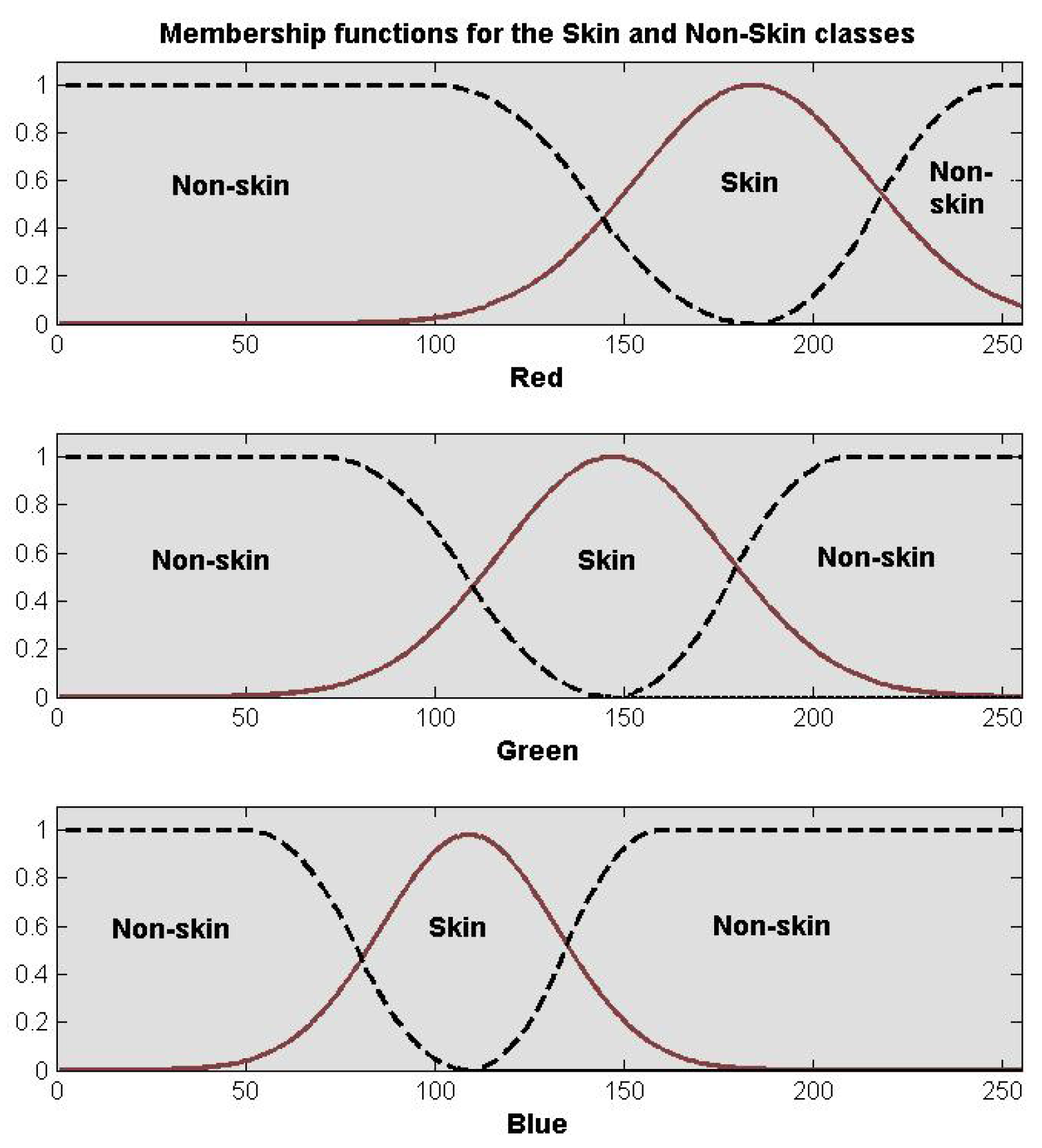
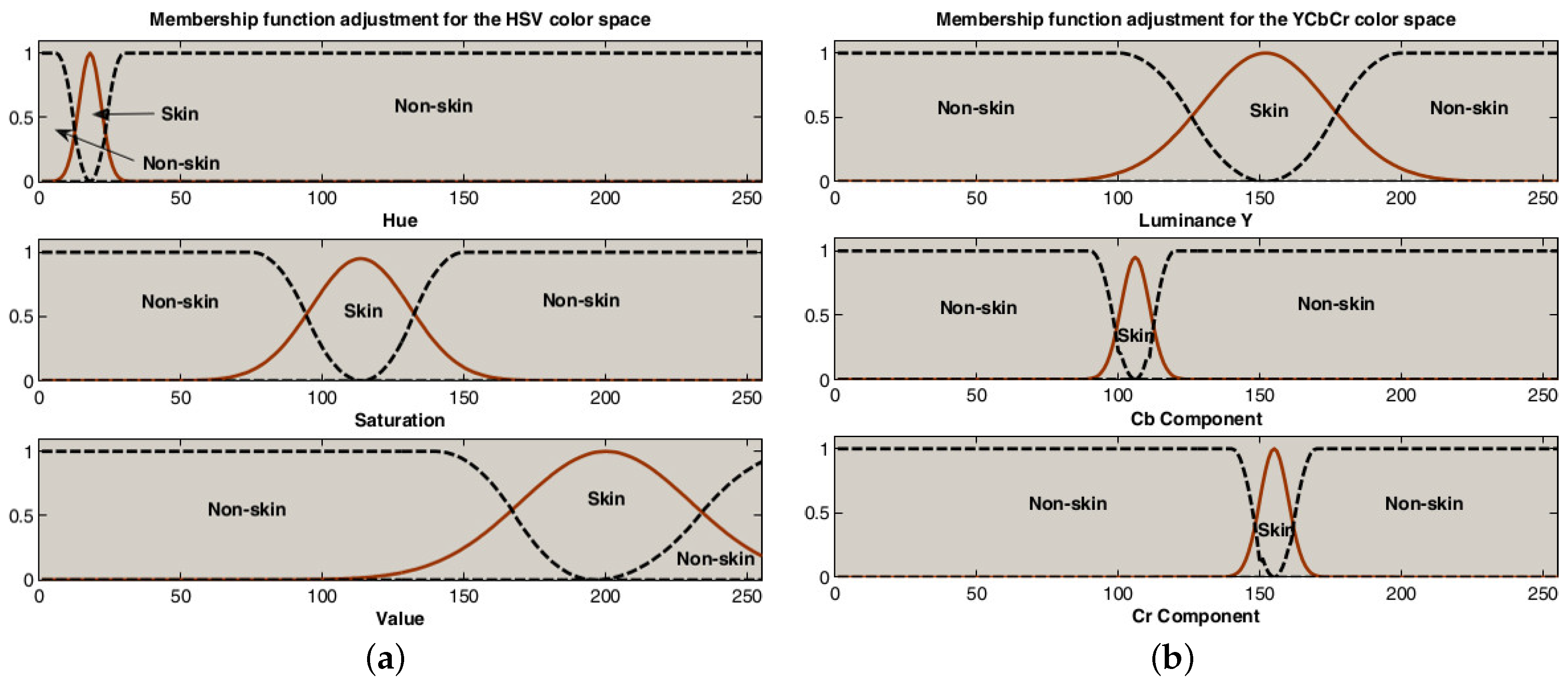
2.2. Fuzzy Sets and Skin Detection
- ;
- ;
- .
2.3. Face Detection
3. Results
3.1. Results for the Proposed Fuzzy Systems
- The XM2VTS face database [36], described before in Section 2.1;
- The VALID database [48], which consists of five recording sessions of 106 subjects over a period of one month. One session is recorded in a studio with controlled lighting and no background noise, and the other four sessions are recorded in office-type scenarios;
- The color FERET database [49], which is composed of 11,338 face images of 994 different persons, taken from different angles of view, over the course of 15 sessions between 1993 and 1996. For our experiments, we used the sets of images fa (images with frontal view) and fb (frontal images from the same individuals but with different facial expression), corresponding to 843 individuals with frontal images only.
3.2. Comparison with Other Methods
3.3. Results on Face Detection
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Hjelmås, E.; Low, B.K. Face Detection: A Survey. Comput. Vis. Image Underst. 2001, 83, 236–274. [Google Scholar] [CrossRef]
- Vezhnevets, V.; Sazonov, V.; Andreeva, A. A Survey on Pixel-Based Skin Color Detection Techniques. Proc. Graphicon 2003, 3, 85–92. [Google Scholar]
- Zhang, C.; Zhang, Z. A Survey of Recent Advances in Face Detection; Technical Report; Microsoft Research: Redmond, WA, USA, 2010. [Google Scholar]
- Albiol, A.; Torres, L.; Delp, E.J. Optimum color spaces for skin detection. ICIP 2001, 1, 122–124. [Google Scholar]
- Yang, M.H.; Kriegman, D.J.; Ahuja, N. Detecting faces in images: A survey. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 34–58. [Google Scholar] [CrossRef]
- Kakumanu, P.; Makrogiannis, S.; Bourbakis, N. A survey of skin-color modeling and detection methods. Pattern Recogn. 2007, 40, 1106–1122. [Google Scholar] [CrossRef]
- Khan, R.; Hanbury, A.; Stöttinger, J.; Bais, A. Color based skin classification. Pattern Recogn. Lett. 2012, 33, 157–163. [Google Scholar] [CrossRef]
- Sun, H.M. Skin detection for single images using dynamic skin color modeling. Pattern Recogn. 2010, 43, 1413–1420. [Google Scholar] [CrossRef]
- Zheng, H.; Daoudi, M.; Jedynak, B. Blocking Adult Images Based on Statistical Skin Detection. Electron. Lett. Comput. Vis. Image Anal. 2004, 4, 1–14. [Google Scholar]
- Kelly, W.; Donnellan, A.; Molloy, D. Screening for Objectionable Images: A Review of Skin Detection Techniques. In Proceedings of the 2008 International Conference Machine Vision and Image Processing, Coleraine, Ireland, 3–5 September 2008; pp. 51–158.
- Chen, H.S.; Wang, T.M.; Chen, S.H.; Liu, J.S. Skin-color correction method based on hue template mapping for wide color gamut liquid crystal display devices. Color Res. Appl. 2011, 36, 335–348. [Google Scholar] [CrossRef]
- Tomaz, F.; Candeias, T.; Shahbazkia, H. Improved Automatic Skin Detection in Color Images. In Proceedings of the VIIth Digital Image Computing: Techniques and Applications, Sydeny, Australia, 10–12 December 2003; pp. 419–428.
- Xiang, F.H.; Suandi, S.A. Fusion of Multi Color Space for Human Skin RegionSegmentation. Int. J. Inf. Electron. Eng. 2013, 3, 172–174. [Google Scholar] [CrossRef]
- Brand, J.; Mason, J.S.; Roach, M.; Pawlewski, M. Enhancing face detection in color images using a skin probability map. In Proceedings of the 2001 International Symposium on Intelligent Multimedia, Video and Speech Processing, Hong Kong, China, 4 May 2001; pp. 344–347.
- Xu, J.; Zhang, X. A Real-Time Hand Detection System during Hand over Face Occlusion. Int. J. Mult. Ubiquitous Eng. 2015, 10, 287–302. [Google Scholar] [CrossRef]
- Liu, Q.; Peng, G.Z. A robust skin color based face detection algorithm. In Proceedings of the 2010 International Asia Conference on Informatics in Control, Automation and Robotics, Wuhan, China, 6–7 March 2010; pp. 525–528.
- Lü, W.; Huang, J. Skin detection method based on cascaded AdaBoost classifier. J. Shanghai Jiaotong Univ. 2012, 17, 197–202. [Google Scholar] [CrossRef]
- Ma, Z.; Leijon, A. Bayesian Estimation of Beta Mixture Models with Variational Inference. IEEE Trans. Pattern Anal. Mach. Intell. 2011, 33, 2160–2173. [Google Scholar] [PubMed]
- Shirali-Shahreza, S.; Mousavi, M.E. A New Bayesian Classifier for Skin Detection. In Proceedings of the 3rd International Conference on Innovative Computing Information and Control, Dalian, China, 18–20 June 2008.
- Hwang, C.L.; Lu, K.D. The Segmentation of Different Skin Colors Using the Combination of Graph Cuts and Probability Neural Network. In Advances in Computational Intelligence; Springer: Berlin/Heidelberg, Germany, 2011; pp. 25–33. [Google Scholar]
- Phung, S.L.; Chai, D.; Bouzerdoum, A. A universal and robust human skin color model using neural networks. In Proceedings of the 2001 International Joint Conference on Neural Networks, Washington, DC, USA, 15–19 July 2001; pp. 2844–2849.
- Wimmer, M.; Radig, B.; Beetz, M. A Person and Context Specific Approach for Skin Color Classification. In Proceedings of the 18th International Conference on Pattern Recognition, Hong Kong, China, 20–24 August 2006; pp. 39–42.
- Yang, M.H.; Ahuja, N. Gaussian mixture model for human skin color and its applications in image and video databases. In Proceedings of the Storage and Retrieval for Image and Video Databases VII, San Jose, CA, USA, 26–29 January 1999; pp. 458–466.
- Yang, J.; Fu, Z.; Tan, T.; Hu, W. Skin color detection using multiple cues. In Proceedings of the 17th International Conference on Pattern Recognition, Cambridge, UK, 23–26 August 2004; pp. 632–635.
- Zhang, L.; Ji, Q. A Bayesian Network Model for Automatic and Interactive Image Segmentation. IEEE Trans. Image Process. 2011, 20, 2582–2593. [Google Scholar] [CrossRef] [PubMed]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Kale, S.; Saradadevi, M. Active Facial Tracking. Asian J. Comput. Sci. Inf. Technol. 2013, 1, 60–63. [Google Scholar]
- Boaventura, I.A.G.; Volpe, V.M.; Silva, I.N.D.; Gonzaga, A. Fuzzy Classification of Human Skin Color in Color Images. In Proceedings of the 2006 IEEE International Conference on Systems, Man and Cybernetics, Taipei, Taiwan, 8–11 October 2006; pp. 5071–5075.
- Selamat, A.; Maarof, M.A.; Chin, T.Y. Fuzzy Mamdani Inference System Skin Detection. In Proceedings of the Ninth International Conference on Hybrid Intelligent Systems, Shenyang, China, 12–14 August 2009; pp. 57–62.
- Kovac, J.; Peer, P.; Solina, F. Human skin color clustering for face detection. In Proceddings of the IEEE Region 8, Eurocon 2003. Computer as a Tool, Ljubljana, Slovenia, 22–24 September 2003; pp. 144–148.
- Truck, I.; Akdag, H.; Borgi, A. A symbolic approach for colorimetric alterations. In Proceedings of the 2nd International Conference in Fuzzy Logic and Technology, Leicester, UK, 5–7 September 2001; pp. 105–108.
- Herrera, F.; Martinez, L. A model based on linguistic 2-tuples for dealing with multigranular hierarchical linguistic contexts in multi-expert decision-making. IEEE Trans. Syst. Man Cybern. 2001, 31, 227–234. [Google Scholar] [CrossRef] [PubMed]
- Bhatia, A.; Srivastava, S.; Agarwal, A. Face Detection Using Fuzzy Logic and Skin Color Segmentation in Images. In Proceedings of the 3rd International Conference on Emerging Trends in Engineering and Technology, Goa, India, 19–21 November 2010; pp. 225–228.
- Hmid, M.B.; Jemaa, Y.B. Fuzzy classification, image segmentation and shape analysis for Human face detection. In Proceedings of the 8th international Conference on Signal Processing, Nice, France, 10–13 December 2006.
- Iraji, M.S.; Tosinia, A. Skin color segmentation in YCBCR color space with adaptive fuzzy neural network (Anfis). Int. J. Image Graph. Signal Process. 2012, 4, 35–41. [Google Scholar] [CrossRef]
- Messer, K.; Matas, J.; Kittler, J.; Luettin, J.; Maitre, G. XM2VTSDB: The extended M2VTS database. In Proceedings of the Second International Conference on Audio and Video-Based Biometric Person Authentication, Washington, DC, USA, 22–24 March 1999; pp. 965–966.
- Murthy, C.A.; Pal, S.K. Fuzzy thresholding: Mathematical framework, bound functions and weighted moving average technique. Pattern Recogn. Lett. 1990, 11, 197–206. [Google Scholar] [CrossRef]
- Nusirwan, A.; Kit, C.W.; John, S. RGB-H-CbCr Skin Colour Model for Human Face Detection. In Proceedings of the MMU International Symposium on Information&Communications Technologies, Petaling Jaya, Malaysia, 16–17 November 2006; pp. 579–584.
- Chitra, S.; Balakrishnan, G. Comparative study for two color spaces HSCbCr and YCbCr in skin color detection. Appl. Math. Sci. 2012, 6, 4229–4238. [Google Scholar]
- Shannon, C.E. A Mathematical Theory of Communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Wu, Y.; Zhou, Y.; Saveriades, G.; Agaian, S.; Noonan, J.P.; Natarajan, P. Local Shannon entropy measure with statistical tests for image randomness. Inf. Sci. 2013, 222, 323–342. [Google Scholar] [CrossRef]
- Abdel-Khalek, S.; Ben Ishak, A.; Omer, O.A.; Obada, A.S. A two-dimensional image segmentation method based on genetic algorithm and entropy. Optik 2017, 131, 414–422. [Google Scholar] [CrossRef]
- Susan, S.; Kumar, A. Auto-segmentation using mean-shift and entropy analysis. In Proceedings of the 3rd International Conference on Computing for Sustainable Global Development, New Delhi, India, 16–18 March 2016; pp. 292–296.
- Bhowmik, M.; Sarkar, A.; Das, R. Shannon entropy based fuzzy distance norm for pixel classification in remote sensing imagery. In Proceedins of the Third International Conference on Computer, Communication, Control and Information Technology, Hooghly, India, 7–8 Febuary 2015.
- Cheng, H.D.; Chen, J.R.; Li, J. Threshold selection based on fuzzy c-partition entropy approach. Pattern Recogn. 1998, 31, 857–870. [Google Scholar] [CrossRef]
- Yin, S.; Zhao, X.; Wang, W.; Gong, M. Efficient multilevel image segmentation through fuzzy entropy maximization and graph cut optimization. Pattern Recogn. 2014, 47, 2894–2907. [Google Scholar] [CrossRef]
- Di Stefano, L.; Bulgarelli, A. A simple and efficient connected components labeling algorithm. In Proceedings of the 1999 International Conference on Image Analysis and Processing, Venice, Italy, 27–29 September 1999; pp. 322–327.
- Fox, N.A.; O’Mullane, B.A.; Reilly, R.B. VALID: A new practical audio-visual database, and comparative results. In Proceedings of the 2005 International Conference on Audio-and Video-Based Biometric Person Authentication, Hilton Rye Town, NY, USA, 20–22 July 2005; pp. 777–786.
- Phillips, P.J.; Moon, H.; Rizvi, S.A.; Rauss, P.J. The FERET evaluation methodology for face-recognition algorithms. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 1090–1104. [Google Scholar] [CrossRef]
- Zhang, X.N.; Jiang, J.; Liang, Z.H.; Liu, C.L. Skin color enhancement based on favorite skin color in HSV color space. IEEE Trans. Consum. Electr. 2010, 56, 1789–1793. [Google Scholar] [CrossRef]
- Huang, D.Y.; Lin, C.J.; Hu, W.C. Learning-based face detection by adaptive switching of skin color models and AdaBoost under varying illumination. J. Inf. Hiding Multimed. Signal Process. 2011, 2, 204–216. [Google Scholar]
- Viola, P.; Jones, M.J. Robust Real-Time Face Detection. Int. J. Comput. Vis. 2004, 57, 137–154. [Google Scholar] [CrossRef]
- Li, H.; Lin, Z.; Shen, X.; Brandt, J.; Hua, G. A Convolutional Neural Network Cascade for Face Detection. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 8–10 June 2015; pp. 5325–5334.










| Algorithm | Incorrect (%) | Correct (%) |
|---|---|---|
| Explicit RGB rules | 12.03 | 87.97 |
| SPM HSV | 22.29 | 77.71 |
| Our proposal (in the RGB system) | 6.47 | 93.53 |
| Algorithm | XM2VTS | VALID | ||||
| FP (%) | FN (%) | Correct (%) | FP (%) | FN (%) | Correct (%) | |
| Explicit RGB rules | 0.12 | 5.75 | 94.14 | 0.40 | 14.47 | 85.13 |
| Explicit HSV rules | 0.47 | 5.12 | 94.41 | 2.19 | 12.91 | 84.91 |
| Explicit YCbCr rules | 0.55 | 4.12 | 95.33 | 0.80 | 15.14 | 84.06 |
| SPM RGB | 1.65 | 3.43 | 94.92 | 6.40 | 17.53 | 76.06 |
| SPM HSV | 0.81 | 6.39 | 92.80 | 0.98 | 13.97 | 85.04 |
| SPM YCbCr | 0.23 | 6.06 | 93.71 | 0.59 | 9.39 | 90.02 |
| Fuzzy RGB | 0.22 | 1.66 | 98.12 | 0.64 | 5.70 | 93.66 |
| Fuzzy HSV | 0.18 | 2.12 | 97.70 | 0.91 | 5.62 | 93.47 |
| Fuzzy YCbCr | 0.18 | 3.31 | 96.52 | 0.60 | 6.38 | 93.02 |
| Algorithm | FERET | Global | ||||
| FP (%) | FN (%) | Correct (%) | FP (%) | FN (%) | Correct (%) | |
| Explicit RGB rules | 3.14 | 2.45 | 94.41 | 1.22 | 7.56 | 91.22 |
| Explicit HSV rules | 6.38 | 4.82 | 88.80 | 3.01 | 7.61 | 89.38 |
| Explicit YCbCr rules | 1.69 | 7.93 | 90.39 | 1.01 | 9.06 | 89.93 |
| SPM RGB | 2.65 | 5.44 | 91.91 | 3.57 | 8.80 | 87.63 |
| SPM HSV | 6.30 | 0.41 | 93.29 | 2.70 | 6.92 | 90.38 |
| SPM YCbCr | 7.10 | 6.16 | 86.74 | 2.64 | 7.20 | 90.16 |
| Fuzzy RGB | 0.75 | 2.56 | 96.69 | 0.54 | 3.31 | 96.16 |
| Fuzzy HSV | 0.60 | 3.13 | 96.27 | 0.56 | 3.62 | 95.82 |
| Fuzzy YCbCr | 0.67 | 4.27 | 95.05 | 0.48 | 4.65 | 94.87 |
| Algorithm | XM2VTS | VALID | ||
| Incorrect (%) | Correct (%) | Incorrect (%) | Correct (%) | |
| Explicit RGB rules | 5.82 | 94.16 | 21.06 | 78.94 |
| SPM HSV | 10.10 | 89.90 | 37.43 | 62.57 |
| Fuzzy RGB | 1.98 | 98.02 | 12.56 | 87.44 |
| Algorithm | FERET | Global | ||
| Incorrect (%) | Correct (%) | Incorrect (%) | Correct (%) | |
| Explicit RGB rules | 9.21 | 90.79 | 12.03 | 87.97 |
| SPM HSV | 19.33 | 80.67 | 22.29 | 77.71 |
| Fuzzy RGB | 4.87 | 95.13 | 6.47 | 93.53 |
© 2017 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pujol, F.A.; Pujol, M.; Jimeno-Morenilla, A.; Pujol, M.J. Face Detection Based on Skin Color Segmentation Using Fuzzy Entropy. Entropy 2017, 19, 26. https://doi.org/10.3390/e19010026
Pujol FA, Pujol M, Jimeno-Morenilla A, Pujol MJ. Face Detection Based on Skin Color Segmentation Using Fuzzy Entropy. Entropy. 2017; 19(1):26. https://doi.org/10.3390/e19010026
Chicago/Turabian StylePujol, Francisco A., Mar Pujol, Antonio Jimeno-Morenilla, and María José Pujol. 2017. "Face Detection Based on Skin Color Segmentation Using Fuzzy Entropy" Entropy 19, no. 1: 26. https://doi.org/10.3390/e19010026
APA StylePujol, F. A., Pujol, M., Jimeno-Morenilla, A., & Pujol, M. J. (2017). Face Detection Based on Skin Color Segmentation Using Fuzzy Entropy. Entropy, 19(1), 26. https://doi.org/10.3390/e19010026







