1. Introduction
It is crucial today to explore technics of energetic and thermal performances enhancement in many fields of science to save on many energy resources. Many simple liquids (water, ethylene glycol, oils) are usually used as heat transfer fluids: in thermal engines (coolants, lubricating oils, etc.), in solar panels of individual water heaters, in the collectors of industrial solar power plants, in power transformers (industry, power distribution network), and in industrial installations (cutting oils, coolants). Unfortunately, these usual liquids all have low thermal conductivities at ambient or industrial temperature. We can find, for example, in [
1], some values of usual thermal conductivity of fluids: water, 0.58 W/(m·K); ethylene glycol, 0.18 W/(m·K), which are very low compared to usual metals such as: iron, 80 W/(m·K); copper, 400 W/(m·K); silver, 430 W/(m·K); graphite, 1000 to 1500 W/(m·K); carbon nanotubes, 2000 to 2500 W/(m·K); suspended graphene, 2500 W/(m·K) and diamond, 2500 W/(m·K). Any increase in the thermal conductivity promotes the exchanges of thermal energy and consequently the extraction ability of the heat from fluids.
The use of fluids containing metallic or semi-conductive particles in homogeneous and stable suspensions is one of the solutions studied for several years for the improvement of thermal transfer. Suspensions of microscopically sized conductive particles are contemplated and used for many years. However, due to the size of the suspended particles, they present problems that limit their industrial applications: abrasion and high risk of sedimentation and clogging. Moreover, the surface-to-volume ratio, which plays a predominant role in all conductive transport phenomena, can be significantly improved with particles of smaller sizes.
With the constant progress of nanotechnologies and the synthesis of specific nanoparticles, the idea of using thermal nanofluids has attracted a lot of interest in the scientific community [
2], but also in industry. The scientific literature on the subject is vast and diverse. It covers both the fundamental (theoretical) aspects of the static thermal modeling, rheological properties of nanofluids and their synthesis, numerical modeling as well as the thermal and rheological characterization of suspensions in the laboratory.
In [
3], a theoretical model is proposed to describe heat transfer performance of the nanofluids. Others works such as [
4] are based on molecular dynamic simulations and aim to explain the differences in thermal conductivity between nanofluids based on metal (Cu) and metal oxide (CuO) nanoparticles. A large part of published works related to the thermal conductivities of nanoparticles suspensions have been based on experimental measurement. In [
5], effective thermal conductivity measurements of alumina/water and copper oxide/water nanofluids are performed and the effects of particle volume fraction, temperature and particle size were investigated. High aspect ratio fillers (carbon nanotubes (CNTs), silver nanowires, copper nanowires) are considered in [
6]. It is found there that silver nanofluid has the highest thermal conductivity compared with copper and CNT nanofluids. In [
7], authors analyze several mechanisms affecting the thermal conductivity of Alumina based nanofluid, such as layering, Brownian motion, clustering, ballistic phonon motion, thermal boundary resistance and mass difference scattering. In [
8], authors look for the specific case when the base fluid is a mixture of ethylene glycol and water. Thermal conductivity has been estimated experimentally at different volume concentrations and temperatures. Other works are related to the coupling with kinematics and rheological response. The effect of viscosity is studied in [
9]. The kinematic effects are also studied in [
10], where an experimental method of studying the heat transfer behavior of buoyancy-driven nanofluids was addressed. These studies open opportunities for many application fields. For example, an interesting applications, related to wind turbines and solar collectors, is found, respectively, in [
11,
12]. The reader can find in [
13] and in the references therein an overview of experimental results about the heat transfer capabilities of nanofluids, which is presented using widely scattered available information from diverse literature sources.
The main aim of the present work is the analysis of thermal properties, in particular the equivalent thermal conductivity, of suspensions involving manometric rods suspended in a Newtonian (purely viscous) fluid. When using particles highly conductive in a poorly conducting matrix, even at very low particle concentration (less than 1 vol.%), it has been observed that the resultant equivalent fluid (suspension) increases (sometimes more than 100%) its apparent thermal conductivity significantly.
In literature, many phenomena are found to be responsible for thermal conductivity enhancement: Brownian motion, ordered liquid layer formation at the nanoparticle surface, interfacial thermal resistance, fractal structuring, cluster formation, thermal conductivity of particles, viscosity of the host fluid, sonication, and surface treatment of the nanoparticles, among many others. In the vast literature about the thermal properties of nanofluids, we can also find a large dispersion of the experimental results. For example, in [
14], it is mentioned, in regard to the effect of the particle volume fraction for example, that enhancements within and beyond the effective medium theory (random dispersion of the nanoparticles through the host fluid) are reported in the literature. The effects of the nanoparticle sizes and nanofluid temperature have also been analyzed in this review; they also show a vast dispersion in the enhancements of the thermal conductivity of nanofluids.
The reasons for these contradictory reports are certainly multiple. We can mention, for example: the choices of the nanoparticle surface chemical treatments; the choice of the host fluid and of the method of the nanoparticle dispersion; and, even sometimes, the choice of the measurement technique.
Taking into account all of these aspects, we have chosen to adopt the following point of view, which consists of analyzing the sole influence of the organization of the nanoparticles within the nanofluid, on its thermal conductivity. The Brownian motion must be viewed in this study as a way to construct two realistic types of structured patterns: fractal skeletons (as observed experimentally and mentioned in [
15]) and micrometric aggregates (as also observed experimentally), and not as a way to promote heat transfer at the microscopic scale.
Thus, we try in this work to answer the following fundamental question: to what extent is the organization of the nanoparticles inside nanofluids essential for improving the thermal conductivity of nanofluids?
This question is fundamental in many aspects. We will prove that the effect of organization is crucial in the enhancement. In addition, the percolation or not of the particles is determinant for final conductivity. This is demonstrated by calculating the heat transfer homogenization based on Fourier’s law without taking into account the Brownian induced conductivity.
In most existing works, the values of the volume fraction considered was much lower than the values used in the present paper. As it has been previously indicated, the present work aims to show the effect of the structure on the thermal conductivity enhancement. In many experiments concerning low viscosity liquids, the Brownian induced conductivity is at the origin of the enhancement of thermal performances at low concentration. In this case, the simulations have to be done with another approach based on the Green–Kubo method, which is used to obtain the thermal conductivity of the nanofluid from the heat autocorrelation function (see for example [
16,
17]). Our strategy in the present work is different. We address heat transfer from the homogenized thermal conductivity related to conduction (Fourier’s law). Such an approach does not take into account Brownian motion for calculating the effective conductivity. Brownian motion has only been used here for developing microstructures (random fractals or clusters) as experimentally observed in many situations where nanoparticles agglomerate inside the host fluid. Moreover, the approach here proposed could be useful to explain thermal conductivity enhancements for some fluids where the viscosity effects are preponderant. In fact, in [
3,
18], we observe almost the same enhancement at a low concentration. Even if it is shown in [
19] that high enhancements of the thermal conductivity can be found for low concentrations, compared to our simulations, it is not in contradiction with our study because we only focused here on structuration effects and not on the other different factors previously mentioned that could promote an extra-thermal conductivity enhancement.
It is well known that particles, suspended into a viscous medium, tend to create aggregates that could reach larger space scales, and, in some cases, they are resolvable at the eyes scale. The modeling of such aggregates requires the consideration of kinetic models at the meso-scale accounting for the flow induced aggregation/disaggregation mechanisms [
20]. As soon as these particles are functionalized in order to avoid aggregation mechanisms, no aggregates are observed at the resolvable scales, and standard models developed for addressing dilute suspensions work well for describing their main rheological features [
21].
In many cases when addressing materials or meta-materials (functionalized materials exhibiting gradients of properties originated by different concentrations and orientations of the dispersed charges) forming processes, after dispersing the particles, a microstructure develops inside and can be frozen by transforming the fluid phase into a solid (e.g., by polymerizing a thermoset resin).
The final properties of the resulting microstructured fluid or solid become radically different from a simple mixing rule as soon as percolation occurs. In these cases, an appropriate homogenization strategy is compulsory for evaluating the final properties. There are numerous works addressing homogenization strategies for systems consisting of perfectly dispersed particles into a matrix (i.e., in the absence of aggregates). In [
22], a reinforced polymer consisting of a population of
nanometric conducting rods immersed into an insulating polymer matrix was assumed. At the microscopic scale, the system can be described from the specification of the position of the centre of gravity
and orientation
of each rod in the population, with
.
The microscopic description, despite the fact of being the finest one, is too heavy from both the computational and the experimental points of view. For this reason, coarser descriptions are preferred. At the mesoscopic scale, the rods’ individuality is substituted with an orientation distribution function
given the fraction of rods that at position
align along direction
. Because this probability distribution function—pdf—is defined in a space of high dimensionality (involving the physical space
and the conformation coordinates
), the solution of its associated balance equation (the so-called Fokker–Planck equation) remains cumbersome, even if advanced numerical discretization techniques have been proposed for alleviating or circumventing the curse of dimensionality that high dimensionality entails [
23,
24].
Finally, macroscopic descriptions constitute the coarsest level of description but the one leading to faster simulations. This description is based on the use of the probability distribution function moments, also known as orientation tensors, being the expression of the second moment given by
In order to quantify the rod network, we introduced in [
22] the density of rod contacts
for a rod with orientation
, depending on the two main microstructure descriptors: (i) the rods concentration
; and (ii) the orientation distribution
. Its evaluation follows the simple geometrical construction depicted in
Figure 1 in which first approximation rods are assumed rigid and straight. Similar descriptors were proposed in [
25,
26,
27,
28].
It can be expected that the conductivity at position along direction scales with the number of contacts . Thus, the conductivity becomes local and directional. One can expect that percolation along direction occurs locally (at position ) when the number of contacts is higher than a threshold value . Lower values imply an infinite local directional resistivity. Thus, percolation could be considered local and directional, allowing us to create a network in which to evaluate the effective conductivity.
When considering electrical properties, the calculation at the network level was carried out by using usual Kirchhoff’s laws [
22]. The question arising immediately concerns the existence of an appropriate fully-macroscopic description modeling thermal conductivity in a perfectly dispersed suspension composed of rods. This modeling framework, with some simplifying assumptions, is described in
Section 2. Then, we will focus on more complex scenarios, the ones involving aggregation mechanics leading to the creation of macroscopic clusters (dispersed into the suspending matrix) and percolated networks, both addressed in
Section 3. The computational thermal homogenization of such complex microstructures is addressed in
Section 4 before then discussing some numerical results in
Section 5.
Different assumptions are considered in the sequel: (i) advective heat fluxes are neglected when the matrix becomes solid in the final part in which the thermal properties are evaluated; (ii) the suspending fluid is assumed viscous and at rest, making possible the particle movement, but remaining insensible to thermal dependencies of its density when addressing thermal homogenization, the viscous forces being preponderant with respect to buoyancy, in all the cases considered here; and (iii) the thermal conductivity contrast between the matrix and the particles is assumed to be large.
4. Calculating the Equivalent Thermal Conductivity
Due to the microscopic heterogeneity (where matrix and particles coexist, the last cluster making part of a single network depending on the microstructure constructor chosen, MDAa or DLAa, respectively, the macroscopic thermal modeling needs a homogenized thermal conductivity that depends on the microscopic details.
We can define the macroscopic temperature gradient
at the RVE level from
where
denotes the microscopic temperature gradient.
We also assume the existence of a localization tensor relating the macroscopic temperature gradient (average of its microscopic counterpart)
with the microscopic local temperature gradient
,
, such that
Now, we consider the microscopic heat flux
at
according to Fourier’s law
and its macroscopic counterpart
that is written
from which the homogenized thermal conductivity can be defined at the RVE level from
As
is perfectly known everywhere in the representative volume element
ω, the definition of the homogenized thermal conductivity tensor only requires the computation of the localization tensor
. Several approaches are proposed in the literature to define this tensor, according to the choice of the boundary conditions. Our objective here is not to discuss such a choice. For the sake of simplicity, we use essential boundary conditions on
corresponding to the assumption of a uniform temperature gradient on the RVE
ω. We consider the general 2D case that involves the solution of the two boundary value problems related to the steady state heat transfer model in the microscopic domain
ω for two different boundary conditions on
:
and
It is easy to prove that both solutions verify
where
denotes the transpose. Thus, the localization tensor finally results as
From a computational point of view, the main difficulty concerns the solution of the two boundary value problems using very fine meshes required to represent accurately all of the microscopic details. In the extreme case of meshes that are too fine, advanced solvers based on the use of separated representations (at the heart of the Proper Generalized Decomposition (PGD)) could be a valuable alternative [
29,
30].
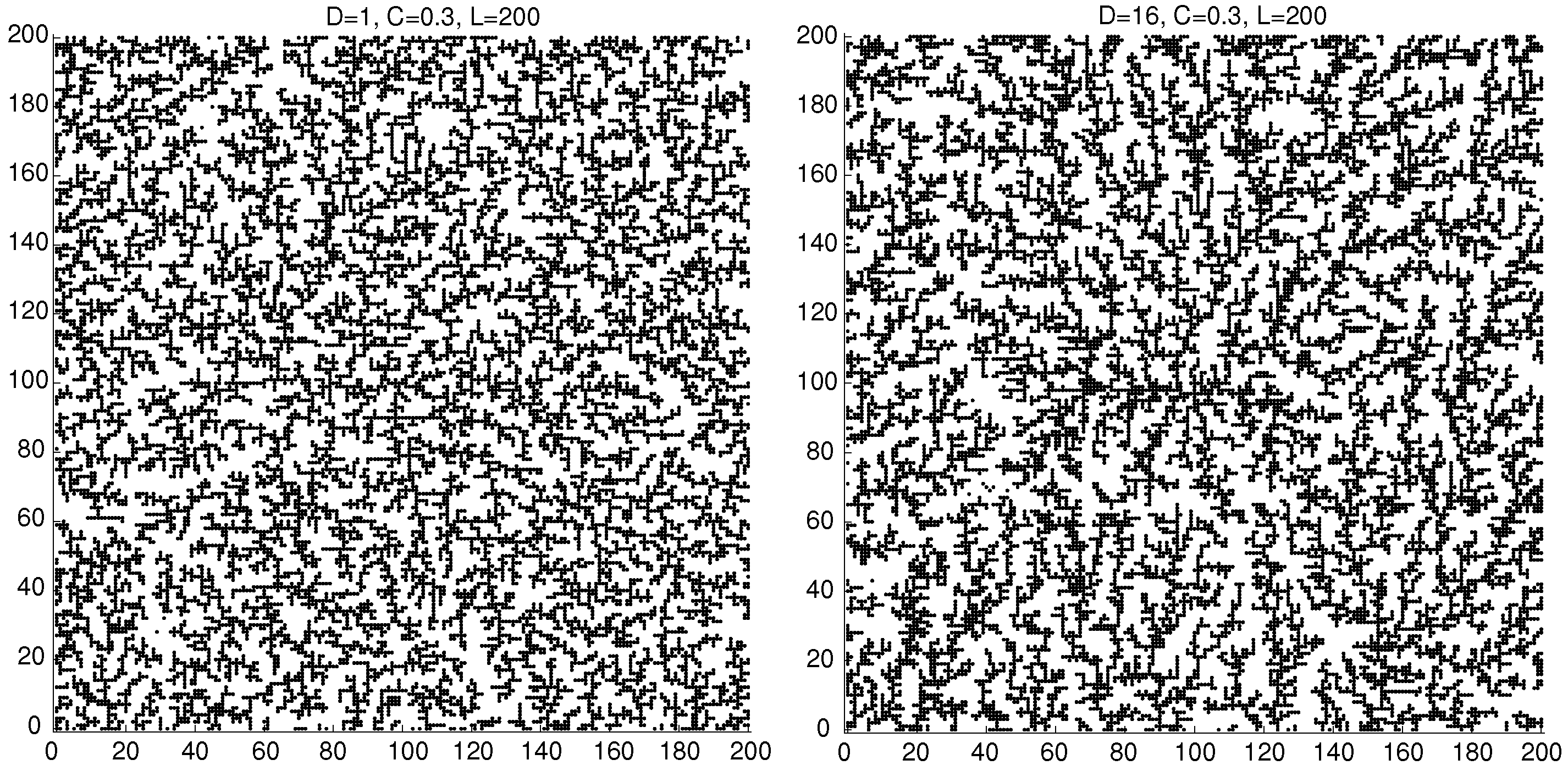
To check the proposed strategy just described, we consider the DLA-based microstructure depicted in
Figure 5.
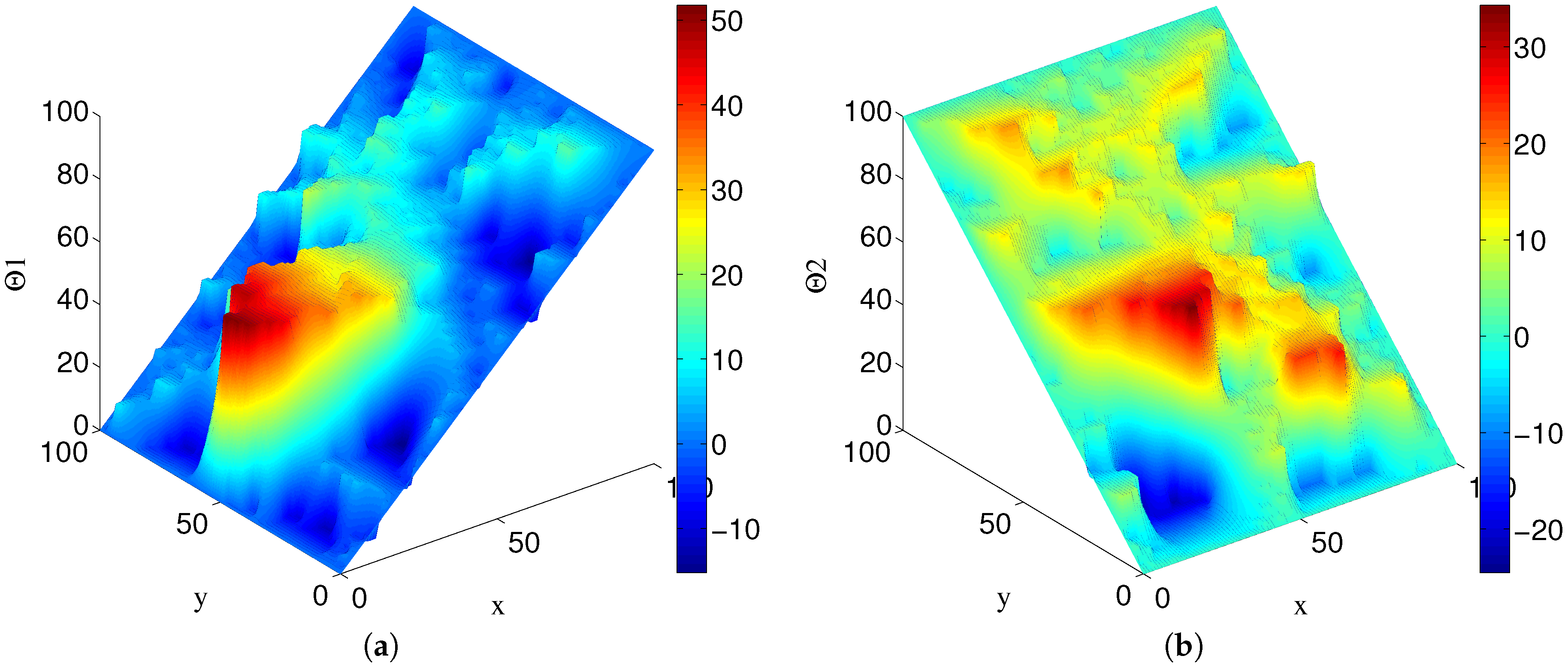
Figure 6 shows both temperature fields
and
.
For the solutions carried out in this study, the mesh size was chosen in order to ensure the numerical convergence, i.e., the mesh-size independence of the computed solutions.
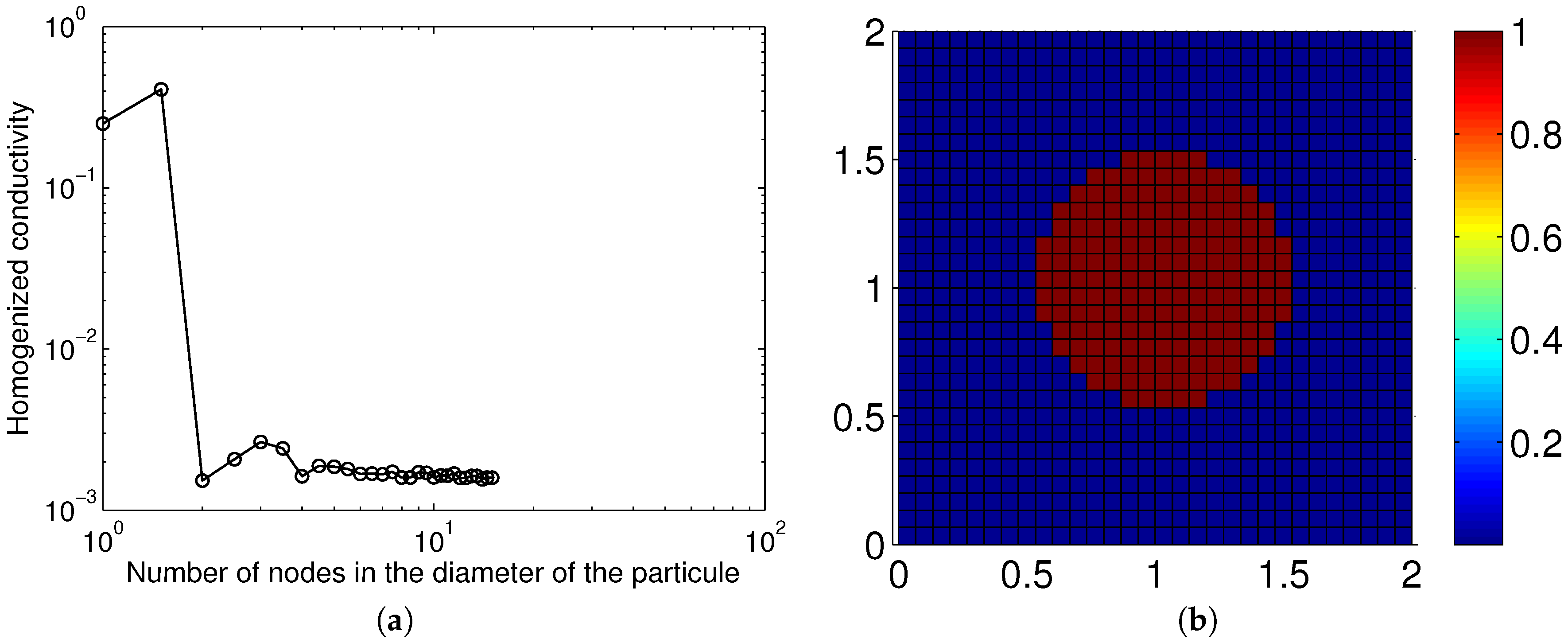
Figure 7 and
Figure 8 analyze the solution dependence as a function of the number of nodes along the particle diameter, for one and many particles, respectively. It can be seen that when considering ten nodes along the particles’ characteristic length, the conductivity becomes almost constant.
5. Numerical Results
In order to compare the homogenized thermal conductivity for different microstructures obtained by using the enhanced DLA and MDA algorithms, we proceed from the same initial particle distribution and different values of the associated concentration. The mesh considered ensured the numerical convergence of all of the thermal analyses carried out in the present study.
The value of concentrations used in the field of nanofluids is usually lower than the maximum range that we have considered in our study. It is generally on the order of 0.1% or to 2%. However, as mentioned previously, the dispersion of the experimental results is such that, in many cases reported in the literature, low volume concentrations of nanoparticles do not always lead to spectacular enhancements of the thermal conductivity. In some specific studies, the volume fraction can reach even values up to 9% [
5,
15]. In the present study, our aim is to focus mainly on the structure-based enhancement effects. For lower concentrations, other numerical strategies are more convenient (the Green–Kubo method and heat autocorrelation function), but, as just indicated, this is not our purpose. In order to compare with some papers in literature,
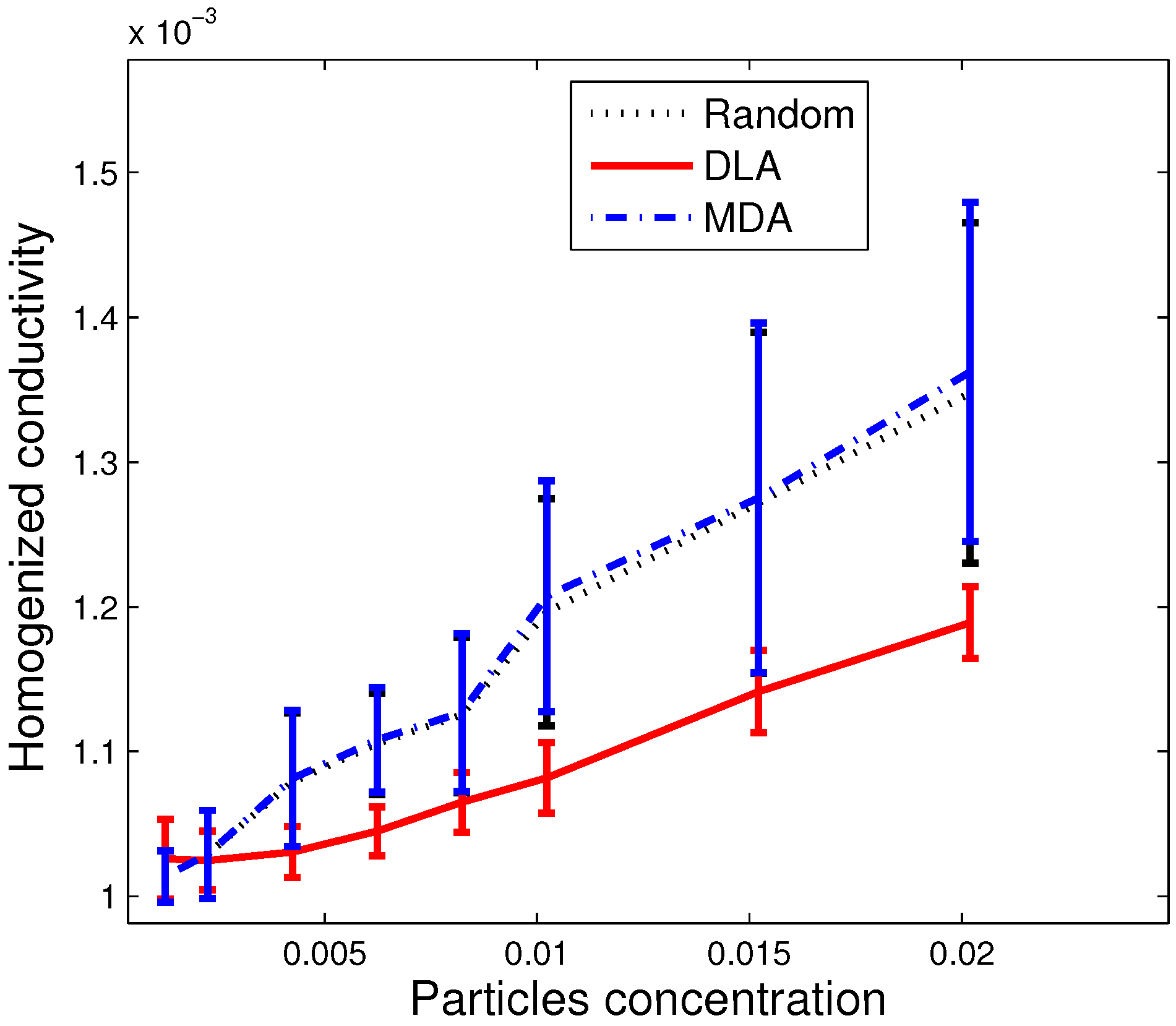
Figure 9 presents an extension of our study results to a volume fraction lower than 2%.
The reported values show the increase of relative conductivity
from 0.001 when there are no particles to 0.014 at 2% of volume fraction. These orders of magnitude are the same that are found in some existing works (e.g., [
3,
18]). Regarding this figure, modification of conductivity is almost the same for random distribution or MD simulation (they almost give the same values of conductivity because low concentration does not promote percolation). However, results of DLA are not significant here as they are related to a small aggregated structure in the middle of the simulation domain.
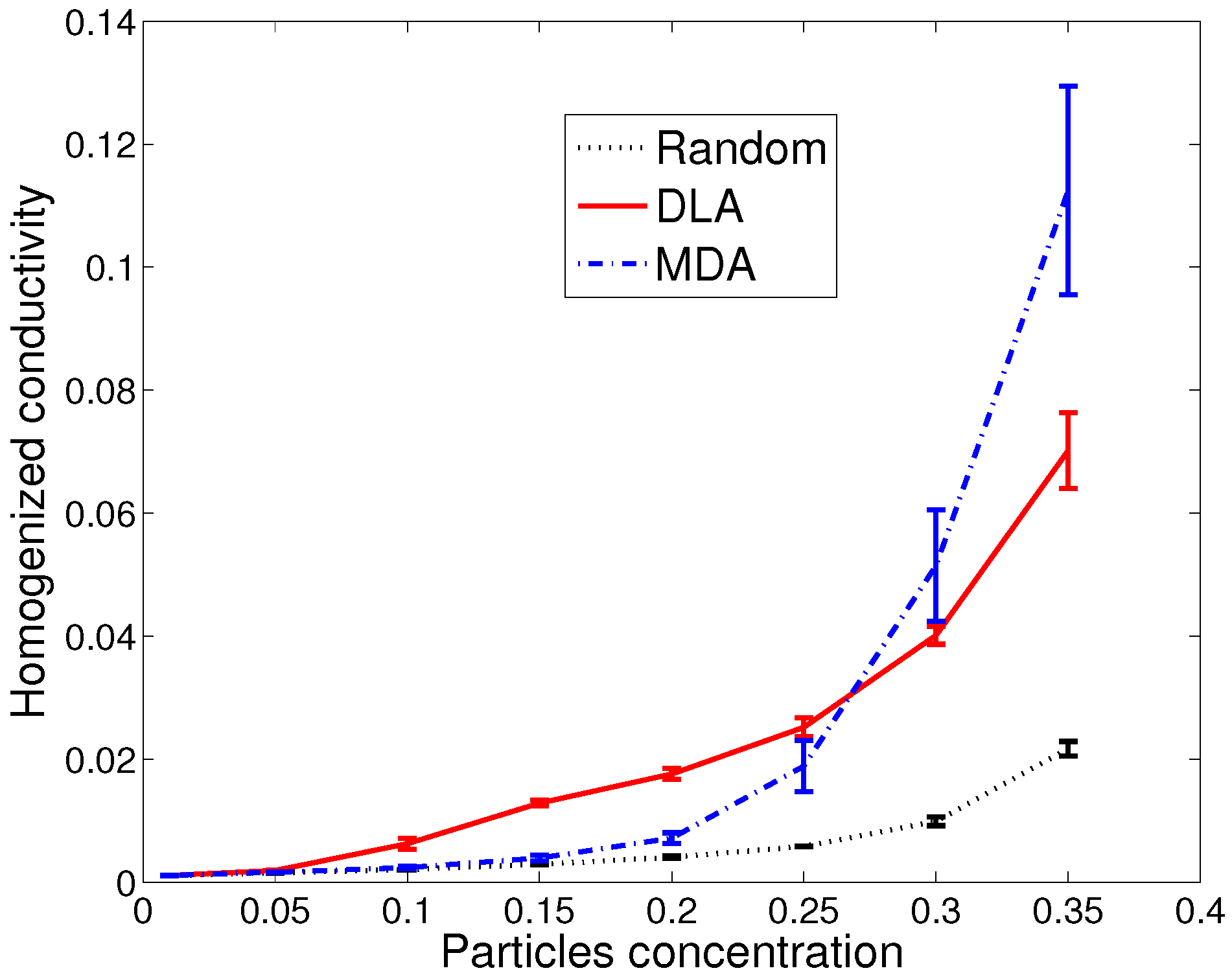
Figure 10 reports the results found for higher concentrations. It can be seen that, as expected for both kinds of microstructures (the one generated by the enhanced-DLAa and the MDAa), the equivalent (homogenized) conductivity increases with the particle concentration. Moreover, the thermal conductivity of the resulting microstructures is larger than the one related to the initial random distribution of particles, all of them being quite similar at very low concentrations. When the concentration increases, the percolated network development seems the most favorable for heat conduction. These numerical results are very similar to the experimental results reported in [
15] on the basis of measurements of the thermal conductivity of magnetically polarizable nanofluids. As can be seen in
Figure 10, at very large concentrations, our computations show that the MD aggregated microstructures are more favorable to heat conduction than the DL ones. This is a quite interesting result, in the sense that the agglomeration of nanoparticles in the form of individual clusters is not an obstacle to the heat conduction through the colloidal suspensions, as long as the sedimentation can be neglected. This facility can be easily understood by comparing the analyzed microstructure morphology depicted in
Figure 11,
Figure 12 and
Figure 13, where the superiority of the percolated MD networks can be easily pointed out.
Figure 11,
Figure 12 and
Figure 13 are generated using three concentrations equal to
,
and
, respectively. For each concentration, we start with a random distribution for the first calculation of homogenized conductivity. Then, we let the random distribution evolve according either to the DLA or the DMA. The DLA tends to build as quickly as possible a network that looks like a fractal. During the simulation, and especially for high concentration, the fractal characterization seems to not be affected by the increase of the network. The topology of the network increases the conductivity by constructing preferential directions for heat conduction. Now, when the structure evolves according to the DMA, the observations are similar to what can be found in [
31]. In fact, a homogeneous nanofluid is described as the dispersion of a discontinuous phase in a continuous one. However, the phase distribution can present three distinct geometric morphologies depending on the volume fraction and shape of the dispersed nanoparticles. These arrangements strongly modify the effective thermo-physical properties at the macro scale. The three geometrical morphologies can be defined as dispersed structure, aggregated structure, and percolated structure. The percolation threshold is defined as the minimum volume fraction that characterizes the formation of a continuous solid path.
At low particle concentrations (less than 1%), it can be seen from our calculations (see
Figure 9) that the organization of particles (in the form of clusters or fractals) has no noticeable effect on the thermal conductivity. The results are even comparable to those obtained with the effective medium theory—EMT—(random distribution of individual nanoparticles). Therefore, any unusual enhancement of the thermal conductivity at a low particle fraction must be explained by other arguments than structuration of the nanoparticles in the form of fractals or clusters. The results are quite different at higher particle fractions. It can be seen from our calculations (see
Figure 10), for concentrations comprised of between 5% and 20%, that the structuration in the form of fractals (DLA) leads to thermal conductivity enhancements well above what is predicted by the EMT. Unfortunately, the formation of a fractal skeleton within the fluid may have a tragic influence on the rheological properties of the nanofluid, which could even make it unusable from a mechanical point of view. On the other hand, what seems very interesting to us is the positive influence of cluster formation on the thermal conductivity enhancement at fractions higher than 25%, well above EMT and even fractal structuration. This is a very promising result in terms of nanofluid industrial applications because, in our opinion, the cluster’s formation has a less damaging influence on the rheological properties of the nanofluid than the fractal skeletons (the validation of this constitutes a work in progress).