The Constant Information Radar
Abstract
:1. Introduction
1.1. Background
1.2. Contributions
- Review the estimation rate for tracking radars
- Examine the traditional target Kalman model
- Augment tracking to include predicted estimation information
- Motivate CIR radar using predicted information
- Demonstrate the results of the CIR in a simulation compared to a traditional radar
2. Radar Tracking and Measurement Model
2.1. Target Motion Model
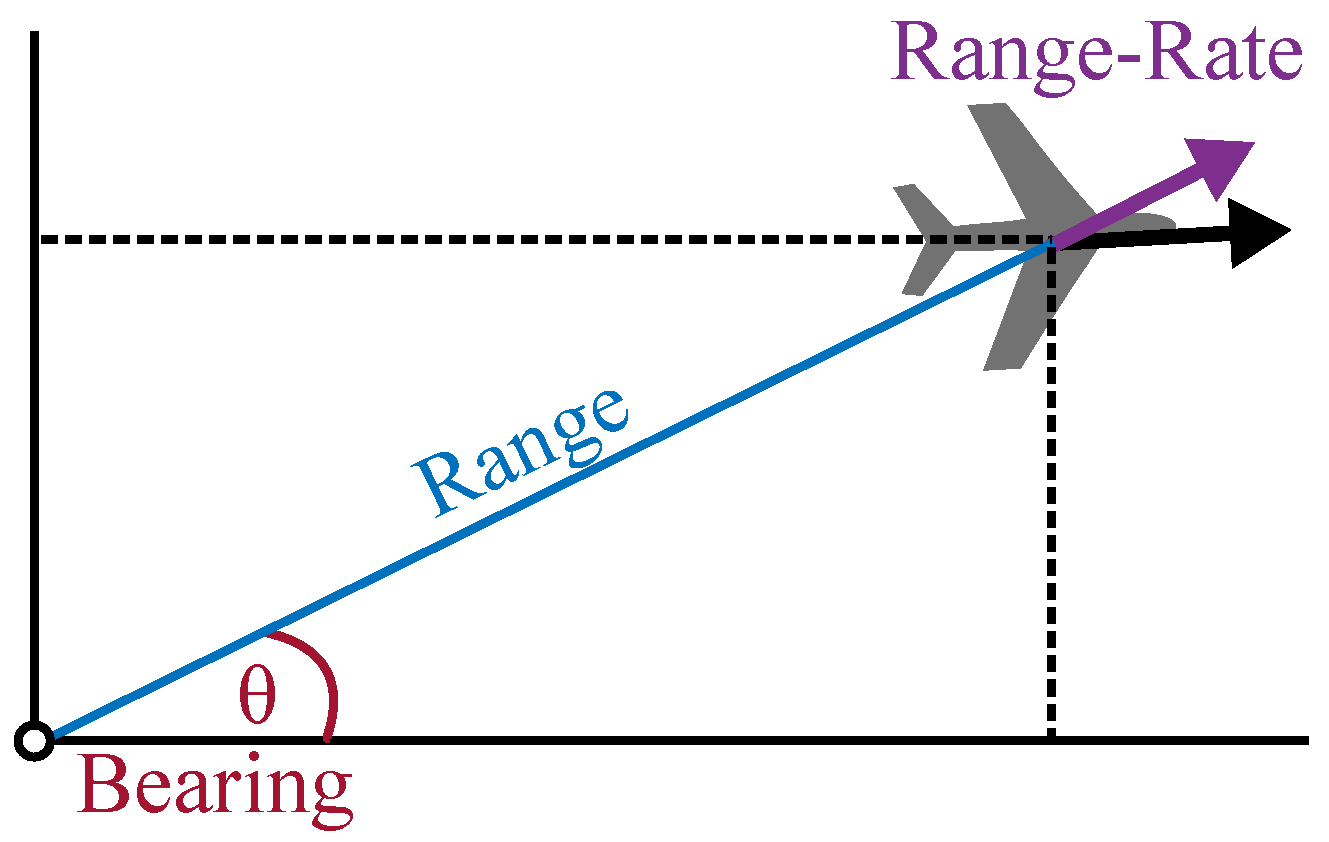
2.2. Target Measurement Model
3. Target Tracking Information
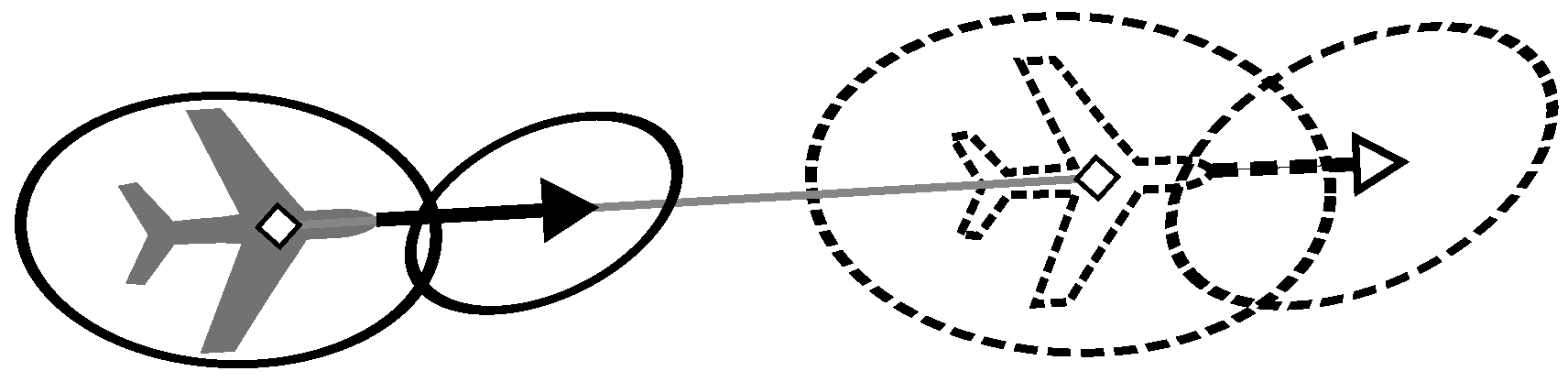
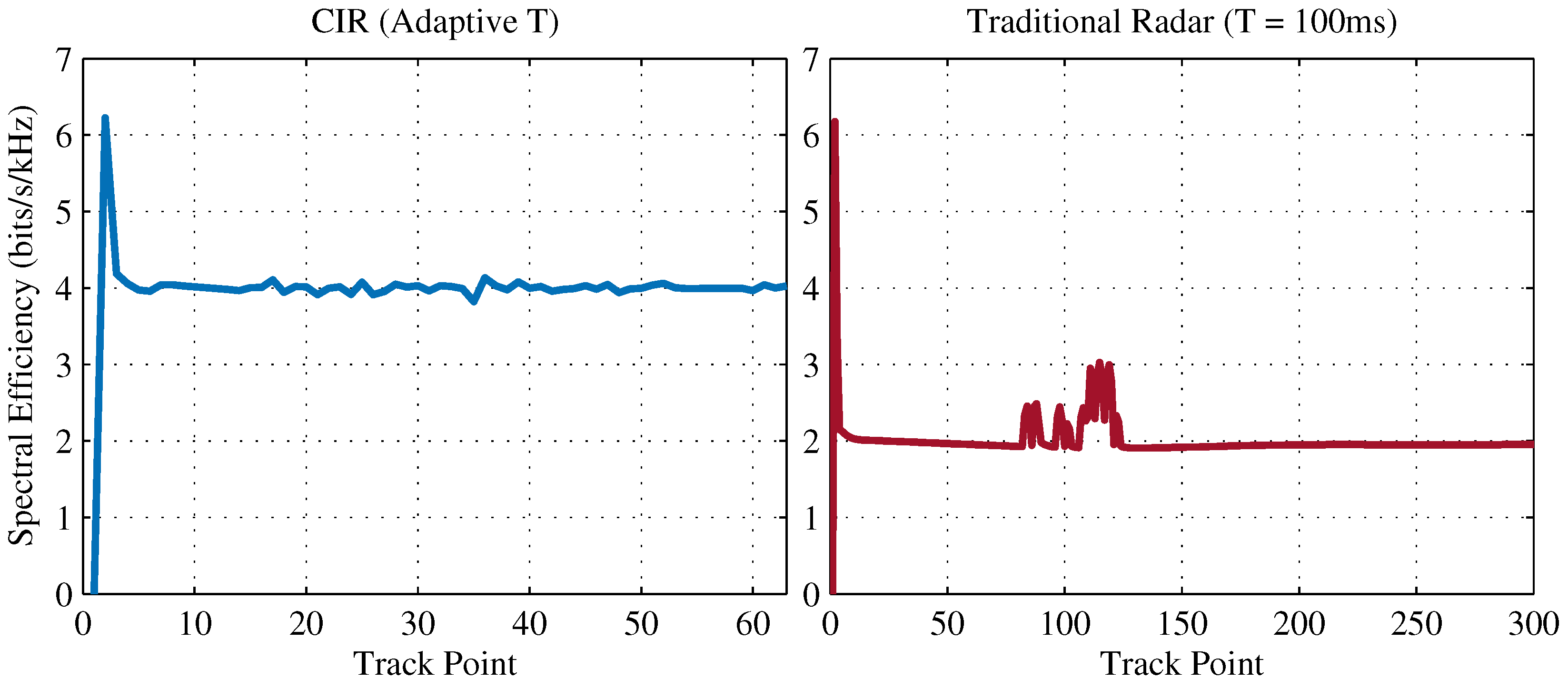
3.1. Radar Estimation Rate
3.2. Target Predicted Information
| Algorithm 1 Revisit Time Modulation (Solving for T) |
|
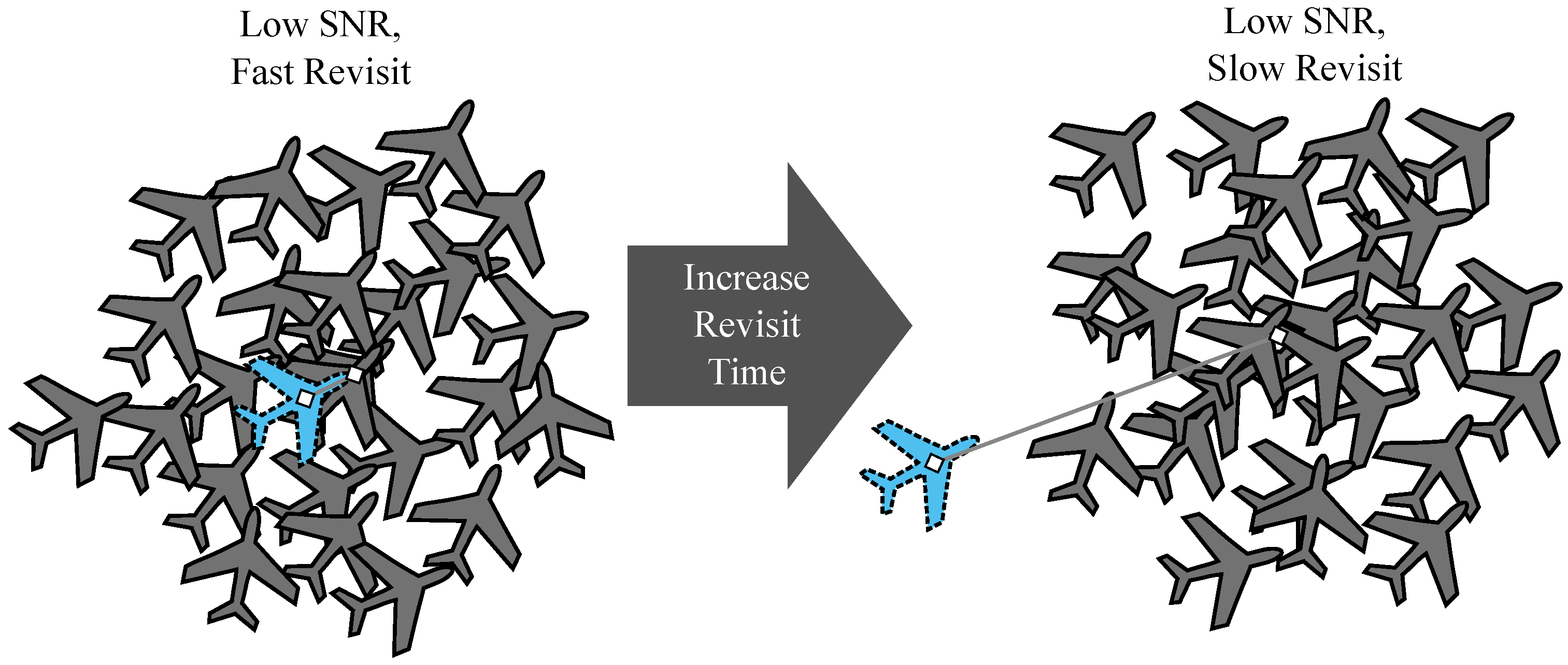
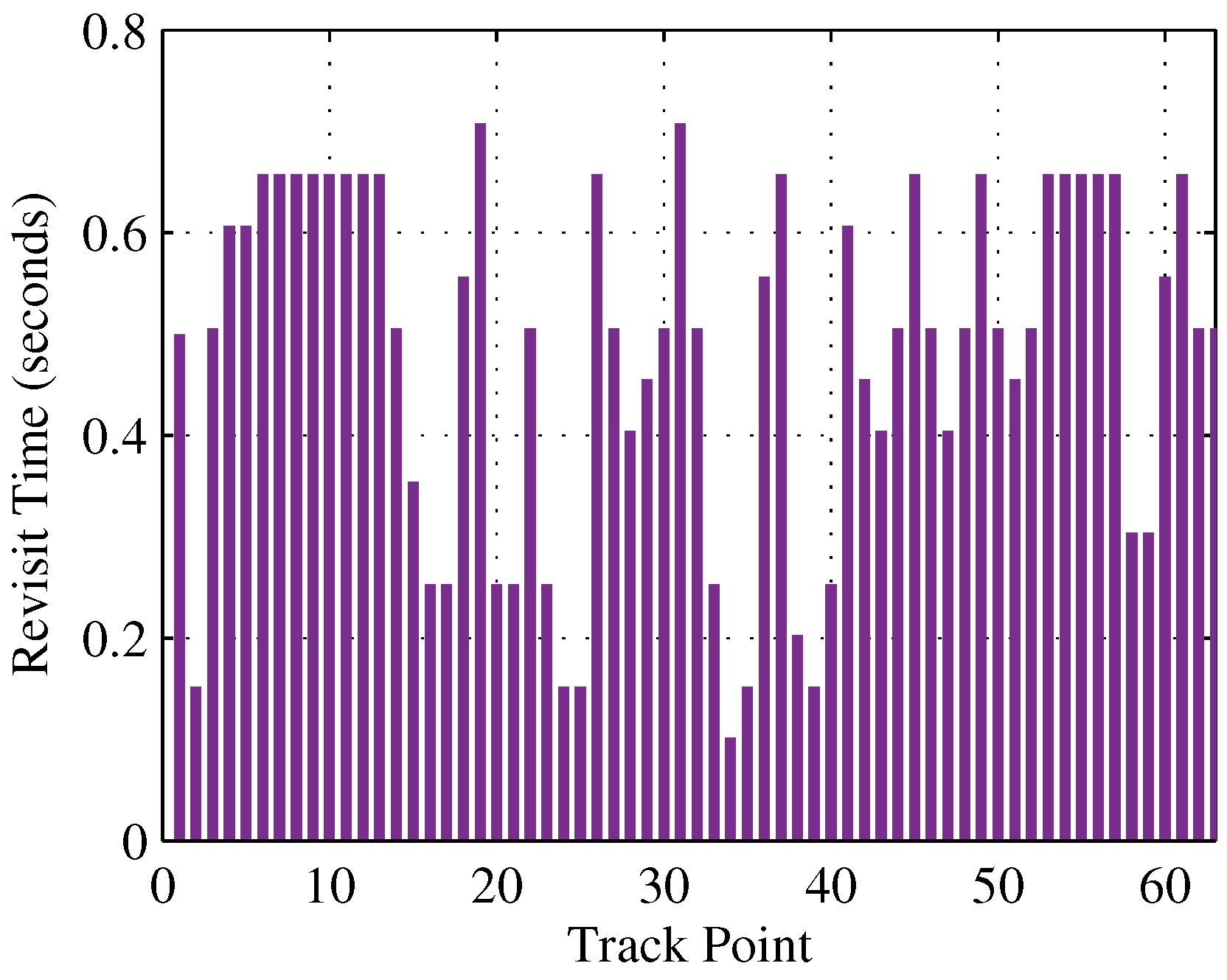
4. Revisit Time Modulation
4.1. Model Mismatch
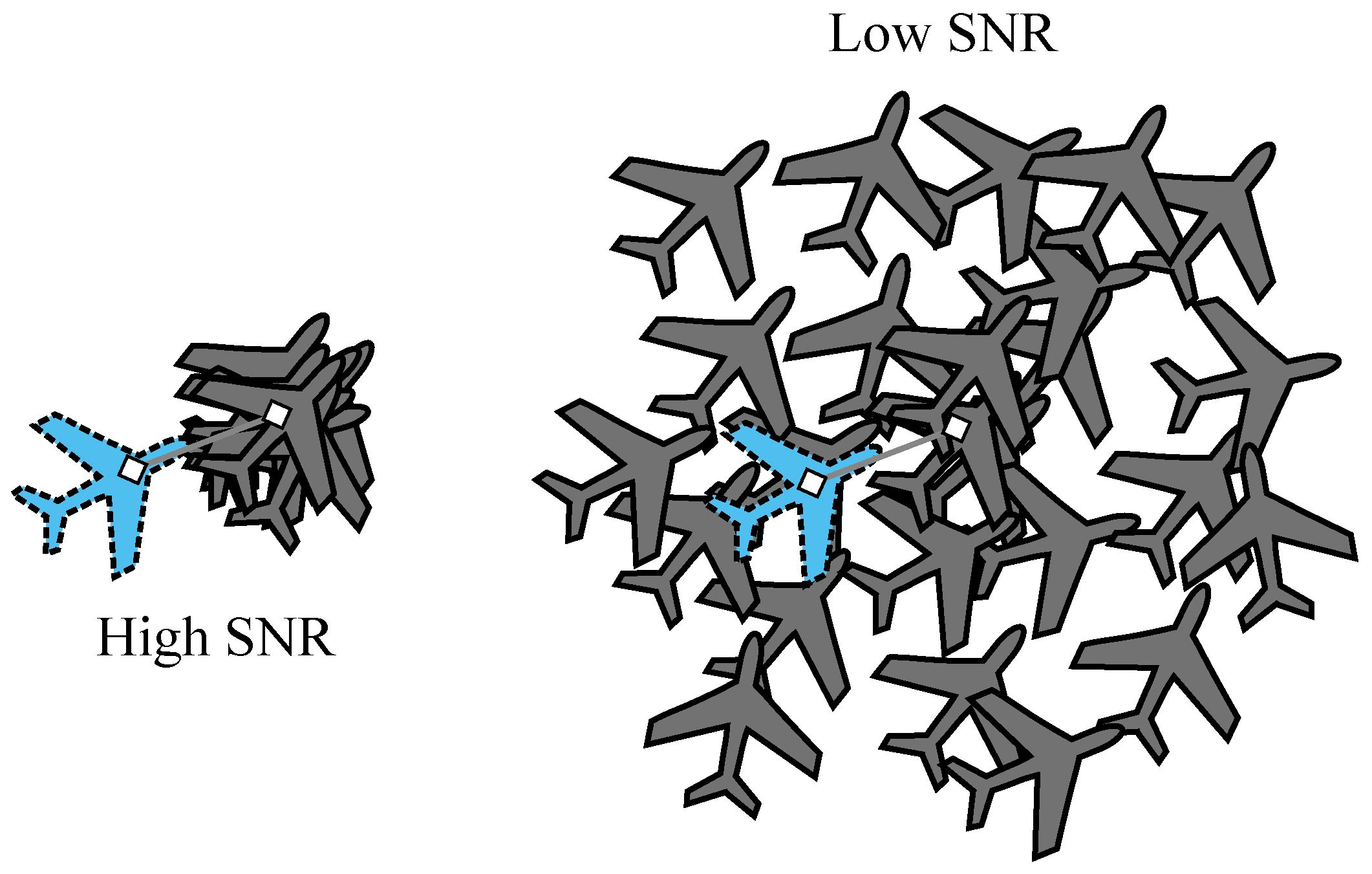
4.2. Signal-to-Noise Ratio
5. Examples
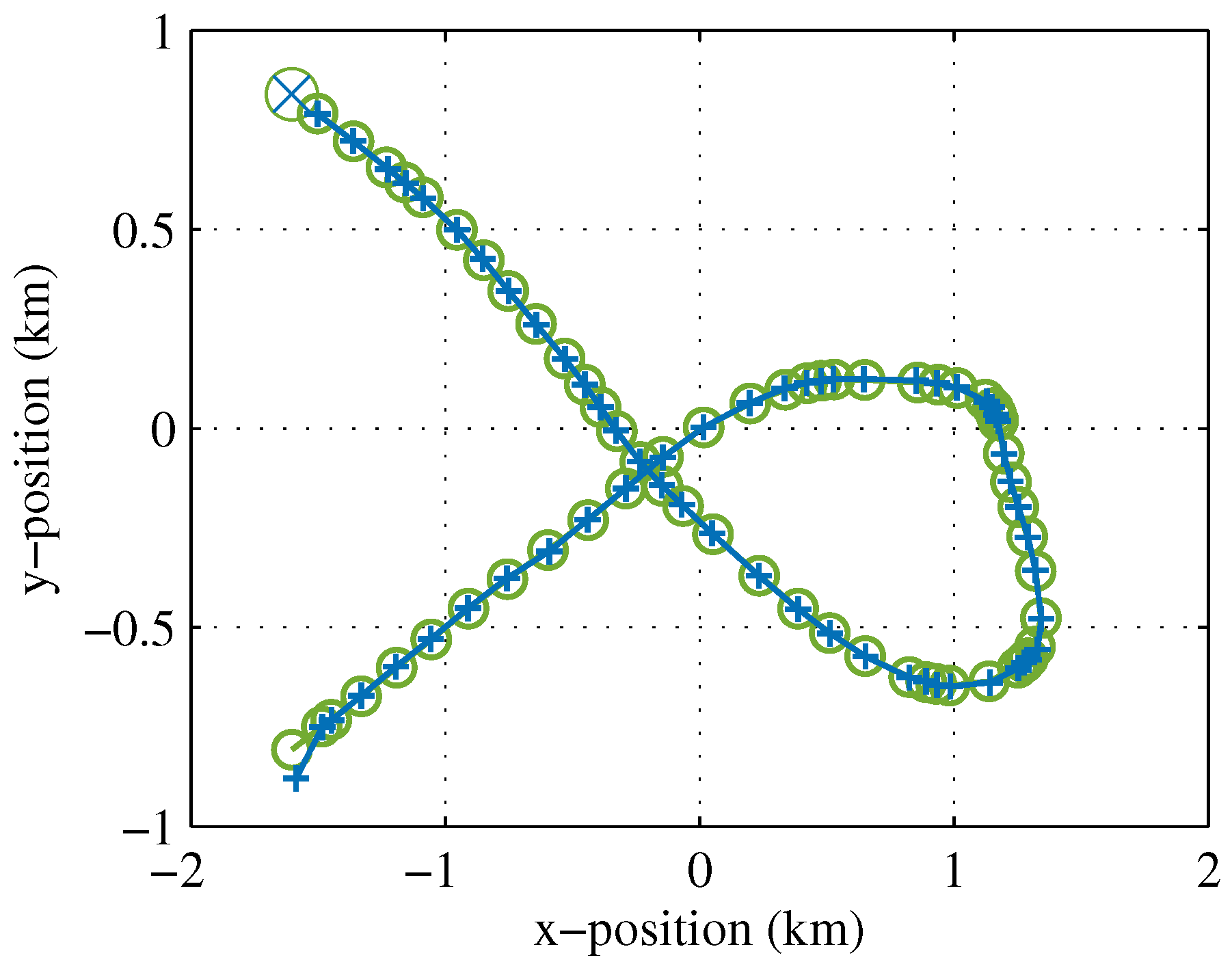
5.1. Looping Track (Model Mismatch Modulation)
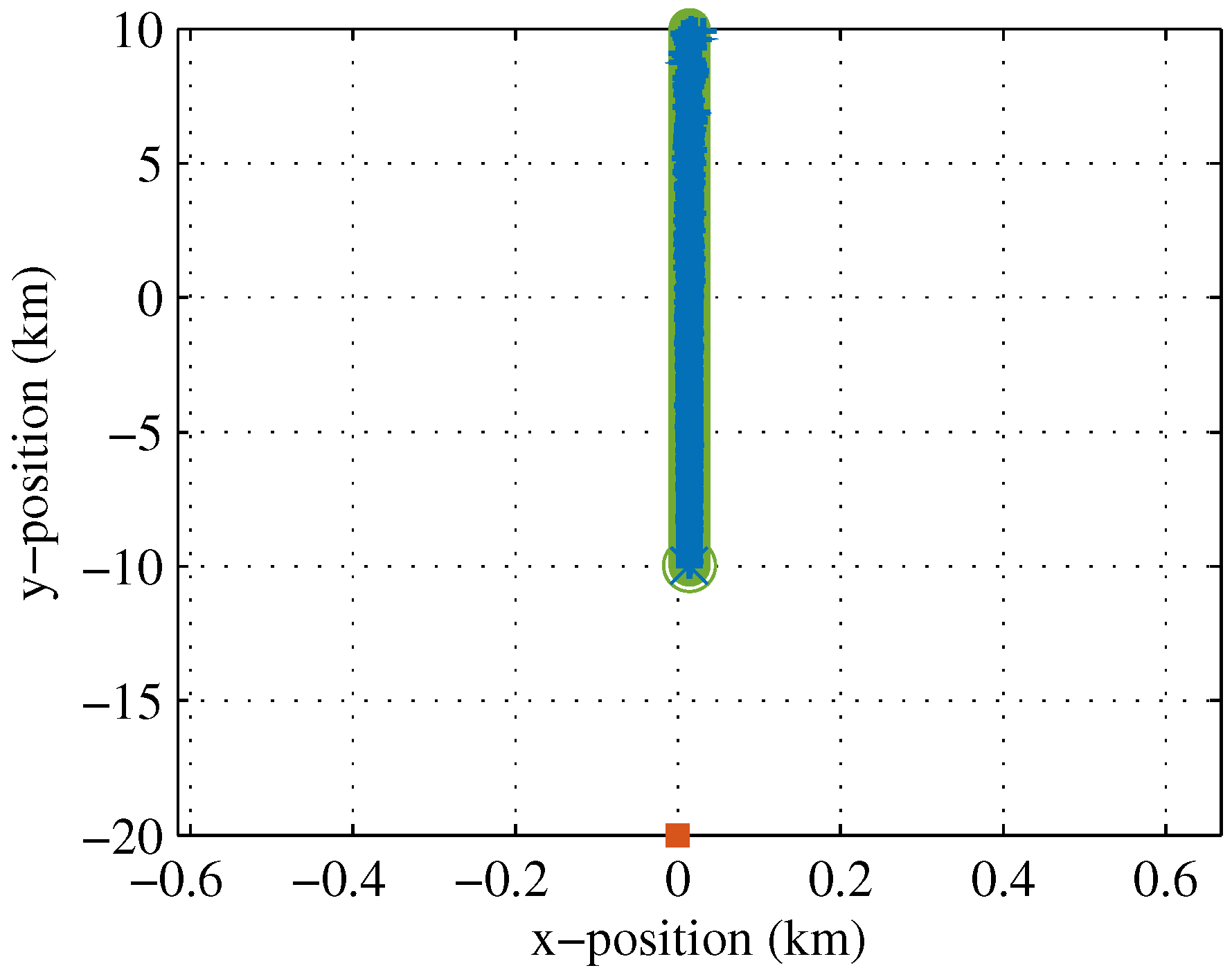
5.2. Approaching Radial Track (SNR Modulation)
5.3. Evasive Track (Global and Local Trending)
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Paul, B.; Bliss, D.W. Constant information radar for dynamic shared spectrum access. In Proceedings of the 49th Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 8–11 November 2015; pp. 1374–1378.
- Bliss, D.W. Cooperative radar and communications signaling: The estimation and information theory odd couple. In Proceedings of the 2014 IEEE Radar Conference, Cincinnati, OH, USA, 19–23 May 2014; pp. 50–55.
- Paul, B.; Bliss, D.W. Extending joint radar-Communications bounds for FMCW radar with Doppler estimation. In Proceedings of the 2015 IEEE Radar Conference, Johannesburg, South Africa, 27–30 October 2015; pp. 89–94.
- Paul, B.; Chiriyath, A.R.; Bliss, D.W. Joint communications and radar performance bounds under continuous waveform optimization: The waveform awakens. In Proceedings of the 2016 IEEE Radar Conference, Philadelphia, PA, USA, 2–6 May 2016; pp. 865–870.
- Chiriyath, A.R.; Bliss, D.W. Joint radar-Communications performance bounds: Data versus estimation information rates. In Proceedings of the 2015 IEEE Military Communications Conference, MILCOM, Tampa, FL, USA, 26–28 October 2015; pp. 1491–1496.
- Chiriyath, A.R.; Bliss, D.W. Effect of clutter on joint radar-Communications system performance inner bounds. In Proceedings of the 49th Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 8–11 November 2015; pp. 1379–1383.
- Chiriyath, A.R.; Paul, B.; Jacyna, G.M.; Bliss, D.W. Inner bounds on performance of radar and communications co-existence. IEEE Trans. Signal Proc. 2016, 64, 464–474. [Google Scholar] [CrossRef]
- Chiriyath, A.R.; Paul, B.; Bliss, D.W. Joint radar-Communications information bounds with clutter: The phase noise menace. In Proceedings of the IEEE Radar Conference, Philadelphia, PA, USA, 2–6 May 2016; pp. 690–695.
- Griffiths, H.; Cohen, L.; Watts, S.; Mokole, E.; Baker, C.; Wicks, M.; Blunt, S. Radar spectrum engineering and management: Technical and regulatory issues. Proc. IEEE 2015, 103, 85–102. [Google Scholar] [CrossRef]
- Chapin, J.M.; Lehr, W.H. Cognitive radios for dynamic spectrum access-the path to market success for dynamic spectrum access technology. IEEE Commun. Mag. 2007, 45, 96–103. [Google Scholar] [CrossRef]
- Bliss, D.W.; Govindasamy, S. Adaptive Wireless Communications: MIMO Channels and Networks; Cambridge University Press: New York, NY, USA, 2013. [Google Scholar]
- Haykin, S. Cognitive radar: A way of the future. IEEE Signal Process. Mag. 2006, 23, 30–40. [Google Scholar] [CrossRef]
- Guerci, J.R.; Guerci, R.M.; Ranagaswamy, M.; Bergin, J.S.; Wicks, M.C. CoFAR: Cognitive fully adaptive radar. In Proceedings of the 2014 IEEE Radar Conference, Cincinnati, OH, USA, 19–23 May 2014; pp. 984–989.
- Sodagari, S.; Khawar, A.; Clancy, T.C.; McGwier, R. A projection based approach for radar and telecommunication systems coexistence. In Proceedings of the IEEE Global Communications Conference (GLOBECOM), Anaheim, CA, USA, 3–7 December 2012; pp. 5010–5014.
- Khawar, A.; Abdel-Hadi, A.; Clancy, T.C. Spectrum sharing between S-band radar and LTE cellular system: A spatial approach. In Proceedings of the IEEE International Symposium on Dynamic Spectrum Access Networks (DYSPAN), McLean, VA, USA, 1–4 April 2014; pp. 7–14.
- Saruthirathanaworakun, R.; Peha, J.M.; Correia, L.M. Opportunistic primary-Secondary spectrum sharing with a rotating radar. In Proceedings of the International Conference on Computing, Networking and Communications (ICNC), Maui, HI, USA, 30 January–2 February 2012; pp. 1025–1030.
- Saruthirathanaworakun, R.; Peha, J.M.; Correia, L.M. Opportunistic sharing between rotating radar and cellular. IEEE J. Sel. Areas Commun. 2012, 30, 1900–1910. [Google Scholar] [CrossRef]
- Setlur, P.; Devroye, N. Adaptive waveform scheduling in radar: An information theoretic approach. In Proceedings of the International Society for Optics and Photonics, Baltimore, MD, USA, 24–26 April 2012.
- Stinco, P.; Greco, M.; Gini, F.; Himed, B. Channel parameters estimation for cognitive radar systems. In Proceedings of the CIP 2014: 4th International Workshop on Cognitive Information Processing, Copenhagen, Denmark, 26–28 May 2014; pp. 1–6.
- Aubry, A.; Maio, A.D.; Naghsh, M.P.M.M.; Soltanalian, M.; Stoica, P. Cognitive radar waveform design for spectral coexistence in signal-dependent interference. In Proceedings of the 2014 IEEE Radar Conference, Cincinnati, OH, USA, 19–23 May 2014; pp. 474–478.
- Paisana, F.; Miranda, J.P.; Marchetti, N.; DaSilva, L.A. Database-Aided sensing for radar bands. In Proceedings of the 2014 IEEE International Symposium on Dynamic Spectrum Access Networks (DYSPAN), McLean, VA, USA, 1–4 April 2014; pp. 1–6.
- Nijsure, Y.; Chen, Y.; Yuen, C.; Chew, Y.H. Location-Aware spectrum and power allocation in joint cognitive communication-Radar networks. In Proceedings of the Sixth International ICST Conference on Cognitive Radio Oriented Wireless Networks and Communications (CROWNCOM), Osaka, Japan, 1–3 June 2011; pp. 171–175.
- Greenspan, M. Potential pitfalls of cognitive radars. In Proceedings of the 2014 IEEE Radar Conference, Cincinnati, OH, USA, 19–23 May 2014; pp. 1288–1290.
- Shannon, C. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 623–656. [Google Scholar] [CrossRef]
- Woodward, P. Information theory and the design of radar receivers. Proc. IRE 1951, 39, 1521–1524. [Google Scholar] [CrossRef]
- Woodward, P.M. Probability and Information Theory, with Applications to Radar; Artech House: Dedham, MA, USA, 1953. [Google Scholar]
- Bell, M.R. Information theory and radar waveform design. IEEE Trans. Inf. Theory 1993, 39, 1578–1597. [Google Scholar] [CrossRef]
- Nijsure, Y.; Chen, Y.; Boussakta, S.; Yuen, C.; Chew, Y.H.; Ding, Z. Novel system architecture and waveform design for cognitive radar radio networks. IEEE Trans. Veh. Technol. 2012, 61, 3630–3642. [Google Scholar] [CrossRef]
- Huang, K.W.; Bică, M.; Mitra, U.; Koivunen, V. Radar waveform design in spectrum sharing environment: Coexistence and cognition. In Proceedings of the 2015 IEEE Radar Conference, Johannesburg, South Africa, 27–30 October 2015; pp. 1698–1703.
- Romero, R.A.; Goodman, N.A. Cognitive radar network: Cooperative adaptive beamsteering for integrated search-and-track application. IEEE Trans. Aerosp. Electron. Syst. 2013, 49, 915–931. [Google Scholar] [CrossRef]
- Hayvaci, H.T.; Tavli, B. Spectrum sharing in radar and wireless communication systems: A review. In Proceedings of the 2014 International Conference on Electromagnetics in Advanced Applications (ICEAA), Palm Beach, Aruba, 3–8 August 2014; pp. 810–813.
- Suvorova, S.; Howard, S.D. Waveform libraries for radar tracking applications: Maneuvering targets. In Proceedings of the 40th Annual Conference on Information Sciences and Systems, Princeton, NJ, USA, 22–24 March 2006; pp. 1424–1428.
- De Jong, E.; Pribić, R. Sparse signal processing on estimation grid with constant information distance applied in radar. EURASIP J. Adv. Signal Process. 2014, 2014, 78. [Google Scholar] [CrossRef]
- Sen, S.; Nehorai, A. Sparsity-based multi-target tracking using OFDM radar. IEEE Trans. Signal Process. 2011, 59, 1902–1906. [Google Scholar] [CrossRef]
- Akcakaya, M.; Sen, S.; Nehorai, A. A novel data-driven learning method for radar target detection in nonstationary environments. IEEE Signal Process. Lett. 2016, 23, 762–766. [Google Scholar] [CrossRef]
- Romero, R.A.; Bae, J.; Goodman, N.A. Theory and application of SNR and mutual information matched illumination waveforms. IEEE Trans. Aerosp. Electron. Syst. 2011, 47, 912–927. [Google Scholar] [CrossRef]
- Watson, G.A.; Blair, W.D. Revisit calculation and waveform control for a multifunction radar. In Proceedings of the 32nd IEEE Conference on Decision and Control, San Antonio, TX, USA, 15–17 December 1993; pp. 456–460.
- Alahmadi, M.S.; Smith, G.E.; Baker, C.J. A recursive approach for adaptive parameters selection in a multifunction radar. In Proceedings of the 2016 IEEE Radar Conference, Philadelphia, PA, USA, 2–6 May 2016; pp. 1–6.
- Guerci, J.R.; Guerci, R.M.; Lackpour, A.; Moskowitz, D. Joint design and operation of shared spectrum access for radar and communications. In Proceedings of the IEEE Radar Conference, Johannesburg, South Africa, 27–30 October 2015; pp. 761–766.
- Reed, J.T.; Odom, J.L.; Causey, R.T.; Lanterman, A.D. Gaussian multiple access channels for radar and communications spectrum sharing. In Proceedings of the IEEE Radar Conference, Philadelphia, PA, USA, 2–6 May 2016; pp. 1–6.
- Turlapaty, A.; Jin, Y. A Joint design of transmit waveforms for radar and communications systems in coexistence. In Proceedings of the IEEE Radar Conference, Cincinnati, OH, USA, 19–23 May 2014; pp. 315–319.
- Li, X.R.; Jilkov, V.P. Survey of maneuvering target tracking. Part I: Dynamic models. Trans. Aerosp. Electron. Syst. 2003, 39, 1333–1364. [Google Scholar]
- Richards, M.A. Fundamentals of Radar Signal Processing, 2nd ed.; McGraw-Hill Education: Raleigh, NC, USA, 2014. [Google Scholar]
- Richards, M.A. Principles of Modern Radar: Basic Principles; SciTech Publishing: Raleigh, NC, USA, 2010. [Google Scholar]
- Van Trees, H.L. Detection, Estimation, and Modulation Theory: Radar-Sonar Signal Processing and Gaussian Signals in Noise; Krieger Publishing Company: Malabar, FL, USA, 1992. [Google Scholar]
- Candy, J.V. Bayesian Signal Processing: Classical, Modern, and Particle Filtering Methods; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Richmond, C.D. Mean-squared error and threshold SNR prediction of maximum-likelihood signal parameter estimation with estimated colored noise covariances. Trans. Inf. Theory 2006, 52, 2146–2164. [Google Scholar] [CrossRef]
- Paul, B.; Bliss, D.W. Estimation information bounds using the I-MMSE formula and Gaussian mixture models. In Proceedings of the 50th Annual Conference on Information Sciences and Systems (CISS), Princeton, NJ, USA, 16–18 March 2016; pp. 292–297.
- Kay, S.M. Fundamentals of Statistical Signal Processing: Estimation Theory, 1st ed.; Prentice-Hall: Upper Saddle River, NJ, USA, 1993. [Google Scholar]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
- Davey, S.J.; Rutten, M.G.; Cheung, B. A comparison of detection performance for several Track-Before-Detect algorithms. In Proceedings of the 11th International Conference on Information Fusion, Cologne, Germany, 30 June–3 July 2008; pp. 1–8.
- Myers, K.A.; Tapley, B.D. Adaptive sequential estimation with unknown noise statistics. Trans. Autom. Control. 1976, 21, 520–523. [Google Scholar] [CrossRef]




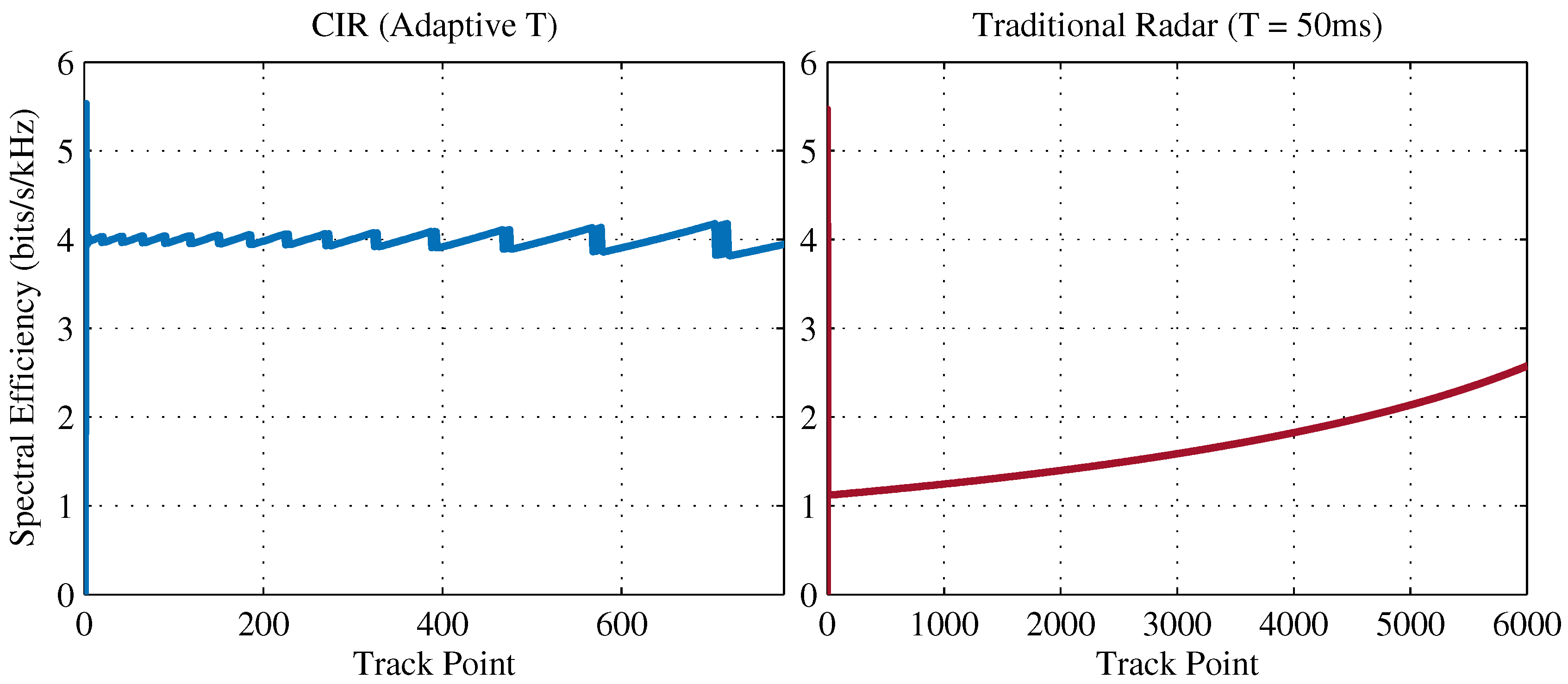
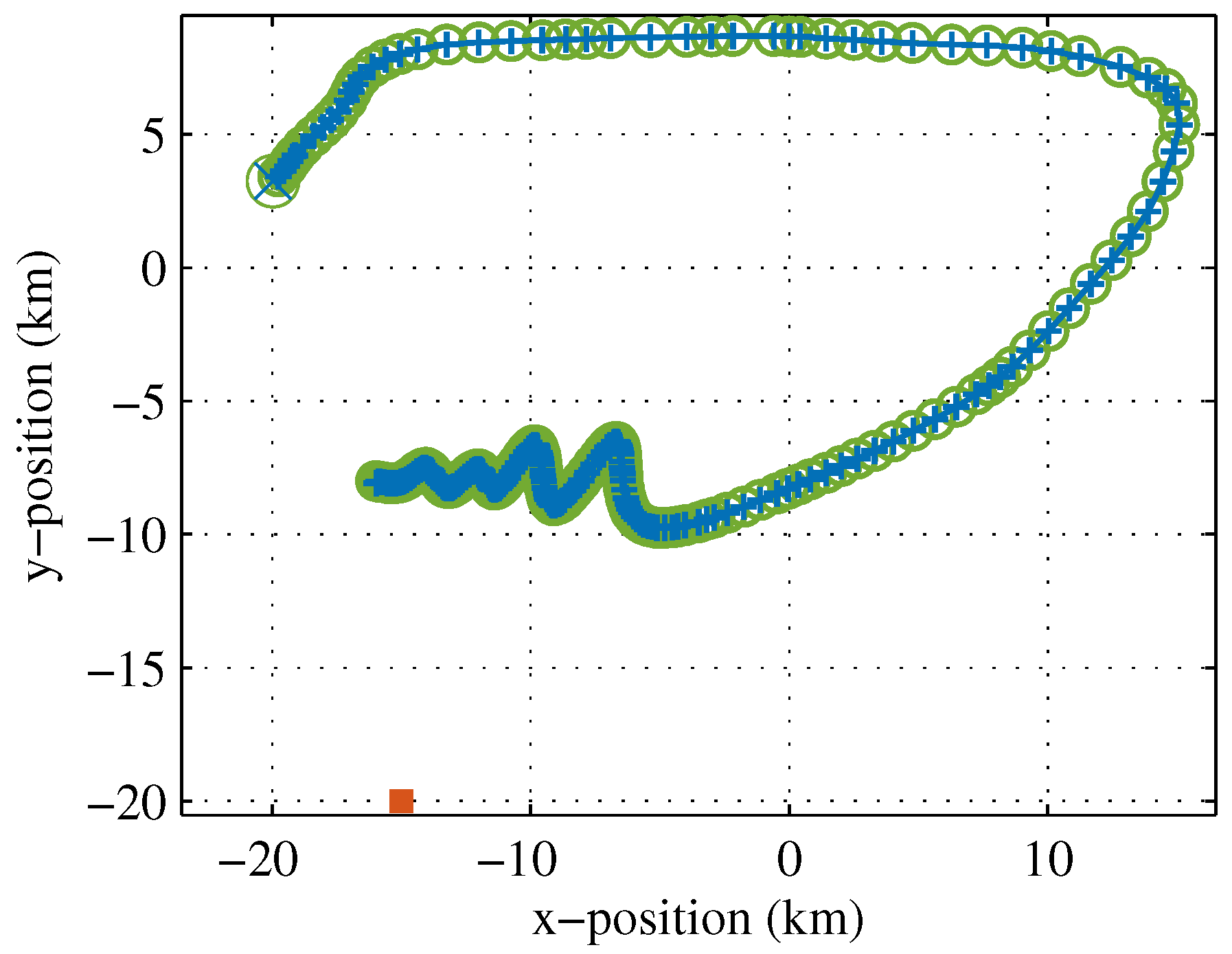
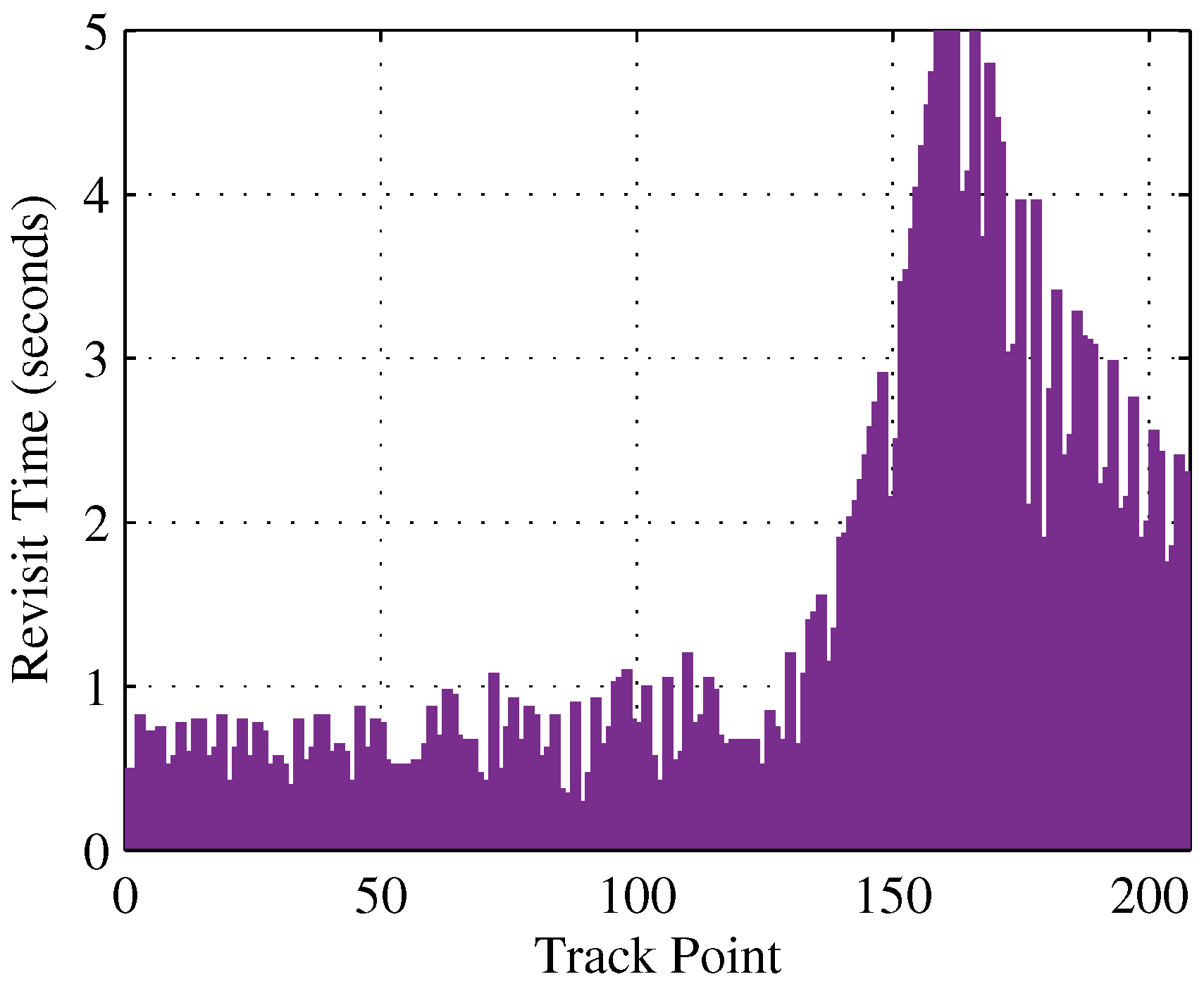
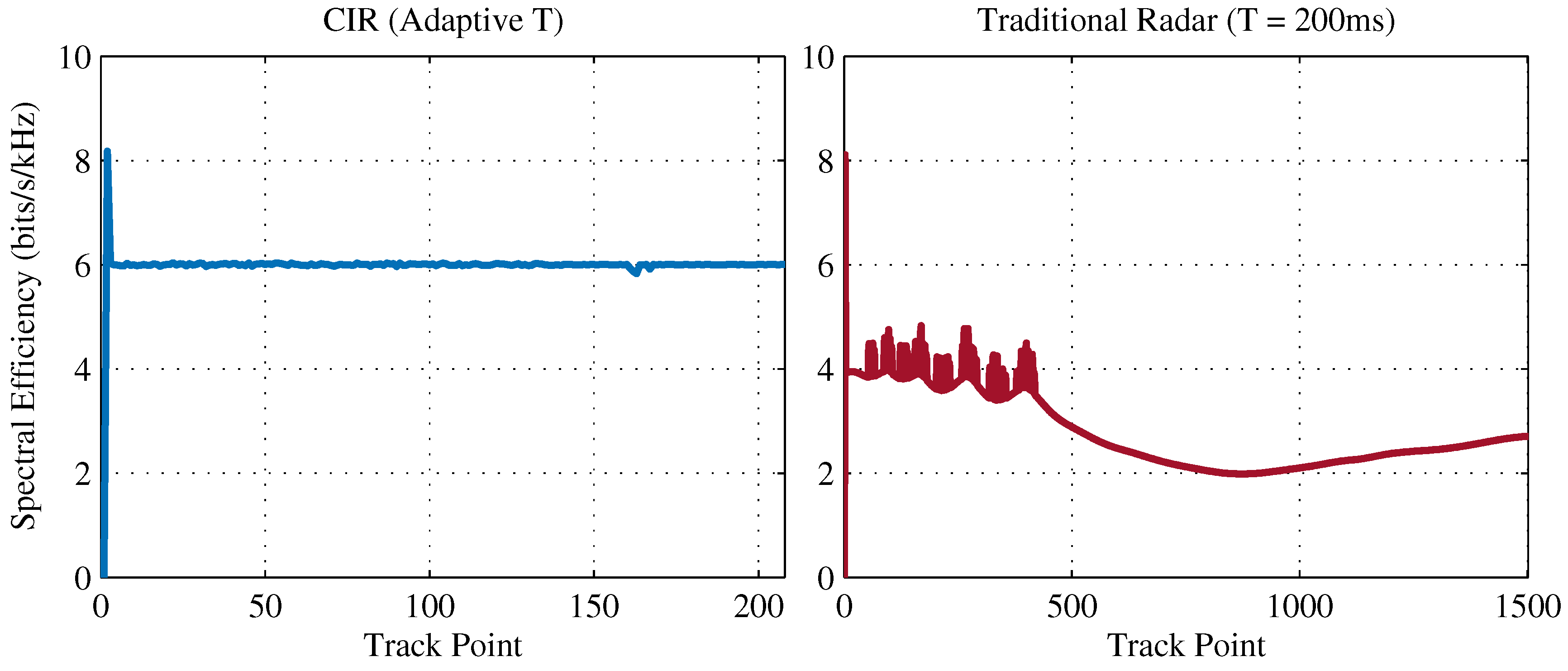
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Bandwidth (B) | 5 MHz | Center Frequency () | 3 GHz |
| Absolute Temperature () | 1000 K | Pulse Duration () | 5 µs |
| Probability of False Alarm (P) | Radar Antenna Gain (G) | 30 dBi | |
| Radar Transmit Power () | 100 kW | Target Cross-Section (σ) | 10 m |
| Chirp Rate | Window Variance | ||
| Wave Speed (c) | m/s | Number of Pulses () | 10 |
| Varied | Number of Array Elements () | 10 |
| Track | Traditional Radar | CIR |
|---|---|---|
| Looping Track | 99.500% (200 targets) | 99.870% (800 targets) |
| Approaching Radial Track | 99.000% (100 targets) | 99.834% (600 targets) |
| Evasive Track | 99.750% (400 targets) | 99.940% (1700 targets) |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Paul, B.; Bliss, D.W. The Constant Information Radar. Entropy 2016, 18, 338. https://doi.org/10.3390/e18090338
Paul B, Bliss DW. The Constant Information Radar. Entropy. 2016; 18(9):338. https://doi.org/10.3390/e18090338
Chicago/Turabian StylePaul, Bryan, and Daniel W. Bliss. 2016. "The Constant Information Radar" Entropy 18, no. 9: 338. https://doi.org/10.3390/e18090338
APA StylePaul, B., & Bliss, D. W. (2016). The Constant Information Radar. Entropy, 18(9), 338. https://doi.org/10.3390/e18090338





