Combined Forecasting of Streamflow Based on Cross Entropy
Abstract
:1. Introduction
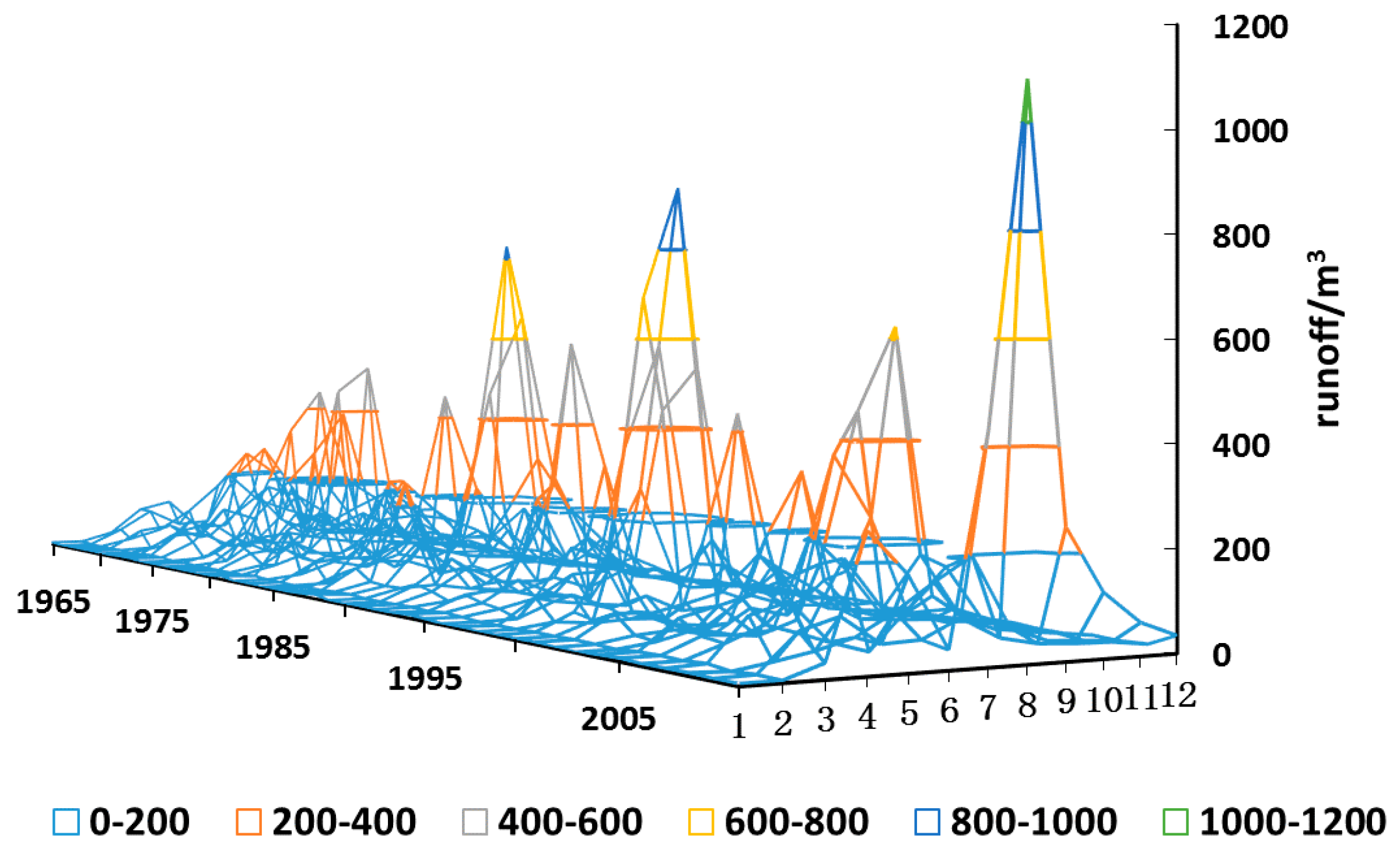
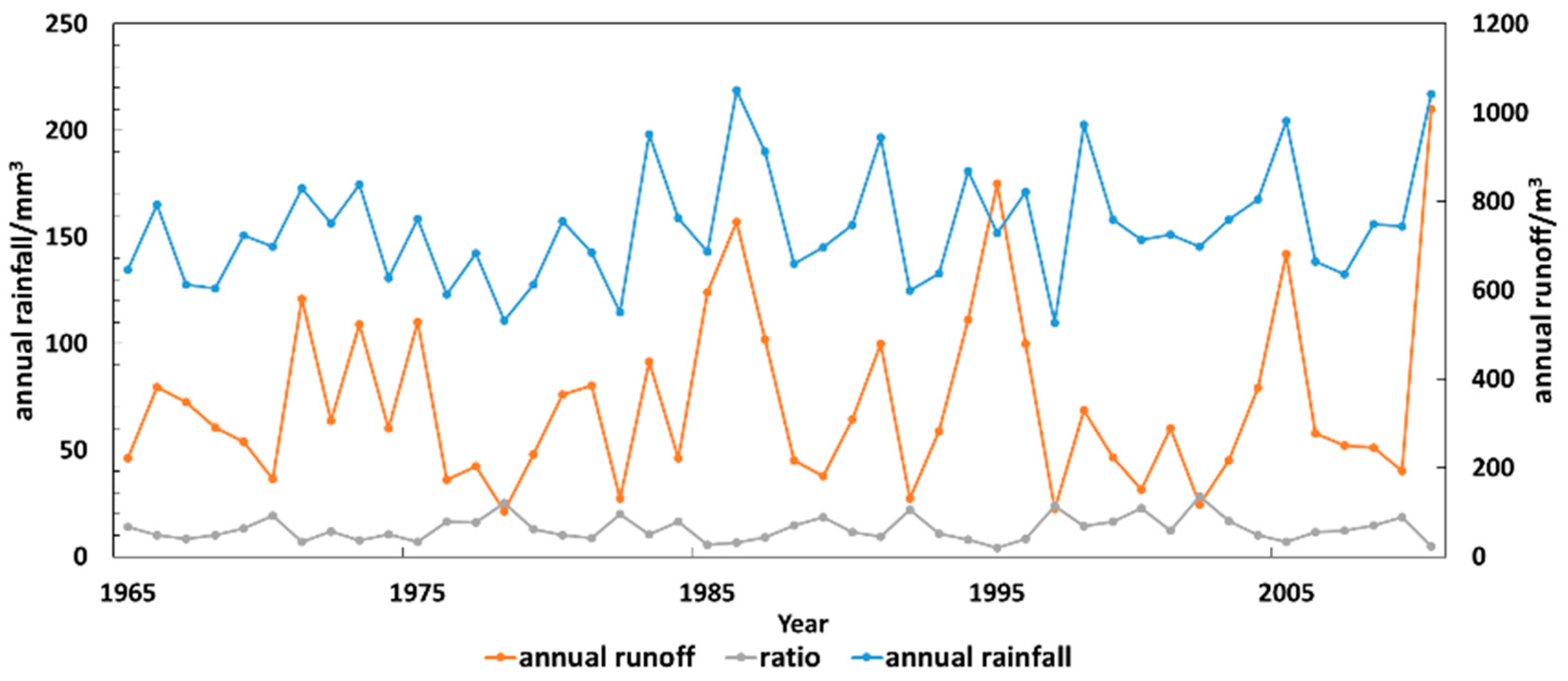
2. Analysis of Streamflow Characteristics
3. Data Processing Method
3.1. Data Preprocessing
3.2. Selecting Similar Years
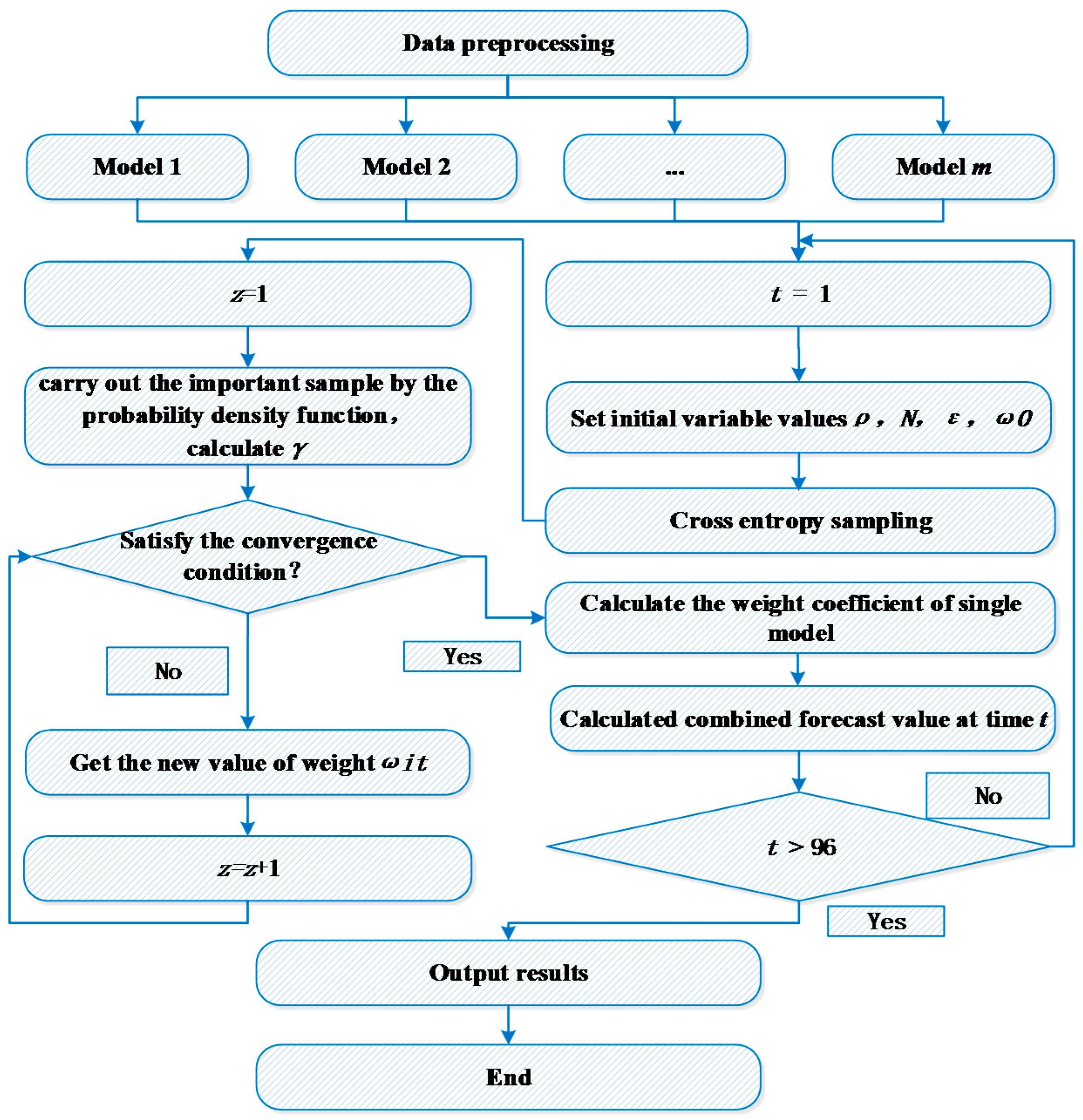
4. Streamflow Forecasting Model Based on CE
4.1. Combined Forecasting Model
4.2. The CE Model
5. Results and Analysis
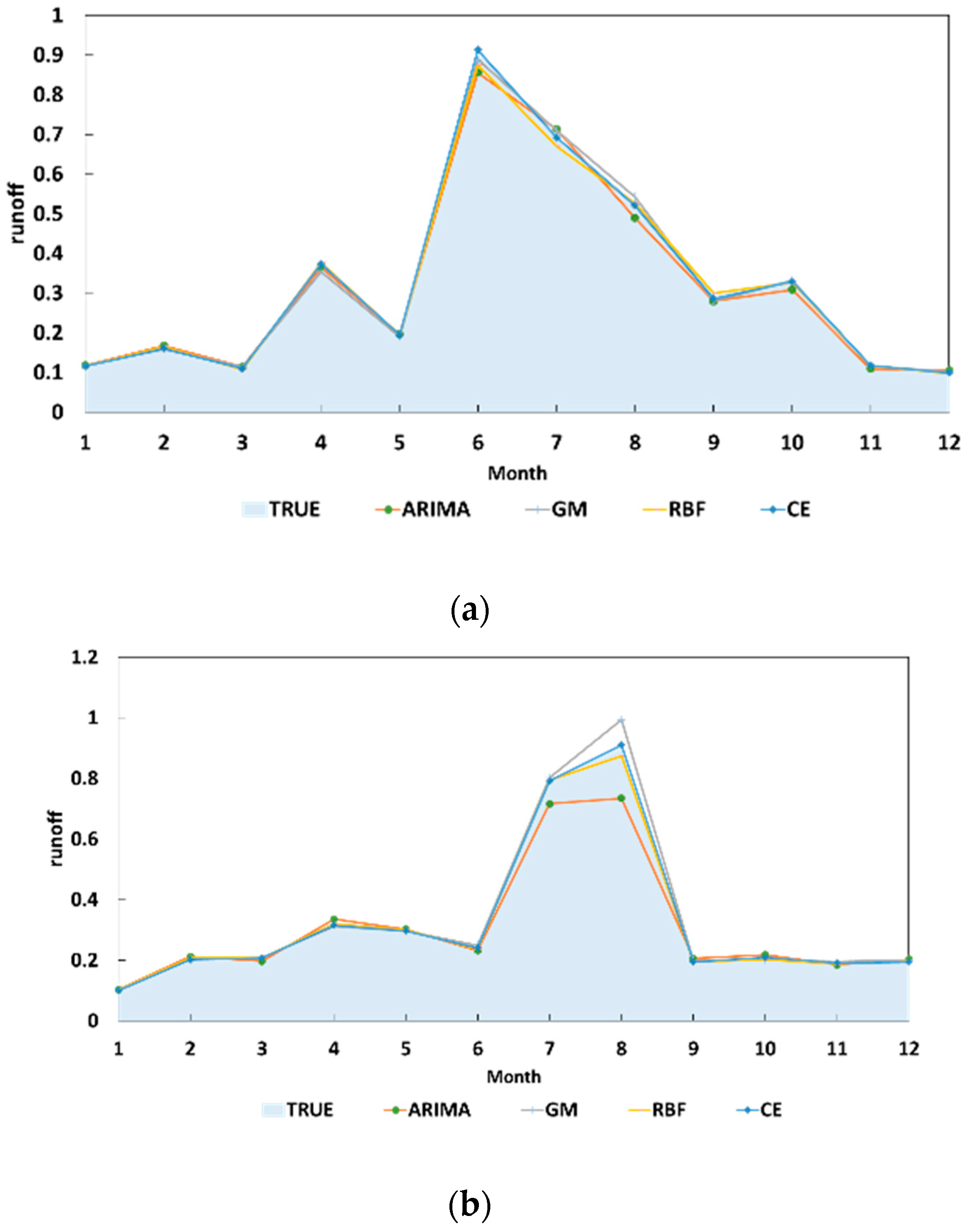
5.1. Comparison of the Results Obtained with a Single Method
5.2. Comparison with Other Combined Forecasting Models
5.3. Influence of the Historical Data Length on the Prediction Results
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Zhang, L.X.; Lei, X.Y. Decomposition of time series model in wulasitai River application of annual runoff prediction. J. Water Resour. Water Eng. 2006, 17, 22–24. [Google Scholar]
- Emili, B.; Alberto, P.; Emilio, S.; Jose, D. Predicting service request in support centers based on nonlinear dynamics ARMA modeling and neural networks. Expert Syst. Appl. 2008, 34, 665–672. [Google Scholar]
- Li, B.; Yuan, P.; Chang, J. GM (1,1) improved model for predicting annual runoff forecasting. Northeast Water Conserv. Hydroelect. 2006, 24, 28–30. [Google Scholar]
- Yu, G.R.; Ye, H.; Xie, Z.Q. Projection pursuit auto regression model in predicting runoff of Yangtze River in application. Hohai Univ. J. 2009, 37, 263–266. [Google Scholar]
- Zhou, H.F.; Li, C. The main stream of the Yellow River Runoff of transient components and frequency analysis and its prediction. Meteor. Sci. 2003, 23, 201–207. [Google Scholar]
- Qiu, L.; An, K.J.; Wang, W.C. Classification of runoff prediction model based on Markov Bayes. Water Conserv. Sci. Technol. Econ. 2011, 17, 1–4. [Google Scholar]
- Wang, Q.H.; Qian, X.; Zhang, Y.C. Application of BP neural network in the prediction of runoff and stream reservoir runoff forecast. Environ. Protect. Sci. 2010, 23, 19–23. [Google Scholar]
- Muhsin, N.; Sinan, U.; Irfan, Y. Side-by-side comparison of horizontal surface flow and free water surface flow constructed wet lands and artificial neural network(ANN)modeling approach. Ecol. Eng. 2009, 35, 1255–1263. [Google Scholar]
- Yun, W.; Guo, S.L.; Xiong, L.H.; Liu, P.; Liu, D. Daily Runoff Forecasting Model Based on ANN and Data Preprocessing Techniques. Water 2015, 7, 4144–4160. [Google Scholar]
- Hao, Z.C.; Hao, F.H.; Singh, V.P. A general framework for multivariate multi-index drought prediction based on Multivariate Ensemble Streamflow Prediction (MESP). J. Hydrol. 2016, 539, 1–10. [Google Scholar] [CrossRef]
- Masselot, P.; Dabo-Niang, S.; Chebana, F.; Ouarda, T.B.M.J. Streamflow forecasting using functional regression. J. Hydrol. 2016, 538, 754–766. [Google Scholar] [CrossRef]
- Arsenault, R.; Poissant, D.; Brissette, F. Parameter dimensionality reduction of a conceptual model for streamflow prediction in Canadian, snowmelt dominated ungauged basins. Adv. Water Resour. 2015, 85, 27–44. [Google Scholar] [CrossRef]
- Bates, J.; Granger, C. The combination of forecast. Oper. Res. Quart. 1969, 20, 451–468. [Google Scholar] [CrossRef]
- Gu, H.Y. Prediction of River Runoff. Master’s Thesis, Northeast Forestry University, Harbin, China, June 2008. [Google Scholar]
- Fan, Y.; Li, Y. Annual runoff combination forecasting method research and application. North Water Conserv. Hydrol. Power 2006, 24, 23–27. [Google Scholar]
- Yin, J.X.; Jiang, Y.Z.; Lu, F. Based on combination forecasting model of long-term forecasting of reservoir runoff. People’s Yellow River 2008, 30, 28–32. [Google Scholar]
- Su, X.H. Study on the Short-Term Load Forecasting Based on Artificial Neural Network. Master’s Thesis, Chongqing University, Chongqing, China, May 2005. [Google Scholar]
- Singh, V.P. Entropy Theory and Its Applications in Environmental and Water Engineering; John Wiley: New York, NY, USA, 2013; p. 662. [Google Scholar]
- Marini, G.; De Martino, G.; Fontana, N.; Fiorentino, M.; Singh, V.P. Entropy approach for 2D velocity distribution in open-channel flow. J. Hydraul. Res. 2011, 49, 784–790. [Google Scholar] [CrossRef]
- Fontana, N.; Marini, G.; De Paola, F. Experimental assessment of a 2-D entropy-based model for velocity distribution in open channel flow. Entropy 2013, 15, 988–998. [Google Scholar] [CrossRef]
- Li, R.; Liu, H.L.; Lu, Y.; Han, B. A combination method for distribution transformer life prediction based on cross entropy theory. Power Syst. Protect. Control 2014, 42, 97–101. [Google Scholar]
- Chen, N.; Sha, Q.; Tang, Y.; Oi, Y.; Zhu, L. A Combination Method for Wind Power Predication Based on Cross Entropy Theory. Proc. CSEE 2012, 32, 29–34. [Google Scholar]
- Liu, J.; Nie, C.X.; Xie, Q. Changes of rainfall runoff relationship and the reasons for the status quo analysis. Anhui Agric. Sci. 2010, 38, 5170–5172. [Google Scholar]
- Liu, H.W. The Feature Selection Algorithm Based on Information Entropy. Master’s Thesis, Jilin University, Jilin, China, June 2010. [Google Scholar]
- Box, G.E.; Jenkins, G.M. Time Series Analysis: Forecasting and Control, revised ed.; Holden Day: San Francisco, CA, USA, 1976; pp. 80–145. [Google Scholar]
- Si, Q. The Gray Prediction Model of Equal Dimension and New Information and the Forecasting Precision—Based on the Analysis and Prediction of the Pension Insurance for Urban Residents of China. Stat. Thinktank 2008, 12, 13–19. (In Chinese) [Google Scholar]
- Pieter-tjerk, D.B.; Kroese, D.P.; Shie, M.; Rubinstein, R.Y. A Tutorial on the Cross-Entropy Method. Annal. Oper. Res. 2005, 134, 19–67. [Google Scholar]
| Year | ARIMA | GM | RBF | CE | ||||
|---|---|---|---|---|---|---|---|---|
| MRPE | RMSE | MRPE | RMSE | MRPE | RMSE | MRPE | RMSE | |
| 2006 | 10.95% | 6.96% | 10.55% | 4.79% | 10.58% | 3.98% | 10.53% | 3.67% |
| 2007 | 10.66% | 5.77% | 9.23% | 5.61% | 9.07% | 4.89% | 8.95% | 5.01% |
| 2008 | 9.71% | 6.01% | 10.12% | 5.85% | 9.25% | 5.28% | 9.77% | 5.32% |
| 2009 | 9.89% | 5.25% | 10.35% | 6.08% | 7.32% | 5.01% | 7.24% | 4.99% |
| 2010 | 11.27% | 7.38% | 11.59% | 8.91% | 8.56% | 7.97% | 8.30% | 6.67% |
| Average | 10.50% | 6.27% | 10.37% | 6.25% | 8.96% | 5.43% | 8.96% | 5.13% |
| Year | EW | RM | CE | |||
|---|---|---|---|---|---|---|
| MPE | RMSE | MPE | RMSE | MPE | RMSE | |
| 2006 | 10.76% | 3.75% | 10.53% | 3.71% | 10.53% | 3.67% |
| 2007 | 9.23% | 5.56% | 9.14% | 5.34% | 8.95% | 5.01% |
| 2008 | 9.74% | 5.30% | 9.78% | 5.29% | 9.77% | 5.32% |
| 2009 | 7.55% | 5.09% | 7.43% | 5.25% | 7.24% | 4.99% |
| 2010 | 10.07% | 7.24% | 9.52% | 7.08% | 8.30% | 6.67% |
| Average | 9.47% | 5.39% | 9.28% | 5.33% | 8.96% | 5.13% |
| Case | RBF | RM | CE | |||
|---|---|---|---|---|---|---|
| MPE | RMSE | MPE | RMSE | MPE | RMSE | |
| Case 1 | 9.01% | 5.62% | 9.31% | 5.37% | 8.98% | 5.14% |
| Case 2 | 9.37% | 5.71% | 9.42% | 5.43% | 9.11% | 5.25% |
| Case 3 | 12.94% | 7.87% | 11.28% | 7.01% | 10.50% | 6.62% |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Men, B.; Long, R.; Zhang, J. Combined Forecasting of Streamflow Based on Cross Entropy. Entropy 2016, 18, 336. https://doi.org/10.3390/e18090336
Men B, Long R, Zhang J. Combined Forecasting of Streamflow Based on Cross Entropy. Entropy. 2016; 18(9):336. https://doi.org/10.3390/e18090336
Chicago/Turabian StyleMen, Baohui, Rishang Long, and Jianhua Zhang. 2016. "Combined Forecasting of Streamflow Based on Cross Entropy" Entropy 18, no. 9: 336. https://doi.org/10.3390/e18090336
APA StyleMen, B., Long, R., & Zhang, J. (2016). Combined Forecasting of Streamflow Based on Cross Entropy. Entropy, 18(9), 336. https://doi.org/10.3390/e18090336





