Characterization of Seepage Velocity beneath a Complex Rock Mass Dam Based on Entropy Theory
Abstract
:1. Introduction
2. Theory
2.1. Information Entropy
2.2. Principle of Maximum Entropy
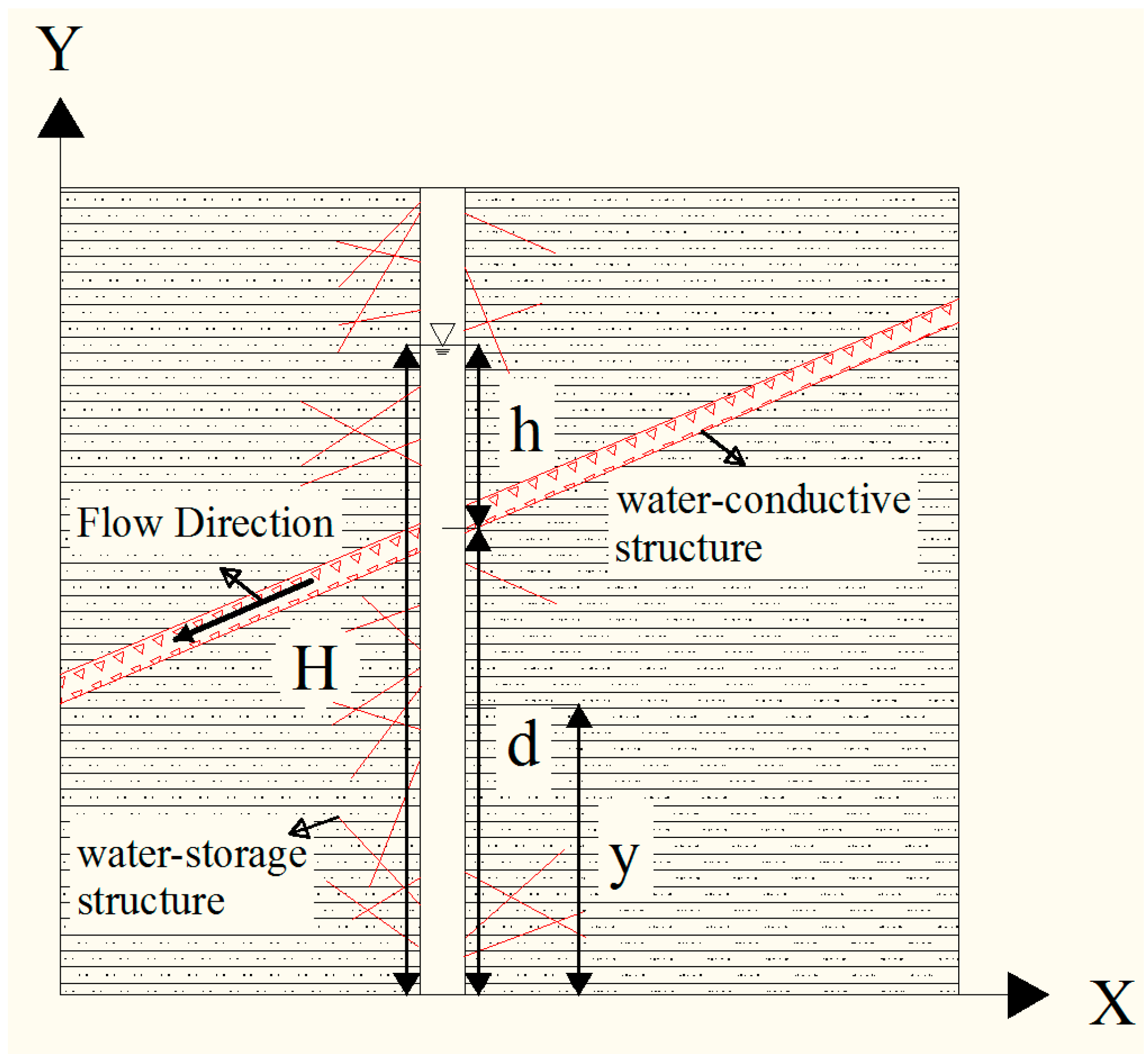
3. Derivation of Seepage Velocity Distribution
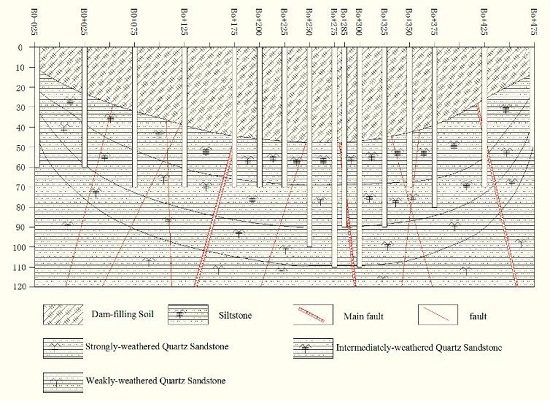
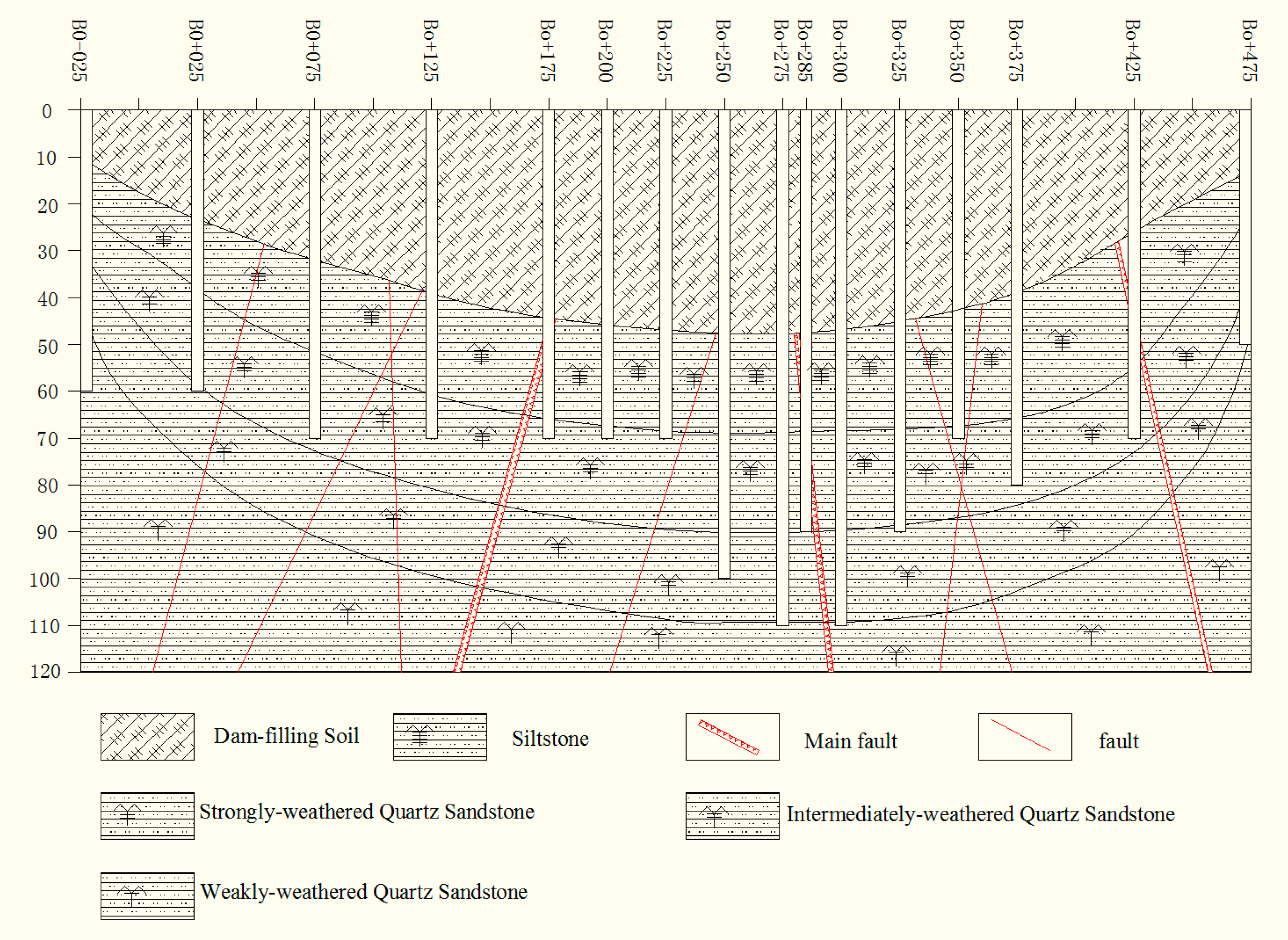
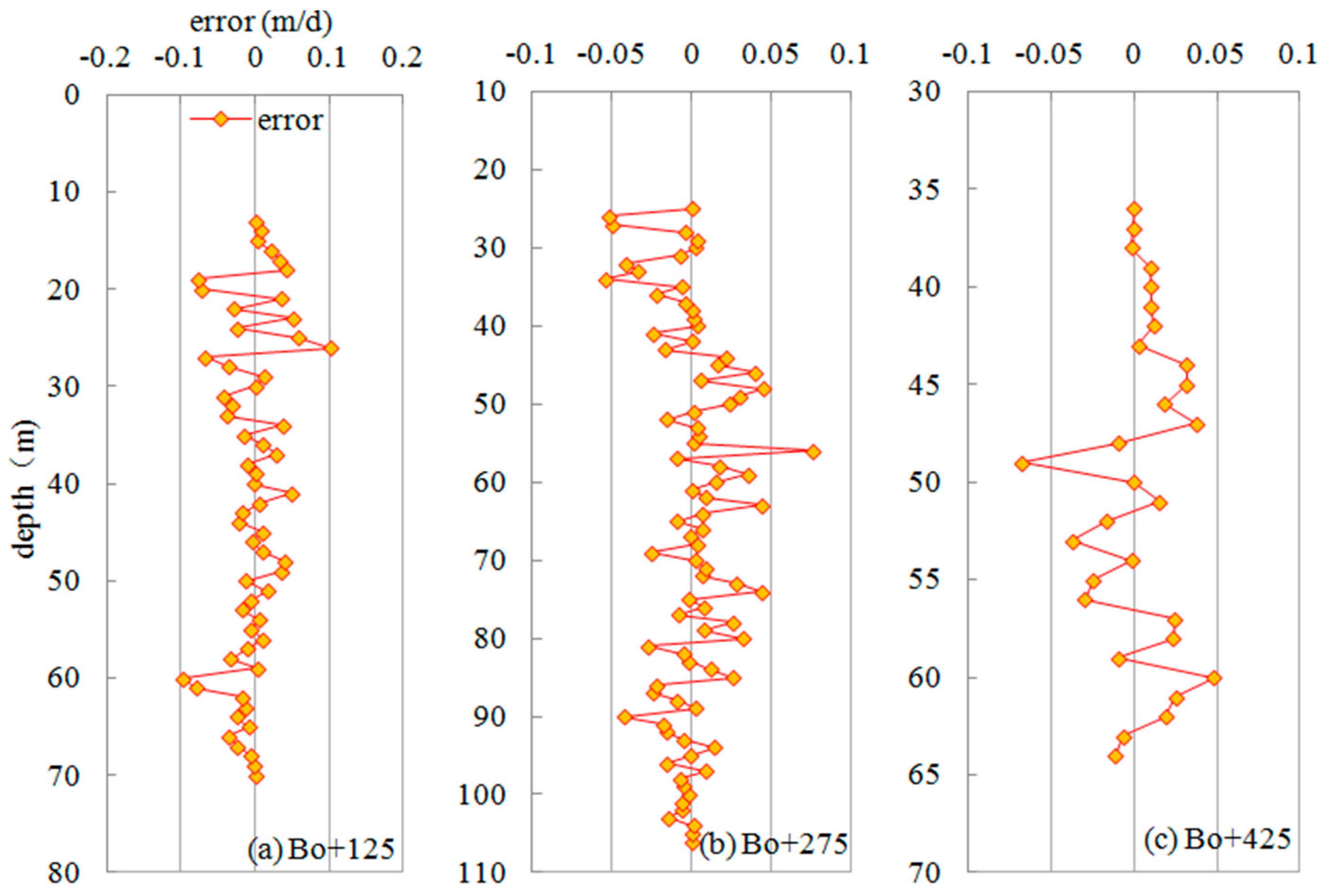
4. Tests and Results
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Mohammadi, Z.; Raeisi, E. Hydrogeological uncertainties in delineation of leakage at karst dam sites, the Zagros Region, Iran. J. Cave Karst Stud. 2007, 69, 305–317. [Google Scholar]
- Mozafari, M.; Raeisi, E.; Zare, M. Water leakage paths in the Doosti Dam, Turkmenistan and Iran. Environ. Earth Sci. 2012, 65, 103–117. [Google Scholar] [CrossRef]
- Zheng, X.; Xu, K.; Wei, Y. Study on the disaster-causing mechanism of the tailings dam falling. J. Saf. Sci. Technol. 2008, 5, 8–12. (In Chinese) [Google Scholar]
- Abdelaziz, R.; Pearson, A.J.; Merkel, B.J. Lattice Boltzmann modeling for tracer test analysis in a fractured Gneiss aquifer. Nat. Sci. 2013, 5, 368–374. [Google Scholar] [CrossRef]
- Abdelaziz, R.; Merkel, B.J. Analytical and numerical modeling of flow in a fractured gneiss aquifer. J. Water Resour. Prot. 2012, 4, 657–662. [Google Scholar] [CrossRef]
- Ge, B.; Zheltov, I. Basic concepts in theory of seepage of homogeneous liquids in fissured rocks. J. Appl. Math. Mech. 1960, 24, 1286–1303. [Google Scholar]
- Srivastava, A.; Babu, G.L.S.; Haldar, S. Influence of spatial variability of permeability property on steady state seepage flow and slope stability analysis. Eng. Geol. 2010, 110, 93–101. [Google Scholar] [CrossRef]
- Cho, S.E. Probabilistic analysis of seepage that considers the spatial variability of permeability for an embankment on soil foundation. Eng. Geol. 2012, 133, 30–39. [Google Scholar] [CrossRef]
- Zhu, H.; Zhang, L.M.; Zhang, L.L.; Zhou, C.B. Two-dimensional probabilistic infiltration analysis with a spatially varying permeability function. Comput. Geotech. 2013, 48, 249–259. [Google Scholar] [CrossRef]
- Singh, V.P. The entropy theory as a tool for modelling and decision-making in environmental and water resources. Water SA 2000, 26, 1–11. [Google Scholar]
- Wang, T.; Chen, J.S.; Wang, T.; Wang, S. Entropy weight-set pair analysis based on tracer techniques for dam leakage investigation. Nat. Hazards 2015, 76, 747–767. [Google Scholar] [CrossRef]
- Contreras, I.A.; Hernández, S.H. Techniques for prevention and detection of leakage in dams and reservoirs. Available online: http://ussdams.com/proceedings/2010Proc/785-814.pdf (accessed on 9 August 2016).
- Chen, L.; Zhao, J.; Li, G.; Zhan, L.; Lei, W. Experimental study of seawall piping under water level fluctuation. Eur. J. Environ. Civ. Eng. 2013, 17, 1–22. [Google Scholar] [CrossRef]
- Chen, L.; Zhao, J.; Zhao, T.; Zhao, X.; Huang, D.; Lu, L. Experimental study of low temperature water seepage detection model of embankment dam. Fresenius Environ. Bull. 2015, 24, 1131–1141. [Google Scholar]
- Chen, J.; Du, G. Radioactive or Natural Tracer Techniques for Leak Determining of Dam Abutment. Nucl. Sci. Tech. 1995, 6, 230–237. [Google Scholar]
- Chen, J.; Dong, H. Generalized physical model of tracer dilution for measuring seepage velocity in well. J. Hydraul. Eng. 2002, 9, 100–107. [Google Scholar]
- Brouyere, S.; Batlle-Aguilar, J.; Goderniaux, P.; Dassargues, A. A New Tracer Technique for Monitoring Groundwater Fluxes: The Finite Volume Point Dilution Method. J. Contam. Hydrol. 2008, 95, 121–140. [Google Scholar] [CrossRef] [PubMed]
- Piqueras, J.A.M.; Pérez, E.S.; Menéndez-Pidal, I. Water seepage beneath dams on soluble evaporite deposits: A laboratory and field study (Caspe Dam, Spain). Bull. Eng. Geol. Environ. 2001, 71, 201–213. [Google Scholar] [CrossRef]
- Ikard, B.S.J.; Revil, A.; Schmutz, M.; Karaoulis, M.; Jardani, A.; Mooney, M. Characterization of Focused Seepage through an Earthfill Dam Using Geoelectrical Methods. Ground Water 2014, 52, 952–965. [Google Scholar] [CrossRef] [PubMed]
- Wang, E.Z.; Yue, Z.Q.; Tham, L.G.; Tsui, Y.; Wang, H.T. A dual fracture model to simulate large-scale flow through fractured rocks. Can. Geotech. J. 2002, 39, 1302–1312. [Google Scholar] [CrossRef]
- Seely, A.J.; Macklem, P.T. Complex systems and the technology of variability analysis. Crit. Care 2005, 8, 367–384. [Google Scholar] [CrossRef] [PubMed]
- Singh, V.P.; Rajagopal, A.K.; Singh, K. Derivation of some frequency distributions using the principle of maximum entropy (POME). Adv. Water Resour. 1986, 9, 91–106. [Google Scholar] [CrossRef]
- Singh, V.P.; Rajagopal, A.K.; Singh, V.P. Some recent advances in the application of the principle of maximum entropy (POME) in hydrology. IAHS Publ. 1987, 164, 353–364. [Google Scholar]
- Singh, V.P.; Fiorentino, M. Entropy and Energy Dissipation in Water Resources; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1992. [Google Scholar]
- Singh, V.P. Entropy-Based Parameter Estimation in Hydrology. J. Environ. Qual. 2000, 29, 1019–1020. [Google Scholar]
- Chiu, C. Entropy and probability concepts in hydraulics. J. Hydraul. Eng. 1987, 113, 583–599. [Google Scholar] [CrossRef]
- Chiu, C. Entropy and 2-D velocity distribution in open channels. J. Hydraul. Eng. 1988, 114, 738–756. [Google Scholar] [CrossRef]
- Chiu, C. Velocity Distribution in Open Channel Flow. J. Hydraul. Eng. 1989, 115, 576–594. [Google Scholar] [CrossRef]
- Chiu, C. Application of Entropy Concept in Open-channel Flow Study. J. Hydraul. Eng. 1991, 117, 615–628. [Google Scholar] [CrossRef]
- Marini, G.; De Martino, G.; Fontana, N.; Fiorentino, M.; Singh, V.P. Entropy approach for 2D velocity distribution in open-channel flow. J Hydraul. Res. 2011, 49, 784–790. [Google Scholar] [CrossRef]
- Greco, M.; Mirauda, D. Entropy Parameter Estimation in Large-Scale Roughness Open Channel. J. Hydrol. Eng. 2015, 20. [Google Scholar] [CrossRef]
- Sato, A.H. Application of spectral methods for high-frequency financial data to quantifying states of market participants. Physica A 2007, 387, 3960–3966. [Google Scholar] [CrossRef]
- Masoumi, F.; Kerachian, R. Assessment of the groundwater salinity monitoring network of the Tehran region: Application of the discrete entropy theory. Water Sci. Technol. 2008, 58, 765–771. [Google Scholar] [CrossRef] [PubMed]
- Nicolae, A.; Nicolae, M.; Predescu, C.; Sohaciu, M.G. Theoretical analysis of the economy-ecology-environment system. Environ. Eng. Manag. J. 2009, 8, 453–456. [Google Scholar]
- Karamanos, K. Characterizing Cantorian sets by entropy-like quantities. Kybernetes 2009, 38, 1025–1032. [Google Scholar] [CrossRef]
- Herrmann, K. Non-extensitivity vs. informative moments for financial models—A unifying framework and empirical results. Europhys. Lett. 2009, 88, 30007. [Google Scholar] [CrossRef]
- Karamouz, M.; Nokhandan, A.K.; Kerachian, R.; Maksimovic, Č. Design of on-line river water quality monitoring systems using the entropy theory: A case study. Environ. Monit. Assess. 2009, 155, 63–81. [Google Scholar] [CrossRef] [PubMed]
- Singh, V.P. Entropy theory for derivation of infiltration equations. Water Resour. Res. 2010, 46, 374–381. [Google Scholar] [CrossRef]
- Mondal, N.C.; Singh, V.P. Entropy-based approach for estimation of natural recharge in Kodaganar River basin, Tamil Nadu, India. Curr. Sci. India 2010, 99, 1560–1569. [Google Scholar]
- Shannon, C.E. A mathematical theory of communications. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Shannon, C.E.; Wyner, A.D. Claude Elwood Shannon: Collected Papers; Wiley: New York, NY, USA, 1993; pp. 127–128. [Google Scholar]
- Soofi, E.S. Generalized Entropy-Based Weights for Multiattribute Value Models. Oper. Res. 1990, 38, 362–363. [Google Scholar] [CrossRef]
- Jaynes, E.T. Information Theory and Statistical Mechanics. Phys. Rev. 1957, 106, 620–630. [Google Scholar] [CrossRef]
- Levine, R.D.; Tribus, M. The Maximum Entropy Formalism; MIT Press: Cambridge, MA, USA, 1979. [Google Scholar]
- Shore, J.; Johnson, R. Axiomatic derivation of the principle of maximum entropy and the principle of minimum cross-entropy. IEEE Trans. Inform. Theory 1980, 26, 26–37. [Google Scholar] [CrossRef]
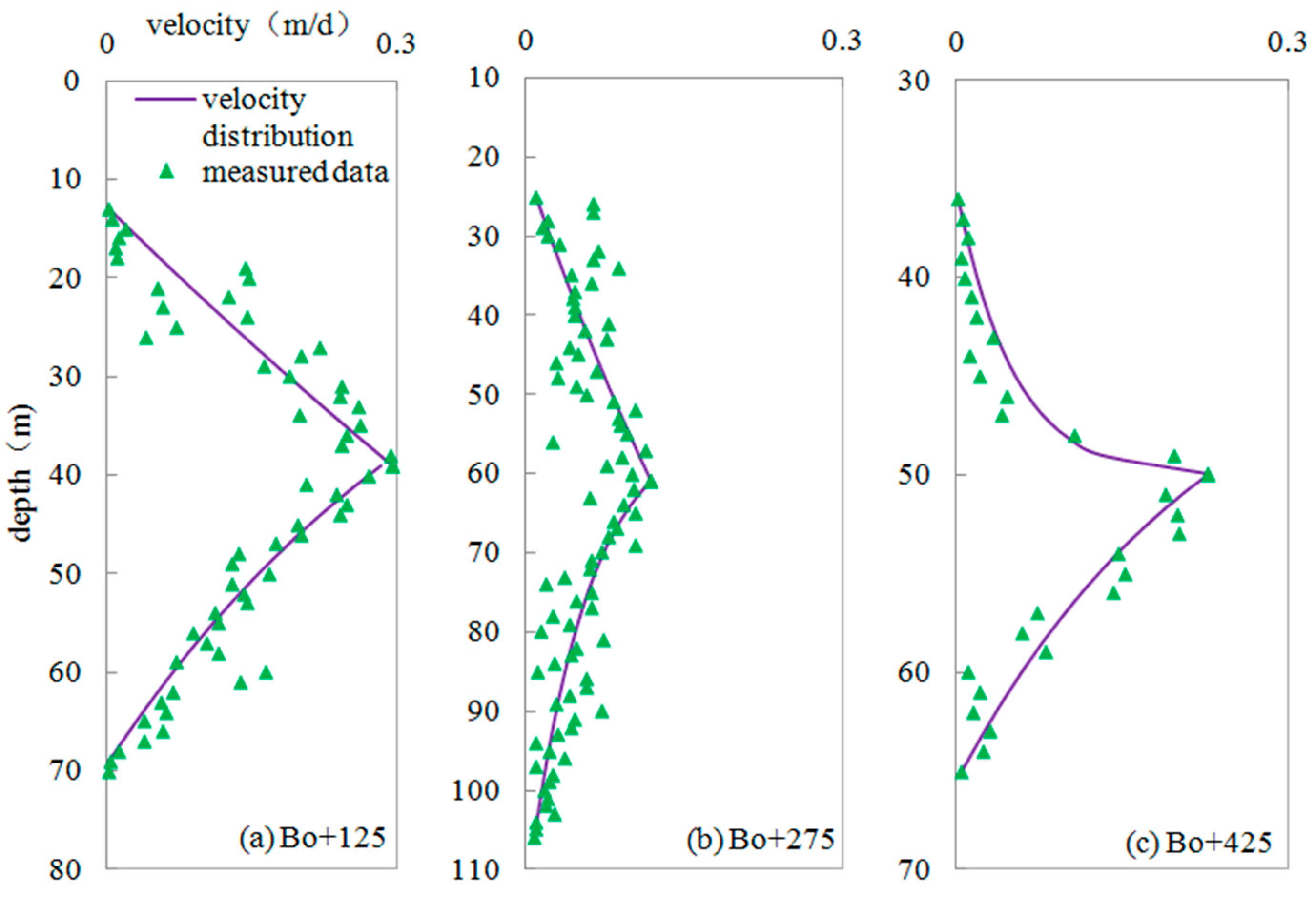
| Borehole | Bo+125UP | Bo+125LP | Bo+275UP | Bo+275LP | Bo+425UP | Bo+425LP |
|---|---|---|---|---|---|---|
| 26 | 31 | 36 | 45 | 15 | 14 | |
| 0.0018 | 0.0016 | 0.0096 | 0.0089 | 0.0040 | 0.0018 | |
| 0.2955 | 0.2955 | 0.1189 | 0.1189 | 0.2275 | 0.2275 | |
| 0.1444 | 0.1306 | 0.0613 | 0.0471 | 0.0986 | 0.0497 | |
| 0.3072 | 2.5700 | 3.3083 | 4.0258 | 4.0021 | 2.9249 | |
| −0.5915 | −2.5147 | −2.9000 | −17.7206 | −19.7375 | −4.1805 | |
| −0.1748 | −0.7431 | −0.3448 | −2.1069 | −4.4909 | −0.9512 | |
| −1.2175 | −1.2379 | −2.0618 | −2.1668 | −2.0181 | −1.5003 | |
| MR | 0.0327 | 0.0201 | 0.0185 | 0.0125 | 0.0162 | 0.0183 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, X.; Chen, J.; Wang, T.; Zhou, H.; Liu, L. Characterization of Seepage Velocity beneath a Complex Rock Mass Dam Based on Entropy Theory. Entropy 2016, 18, 293. https://doi.org/10.3390/e18080293
Chen X, Chen J, Wang T, Zhou H, Liu L. Characterization of Seepage Velocity beneath a Complex Rock Mass Dam Based on Entropy Theory. Entropy. 2016; 18(8):293. https://doi.org/10.3390/e18080293
Chicago/Turabian StyleChen, Xixi, Jiansheng Chen, Tao Wang, Huaidong Zhou, and Linghua Liu. 2016. "Characterization of Seepage Velocity beneath a Complex Rock Mass Dam Based on Entropy Theory" Entropy 18, no. 8: 293. https://doi.org/10.3390/e18080293
APA StyleChen, X., Chen, J., Wang, T., Zhou, H., & Liu, L. (2016). Characterization of Seepage Velocity beneath a Complex Rock Mass Dam Based on Entropy Theory. Entropy, 18(8), 293. https://doi.org/10.3390/e18080293