The Logical Consistency of Simultaneous Agnostic Hypothesis Tests
Abstract
:1. Introduction
- Monotonicity: if A implies B, then a test that does not reject A should not reject B.
- Invertibility: A test should reject A if and only if it does not reject not-A.
- Union consonance: If a test rejects A and B, then it should reject .
- Intersection consonance: If a test does not reject A and does not reject B, then it should not reject .
2. Agnostic Testing Schemes
3. Coherence Properties
3.1. Monotonicity
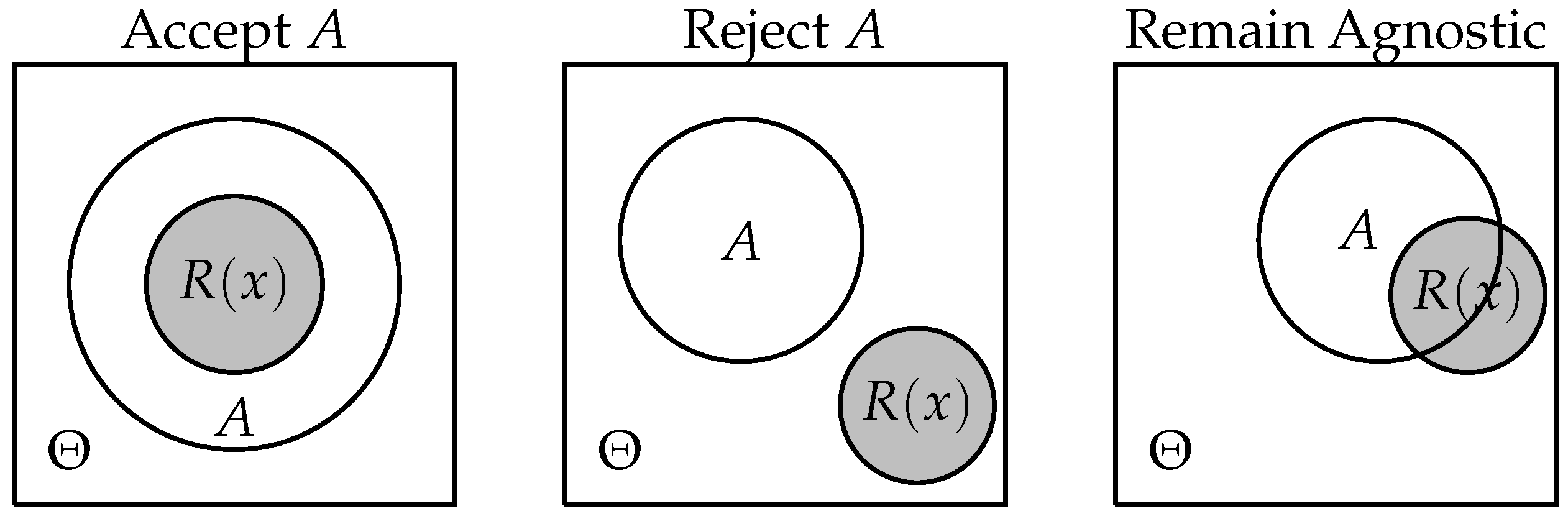
- if accepts A, then it also accepts B.
- if remains agnostic about A, then it either remains agnostic about B or accepts B.
3.2. Union Consonance
3.3. Intersection Consonance
3.4. Invertibility
4. Satisfying All Properties
4.1. Weak Desiderata
- 1.
- Monotonicity for every prior distribution if, and only if, for every with and
- 2.
- Weak union consonance for every prior distribution if, and only if, for every such that ,
- 3.
- Weak intersection consonance for every prior distribution if, and only if, for every such that ,
- 4.
- Invertibility for every prior distribution if, and only if, for every ,
4.2. Strong Desiderata
4.3. n-Weak Desiderata
5. Decision-Theoretic Perspective
5.1. Monotonicity
5.2. Union Consonance
5.3. Intersection Consonance
5.4. Invertibility
6. Final Remarks
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
- .
- .
- If for every with and , then for every , , and . It follows that monotonicity holds.
- If for every such that , , then for every , and implies that . It follows that union consonance holds.
- If for every such that , , then for every , and implies that . It follows that intersection consonance holds.
- If for every , , then for every , if, and only if, . Similarly, if, and only if, . It follows that invertibility holds.
- If , then .
- If , then .
References
- Wiener, Y.; El-Yaniv, R. Agnostic selective classification. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 2011; pp. 1665–1673. [Google Scholar]
- Balsubramani, A. Learning to abstain from binary prediction. 2016; arXiv:1602.08151. [Google Scholar]
- Izbicki, R.; Esteves, L.G. Logical consistency in simultaneous statistical test procedures. Logic J. IGPL 2015, 23, 732–758. [Google Scholar] [CrossRef]
- Finner, H.; Strassburger, K. The partitioning principle: A powerful tool in multiple decision theory. Ann. Stat. 2002, 30, 1194–1213. [Google Scholar] [CrossRef]
- Sonnemann, E. General solutions to multiple testing problems. Biom. J. 2008, 50, 641–656. [Google Scholar] [CrossRef] [PubMed]
- Patriota, A.G. S-value: An alternative measure of evidence for testing general null hypotheses. Cienc. Nat. 2014, 36, 14–22. [Google Scholar]
- Da Silva, G.M.; Esteves, L.G.; Fossaluza, V.; Izbicki, R.; Wechsler, S. A bayesian decision-theoretic approach to logically-consistent hypothesis testing. Entropy 2015, 17, 6534–6559. [Google Scholar] [CrossRef]
- Berg, N. No-decision classification: An alternative to testing for statistical significance. J. Socio-Econ. 2004, 33, 631–650. [Google Scholar] [CrossRef]
- Babb, J.; Rogatko, A.; Zacks, S. Bayesian sequential and fixed sample testing of multihypothesis. In Asymptotic Methods in Probability and Statistics; Elsevier: Amsterdam, The Netherlands, 1998; pp. 801–809. [Google Scholar]
- Ripley, B.D. Pattern Recognition and Neural Networks; Cambridge University Press: Cambridge, UK, 1996. [Google Scholar]
- De Bragança Pereira, C.A.; Stern, J.M. Evidence and credibility: Full bayesian significance test for precise hypotheses. Entropy 1999, 1, 99–110. [Google Scholar] [CrossRef]
- Berger, J.O.; Delampady, M. Testing precise hypotheses. Stat. Sci. 1987, 2, 317–335. [Google Scholar] [CrossRef]
- Benjamini, Y.; Hochberg, Y. Controlling the false discovery rate: A practical and powerful approach to multiple testing. J. R. Stat. Soc. 1995, 57, 289–300. [Google Scholar]
- Jaynes, E.T. Confidence intervals vs. Bayesian intervals. In Foundations of Probability Theory, Statistical Inference, and Statistical Theories of Science; Springer: Dodrecht, The Netherlands, 1976. [Google Scholar]
- Gabriel, K.R. Simultaneous test procedures—Some theory of multiple comparisons. Ann. Math. Stat. 1969, 41, 224–250. [Google Scholar] [CrossRef]
- Fossaluza, V.; Izbicki, R.; da Silva, G.M.; Esteves, L.G. Coherent hypothesis testing. Am. Stat. 2016. submitted for publication. [Google Scholar]
- Sonnemann, E.; Finner, H. Vollständigkeitssätze für multiple testprobleme. In Multiple Hypothesenprüfung; Bauer, P., Hommel, G., Sonnemann, E., Eds.; Springer: Berlin, Germany, 1988; pp. 121–135. (In German) [Google Scholar]
- Lavine, M.; Schervish, M. Bayes factors: What they are and what they are not. Am. Stat. 1999, 53, 119–122. [Google Scholar]
- Izbicki, R.; Fossaluza, V.; Hounie, A.G.; Nakano, E.Y.; Pereira, C.A.B. Testing allele homogeneity: The problem of nested hypotheses. BMC Genet. 2012, 13. [Google Scholar] [CrossRef] [PubMed]
- Schervish, M.J. p values: What they are and what they are not. Am. Stat. 1996, 50, 203–206. [Google Scholar] [CrossRef]
- Hochberg, Y.; Tamhane, A.C. Multiple Comparison Procedures; John Wiley & Sons: New York, NY, USA, 1987. [Google Scholar]
- Borges, W.; Stern, J.M. The rules of logic composition for the bayesian epistemic e-values. Logic J. IGPL 2007, 15, 401–420. [Google Scholar] [CrossRef]
- Johnson, R.A.; Wichern, D.W. Applied Multivariate Statistical Analysis, 6th ed.; Pearson: Upper Saddle River, NJ, USA, 2007. [Google Scholar]
- Schervish, M.J. Theory of Statistics; Springer: New York, NY, USA, 1997. [Google Scholar]
- Robert, C. The Bayesian Choice: From Decision-Theoretic Foundations to Computational Implementation, 2nd ed.; Springer: New York, NY, USA, 2007. [Google Scholar]
| Decision | State of Nature | |
|---|---|---|
| 0 (accept A) | 0 | |
| (remain agnostic about A) | ||
| 1 (reject A) | 0 | |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Esteves, L.G.; Izbicki, R.; Stern, J.M.; Stern, R.B. The Logical Consistency of Simultaneous Agnostic Hypothesis Tests. Entropy 2016, 18, 256. https://doi.org/10.3390/e18070256
Esteves LG, Izbicki R, Stern JM, Stern RB. The Logical Consistency of Simultaneous Agnostic Hypothesis Tests. Entropy. 2016; 18(7):256. https://doi.org/10.3390/e18070256
Chicago/Turabian StyleEsteves, Luís G., Rafael Izbicki, Julio M. Stern, and Rafael B. Stern. 2016. "The Logical Consistency of Simultaneous Agnostic Hypothesis Tests" Entropy 18, no. 7: 256. https://doi.org/10.3390/e18070256
APA StyleEsteves, L. G., Izbicki, R., Stern, J. M., & Stern, R. B. (2016). The Logical Consistency of Simultaneous Agnostic Hypothesis Tests. Entropy, 18(7), 256. https://doi.org/10.3390/e18070256