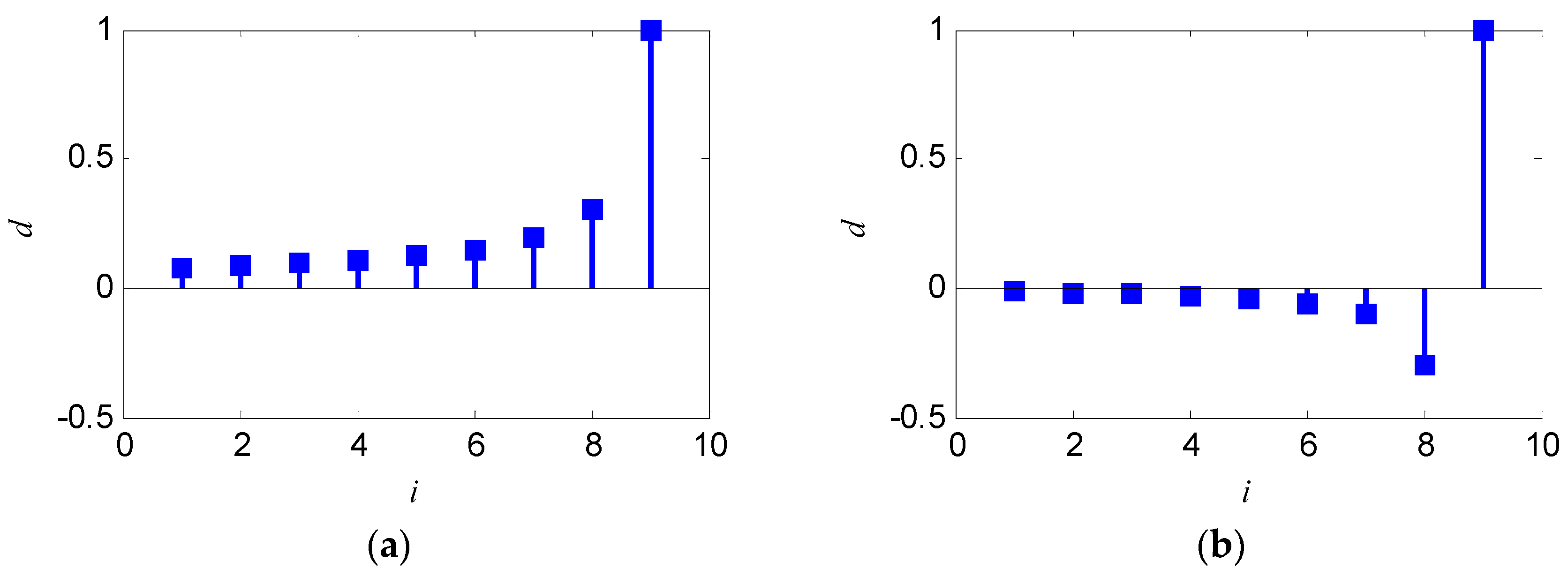1. Introduction
Non-equidistant sequences, whose sampling times are taken to be not equally spaced, exist widely in many applications due to missing data, event-triggered phenomena, imperfect sensors and clocks [
1]. Especially, compressive sensing theory and random sampling techniques [
2,
3] have been developed so that a number of applications use the non-uniform sampling inherently or by choice. It is important to predict the development of processes and systems based on non-equidistant sequences.
Grey prediction method is an effective tool for handling an uncertain system with limited data and partially-known information [
4,
5]. It has been widely applied to various fields with better predicting accuracy, including natural science, mechanical engineering, and economic fields. NGM(1,1), the non-equidistant grey model with first-order differential equation and a single variable, is the most commonly-used grey prediction model for non-equidistant sequences. In order to improve its predicting accuracy, matrix analysis [
6], trend and potency tracking method [
7], and the exponential trait [
8] were employed to reconstruct background values of NGM(1,1). The reciprocal [
9] and class ratio [
10] of the original sequence was also modeled with NGM(1,1). The accumulated method [
11], Euler formula [
12], and Taylor approximation method [
13] were used to estimate parameters of NGM(1,1). Moreover, non-equidistant grey Verhulst model [
14], non-equidistant DGM(2,1) [
15], and non-equidistant grey power model [
16] have been proposed for non-equidistant sequences. In the above grey models, original sequences are mostly transformed into accumulated sequences based on the first-order accumulated generating operation (1-AGO). However, these accumulated data do not always follow the grey exponential law completely, so the existing grey model cannot accurately predict for many actual systems.
With the development of fractional calculus, it has been demonstrated that calculus equations with the non-integer/fractional order can describe dynamical behavior of processes and systems with high accuracy and concise models in various fields [
17,
18,
19]. According to the definition of fractional calculus, Wu [
20] proposed the fractional-order accumulated generating operation (
r-AGO), which extended the first or positive integer-order into the positive fractional one. Various grey models with the fractional order accumulation, such as the fractional-order time-lag grey model [
21], reverse accumulative grey model [
22], grey discrete power model [
23], and non-homogenous discrete grey model [
24], were proposed to improve the predicting accuracy in some fields. Mao [
25] developed another fractional grey model, which was an extension of the basic grey model in that first-order differential equations were transformed into fractional differential equations. Meng [
26] derived the analytical expression of the fractional order reducing generation operator and verified that this operator satisfied the commutative and exponential law. However, these fractional-order grey models are still based on equidistant sequences. More deviations could be yielded if they are used directly to non-equidistant sequences.
A novel fractional-order non-equidistant accumulated generating operation (r-NAGO) is proposed for the non-equidistant sequence in this paper, and the accumulated order is extended to the negative fraction in order to improve the exponential law of the accumulated sequence. Thus, a new grey prediction method (r-NGM(1,1)) is developed based on r-NAGO and the basic grey model GM(1,1) to enhance the predicting accuracy for the non-equidistant sequence. Some practical cases are employed to compare the predicting accuracy of the proposed r-NGM(1,1) with the traditional non-equidistant grey model (NGM(1,1)).
The work procedure is shown as follows.
Section 2 reviews the basic theories about
r-AGO and NGM(1,1). Then,
r-NAGO and
r-NGM(1,1) for the non-equidistant sequence is developed in
Section 3. Moreover, three practical cases are illustrated to validate the proposed
r-NGM(1,1) in
Section 4.
Section 5 analyzes further its applicability and sampled intervals. Finally, conclusions and future works are presented in
Section 6.
2. Basic Theories
A grey system is one in that some information is known and some unknown [
4,
5]. In actual applications, many systems can be considered as grey systems because there are always some uncertainties. The partially-known information contains a certain governing relation, though it is too complex or chaotic. The main task of grey system theory is to extract the realistic governing relation of the system from the partially known data. The accumulated generating operation usually smoothes the randomness of the original sequence. Then grey model is used to describe the inherent functional relations with differential equations. GM(1,1), a grey model with a first-order differential equation and a single variable, is the most commonly-used grey prediction model. The estimated sequence is calculated by the grey model and the original sequence can be reverted to describe systemic behavior using an inverse accumulated generating operation. Grey system theory has become an effective method to solve uncertainty systems with less sample size and poor information.
2.1. r-AGO
Assuming that
is the original nonnegative sequence, when the first-order accumulated generating operation (1-AGO) is applied on
, its first-order accumulated sequence
could be obtained as:
Equation (1) can be expressed with the matrix as:
where
D is the first-order accumulated matrix:
So the
k-th value in
is:
The corresponding second-order and
M-order accumulated sequences are:
The
M-order accumulated matrix
is equal to the
M-th power of
D when
M is the positive integer. Their values in
can be written as:
Thus, the
k-th accumulated data in
is:
Wu [
14] extended the positive integer-order accumulated generating operation into any positive fractional one based on the concepts of fractional calculus. Thus, the fractional-order accumulated sequence
can be written as:
where
r is the accumulated order. It can be called as the fractional order when
r is set as the fractional number. According to Equation (7),
can be obtained as the follows when
:
Based on the Gamma function
[
26],
can be written as:
where
r is the positive fraction and integer,
. More precisely, it can be obtained that
and
when
, so
, and
when
according to Equation (11).
Then the
k-th accumulated data in
is:
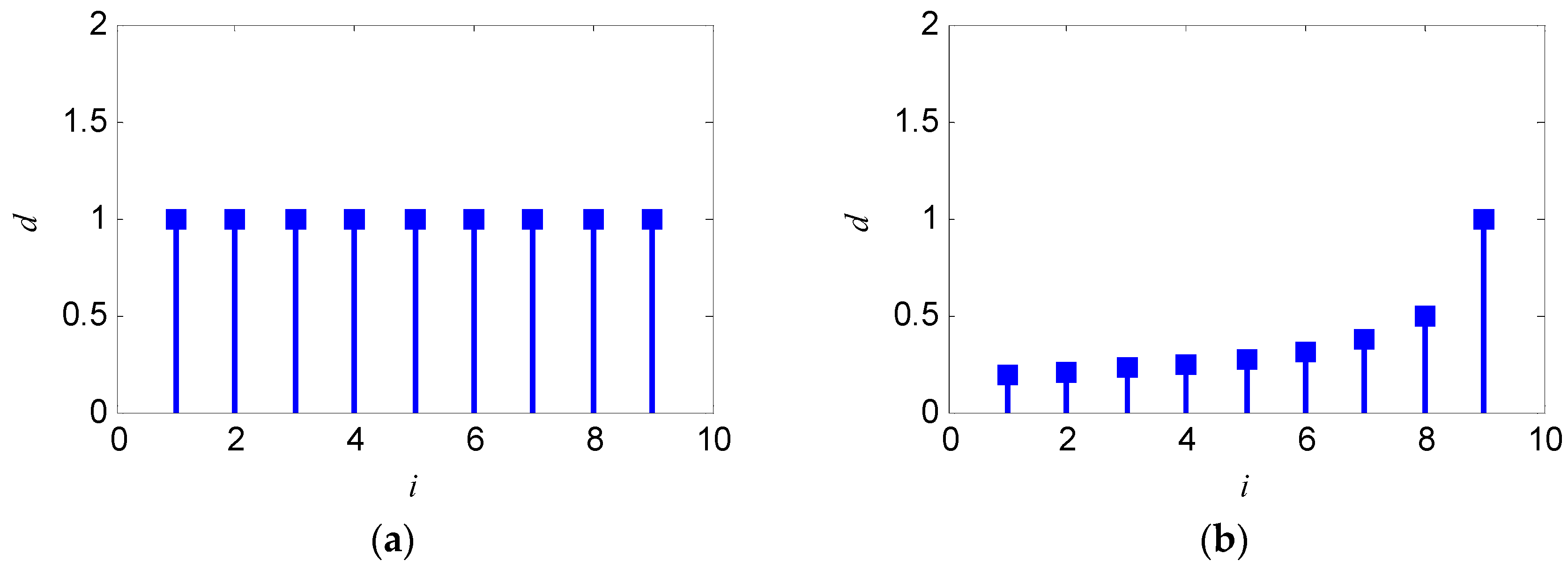
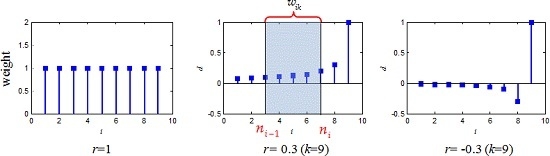
Equation (12) is equal to Equation (4) when r = 1. The original sequence is accumulated to construct in the weighted form according to Equation (12). Decreasing r can reduce the weight of previous data and put more emphasis on new data, and the weight of the i-th original data varied with k in the k-th accumulated data .
2.2. The Traditional NGM(1,1)
Assume that is the original sequence, where denotes the datum at time . If all time intervals, (k = 2, 3, …, m), are not equal to the constant, is called the non-equidistant sequence.
Based on the first-order non-equidistant accumulated generating operation (1-NAGO) [
8], its corresponding accumulated sequence
can be obtained:
The grey differential equation of NGM(1,1) and its whitening equation is defined, respectively:
where
is the background value,
a and
b are parameters that can be estimated using the least square method:
with:
Then the solution of Equation (15) at time
is:
The estimated sequence
of the original sequence
can be obtained using the first-order inverse accumulated generating operation [
8]:
where
.
4. Computational Cases
Three practical cases are employed to test the accuracy of the proposed r-NGM(1,1) compared with the traditional NGM(1,1). These non-equidistant sequences are monotonic decreasing, monotonic inceasing, and oscillating, respectively. The maximum iteration is set as 200, the threshold of the gradient is 10−6, and the factor of is 0.1 in the optimization of the fractional order.
4.1. Case 1
Data comes from [
8], which are the experimental data on the fatigue strength (σ
−1, MPa) of titanium alloy with different temperatures (
Te, °C) under the action of a symmetrical cyclic load, shown in
Table 1. It is the monotonic decreasing non-equidistant sequence. All data are used to construct different grey models. The sampling interval is set as
T = 10 in
r-NGM(1,1). Actual and estimated values of several grey models are presented in
Table 1 and
Table 2.
When the fractional order is limited to be positive, 0.995 is the best accumulated order, which means that 0.995-NGM(1,1) yields the lowest RMSE and APD for this case. When the fractional order is not limited, −0.017-NGM(1,1) provides better performance with APD of 0.22% and RMSE of 1.55, which indicates the reasonable modeling accuracy.
Some modified methods of the traditional NGM(1,1) were proposed to model the fatigue strength data [
8,
9,
29]. The exponential trait and integral [
8] was employed to determine the background value so that APD and RMSE were 0.37% and 2.67. Zou [
9] put forward the NGM(1,1) based on the reciprocal accumulated generating operation, whose APD and RMSE were 2.34 and 0.35%, respectively. The step-by-step optimum new information method [
29] was used to establish NGM(1,1). In this circumstance, its RMSE and APD were 3.31 and 0.55%.
It can be seen that APD obtained using −0.007-NGM(1,1) is less than the traditional NGM(1,1) and three modified NGM(1,1) models [
8,
9,
29]. The proposed
r-NGM(1,1) could give an appropriate modeling accuracy for the increasing non-equidistant sequence.
4.2. Case 2
The original sequence is from [
30], which is a monotonic increasing non-equidistant sequence. Four data are used to construct different grey models and the fifth datum is predicted. The sampling interval is set as
T = 1 in
r-NGM(1,1),
i.e.,
The background value of the traditional NGM(1,1) is the mean of two adjacent accumulated data,
i.e.,
, while the background value of NGM(1,1) in [
30] is set as the accumulated values,
i.e.,
. Results of different non-equidistant grey models are listed in
Table 3 and
Table 4.
As can be seen from
Table 4, the optimal accumulated order is 0.93 in
r-NGM(1,1) when
r > 0. The modeling RMSE and APD of 0.93-NGM(1,1) are 0.001 and 0.068% less than that of the traditional NGM(1,1). When
r is not limited, the modeling and predicting errors of the −0.13-NGM(1,1) are lowest among these grey models. It gives better performance compared with other grey models. The proposed
r-NGM(1,1) could provide the satisfactory modeling and predicting accuracy for the increasing non-equidistant sequences.
4.3. Case 3
The original sequence is collected from [
31], which is the strapdown inertial measurement unit. It is an oscillating non-equidistant sequence. Nine data are used to construct different grey models and the tenth datum is predicted. The sampling interval is set as
T = 1 in
r-NGM(1,1). The modeling and predicting values of different grey models are presented in
Table 5 and
Table 6.
The optimal accumulated order is 1.01 in r-NGM(1,1) when r is limited to the positive numbers, whose predicting APD and RMSE are 0.38% and 0.008, respectively. −0.01-NGM(1,1) is the best modeling and predicting performance without restriction of the fractional order. Its predicting APD and RMSE are 0.20% and 0.004.
Moreover, the non-equidistant sequence is adjusted to equidistant one by means of cubic spline interpolation and built the grey model GM(1,1) in [
31]. The predicting value of the tenth datum was 2.179121, whose relative error was 0.5% higher than that of −0.01-NGM(1,1) and 1.01-NGM(1,1). The proposed
r-NGM(1,1) can greatly improve the modeling and predicting accuracy of non-equidistant sequences.
5. Discussion
5.1. Applicability of the Proposed Method
The proposed r-NGM(1,1) in this paper is based on the non-equidistant accumulated generating operation and the basic grey model, GM(1,1), thus, its suitable range and condition is the same as GM(1,1). Firstly the number of the original sequence is more than four in r-NGM(1,1). The second condition is that the r-NGM(1,1) can only be used in positive sequences according to the condition of GM(1,1), but there exist some negative values in the actual applications, especially the accumulated values could be negative when the fractional order is negative. Thus, it is necessary to find a positive value, which is added to the sequence and used to convert into a non-negative sequence. Finally, the original and accumulated sequence should satisfy the quasi-smooth and quasi-exponential checking conditions in conducting the r-NGM(1,1). In case these sequences do not satisfy these conditions, another positive value is added to the sequence and the formed sequence can pass the checking conditions. How to select these two positive values needs to depend on the case analysis.
5.2. The Sampled Interval
The coefficients
, and
of
r-NGM(1,1) in Equation (34) are estimated according to the least square method, and the fractional order
r is optimized through the Levenberg–Marquardt algorithm in this paper. However, the sampled interval
T is given to meet the requirements that every value in a new time sequence is a positive integer according to Equation (19). Different sampled intervals are set to analyze their influences on the modeling and predicting performances of the
r-NGM(1,1). Results of three cases are listed in
Table 7 under different sampled intervals. Each set of parameters is run five times. The modeling and predicting performances are the most accurate result and the running time is the average one of the five-time runs.
APD and RMSE of the modeling and predicting data are very similar in three cases when the sampled intervals decrease from 10 to 0.01. The optimal fractional orders r are the same in Case 2 and Case 3, while they are different in Case 1, which shows that the sequence in Case 1 is more sensitive to the fractional order. Moreover, the maximal time and running time increase dramatically when the sampled interval decreases. The sampled intervals affect the modeling and predicting performance of r-NGM(1,1) less, so the main factor to select the sampled interval is the running time.
5.3. Comparison with Other Method
An artificial neural network (ANN) [
32] is employed to compare with the proposed
r-NGM(1,1) in this paper.
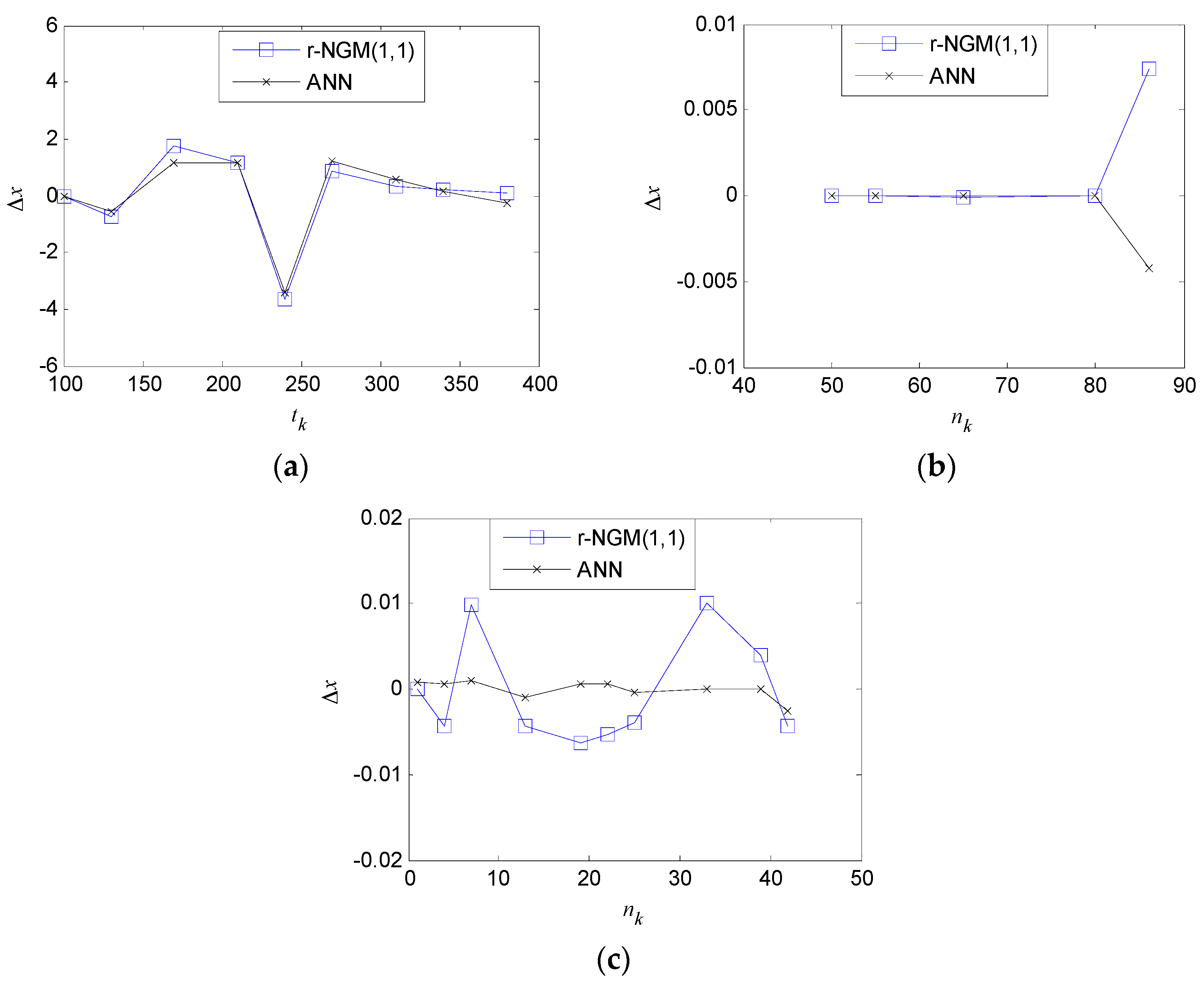
Figure 4 shows errors Δ
x between the original and estimated values obtained by two models, and their comparison results are listed in
Table 8. A three-layered ANN is used to predict the non-equidistant sequences, consisting of an input layer, hidden layer, and output layer. The number of neurons in the hidden layer is chosen empirically by adjusting the number of neurons until the effective number of parameters reaches a constant value.
As shown in
Figure 4 and
Table 8, the RMSE and APD of the ANN is smaller than one of the proposed
r-NGM(1,1), which indicates less deviation between the estimated and original values for the ANN. A greater number of neurons in the hidden layer in the ANN could provide more accurate prediction, but significantly increase the model complexity. The proposed grey model is simpler than the neural network under the same modeling and predicting performance. Compared with the ANN, the proposed
r-NGM(1,1) gives better performance with satisfactory accuracy and concise explicit models for non-equidistant sequences.
6. Conclusions and Future Work
A novel fractional-order non-equidistant grey model, r-NGM(1,1), is proposed to deal with the predicting problem of non-equidistant sequences. The fractional-order non-equidistant accumulated generating operation is developed to extend the application of grey models with fractional order accumulation. Some cases have been carried out to evaluate the proposed r-NGM(1,1) in comparison with the traditional NGM(1,1). Results show that the proposed r-NGM(1,1) remarkably increases the modeling and predicting accuracy of non-equidistant sequence.
The proposed r-NGM(1,1) is constructed through the partially-known information, so it is not more suitable for the systems with the distinct inherent mechanism, and it is difficult to obtain more accuracy for the long-term prediction due to the limitation of time effect. Moreover, the effectiveness of the proposed r-NGM(1,1) is only validated based on some practical cases in this paper. More cases and applications are employed to validate the modeling and predicting performance of r-NGM(1,1). It is important to give the theoretical analysis of r-NAGO and r-NGM(1,1), which will be carried out in the next work. The proposed r-NGM(1,1) in this paper is still based on first-order grey differential equations with r-AGO, so it is necessary to further discuss its relationship with the fractional-order grey differential equations with 1-AGO or fractional-order ones with r-AGO.
As a future work, optimal initial values and background values should be considered to further improve the modeling and predicting performance of r-NGM(1,1), and an effective optimization technique is developed to derive the global optimal solutions of the fractional order and coefficients in r-NGM(1,1) due to the nonlinear objective function shown in Equation (35). Meanwhile, the proposed r-NAGO is introduced into other non-equidistant grey models, such as the discrete grey model, grey Verhulst model, and grey power model.