Entropy Generation on Nanofluid Flow through a Horizontal Riga Plate
Abstract
:1. Introduction
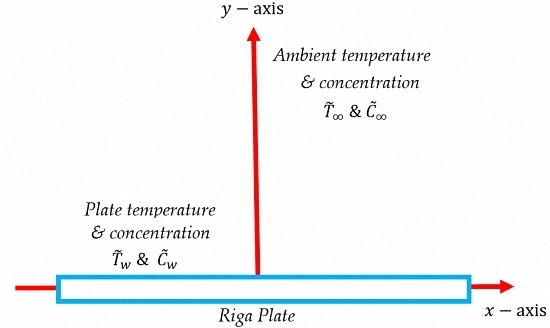
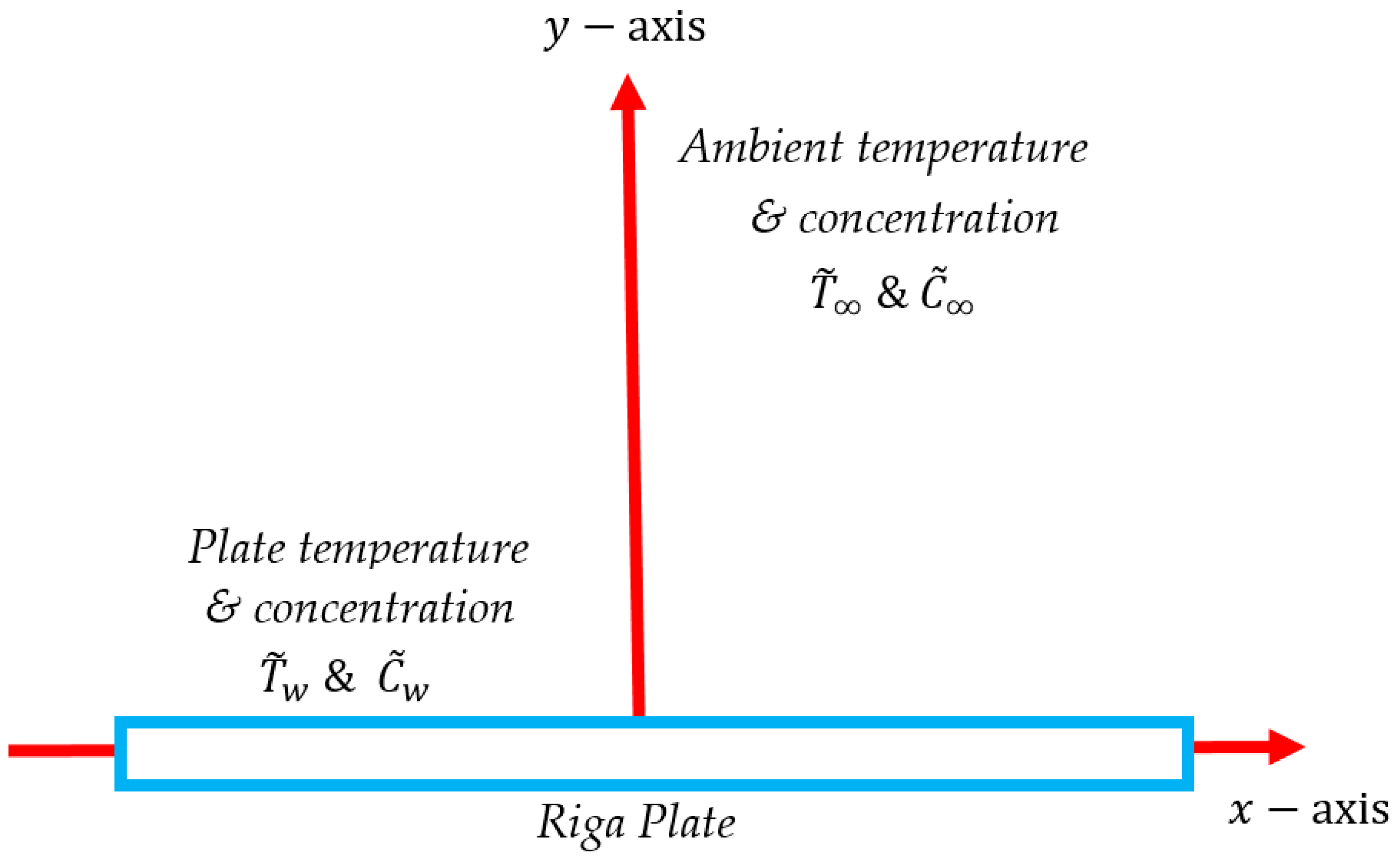
2. Mathematical Formulation
3. Entropy Generation Analysis
4. Numerical Method
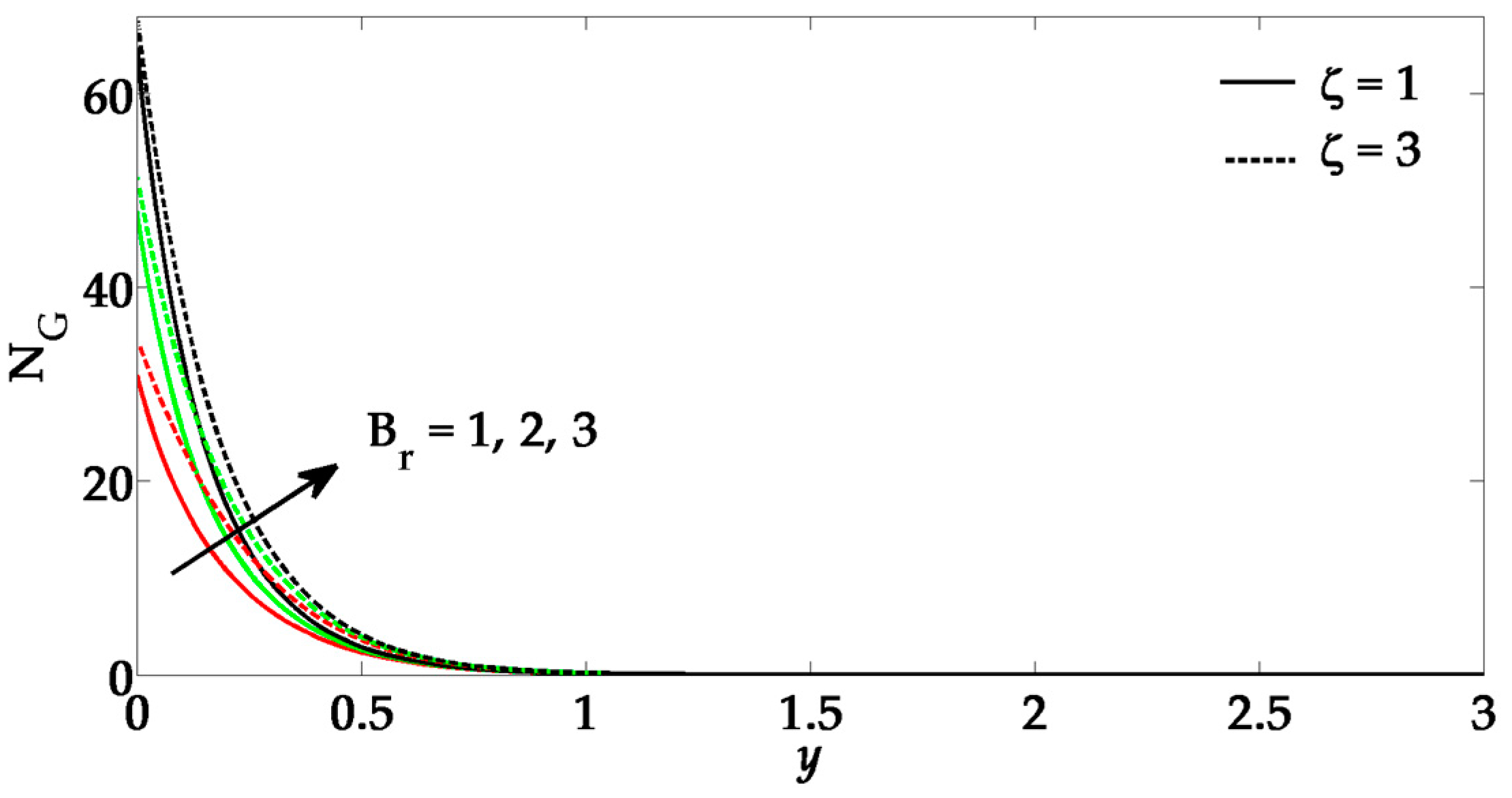
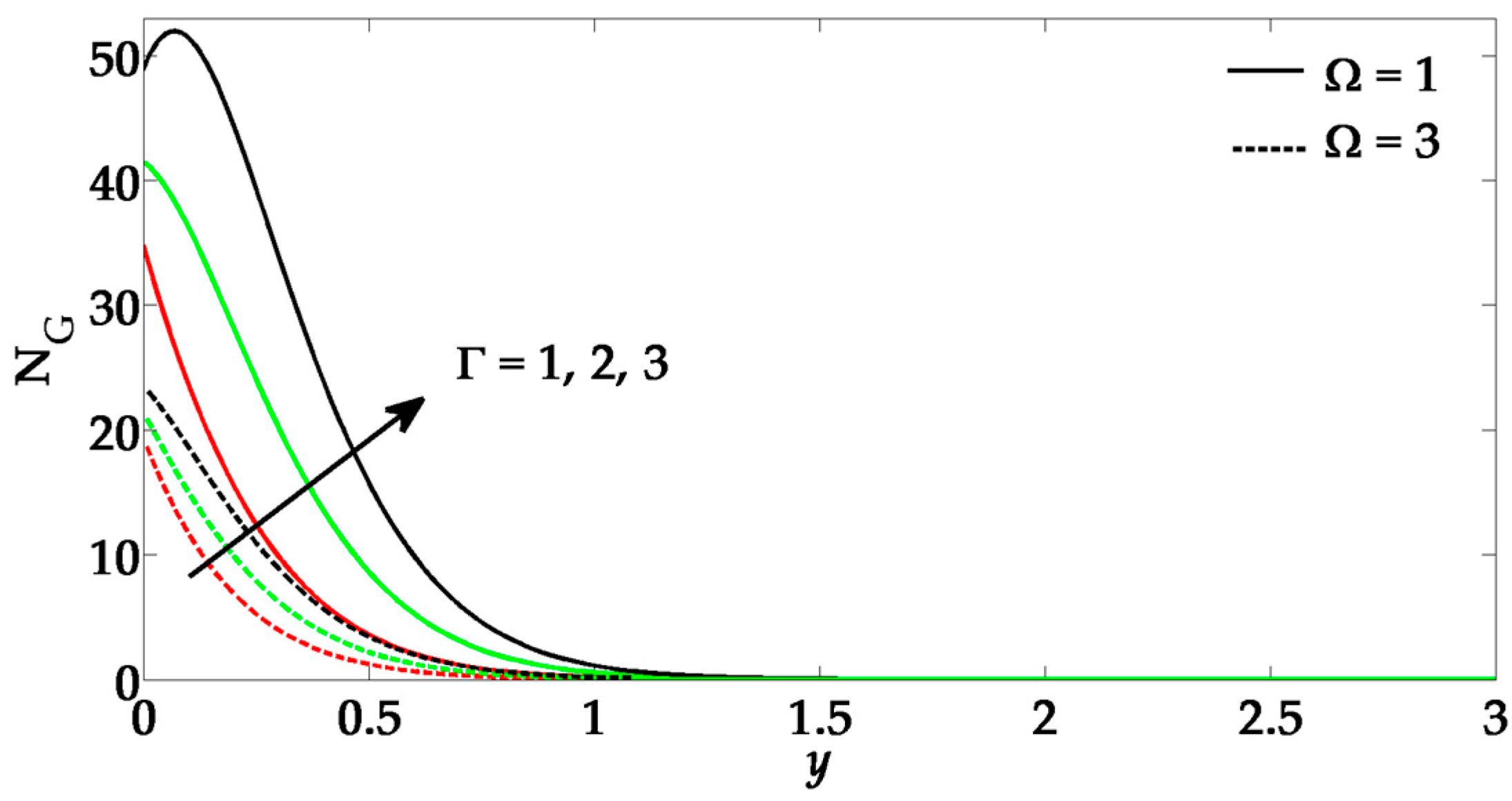
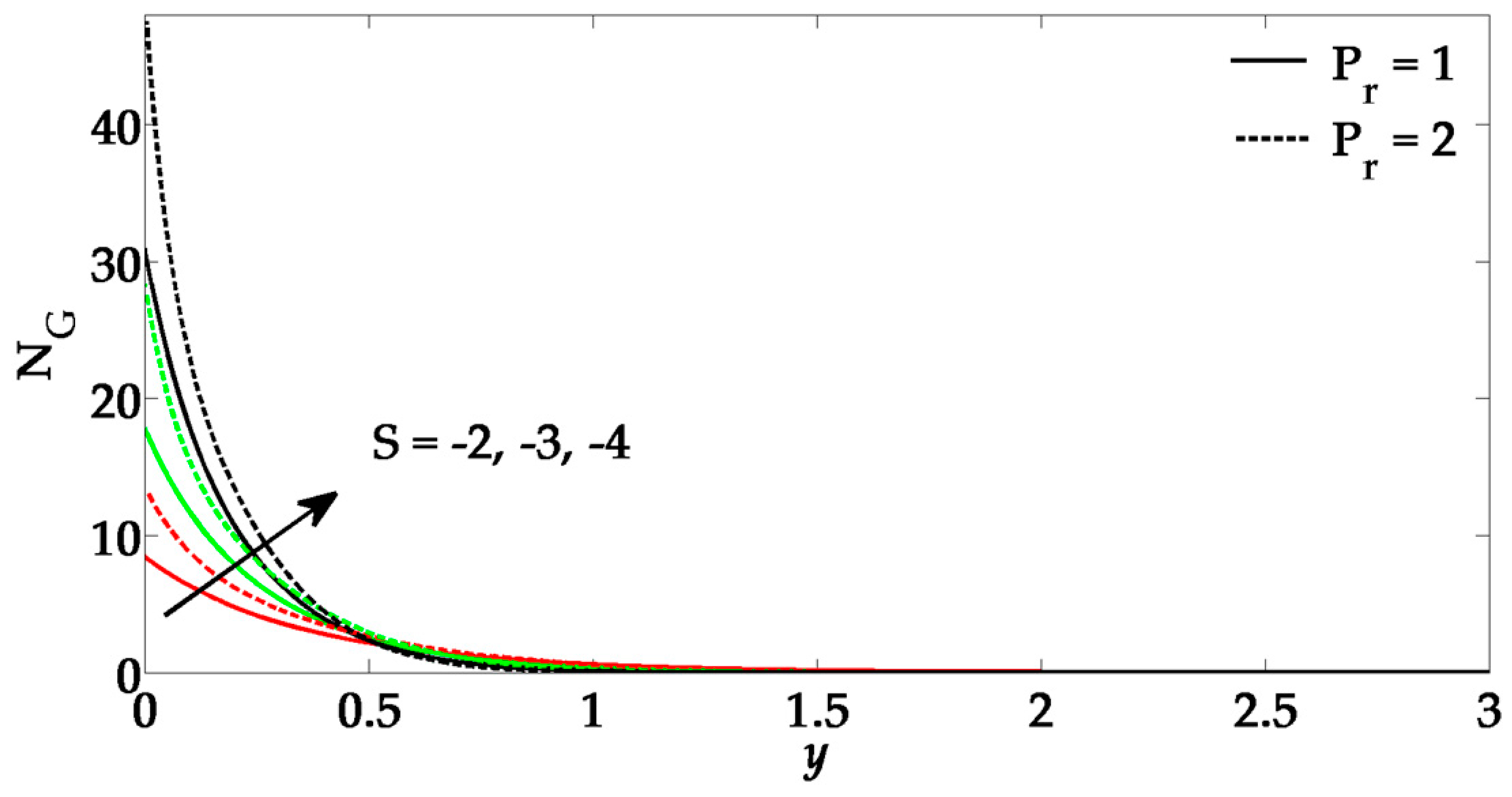
5. Numerical Results and Discussion
6. Conclusions
- (i)
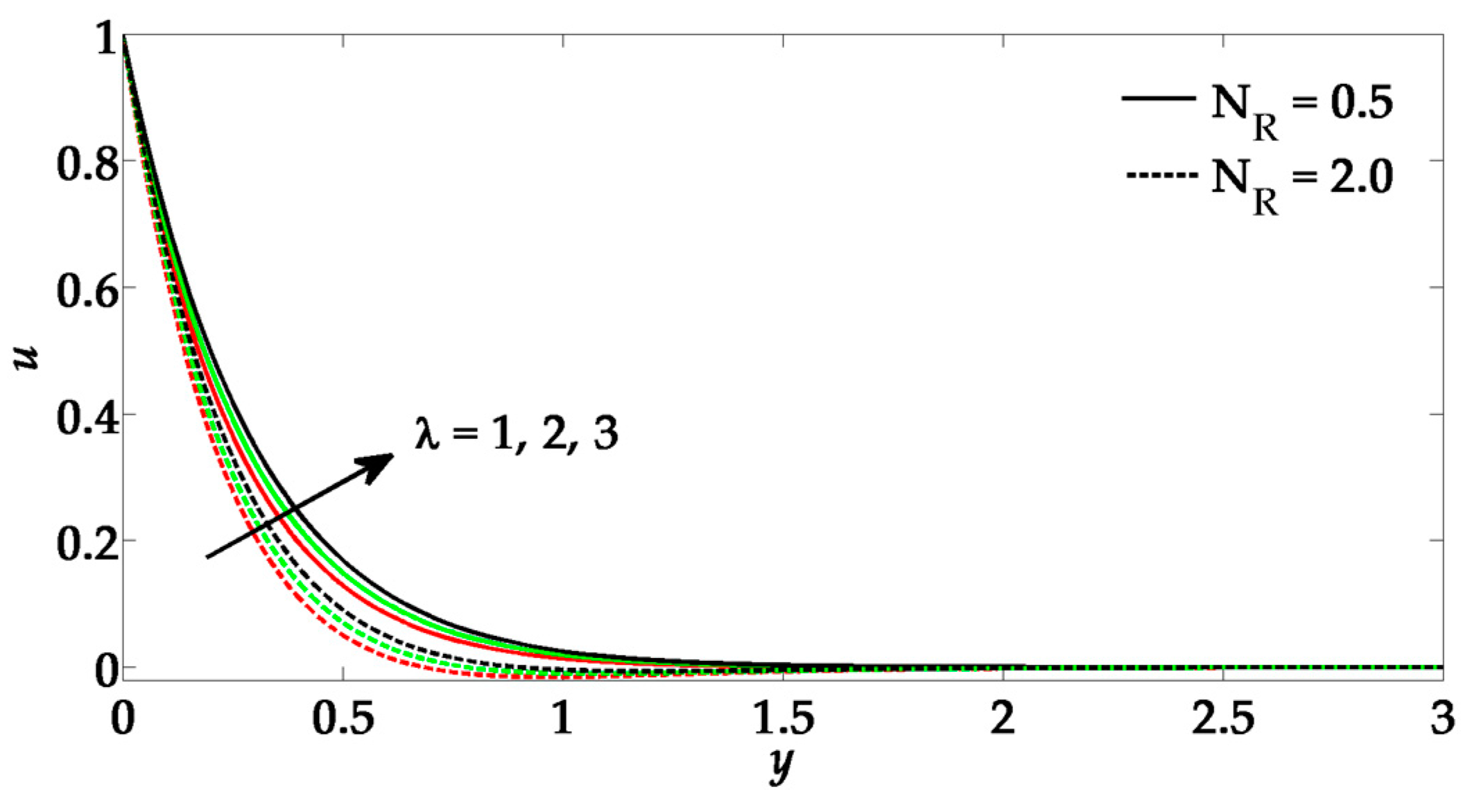
- The Richardson number enhances the velocity; however, nanoparticle flux parameter opposes the flow.
- (ii)
- By increasing Prandtl number, the velocity profile tends to rise.
- (iii)
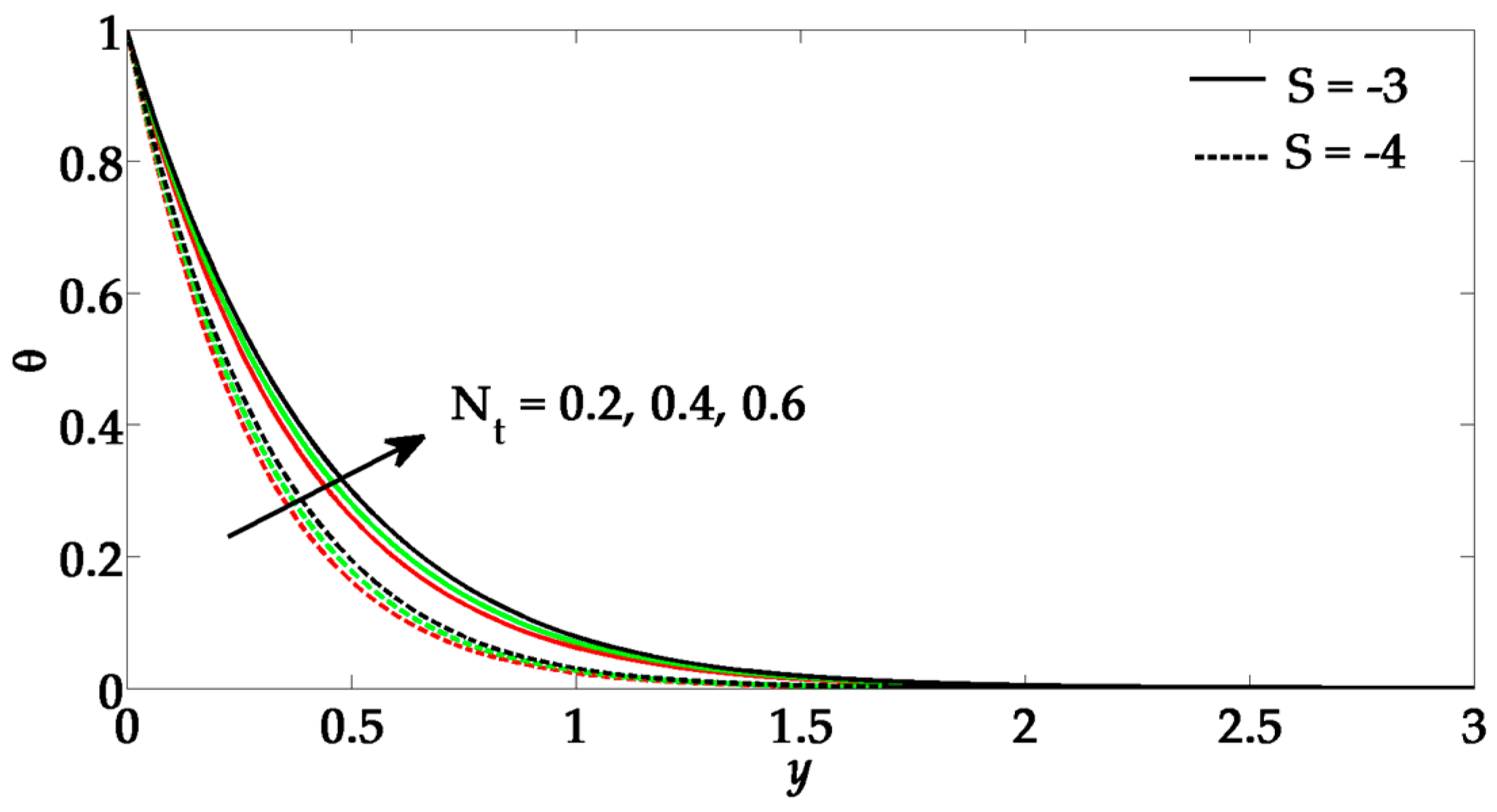
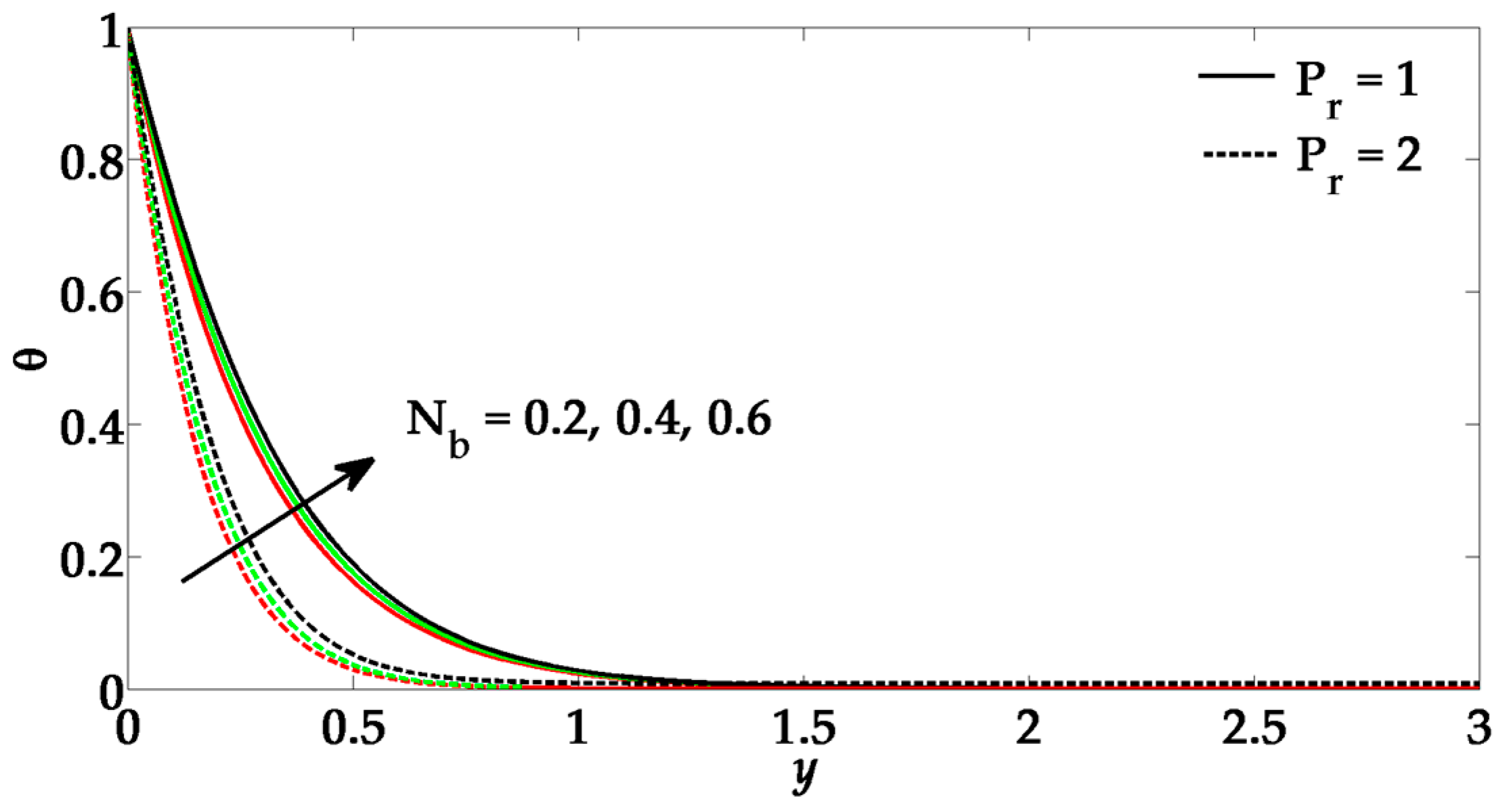
- The Brownian motion parameter and thermophoresis parameter also enhances the temperature profile and its boundary layer thickness.
- (iv)
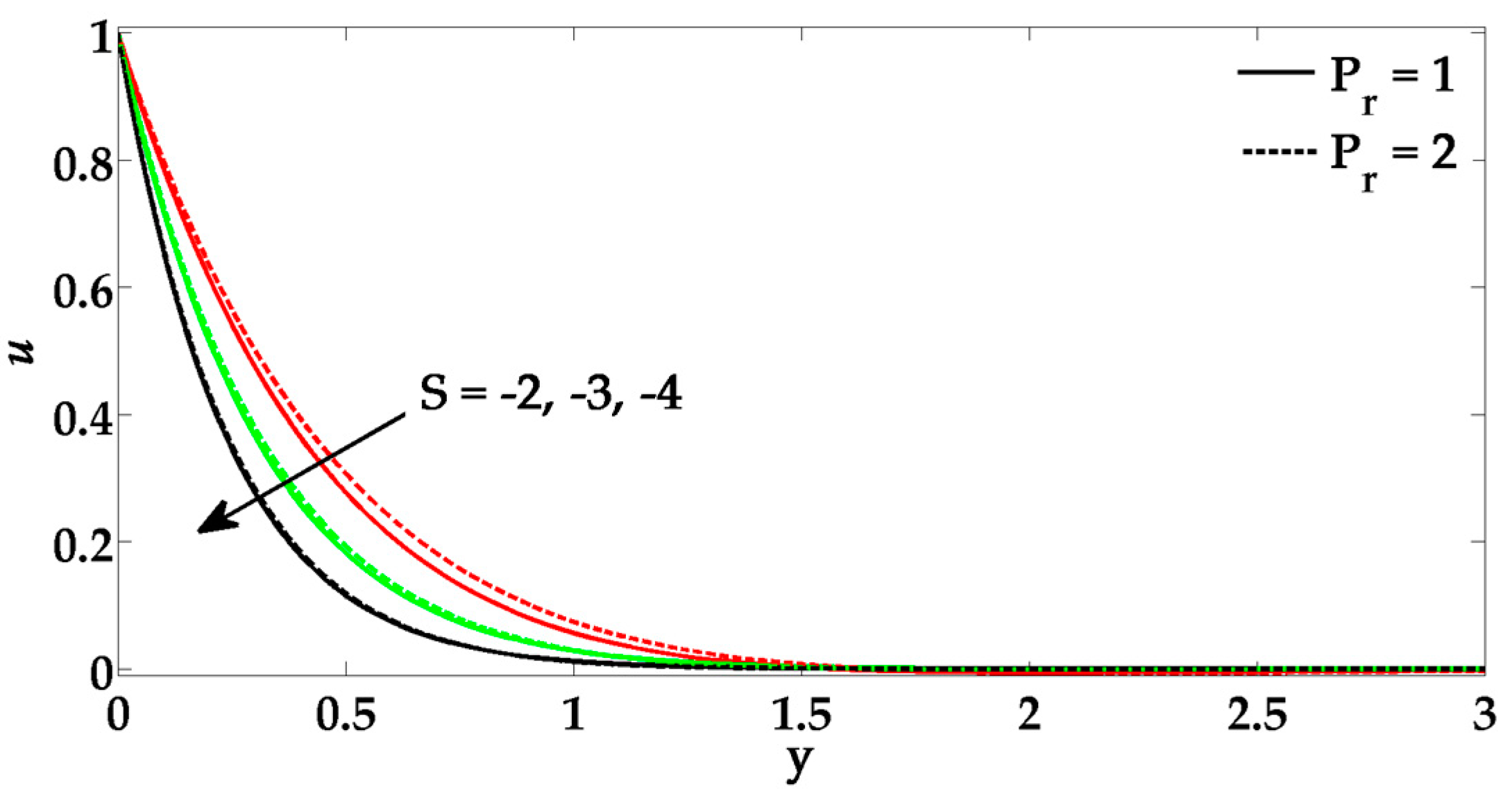
- Due to a greater influence of Prandtl number and suction parameter, the temperature profile tends to diminish.
- (v)
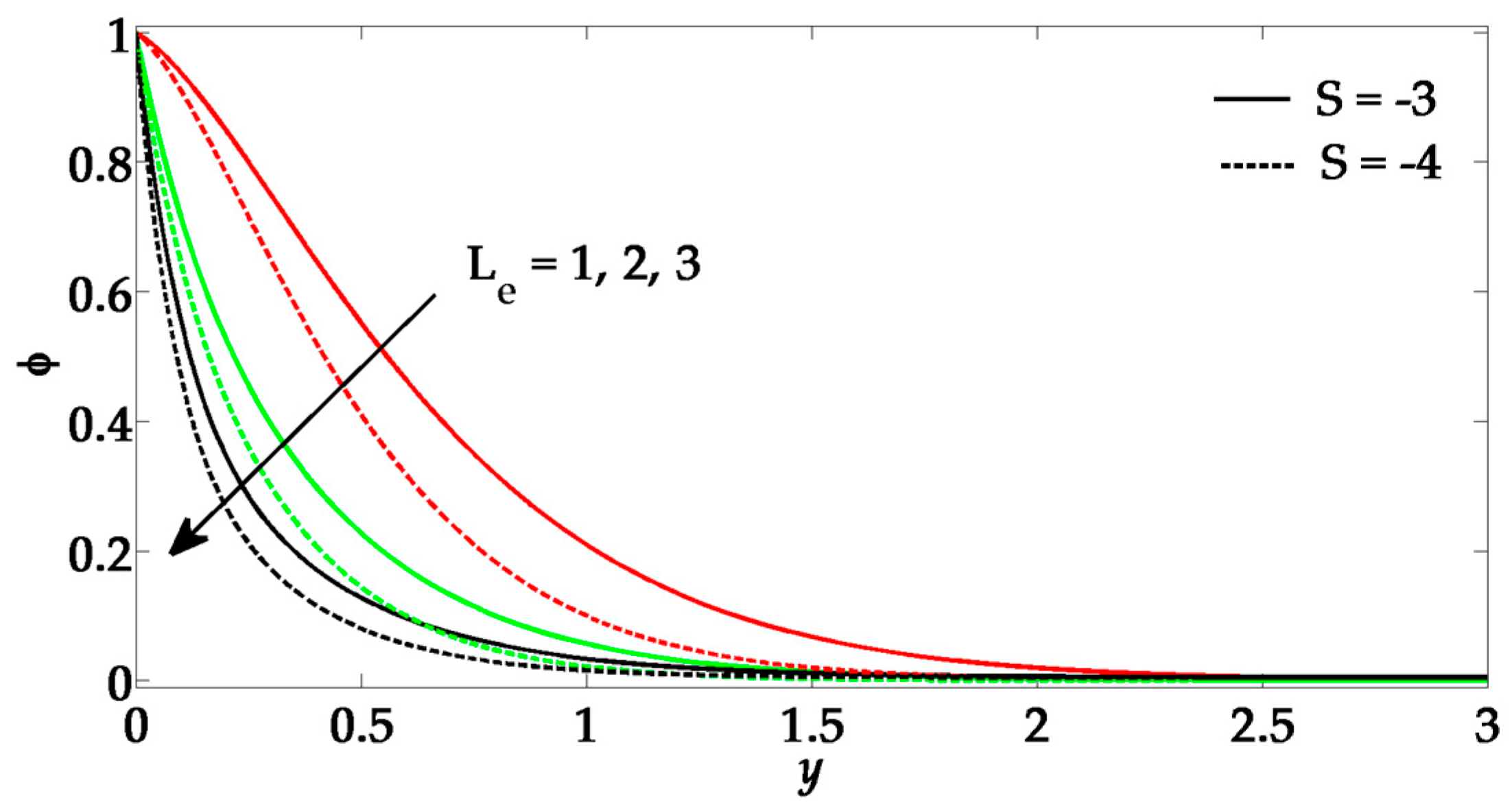
- The Prandtl number enhances the nanoparticle concentration profile and its boundary layer thickness.
- (vi)
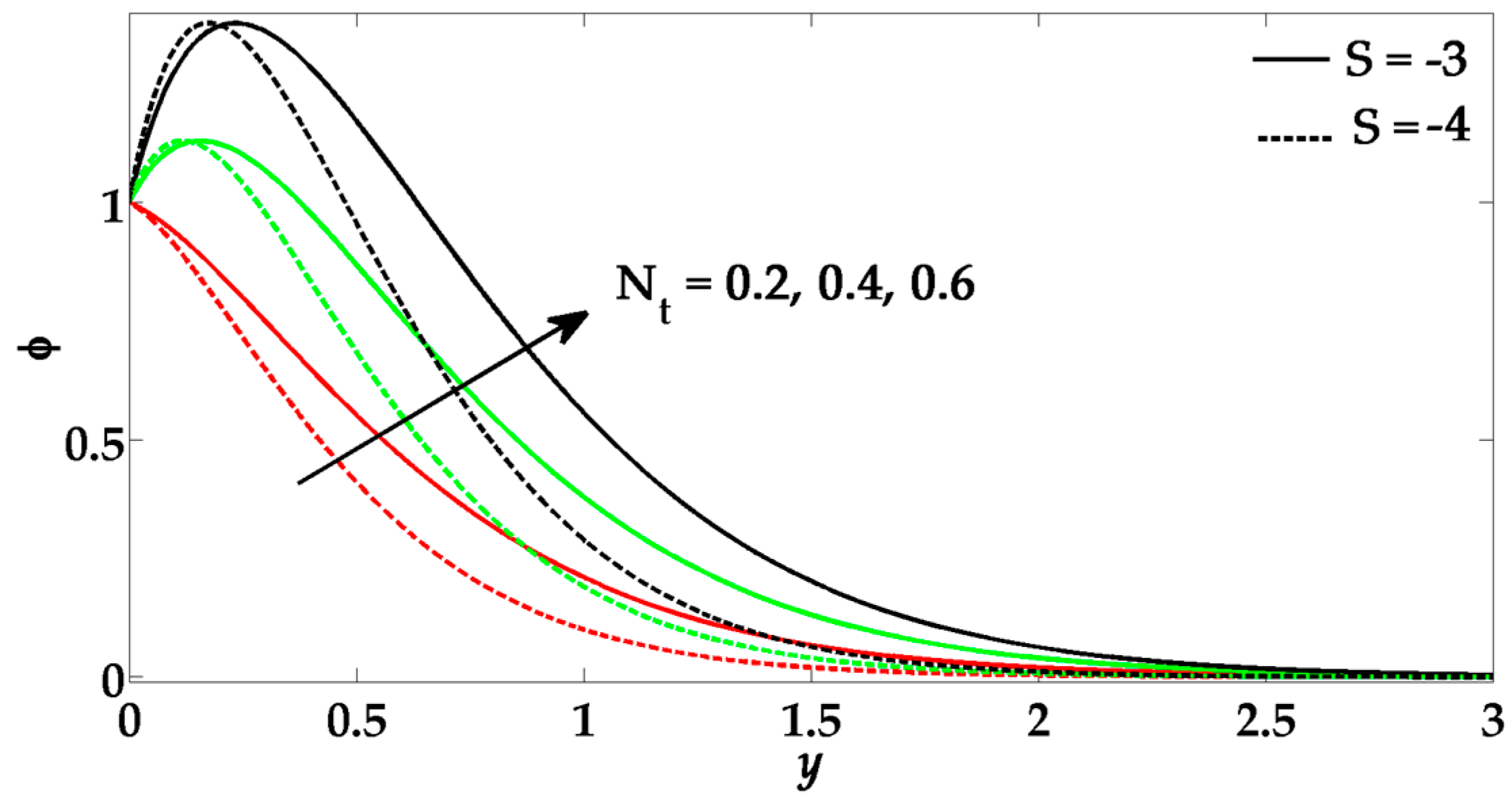
- The thermophoresis parameter and Brownian motion parameter show alternate behavior on nanoparticle concentration profile.
- (vii)
- The entropy profile behaves as an increasing function of all the pertinent parameters.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Ahmad, A.; Asghar, S.; Afzal, S. Flow of nanofluid past a Riga plate. J. Magn. Magn. Mater. 2016, 402, 44–48. [Google Scholar] [CrossRef]
- Kuznetsov, A.V.; Nield, D.A. Natural convective boundary-layer flow of a nanofluid past a vertical plate. Inter. J. Therm. Sci. 2010, 49, 243–247. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Ganji, D.D.; Javed, M.Y.; Ellahi, R. Effect of thermal radiation on magnetohydrodynamics nanofluid flow and heat transfer by means of two phase model. J. Magn. Magn. Mater. 2015, 374, 36–43. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Ganji, D.D. Heat transfer of Cu-water nanofluid flow between parallel plates. Powder Technol. 2013, 235, 873–879. [Google Scholar] [CrossRef]
- Zeeshan, A.; Baig, M.; Ellahi, R.; Hayat, T. Flow of viscous nanofluid between the concentric cylinders. J. Comput. Theor. Nanosci. 2014, 11, 646–654. [Google Scholar] [CrossRef]
- Pantzali, M.N.; Kanaris, A.G.; Antoniadis, K.D.; Mouza, A.A.; Paras, S.V. Effect of nanofluids on the performance of a miniature plate heat exchanger with modulated surface. Int. J. Heat Fluid Flow 2009, 30, 691–699. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Ellahi, R. Electrohydrodynamic nanofluid hydrothermal treatment in an enclosure with sinusoidal upper wall. Appl. Sci. 2015, 5, 294–306. [Google Scholar] [CrossRef]
- Rahman, S.U.; Ellahi, R.; Nadeem, S.; Zia, Q.Z. Simultaneous effects of nanoparticles and slip on Jeffrey fluid through tapered artery with mild stenosis. J. Mol. Liquids 2016, 218, 484–493. [Google Scholar] [CrossRef]
- Zeeshan, A.; Majeed, A.; Ellahi, R. Effect of magnetic dipole on viscous ferro-fluid past a stretching surface with thermal radiation. J. Mol. Liquids 2016, 215, 549–554. [Google Scholar] [CrossRef]
- Rashidi, S.; Dehghan, M.; Ellahi, R.; Riaz, M.; Jamal-Abad, M.T. Study of stream wise transverse magnetic fluid flow with heat transfer around an obstacle embedded in a porous medium. J. Magn. Magn. Mater. 2015, 378, 128–137. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Ellahi, R. Three dimensional mesoscopic simulation of magnetic field effect on natural convection of nanofluid. Int. J. Heat Mass Tran. 2015, 89, 799–808. [Google Scholar] [CrossRef]
- Ellahi, R.; Hassan, M.; Zeeshan, A. Study of natural convection MHD nanofluid by means of single and multi-walled carbon nanotubes suspended in a salt-water solution. IEEE Trans. Nanotechnol. 2015, 14, 726–734. [Google Scholar] [CrossRef]
- Kandelousi, M.S.; Ellahi, R. Simulation of ferrofluid flow for magnetic drug targeting using the Lattice Boltzmann method. Z. Naturforsch. A Phys. 2015, 70, 115–124. [Google Scholar] [CrossRef]
- Akbar, N.S.; Raza, M.; Ellahi, R. Influence of induced magnetic field and heat flux with the suspension of carbon nanotubes for the peristaltic flow in a permeable channel. J. Magn. Magn. Mater. 2015, 381, 405–415. [Google Scholar] [CrossRef]
- Ellahi, R.; Aziz, S.; Zeeshan, A. Non-Newtonian nanofluid flow through a porous medium between two coaxial cylinders with heat transfer and variable viscosity. J. Porous Media 2013, 16, 205–216. [Google Scholar] [CrossRef]
- Ellahi, R.; Hassan, M.; Zeeshan, A. Shape effects of nanosize particles in Cu-H2O nanofluid on entropy generation. Int. J. Heat Mass Tran. 2015, 81, 449–456. [Google Scholar] [CrossRef]
- Zeeshan, A.; Majeed, A. Non Darcy Mixed Convection Flow of Magnetic Fluid over a Permeable Stretching Sheet with Ohmic Dissipation. J. Magn. 2016, 21, 153–158. [Google Scholar] [CrossRef]
- Rashidi, M.M.; Abelman, S.; Mehr, N.F. Entropy generation in steady MHD flow due to a rotating porous disk in a nanofluid. Int. J. Heat Mass Tran. 2013, 62, 515–525. [Google Scholar] [CrossRef]
- Nawaz, M.; Zeeshan, A.; Ellahi, R.; Abbasbandy, S.; Rashidi, S. Joules and Newtonian heating effects on stagnation point flow over a stretching surface by means of genetic algorithm and Nelder-Mead method. Int. J. Numer. Method Heat Fluid Flow 2015, 25, 665–684. [Google Scholar] [CrossRef]
- Abolbashari, M.H.; Freidoonimehr, N.; Nazari, F.; Rashidi, M.M. Entropy analysis for an unsteady MHD flow past a stretching permeable surface in nano-fluid. Powder Technol. 2014, 267, 256–267. [Google Scholar] [CrossRef]
- Abolbashari, M.H.; Freidoonimehr, N.; Nazari, F.; Rashidi, M.M. Analytical modeling of entropy generation for Casson nano-fluid flow induced by a stretching surface. Adv. Powder Technol. 2015, 26, 542–552. [Google Scholar] [CrossRef]
- Qing, J.; Bhatti, M.M.; Abbas, M.A.; Rashidi, M.M.; Ali, M.E.S. Entropy Generation on MHD Casson Nanofluid Flow over a Porous Stretching/Shrinking Surface. Entropy 2016, 18. [Google Scholar] [CrossRef]
- Bhatti, M.M.; Rashidi, M.M. Effects of thermo-diffusion and thermal radiation on Williamson nanofluid over a porous shrinking/stretching sheet. J. Mol. Liquids 2016. [Google Scholar] [CrossRef]
- Zeeshan, A.; Hassan, M.; Ellahi, R.; Nawaz, M. Shape effect of nanosize particles in unsteady mixed convection flow of nanofluid over disk with entropy generation. J. Process Mech. Eng. 2016. [Google Scholar] [CrossRef]
- Bhatti, M.M.; Abbas, T.; Rashidi, M.M.; Ali, M.E.S. Numerical simulation of entropy generation with thermal radiation on MHD Carreau nanofluid towards a shrinking sheet. Entropy 2016, 18. [Google Scholar] [CrossRef]

| - | - | - | |||
| - | - | - | |||
| - | - | - | |||
| - | - | - | |||
| - | - | - | |||
| - | - | - | |||
| - | - | - | |||
| - | - | - | |||
| - | - | - | |||
| - | - | - | |||
| - | - | - |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abbas, T.; Ayub, M.; Bhatti, M.M.; Rashidi, M.M.; Ali, M.E.-S. Entropy Generation on Nanofluid Flow through a Horizontal Riga Plate. Entropy 2016, 18, 223. https://doi.org/10.3390/e18060223
Abbas T, Ayub M, Bhatti MM, Rashidi MM, Ali ME-S. Entropy Generation on Nanofluid Flow through a Horizontal Riga Plate. Entropy. 2016; 18(6):223. https://doi.org/10.3390/e18060223
Chicago/Turabian StyleAbbas, Tehseen, Muhammad Ayub, Muhammad Mubashir Bhatti, Mohammad Mehdi Rashidi, and Mohamed El-Sayed Ali. 2016. "Entropy Generation on Nanofluid Flow through a Horizontal Riga Plate" Entropy 18, no. 6: 223. https://doi.org/10.3390/e18060223
APA StyleAbbas, T., Ayub, M., Bhatti, M. M., Rashidi, M. M., & Ali, M. E.-S. (2016). Entropy Generation on Nanofluid Flow through a Horizontal Riga Plate. Entropy, 18(6), 223. https://doi.org/10.3390/e18060223