Magnetically-Driven Quantum Heat Engines: The Quasi-Static Limit of Their Efficiency
Abstract
:1. Introduction
2. General Theory
2.1. Relaxation to Equilibrium
2.2. Quasi-Static Evolution
3. Magnetically-Driven Quantum Engine on a Quantum Dot Array
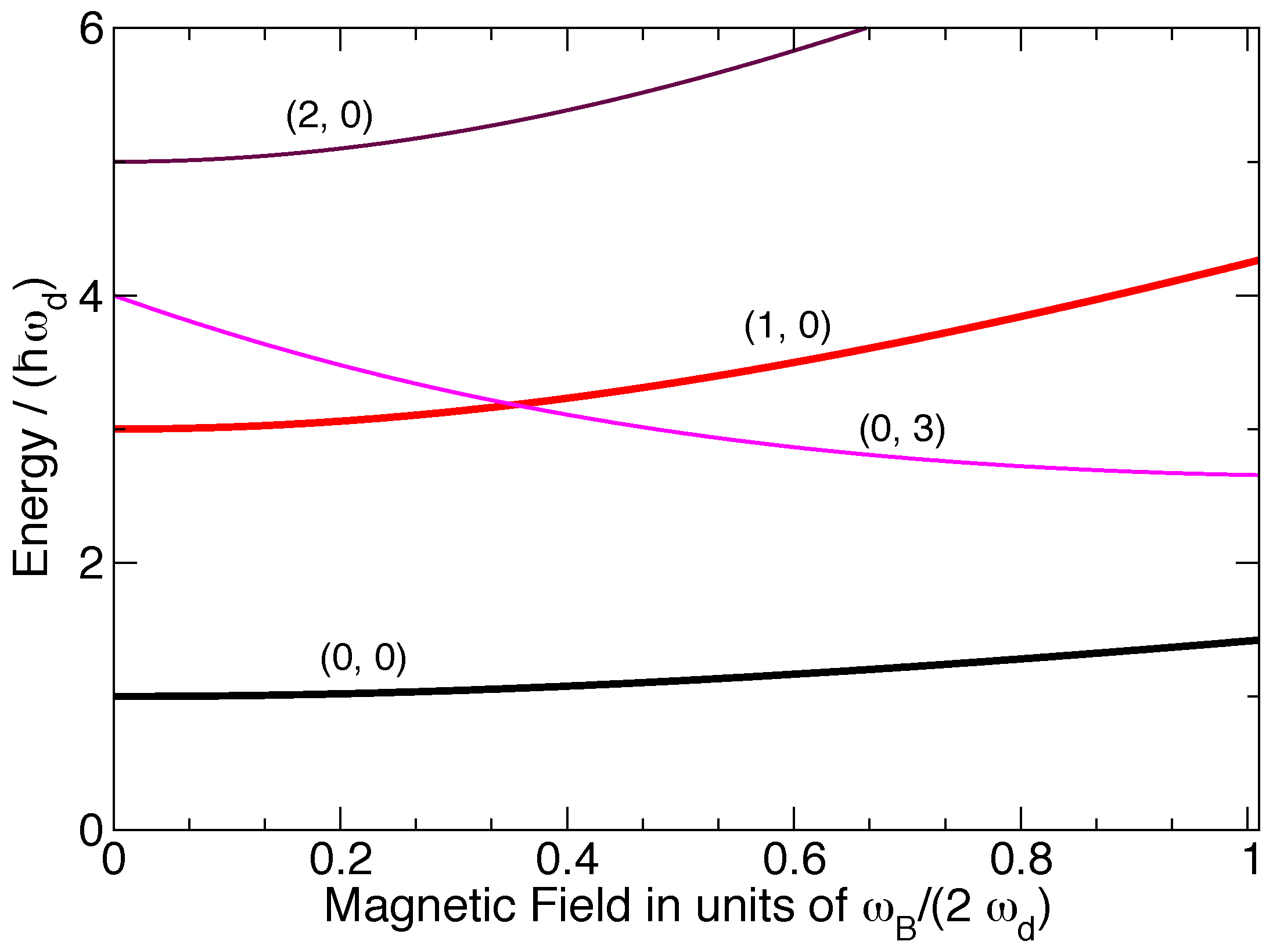
3.1. The Single-Particle Spectrum in a Cylindrical Quantum Dot under an External Magnetic Field
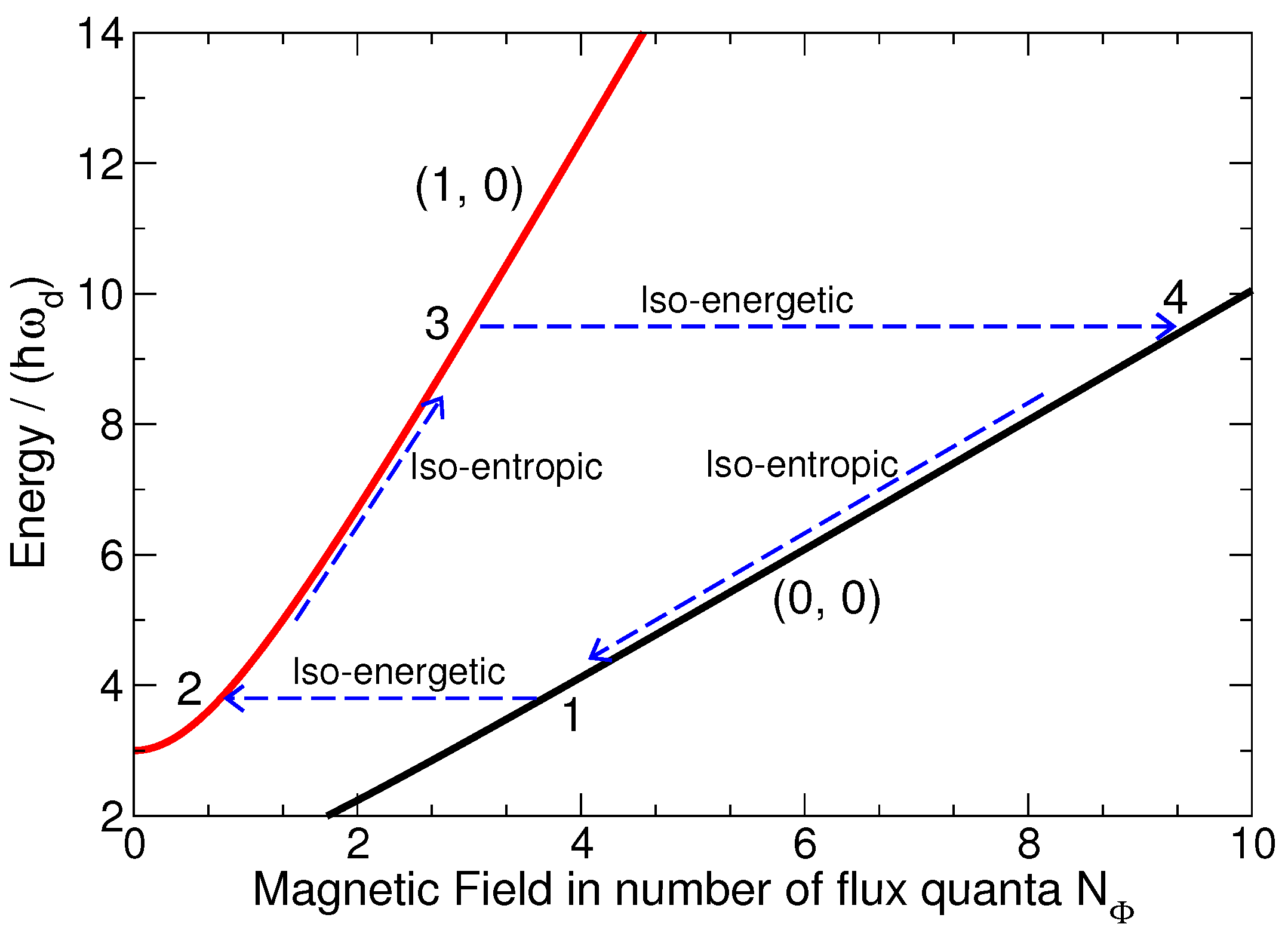
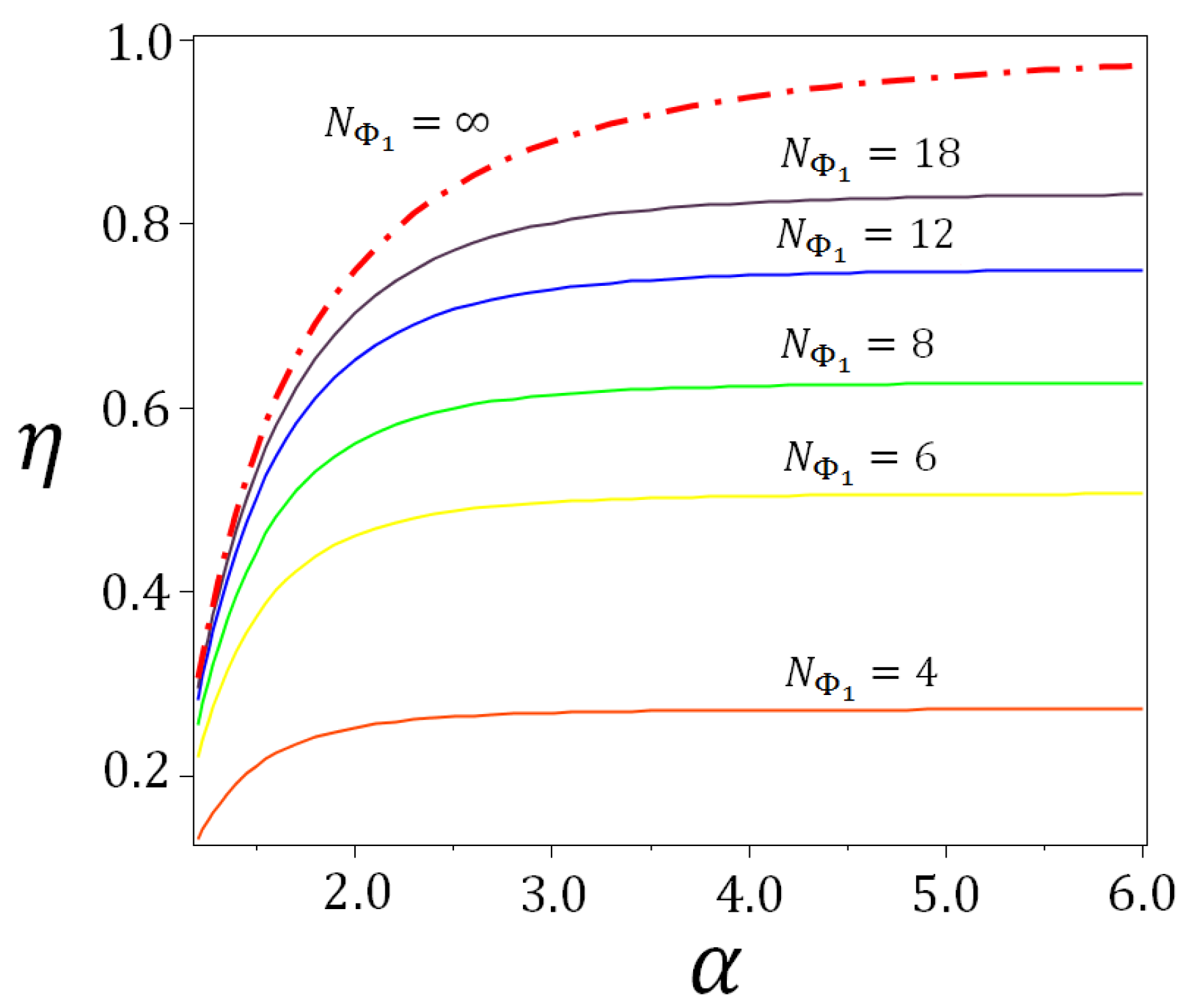
3.2. The Iso-Energetic Cycle
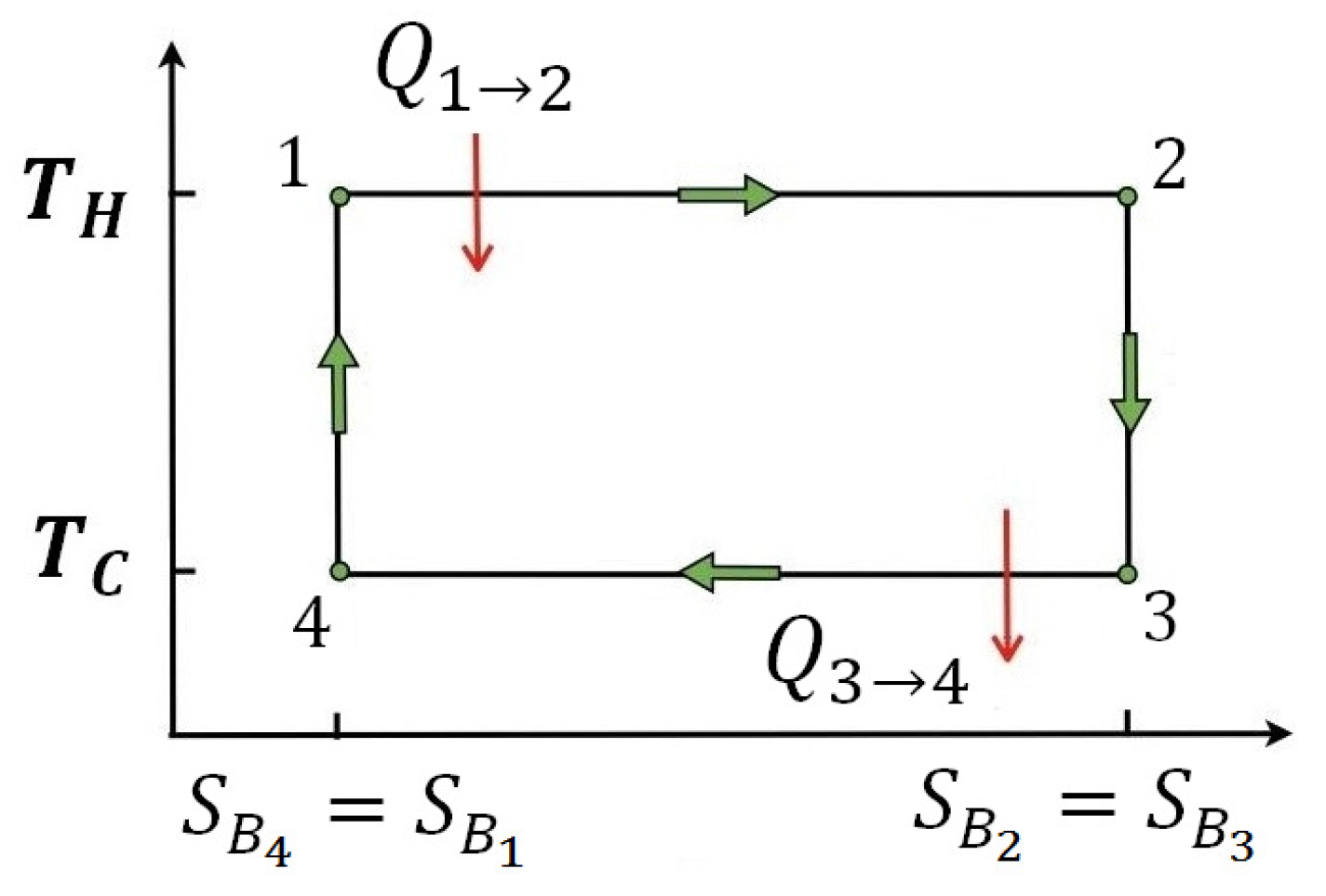
3.3. The Quantum Carnot Cycle
4. A Magneto-Strain-Driven Quantum Engine on a Graphene Layer
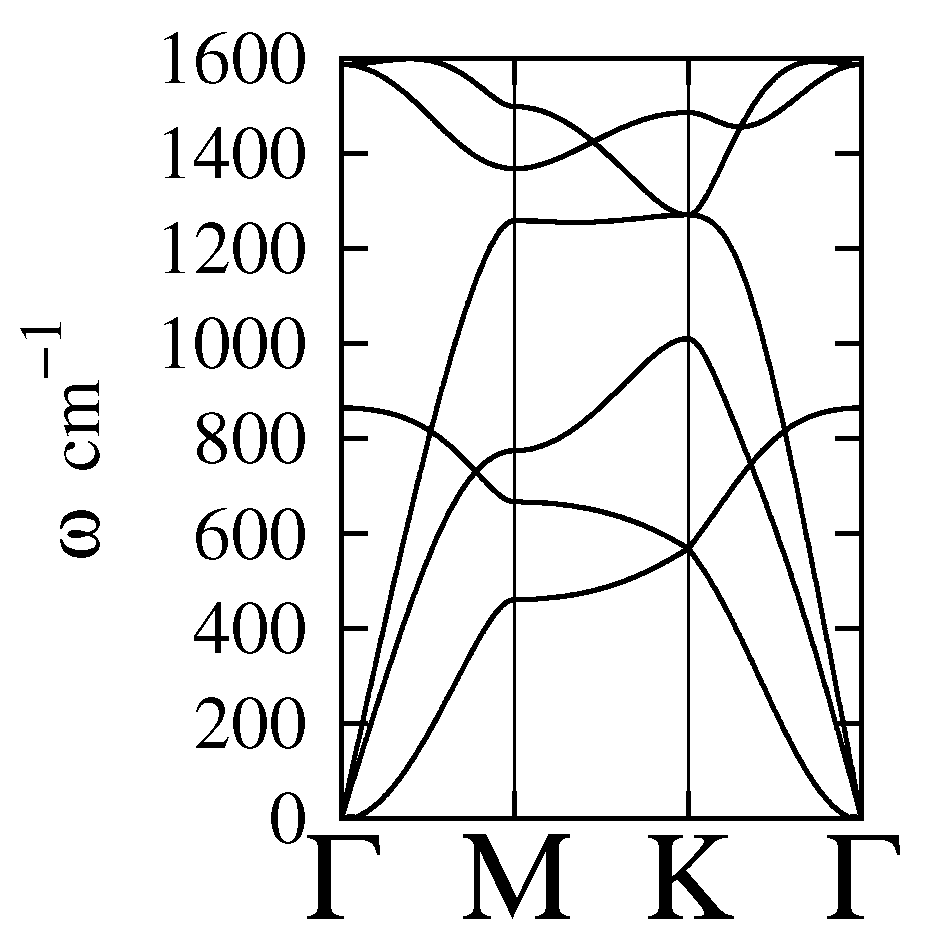
4.1. The Single-Particle Spectrum
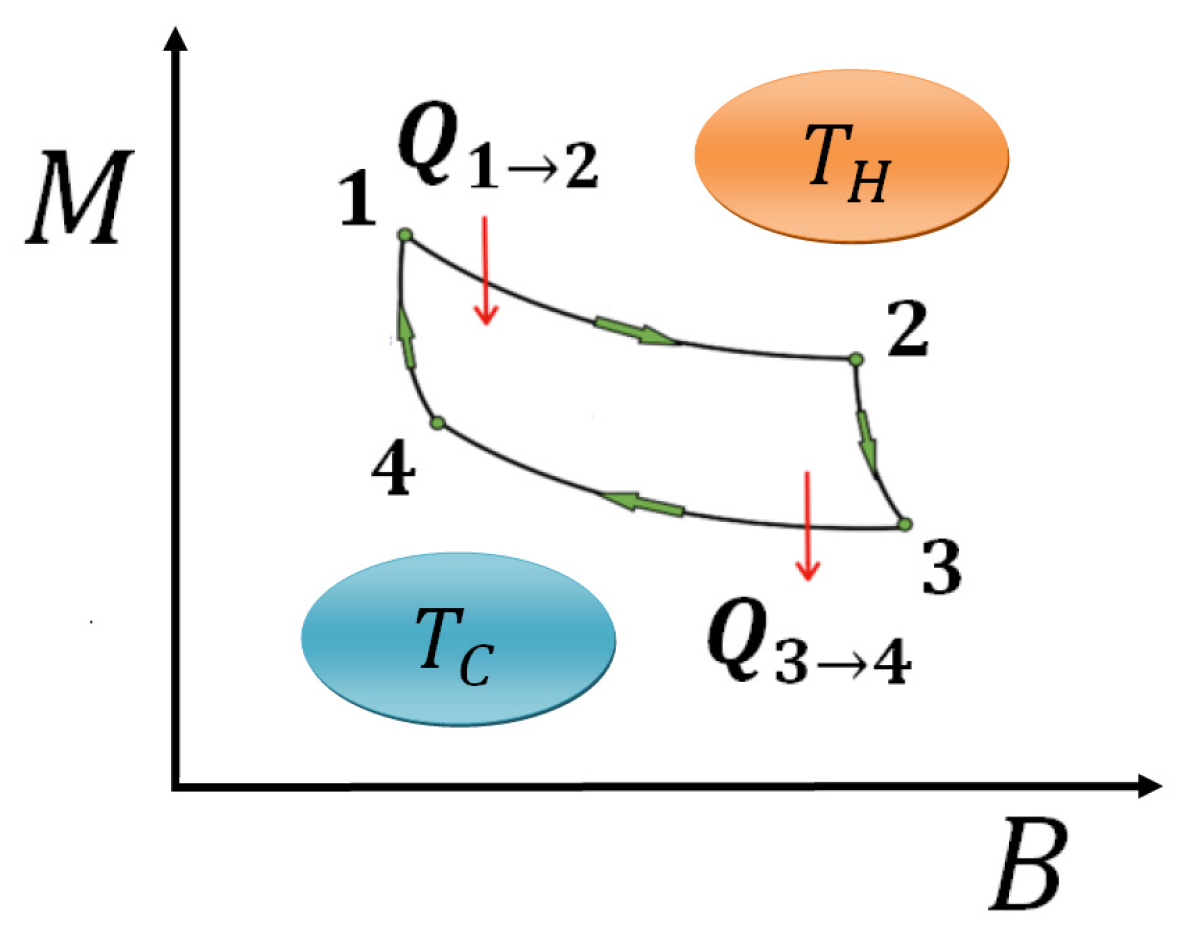
4.2. The Quantum Engine Cycle
5. Discussion
Acknowledgments
Author Contributions
Conflicts of Interest
References and Notes
- Kosloff, R. Quantum thermodynamics: A dynamical viewpoint. Entropy 2013, 15, 2100–2128. [Google Scholar] [CrossRef]
- Breuer, H.P.; Petruccione, F. The Theory of Quantum Open Systems; Oxford University Press: New York, NY, USA, 2010. [Google Scholar]
- Uzdin, R.; Levy, A.; Kossloff, R. Equivalence of quantum heat machines, and quantum-thermodynamic signatures. Phys. Rev. X 2015, 5, 031044. [Google Scholar] [CrossRef]
- Bender, C.M.; Brody, D.C.; Meister, B.K. Entropy and Temperature of a quantum Carnot engine. Proc. R. Soc. Lond. A 2002, 458, 1519–1526. [Google Scholar] [CrossRef]
- Bender, C.M.; Brody, D.C.; Meister, B.K. Quantum-Mechanical Carnot Engine. J. Phys. A 2000, 33. [Google Scholar] [CrossRef]
- Wang, J.; He, J.; He, X. Performance analysis of a two-state quantum heat engine working with a single-mode radiation field in a cavity. Phys. Rev. E 2011, 84, 041127. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; He, J. Optimization on a three-level heat engine working with two noninteracting fermions in a one-dimensional box trap. J. Appl. Phys. 2012, 111, 043505. [Google Scholar] [CrossRef]
- Arnaud, J.; Chusseau, L.; Philippe, F. Carnot cycle for an oscillator. Eur. J. Phys. 2002, 23, 489–500. [Google Scholar] [CrossRef]
- Latifah, E.; Purwanto, A. Multiple-state quantum carnot engine. J. Mod. Phys. 2011, 2, 1366–1372. [Google Scholar] [CrossRef]
- Quan, H.T.; Liu, Y.-X.; Sun, C.P.; Nori, F. Quantum thermodynamic cycles and quantum heat engines. Phys. Rev. E 2007, 76, 031105. [Google Scholar] [CrossRef] [PubMed]
- Scully, M.O.; Zubairy, M.S.; Agarwal, G.S.; Walther, H. Extracting work from a single heath bath via vanishing quantum coherence. Science 2003, 299, 862–864. [Google Scholar] [CrossRef] [PubMed]
- Scully, M.O.; Chapin, K.R.; Dorfman, K.E.; Kim, M.B.; Svidzinsky, A. Quantum heat engine power can be increased by noise-induced coherence. Proc. Natl. Acad. Sci. USA 2011, 108, 15097–15100. [Google Scholar] [CrossRef] [PubMed]
- Quan, H.T.; Zhang, P.; Sun, C.P. Quantum-classical transition of photon-Carnot engine induced by quantum decoherence. Phys. Rev. E 2006, 73, 036122. [Google Scholar] [CrossRef] [PubMed]
- Dong, C.D.; Lefkidis, G.; Hübner, W. Quantum isobaric process in Ni2. J. Supercond. Nov. Mag. 2013, 26, 1589–1594. [Google Scholar] [CrossRef]
- Dong, C.D.; Lefkidis, G.; Hübner, W. Magnetic quantum diesel engine in Ni2. Phys. Rev. B 2013, 88, 214421. [Google Scholar] [CrossRef]
- Hübner, W.; Lefkidis, G.; Dong, C.D.; Chaudhuri, D.; Chotorlishvili, L.; Berakdar, J. Spin-dependent Otto heat engine based on a molecular substance. Phys. Rev. B 2014, 90, 024401. [Google Scholar] [CrossRef]
- Alecce, A.; Galve, F.; Lo Gullo, N.; Dell’Anna, L.; Plastina, F.; Zambrini, R. Quantum Otto cycle with inner friction: Finite-time and disorder effects. New J. Phys. 2015, 17, 075007. [Google Scholar] [CrossRef]
- Hofer, P.P.; Souquet, J.R.; Clerk, A.A. Quantum heat engine based on photon-assisted Cooper pair tunneling. Phys. Rev. E 2016, 93, 041418(R). [Google Scholar] [CrossRef]
- Feldmann, T.; Kosloff, R. Characteristics of the limit cycle of a reciprocating quantum heat engine. Phys. Rev. E 2004, 70, 046110. [Google Scholar] [CrossRef] [PubMed]
- Gardas, B.; Deffner, S. Thermodynamic universality of quantum Carnot engines. Phys. Rev. E 2015, 92, 042126. [Google Scholar] [CrossRef] [PubMed]
- Dorfman, K.E.; Voronine, D.V.; Mukamel, S.; Scully, M.O. Photosynthetic reaction center as a quantum heat engine. Proc. Natl. Acad. Sci. USA 2013, 110, 2746–2751. [Google Scholar] [CrossRef] [PubMed]
- Roßnagel, J.; Abah, O.; Schmidt-Kaler, F.; Singer, K.; Lutz, E. Nanoscale heat engine beyond the Carnot limit. Phys. Rev. Lett. 2014, 112, 030602. [Google Scholar] [CrossRef] [PubMed]
- Huang, X.L.; Xu, H.; Niu, X.Y.; Fu, Y.D. A special entangled quantum heat engine based on the two-qubit Heinsenberg XX model. Phys. Scr. 2013, 88, 065008. [Google Scholar] [CrossRef]
- Li, H.; Zou, J.; Yu, W.L.; Xu, B.M.; Shao, B. Negentropy as a source of efficiency: A nonequilibrium quantum Otto cycle. Eur. Phys. J. D 2013, 67, 134. [Google Scholar] [CrossRef]
- Leggio, B.; Antezza, M. Otto engine beyond its standard quantum limit. Phys. Rev. E 2016, 93, 022122. [Google Scholar] [CrossRef] [PubMed]
- Muñoz, E.; Peña, F.J. Quantum heat engine in the relativistic limit: The case of a Dirac particle. Phys. Rev. E 2012, 86, 061108. [Google Scholar] [CrossRef] [PubMed]
- Muñoz, E.; Peña, F.J. Magnetically driven quantum heat engine. Phys. Rev. E 2014, 89, 052107. [Google Scholar] [CrossRef] [PubMed]
- Peña, F.J.; Muñoz, E. Magnetostrain-driven quantum engine on a graphene flake. Phys. Rev. E 2015, 91, 052152. [Google Scholar] [CrossRef] [PubMed]
- Lamb, W.E.; Retherford, R.C. Fine Structure of the Hydrogen Atom by a Microwave Method. Phys. Rev. 1947, 72, 241–243. [Google Scholar] [CrossRef]
- Von Neumann, J. Mathematical Foundations of Quantum Mechanics; Princeton University Press: Princeton, NJ, USA, 1955. [Google Scholar]
- Jacak, L.; Hawrylak, P.; Wójs, A. Quantum Dots; Springer-Verlag: Berlin, Germany, 1998. [Google Scholar]
- Muñoz, E.; Barticevic, Z.; Pacheco, M. Electronic spectrum of a two-dimensional quantum dot array in the presence of electric and magnetic fields in the Hall configuration. Phys. Rev. B 2005, 71, 165301. [Google Scholar] [CrossRef]
- A necessary condition for entropy to remain constant is This is clearly less stringent than the sufficient condition for all n.
- Callen, H.B. Thermodynamics and an Introduction to Thermostatistics, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 1985. [Google Scholar]
- Englund, D.; Fattal, D.; Waks, E.; Solomon, G.; Zhang, B.; Nakaoka, T.; Arakawa, Y.; Yamamoto, Y.; Vučović, J. Controlling the spontaneous emission rate of single quantum dots in a two-dimensional photonic crystal. Phys. Rev. Lett. 2005, 95, 013904. [Google Scholar] [CrossRef] [PubMed]
- Agarwal, G. Quantum Optics, 1st ed.; Cambridge University Press: New York, NY, USA, 2013; Chapter 7. [Google Scholar]
- Tolman, R.C. The Principles of Statistical Mechanics; Oxford University Press: Oxford, UK, 1938. [Google Scholar]
- Muñoz, E.; Singh, A.K.; Ribas, M.A.; Penev, E.S.; Yakobson, B.I. The ultimate diamond slab: GraphAne versus graphEne. Diam. Relat. Mater. 2010, 19, 368–373. [Google Scholar] [CrossRef]
- Castro, A.H.; Guinea, F.; Peres, N.M.R.; Novoselov, K.S.; Geim, A.K. The electronic properties of graphene. Rev. Mod. Phys. 2009, 81, 109. [Google Scholar] [CrossRef]
- Guinea, F.; Katsnelson, M.I.; Geim, A.K. Energy gaps and zero-field quantum Hall effect in graphene by strain engineering. Nat. Phys. 2010, 6, 30–33. [Google Scholar] [CrossRef]
- Guinea, F.; Geim, A.K.; Katsnelson, M.I.; Novoselov, K.S. Generating quantizing pseudo magnetic fields by bending graphene ribbons. Phys. Rev. B 2010, 81, 035408. [Google Scholar] [CrossRef]
- Peres, N.M.R. Colloquium: The transport properties of graphene. Rev. Mod. Phys. 2010, 82, 2673–2700. [Google Scholar] [CrossRef]
- Muñoz, E.; Lu, J.; Yakobson, B.I. Ballistic thermal conductance of graphene ribbons. Nano Lett. 2010, 10, 1652–1656. [Google Scholar] [CrossRef] [PubMed]
- Muñoz, E. Phonon-limited transport coefficients in extrinsic graphene. J. Phys. Condens. Matter 2012, 24, 195302. [Google Scholar] [CrossRef] [PubMed]
- Booth, T.J.; Blake, P.; Nair, R.; Jiang, D.; Hill, E.W.; Bangert, U.; Blecloch, A.; Gass, M.; Novoselov, K.S.; Katsnelson, M.I.; et al. Macroscopic Graphene membranes and their extraordinary stiffness. Nano Lett. 2008, 8, 2442–2446. [Google Scholar] [CrossRef] [PubMed]
- Balandin, A.A.; Ghosh, S.; Bao, W.; Calizo, I.; Teweldebrhan, D.; Miao, F.; Lau, C.N. Superior thermal conductivity of single-layer graphene. Nano Lett. 2008, 8, 902–907. [Google Scholar] [CrossRef] [PubMed]
- Saito, R.; Dresselhaus, G.; Dresselhaus, M.S. Physical Properties of Carbon Nanotubes; Imperial College Press: London, UK, 1998. [Google Scholar]
- Levy, N.; Burke, S.A.; Meaker, K.L.; Panlasigui, M.; Zettl, A.; Guinea, F.; Neto, A.H.C.; Crommie, M.F. Strain-induced pseudo-magnetic fields greater than 300 Tesla in graphene nanobubbles. Science 2010, 329, 544–547. [Google Scholar] [CrossRef] [PubMed]
- De Juan, F.; Mañes, J.L.; Vozmediano, M.A.H. Gauge fields from strain in graphene. Phys. Rev. B 2013, 87, 165131. [Google Scholar] [CrossRef]
- Goerbig, M.O. Electronic properties of graphene in a strong magnetic field. Rev. Mod. Phys. 2011, 83, 1193. [Google Scholar] [CrossRef]
- De Juan, F.; Sturla, M.; Vozmediano, M.A.H. Space dependent Fermi velocity in strained graphene. Phys. Rev. Lett. 2012, 108, 227205. [Google Scholar] [CrossRef] [PubMed]
- Mañes, J.L.; de Juan, F.; Sturla, M.; Vozmediano, M.A.H. Generalized effective Hamiltonian for graphene under nonuniform strain. Phys. Rev. B 2013, 88, 155405. [Google Scholar] [CrossRef]
- Zhang, Y.; Jiang, Z.; Small, J.P.; Purewal, M.S.; Tan, Y.W.; Fazlollahi, M.; Chudow, J.D.; Jaszczak, J.A.; Stormer, H.L.; Kim, P. Landau-level splitting in graphene in high magnetic fields. Phys. Rev. Lett. 2006, 96, 136806. [Google Scholar] [CrossRef] [PubMed]
- Ferone, R.; Wallbank, J.R.; Zólyomi, V.; McCann, E.; Fal’ko, V.I. Manifestation of LO-LA phonons in Raman scattering in graphene. Solid State Commun. 2011, 151, 1071–1074. [Google Scholar] [CrossRef]

© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Muñoz, E.; Peña, F.J.; González, A. Magnetically-Driven Quantum Heat Engines: The Quasi-Static Limit of Their Efficiency. Entropy 2016, 18, 173. https://doi.org/10.3390/e18050173
Muñoz E, Peña FJ, González A. Magnetically-Driven Quantum Heat Engines: The Quasi-Static Limit of Their Efficiency. Entropy. 2016; 18(5):173. https://doi.org/10.3390/e18050173
Chicago/Turabian StyleMuñoz, Enrique, Francisco J. Peña, and Alejandro González. 2016. "Magnetically-Driven Quantum Heat Engines: The Quasi-Static Limit of Their Efficiency" Entropy 18, no. 5: 173. https://doi.org/10.3390/e18050173
APA StyleMuñoz, E., Peña, F. J., & González, A. (2016). Magnetically-Driven Quantum Heat Engines: The Quasi-Static Limit of Their Efficiency. Entropy, 18(5), 173. https://doi.org/10.3390/e18050173







