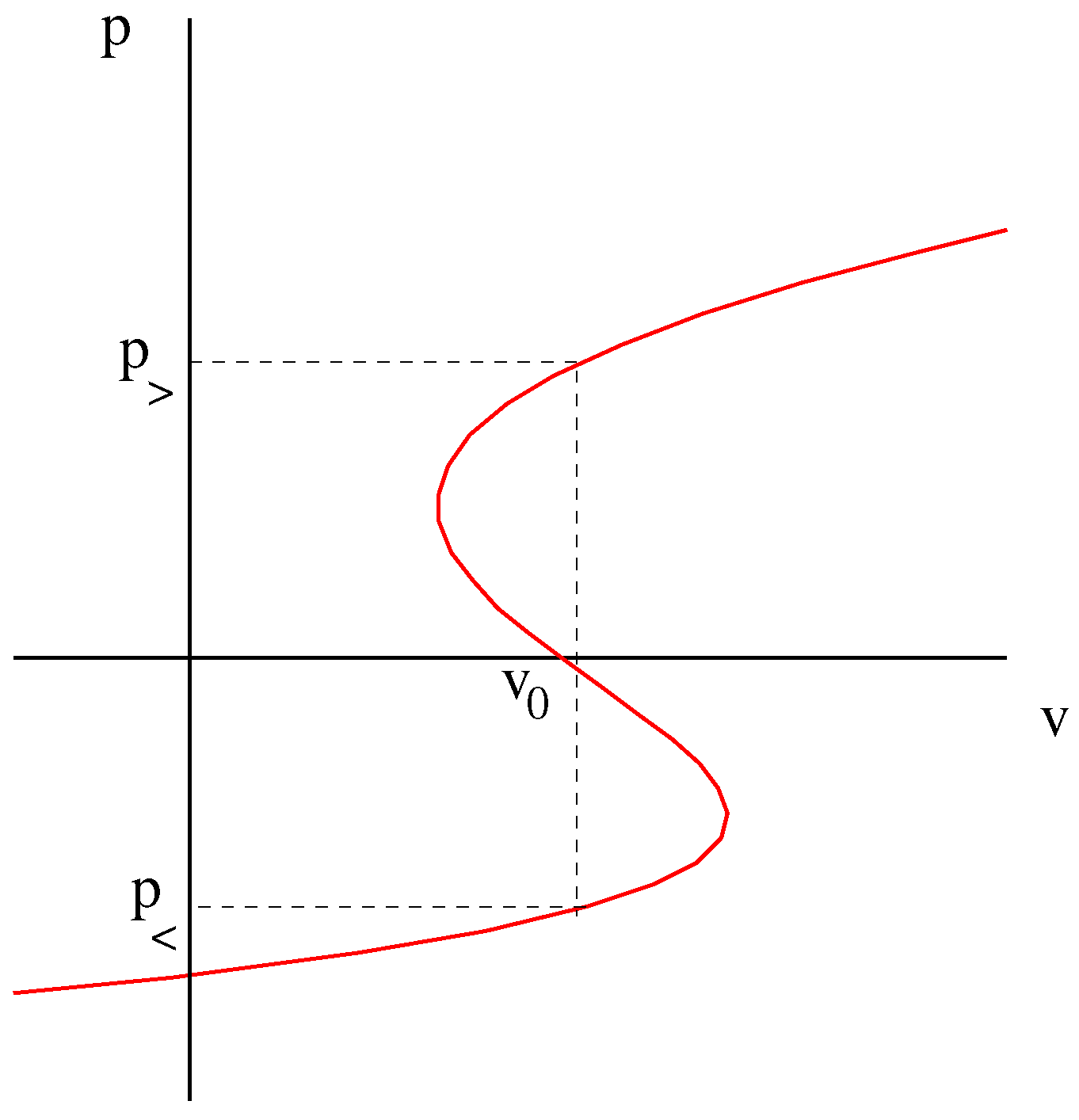1. Introduction
Ever since Bekenstein’s discovery of the relation between entropy and the area of a black hole’s event horizon [
1,
2] and Hawking’s subsequent observation that black holes have an intrinsic temperature associated with them [
3,
4,
5], the subject of black hole thermodynamics has been a fascinating area of research. Indeed black hole thermodynamics now has potentially great usefulness in providing insights into the thermodynamics of conformal theories via the AdS/CFT correspondence [
6].
An interesting aspect of black hole thermodynamics is the role of the cosmological constant, Λ, as a thermodynamic variable: an idea originally considered in [
7,
8] and re-visited in [
9]. Since Λ has the natural physical interpretation of pressure in the bulk, the conjugate variable is a volume, and this has led to some intriguing recent results for the pressure and volume of black holes, with phase transitions and critical points showing very similar properties to liquid-gas phase transitions [
10,
11]. For Einstein gravity in the bulk, the critical exponents are mean field for all black hole solutions studied to date, leading to an analogy with the liquid-gas transition of a van der Waals fluid.
In the context of AdS/CFT, it was suggested in [
9,
12] that varying the cosmological constant in the bulk should be associated with varying the number of colours in the boundary CFT, and this proposal was investigated in more detail in [
13], where the thermodynamically-conjugate variable to Λ was interpreted as a kind of chemical potential for colour.
An alternative approach is followed here based on a different interpretation of the thermodynamic significance of Λ, which provides a length scale in the CFT. When global AdS coordinates are used, the CFT on the boundary has a finite volume, determined by Λ; hence, varying Λ in the bulk corresponds to varying the volume of the CFT on the boundary. If Λ gives the volume of the CFT, then the thermodynamically-conjugate variable is the pressure, and one is led to the construction of
diagrams for the CFT, in which the pressure and volume are interchanged relative to their roles in the bulk. This can be achieved while keeping the number of colours fixed provided the higher dimensional Newton’s constant is adjusted as Λ is varied, as suggested in [
14]. In 10-dimensional string theory, for example, Newton’s constant is related to the string coupling constant and tension by
, so varying
can be thought of as varying
with the tension fixed.
In this paper the
diagram associated with four-dimensional
SUSY
Yang–Mills theory at large
N is investigated using the AdS/CFT correspondence. When the bulk contains a black hole there is a first order phase transition [
15] which is associated with the deconfining transition for the quark-gluon plasma on the boundary [
16,
17]. When the black hole carries a
charge, corresponding to
R-charge in the Yang–Mills theory, this phase transition is one end of a line of first order phase transitions, while the other end terminates at a second order transition where the heat capacity at constant volume for the Yang–Mills theory diverges [
18].
The critical exponents in the bulk gravitational theory, with charge as the order parameter and temperature as the control parameter, are known to be mean field [
19], and so,
is finite at the critical point for the black hole in the bulk. At first sight, this is at odds with the statement in [
18] that there is a critical point in the CFT at which
diverges. We shall show that there is no contradiction here, and when interpreted correctly, the boundary CFT has mean field exponents. In terms of pressure and volume, there is a number of aspects of the phase transition that make it different from more usual cases. Firstly, there is a single phase at low temperatures, and the two-phase regime exists for temperatures above the critical point [
18]; secondly, above the critical point, along the line of first order phase transitions, it is the pressure that jumps across the phase transition, not the volume, so it is more appropriate to use the pressure as an order parameter rather than the more usual volume; thirdly, the conformal symmetry dictates that volume and temperature are not fully independent, and it is better to use charge as the control parameter rather than the temperature. This last point of view is more in keeping with the notion of the phase transition being a quantum phase transition rather than a thermal phase transition. With this interpretation, the critical exponents for pressure and volume of the Yang–Mills theory are calculated in the large
N limit and shown to be mean field.
The general structure is the same for the three-dimensional and six-dimensional CFTs considered in [
20]; in particular, the critical exponents at large
N are mean field in all three conformal field theories.
In
Section 2, the black hole thermodynamics of the relevant bulk solution is summarized and is related to that of the boundary CFT in
Section 3.
Section 4 analyses the case of
SUSY Yang–Mills in detail; the
diagram is constructed, and critical exponents for the deconfining phase transition in the large
N limit are calculated. Finally
Section 5 summarizes the results. Some technical details are in the
Appendix.
2. The Bulk
In
D space-time dimensions, the Lagrangian for Einstein gravity, with a cosmological constant Λ, coupled to a
gauge field, is:
The normalization of
F is the same as in [
18]; it has dimensions of inverse length.
A solution of the equations of motion arising from Equation (1), corresponding to a spherical charged asymptotically AdS black hole in
D space-time dimensions, is easily written down. In global co-coordinates, the gauge potential is:
where
is the volume of a unit
-sphere. The constant
accommodates some freedom in the choice of gauge.
The normalization of the
charge
here is determined by requiring that the gauge field
satisfies the Gauss law:
where
is a sphere containing the charge.
The line element is:
where:
and is the line element on a unit sphere. There is an event horizon, and the largest root of will be denoted by . It is natural to choose a gauge in which the potential above vanishes at the outer horizon, .
The parameters
q and
μ are then related to
and the mass
M of the black hole by:
and:
(we use units with
, but keep the
D-dimensional Newton’s constant explicit).
From Equation (
5), with
, and Equation (
7):
The area of the event horizon is
, and the Bekenstein–Hawking entropy is:
From the point of view of black hole thermodynamics, the mass is interpreted as the internal energy of the system,
, and the Bekenstein–Hawking temperature is:
It will prove useful to define dimensionless variables,
and
, which can be used in lieu of
S and the charge. In terms of these variables:
and:
In the context of superstring theory, the
D-dimensional Newton’s constant
is descended from Newton’s constant in the full
-dimensional theory (
or 11). Compactifying the higher dimensional theory on a
-dimensional compact space
, with size
L, allows for a direct product
-dimensional space-time
, where
is asymptotically
, with line-element Equation (4), and:
where
C is a dimensionless number determined by the metric on
. The AdS length scale
L is not intrinsic to the
-dimensional action, but is merely a parameter in a classical solution of the
-dimensional theory, and it is perfectly reasonable to consider varying
L in the solution.
3. Thermodynamics of the Boundary Field Theory
In the AdS/CFT correspondence, the boundary CFT theory has
space dimensions. With the global coordinates used in the previous section, the
-dimensional space-time metric at fixed
r is:
which is conformal to a
-dimensional space-time with constant time spatial volume:
and this can be interpreted as the spatial volume of the boundary conformal field theory.
The dimensionless ratio of the AdS length scale
L to the
-dimensional Planck length in the bulk determines the number of degrees of freedom in the boundary field theory [
20].
The most studied case is
compactified on
, with
. the boundary CFT is then
SUSY
Yang–Mills theory, when the classical solution in the bulk Equation (4) is relevant for large
N. This has
degrees of freedom (
bosonic and
fermionic), and the large
N limit is the weak gravity limit:
is of course related to the 10-dimensional Planck length, , and as usual, large N is related to the classical limit of the bulk theory, in which .
The CFT is on a three-sphere with volume:
and the inverse of the five-dimensional Planck length Equation (
16) is related to the number of degrees of freedom per unit volume of the CFT:
so varying the volume of the CFT, keeping
fixed, is completely equivalent to varying the five-dimensional Planck length.
The entropy is proportional to
(with
as before):
as is the dimensionless charge:
where
.
On dimensional grounds, the internal energy
is of the form:
with
a dimensionless function of dimensionless variables. The thermodynamics of the CFT is determined by the functional dependence of the mass on
S,
Q and
V (or equivalently,
x,
y and
L), explicitly:
Two other interesting cases are the three-dimensional CFT obtained from M-theory in
compactified on
(more generally,
for integral
k [
6,
18]) and the six-dimensional CFT obtained from M-theory in
compactified on
. For these two cases, the
behaviour of the “extensive” quantities
M,
S and
Q is replaced with
and
, respectively, and the powers of
x change as in Equation (
11) and Equation (
12); but otherwise, the analysis of the thermodynamics is similar to the case
and
studied in
Section 4 below.
4. The Thermodynamics of SUSY Yang–Mills
To explore the thermodynamics of the CFT fully, we wish to fix
N and allow
S,
Q and
V to vary. This means we must vary
L, but at the same time vary the
-dimensional Newton constant in such a way that
is fixed in the first equation of Equation (
16) [
14].
For concreteness, we shall focus on
; the general structure is the same as the other two cases; in particular, the critical exponents are the same. Thermodynamically, we interpret
in Equation (
22) as the internal energy of the large
N Yang–Mills theory at strong coupling,
Note that, while the mass in the bulk is classical, the internal energy of the CFT is quantum mechanical and vanishes as with x and y fixed.
The temperature is then:
In the deconfined phase, this is interpreted as the temperature of the quark-gluon plasma [
16,
17,
18].
The pressure is [
14]:
where
is the energy density. Hence:
and the speed of sound is given by:
simple consequences of the fact that dimensionally,
.
Lastly, the chemical potential is:
These expressions simplify at high
T (large
x) when the event horizon curvature and the charge are negligible. This is deep into the de-confined phase of the quark-gluon plasma, and in this limit:
Since , we see that the pressure and the chemical potential here are of quantum mechanical origin.
At fixed charge and temperature, there is a phase transition [
18], an extension of the
Hawking–Page phase transition in the bulk [
15], which is interpreted as the deconfining phase transition in the boundary Yang–Mills theory [
16,
17]. The heat capacity:
diverges when
vanishes, and there is a critical point when
. This happens at:
a critical point that was first found in [
18]. The critical temperature is given by:
Conformal invariance dictates that only the combination
is determined at the critical point;
V and
T are not fixed separately (finite temperature field theory is associated with periodicity in Euclidean time with period
, and Euclidean time parameterizes a circle
of radius
. The spatial geometry is
with radius
L, and because the theory is conformal, the physics can only depend on the ratio of the radii of these two spheres, namely
. The physics depends on
, not on
V and
T separately [
16,
17]).
The critical exponent
α for the specific heat can easily be determined by fixing
and expanding
around
. With
:
α can be extracted by similarly expanding the reduced temperature at constant volume,
which gives:
The critical exponent follows from
with:
This singularity in the heat capacity was not found in the bulk thermodynamics of higher dimensional asymptotically AdS charged black holes studied in [
19,
21]; these authors found a critical point in the bulk; but the exponents were mean field, and
is finite there. To understand this apparent contradiction, we write the full equation of state in terms of
Q and Φ. Using Equation (
20) and Equation (
28) to eliminate
x in favour of
Q and Φ in Equation (
24) gives the equation of state:
Expanding about the critical point Equation (31) with
,
and
, where
, leads to:
Aside from a change in the sign of
t, this has the same analytic structure as the equation of state for a van der Waals gas [
19], which, in reduced variables
and
, reads:
The van der Waals equation of state has mean field exponents, so one expects
. The previous calculation gave
, because
Q was held fixed (fixed
η), but the order parameter for the liquid-gas phase transition in the van der Waals gas is
v, which would be analogous to
φ in Equation (
38). Indeed,
is perfectly finite [
18], so
α is indeed zero for fixed Φ, which is the analogue of the van der Waals case.
If
Q is the order parameter, the usual exponents are defined by:
and the response function,
behaves as:
when
.
The equation of state Equation (
38) results in:
While these exponents, together with
, do satisfy the Rushbrooke and Widom scaling relations:
there is a difficulty in that
γ is negative, so the response function vanishes at the critical point , rather than diverging. As indicated in Equation (
42), the response function
can be negative near the critical point,
and this is the instability found in [
22] (the same instability is also present for rotating Myers–Perry black holes with fixed angular momenta, which have a second order phase transition at a critical value of the angular momenta [
23,
24]). It was also shown in [
22] that Φ jumps across the phase transition in the two-phase regime, suggesting that Φ is the order parameter for this transition.
If Q is just fixed from the start and not varied, then there is no problem; diverges with exponent , and β, γ and δ are not relevant. However, if we wish to probe the system by adjusting Q, then Φ should be viewed as the order parameter, not Q. In that case, diverges as , rather than , because it should be calculated for and not .
The other exponents,
and
, are easily obtained from Equation (
38) in the usual way and are found to be mean field:
In particular, the heat capacity
is finite (and negative) at the critical point [
18]. Mean field behaviour with Φ as the order parameter for the black hole in the bulk was first found in [
19].
Alternatively, the equation of state can be written in terms of the pressure rather than the chemical potential to study the compressibility. The adiabatic compressibility of the plasma follows easily from Equation (
25) and is:
but the isothermal properties are more interesting.
It is shown in
Appendix A that the isothermal compressibility,
, is given by:
Hence, vanishes at the critical point and is negative along close to the critical point when diverges. Thus, the response function, , behaves the same way as the Q-Φ response function . This suggests that the order parameter here is P rather than V.
If this is a valid point of view, we should focus on the heat capacity at constant pressure,
, rather than
. Using the standard relation:
Equation (
47) and Equation (
48) give:
which is finite and negative when
diverges, just as
is. In particular, at the critical point:
Thus, with P as the order parameter, is mean field. The negative value of at the critical point is a reflection of the instability found above in .
There is a subtlety in trying to extract β and δ, as there is no independent definition of a critical volume; V and T are linked due to conformal invariance. In particular, it would be wrong to use the usual scaling relations to derive β and δ from α and γ above, as conformal invariance imposes an extra constraint.
A reduced volume can be defined as:
but this is not a new variable, since conformal invariance relates it directly to
t,
As a consequence the usual definitions of the exponents
β and
δ do not apply.
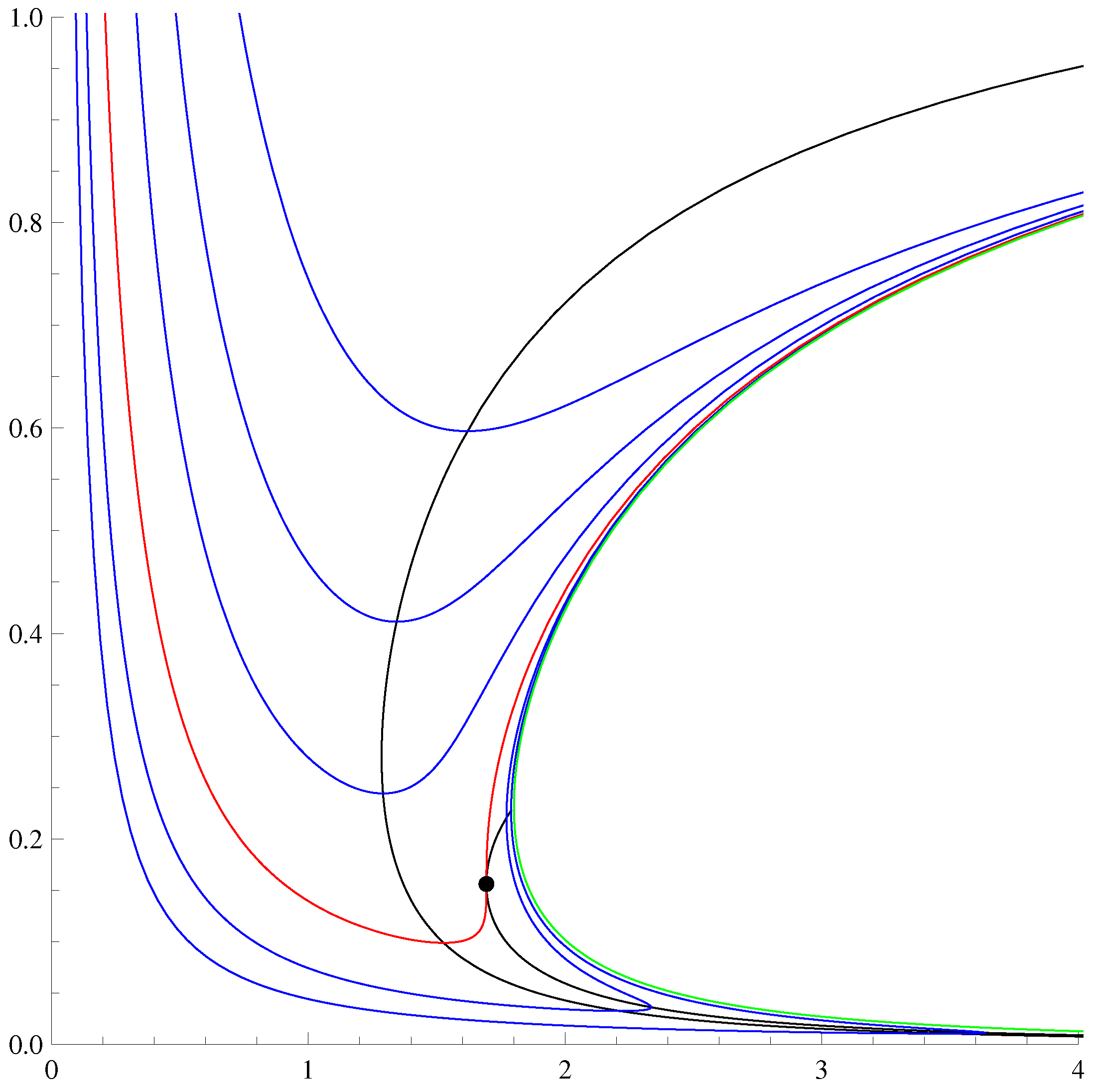
Since
v and
t are not independent, it is better, when discussing pressure and volume, to use
η to probe the physics near the critical point rather than
t. Lines of equal charge in the
plane are plotted in
Figure 1 where
P and
V are rendered dimensionless by multiplying by appropriate powers of
T. The isothermal compressibility is positive when the slope of the plotted curves is negative, and there are two regions in the
plane where this is the case; the critical point lies on the boundary of the rightmost of these regions, which corresponds to
and
(hence,
,
i.e., the high temperature regime). The pressure of the system jumps across the phase transition.
To calculate critical exponents, first define a reduced pressure:
at fixed volume. (One can also use the temperature to render
P dimensionless and define the reduced pressure as
. This does not change the critical behaviour; in particular, it gives the same critical exponents). Then, with
p as the order parameter and
Q as the control variable,
β and
δ are defined by:
in analogy with the usual definition of
β, but with
t replaced by
η and
p as the order parameter (so,
p and
v are interchanged). Similarly:
Lastly, the relevant response function is:
γ then follows from:
We leave the details to an
Appendix and here quote the result that
β,
γ and
δ are indeed mean field. We conclude that, with the proper identification of the order parameter as being the thermodynamic variable that jumps across the line of first order phase transformations, the exponents are always mean field in the large
N limit, both in the Φ-
Q plane and the
plane.
5. Summary
The critical point of
SUSY
Yang–Mills in the large
N limit, first found in [
18,
22], is also visible in the
diagram of the quark-gluon plasma. The volume here is provided by the cosmological constant in the 5D bulk,
, which is related to the volume of three-space,
, in the boundary Yang–Mills theory by
. The pressure is then defined through the thermodynamic relation
, where
U is the internal energy of the thermodynamic system, identified with the mass of the black hole in the bulk. This is in contrast to the thermodynamics of the black hole itself, where the roles of pressure and volume are reversed so that, on the gravity side, the cosmological constant provides the pressure; the thermodynamically-conjugate variable is a volume; the black hole mass is the enthalpy of the system [
9].
There is a constraint on the thermodynamic variables, due to the fact that the boundary field theory is conformal, and only the combination is relevant to the phase structure, not V and T separately. As a consequence, it seems better to use the charge rather than the temperature as the control parameter in discussing the thermodynamics. Then, the pressure jumps across the phase transition in the two-phase regime. In the approximation in which the fluid is treated as a gas of non-interacting particles—quarks and gluons in the plasma and non-interacting hadrons in the confined phase—this jump may be viewed as simply due to a change in the number of degrees of freedom: each degree of freedom contributes equally to the pressure; any change across the phase transition in the number of effective degrees of freedom contributes to a change in pressure.
With pressure as the order parameter in the plane, the exponents are mean field, and the phase transition is in the same universality class as the van der Waals gas. Mean field exponents also characterize the phase transition in the Φ-Q plane.
An unsatisfactory feature of the analysis is the instability associated with the negative value of
at the critical point, implying that the system is unstable there when the pressure is fixed. Although
is positive in the region enclosed by the black curve to the right of the critical point in
Figure 1, both
and
are negative there. The only region of the
plane that has all three of
,
and
positive is the region to the left of the left-hand black curve in the figure, the single-phase region.
to the right of this curve.
Instability in black hole thermodynamics is not new and indeed lies behind the phenomenon of black hole evaporation; an asymptotically flat Schwarzschild black hole also has negative . Whether or not negative is a problem is a question of time-scales; for Hawking radiation, the time-scale for black hole evaporation can be very large, so large that the system is essentially quasi-static equilibrium, and thermodynamic principles can still be applied, at least at early times before the evaporation process has gone too far. It is not clear whether the same thing can be said for the quark-gluon plasma or what the physical interpretation of the instability should be in this case.
Although the analysis here has focused on the case of four-dimensional SUSY Yang–Mills, associated with string theory in compactified on , the thermodynamics of the three-dimensional and six-dimensional CFTs, obtained from M-theory in compactified on and on , respectively, is essentially similar: the critical exponents are mean field in all three cases.
It would be of great interest to evaluate
corrections to the exponents, but the method employed here relies on a representation of the thermodynamic potentials arising from an exact solution of the Einstein equations in the bulk. The paucity of known exact solutions relevant to the problem is an obstacle to realizing
corrections with this method. However, it may be possible to make some progress in studying
corrections by adding a Gauss–Bonnet term to the 5D Einstein action [
25].