Abstract
Coordination games provide ubiquitous interaction paradigms to frame human behavioral features, such as information transmission, conventions and languages as well as socio-economic processes and institutions. By using a dynamical approach, such as Evolutionary Game Theory (EGT), one is able to follow, in detail, the self-organization process by which a population of individuals coordinates into a given behavior. Real socio-economic scenarios, however, often involve the interaction between multiple co-evolving sectors, with specific options of their own, that call for generalized and more sophisticated mathematical frameworks. In this paper, we explore a general EGT approach to deal with coordination dynamics in which individuals from multiple sectors interact. Starting from a two-sector, consumer/producer scenario, we investigate the effects of including a third co-evolving sector that we call public. We explore the changes in the self-organization process of all sectors, given the feedback that this new sector imparts on the other two.
PACS:
02.50.Le; 89.65.-s; 89.75.Fb; 02.50.Ga
1. Introduction
Coordination games are pervasive in social interactions. It is argued that coordination games are the cornerstone of our institutions and the so-called social contract [1]. Even information transfer, often modeled as a signaling game, exhibits typical coordination game features [1,2,3,4,5]. Furthermore, the connection between coordination and cooperation is certainly close. The well-known Prisoner’s Dilemma (PD) is paramount in the study of cooperation [6,7,8,9], and indeed this interaction metaphor provides the most stringent scenario for cooperation to thrive [6]. Yet, coordination games, taken also as relaxed cooperative dilemmas [6], are said to be the ancient source of human cooperative behaviors [10] and a principal motive for the singularity of human social thinking [10,11]. The shared intentionality hypothesis suggests that the uniqueness of human thinking stems from essential adaptations for dealing with problems of social coordination, e.g., collective hunting or foraging [11]. Interestingly, coordination dilemmas also arise in games where fairness plays a central role [12,13].
Coordination games are characterized by multiple Nash equilibria from which no player has an incentive to unilaterally deviate. In such situations, the use of dynamic models to study the set of possible equilibrium states becomes particularly relevant [1,4,8,14,15] by enabling the analysis of why individuals evolve to a specific equilibrium state and in what conditions they depart from it. This endeavor is especially relevant for social and biological sciences where one not only finds multiple states that constitute preferred alternatives to each other, but also many commonalities between problems occurring in both scientific domains [16,17,18,19,20].
Traditionally, coordination game models encompass interactions within a single class of individuals. Consider the following example: two men are in a boat and they can either row or keep comfortably still, both being equivalent regarding the problem at stake. They are expected to make a simultaneous decision. Only if they both row together they manage to proceed and reach their destination. If only one rows, the effort will be vain. The best result is naturally achieved if they both coordinate for rowing. Yet, this outcome may be undermined by the fear of rowing alone, as that would result in making an effort for nothing [1,21]. This simple example, depicted by Hume in A Treatise of Human Nature [21], evidences a paradigmatic interaction that requires some form of correlated action between two individuals, in order to achieve the best possible outcome. What kind of behavior will they coordinate into and what do the boat riders need to get coordinated?
A first solution comes expeditiously: individuals have to communicate, share information and ultimately reach an agreement. Alternatively, let us imagine a world in which the whole population faces the same problem of riding the same kind of boat. Individuals often observe the trail of other boats and assess the actions of the boat riders concomitantly. They use the information gathered to derive simple strategy rules. As time goes by, they may learn to behave distinctly, given two possible strategy profiles: (1) to row means success, thereby I should row or (2) to row means wasting valuable time and energy, so I should keep still. What is interesting to note is that the learned behavior strongly depends on the population culture and status quo. If the large majority of individuals row, that activity is perceived as successful, as those that row frequently find peers that also do so. Their boats readily reach the destination. If the large majority of individuals keep still, those that row will probably do it alone, thereby wasting energy for nothing. As such, rowing will be perceived as unsuccessful. Without any kind of top-down control, and only resorting to simple local imitation of successful behaviors, a population of boat riders—initially composed by those who row and those who avoid it—will self-organize into an homogenous state with everyone rowing or everyone keeping quiet.
This dynamical approach is intimately related to the study of complex adaptive systems [16,22,23]. We consider the existence of (a large number of) individuals that, by simple local rules of influence, drive the overall state of the population to one out of two possible equilibrium configurations. No central authority or top-down control is considered, and the final outcome is dictated by the population history (or path dependency).
Coordination games have a singular link with the study of complex systems and population dynamics in social settings and problems of different nature. In this regard, the works of Schelling and Skyrms on dynamical models of coordination [1,4,23] are paramount. Other applications include the so-called signaling games used to uncover the dynamics of information transfer, the evolution of languages and meaning [1,3,4,5] and games related to the problem of information communication and coordination [5,15,24,25,26], among many other. All these problems involve information production and exchange, with concomitant entropy variation [27]. For instance, in signaling games, information content in signals identifying states has been measured in terms of the Kullback–Leibler distance [5]. Here, however, we shall be more interested in the changes taking place throughout the self-organizing trajectories of a population of individuals exhibiting a limited numbers of traits.
Common to most of the games and models is a single class of individuals, as in the boat-example above. However, many social problems are in fact co-evolutionary problems, where, for example, the (un)success of a given strategy in a population of individuals of type A depends on the (un)success of another population of individuals of type B and vice-versa. Examples of this type of interaction abound in society such as the relations between the government and the private sector, social activism towards/against government or market policies and actions, among many others. Conjuncture (time) and context (space) may dictate an overall equilibrium configuration for all populations involved, as a result of a co-evolutionary process. Again, different status at given times, combined with their continuous adaptation and co-evolution, may lead the world to different equilibrium states.
Evolutionary game theory, applied to the study of interdependent sectors of society, can thus help to understand the conditions that explain the status-quo, as well as unfold possible future equilibrium states. Furthermore, it can be instrumental in helping one devise necessary measures and/or actions to be taken in order to promote the shift towards alternative equilibrium states, in some sense more desirable. These transitions, together with the associated actors and challenges, can be conceived at different scales. For instance, at a supranational level, this is particularly relevant when trying to mitigate current climate change problems, by changing to a political coordination that can effectively guarantee the future sustainability of humanity as a whole [18,28,29,30,31,32]. At smaller, city scale, the so-called parallel distributed planning suggests a multiplicity of actors organized in different sectors with interdependent interests (e.g., families, firms, planning administration) [33], that are able to take decisions able to impact (and hopefully steer to the most desirable coordination) processes such as the integration of immigrants [34], which constitutes, at present, an important conundrum.
The focus of the present paper is to review existing mathematical tools in evolutionary game theory and employ them to analyze the self-organization process stemming from coordination dynamics between and among different sectors of society. The study of evolutionary dynamics and strategy stability within multi-population models is typically addressed assuming two (infinite) populations and two available strategies [35,36]. Here we extend this framework to include three populations, given the problem at stake. We set the stage by defining a two-sector dynamics in the framework of a producer/consumer interaction. Subsequently, we extend the framework to address the dynamics of producer/consumer/public interactions. The addition of individuals from a third sector (public) introduces important non-linear feedbacks, provided that their decisions can simultaneously influence and be influenced by the dynamics of the previous two sectors. Given the multi-dimensional analysis that considering a third sector implies, those feedbacks are non-trivial to anticipate. We depict the global dynamics for some specific examples. Then, by resorting to stability theory and by taking advantage of the fact that we are dealing with coordination dynamics, we focus on the characterization of the ensuing equilibria, putting emphasis on the qualitative changes that the new sector introduces, using the previous two-sector coordination dynamics as a reference. We show that the new sector can promote or prevent the self-organization of producers/consumers into the socially desirable equilibria, which naturally depends on the mechanisms employed by the public but also on the subtle reward that producers/consumers may feedback into the public sector.
2. Evolutionary Game Theory
The toy example of boat riders provided in the introduction has a set of interesting ingredients: (1) individuals interact strategically, in the sense that their gains depend both on their strategies and on the strategies of their opponents [37]; this means that (2) the success of a given strategy naturally depends on the ecology of behaviors present, at that time, in the population (frequency-dependence) and (3) the new behavior adopted by an individual followed a simple social learning rule, one in which individuals observe their peers and imitate those behaviors of theirs perceived as more successful (a learning mechanism that, despite being conceptually very simple, stands as a heuristic often employed by humans [38,39,40]).
The features of this analysis place us in a territory remarkably close to evolutionary biology [16,17,18,19,20]. In this field, the dynamics of traits (instead of behaviors) is studied as the byproduct of natural selection. Also here, the advantages of one trait depend both on the environment and on the other traits present in the population. Although the nomenclature is different, the framework usually employed to study this frequency-dependent trait dynamics is also evolutionary game theory (EGT) [35,41,42]. Conveniently, we will apply this framework to analyze a set of coordination dynamics that may arise in political and socio-economic contexts. We extend the previous analysis through the addition of coordination dynamics between individuals belonging to different sectors of society.
Let us suppose that we want to study one infinitely large population in which individuals can adopt one out of two strategies, named C (historically meaning Cooperate) and D (Defect). A fraction x of individuals adopts C and we are concerned with studying how this quantity evolves. The social learning mechanism introduced above suggests that the adoption of strategy C by and individual D implies that this individual has imitated another with strategy C. Let us consider that imitation is more probable if the fitness of the role model is higher than the fitness of the imitator. Successful strategies are imitated [38]. Here we say that the success of C is measured by fC (fitness of C), and similarly, fD stands for the success of D. Both quantities depend on the frequency of strategies in the population. How does the fraction x evolve? The famous replicator equation [35,43] translates the following intuition: Strategies that do better than average will grow, whereas those that do worse than average will dwindle. Denoting by F the average fitness of the population, the evolution of x is thereby summarized in the gradient of selection . By noting that F = xfC + (1 − x)fD and using ΔfC,D(x) = fC(x) − fD(x) the gradient can be rewritten in the form:
The mathematical setup described above holds for single evolving populations. However, it is possible to generalize the aforementioned equations to consider multiple co-evolving populations.
Let us restrict the analysis to situations in which imitation occurs within populations and success is derived from games between populations. Considering that individuals may again opt for one out of two strategies, we move now into a multi-dimensional system of equations; g(x), becomes now:
where represents the gradient of selection corresponding to population i. This implies the definition of , i.e., the fitness difference for individuals in population i, given the overall state of all populations, .
The replicator equation, g(x) (and naturally its multi population generalization, ), has interesting properties for the analysis of coordination dynamics. The sign of g(x) indicates the direction of evolution. If g(x) > 0, the population will evolve towards an increase in Cs. Contrarily, when g(x) < 0, the fraction of Ds increases. The values x* satisfying g(x*) = 0 are the fixed points of the evolutionary dynamics, which in the simplest scenario of one population and two strategies can be characterized as stable (g’(x*) < 0) or unstable (g’(x*) > 0). If g’(x*) > 0, x* is also called coordination point [8] providing an essential ingredient to unveil the coordination dynamics of the populating being studied. If, instead of having infinite populations, we consider a more realistic setting in which populations or sectors involve a finite number of individuals, then one must modify the dynamics in order to take into consideration stochastic effects that in some cases, may be important [44,45]. In this regime, one is typically concerned with the time evolution of the probability distribution over the phase space, which can be modeled by resorting to a master equation [46,47]. Under specific circumstances—large but finite population sizes—these equations can be approximated by a Fokker–Plank equation [48]. Notably, this approximation of a discrete model by a continuous counterpart is an exercise with particularities (e.g., the scaling between population size and time-scales) that may impact the resulting description of the system [49]. By focusing on infinite populations, in this paper we resort to dynamical portraits that leave stochastic effects out for two main reasons:
- (1)
- We are concerned with providing an example of multi-sector dynamics and as we will see, the analytical challenges of these dynamics can be grasped even considering the infinite population assumption and the analytical framework that this limit entails.
- (2)
- The coordination nature of the games under study puts special relevance in the comprehension of the resulting self-organizing dynamics, namely, the characterization of each equilibrium, the phase space that leads to them and the qualitative changes (in the dynamical portrait) that result from adding new sectors.
A Simple Game—One Population, Two Strategies
The interaction example provided so far deals with a single class of individuals (say, boat riders) that may choose between two actions (rowing or keep quiet). As Table 1 depicts, we can generalize the metaphor by also assuming Cooperation (C) and Defection (D) as possible strategies. In this way, payoffs are traditionally segmented into Reward (R), earned by a C that also meets a C; Suckers payoff (S), earned by a C that is cheated by a D; Temptation (T) that is earned by a D that (potentially) exploits a C and finally Punishment (P), provided when both individuals are D. Coordination games are characterized by R > T > P > S [50,51] and are regarded as a relaxed cooperative dilemma [6]. For simplicity, we fix P = 0, R = 1, T = 0.5 and analyze the different outcomes that are engendered by varying S < P.

Table 1.
Generic payoff matrix of a two-person, two-strategy game within one population. Each cell dictates the payoff earned by the row player for each possible strategy profile. We test the specific coordination game occurring when R = 1, T = 0.5, P = 0 and S ranging from −1.5 to 0.
As depicted in Figure 1, varying S has significant effects on the game dynamics. Although not being a part of the payoff earned in the equilibrium strategy profiles, S provides a source of risk and incentive that ultimately shapes decision-making [9]. Using the EGT interpretation of risk-dominance (i.e., a strategy is risk-dominant if its basin of attraction is larger than ½ [7,8]), Figure 1b shows that increasing the absolute value of S has the effect of turning D a risk-dominant strategy, although C is always the payoff dominant strategy. Thereby, a coordination failure is likely to occur (understood as failing to coordinate at the optimal equilibrium).
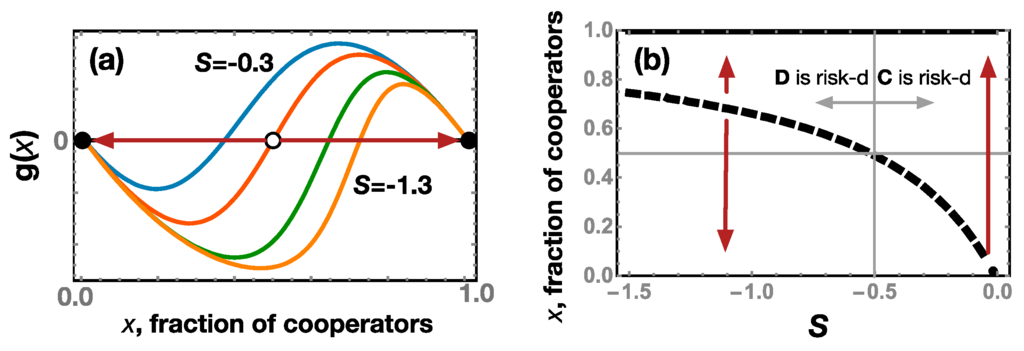
Figure 1.
(a) Gradient of selection for the game in Table 1. Assuming that Z is infinitely large (Equation (1)), there is an interior unstable fixed point (open circle) whose position (x*) depends on S as x* = S/(S − 0.5) [52]. (b) Position of the interior unstable fixed point (dashed line) when S varies. S defines which equilibrium (C or D) is risk-dominant, i.e., has a basin of attraction larger than ½.
This single sector game can naturally encompass all previous mentioned game metaphors of coordination dynamics but it does not answer the question of how these dynamics change when different sectors (or types) interact: Employees and Employers, Producers and Consumers, Predators and Preys or Senders and Receivers, to name a few examples. In all cases, interaction occurs between sectors but social learning is constrained within sectors.
In the next section, we present simple examples of the evolutionary dynamics between individuals from multiple sectors. Naturally, the framework can be applied to any game, yet, we focus on toy examples that exhibit typical coordination dynamics.
3. Models for Multi-Sector Populations
3.1. Two Sectors, Two Strategies
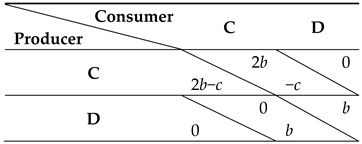
Consider that two players get together in a typical market environment: one as Producer and the other as Consumer. They will both earn a benefit b > 0 if a transaction occurs, which happens whenever their strategies are aligned: what one wants to sell, the other seeks to buy (and vice-versa). Both can choose between two products C or D. Product C has a higher quality but also an extra-cost c > 0 to be produced (for simplicity we assume that the producer will assume this extra-cost and will not transfer it to the consumer). A product C, with high quality, provides a good reputation to its Producer and adds an obvious benefit to its Consumers. This payoff structure is summarized in Table 2. We are dealing with a coordination game, in which Producers and Consumers are in Nash equilibrium when they both play C or D. Although both (C,C) and (D,D) are Nash Equilibria, the pair (C,C) stands as the social optimum, and coordination into (D,D) means typically coordination failure.

Table 2.
Producer-Consumer game. When a transaction occurs (strategies of Producer and Consumer are the same) there is a benefit for both. Producing a product C has an increased cost (c > 0) given the high quality of the product. The benefit earned by transacting a high quality product (2b > 0) is higher than in the low quality case (b > 0).
Using x and y to designate the fraction of Producers and Consumers adopting strategy C, the fitness difference between a C and D Producer is given by (difference in the average payoff of C and D, given the population composition, (x,y)) whereas in the case of a Consumer that amount reads as . Equation (2) boils down to:
The fixed points are given by setting , which results in the trivial solutions (0,0), (1,0), (0,1) and (1,1) and also the internal fixed point . Close to this point, it is straightforward to classify its stability and nature, resorting to a linear approximation of [35,53]. For that, we study the Jacobian matrix of :
We note that and , i.e., whenever the internal fixed point exists () it is a saddle point () [53]. We are thus in the presence of a coordination dynamics with the saddle pushing the system towards the multiple equilibria. Moreover, the eigenvalues of J at provide us information about those equilibrium points; those eigenvalues read as and the corresponding eigenvectors as . The fact that the eigenvector with positive component in x has the corresponding eigenvalue positive means that, near the internal fixed point, an increase in C-Producers (D-Producers) yields an increase in C-Consumers (D-Consumers), which allows us to infer that (C,C) and (D,D) are the stable equilibrium points. Assuming that c and b are always positive, the same is to say that the condition 2b > c should be verified. In this simplest case of non-frequency dependent payoff values, a simple look into the payoff matrix could derive the same conclusions. A more interesting scenario results from a payoff structure in which, e.g., economies of scale are accommodated. This implies the addition of an intra-sector dynamics. Let us take the example in which the benefits of producing a high-quality product increase, as more Producers are willing to do so (complementary goods). For that, we assume that the factor 2b in Table 2 is multiplied by x, the fraction of Producers adopting a D strategy:
Besides the movement of the internal fixed point (now at ), a new fixed point appears in the edge (y = 1) of the phase space, at position . Following the same method above, it is straightforward to show that the new fixed point is also associated with a saddle point (2b < 3c). There, J has an eigenvector (1,0) and a corresponding eigenvalue positive, which means that there is a coordination dynamics, not only between Producers and Consumers, but even inside the Producer sector.
We can now depict a specific example of this interaction, by plotting the gradient of selection in a two dimensional space (Equation (2)). This is represented in Figure 2, for b = 2, c = 1. The game for Consumers is symmetric and thus Producers will shift from C to D (D to C) when their consumers’ base is more (less) than ½. However, the gain in reputation derived from product C, alongside with the extra-investment needed to produce it, creates an asymmetry in the Producers’ game and in the corresponding Consumer’s response. As such, the joint dynamics of a majority of C Producers and ½ of C consumers takes the system to state (C,C). This basin of attraction is represented by a gray shade in Figure 2.
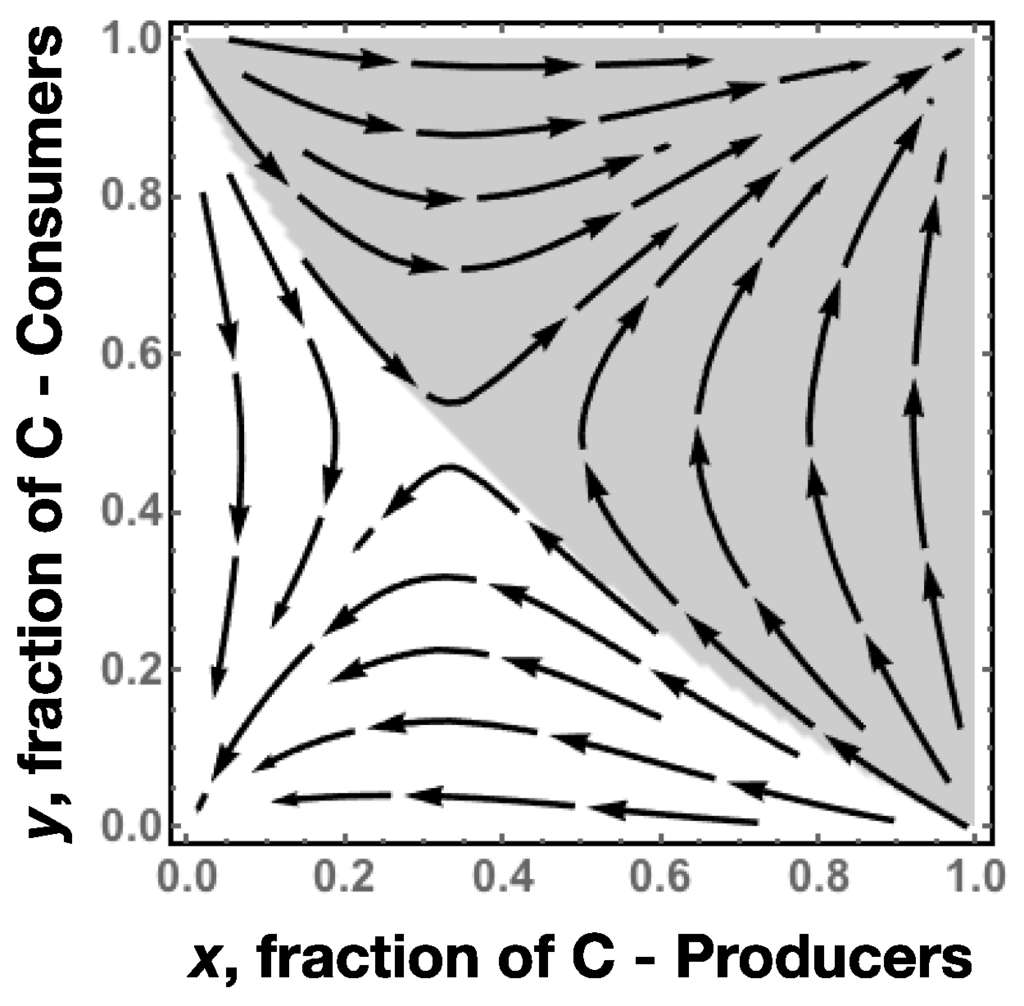
Figure 2.
Gradient of selection (Equation (2)) of the game represented in Table 2, when b = 2, c = 1. State (C,C) corresponds to point (1,1) whereas state (D,D) corresponds to (0,0).
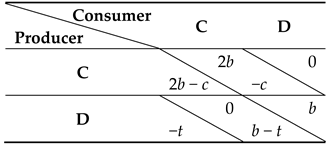
Note, however, that the white basin of attraction in Figure 2 leads to a coordination failure. This could be overcome if the payoff structure of this game is slightly modified, given that an external factor (e.g., a regulatory organization, other production-chain intermediary players, government policies, etc.) imposes an extra-cost to companies opting for D. This slight payoff modification can again be represented in a table form (Table 3) and the dynamical outcome shown in Figure 3.

Table 3.
Producer-Consumer game with external intervention. An extra-cost (t) is applied to Producers that assemble the low-quality product D. Interestingly, the case in which t < 0 models a corruptive external intervention, where low-quality products are perversely favored.
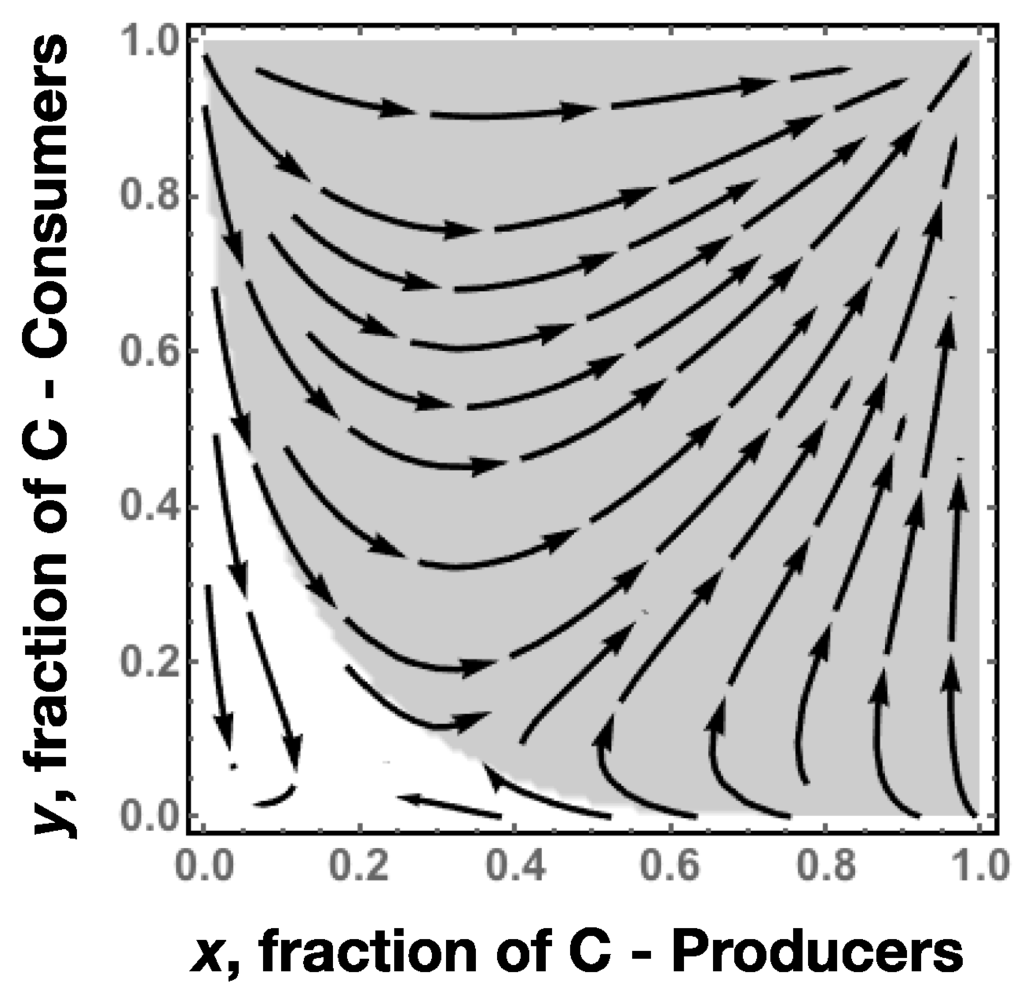
Figure 3.
Gradient of selection (Equation (2)) of the game represented in Table 3, when b = 2, c = 1, t = 2.5. State (C,C) corresponds to point (1,1) whereas state (D,D) corresponds to (0,0).
The basin of attraction towards (C,C) is significantly enlarged (gray area) due to an external intervention that confers a larger asymmetry to the Consumers’ game. The coordination point that defines the dominance of strategy C in both populations indicates a more rapid response of Producers to consumers’ interests, when they opt for C.
Table 3 includes one additional parameter that is exogenous to the game played by Producers and Consumers. This, however, needs not to be true, in the sense that, often, the exogenous term originates from an interdependence that actually occurs endogenously, though originating from another player not yet identified. This typically means considering a new sector which, together with the other two, will also respond to the strategic landscape of the coordination game. We introduce this idea in the next section where we model a game between three interdependent sectors and two strategies in each.
3.2. Three Sectors, Two Strategies
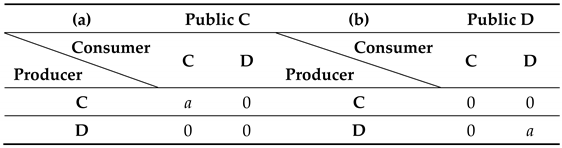
We now focus on the case in which three sectors co-evolve. We assume that there is a Public body that, when choosing C, will be active in applying a tax to low-quality products (offered by D Producers). This sector is sensitive to the other sectors’ opinion (e.g., given the existence of elections). For simplicity, in this illustrative model we assume that the Public sector earns a payoff a when the two sectors are in agreement with its policies. Table 4 summarizes this new payoff structure. This way of formulating the game, again, assumes that imitation occurs within populations and success is derived from games between populations. Because interactions between individuals of the same sector are not explicitly included, this assumption implies that interactions always involve one individual from each sector, a subclass of all possible game types involving three sectors.

Table 4.
Payoffs accruing to the Public sector while interacting with Producers and Consumers. A Public agent (with strategy C or D) will earn payoff a when interacting with individuals with the same strategy (respectively, C or D) from other sector. This creates an extra coordination, between Public and the other sectors.
Combining the payoff structure defined by Table 3 and Table 4, the dynamical system describing the interaction of the three sectors (Equation (2)) reads as:
As it is well known, a system of three or more non-linear differential equations provides challenging barriers to a qualitative analysis of the whole range of resulting dynamics [53]. This said, the introduction of a third sector makes perfectly sense under a wide plethora of socio-economic situations, however, it entails important analytical issues. Here we are concerned in motivating the need to evaluate the full 3-sector system (previously with just 2 sectors) and not so much to tackle the current technical difficulties that the problem poses. We focus on studying the structure of the previous equilibria and its qualitative changes.
Repeating the same methodology, we find that the previous 2-sector coordination between Producers and Consumers (Table 2) exists only whenever . The fixed point, once again, can only be a saddle point, this time located at .
Naturally, the previous condition, 2b > c, do not remain as a guarantee that (C,C,-) and (D,D,-) are indeed an equilibrium. Let us analyze the eigenvalues of the Jacobian matrix (J) of :
near the trivial solutions of and again assuming that b > 0 and c > 0, we verify that, e.g., (C,C,C) is only stable (J|(C,C,C) has three negative eigenvectors) whenever c < t + 2b and a > 0. In this way, when the condition 0 < 2b − c< −t is satisfied, (C,C,C) looses its stability in this 3-sector extension. Additionally, a > 0 results in a pernicious dynamics whereby the only asymptotically stable state [35] is (D,D,D), in which Consumers are impaired. In this case, a < 0 would result in the stability of (C,C,D). Naturally, the effect of parameter a in providing the needed stability to a state in which both Producers and Consumers are coordinated into (C,C) is completely extraneous in the 2-sector analysis. Interestingly, this 3-sector study allows us to observe that, on top of the common assumption about external entities (public) being needed to solve coordination failures of producers/consumers, the feedback provided by the consumers/public into the public sector also provides an important contribution to the overall dynamics. The difficulties in apprehending the resulting three sector dynamics would be more pronounced if we had extended the scenario assuming increasing benefits (of scale) of Producers (as in Equation (5)). Furthermore, we focus on one-shot interactions, not considering iterated plays or strategies conditioned on past information (that could be modeled as asymmetric, depending on the specific sector), as that would result in an extended strategy space that would prevent a tractable exposition of the global dynamics involved in a three-sector dynamics.
As Figure 1, Figure 2 and Figure 3 already suggest, the particularities of the coordination dynamics are not fully apprehended by solely relying on a stability analysis of Equation 6. Indeed, the existence of multiple equilibria puts special emphasis in the study of out-of-equilibrium properties of the system, such as the relative sizes of the basins of attraction that lead to each equilibrium state. For pedagogical purposes, we proceed through this way in three incremental steps, by showing some numerical examples regarding (1) the dynamical portrait for the extreme cases where public sector is all D or all C; (2) the full dynamical portrait with colored basins of attraction indicating the respective attractor and (3) the relative size of the basins of attraction towards the socially desirable C strategy, for a wide range of t (the incentive by the public sector).
Following Equation (2), the gradient of selection can be represented in a three-dimensional cube (Figure 4), with the corners representing monomorphic states in which all the sectors fully adopt one of the strategies (C or D). We refer to (C (D),C (D),C (D)) as the monomorphic state in which Public is fully adopting C (D), Producers are fully adopting C (D), and Consumers are fully adopting C (D). In the three dimensional cube, the vertex with position (0,0,0) corresponds to (D,D,D) while (1,1,1) corresponds to (C,C,C).
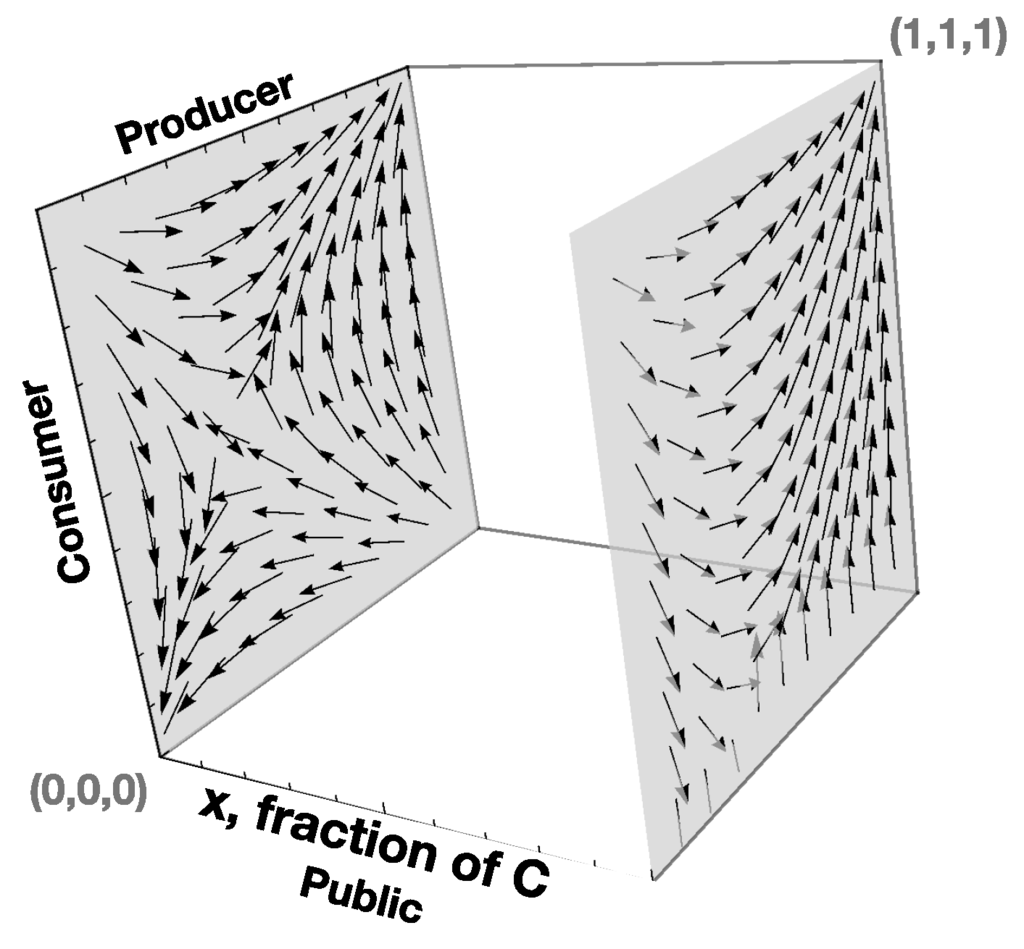
Figure 4.
Gradient of selection of the overall game played by the three sectors, represented only when all Public is C or D. The game is a synthesis of the games governed by payoff structures in Table 1, Table 2 and Table 3. Here, the three sectors co-evolve. Other parameters: b = 2, c = 1, t = 2.5.
In Figure 4 we represent the same gradients as in Figure 2 and Figure 3, yet placed in the full state space that embodies the co-evolving process of the three sectors. That space is well-captured by a cube. By incorporating the Public sector it is possible to analyse not only its impact on the Producers and Consumers but also to study its own dynamics in response to the behaviour of the other two sectors. In Figure 5 we explicitly represent the full gradient considering the three sectors. Naturally, the increased complexity proves challenging regarding visualization techniques that allow the interpretation of the evolutionary dynamics. In Figure 5 we colour each vector of the gradient according to the final destination of the trajectory that passes by its origin. If the destination is (C,C,C), the colour used is blue. If the path ends in (D,D,D), we use gray. This way, we have a visual hint of the size of the basins of attraction. The basin of attraction towards (D,D,D) and (C,C,C) provide an intuition for how easy it is to overcome the lock-in status-quo and move the population to the most favourable equilibrium (C,C,C).
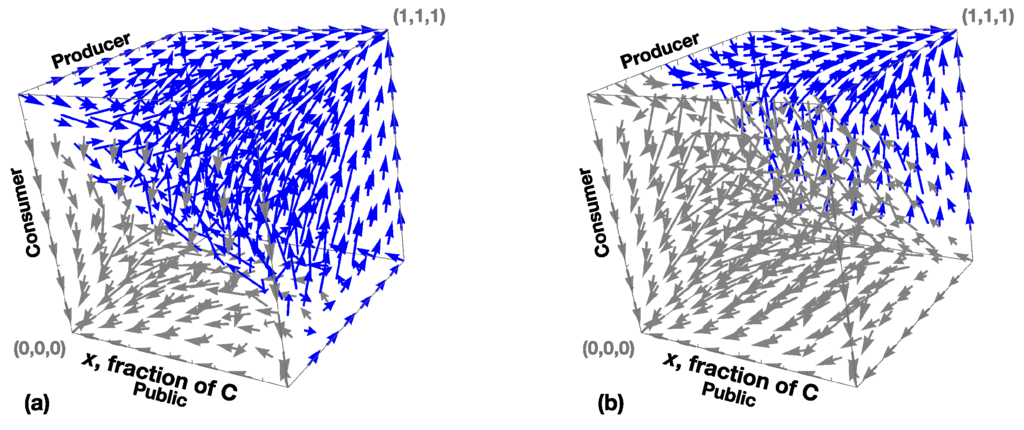
Figure 5.
Gradient of selection of the overall game played by the three sectors. The game is a synthesis of the games governed by payoff structures in Table 1, Table 2 and Table 3. Here, the three sectors co-evolve. For each possible configuration there is an associated vector that translates the most probable dynamic, given the gradient of selection (see Section 2). The configurations that are parte of paths leading to (0,0,0) are colored with gray; configurations that are part of paths leading to (1,1,1) are colored with blue (a) b = 2, c = 1, t = 4, a = 2; (b) b = 2, c = 4, t = 1, a = 2.
Wrapping up, it is easy to grasp that the game played by individuals whose dynamic is depicted in Figure 5a is more capable of preventing a coordination failure than the game corresponding to Figure 5b. Figure 5 shows that the preferred equilibrium is strongly affected by the fact that three sectors co-evolve and, naturally, by the considered payoff structure. As the tax applied by the Public body increases, which happens from Figure 5a to Figure 5b, the basin of attraction towards (C,C,C) increases, with more initial conditions leading to this configuration.
Note that, as we traverse the interior of the cube along a direction perpendicular to the Consumer-Producer plane, the impact of this parameter t is changing, depending on the relative proportion of individuals of type C in the new sector. Naturally, Figure 4 and Figure 5 provide a specific instance of an interaction that can be rather generalized. By picking a grid of initial conditions and proceeding through numerical integration, we compute an approximation for the fraction of the state space leading to the final adoption of strategy C, by each of the three sectors. To exemplify this procedure, we input as initial conditions all the points (x,y,z) such that 0 < x,y,z < 1 (i.e., interior points) and with x,y,z as multiples of 0.05. We compute the numerical solution of Equation (6) at time 1000 (which was verified to be enough in order to reach an equilibrium point) and, for different values of parameters t and a, we keep track of the initial conditions leading to a point where all Producers, Consumers and Public end up employing strategy C. The results are showed in Figure 6 and evidence that the introduction of a third sector has not only a huge impact in the rendering stable/unstable previous two-sector stable equilibrium points (see stability analysis above), but also when (C,C,-) and (D,D,-) are both equilibrium points (2b – c > −t, see above), it ultimately shapes the basins of attraction that lead to each equilibrium, thus making easier or harder to overcome the two-sector coordination barrier.
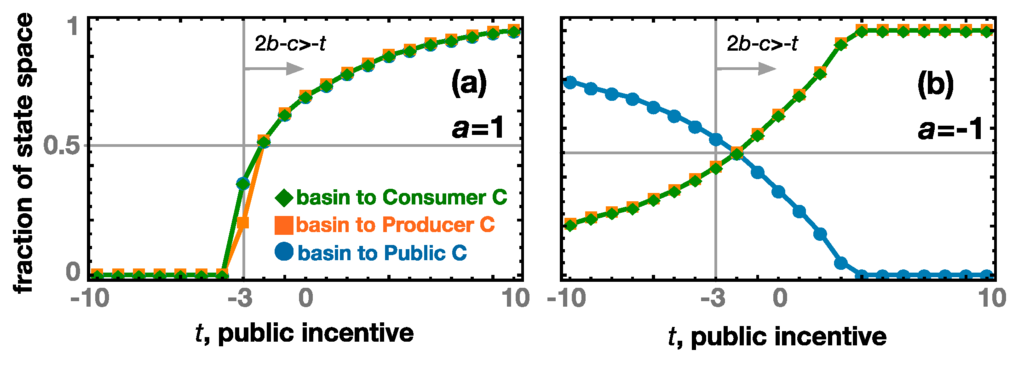
Figure 6.
Relative size of the basins of attraction leading to full adoption of C. We calculate, numerically, the solutions of Equation (6) given a grid of initial conditions (x,y,z) such that 0 < x,y,z < 1 and x,y,z being multiples of 0.05. We compute the fraction of initial conditions that, at time 1000, lead to a fraction of C adopters higher than 0.9, thus, for a wide range of t and given (a) a = 1, (b) a = −1, we calculate an approximation for the fraction of the state space leading to the full adoption of C by each of the three sectors. As the differences in (a) and (b) show, the impact of Public policy (t) in routing Producers/Consumers to C is contingent on the feedback provided by Producers/Consumers to Public (parameter a). (a) Whenever t < −3, the monomorphic state (C,C,C) is no longer stable, as we show below through a stability analysis. Notwithstanding, when both (C,C,C) and (D,D,D) are stable (t > −3), coordinating into C can be easier/harder given the role of the public sector through parameter t. (b) when a < 0, the public sector is anti-coordinated with producers/consumers, which is here observable by the impact of parameter t in decreasing (increasing) the basin of attraction of public (producers/consumers) towards C. Other parameters: b = 2, c = 1.
It is important to retain the message that the introduction of a third sector (1) makes sense from the socio-economic point of view in light of the particular processes being modeled, however, even considering the comfortable deterministic analysis of an infinite population, we can see that the third sector (2) introduces significant technical challenges concerning the available analytical approaches to systematically study the resulting dynamics at the same time that (3) implies significant changes in both the structure of equilibria and corresponding basins of attraction, unforeseen in a 2-sector scenario.
These features arise naturally in this context, leading to richer dynamics, and the conclusions can be adapted to a wider range of situations that cannot be accounted for by a single-sector model.
4. Conclusions
In this paper we analyze the ubiquitous coordination dynamics of populations in which interactions involve multiple sectors of a society. These are of particular importance in cases where there is a need to shift the current overall status-quo in order to move into another overall equilibrium state that, e.g., may bring long-term benefits to society as a whole. Traditionally, coordination games incorporate mostly interactions between individuals of a single class. Some are specially relevant for understanding the role of information transmission in human societies [1,2,3,4,8,24,25]. However, the intrinsic complexity of socio-political relations calls for modeling techniques that account for typical properties of complex systems, such as self-organization and historical contingency. Evolutionary game theory stands as a toolbox capable of providing the needed formalism to model the coordination dynamics. In this context, the inclusion of multiple sectors stands as a requirement to cope with the intricate and co-evolving nature of actual socio-economic systems. Here, we extended the toolbox of EGT to incorporate a set of multi-sector coordination dynamics.
We devised a conceptually simple Producer-Consumer model, involving coordination between these two sectors. We showed how the quantification of costs and benefits in each sector may fundamentally change the overall basins of attraction and, as such, the preferred order of the equilibria as well as the approach to equilibrium. We did so by introducing an exogenous parameter that, in fact, can be naturally viewed as endogenous, to the extent that we enlarge the number of sectors from two to three. Naturally, this third population can differ depending on the problem being studied.
A comprehensive description of the whole dynamics portfolio accruing from a game interaction is feasible in the case of one sector and two strategies (Table 1). As the number of interacting populations increases, the sum of strategic arrangements rises concomitantly. When reaching the scenario of three sectors and two strategies, the number of payoff entries (possible encounters times the number of sectors) amounts to 24. Naturally, this precludes any attempt to characterize the full range of possible dynamics. Here we opt to focus on a payoff structure that reproduces a typical coordination dilemma. Producers and Consumers interact in such a way that it is easy to identify a payoff and risk dominant equilibrium, with the corresponding basins of attraction sized by a few parameters (b, c). A third sector (Public) coordinates with the previous in a way determined by (1) the impact it provides in the social undesirable equilibrium (parameter t, which can go from a Pigouvian tax to a corruptive incentive) and (2) the response provided by the coordinated Producers and Consumers (a). In contexts of policy making, recognizing and understating these dynamics of cooperation becomes important to anticipate the effectiveness of new policies or to identify possible drawbacks difficult to unveil without the use of a multi-population approach, such as the one we discuss here.
The above multi-sectorial analysis implies a higher difficulty in model design and analysis, due to the increased dimensionality. New tools for visualization of results and their analysis are needed in order to improve and facilitate its widespread adoption in research across many fields and its application in real world contexts.
Acknowledgments
We thank Hermann Haken for valuable suggestions. This research was supported and carried out in the framework of the projects: (1) Diffusion of Mass E-Mobility and Integrating Renewable Energy in Smart Grids and Cities: Intelligent Agents for Efficient Energy Consumption, funded by the Israeli Ministry of Energy and Water (SE and JP); and (2) by Fundação para a Ciência e Tecnologia (FCT) through project grants SFRH/BD/94736/2013 (FPS), PTDC/EEI-SII/5081/2014 (SE, FPS, FCS, JMP), PTDC/MAT/STA/3358/2014 (SE, FPS, FCS, JMP) and by multi-annual funding of CBMA, INESC-ID and CICS.NOVA (under the projects UID/BIA/04050/2013, UID/CEC/50021/2013 and UID/SOC/04647/2013) also provided by FCT.
Author Contributions
This paper results from the original suggestion of Juval Portugali to investigate the interdependence between different sectors of society using game theoretical methods. Fernando P. Santos, Sara Encarnação, Francisco C. Santos and Jorge M. Pacheco designed and performed the research and analyzed the data. All authors wrote the paper. All authors have read and approved the final manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Skyrms, B. The Stag Hunt and the Evolution of Social Structure; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Huttegger, S.; Skyrms, B.; Tarrès, P.; Wagner, E. Some dynamics of signaling games. Proc. Natl. Acad. Sci. USA 2014, 111 (Suppl. 3), 10873–10880. [Google Scholar] [CrossRef] [PubMed]
- Lewis, D. Convention: A Philosophical Study; Wiley: Hoboken, NJ, USA, 2008. [Google Scholar]
- Skyrms, B. Evolution of the Social Contract; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- Skyrms, B. Signals: Evolution, Learning, and Information; Oxford University Press: Oxford, UK, 2010. [Google Scholar]
- Rand, D.G.; Nowak, M.A. Human cooperation. Trends Cogn. Sci. 2013, 17, 413–425. [Google Scholar] [CrossRef] [PubMed]
- Nowak, M.A. Five rules for the evolution of cooperation. Science 2006, 314, 1560–1563. [Google Scholar] [CrossRef] [PubMed]
- Nowak, M.A. Evolutionary Dynamics; Harvard University Press: Cambridge, MA, USA, 2006. [Google Scholar]
- Capraro, V. A model of human cooperation in social dilemmas. PLoS ONE 2013, 8, e72427. [Google Scholar] [CrossRef] [PubMed]
- Tomasello, M.; Melis, A.P.; Tennie, C.; Wyman, E.; Herrmann, E. Two key steps in the evolution of human cooperation. Curr. Anthropol. 2012, 53, 673–692. [Google Scholar] [CrossRef]
- Tomasello, M. A Natural History of Human Thinking; Harvard University Press: Cambridge, MA, USA, 2014. [Google Scholar]
- Santos, F.P.; Santos, F.C.; Paiva, A.; Pacheco, J.M. Evolutionary dynamics of group fairness. J. Theor. Biol. 2015, 378, 96–102. [Google Scholar] [CrossRef] [PubMed]
- Nowak, M.A.; Page, K.M.; Sigmund, K. Fairness versus reason in the ultimatum game. Science 2000, 289, 1773–1775. [Google Scholar] [CrossRef] [PubMed]
- Pacheco, J.M.; Santos, F.C.; Souza, M.O.; Skyrms, B. Evolutionary dynamics of collective action in N-person stag hunt dilemmas. Proc. R. Soc. Lond. B 2009, 276, 315–321. [Google Scholar] [CrossRef] [PubMed]
- Pacheco, J.M.; Vasconcelos, V.V.; Santos, F.C.; Skyrms, B. Co-evolutionary Dynamics of Collective Action with Signaling for a Quorum. PLoS Comput. Biol. 2015, 11, e1004101. [Google Scholar] [CrossRef] [PubMed]
- May, R.M.; Levin, S.A.; Sugihara, G. Complex systems: Ecology for bankers. Nature 2008, 451, 893–895. [Google Scholar] [CrossRef] [PubMed]
- Levin, S.; Xepapadeas, T.; Crépin, A.-S.; Norberg, J.; de Zeeuw, A.; Folke, C.; Hughes, T.; Arrow, K.; Barrett, S.; Daily, G. Social-ecological systems as complex adaptive systems: Modeling and policy implications. Environ. Dev. Econ. 2013, 18, 111–132. [Google Scholar] [CrossRef]
- Tavoni, A.; Levin, S. Managing the climate commons at the nexus of ecology, behaviour and economics. Nat. Clim. Chang. 2014, 4, 1057–1063. [Google Scholar] [CrossRef]
- Levin, S.A. Public goods in relation to competition, cooperation, and spite. Proc. Natl. Acad. Sci. USA 2014, 111 (Suppl. 3), 10838–10845. [Google Scholar] [CrossRef] [PubMed]
- Levin, S.A.; Lo, A.W. Opinion: A new approach to financial regulation. Proc. Natl. Acad. Sci. USA 2015, 112, 12543–12544. [Google Scholar] [CrossRef] [PubMed]
- Hume, D. A Treatise of Human Nature; Courier Corporation: North Chelmsford, MA, USA, 2012. [Google Scholar]
- Miller, J.H.; Page, S.E.; LeBaron, B. Complex adaptive systems: An introduction to computational models of social life. J. Econ. Lit. 2008, 46, 427–428. [Google Scholar]
- Schelling, T.C. Micromotives and Macrobehavior; W.W. Norton & Company: New York, NY, USA, 2006. [Google Scholar]
- Lamport, L.; Shostak, R.; Pease, M. The Byzantine generals problem. ACM Trans. Program. Lang. Syst. (TOPLAS) 1982, 4, 382–401. [Google Scholar] [CrossRef]
- Rubinstein, A. The Electronic Mail Game: Strategic Behavior Under “Almost Common Knowledge”. Am. Econ. Rev. 1989, 79, 385–391. [Google Scholar]
- Santos, F.C.; Pacheco, J.M.; Skyrms, B. Co-evolution of pre-play signaling and cooperation. J. Theor. Biol. 2011, 274, 30–35. [Google Scholar] [CrossRef] [PubMed]
- Haken, H.; Portugali, J. Information Adaptation: The Interplay between Shannon Information and Semantic Information in Cognition; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Tavoni, A.; Dannenberg, A.; Kallis, G.; Löschel, A. Inequality, communication, and the avoidance of disastrous climate change in a public goods game. Proc. Natl. Acad. Sci. USA 2011, 108, 11825–11829. [Google Scholar] [CrossRef] [PubMed]
- Santos, F.C.; Pacheco, J.M. Risk of collective failure provides an escape from the tragedy of the commons. Proc. Natl. Acad. Sci. USA 2011, 108, 10421–10425. [Google Scholar] [CrossRef] [PubMed]
- Climate Change 2014: Synthesis Report. Available online: http://ar5-syr.ipcc.ch/ipcc/ipcc/resources/pdf/IPCC_SynthesisReport.pdf (accessed on 14 April 2016).
- Pacheco, J.M.; Vasconcelos, V.V.; Santos, F.C. Climate change governance, cooperation and self-organization. Phys. Life Rev. 2014, 11, 573–586. [Google Scholar] [CrossRef] [PubMed]
- Vasconcelos, V.V.; Santos, F.C.; Pacheco, J.M.; Levin, S.A. Climate policies under wealth inequality. Proc. Natl. Acad. Sci. USA 2014, 111, 2212–2216. [Google Scholar] [CrossRef] [PubMed]
- Portugali, J. Self-Organization and the City; Springer: Berlin/Heidelberg, Germany, 1999. [Google Scholar]
- Portugali, J.; Benenson, I. Artificial planning experience by means of a heuristic cell-space model: Simulating international migration in the urban process. Environ. Plan. A 1995, 27, 1647–1665. [Google Scholar] [CrossRef]
- Hofbauer, J.; Sigmund, K. Evolutionary Games and Population Dynamics; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]
- Weibull, J.W. Evolutionary Game Theory; MIT Press: Cambridge, MA, USA, 1997. [Google Scholar]
- Von Neumann, J.; Morgenstern, O. Theory of Games and Economic Behavior; Princeton University Press: Princeton, NJ, USA, 2007. [Google Scholar]
- Rendell, L.; Boyd, R.; Cownden, D.; Enquist, M.; Eriksson, K.; Feldman, M.W.; Fogarty, L.; Ghirlanda, S.; Lillicrap, T.; Laland, K.N. Why copy others? Insights from the social learning strategies tournament. Science 2010, 328, 208–213. [Google Scholar] [CrossRef] [PubMed]
- Tomasello, M.; Call, J. Primate Cognition; Oxford University Press: New York, NY, USA, 1997. [Google Scholar]
- Fudenberg, D.; Levine, D.K. The Theory of Learning in Games; MIT Press: Cambridge, MA, USA, 1998. [Google Scholar]
- Smith, J.M. Evolution and the Theory of Games; Cambridge University Press: Cambridge, UK, 1982. [Google Scholar]
- Smith, J.M.; Price, G.R. The Logic of Animal Conflict. Nature 1973, 246, 15–18. [Google Scholar] [CrossRef]
- Taylor, P.D.; Jonker, L.B. Evolutionary stable strategies and game dynamics. Math. Biosci. 1978, 40, 145–156. [Google Scholar] [CrossRef]
- Nowak, M.A.; Sasaki, A.; Taylor, C.; Fudenberg, D. Emergence of cooperation and evolutionary stability in finite populations. Nature 2004, 428, 646–650. [Google Scholar] [CrossRef] [PubMed]
- Santos, F.P.; Santos, F.C.; Pacheco, J.M. Social Norms of Cooperation in Small-Scale Societies. PLoS Comput. Biol. 2016, 12, e1004709. [Google Scholar] [CrossRef] [PubMed]
- Haken, H. Synergetics: Introduction and Advanced Topics; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Weidlich, W. Sociodynamics—A systematic approach to mathematical modelling in the social sciences. Nonlinear Phenom. Complex Syst. 2002, 5, 479–487. [Google Scholar] [CrossRef]
- Traulsen, A.; Claussen, J.C.; Hauert, C. Coevolutionary dynamics: From finite to infinite populations. Phys. Rev. Lett. 2005, 95, 238701. [Google Scholar] [CrossRef] [PubMed]
- Chalub, F.A.C.C.; Souza, M.O. From discrete to continuous evolution models: A unifying approach to drift-diffusion and replicator dynamics. Theor. Popul. Biol. 2009, 76, 268–277. [Google Scholar] [CrossRef] [PubMed]
- Macy, M.W.; Flache, A. Learning dynamics in social dilemmas. Proc. Natl. Acad. Sci. USA 2002, 99 (Suppl. 3), 7229–7236. [Google Scholar] [CrossRef] [PubMed]
- Santos, F.C.; Pacheco, J.M.; Lenaerts, T. Evolutionary dynamics of social dilemmas in structured heterogeneous populations. Proc. Natl. Acad. Sci. USA 2006, 103, 3490–3494. [Google Scholar] [CrossRef] [PubMed]
- Traulsen, A.; Nowak, M.A.; Pacheco, J.M. Stochastic dynamics of invasion and fixation. Phys. Rev. E 2006, 74, 011909. [Google Scholar] [CrossRef] [PubMed]
- Hirsch, M.W.; Smale, S.; Devaney, R.L. Differential Equations, Dynamical Systems, and an Introduction to Chaos; Academic Press: Cambridge, MA, USA, 2012. [Google Scholar]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).