The theoretical framework for quantification of any system complexity is provided by information theory, in general. First, we may refer two seminal works on this field [
7,
8]. Entropy represents the most known quantitative measure of expected amount of information required to describe the state of a system, and builds a basic framework for the development of complexity theory [
9,
10]. Entropy is used for measuring the complexity of supply chains [
11,
12,
13,
14,
15,
16,
17]. These papers bring manifold topics and approaches, and show also more or less connections with inventory control theory, in general. Another field of applications is focused on system complexity analysis, where there is engineering design and manufacturing chains, see [
18,
19,
20,
21]. In general, the complexity of a system increases with the increasing level of disorder and uncertainty of its states, as presented in [
22]. A theoretical framework for joint conditional complexity is presented in [
23]. Application of entropy for analysis and classification of numerical algorithms and the corresponding computational complexities is discussed in [
24,
25]. Paper [
26] brings a good review of various multi-scale entropy algorithms and some applications, too. Two-echelon supply chain games and their information characteristics, in particular, are discussed in [
27]. Finally, the papers [
28,
29,
30] are concerned with measuring the operational complexity of supplier-customer systems, and initiated our serious interest in the field.
2.1. Entropy Used to Measure Operational Complexity
Basically, we use classical Shannon information-theoretic measure and corresponding entropy defined for any information system with
N states being characterized with a discrete probability distribution,
i.e., each system state may appear with probability
pi ≥ 0, with
The Shannon entropy is given by following formula, which corresponds to Equation (1) taking
c = 1 and
b = 2:
where
H is used to denote entropy calculated using log
2(
) in particular, whilst the entropy calculated with natural logarithms log(
),
i.e., with
b =
e, will be denoted by
S from here on.
The maximal value of
attainable is given for uniform distribution, and takes the form:
Recently, generalized (
c,
d)-entropy was presented in [
31], which is particularly interesting. It provides a versatile tool for quantitatively measuring complex systems, which are often inherently non-ergodic and non-Markovian ones, thus relaxing the rigorous need to apply Shannon entropy. Moreover, the (
c,
d)-entropy, with system-specific scaling exponents,
c and
d, has yet another attractive feature. This entropy contains many known entropy functionals as special cases, including Shannon entropy among others.
Following [
31], the (
c,
d)-entropy is defined as follows:
using natural logarithmic function log(
), and incomplete gamma function Γ(
), as key-tools.
The incomplete gamma function is given by:
when relaxing the lower integration bound of the Euler gamma function:
which provides useful extension of the factorial, where (
n − 1)! = Γ(
n), for any positive integer
n.
The Boltzmann–Gibbs entropy originated in thermodynamics:
It differs from Shannon entropy quantitatively just by using natural logarithms instead of logarithms with base 2. Hence, it is usually denoted by the symbol SBGS and called Boltzmann–Gibbs–Shannon entropy, in the most correct sense.
Following [
31], the relation between (
c,
d)-entropy and the Boltzmann–Gibbs–Shannon entropy is established for
c = 1, and
d = 1:
This relation has motivated us to reformulate the additive term in Equation (3) in order to remove the additive constant −1 from Equation (7) intrinsically. Hence, we propose the modified formula in the following form:
and call it (
c,
d)-entropy as well, which still provides the desired smart relation:
Let denote the discrete distribution of any given probabilistic system thus providing a way to write the next formulae and equations in a more compact way.
Given , the can be investigated as a function of arguments (c,d) over a region Ω 2, which helps significantly to elucidate Equations (7) and (9).
We have used Mathematica® (version 10.1) to perform our numerical experiments with (c,d)-entropy given by Equation (8), as well as to discover a more general relation between (c,d)-entropy and SBGS than given by Equations (7) or (9), respectively.
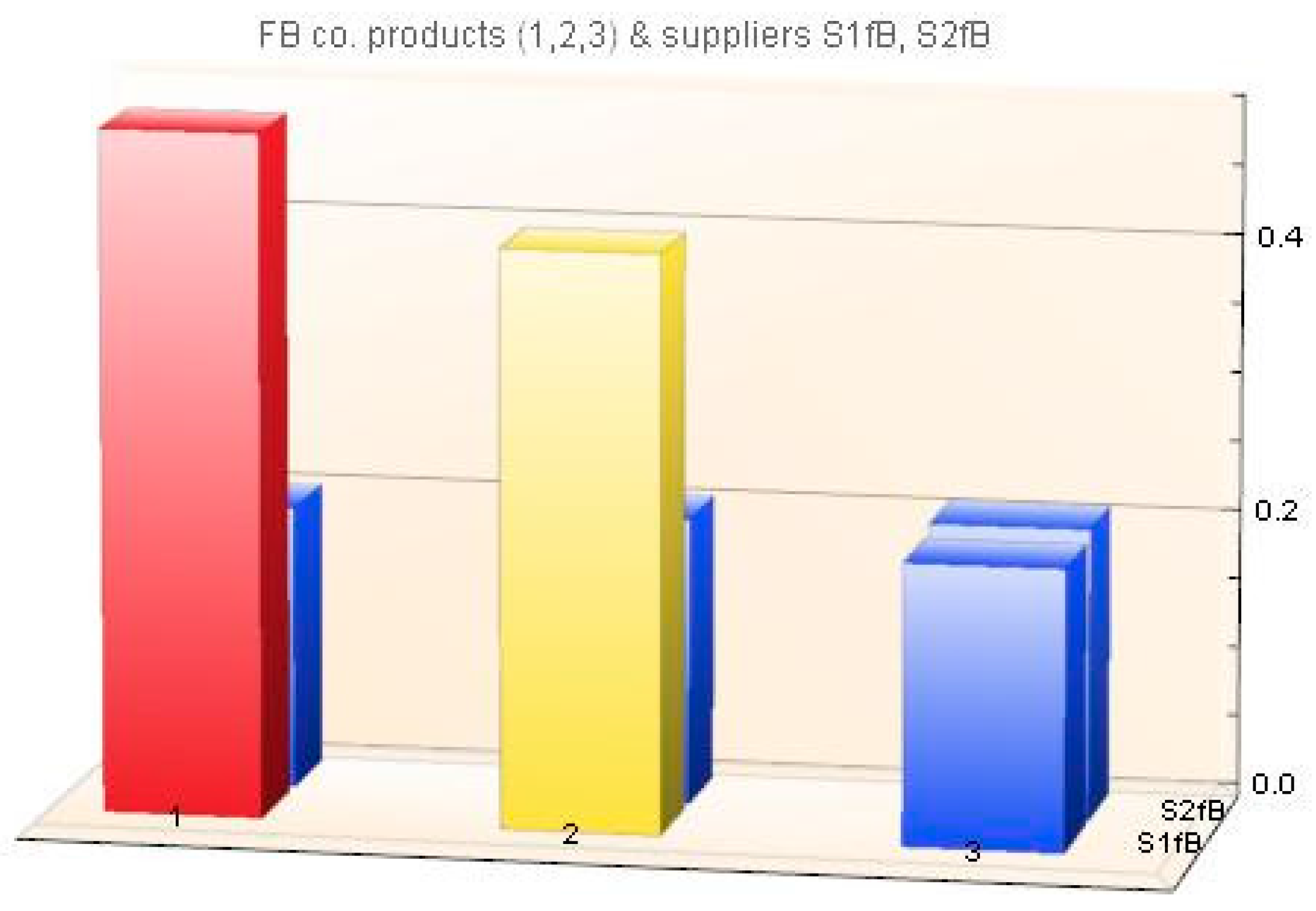
Set (c,d) Ω = [0.1, 5] × [0.1, 5] 2, where × denotes a Cartesian product of two sets. The distribution is constructed from finite samples of random numbers generated by integer pseudo-random generators. In general, L will denote the length of list of such numbers, and their range will be {0, 1, …, kmax}, thus N = kmax + 1.
We use the Mathematica function Random Integer [kmax, L], which serves exactly that purpose to give a list of L pseudorandom integers ranging from 0 to kmax desired. Sorting the list for given kmax, the frequencies and corresponding empirical distribution will be calculated as an approximation of a uniform distribution of probabilistic system with N states.
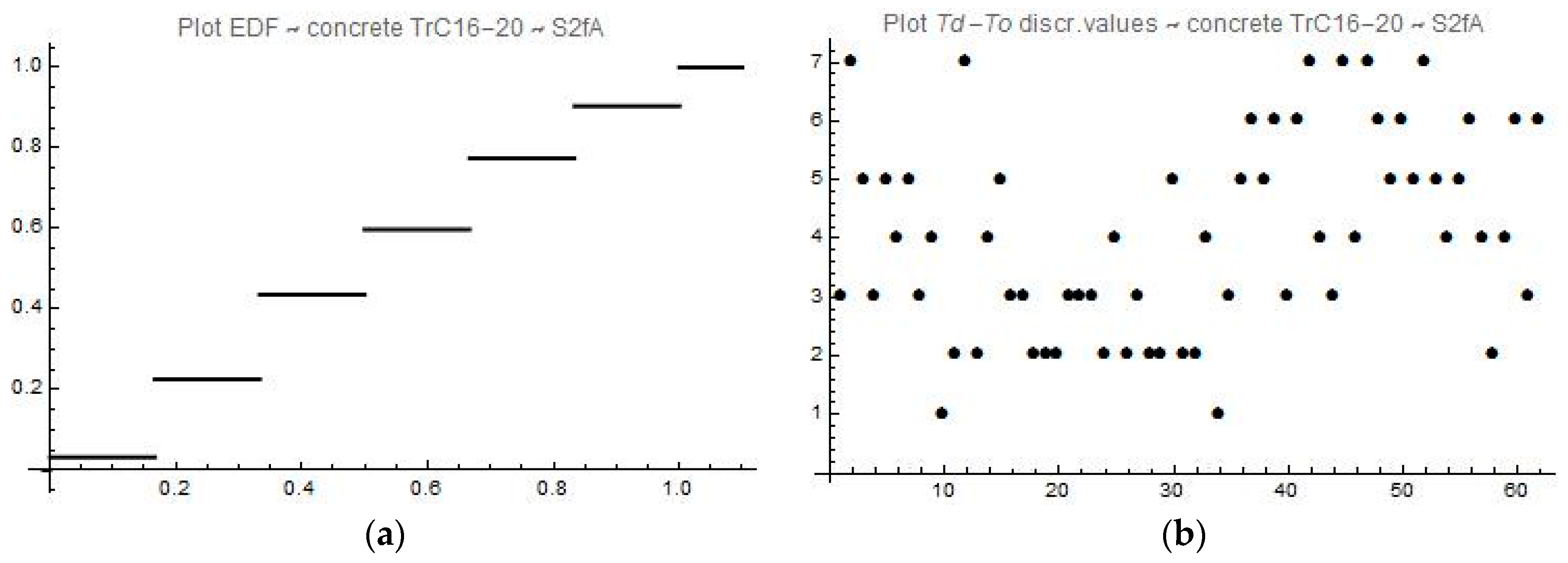
We have run several numerical experiments varying both
L and
kmax. Since the results were very similar, we present just the following ones, see
Figure 1 and
Figure 2. Raw data of the generated probabilistic system are given in
Table 1. In the first row, there are particular system states selected,
i.e., ten bins denoted 0, …, 9 in sequel, which makes
N = 10 as
kmax = 9. In the second row, there are the corresponding frequencies of state occurrences. Further, the
Table 2 gives the corresponding probabilities
p1, …,
p10, and thus the distribution
is easily obtained from
Table 1.
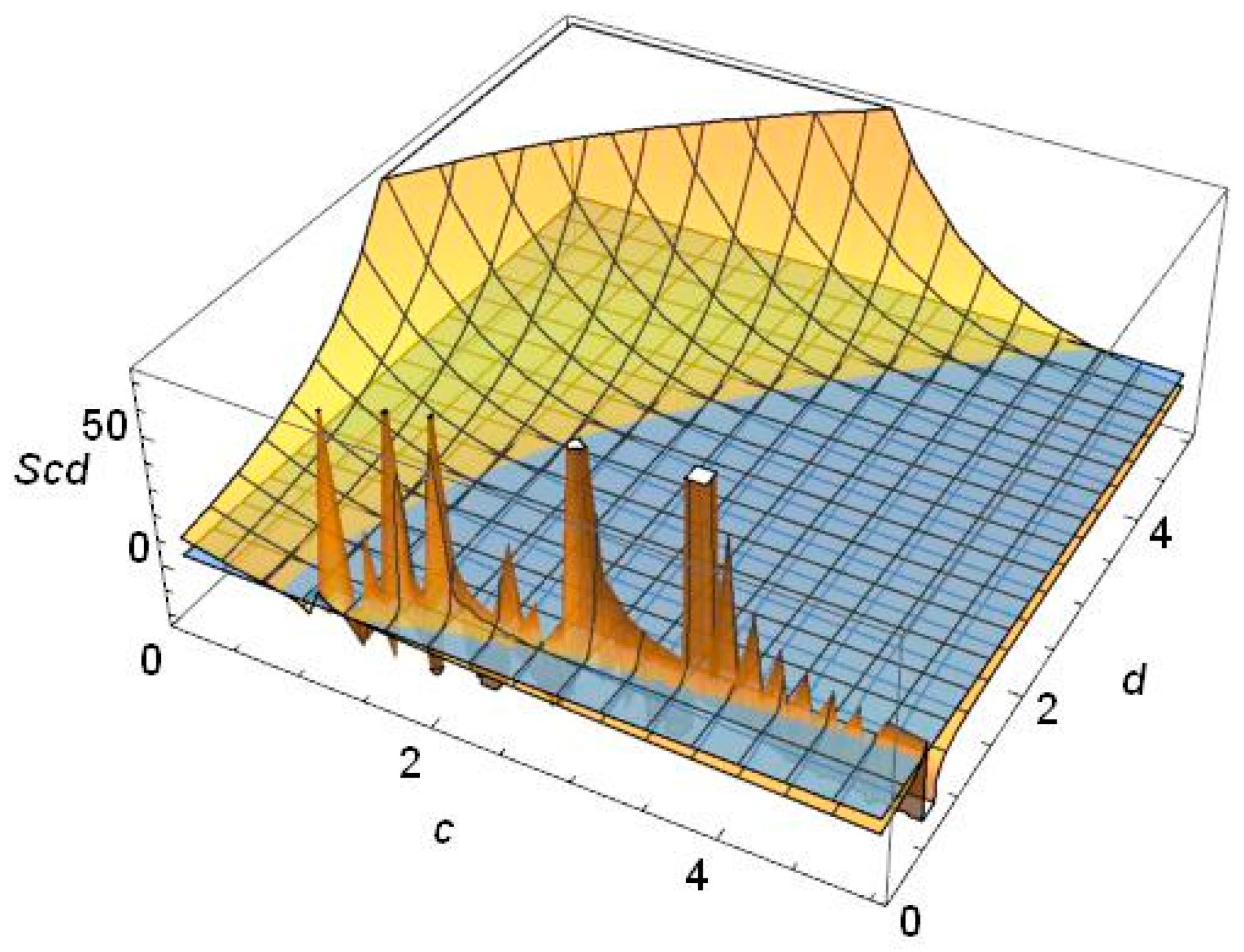
The functions
and
are plotted in
Figure 1, where the blue horizontal plane represents
to be constant over (
c,
d)
Ω = [0.1, 5] × [0.1, 5], as it does not depend upon (
c,
d) at all just by its definition. For given empirical distribution
presented in
Table 2, the
= 2.29809, which is a little bit lower than 2.30259, as being calculated in case of exact uniform distribution, precisely.
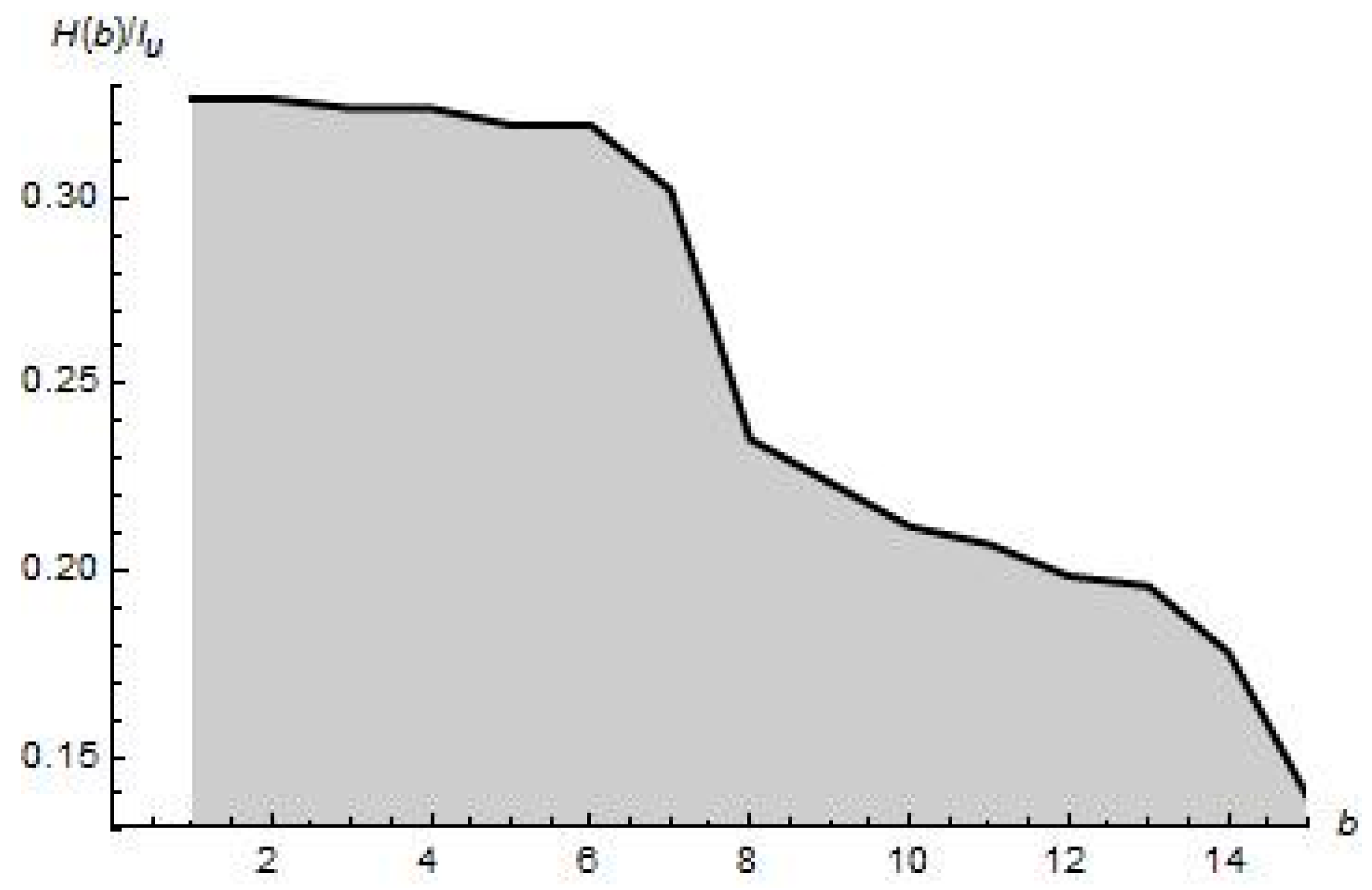
The complicated surface of
representing (
c,
d)-entropy being calculated for the same distribution
within a sub-region (
c,
d)
[1, 5] × [0.1, 0.75] is due to the numerical properties of incomplete gamma function calculations for the corresponding arguments. This surprising result has issued a question to investigate an intersection
over (
c,
d)
Ω = [0.1, 5] × [0.1, 5] in more details. The result is given in
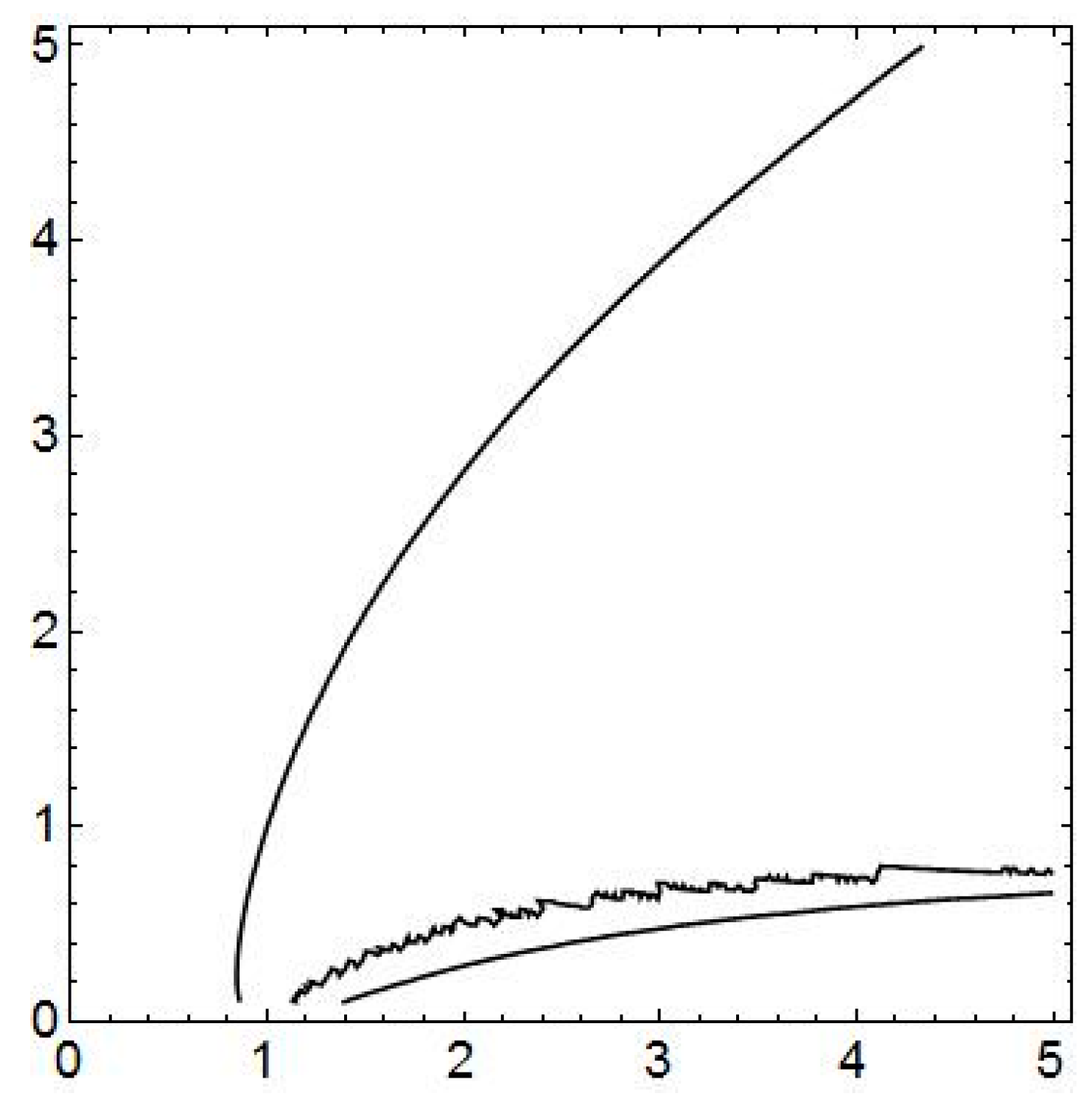
Figure 2, which shows the detected intersection.
In general, there are three curves representing the intersection of surface
with the horizontal plane
over (
c,
d)
Ω = [0.1, 5] × [0.1, 5], which are plotted in
Figure 2. Given
, the analytic definition of set of points forming the intersection is the following:
Provided Ω = Ω
1 Ω
2, we are able to localize the curves more distinctly. The mutually disjoint sub-regions Ω
1, Ω
2, are defined using suitable separating line given by two incidence points, e.g., (1,0) and (5,5), in the following way:
Hence, the sub-region Ω
1 contains just one curve, denoted
λ1, and called the
main branch of the intersection,
over (
c,
d)
Ω, while sub-region Ω
2 contains two other curves, called secondary branches, on the contrary. The point (
c,
d) = (1,1), which stands in Equations (7) and (9) [
31], thus belongs to
λ1 evidently. Concluding, the curve
λ1,
i.e., the
main branch, is given by:
Hence, given
, the desired generalization of Equation (9) is the following:
Of course, the secondary branches allow one to express relations similar to Equation (13), and could be also interesting, but we do not mention them in more details here. At the end of this section, we may conclude the relation between BGS-entropy and (c,d)-entropy is more complicated than a single-valued relation given just by (c,d) = (1,1), as in the Equations (9) and (7), respectively. Given the probability distribution, the value of BGS-entropy induces the iso-quant curves on the surface of (c,d)-entropy being calculated for the same probability distribution. The main branch of such iso-quant curves given by Equation (12), is that one which is incident with the (c,d) = (1,1) point, exactly.