1. Introduction
Information entropy is considered a measure of uncertainty and its maximization guarantees the best solutions for the maximal uncertainty [
1,
2,
3,
4,
5]. Information entropy characterizes uncertainty caused by random parameters of a random system and measurement noise in the environment [
6]. Entropy has been used for information retrieval such as systemic parametric and nonparametric estimation based on real data, which is an important topic in advanced scientific disciplines such as econometrics [
1,
2], financial mathematics [
4], mathematical statistics [
3,
4,
6], control theory [
5,
7,
8], signal processing [
9], and mechanical engineering [
10,
11]. Methods developed within this framework consider model parameters as random quantities and employ the informational entropy maximization principle to estimate these model parameters [
6,
9].
System entropy describes disorder or uncertainty of a physical system and can be considered to be a significant system property [
12]. Real physical systems are always modeled using stochastic partial differential dynamic equation in the spatio-temporal domain [
12,
13,
14,
15,
16,
17]. The entropy of thermodynamic systems has been discussed in [
18,
19,
20]. The maximum entropy generation of irreversible open systems was discussed in [
20,
21,
22]. The entropy of living systems was discussed in [
19,
23]. The system entropy of stochastic partial differential systems (SPDSs) can be measured as the logarithm of system randomness, which can be obtained as the ratio of output signal randomness to input signal randomness from the entropic point of view. Therefore, if system randomness can be measured, the system entropy can be easily obtained from its logarithm. The system entropy of biological systems modeled using ordinary differential equations was discussed in [
24]. However, since many real physical and biological systems are modeled using partial differential dynamic equations, in this study, we will discuss the system entropy of SPDSs. In general, we can measure the system entropy from the system characteristics of a system without measuring the system signal or input noise. For example, a low-pass filter, which is a system characteristic, can be determined from its transfer function or system’s frequency response without measuring its input/output signal. Hence, in this study, we will measure the system entropy of SPDSs from the system’s characteristics. Actually, many real physical and biological systems are only nonlinear, such as the large-scale systems [
25,
26,
27,
28], the multiple time-delay interconnected systems [
29], the tunnel diode circuit systems [
30,
31], and the single-link rigid robot systems [
32]. Therefore, we will also discuss the system entropy of nonlinear system as a special case in this paper.
However, because direct measurement of the system entropy of SPDSs in the spatio-temporal domain using current methods is difficult, in this study, an indirect method for system entropy measurement was developed through the minimization of its upper bound. That is, we first determined the upper bound of the system entropy and then decreased it to the minimum possible value to achieve the system entropy. For simplicity, we first measure the system entropy of linear stochastic partial differential systems (LSPDSs) and then the system entropy of nonlinear stochastic partial differential systems (NSPDSs) by solving a nonlinear Hamilton–Jacobi integral inequality (HJII)-constrained optimization problem. We found that the intrinsic random fluctuation of SPDSs will increase the system entropy.
To overcome the difficulty in solving the system entropy measurement problem due to the complexity of the nonlinear HJII, a global linearization technique was employed to interpolate several local LSPDSs to approximate a NSPDS; a finite difference scheme was employed to approximate a partial differential operator with a finite difference operator at all grid points. Hence, the LSPDSs at all grid points can be represented by a spatial stochastic state space system and the system entropy of the LSPDSs can be measured by solving a linear matrix inequalities (LMIs)-constrained optimization problem using the MATLAB LMI toolbox [
12]. Next, the NSPDSs at all grid points can be represented by an interpolation of several local linear spatial state space systems; therefore, the system entropy of NSPDSs can be measured by solving the LMIs-constrained optimization problem.
Finally, based on the proposed systematic analysis and measurement of the system entropy of SPDSs, two system entropy measurement simulation examples of heat transfer system and biochemical system are given to illustrate the proposed system entropy measurement procedure of SPDSs.
2. General System Entropy of LSPDSs
For simplicity, we will first calculate the entropy of linear partial differential systems (LPDSs). Then, the result will be extended to the measure of NSPDSs. Consider the following LPDS [
15,
16]:
where
is the space variable,
is the state variable,
is the random input signal, and
,…
is the output signal.
and
are the space and time variable, respectively. The space domain
is a two-dimensional bounded domain. The system coefficients are
,
,
, and
. The Laplace (diffusion) operator
is defined as follows [
15,
16]:
Suppose that the initial value
. For simplicity, the boundary condition is usually given by the Dirichlet boundary condition,
i.e.,
a constant on
, or by the Neumann boundary condition
on
, where
is a normal vector to the boundary
[
15,
16]. The randomness of the random input signal is measured by the average energy in the domain
and the entropy of the random input signal is measured by the logarithm of the input signal randomness as follows [
1,
2,
24]:
where
E denotes the expectation operator and
tf denotes the period of the random input signal,
i.e.,
. Similarly, the entropy of the random output signal
is obtained as:
In this situation, the system entropy
S of the LPDS given in Equation (1) can be obtained from the differential entropy between the output signal and input signal,
i.e., input signal entropy minus output signal entropy, or the net signal entropy of the LPDS [
33]:
Let us denote the system randomness as the following normalized randomness:
Then, the system entropy
That is, if system randomness can be obtained, the system entropy can be determined from the logarithm of the system randomness. Therefore, our major work of measuring the entropy of the LPDS given in Equation (1) first involves the calculation of the system randomness
given in Equation (4). However, it is not easy to directly calculate the normalized randomness
in Equation (4) in the spatio-temporal domain. Suppose there exists an upper bound of
as follows:
and we will determine the condition with that
has an upper bound
. Then, we will decrease the value of the upper bound
as small as possible to approach
, and then obtain the system entropy using
.
Remark 1. (i) From the system entropy of LPDS Equation (1), if the randomness of the input signal is larger than the randomness of the output signal , i.e.,:then and . A negative system entropy implies that the system can absorb external energy to increase the structure order of the system. All the biological systems are of this type, and according to Schrödinger’s viewpoint, biological systems consume negative entropy, leading to construction and maintenance of their system structures, i.e., life can access negative entropy to produce high structural order. (ii) If the randomness of the output signal is larger than the randomness of the input signal , i.e.,:then and . A positive system entropy indicates that the system structure disorder increases and the system can disperse entropy to the environment. (iii) If the randomness of the input signal is equal to the randomness of the system signal , i.e.,:then and . In this case, the system structure order is maintained constantly with zero system entropy. (iv) If the initial value then the system randomness in Equation (4) should be modified as:for a positive Lyapunov function , and the randomness due to the initial condition should be considered a type of input randomness. Based on the upper bound of the system randomness as given in Equation (5), we get the following result:
Proposition 1. For the LPDS in Equation (1), if the following HJII holds for a Lyapunov function and with :then the system randomness has an upper bound as given in Equation (5). Since
is the upper bound of
, it can be calculated by solving the following HJII-constrained optimization problem:
Consequently, we can calculate the system entropy using .
Remark 2. If the system in Equation (1) is free of a partial differential term , i.e., in the case of the following conventional linear dynamic system:then the system entropy of linear dynamic system in Equation (12) is written as [24]: Therefore, the result of Proposition 1 is modified as the following corollary.
Corollary 1. For the linear dynamic system in Equation (12), if the following Riccati-like inequality holds for a positive definite symmetric :or equivalently (by the Schur complement [12]):then the system randomness of the linear dynamic system in Equation (12) has an upper bound .
Thus, the randomness
of the linear dynamic system in Equation (12) is obtained by solving the following LMI-constrained optimization problem:
Hence, the system entropy of the linear dynamic system in Equation (12) can be calculated using
. The LMI-constrained optimization problem given in Equation (16) is easily solved by decreasing
until no positive definite solution
exists for the LMI given in Equation (15), which can be solved using the MATLAB LMI toolbox [
12]. Substituting
into
in Equation (14), we get:
The right hand side of Equation (17) can be considered as an indication of the system stability. If the eigenvalues of are more negative (more stable), i.e., the right hand side is more large, then and the system entropy , are smaller. Obviously, the system entropy is inversely related to the stability of the dynamic system. If is fixed, then the increase in input signal coupling may increase and .
Remark 3. If the LPDS in Equation (1) suffers from the following intrinsic random fluctuation:where the constant matrix denotes the deterministic part of the parametric variation of system matrix and is a stationary spatio-temporal white noise to denote the random source of intrinsic parametric variation [34,35], then the LSPDS in Equation (18) can be rewritten in the following differential form:where with being the Wiener process or Brownian motion in a zero mean Gaussian random field with unit variance at each location x [15]. For the LSPDS in Equation (19), we get the following result.
Proposition 2. For the LSPDS in Equation (19), if the following HJII holds for a Lyapunov function with :then the system randomness has an upper bound as given in (5). Since
is the upper bound of
, it could be calculated by solving the following HJII-constrained optimization problem:
Hence, the system entropy of LSPDS in Equations (18) or (19) could be obtained using , where is the system randomness solved from Equations (21).
Remark 4. Comparing the HJII in Equation (20) with the HJII in Equation (10) and replacing with , we find that Equation (20) has an extra positive term due to the intrinsic random parametric fluctuation given in Equation (18). To maintain the left-hand side of Equation (20) as negative, the system randomness in Equation (20) must be larger than the randomness in Equation (10), i.e., the system entropy of the LPDS in Equations (18) or (19) is larger than that of the LPDS in Equation (1) because the intrinsic random parametric variation in Equation (18) can increase the system randomness and the system entropy.
Remark 5. If the LSPDS in Equation (18) is free of the partial differential term , i.e., in the case of the conventional linear dynamic system:or the following form:then we modify Proposition 2 as the following corollary. Corollary 2. For the linear dynamic system in Equations (22) or (23), if the following Riccati-like inequality holds for a positive definite symmetric :or equivalently:then the system randomness of the linear dynamic system in Equations (22) or (23) has a upper bound . Therefore, the system randomness
of the linear stochastic system in Equations (22) or (23) can be obtained by solving the following LMI-constrained optimization problem:
Hence, the system entropy Equation (13) of the linear stochastic system in Equations (22) or (23) can be calculated using , where the system randomness is the optimal solution of Equation (26).
By substituting
calculated by Equation (26) into Equation (24), we can get:
Remark 6. Comparing Equation (27) with Equation (17), it can be seen that the term due to the intrinsic random parametric fluctuation in Equation (22) can increase the system randomness which consequently increases the system entropy .
3. The System Entropy Measurement of LSPDSs via a Semi-Discretization Finite Difference Scheme
Even though the entropy of the linear systems in Equations (12) and (22) can be easily measured by solving the optimization problem in Equations (16) and (26), respectively, using the LMI toolbox in MATLAB, it is still not easy to solve the HJII-constraint optimization problem in Equations (11) and (21) for the system entropy of the LPDS in Equation (1) and the LSPDS in Equation (18), respectively. To simplify this system entropy problem, the main method is obtaining a more suitable spatial state space model to represent the LPDSs. For this purpose, the finite difference method and the Kronecker product are used together in this study. The finite difference method is employed to approximate the partial differential term
in Equation (1) in order to simplify the measurement procedure of entropy [
14,
16].
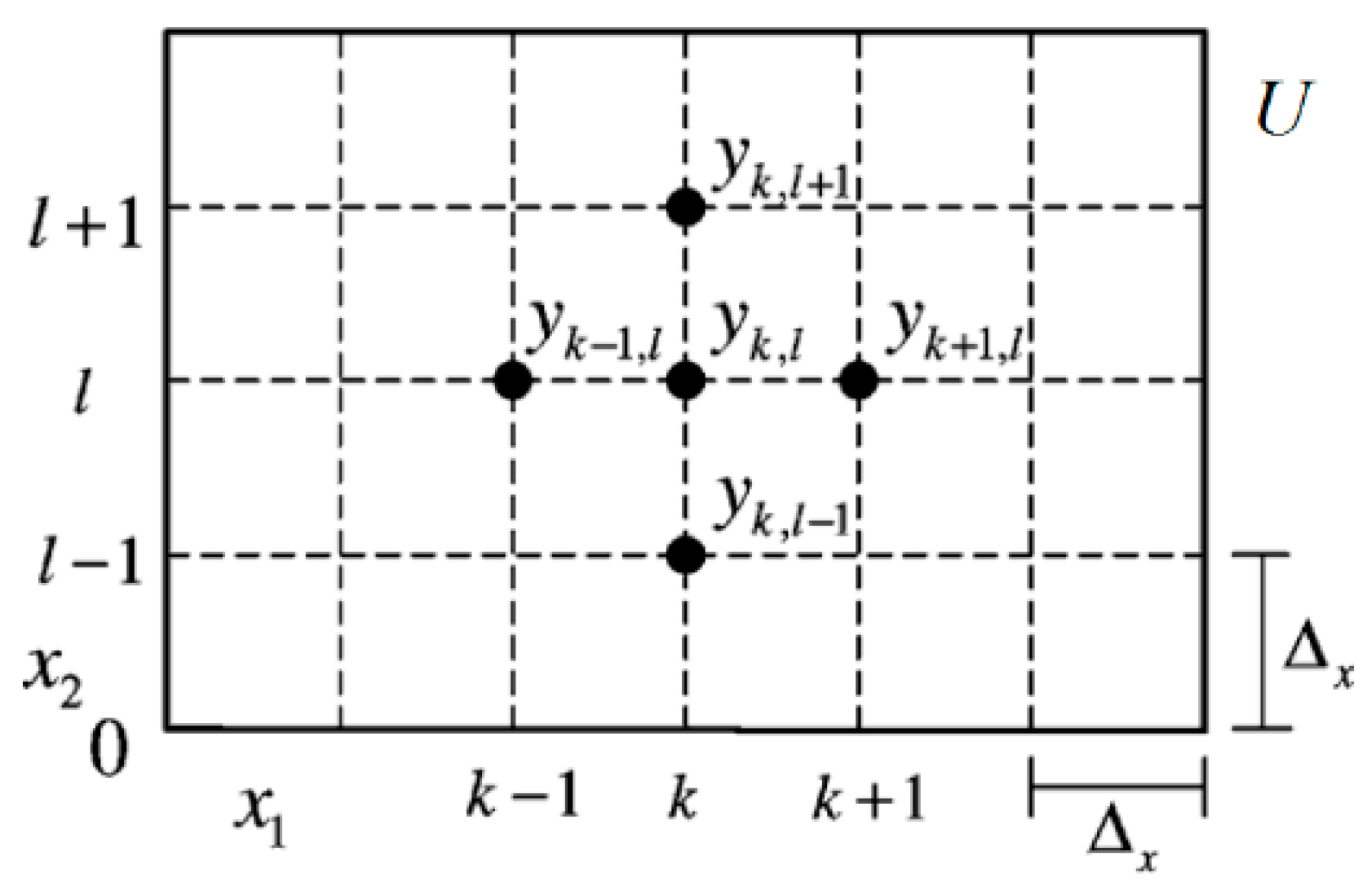
Consider a typical mesh grid as shown in
Figure 1. The state variable
is represented by
at the grid node
, where
and
,
i.e.,
at the grid point
, and the finite difference approximation scheme for the partial differential operator can be written as follows [
14,
16]:
.
Based on the finite difference approximation in Equation (28), the LPDS in Equation (1) can be represented by the following finite difference system:
.
Let us denote:
then we get:
For the simplification of entropy measurement for the LPDS in Equation (1), we will define a spatial state vector
at all grid node in
Figure 1. For the Dirichlet boundary conditions [
16], the values of
at the boundary are fixed. For example,
, where
. We have
at
or
. Therefore, the spatial state vector
for state variables at all grid nodes is defined as follows:
where
. Note that
is the dimension of the vector
for each grid node and
is the number of grid nodes. For example, let
and
, then we have
. To simplify the index of the node
in the spatial state vector
, we will denote the symbol
to replace
. Note that the index
is from 1 to
N,
i.e.:
where
in Equation (32). Thus, the linear difference model of two indices in Equation (31) could be represented with only one index as follows:
where
with
and
is defined as follows:
where
and
denote the
zero matrix and
identity matrix, respectively.
We will collect all states
of the grid nodes given in Equation (33) to the spatial state vector given in Equation (32). The Kronecker product can be used to simplify the representation. Using the Kronecker product, the systems at all grid nodes given in Equation (33) can be represented by the following spatial state space system (
i.e., the linear dynamic systems of Equation (33) at all grid points within domain
in
Figure 1 are represented by a spatial state space system [
14]):
where
,
, and
denotes the Kronecker product between
and
.
Definition 1. [
17,
36]: Let
,
. Then the Kronecker product of
and
is defined as the following matrix:
Remark 7. Since the spatial state vector in Equation (32) is used to represent at all grid points, in this situation, , , and in the measurement of system randomness in Equations (5) or (9) could be modified by the temporal forms , , and , respectively, for the spatial state space system in (35), where the Lyapunov function is related to the Lyapunov function as . Therefore, for the spatial state space system in Equation (35), the system randomness in Equations (5) or (9) is modified as follows:or: Hence, our entropy measurement problem of the LPDS in Equation (1) becomes the measurement of the entropy of the spatial state system Equation (35), as given below.
Proposition 3. For the linear spatial state space system in Equation (35), if the following Riccati-like inequality holds for a positive definite matrix :or equivalently:where , then the system randomness in Equations (36) or (37) of linear spatial state space system in Equation (35) has the upper bound . Proof. The proof is similar to the proof of Corollary 1 in
Appendix B and can be obtained by replacing
, and
with
, and
, respectively. ☐
Therefore, the randomness
of the linear spatial state space system in Equation (35) can be obtained by solving the following LMI-constrained optimization problem:
Hence, the system entropy of the linear spatial state space system in Equation (33) can be calculated using .
Remark 8. (i) The Riccati-like inequality in Equation (38) or the LMI in Equation (39) is an approximation of the HJII in Equation (10) with the finite difference scheme given in Equation (28). If the finite difference, shown in Equation (28), , then in Equation (40) will approach in Equation (11). (ii) Substituting into Equation (38), we get: If the eigenvalues of
are more negative (more stable), the randomness
as well as the entropy
is smaller. Similarly, the LSPDS in Equation (18) can be approximated by the following stochastic spatial state space system
via finite difference scheme [
14]:
where
, and the Hadamard product of matrices (or vectors)
and
of the same size is the entry-wise product denoted as
.
Then we can get the following result.
Corollary 3. For the linear stochastic spatial state space system Equation (42), if the following Riccati-like inequality holds for a positive definite symmetric :or equivalently, the following LMI has a positive definite symmetric solution :then the system randomness of the stochastic state space system in Equation (
42) has an upper bound , where . Proof. The proof is similar to the proof of
Corollary 2 in
Appendix D. ☐
Therefore, the system randomness
of the linear stochastic state space system Equation (42) can be obtained by solving the following LMI-constrained optimization problem:
and hence the system entropy
of the stochastic spatial state space system in Equation (42) can be obtained using
. Substituting
into (43), we get:
Remark 9. Comparing Equation (41) with Equation (46), because of the term from the intrinsic random fluctuation, it can be seen that the LSPDS with random fluctuations will lead to a larger and a larger system entropy S. ☐
4. System Entropy Measurement of NSPDSs
Most partial dynamic systems are nonlinear; hence, the measurement of the system entropy of nonlinear partial differential systems (NPDSs) will be discussed in this section. Consider the following NPDSs in the domain
:
where
,
and
are the nonlinear functions with
,
, and
, respectively. The nonlinear diffusion functions
satisfy
, and
. If the equilibrium point of interest is not at the origin, for the convenience of analysis, the origin of the NPDS must be shifted to the equilibrium point (shifted to zero). The initial and boundary conditions are the same as the LPDS in Equation (1); then, we get the following result.
Proposition 4. For the NPDS in Equation (47), if the following HJII holds for a Lyapunov function with :then the system randomness of the NPDS in Equation (47) has an upper bound as given in Equation (5). Based on the condition of upper bound
given in Equation (48), the system randomness
could be obtained by solving the following HJII-constrained optimization problem:
Hence, the system entropy of NPDS in Equation (47) can be obtained using
. If the NPDS in Equation (47) is free of the diffusion operator
as with the following conventional nonlinear dynamic system:
then the result of Proposition 4 is reduced to the following corollary.
Corollary 4. For the nonlinear dynamic system Equation (50), if the following HJII holds for a positive Lyapunov function with :then the system randomness of the nonlinear dynamic system in Equation (50) has an upper bound Proof. The proof is similar to that of Proposition 4 without consideration of the diffusion operator and spatial integration on the domain .
Hence, the system randomness of the nonlinear dynamic system in Equation (50) can be obtained by solving the following HJII-constrained optimization problem:
and the system entropy is obtained using
. If the NPDS in Equation (47) suffers from random intrinsic fluctuations as with the NSPDSs:
where
denotes the random intrinsic fluctuation, then the NSPDS in Equation (53) can be written in the following
form:
Therefore, we can get the following result:
Proposition 5. For the NSPDS in Equations (53) or (54), if the following HJII holds for a Lyapunov function with :then the system randomness of the NSPD S in Equations (53) or (54) can be obtained by solving the following HJII-constrained optimization problem: Remark 10. By comparing the HJII in Equation (48) with the HJII in Equation (55), due to the extra term from the random intrinsic fluctuation in Equation (53), it can be seen that the system randomness of the NSPDS in Equation (53) must be larger than the system randomness of the NPDS in Equation (47). Hence, the system entropy of the NSPDS in Equation (53) is larger than that of the NPDS in Equation (47).
5. System Entropy Measurement of NSPDS via Global Linearization and Semi-Discretization Finite Difference Scheme
In general, it is very difficult to solve the HJII in Equations (48) or (55) for the system entropy measurement of the NPDS in Equation (47) or the NSPDS in Equation (53), respectively. In this study, the global linearization technique and a finite difference scheme were employed to simplify the entropy measurement of the NPDS in Equation (47) and NSPDS in Equation (53). Consider the following global linearization of the NPDS in Equation (47), which is bounded by a polytope consisting of
L vertices [
12,
37]:
where
denotes the convex hull of a polytope with
vertices defined in Equation (57). Then, the trajectories of
for the NPDS in Equation (47) will belong to the convex combination of the state trajectories of the following
linearized PDSs derived from the vertices of the polytope in Equation (57):
From the global linearization theory [
16,
37], if Equation (57) holds, then every trajectory of the NPDS in Equation (47) is a trajectory of a convex combination of
linearized PDSs in Equation (58), and they can be represented by the convex combination of
linearized PDSs in Equation (58) as follows:
where the interpolation functions are selected as
and they satisfy
and
. That is, the trajectory of the NPDS in Equation (47) can be approximated by the trajectory of the interpolated local LPDS given in Equation (59).
Following the semi-discretization finite difference scheme in Equations (28)–(34), the spatial state space system of the interpolated PDS in Equation (59) can be represented as follows:
where
and
are defined in (35). That is, the NPDS in Equation (47) is interpolated through local linearized PDSs in Equation (59) to approximate the NPDS in Equation (47) using global linearization and semi-discretization finite difference scheme.
Remark 11. In fact, there are many interpolation schemes for approximating a nonlinear dynamic system with several local linear dynamic systems such as Equation (60); for example, fuzzy interpolation and cubic spline interpolation methods [13]. Then, we get the following result. ☐
Proposition 6. For the linear dynamic systems in Equation (60), if the following Riccati-like inequalities hold for a positive definite symmetric :or equivalently:where , , and are defined as , and , respectively, then the system randomness of the NPDSs in Equation (47) or the interpolated dynamic systems in Equation
(60) have an upper bound . Therefore, the system randomness
of the NPDSs in Equation (47) or the interpolated dynamic systems in Equation (60) can be obtained by solving the following LMIs-constrained optimization problem:
Hence, the system entropy
of the NPDSs in Equation (47) or the interpolated dynamic systems in Equation (60) can be obtained using
. By substituting
into the Riccati-like inequalities in Equation (61), we can obtain:
Obviously, if the eigenvalues of local system matrices are more negative (more stable), the randomness is smaller and the corresponding system entropy is also smaller, and vice versa.
The NSPDs given in Equation (54) can be approximated using the following global linearization technique [
12,
37]:
Then, the NSPDs with the random intrinsic fluctuation given in Equation (53) can be approximated by the following interpolated spatial state space system [
14]:
i.e., we could interpolate
local interpolated stochastic spatial state space systems to approximate the NSPDs in Equation (53). Then, we get the following result.
Proposition 7. For the NSPDs in Equation (54) or the linear interpolated stochastic spatial state space systems in (66), if the following Riccati-like inequalities hold for a positive definite symmetric :or equivalently:where , then the system randomness of the NSPDs in Equation (53) or the interpolated stochastic systems in Equation (66) can be obtained by solving the following LMIs-constrained optimization problem: Then, the system entropy of NSPD in Equation (53) or the interpolated stochastic systems in Equation (66) could be obtained as .
Substituting
into in Equation (67), we get:
Comparing (64) with Equation (70),
of the NSPDS in Equation (53) is larger than
of the NPDS in Equation (47),
i.e., the random intrinsic fluctuation
will increase the system entropy of the NSPDS. Based on the above analysis, the proposed system entropy measurement procedure of NSPDSs is given as follows:
- Step 1:
Given the initial value of state variable, the number of finite difference grids, the vertices of the global linearization, and the boundary condition.
- Step 2:
Construct the spatial state space system in Equation (60) by finite difference scheme.
- Step 3:
Construct the interpolated state space system Equation (66) by global linearization method.
- Step 4:
If the error between the original model Equation (54) and the approximated model Equation (66) is too large, we could adjust the density of grid nodes of finite difference scheme and the number of vertices of global linearization technique and return to Step 1.
- Step 5:
Solve the eigenvalue problem in Equation (69) to obtain and , and then system entropy .
6. Computational Example
Based on the aforementioned analyses for the system entropy of the considered PDSs, two computational examples are given below for measuring the system entropy.
Example 1. Consider a heat transfer system in a 1m × 0.5m thin plate with a surrounding temperature of 0 °C as follows [
38]:
and
y(
x,
t) = 0 °C, ∀
t, ∀
x on the boundary of
U =[0,1]×[0,0.5]. Here,
y(
x,t) is the temperature function, location
x is in meters, time
t is in s,
is the thermal diffusivity [
4,
5,
6,
7,
9], and the term
with
denotes the thermal dissipation when the temperature of the plate is greater than the surrounding temperature,
i.e.,
°C, or the thermal absorption when the temperature on the plate is less than the surrounding temperature,
i.e.,
°C. The output coupling
.
is the environmental thermal fluctuation input with
. We can estimate the system entropy of the heat transfer system in Equation (71). Based on
Proposition 3 and the LMI-constrained optimization problem Equation (40), we can calculate the system entropy of the heat transfer system in Equation (71) as
. In this calculation of the system entropy, the grid spacing
of the finite difference scheme was chosen as 0.125m such that there are
interior grid points and 24 boundary points in
. The temperature distributions
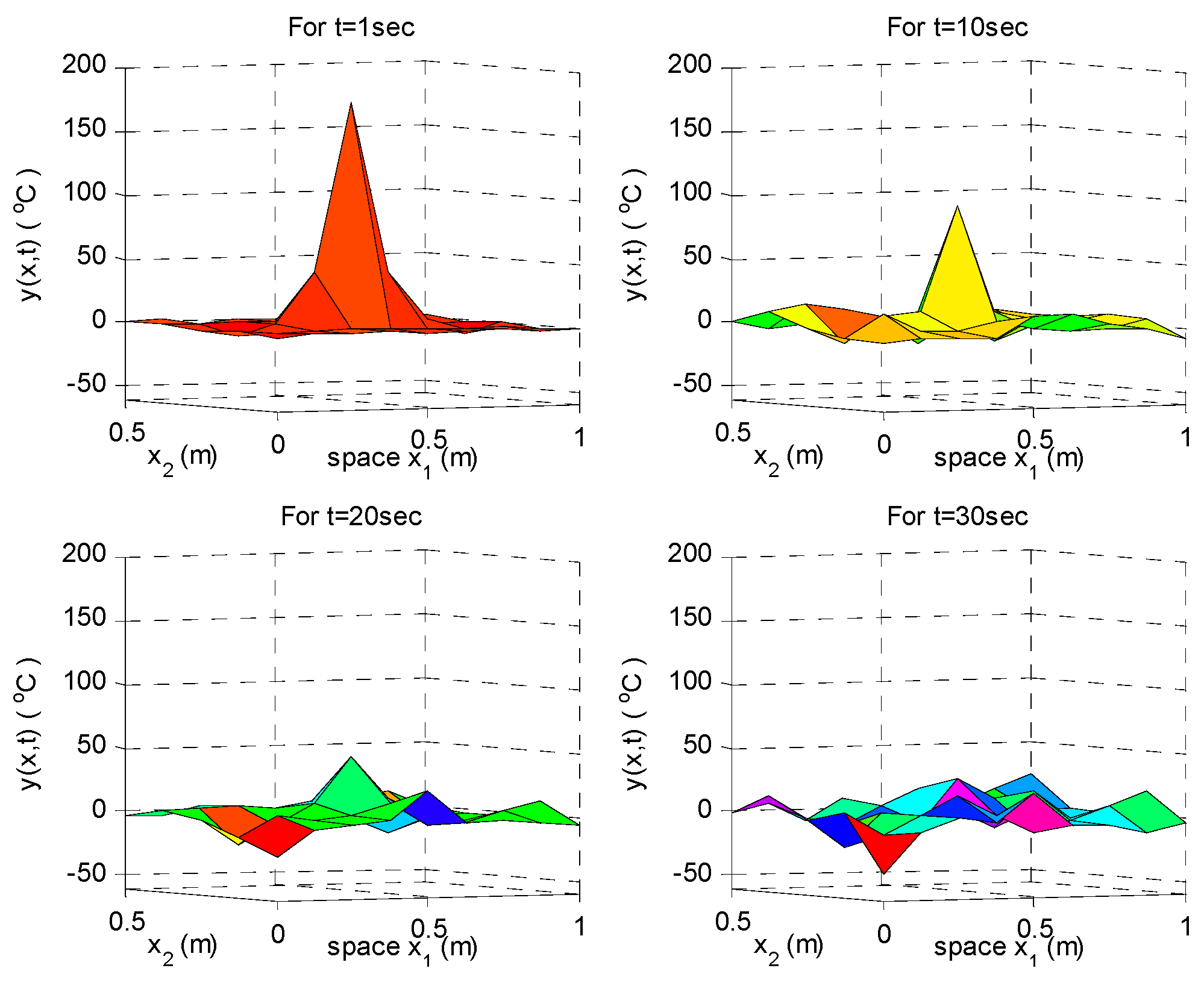
of the heat transfer system in Equation (71) at
, 10, 30 and 50 s are shown in
Figure 2 with
. Due to the diffusion term
, the heat temperature of transfer system Equation (71) will be uniformly distributed gradually. Even if the thin plate has initial value (heat source) or some other influences like input signal and intrinsic random fluctuation, the temperature of the thin plate will gradually achieve a uniform distribution to increase the system entropy. This phenomenon can be seen in
Figure 2,
Figure 3,
Figure 4 and
Figure 5.
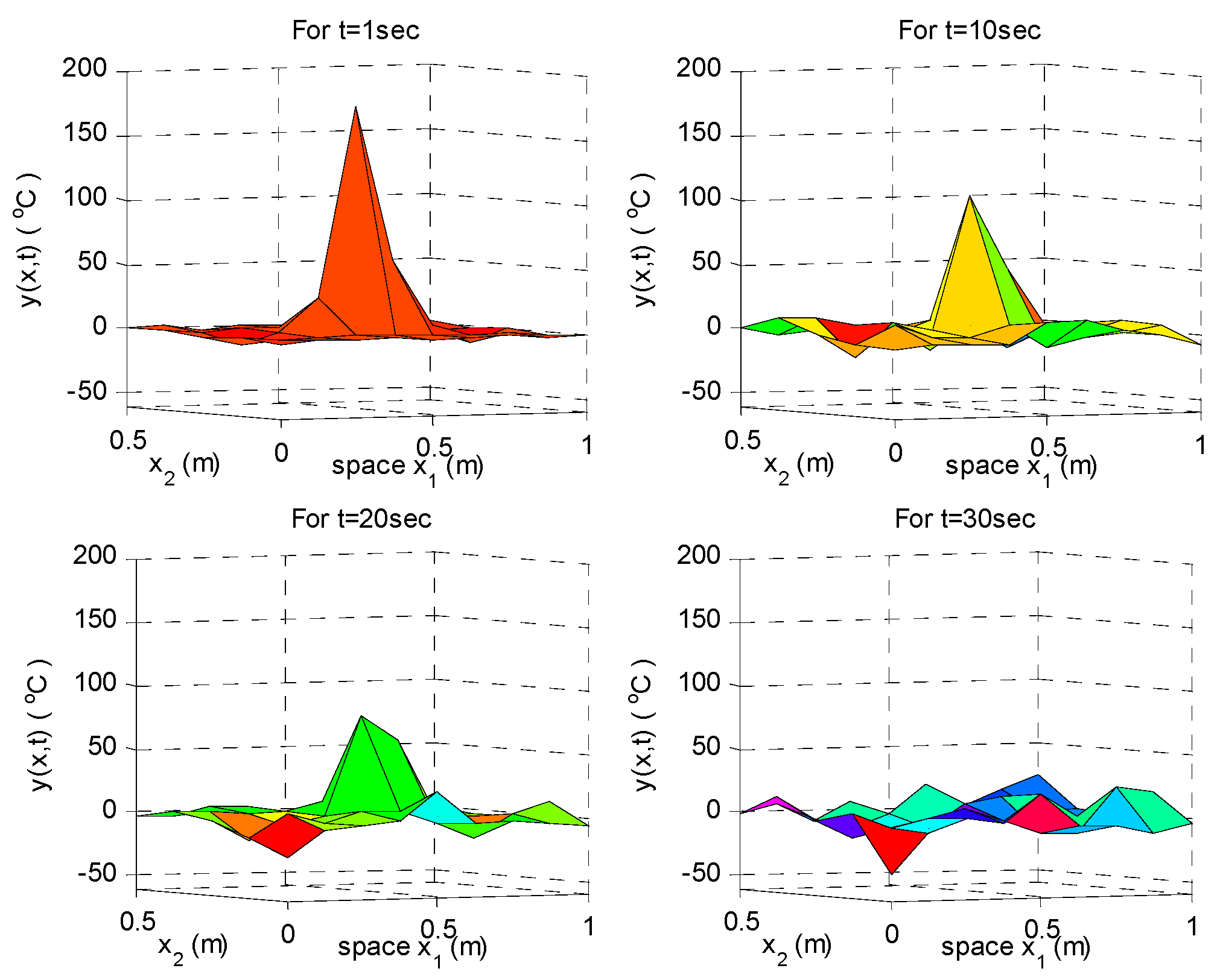
Suppose that the heat transfer system in Equation (71) suffers from the following random intrinsic fluctuation:
where the term
with
is due to the random parameter variation of the term
. Then, the temperature distributions
of the heat transfer system in Equation (72) at
1, 10, 30 and 50 s are shown in
Figure 3. Based on the Corollary 3 and the LMI-constrained optimization problem in Equation (45), we can calculate the system entropy of the stochastic heat transfer system in Equation (72) as
. Obviously, it can be seen that the system entropy of the stochastic heat transfer system in Equation (72) is larger than the heat transfer system in Equation (71) without intrinsic random fluctuation.
Example 2. A biochemical enzyme system is used to describe the concentration distribution of the substrate in a biomembrane. For the enzyme system, the thickness
of the artificial biomembrane is 1 μm. The concentration of the substrate is uniformly distributed inside the artificial biomembrane. Since the biomembrane is immersed in the substrate solution, the reference axis is chosen to be perpendicular to the biomembrane. The biochemical system can be formulated as follows [
13]:
where
is the concentration of the substrate in the biomembrane,
is the substrate diffusion coefficient,
is the maximum activity in one unit of the biomembrane,
is the Michaelis constant, and
is the substrate inhibition constant. The parameters of the biochemical enzyme system are given by
,
,
,
and the output coupling
. Note that the equilibrium point in
Example 2 is at zero. The concentration of the initial value of the substrate is given by
. The boundary conditions used to restrict the concentration are zero at
and
,
i.e.,
,
. A more detailed discussion about the enzyme can be found in [
13]. Suppose that the biochemical enzyme system is under the effect of an external signal
. For the convenience of computation, the external signal
is assumed as a zero mean Gaussian noise with a unit variance. The influence function of external signal is defined as
at
and
(μm). Based on the global linearization in Equation (57), we get
and
, as shown in detail in
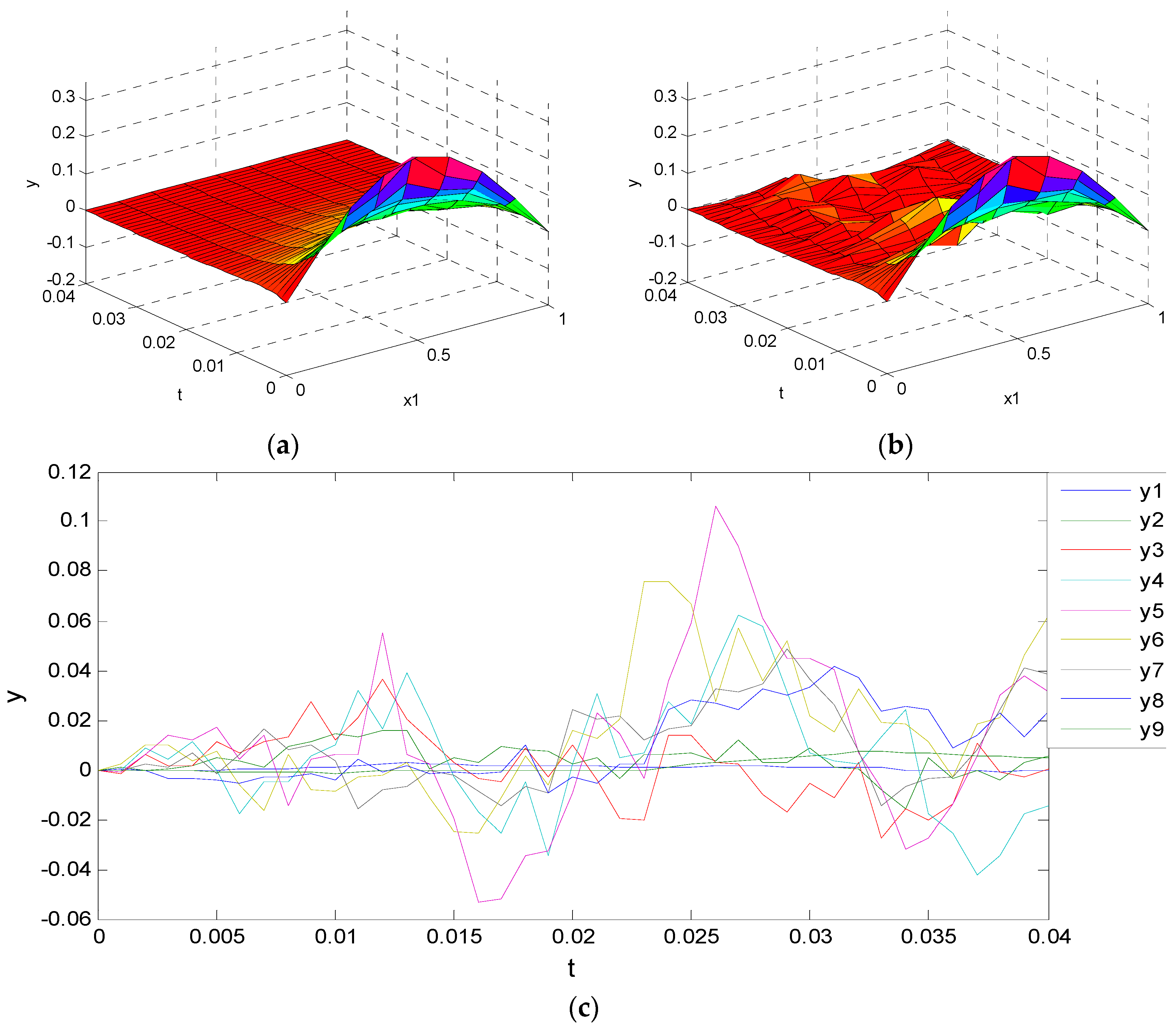
Appendix I. The concentration distributions
of the real system and approximated system are given in
Figure 4 with
,
i.e.,
. Clearly, the approximated system based on the global linearization technique and finite difference scheme efficiently approach the nonlinear function. Based on
Proposition 6 and the LMIs-constrained optimization given in Equation (63), we can obtain
as shown in detail in Appendix J and calculate the system entropy of the enzyme system in Equation (73) as
.
Therefore, it is clear that the approximated system in Equation (60) can efficiently approximate biochemical enzyme system in Equation (73). In this simulation,
. Suppose that the biochemical system in Equation (73) suffers from the following random intrinsic fluctuation:
where the term
with
is the random parameter variation from the term
. Based on the global linearization in Equation (65), we can get
as shown in detail in Appendix K. Based on the
Proposition 7 and the LMIs-constrained optimization given in Equation (69), we can solve
as shown in detail in Appendix L and calculate the system entropy of the enzyme system in Equation (74) as
.
Clearly, because of the intrinsic random parameter fluctuation, the system entropy of the stochastic enzyme system given in Equation (74) is larger than that of the enzyme system given in Equation (73).
The computation complexities of the proposed LMI-based indirect entropy measurement method is about
in solving LMIs, where
is the dimension of
,
is the number of global interpolation points. We also calculate the elapsed time of the simulations examples by using MATLAB. The computation times including the drawing of the corresponding figures to solve the LMI constrained optimization problem are given as follows: in Example 1, the case of heat transfer system in Equation (71) is 183.9 s; the case of heat transfer system with random fluctuation in Equation (72) is 184.6 s. In Example 2, the case of biochemical system in Equation (73) is 17.7 s, the case of biochemical system with random fluctuation in Equation (74) is 18.6 s. The RAM of the computer is 4.00 GB, the CPU we used is AMD A4-5000 CPU with Radeon(TM) HD Graphics, 1.50 GHz. The results are reasonable. Because the dimension of grid nodes in Example 1 is
and the dimension of grid nodes in Example 2 is
, obviously, the computation time in Example 1 is much larger than in Example 2. Further, the time spent of the system without the random fluctuation is slightly faster than the system with the random fluctuation. The conventional algorithms of calculating entropy have been applied in image processing, digital signal processing, and particle filters, like in [
39,
40,
41]. The conventional algorithms for calculating entropy just can be used in linear discrete systems, but in fact many systems are nonlinear and continuous. The indirect entropy measurement method we proposed can deal with the nonlinear stochastic continuous systems. Though the study in [
24] is about the continuous nonlinear stochastic system, many physical systems are always modeled using stochastic partial differential dynamic equation in the spatio-temporal domain. The indirect entropy measurement method we proposed can be employed to solve the system entropy measurement in nonlinear stochastic partial differential system problem.