Abstract
In this paper, we use Boltzmann statistics and the maximum likelihood distribution derived from Bayes’ Theorem to infer parameter values for a Pake Doublet Spectrum, a lineshape of historical significance and contemporary relevance for determining distances between interacting magnetic dipoles. A Metropolis Hastings Markov Chain Monte Carlo algorithm is implemented and designed to find the optimum parameter set and to estimate parameter uncertainties. The posterior distribution allows us to define a metric on parameter space that induces a geometry with negative curvature that affects the parameter uncertainty estimates, particularly for spectra with low signal to noise.
1. Intoduction
Parameter inference is an important task in the interpretation of magnetic resonance spectra and may be accomplished by a variety of means. One approach of particular note is the early and important work of Bretthorst who established methods for the analysis of high resolution Nuclear Magnetic Resonance (NMR) lineshapes that are complementary to the Markov Chain Monte Carlo methods developed in this work [1,2,3]. Markov Chain Monte Carlo simulations are frequently used in statistics for sampling probability distributions to compute quantities that would otherwise be difficult to evaluate by conventional means. In this paper we will discuss a Markov Chain Monte Carlo algorithm optimized for parameter inference of the absorption lineshape of a Pake Doublet, which arises from the magnetic dipole-dipole interaction between coupled spins. This Lineshape is important in both NMR and Electron Paramagnetic Resonance (EPR). In modern applications, the details of the lineshape can provide distance information for various spin systems [4]. For the purposes of this paper, we will explore the process of parameter inference for a case of historical interest and reanalyze Pake’s original distance determination of a hydrated gypsum crystal [5].
The probability of absorption is [5,6]:
This distribution (1) is convolved with a Gaussian to represent inhomogeneities in the magnetic field as well as contributions from neighboring atoms. The Gaussian has the form:
and the lineshape has the form:
shown in Figure 1.

Figure 1.
Absorption probability for α = 5.4 in red. The result of (3) in blue with β = 1.54.
Note that the absorption lineshape (3) is normalized and is non-negative, and so may be treated as a probability mass function [7].
In this work we will study two cases, one with a SNR = 7, Figure 2a, and the second with a SNR = 70, Figure 2b, with emphasis on the latter since it is more sensitive to the explicit values of the parameters. SNR is the signal to noise ratio and is defined as the ratio of the maximum amplitude of the signal to the root mean square noise width of the signal.
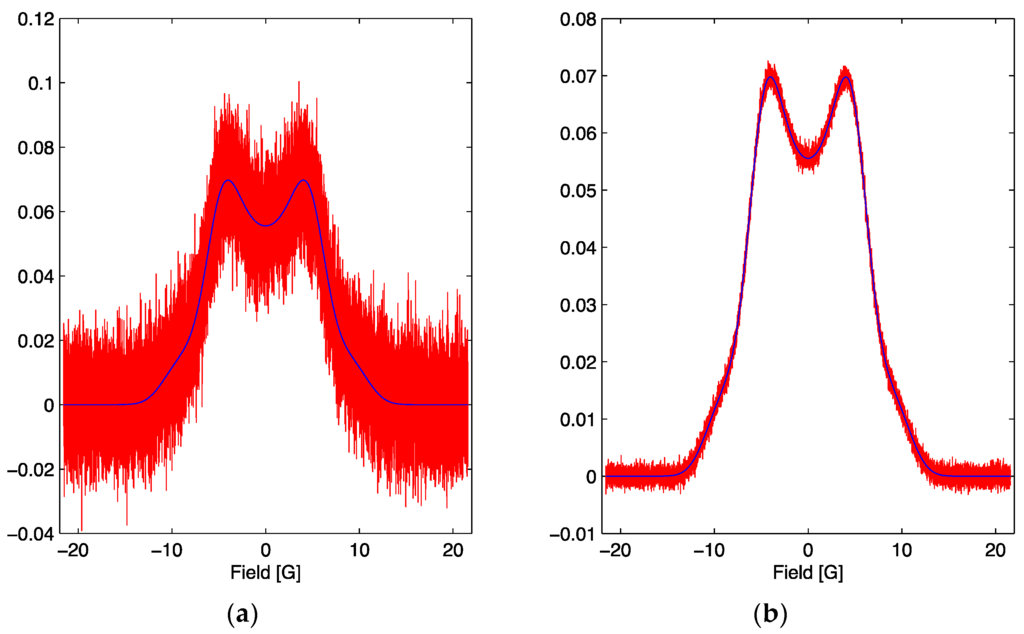
Figure 2.
(a) The simulated signal for the optimum parameter set with the addition of noise (red) and the noiseless lineshape (blue). The red signal corresponds to a signal to noise ratio of 7. (b) The simulated signal for the optimum parameter set with the addition of noise (red) and the noiseless lineshape (blue). The red signal corresponds to a signal to noise ratio of 70.
We will use the maximum likelihood distribution [8]:
which can be derived from manipulation of Bayes’ Theorem. In (4), F is the model (3), σ is the width of the noise (Nk/n, where Nk is the normal noise generated in MATLAB (version R2013a), which has a width = 1 which is then scaled by n to obtain the desired SNR), {X} represents a set of parameters (in this case α and β), our signal , and the k subscript indicates a specific observation frequency in the bandwidth of the spectrum. Here, {Xo} is the optimum parameter set, {αo, βo}.
The maximum likelihood distribution (4) is analogous to the canonical ensemble (5) [9]:
We can obtain equality if we set and or , the analog to temperature used in Boltzmann statistics [9,10]. Note that we measure our pseudotemperature T in units of Ek. We can normalize Equation (4) by constructing a probability mass function whose evidence (or partition function) may be defined by using Equations (4) and (6):
The probability mass function then takes the form:
where {Xi} is the i-th set of parameters being evaluated, {αi, βi}.
By analogy to the canonical distribution, we observe that there are many computable quantities with connections to classical thermodynamics such as the heat capacity, which in this case gives a measure of the fluctuations of the mean-squared residual in the presence of noise; the expectation of the residual, which is controlled by the pseudo temperature ; and the Shannon and Boltzmann entropy [10]. The residual squared:
is expected to be a minimum at the parameter optimum {X0}.
At the optimum parameter set, [5] and a signal to noise ratio of 70 our probability mass function (8) is shown in Figure 3. This is the optimum set used in all simulations discussed. An example simulated signal with parameter set with a signal to noise ratio of 70 is shown in Figure 4 and the resulting probability mass function (8) in Figure 5.
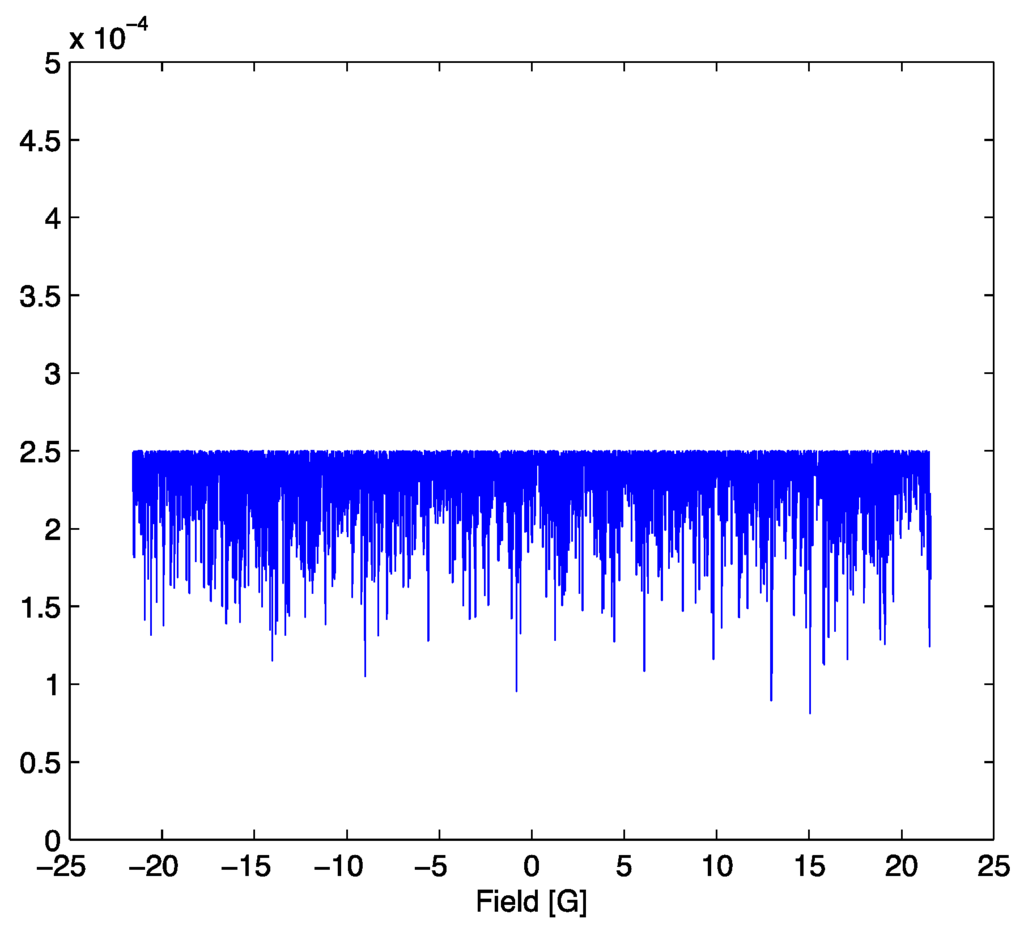
Figure 3.
Probability mass function (8) evaluated at the optimal parameter set and SNR = 70.
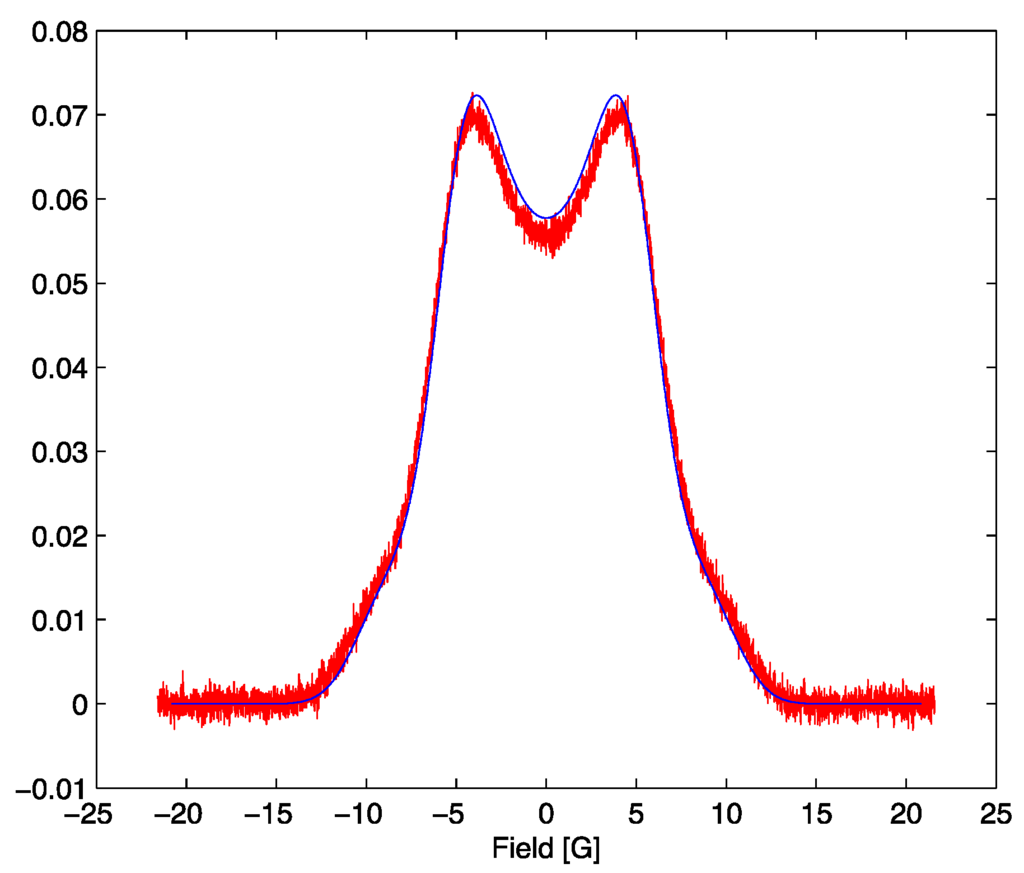
Figure 4.
The simulated signal for the optimum parameter set with SNR = 70 in red and the model lineshape evaluated at α = 5.2, β = 1.49 in blue.

Figure 5.
Probability mass function (8) evaluated at α = 5.2 and β = 1.49 and SNR = 70.
Note that the maximum amplitude of the probability mass function in Figure 5 is slightly higher than that in Figure 3. This is a result of a decrease in the value of the normalization constant, the partition function (7), which leads to a slight increase in the probability of points far from the center of the distribution where the model and signal still coincide. The decrease in the partition function arises because deviations from the optimum parameter set distort the probability mass function. This may be interpreted in a thermodynamic analogy as a non-equilibrium state where the residual is treated as a distortion energy. When the parameter set is non-optimum, the distortion energy increases, corresponding to a “perturbation” away from equilibrium. During a successful search process, the mean squared residual approaches a minimum and “equilibrium” is achieved at the optimum parameter set. In order to accurately estimate the uncertainties in the parameters, it is necessary to quantify precisely how the mean-squared distortion energy changes in the neighborhood of the parameter optimum. In some sense, we need a measure of how far “apart” different posteriors are. The tool of choice for this purpose is the Fisher information matrix which can be treated as a metric in the space of lineshape model parameters [7]. The Fisher information matrix induces a geometry on parameter space. For the particular case studied here, we will show in Section 3 that the resulting geometry has negative curvature, analogous to the surface of a saddle, and this has consequences for accurate computation of parameter uncertainties. The Appendix contains a brief formulary for some needed results from differential geometry for the computation of quantities related to curvature. Some of these results are only valid for the two dimensional parameter space treated here. The references should be consulted for the extensions needed to accommodate parameter spaces of higher dimension.
2. Methods
2.1. MCMC Simulation
A Markov Chain Monte Carlo algorithm was written using MATLAB to find the optimal parameter set. This algorithm searches parameter space, seeking the absolute maximum of the partition function, which corresponds to the state of maximum entropy. Typically, Metropolis Hastings MCMC algorithms sample the posterior probability when the total distribution is unknown [8]. A set of parameters is taken and compared to a new position and if the new set has a higher probability, the old parameter set is deprecated. Here, (8) is the probability based on the magnetic field, α and β while the partition function is the numerator marginalized over the field. If we also marginalize the denominator over all probability space (field, α and β) and the numerator over the field, we obtain a new probability distribution that consists of the partition function divided by some normalization. When the algorithm compares the probabilities at each step, the normalizations (Π) cancel and only the partition functions remain:
Hence when this algorithm takes a step that changes the parameter combination, it generates a new model lineshape to be compared to the signal via Equation (8). The partition function is calculated for both the new parameter set and the old, which are then compared as a ratio:
The algorithm accepts the new set as the new worst set if the new set has a higher value for the partition function than the previous set and then proceeds to sample more sets. Acceptance rates (the ratio of number of steps taken that yield a higher partition function to total number of steps taken) for α and β are monitored so that the step size (with an initial value of 0.5 which either grows or decays exponentially based on the acceptance rate) for each of the parameters can be adjusted to suit the landscape. The new parameter set is randomly chosen at an arbitrary step size away from the current parameter set. This random selection is equivalent to a biased coin toss. The bias is calculated using the ratio of the two partition functions to control the direction the algorithm moves in. If the new partition function is larger than the previous on, the probability of a step size in that direction will be slightly higher. A flow chart is shown below in Figure 6 to help visualize the steps involved in the algorithm.
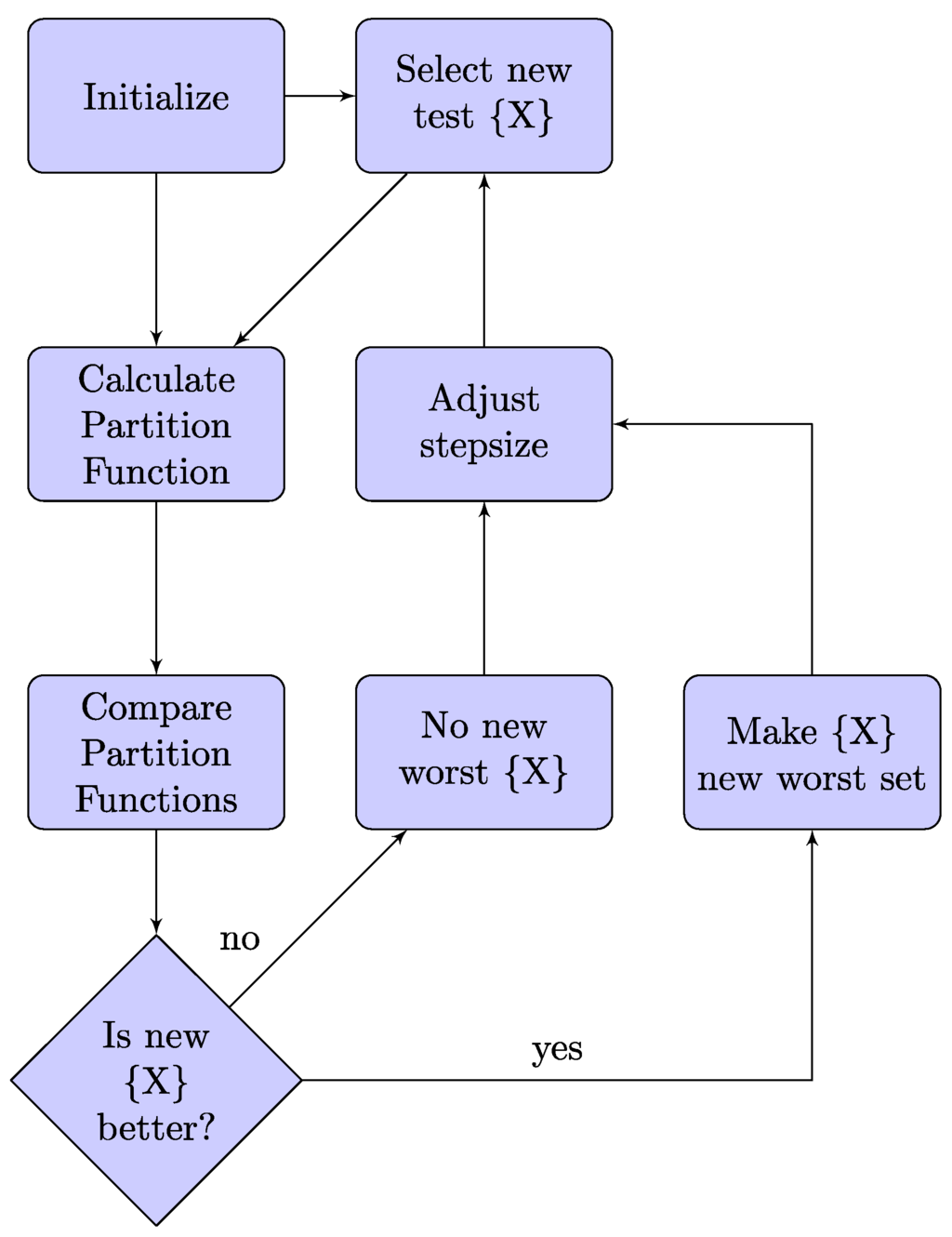
Figure 6.
A flow chart of the algorithm developed for the computations reported on in this work.
2.2. Computation of Parameter Uncertainties
Given the mean-squared residual at the optimum parameter set and its behavior in the neighborhood of the optimum parameter set, the usual procedure is to estimate parameter uncertainties from the Hessian matrix (12) computed from partial derivatives of the mean-squared residual (9) with respect to parameters Xm, Xn, where Xm, Xn are chosen from the set {α, β}. In this two parameter model, one obtains a 2 × 2 matrix. The (1,1) component of this matrix is the second partial derivative of the residual (9) with respect to parameter 1 (in this case derivatives with respect to α); off diagonal components are partial derivatives to α and β.
It is here that curvature effects enter. If the parameter space were flat, which is the usual assumption, then no curvature effects need to be accounted for. As we have shown previously [7], the parameter space for the lineshape model can be curved, and we need the tools of differential geometry to accommodate this curvature (cf. Appendix).
The starting point for these investigations requires that we specify a metric on parameter space. We have shown [7] that a suitable choice for the lineshape problem is the Fisher information (13) [11]:
The Fisher information gives us a notion of “distance” between models in parameter space. In order to describe the curvature of this space, we need derivatives of the metric known as Christoffel symbols [12] (14). The required derivatives are evaluated analytically and implemented in the code. These derivatives depend on differentiation of (3), due to repeated application of the chain rule. By appropriate reuse of code, analytical evaluation of the derivatives is tedious but straightforward, and is preferred over numerical differentiation due to instabilities inherent in numerical differentiation. The closed form expression for the required Christoffel symbols is:
Here, the quantity is the matrix inverse of the quantity defined in (13). We are also using the Einstein summation convention where repeated indices are summed over. If the parameter space is flat, which is the usual assumption in parameter inference, then the Christoffel symbols vanish. Note that the curvature of the parameter space is independent of the particular parameterization chosen, so that there is no clever coordinate transformation that will transform the curvature away.
We now return to the problem of computing the Hessian. From a mathematical perspective the quantity defined in (9) is a scalar. It is a standard result of differential geometry that partial derivatives of scalar functions do not require curvature corrections. So, the array of first derivatives of (9) computed as an intermediate step in the computation of the Hessian do not need to be corrected. It is important to note, however, that this array of first derivatives does depend on the chosen parameterization and transforms as a vector under arbitrary coordinate transformations. Differential geometry informs us that the second derivative matrix of a scalar function, in this case the Hessian, will require curvature corrections. The form of the Hessian that incorporates Riemannian corrections is:
3. Results
MCMC Simulation Results
Below we show surface plots of the partition function in parameter space for SNR = 7, Figure 7a, and SNR = 70, Figure 7b. The landscape of the SNR = 70 case has many more features in parameter space than the SNR = 7 case. For cases of higher SNR, the parameter landscape may be approximated by a flat landscape with a delta function at the optimum parameter set. This requires a better ‘initial guess’ of starting parameters for the algorithm. For the SNR = 7 case, we start with {X} = {1.6, 0.5} and for the SNR = 70 case {X} = {4.95, 1.38}.
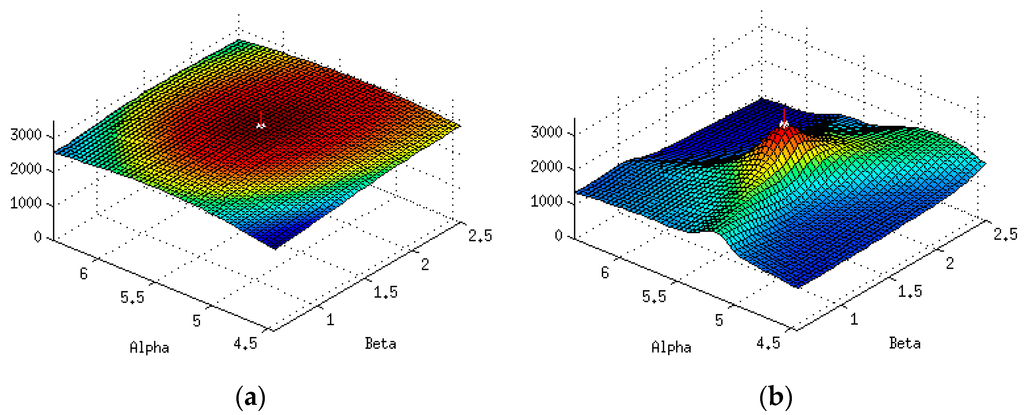
Figure 7.
(a) The partition function (7) at SNR = 7 for α values from 4.5 to 6.5 and β values from 0.5 to 1.5. (b) The partition function (7) at SNR = 70 for α values from 4.5 to 6.5 and β from 0.5 to 1.5. For both plots, the red vertical line indicates the optimum parameter set.
Here we show (in Figure 8a,b and Figure 9a,b) parameter values obtained by the Monte Carlo simulation, which are the root mean square (RMS) of one thousand iterations, for signal to noise ratios of 7 and 70. The same starting parameters are used for all simulations except that the SNR = 70 case uses starting parameters that are closer to the optimal parameter set to improve the convergence properties. We note that it is often found in practice, regardless of the method used, that parameter inference on spectra with a high SNR requires starting values closer to the optimized parameter set than is required for the low SNR case.
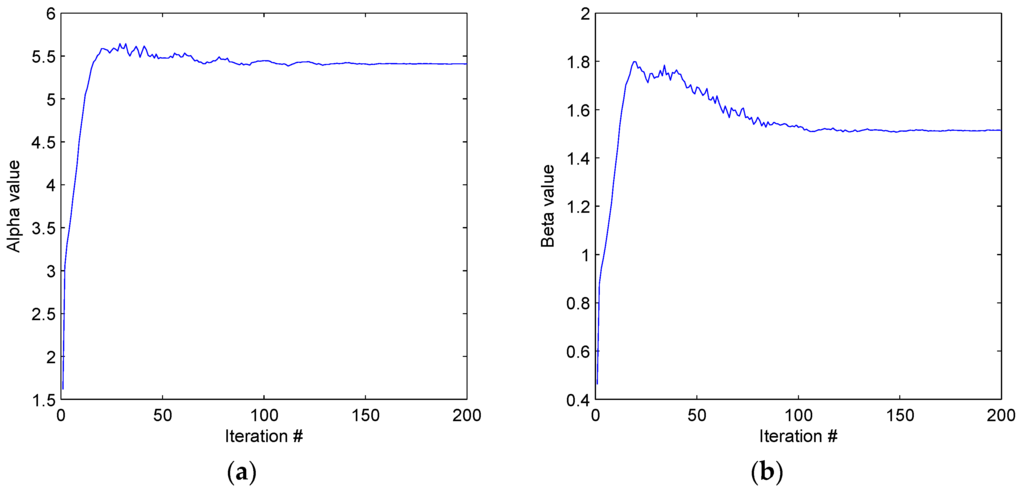
Figure 8.
(a) Results of the algorithm described in this work for SNR = 7 yield α = 5.4067 ± 0.26G. (b) Results of the algorithm described in this work for SNR = 7 yield β = 1.5099 ± 0.77G.
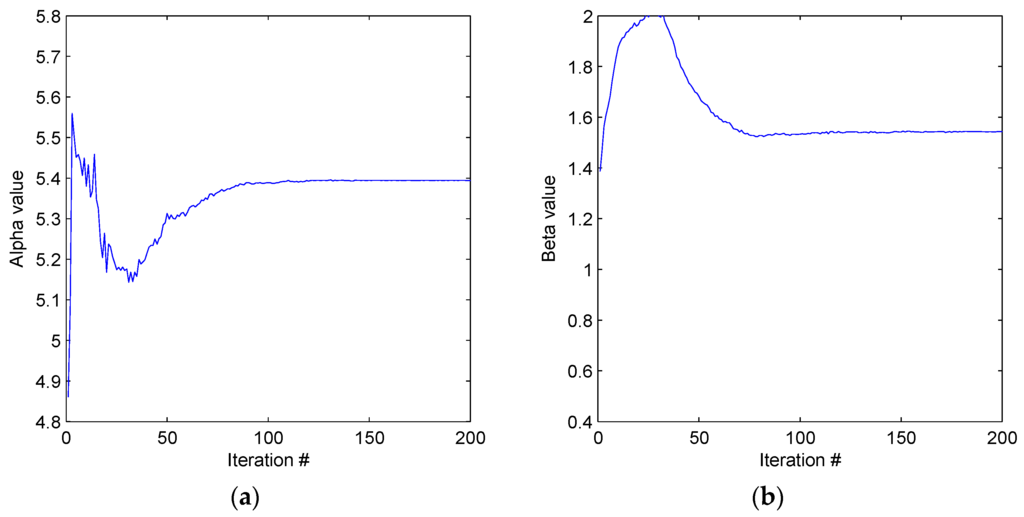
Figure 9.
(a) Results of the algorithm described in this work for SNR = 70 yield α = 5.3996 ± 2.09 × 10−4G. (b) Results of the algorithm described in this work for SNR = 70 yield β = 1.5391 ± 1.4 × 10−3G.
These values are calculated from the RMS of the last 50, stable, components. The deviation is calculated similarly. The convergence of the algorithm on the optimum parameter set in the SNR = 70 case is 98.62±3.6%. This is calculated by performing 5000 iterations of the algorithm and finding which of these paths reach the optimum parameter set. It is binned into groups of 10 and the variance is calculated by the deviation in bin values.
The lower signal to noise ratio parameter optimization follows a very smooth path to the expected optimal set, consistent with the observation that the parameter landscape is relatively flat. As noted above, the higher signal to noise ratio case generates a parameter landscape with more features. Qualitatively, the search algorithm is more likely to “slip off the ridge” where the maximum partition function is found in cases of higher signal to noise.
Figure 10 shows the RMS path for SNR = 70.
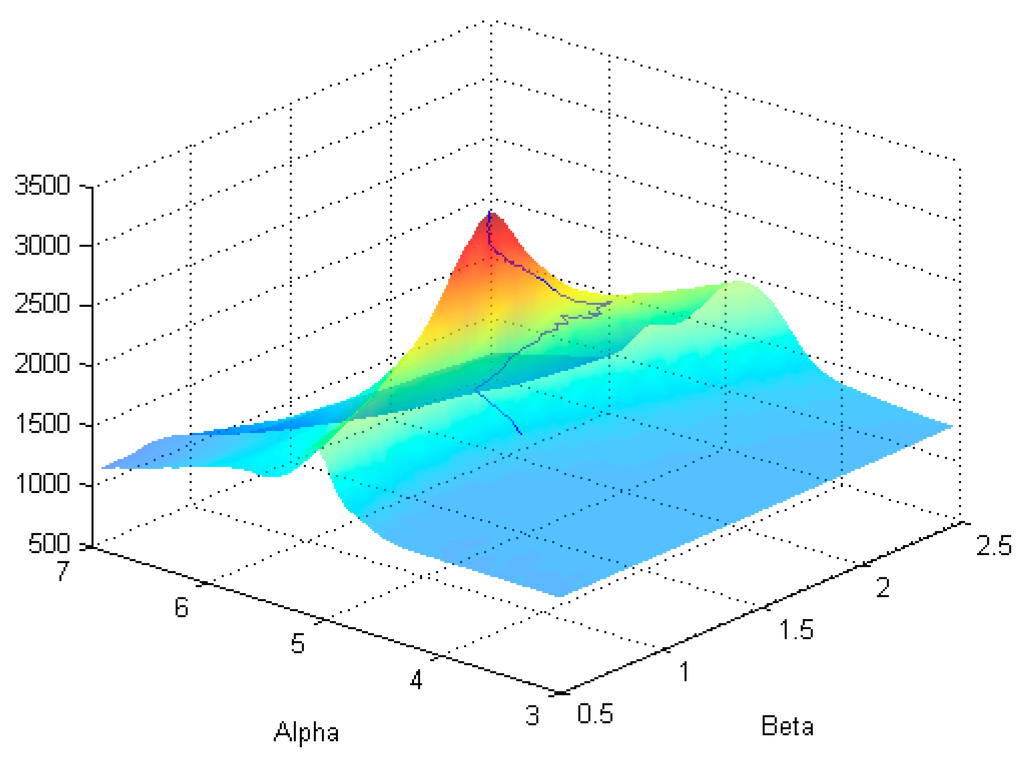
Figure 10.
Path of the algorithm cast on the surface of the partition function.
Figure 11a,b shows the performance of the MCMC algorithm compared to the performance of a Nelder–Mead algorithm [13]. For this comparison, we used the fminsearch function built into MATLAB, which uses the Nelder–Mead Simplex algorithm. Both algorithms perform well in the ranges shown for the SNR = 7 case. When we extend the scan to the SNR = 70 case, we can start to see a breakdown in the performance of the Nelder–Mead as opposed to the reliability of the MCMC algorithm used in this work.
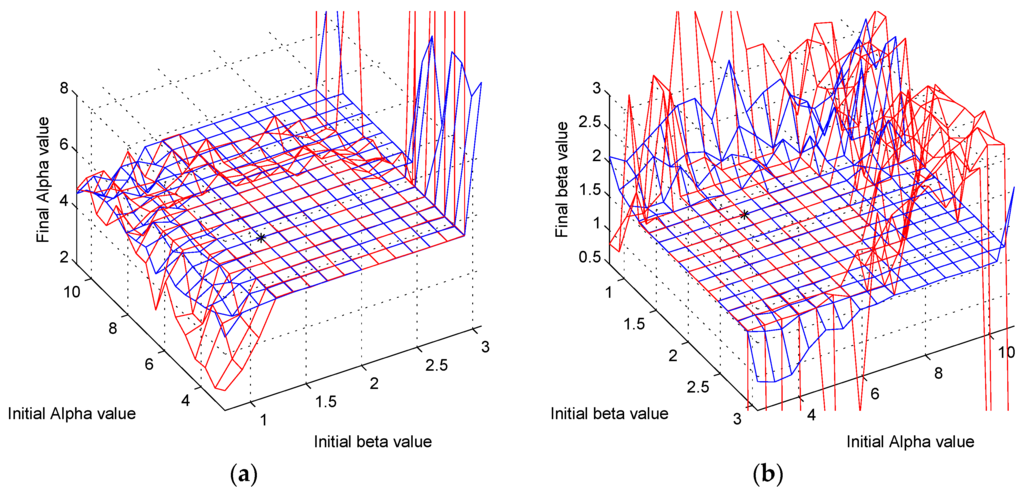
Figure 11.
(a) A scan comparing the Nelder–Mead optimization algorithm (red) with the MCMC algorithm discussed in this paper (blue) for various starting parameters of alpha and beta and the final value for alpha. (b) A scan comparing the Nelder-Mead optimization algorithm (red) with the MCMC algorithm discussed in this paper (blue) for various starting parameters of alpha and beta and the final value for beta.
Using the expressions given in the Appendix, we show the effect of curvature in the parameter space for low signal to noise in Figure 12a, and good signal to noise in Figure 12b.
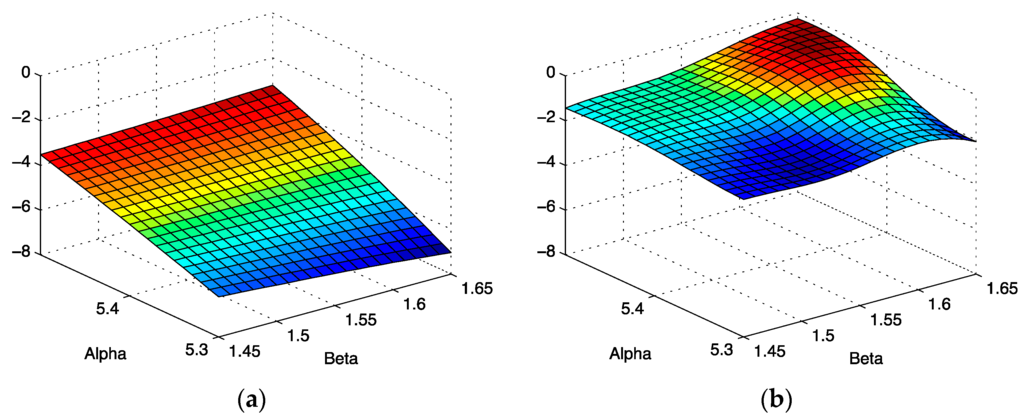
Figure 12.
(a) Gaussian curvature K as a function of model parameters for SNR = 7. (b) Gaussian curvature K as a function of model parameters for SNR = 70.
The variances obtained by taking the inverse of the Hessian Matrix (12) for the case SNR = 7 are found to be 0.22 for , and 0.71 for ; the curvature corrected variances computed from the Hessian matrix (15) are found to be 0.26 for , and 0.77 for . For the SNR = 70 case, the “Euclidean” variance values are 2.7×10−3 for , and 7.8×10−3 for , while the curvature corrected variances are found to be 2.8×10−3 for , and 7.9×10−3 for . Note that the curvature corrections are more significant in the low SNR case than the high SNR case.
4. Discussion
Our motivation for studying this problem was to extend the methods of [7] which were applied to a simple absorption line to a more complex problem. As noted in the introduction, the work of Bretthorst provides an alternative perspective and approach [1,2,3]. In addition, we wanted to further explore the consequences of the curvature corrections implied by the probability mass function introduced in [10], which explicitly accounts for noise in the spectrum. These considerations encouraged us to develop an algorithm for finding the optimum parameter set of an inhomogeneously broadened Pake doublet spectrum in the presence of noise. This algorithm proves to be accurate and reliable in cases with good signal to noise; its accuracy drops off in both the high and low SNR regions. For these cases, a nested sampling algorithm [8] was used but is not discussed in this paper. The algorithm also requires a sampling procedure that can accurately accommodate the inverse square root singularity of Euqation (1). It does exemplify how the principles of a Metropolis Hastings Markov Chain Monte Carlo algorithm can be adapted to suit the requirements of parameter optimization for a magnetic resonance lineshape of importance for distance determinations [4,5]. It should be noted that the cases treated in this work do not account for the systematic errors that certainly complicate parameter inference in practical applications. As illustrative but by no means exhaustive examples, we have considered the effects of an unmodeled background signal, as well as an admixture of dispersion into the Pake doublet spectrum, as summarized elsewhere [10]. Athough we have shown that systematic errors can be accommodated by our methods [10], we felt that explicit consideration of such errors would detract from our principle aim in the work reported on here, which was to estimate and demonstrate the effets of parameter space curvature in idealized cases.
Our results provide some justification for standard error estimate practices for spectra with good signal to noise [11], exemplified by the spectrum shown in Figure 2. The scalar curvature for this case, shown in Figure 12b, is smaller in magnitude over the entire parameter space explored than the scalar curvature for the low signal to noise ratio case shown in Figure 12a. A scalar curvature of zero corresponds to a flat, or Euclidean geometry. In computing error estimates, the standard computation uses a Hessian constructed under the assumption that curvature effects may be neglected, or equivalently, that the Christoffel symbols are all zero in this space. We see that for high signal to noise, this is a well-justified assumption, but our results do indicate that it is an approximation. For the case of low signal to noise ratio, error estimates computed without curvature corrections are even more of an approximation than one might otherwise suppose. In applications, the parameter uncertainties are important criteria for assessing the reliability of the parameter inference for models of the environments in which the spin-bearing moments are found with consequences for what structural information may be trusted. In addition, the signal to noise is often sub-optimal for samples of biological interest. For these cases, the methods developed in this work permit significant refinements over conventional methods.
The methods reported on here may be applied to any lineshape model for which analytical derivatives are available. Numerical derivatives may be used when necessary, but the number of required derivatives for curvature calculations, as many as four, can result in significant loss of accuracy if the computations are performed without care. MATLAB scripts comprising an implementation of the algorithm described here are available for download from the Earle research website: earlelab.rit.albany.edu.
5. Conclusions
Boltzmann statistics and the maximum likelihood distribution provided the basis for a novel parameter optimization algorithm. The maximum likelihood function also allowed us to develop a metric on parameter space and define a consistent information geometry. The Metropolis Hastings Markov Chain Monte Carlo algorithm was modified for application to parameter optimization. It performed reliably for the two-parameter, Pake Doublet spectrum model system studied here, even with lineshapes that had a low signal to noise ratio. Information geometry allowed us to show that the parameter space geometry induced by the posterior distribution arising from the lineshape has negative curvature. This negative curvature altered parameter uncertainties by providing Riemannian corrections to the Hessian from which the parameter uncertainties were computed.
Acknowledgments
Kiel Hock thanks Kevin Knuth of the University at Albany Physics Department for several useful discussions. Keith Earle thanks David Schneider of Cornell University for numerous discussions. In addition, Keith Earle thanks the National Institutes of Health Advanced ESR Technology (NIH ACERT) resource at Cornell University for the use of their resources during the preparation of this manuscript. Keith Earle also thanks the University at Albany for partial support of this work via a Faculty Research Award Program grant and the Biomedical EPR Center at the Medical College of Wisconsin for partial support as a participant in the Advanced Visitor Training Program during a sabbatical visit while this manuscript was in preparation.
Author Contributions
Kiel Hock developed the code used in this paper. Keith Earle suggested the problem and developed the theoretical formalism used. This paper was written by Kiel Hock and Keith Earle. Both authors have read and approved the final manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix
In this appendix we will state without proof some basic results of differential geometry that are needed to follow the discussion of curvature in the main text. The Riemann curvature tensor characterizes the intrinsic curvature of a space. For example, from local measurements on the surface of a sphere, one may infer that the surface is positively curved. Using the methods developed in [7], one may show that a simple absorption lineshape has negative curvature, sometimes called a saddle geometry. In terms of the metric tensor, here, the Fisher information, and the Christoffel symbols introduced in (12) and (13), one may write elements of the curvature tensor as follows:
Here, the indices span the parameter space. We are also using the Einstein summation convention that repeated indices are summed over. For the case that we are studying, we have a space that is intrinsically two dimensional, characterized by and . Even with two parameters one could have, in principle, sixteen components for a tensor with four indices. For the special case of two dimensions, however, one can exploit symmetries of the curvature tensor to show that there is only one independent component. Choosing the labels and the sole independent component of the curvature tensor may be written explicitly as follows:
A good resource for this material may be found in [12]. In practical applications, it is often useful to work with tensors that summarize the full information provided by the Riemann curvature tensor. An example is the Ricci curvature tensor. In two dimensions, this symmetric tensor takes the following form:
Note that the Ricci tensor has four components in this two dimensional space and is proportional to the Fisher information. In higher dimensions, this proportionality is not maintained in general. We have also introduced the quantity:
which is the determinant of the Fisher information matrix. A further summary of the curvature information available from the Riemann curvature tensor is provided by the scalar curvature, which takes the following form in a two dimensional space:
As a side note, the Ricci curvature tensor and the scalar curvature are key elements appearing in the Einstein field equations [14]. Historically, the Gaussian curvature:
was developed to describe the intrinsic curvature of two dimensional surfaces. It differs by a trivial factor from the scalar curvature. When comparing expressions for the Gaussian curvature in the literature, it is important to determine the sign of the determinant in Equation (A4). In the work reported on here, the determinant is positive definite. In the field of General Relativity, the determinant of the metric is negative, so some authors [14] insert an extra minus sign in equations analogous to (A6). The sign of the determinant of the metric is not directly related to curvature effects. For example, the metric , , describes a “hyperbolic sphere”, a surface with intrinsically negative curvature. Observe that the metric in this case is positive definite.
References
- Bretthorst, G.L. Bayesian Analysis I. Parameter Estimation Using Quadrature NMR Models. J. Magn. Reson. 1990, 88, 533–551. [Google Scholar] [CrossRef]
- Bretthorst, G.L. Bayesian Analysis II. Parameter Estimation Using Quadrature NMR Models. J. Magn. Reson. 1990, 88, 552–570. [Google Scholar]
- Bretthorst, G.L. Bayesian Analysis III. Parameter Estimation Using Quadrature NMR Models. J. Magn. Reson. 1990, 88, 571–595. [Google Scholar]
- Berliner, L.J.; Eaton, S.S.; Eaton, G.R. (Eds.) Distance Measurements in Biological Systems by EPR. In Biological Magnetic Resonance; Kluwer Academic/Plenum Publishers: New York, NY, USA, 2000.
- Pake, G.E. Nuclear Resonance Absorption in Hydrated Crystals: Fine Structure of the Proton Line. J. Chem. Phys. 1948, 16, 327–336. [Google Scholar] [CrossRef]
- Abragam, A. The Principles of Nuclear Magnetism; Oxford University Press: London, UK, 1961. [Google Scholar]
- Earle, K.A.; Mainali, L.; Dev Sahu, I.; Schneider, D.J. Magnetic Resonance Spectra and Statistical Geometry. Appl. Magn. Reson. 2010, 37, 865–880. [Google Scholar] [CrossRef] [PubMed]
- Sivia, D.S.; Skilling, J. Data Analysis: A Bayesian Tutorial; Oxford University Press: New York, NY, USA, 2010. [Google Scholar]
- Ben-Naim, A. A Farewell to Entropy: Statistical Thermodynamics Based on Information; World Scientific Publishing: Singapore, 2011. [Google Scholar]
- Hock, K.; Earle, K. Information Theory Applied to Parameter Inference of Pake Doublet Spectra. Appl. Magn. Reson. 2014, 45, 859–879. [Google Scholar] [CrossRef]
- Rao, C.R. Information and the Accuracy Attainable in the Estimation of Statistical Parameters. In Breakthroughs in Statistics; Springer: New York, NY, USA, 1992. [Google Scholar]
- Lee, J.M. Riemannian Manifolds: An Introduction to Curvature; Springer: New York, NY, USA, 1997. [Google Scholar]
- Lagaris, J.C.; Reeds, J.A.; Wright, M.H.; Wright, P.E. Convergence Properties of the Nelder-Mead Simplex Method in Low Dimensions. SIAM J. Optim. 1998, 9, 112–147. [Google Scholar] [CrossRef]
- Weinberg, S. Gravitation and Cosmology: Principles and Applications of the General Theory of Relativity; Wiley: New York, NY, USA, 1972. [Google Scholar]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).