Entropy Generation through Deterministic Spiral Structures in Corner Flows with Sidewall Surface Mass Injection
Abstract
:1. Introduction

2. Selection of Heated Air as the Working Substance
3. Review of Program Components
3.1. Steady-Flow Boundary-Layer Development: Velocity Gradients
3.2. Modified Lorenz-Form Equations: Spectral Velocity Components
3.3. Synchronization Properties of the Modified Lorenz Equations
3.4. Power Spectral Density within the Deterministic Spectral Velocity Fluctuations
3.5. Empirical Entropies from Singular Value Decomposition
3.6. Empirical Entropic Indices for the Ordered Structures
3.7. Empirical Intermittency Exponents for the Ordered Structures
3.8. Kinetic Energy Available for Dissipation
3.9. Entropy Generation Rates through the Ordered Structures
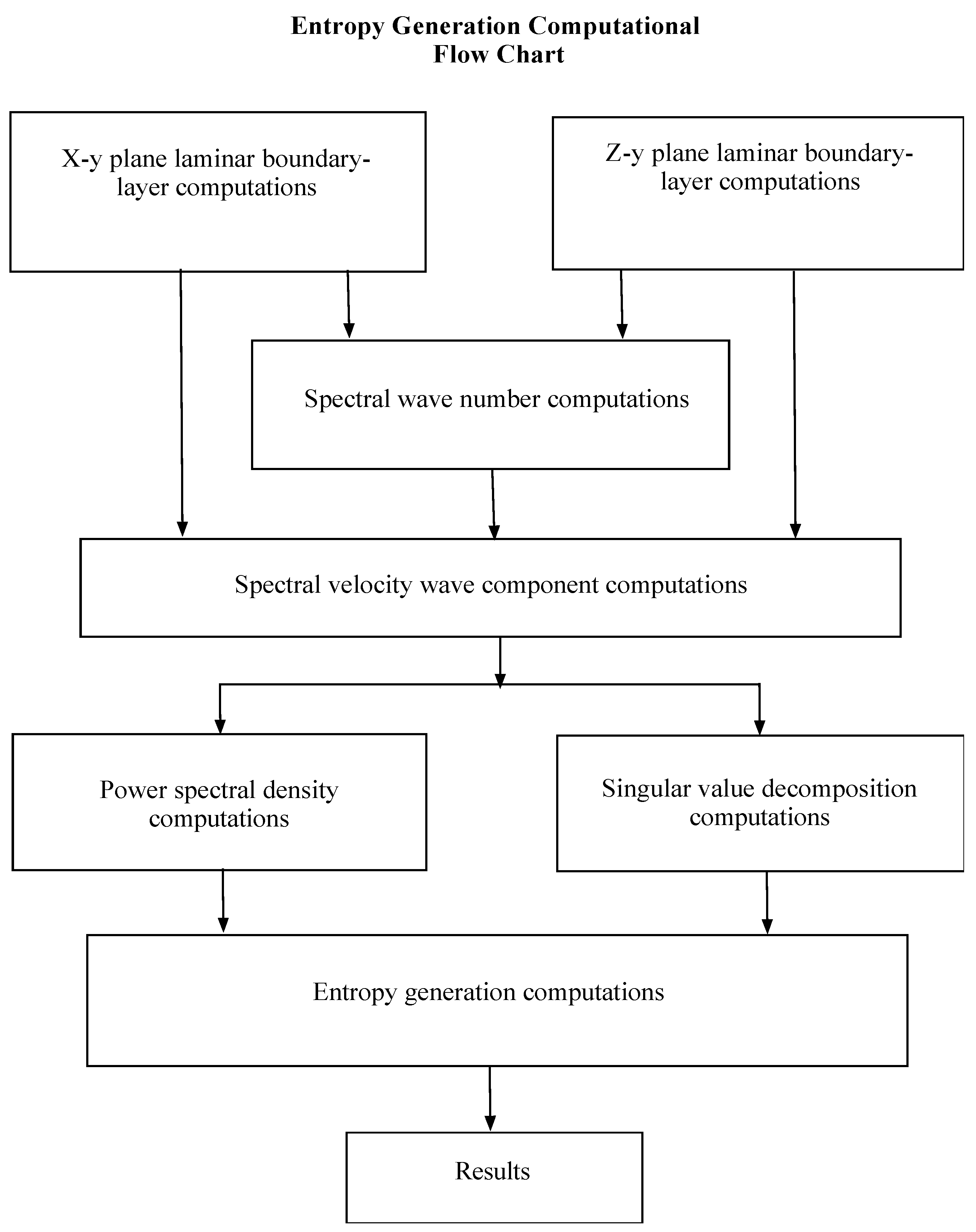
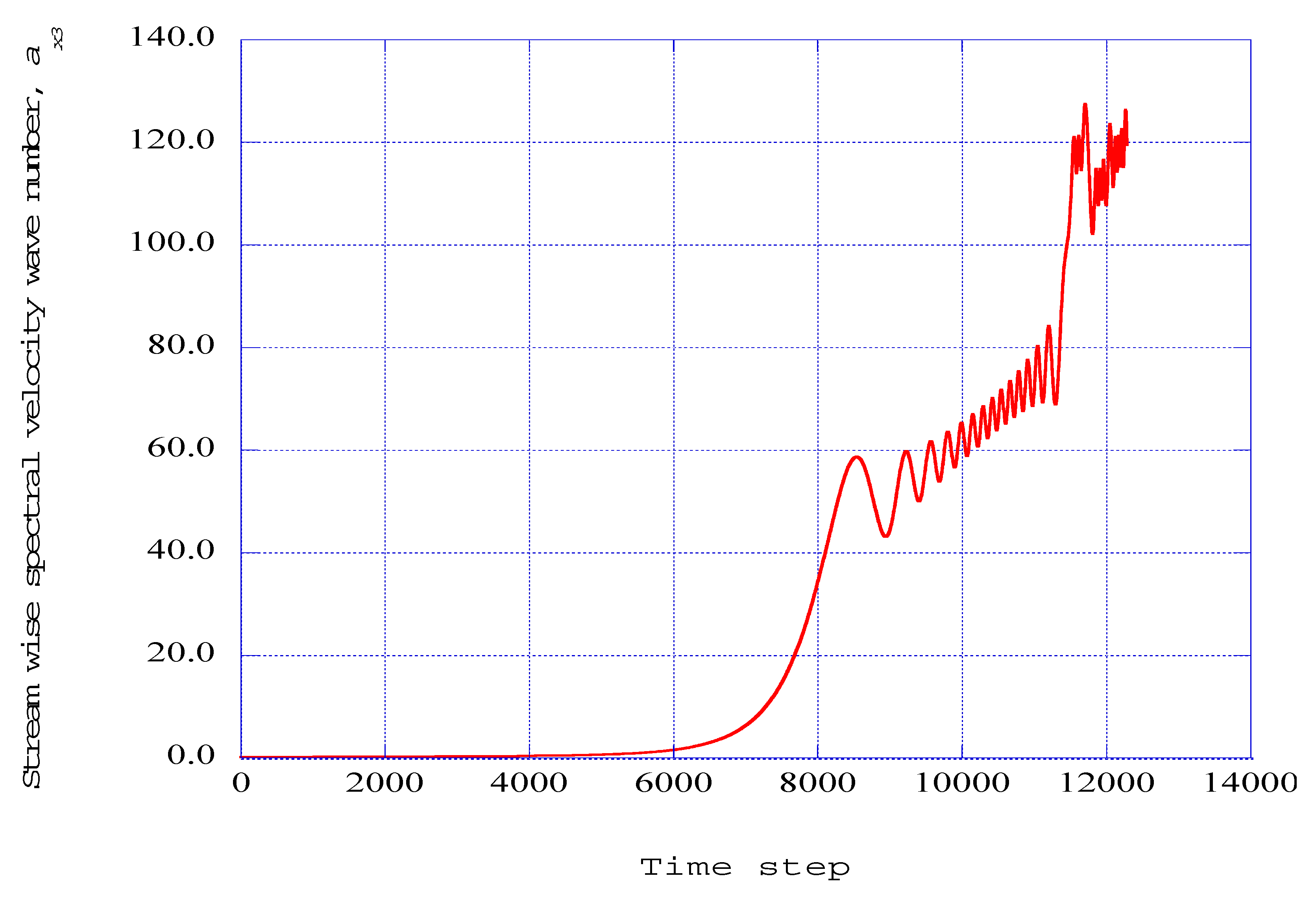
4. Results
Computational Results for the Receiver Stations
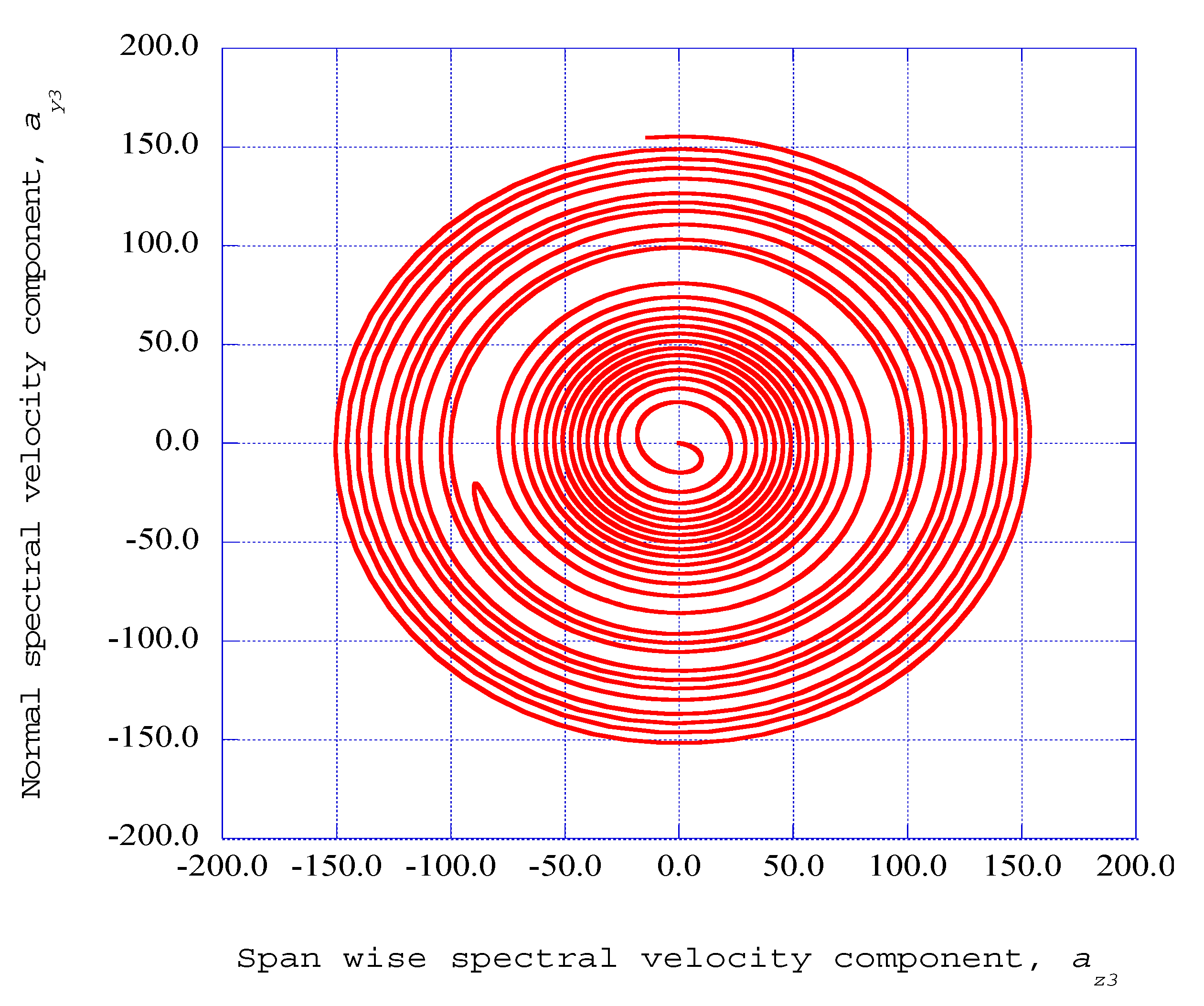


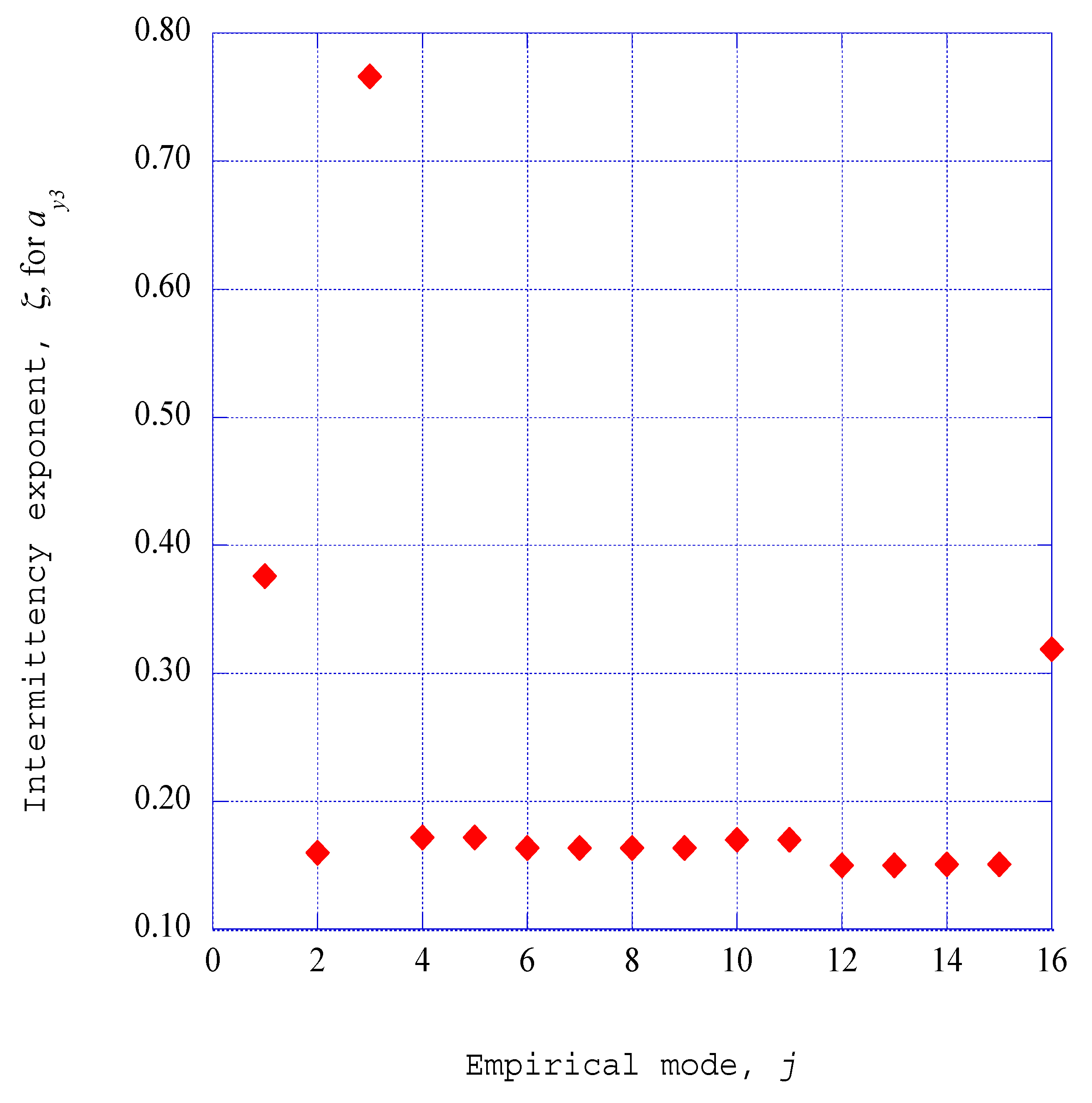
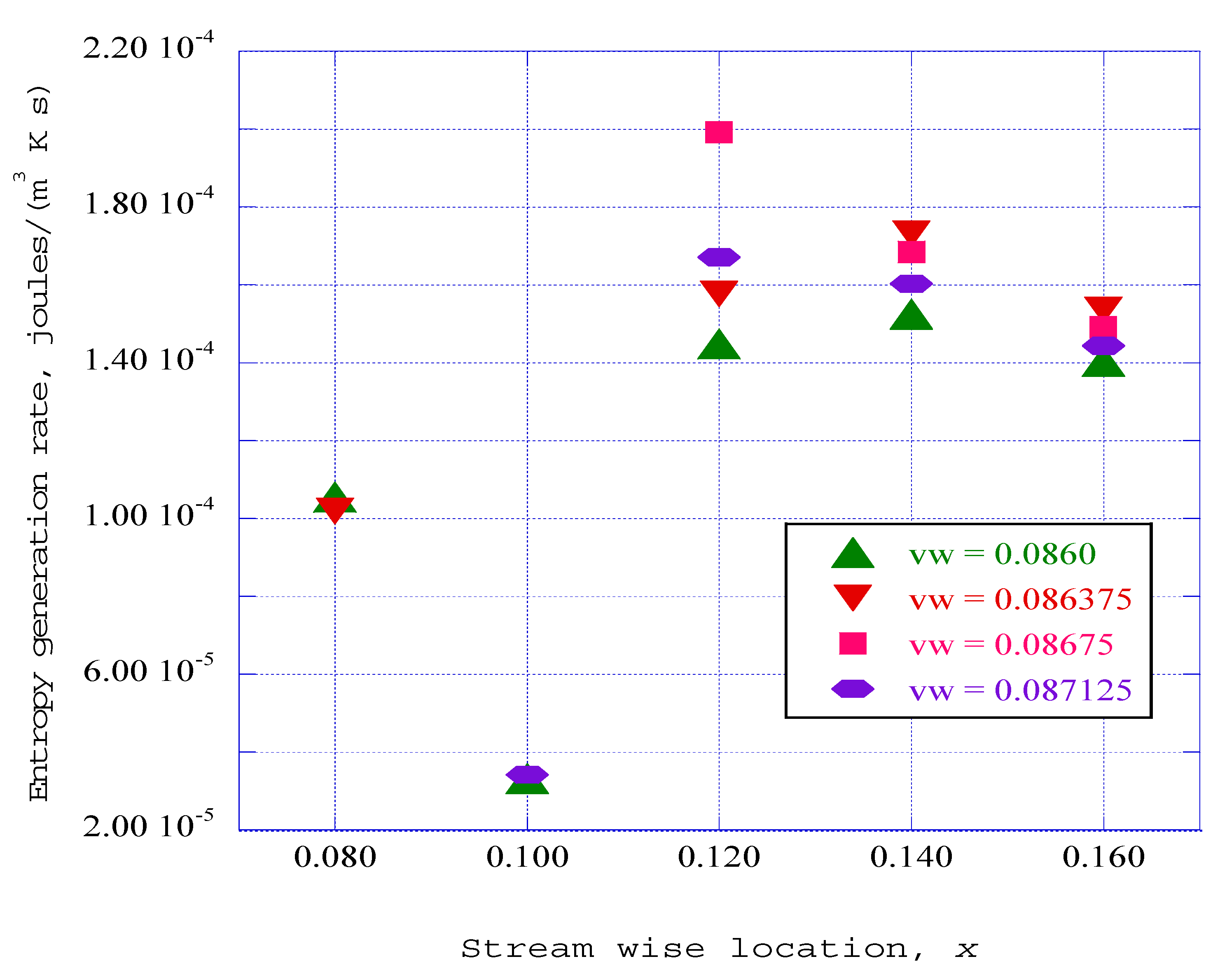
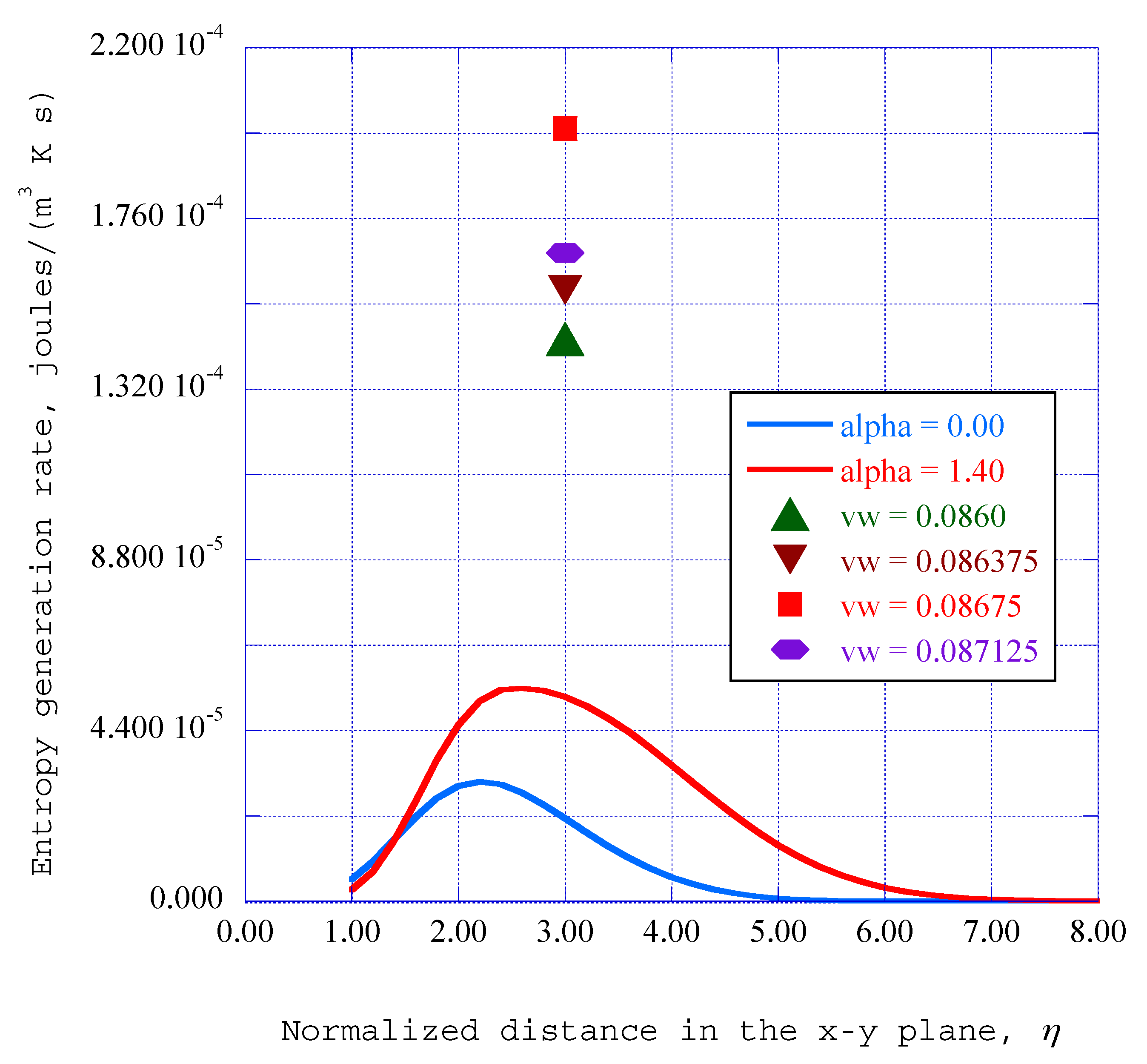
5. On the Transition of Non-Equilibrium Ordered Structures into Equilibrium Thermodynamic States

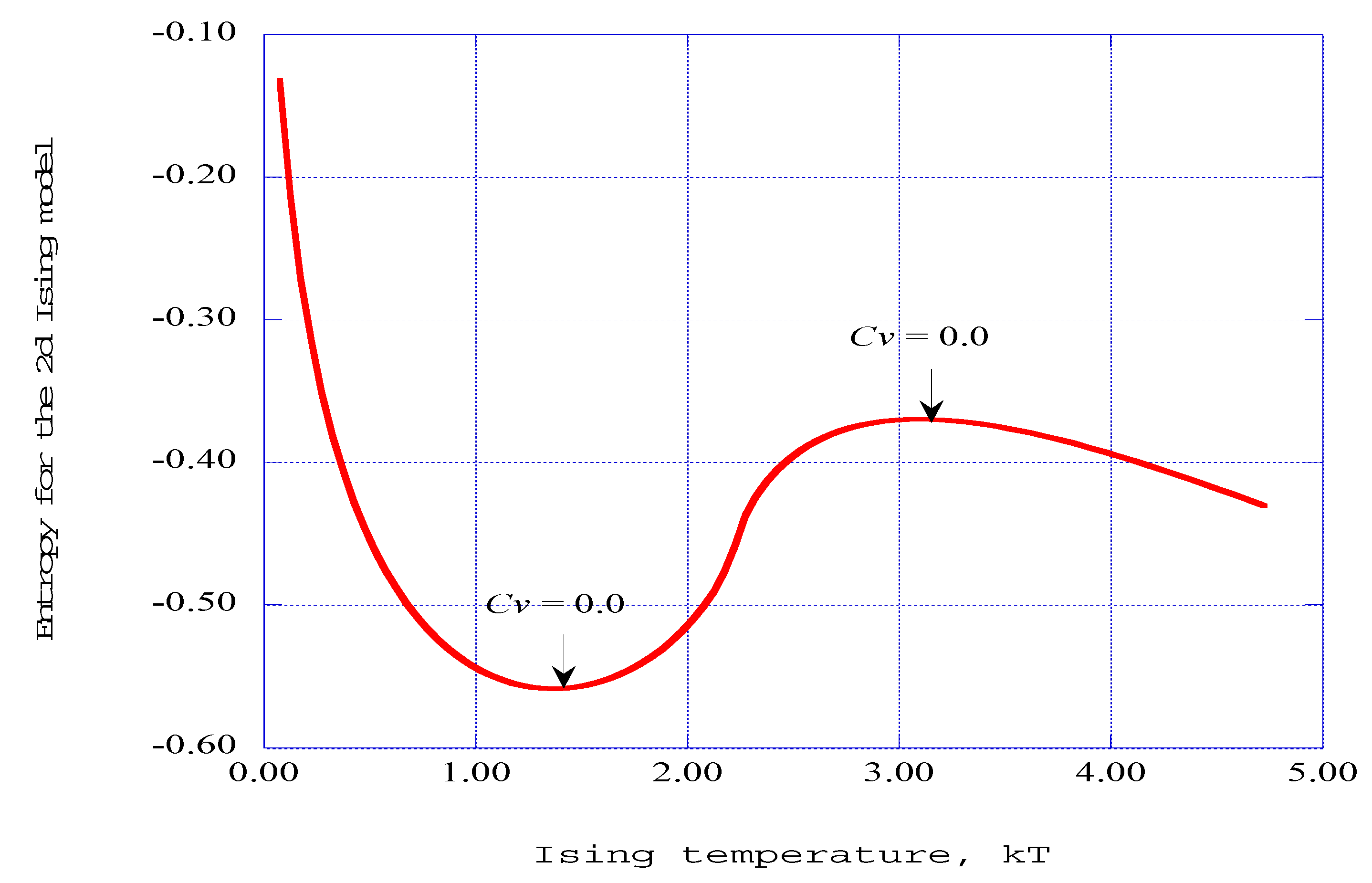
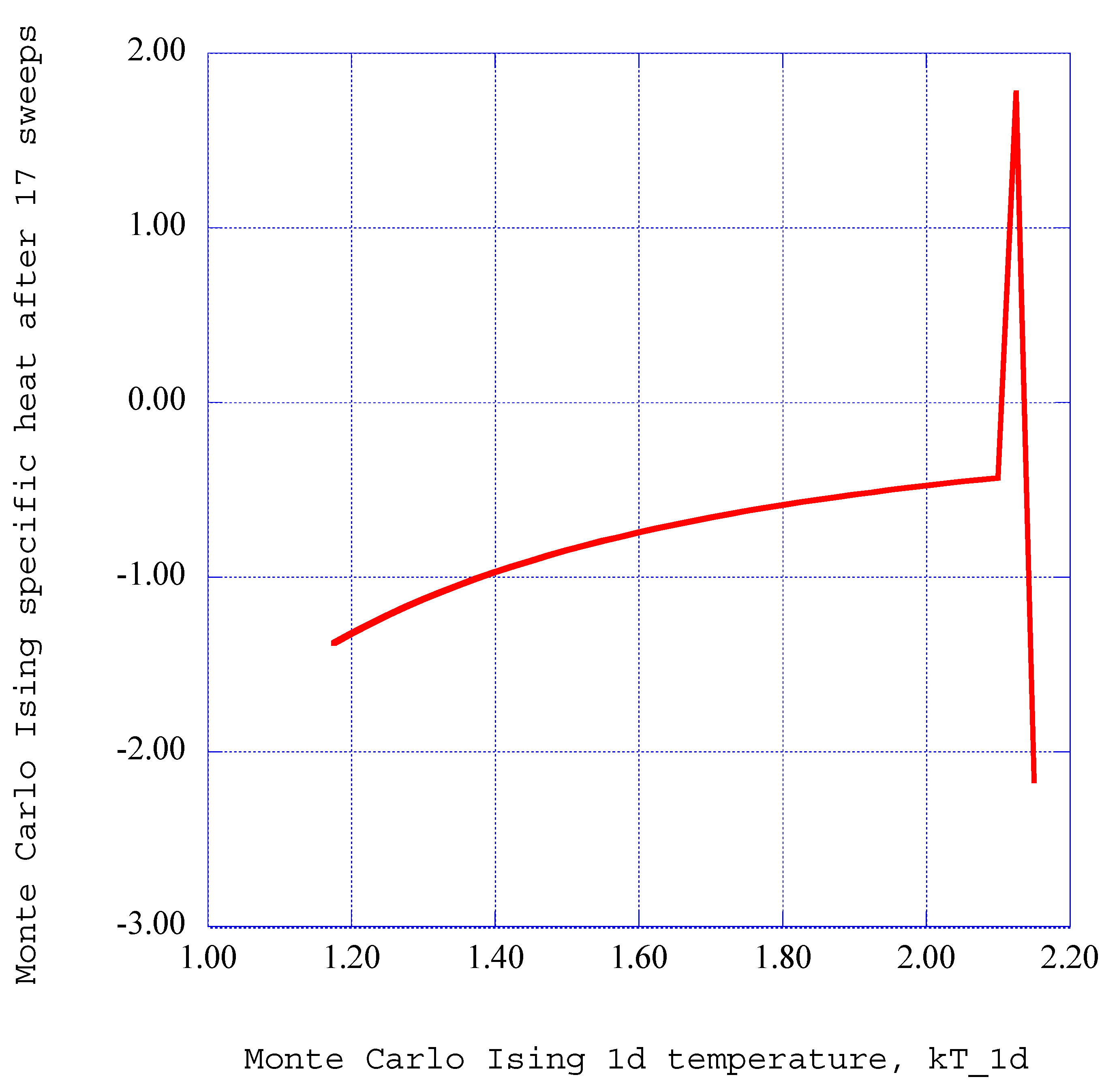
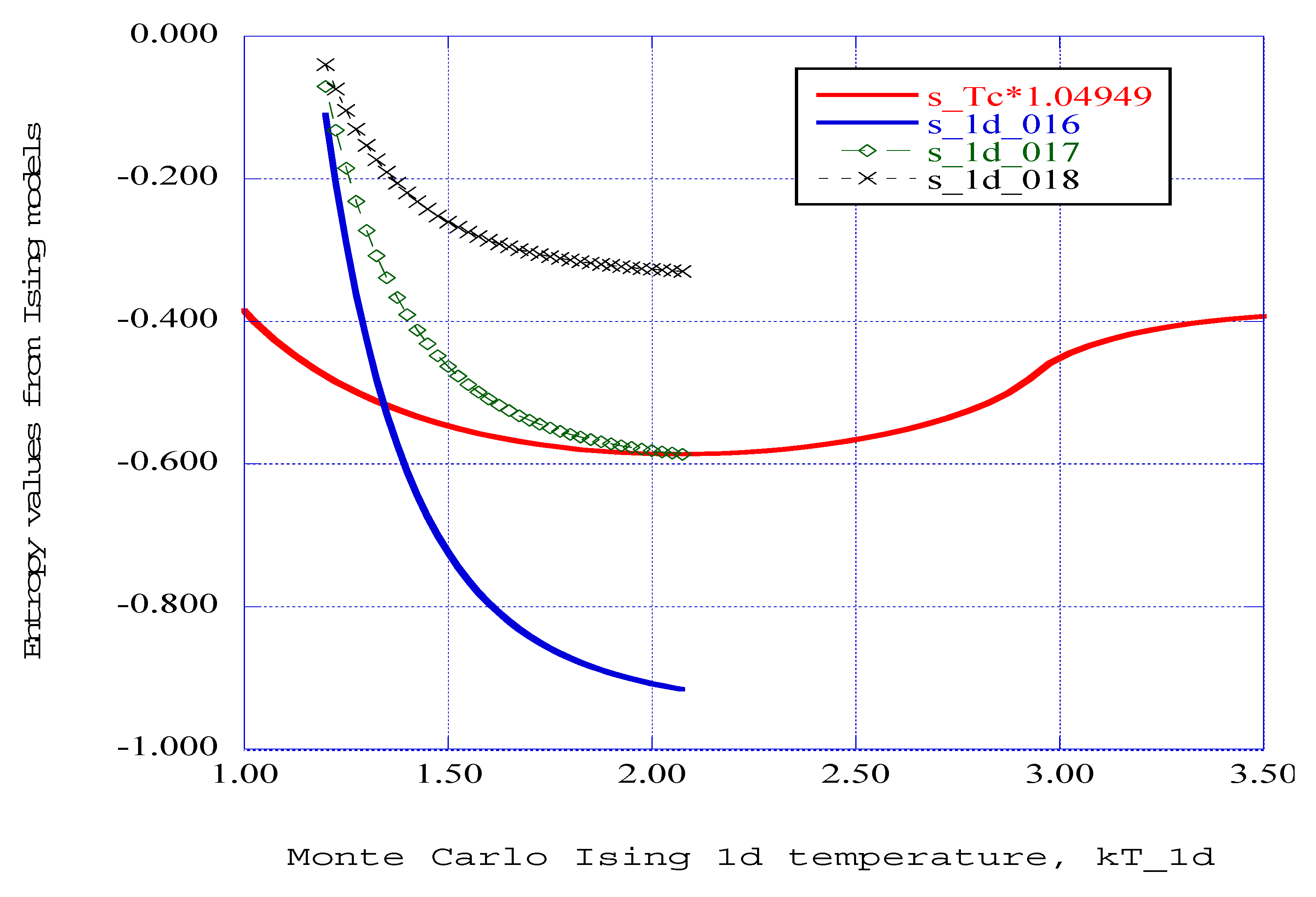
6. Discussion
7. Conclusions
Conflicts of Interest
References
- Isaacson, L.K. Entropy Generation through Deterministic Spiral Structures in a Corner Boundary-Layer Flow. Entropy 2015, 17, 5304–5332. [Google Scholar] [CrossRef]
- Isaacson, L.K. Ordered Regions within a Nonlinear Time Series Solution of a Lorenz Form of the Townsend Equations for a Boundary-Layer Flow. Entropy 2013, 15, 53–79. [Google Scholar] [CrossRef]
- Isaacson, L.K. Spectral Entropy, Empirical Entropy and Empirical Exergy for Deterministic Boundary-Layer Structures. Entropy 2013, 15, 4134–4158. [Google Scholar] [CrossRef]
- Isaacson, L.K. Spectral Entropy in a Boundary Layer Flow. Entropy 2011, 13, 1555–1583. [Google Scholar] [CrossRef]
- Isaacson, L.K. Entropy Generation through a Deterministic Boundary-Layer Structure in Warm Dense Plasma. Entropy 2014, 16, 6006–6032. [Google Scholar] [CrossRef]
- Attard, P. Non-Equilibrium Thermodynamics and Statistical Mechanics: Foundation and Applications; Oxford University Press: Oxford, UK, 2012. [Google Scholar]
- Hansen, A.G. Similarity Analyses of Boundary Value Problems in Engineering; Prentice-Hall, Inc.: Englewood Cliffs, NJ, USA, 1964; pp. 86–92. [Google Scholar]
- Cebeci, T.; Bradshaw, P. Momentum Transfer in Boundary Layers; Hemisphere: Washington, DC, USA, 1977; pp. 319–321. [Google Scholar]
- Cebeci, T.; Cousteix, J. Modeling and Computation of Boundary-Layer Flows; Horizons Publishing Inc.: Long Beach, CA, USA, 2005. [Google Scholar]
- Townsend, A.A. The Structure of Turbulent Shear Flow, 2nd ed.; Cambridge University Press: Cambridge, UK, 1976. [Google Scholar]
- Isaacson, L.K. Transitional Intermittency Exponents through Deterministic Boundary-Layer Structures and Empirical Entropic Indices. Entropy 2014, 16, 2729–2755. [Google Scholar] [CrossRef]
- Mathieu, J.; Scott, J. An Introduction to Turbulent Flow; Cambridge University Press: New York, NY, USA, 2000; pp. 251–261. [Google Scholar]
- Manneville, P. Dissipative Structures and Weak Turbulence; Academic Press, Inc.: San Diego, CA, USA, 1990. [Google Scholar]
- Pecora, L.M.; Carroll, T.L. Synchronization in chaotic systems. In Controlling Chaos: Theoretical and Practical Methods in Nonlinear Dynamics; Kapitaniak, T., Ed.; Academic Press Inc.: San Diego, CA, USA, 1996; pp. 142–145. [Google Scholar]
- Pérez, G.; Cerdeiral, H.A. Extracting messages masked by chaos. In Controlling Chaos: Theoretical and Practical Methods in Nonlinear Dynamics; Kapitaniak, T., Ed.; Academic Press Inc.: San Diego, CA, USA, 1996; pp. 157–160. [Google Scholar]
- Cuomo, K.M.; Oppenheim, A.V. Circuit implementation of synchronized chaos with applications to communications. In Controlling Chaos: Theoretical and Practical Methods in Nonlinear Dynamics; Kapitaniak, T., Ed.; Academic Press Inc.: San Diego, CA, USA, 1996; pp. 153–156. [Google Scholar]
- Chen, C.H. Digital Waveform Processing and Recognition; CRC Press, Inc.: Boca Raton, FL, USA, 1982; pp. 131–158. [Google Scholar]
- Press, W.H.; Teukolsky, S.A.; Vetterling, W.T.; Flannery, B.P. Numerical Recipes in C: The Art of Scientific Computing, 2nd ed.; Cambridge University Press: Cambridge, UK, 1992. [Google Scholar]
- Holmes, P.; Lumley, J.L.; Berkooz, G.; Rowley, C.W. Turbulence, Coherent Structures, Dynamical Stations and Symmetry, 2nd ed.; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Rissanen, J. Information and Complexity in Statistical Modeling; Springer: New York, NY, USA, 2007. [Google Scholar]
- Tsallis, C. Introduction to Nonextensive Statistical Mechanics; Springer: New York, NY, USA, 2009; pp. 37–43. [Google Scholar]
- Arimitsu, T.; Arimitsu, N. Analysis of fully developed turbulence in terms of Tsallis statistics. Phys. Rev. E 2000, 61, 3237–3240. [Google Scholar] [CrossRef]
- De Groot, S.R.; Mazur, P. Non-Equilibrium Thermodynamics; North-Holland Pub. Co.: Amsterdam, The Netherlands, 1962. [Google Scholar]
- Truitt, R.W. Fundamentals of Aerodynamic Heating; The Ronald Press Company: New York, NY, USA, 1960. [Google Scholar]
- Bejan, A. Entropy Generation Minimization; CRC Press LLC: Boca Raton, FL, USA, 1996. [Google Scholar]
- Ghasemisahebi, E. Entropy Generation in Transitional Boundary Layers; LAP LAMBERT Academic Publishing: Saarbrücken, Germany, 2013. [Google Scholar]
- Glansdorff, P.; Prigogine, I. Thermodynamic Theory of Structure, Stability and Fluctuations; John Wiley & Sons Ltd.: London, UK, 1971. [Google Scholar]
- Mariz, A.M. On the irreversible nature of the Tsallis and Renyi entropies. Phys. Lett. A 1992, 165, 409–411. [Google Scholar] [CrossRef]
- Mazellier, N.; Vassilicos, J.C. Turbulence without Richardson-Kolmogorov cascade. Phys. Fluids 2010, 22, 075101. [Google Scholar] [CrossRef]
- Hatsopoulos, G.N.; Keenan, J.H. Principles of General Thermodynamics; John Wiley & Sons, Inc.: New York, NY, USA, 1965. [Google Scholar]
- Anderson, T.D.; Lim, C.C. Introduction to Vortex Filaments in Equilibrium; Springer Science + Business Media: New York, NY, USA, 2014. [Google Scholar]
- Huang, K. Statistical Mechanics; John Wiley & Sons, Inc.: New York, NY, USA, 1963. [Google Scholar]
- Landau, D.P.; Binder, K. A Guide to Monte Carlo Simulations in Statistical Physics; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Baxter, R.L. Exactly Solved Models in Statistical Mechanics; Dover Publications, Inc.: Mineola, NY, USA, 2007. [Google Scholar]
- Newman, M.E.J.; Barkema, G.T. Monte Carlo Methods in Statistical Physics; Oxford University Press Inc.: New York, NY, USA, 2002. [Google Scholar]
- Lim, C.; Nebus, J. Vorticity, Statistical Mechanics, and Monte Carlo Simulation; Springer Science + Business Media, LLC: New York, NY, USA, 2007. [Google Scholar]
- Liang, F.; Liu, C.; Carroll, R.J. Advanced Markov Chain Monte Carlo Methods: Learning from Past Examples; John Wiley & Sons Ltd.: West Sussex, UK, 2010. [Google Scholar]
© 2016 by the author; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Isaacson, L.K. Entropy Generation through Deterministic Spiral Structures in Corner Flows with Sidewall Surface Mass Injection. Entropy 2016, 18, 47. https://doi.org/10.3390/e18020047
Isaacson LK. Entropy Generation through Deterministic Spiral Structures in Corner Flows with Sidewall Surface Mass Injection. Entropy. 2016; 18(2):47. https://doi.org/10.3390/e18020047
Chicago/Turabian StyleIsaacson, LaVar King. 2016. "Entropy Generation through Deterministic Spiral Structures in Corner Flows with Sidewall Surface Mass Injection" Entropy 18, no. 2: 47. https://doi.org/10.3390/e18020047
APA StyleIsaacson, L. K. (2016). Entropy Generation through Deterministic Spiral Structures in Corner Flows with Sidewall Surface Mass Injection. Entropy, 18(2), 47. https://doi.org/10.3390/e18020047




