Abstract
The interactions between three or more random variables are often nontrivial, poorly understood and, yet, are paramount for future advances in fields such as network information theory, neuroscience and genetics. In this work, we analyze these interactions as different modes of information sharing. Towards this end, and in contrast to most of the literature that focuses on analyzing the mutual information, we introduce an axiomatic framework for decomposing the joint entropy that characterizes the various ways in which random variables can share information. Our framework distinguishes between interdependencies where the information is shared redundantly and synergistic interdependencies where the sharing structure exists in the whole, but not between the parts. The key contribution of our approach is to focus on symmetric properties of this sharing, which do not depend on a specific point of view for differentiating roles between its components. We show that our axioms determine unique formulas for all of the terms of the proposed decomposition for systems of three variables in several cases of interest. Moreover, we show how these results can be applied to several network information theory problems, providing a more intuitive understanding of their fundamental limits.
1. Introduction
Interdependence is a key concept for understanding the rich structures that can be exhibited by biological, economic and social systems [1,2]. Although this phenomenon lies at the heart of our modern interconnected world, there is still no solid quantitative framework for analyzing complex interdependencies, this being crucial for future advances in a number of disciplines. In neuroscience, researchers desire to identify how various neurons affect an organism’s overall behavior, asking to what extent the different neurons are providing redundant or synergistic signals [3]. In genetics, the interactions and roles of multiple genes with respect to phenotypic phenomena are studied, e.g., by comparing results from single and double knockout experiments [4]. In graph and network theory, researchers are looking for measures of the information encoded in node interactions in order to quantify the complexity of the network [5]. In communication theory, sensor networks usually generate strongly-correlated data [6]; a haphazard design might not account for these interdependencies and, undesirably, will process and transmit redundant information across the network, degrading the efficiency of the system.
The dependencies that can exist between two variables have been extensively studied, generating a variety of techniques that range from statistical inference [7] to information theory [8]. Most of these approaches require to differentiate the role of the variables, e.g., between a target and a predictor. However, the extension of these approaches to three or more variables is not straightforward, as a binary splitting is, in general, not enough to characterize the rich interplay that can exist between variables. Moreover, the development of more adequate frameworks has been difficult, as most of our theoretical tools are rooted in sequential reasoning, which is adept at representing linear flows of influences, but is not as well-suited for describing distributed systems or complex interdependencies [9].
In this work, our approach is to understand interdependencies between variables as information sharing. In the case of two variables, the portion of the variability that can be predicted corresponds to information that a target and a predictor have in common. Following this intuition, we present a framework that decomposes the total information of a distribution according to how it is shared among the variables. Our framework is novel in combining the hierarchical decomposition of higher-order interactions, as developed in [10], with the notion of synergistic information, as proposed in [11]. In contrast to [10], we study the information that exists in the system itself without comparing it to other related distributions. In contrast to [11], we analyze the joint entropy instead of the mutual information, looking for symmetric properties of the system. Note that a different approach for relating the tools presented in [10] and the idea of synergistic information has been presented independently in [12].
One important contribution of this paper is to distinguish shared information from predictability. Predictability is a concept that requires a bipartite system divided into predictors and targets. As different splittings of the same system often yield different conclusions, we see predictability as a directed notion that strongly depends on one’s “point of view”. In contrast, we see shared information as a property of the system itself, which does not require differentiated roles between its components. Although it is not possible in general to find a unique measure of predictability, we show that the shared information can be uniquely defined for systems of three variables in a number of interesting scenarios.
Additionally, our framework provides new insight into various problems of network information theory. Interestingly, many of the problems of network information theory that have been solved are related to systems that present a simple structure in terms of shared information and synergies, while most of the open problems possess a more complex mixture of them.
The rest of this article is structured as follows. First, Section 2 introduces the notions of the hierarchical decomposition of dependencies and synergistic information, reviewing the state of the art and providing the necessary background for the unfamiliar reader. Section 3 presents our axiomatic decomposition for the joint entropy, focusing on the fundamental case of three random variables. Then, we illustrate the application of our framework for various cases of interest: pairwise independent variables in Section 4, pairwise maximum entropy distributions and Markov chains in Section 5 and multivariate Gaussians in Section 6. After that, Section 7 presents the first application of this framework in settings of fundamental importance for network information theory. Finally, Section 8 summarizes our conclusions.
2. Preliminaries and the State of the Art
One way of analyzing the interactions between the random variables is to study the properties of the correlation matrix . However, this approach only captures linear relationships, and hence, the picture provided by is incomplete. Another possibility is to study the matrix of mutual information terms. This matrix captures the existence of both linear and nonlinear dependencies [13], but its scope is restricted to pairwise relationships and, thus, misses all higher-order structure. To see an example of how this can happen, consider two independent fair coins and , and let be the output of an exclusive-or logic gate. The mutual information matrix has all its off-diagonal elements equal to zero, making it indistinguishable from an alternative situation where is just another independent fair coin.
For the case of , a possible next step would be to consider higher-order moment matrices, such as co-skewness and co-kurtosis. We seek their information-theoretic analogs, which complement the description provided by . One method of doing this is by studying the information contained in marginal distributions of increasingly larger sizes; this approach is presented in Section 2.1. Other methods try to provide a direct representation of the information that is shared between the random variables; they are discussed in Section 2.2, Section 2.3 and Section 2.4.
2.1. Negentropy and Total Correlation
When the random variables that compose a system are independent, their joint distribution is given by the product of their marginal distributions. In this case, the marginals contain all that is to be learned about the statistics of the entire system. For an arbitrary joint probability density function (pdf), knowing the single variable marginal distributions is not enough to capture all there is to know about the statistics of the system.
To quantify this idea, let us consider the information stored in N discrete random variables with joint pdf , where each takes values in a finite set with cardinality . Here, we refer to a Bayesian interpretation of the Shannon information as described in [14], which corresponds to the state of knowledge that an observer has with respect to a system as described by its probability distribution; in this context, uncertainty in the system corresponds to information that can be extracted by performing measurements. The maximal amount of information that could be stored in is , which corresponds to the entropy of the pdf , where is the uniform distribution for each random variable . On the other hand, the joint entropy with respect to the true distribution measures the actual uncertainty that the system possesses. Therefore, the difference
corresponds to the decrease of the uncertainty about the system that occurs when one learns its pdf, i.e., the information about the system that is contained in its statistics. This quantity is known as negentropy [15] and can also be computed as
where is the marginal of the variable and is the Kullback–Leibler divergence. In this way, Equation (3) decomposes the negentropy into a term that corresponds to the information given by simple marginals and a term that involves higher-order marginals. The second term is known as the total correlation (TC) [16] (also known as multi-information [17]), which is equal to the mutual information for the case of . Because of this, the TC has been suggested as an extension of the notion of mutual information for multiple variables.
An elegant framework for decomposing the TC can be found in [10] (for an equivalent formulation that does not rely on information geometry, see [18]). Let us call k-marginals the distributions that are obtained by marginalizing the joint pdf over variables. Note that the k-marginals provide a more detailed description of the system than the -marginals, as the latter can be directly computed from the former by marginalizing the corresponding variables. In the case where only the one-marginals are known, the simplest guess for the joint distribution is . One way of generalizing this for the case where the k-marginals are known is by using the maximum entropy principle [14], which suggests choosing the distribution that maximizes the joint entropy while satisfying the constrains given by the partial (k-marginal) knowledge. Let us denote by the pdf that achieves the maximum entropy while being consistent with all of the k-marginals, and let denote its entropy. Note that , since the number of constrains that are involved in the maximization process that generates increases with k. It can therefore be shown that the following generalized Pythagorean relationship holds for the total correlation:
Above, measures the additional information that is provided by the k-marginals that was not contained in the description of the system given by the -marginals. In general, the information that is located in terms with higher values of k is due to dependencies between groups of variables that cannot be reduced to combinations of dependencies between smaller groups.
It has been observed that in many practical scenarios, most of the TC of the measured data is provided by the lower marginals. It is direct to see that
Therefore, if there exists a , such that all are small for , then provides an accurate approximation for from the point of view of the Kullback–Leibler divergence. In fact, it has been shown that pairwise maximum entropy models (i.e., ) can provide an accurate description of the statistics of many biological systems [19,20,21,22] and also some social organizations [23,24].
2.2. Internal and External Decompositions
An alternative approach to study the interdependencies between many random variables is to analyze the ways in which they share information. This can be done by decomposing the joint entropy of the system. For the case of two variables, the joint entropy can be decomposed as
suggesting that it can be divided into shared information, , and into terms that represent information that is exclusively located in a single variable, i.e., for and for .
In systems with more than two variables, one can compute the total information that is exclusively located in one variable as , where denotes all of the system’s variables, except . The difference between the joint entropy and the sum of all exclusive information terms, , defines a quantity known [25] as the dual total correlation (DTC):
which measures the portion of the joint entropy that is shared between two or more variables of the system (the superscripts and subscripts are used to reflect that ). When , then , and hence, the DTC has also been suggested in the literature as a measure for the multivariate mutual information. Note that the DTC is also known as excess entropy in [26], whose definition differs from its typical use of this term in the context of time series, e.g., [27].
By comparing Equations (4) and (7), it would be appealing to look for a decomposition of the DTC of the form , where would measure the information that is shared by exactly k variables [28]. With this, one could define an internal entropy as the information that is shared between at most j variables, in contrast to the external entropy , which describes the information provided by the j-marginals. These entropies would form a non-decreasing sequence
This layered structure, and its relationship with the TC and the DTC, is graphically represented in Figure 1.
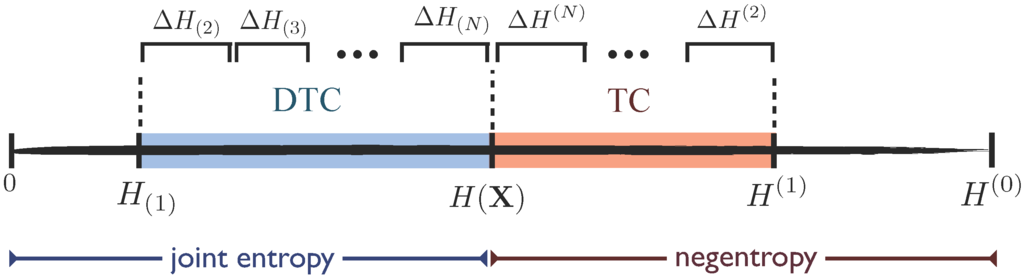
Figure 1.
Layers of internal and external entropies that decompose the dual total correlation (DTC) and the TC. Each shows how much information is contained in the j-marginals, while each measures the information shared between exactly j variables.
One of the main goals of this paper is to find expressions for for the case of . It is interesting to note that even though the TC and DTC coincide for the case of , these quantities are in general different for larger system sizes.
2.3. Inclusion-Exclusion Decompositions
Perhaps the most natural approach to decompose the DTC and joint entropy is to apply the inclusion-exclusion principle, using a simplifying analogy that the entropies and areas have similar properties. A refined version of this approach can be found also in the I-measures [29] and in the multi-scale complexity [30]. For the case of three variables, this approach gives
The last term is known as the co-information [31] (being closely related to the interaction information [32]) and can be defined using the inclusion-exclusion principle as
As , the co-information has also been proposed as a candidate for extending the mutual information to multiple variables. For a summary of the various possible extensions of the mutual information, see Table 1 and also additional discussion in [33].

Table 1.
Summary of the candidates for extending the mutual information.
| Name | Formula |
|---|---|
| Total correlation | |
| Dual total correlation | |
| Co-information |
It is tempting to coarsen the decomposition provided by Equation (9) and associate the co-information with and the remaining terms with , obtaining a decomposition similar to the one presented in [30]. This idea is equivalent to building a Venn diagram for the information sharing between three variables as the one shown in Figure 2. However, the resulting decomposition and diagram (which differ from what is presented in Section 3.4) are not very intuitive, since the co-information can be negative.
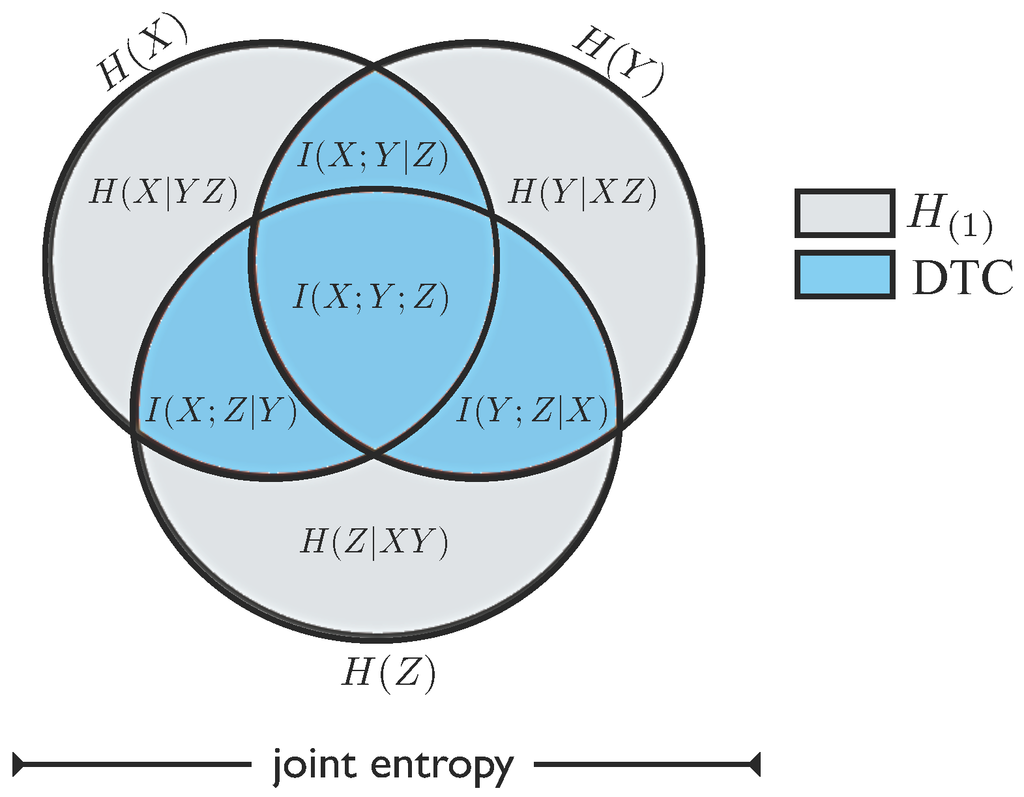
Figure 2.
An approach based on the inclusion-exclusion principle decomposes the total entropy of three variables into seven signed areas.
As part of this temptation, it is appealing to consider the conditional mutual information as the information contained in and that is not contained in , just as the conditional entropy is the information that is in and not in . However, the latter interpretation works because conditioning always reduces entropy (i.e., ), while this is not true for mutual information; that is, in some cases, the conditional mutual information can be greater than . This suggests that the conditional mutual information can capture information that extends beyond and , incorporating higher-order effects with respect to . Therefore, a better understanding of the conditional mutual information is required in order to refine the decomposition suggested by Equation (9).
2.4. Synergistic Information
An extended treatment of the conditional mutual information and its relationship to the mutual information decomposition can be found in [34,35]. For presenting these ideas, let us consider two random variables and , which are used to predict Y. The predictability of Y, understood as the benefit of knowing the realization of and for performing inference over Y, is directly related to if a natural data processing property is to be satisfied [36] (for simplicity, through the paper, we use the shorthand notation ). Using the chain rule of the mutual information, the predictability can be decomposed as
It is natural to think that the predictability provided by , which is given by the term , can be either unique or redundant with respect of the information provided by . On the other hand, due to Equation (12), it is clear that the unique predictability contributed by must be contained in . However, the fact that can be larger than , while the latter contains both the unique and redundant contributions of , suggests that there can be an additional predictability that is accounted for only by the conditional mutual information.
Following this rationale, we denote as synergistic predictability the part of the conditional mutual information that corresponds to evidence about the target that is not contained in any single predictor, but is only revealed when both are known. Is to be noticed that this notion is based on the asymmetrical roles played by predictors and the target. As an example of synergistic predictability, consider again the case in which and are independent random bits and . Then, it can be seen that but . Hence, neither nor individually provide information about Y, although together, they fully determine it.
Further discussions about the notion of synergistic predictability can be found in [11,12,37,38,39].
3. A Non-Negative Joint Entropy Decomposition
Following the discussions presented in Section 2.2 and Section 2.4, we search for a decomposition of the joint entropy that reflects the private, common and synergistic modes of information sharing. In this way, we want the decomposition to distinguish information that is shared only by a few variables from information that is accessible from the entire system.
Our framework is based on distinguishing the directed notion of predictability from the undirected one of information. By predictability, we understand “the reduction in optimal prediction risk in the presence of side information” [36]. The predictability is intrinsically a directed notion, which is based on a distinction between predictors and the target variable. On the contrary, we use the term information to exclusively refer to intrinsic statistical properties of the whole system, which do not rely on such a distinction. Currently, there is an ongoing debate about the best way of characterizing and computing predictability—although without using the same terminology—in arbitrary systems (see, for example, [38] and the references therein). Nevertheless, our approach in this work is to explore how far one can reach based on an axiomatic approach. In this way, our results are going to be consistent with any choice of formula that is consistent with the discussed axioms.
In the following, Section 3.1, Section 3.2 and Section 3.3 discuss the basic features of predictability and information. After these necessary preliminaries, Section 3.4 finally presents our formal decomposition for the joint entropy of discrete and continuous variables. Note that the rest of this article is focused on the case of three variables, leaving possible extensions for future work.
3.1. Predictability Axioms
Let us consider two variables and that are used to predict a target variable . Intuitively, quantifies the predictability of Y that is provided by . In the following, we want to find a function that measures the redundant predictability provided by with respect to the predictability provided by , and a function that measures the unique predictability that is provided by , but not by . Following [11], we first determine a number of desired properties that these functions should have.
Definition
A predictability decomposition is defined by the real-valued functions and over the distributions of and , which satisfy the following axioms:
- (1)
- Non-negativity: .
- (2)
- .
- (3)
- .
- (4)
- Weak symmetry I: .
The requirement that and depend only on the pairwise marginals of and , and not on their joint distribution, was first proposed in [39]. Although this property is not required in some of the existent literature (for example, in [38]), most of the predictability decompositions proposed so far respect it [11,37,39]. Furthermore, Axiom (3) states that the sum of the redundant and corresponding unique predictabilities given by each variable cannot be larger than the total predictability —in fact, the difference between the right and left hand terms of Axiom (3) gives the synergistic predictability, whose analysis will not be included in this work to avoid confusing it with the synergistic information, introduced in Section 3.2. Finally, Axiom (4) states that the redundant predictability is independent of the ordering of the predictors.
The following lemma determines the bounds for the redundant predictability (the proof is given in Appendix A).
Lemma 1.
The functions and satisfy Axioms (1)–(3) if and only if
where .
Corollary 1.
For variables and Y following an arbitrary joint pdf , there exists at least one predictability decomposition that satisfies Axioms (1)–(4) defined by
Proof.
Being a symmetric function on and , Equation (14) satisfies Axiom (4). Furthermore, as Equation (14) is equal to the upper bound given in Lemma 1, Axioms (1)–(3) are satisfied due to Lemma 2. ☐
Above, the subscript MMI corresponds to “minimal mutual information”. Note that was introduced in [40] and has also been studied in [12,41].
In principle, the notion of redundant predictability takes the point of view of the target variable and measures the parts that can be predicted by both and when they are used by themselves, i.e., without combining them with each other. It is appealing to think that there should exist a unique function that provides such a measure. Nevertheless, these axioms define only very basic properties that a measure of redundant predictability should satisfy, and hence, in general, they are not enough for defining a unique function. In fact, a number of different predictability decompositions have been proposed in the literature [37,38,39,41].
From all of the candidates that are compatible with the axioms, the decomposition given in Corollary 1 gives the largest possible redundant predictability measure. It is clear that in some cases, this measure gives an over-estimate of the redundant predictability given by and ; for an example of this, consider and to be independent variables and . Nevertheless, Equation (14) has been proposed as a adequate measure for the redundant predictability of multivariate Gaussians [41] (for a corresponding discussion, see Section 6).
3.2. Shared, Private and Synergistic Information
Let us now introduce an additional axiom, which will form the basis for our proposed information decomposition.
Definition
A symmetrical information decomposition is given by the real valued functions and over the marginal distributions of , and , which satisfy Axioms (1)–(4) for and , while also satisfying the following property:
- (5)
- Weak symmetry II: .
The role of Axiom (5) can be related to the role of the fifth of Euclid’s postulates, as, while seeming innocuous, their addition has interesting consequences in the corresponding theory. The following lemma explains why this decomposition is denoted as symmetrical and also shows fundamental bounds for these information functions (note that equivalent bounds for predictability decompositions can also be derived using Lemma 1). The proof is presented in Appendix C.
Lemma 2.
The functions that compose a symmetrical information decomposition satisfy the following properties:
- (a)
- Strong symmetry: and are symmetric on their three arguments.
- (b)
- Bounds: these quantities satisfy the following inequalities:
The strong symmetry property was first presented in [40], where it was shown that it is not compatible with the axioms presented in [11]. Regardless of this, strong symmetry is a highly desirable property when looking for a decomposition of the joint entropy. Discussions about strong symmetry can also be found in [34,38].
A symmetrical information decomposition can be used to decompose the following mutual information as
In contrast to a decomposition based on the predictability, these measures address properties of the system as a whole, without being dependent on how it is divided between target and predictor variables (for a parallelism with respect to the corresponding predictability measures, see Table 2). Intuitively, measures the shared information that is common to , and ; quantifies the private information that is shared by and , but not , and captures the synergistic information that exist between . The latter is a non-intuitive mode of information sharing, whose nature we hope to clarify through the analysis of particular cases presented in Section 4 and Section 6.

Table 2.
Parallelism between predictability and information measures.
| Directed Measures | Symmetrical Measures |
|---|---|
| Redundant predictability | Shared information |
| Unique predictability | Private information |
| Synergistic predictability | Synergistic information |
Note also that the co-information can be expressed as
Hence, strictly positive (resp. negative) co-information is a sufficient, although not necessary, condition for the system to have non-zero shared (resp. synergistic) information.
3.3. Further Properties of the Symmetrical Decomposition
At this point, it is important to clarify a fundamental distinction that we make between the notions of predictability and information. The main difference between the two notions is that, in principle, the predictability only considers the predictable parts of the target, while the shared information also considers the joint statistics of the predictors. Although this distinction will be further developed when we address the case of Gaussian variables (cf. Section 6.3), let us for now present a simple example to help develop the intuitions about this issue.
Example
Define the following functions:
It is straightforward that these functions satisfy Axioms (1)–(5) and therefore constitute a symmetric information decomposition. In contrast to the decomposition given in Corollary 1, this can be seen to be strongly symmetric and also dependent on the three marginals , and .
In the following lemma, we will generalize the previous construction, whose simple proof is omitted.
Lemma 3.
For a given predictability decomposition with functions and , the functions
provide a symmetrical information decomposition, which is called the canonical symmetrization of the predictability.
Corollary 2.
For variables and following an arbitrary joint pdf , there exists at least one symmetric information decomposition.
Proof.
This is a direct consequence of the previous lemma and Corollary 1. ☐
May be the most remarkable property of symmetrized information decompositions is that, in contrast to directed ones, as defined in Section 3.1, they are uniquely determined by Axioms (1)–(5) for a number of interesting cases.
Theorem 1.
The symmetric information decomposition is unique if the variables form a Markov chain or two of them are pairwise independent.
Proof.
Let us consider the upper and lower bound for given in Equation (15), denoting them as and . These bounds restrict the possible functions to lay in the interval of length
Therefore, the framework will provide a unique expression for the shared information if (at least) one of the above six terms is zero. These scenarios correspond either to Markov chains, where one conditional mutual information term is zero, or pairwise independent variables, where one mutual information term vanishes. ☐
Pairwise independent variables and Markov chains are analyzed in Section 4 and Section 5.1, respectively.
3.4. Decomposition for the Joint Entropy of Three Variables
Now, we use the notions of redundant, private and synergistic information functions for developing a non-negative decomposition of the joint entropy, which is based on a non-negative decomposition of the DTC. For the case of three discrete variables, by applying Equations (18) and (19) to Equation (9), one finds that
From Equations (7) and (25), one can propose the following decomposition for the joint entropy:
where
In contrast to Equation (9), here, each term is non-negative because of Lemma 2. Therefore, Equation (26) yields a non-negative decomposition of the joint entropy, where each of the corresponding terms captures the information that is shared by one, two or three variables. Interestingly, and are homogeneous (being the sum of all of the exclusive information or private information of the system), while is composed by a mixture of two different information sharing modes. Interestingly, it can be seen from Equations (18) and (19) that the co-information is sometimes negative for compensating the triple counting of the synergy due to the sum of the three conditional mutual information terms.
An analogous decomposition can be developed for the case of continuous random variables. Nevertheless, as the differential entropy can be negative, not all of the terms of the decomposition can be non-negative. In effect, following the same rationale that leads to Equation (26), the following decomposition can be found:
Above, denotes the differential entropy of X, and are as defined in Equations (28) and (29), and
Hence, although both the joint entropy and can be negative, the remaining terms conserve their non-negative condition.
It can be seen that the lowest layer of the decomposition is always trivial to compute, and hence, the challenge is to find expressions for and . In the rest of the paper, we will explore scenarios where these quantities can be characterized. Note that in general, , although it is appealing to believe that there should exist a relationship between them. These issues are explored in the following sections.
4. Pairwise Independent Variables
In this section, we focus on the case where two variables are pairwise independent while being globally connected by a third variable. The fact that pairwise independent variables can become correlated when additional information becomes available is known in the statistics literature as the Bergson’s paradox or selection bias [42] or as the explaining away effect in the context of artificial intelligence [43]. As an example of this phenomenon, consider and to be two pairwise independent canonical Gaussians variables and a binary variable that is equal to one if and zero otherwise. Then, knowing that implies that , and hence, knowing the value of effectively reduces the uncertainty about .
In our framework, Bergson’s paradox can be understood as synergistic information that is introduced by the third component of the system. In fact, we will show that in this case, the synergistic information function is unique and given by
which is, in fact, a measure of the dependencies between and that are created by . In the following, Section 4.1 presents the unique symmetrized information decomposition for this case. Then, Section 4.2 focuses on the particular case where is a function of the other two variables.
4.1. Uniqueness of the Entropy Decomposition
Let us assume that and are pairwise independent, and hence, the joint pdf of , and has the following structure:
It is direct to see that in this case , but . Therefore, as , it is direct from Axioms (1) and (2) that any redundant predictability function satisfies . However, the axioms are not enough to uniquely determine , as the only restriction that the bound presented in Lemma 2 provides is (note that in this case ). Nevertheless, the symmetrized decomposition is uniquely determined, as shown in the next corollary that is a consequence of Theorem 1.
Corollary 3.
If , and follow a pdf as Equation (33), then the shared, private and synergetic information functions are unique. They are given by
Proof.
The fact that there is no shared information follows directly from the upper bound presented in Lemma 2. Using this, the expressions for the private information can be found using Axiom (2). Finally, the synergistic information can be computed as
The second formula for the synergistic information can be found then using the fact that . ☐
With this corollary, the unique decomposition of the that is compatible with Equations (28) and (29) can be found to be
Note that the terms and can be bounded as follows:
The bound for follows from the basic fact that . The second bound follows from
4.2. Functions of Independent Arguments
Let us focus in this section on the special case where is a function of two independent random inputs and study its corresponding entropy decomposition. We will consider and as inputs and to be the output. Although this scenario fits nicely in the predictability framework, it can also be studied from the shared information framework’s perspective. Our goal is to understand how F affects the information sharing structure.
As , we have
The term hence measures the information of the inputs that is not reflected by the output. An extreme case is given by a constant function , for which .
The term measures how much of F can be predicted with knowledge that comes from one of the inputs, but not from the other. If is large, then F is not “mixing” the inputs too much, in the sense that each of them is by itself able to provide relevant information that is not given also by the other. In fact, a maximal value of for given marginal distributions for and is given by , where , and the bound provided in Equation (41) is attained.
Finally, due to Equation (34), there is no shared information, and hence, is just proportional to the synergy of the system. By considering Equation (42), one finds that F needs to leave some ambiguity about the exact values of the inputs in order for the system to possess synergy. For example, consider a 1-1 function F for which for every output ; one can find the unique values and that generate it. Under this condition , and hence, because of Equation (42), it is clear that a 1-1 function does not induce synergy. On the other extreme, we showed already that constant functions have , and hence, the case where the output of the system gives no information about the inputs also leads to no synergy. Therefore, synergistic functions are those whose output values generate a balanced ambiguity about the generating inputs. To develop this idea further, the next lemma studies the functions that generate a maximum amount of synergy by generating for each output value different 1-1 mappings between their arguments.
Lemma 4.
Let us assume that both and take values over and are independent. Then, the maximal possible amount of information synergy is created by the function
when both input variables are uniformly distributed.
Proof.
Using Equations (37) and (46), it can be shown that if F is an arbitrary function, then
where the last inequality follows from the fact that both inputs are restricted to alphabets of size K.
Now, consider to be the function given in Equation (48) and assume that and are uniformly distributed. It can be seen that for each , there exist exactly K ordered pairs of inputs , such that , which define a bijection from to . Therefore,
and hence
showing that the upper bound presented in Equation (52) is attained. ☐
Corollary 4.
The XOR logic gate generates the largest amount of synergistic information possible for the case of binary inputs.
The synergistic nature of the addition over finite fields helps to explain the central role it has in various fields. In cryptography, the one-time-pad [44] is an encryption technique that uses finite-field additions for creating a synergistic interdependency between a private message, a public signal and a secret key. This interdependency is completely destroyed when the key is not known, ensuring no information leakage to unintended receivers [45]. Furthermore, in network coding [46,47], nodes in the network use linear combinations of their received data packets to create and transmit synergistic combinations of the corresponding information messages. This technique has been shown to achieve multicast capacity in wired communication networks [47] and has also been used to increase the throughput of wireless systems [48].
5. Discrete Pairwise Maximum Entropy Distributions and Markov Chains
This section studies the case where the system’s variables follow a pairwise maximum entropy (PME) distribution. These distributions are of great importance in the statistical physics and machine learning communities, where they are studied under the names of Gibbs distributions [49] or Markov random fields [50].
Concretely, let us consider three pairwise marginal distributions and for the discrete variables , and . Let us denote as the set of all of the joint pdfs over that have those as their pairwise marginals distributions. Then, the corresponding PME distribution is given by the joint pdf that satisfies
For the case of binary variables (i.e., ), the PME distribution is given by an Ising distribution [51]
where Z is a normalization constant and an energy function given by , being the coupling terms. In effect, if for all i and k, then can be factorized as the product of the unary-marginal pdfs.
In the context of the framework discussed in Section 2.1, a PME system has while . In contrast, Section 5.1 studies these systems under the light of the decomposition of the DTC presented in Section 3.4. Then, Section 5.2 specifies the analysis for the particular case of Markov chains.
5.1. Synergy Minimization
It is tempting to associate the synergistic information with that which is only in the joint pdf, but not in the pairwise marginals, i.e., with . However, the following result states that there can exist some synergy defined by the pairwise marginals themselves.
Theorem 2.
PME distributions have the minimum amount of synergistic information that is allowed by their pairwise marginals.
Proof.
Note that
Therefore, maximizing the joint entropy for fixed pairwise marginals is equivalent to minimizing the synergistic information. Note that the last equality follows from the fact that by definition only depends on the pairwise marginals. ☐
Corollary 5.
For an arbitrary system , the synergistic information can be decomposed as
where is as defined in Equation (4) and is the synergistic information of the corresponding PME distribution.
Proof.
This can be proven noting that, for an arbitrary pdf , it can be seen that
Above, the first equality corresponds to the definition of , and the second equality comes from using Equation (59) on each joint entropy term and noting that only the synergistic information depends on more than the pairwise marginals. ☐
The previous corollary shows that measures only one part of the information synergy of a system, the part that can be removed without altering the pairwise marginals. Therefore, by considering Equations (29) and (60), one can find that for systems of three variables
Note that PME systems with non-zero synergy, i.e., systems where the above inequality is strict, are easy to find. For example, consider and to be two independent equiprobable bits, and . It can be shown that for this case, one has [18]. On the other side, as the inputs are independent, the synergy can be computed using Equation (37), and therefore, a direct calculation shows that
From the previous discussion, one can conclude that only a special class of pairwise distributions and is compatible with having null synergistic information. This is a remarkable result, as the synergistic information is usually considered to be an effect purely related to high-order marginals. For example, in [39] property is introduced, which states that for given and there exists a joint pdf that is compatible with them while having zero synergistic predictability. In contrast, the above discussion has shown that in our framework, a symmetrized extension of is not true, i.e., it is not always possible to find a joint pdf with zero synergistic information when the three pairwise marginals are given.
It would be interesting to have an expression for the minimal information synergy that a set of pairwise distributions requires, or equivalently, a symmetrized information decomposition for PME distributions. A particular case that allows a unique solution is discussed in the next section.
5.2. Markov Chains
Markov chains maximize the joint entropy subject to constraints on only two of the three pairwise distributions. In effect, following the same rationale as in the proof of Theorem 2, it can be shown that
Then, for fixed pairwise distributions and , maximizing the joint entropy is equivalent to minimizing the conditional mutual information. Moreover, the maximal entropy is attained by the pdf that makes , which is precisely the Markov chain with joint distribution
For the binary case, it can be shown that a Markov chain corresponds to an Ising distribution, like Equation (56), where the interaction term is equal to zero.
It is direct to see that two of the redundant predictability terms of a Markov chain are unique, given by Equation (13) as . However, the third redundant predictability term, , is not uniquely defined, as the bounds only guarantee
Due to the well-known data processing inequality [8], both and can be strictly larger than , and hence, this bound does not provide in general a unique definition. In contrast, Theorem 1 showed that the symmetric information decomposition for Markov chains is unique. We develop this decomposition in the following corollary.
Corollary 6.
If is a Markov chain, then their unique shared, private and synergistic information functions are given by
In particular, Markov chains have no synergistic information.
Proof.
For this case, one can show that
where the first equality is a consequence of the data process inequality and the second of the fact that . The above equality shows that the bounds for the shared information presented in Lemma 2 give the unique solution . The other equalities are obtained directly using this result and the definition of and . ☐
Using this corollary, the unique decomposition of the for Markov chains that is compatible with Equations (28) and (29) is given by
Hence, Corollary 6 states that a sufficient condition for three pairwise marginals to be compatible with zero information synergy is for them to satisfy the Markov condition . The question of finding a necessary condition is an open problem, intrinsically linked with the problem of finding a good definition for the shared information for arbitrary PME distributions.
To conclude, let us note an interesting duality that exists between Markov chains and the case where two variables are pairwise independent, which is illustrated in Table 3.

Table 3.
Duality between Markov chains and pairwise independent variables.
| Markov Chains | Pairwise Independent Variables |
|---|---|
| Conditional pairwise independency | Pairwise independency |
| No between and | No between and |
| No synergistic information | No shared information |
6. Entropy Decomposition for the Gaussian Case
In this section, we study the entropy-decomposition for the case where follow a multivariate Gaussian distribution. As the entropy is not affected by translation, we assume, without loss of generality, that all of the variables have zero mean. The covariance matrix is denoted as
where is the variance of , α is the correlation between and , β is the correlation between and and γ is the correlation between and . The condition that the matrix Σ should be positive semi-definite yields the following condition
Unfortunately, it is not possible to derive directly from Theorem 1 a unique information decomposition for multivariate Gaussian variables with an arbitrary covariance matrix. However, it has been recently shown that the predictability decomposition for multivariate Gaussians is unique [41]. In the sequel, Section 6.1 and Section 6.2 present a discussion on some properties of the shared and synergistic information of multivariate Gaussians, which lead to an intuitive understanding of the predictability decomposition introduced in [41]. Based on this measure, Section 6.3 builds a symmetrical information decomposition and explores some of its consequences.
6.1. Understanding the Synergistic Information Between Gaussians
The simplistic structure of the joint pdf of multivariate Gaussians, which is fully determined by mere second order statistics, could make one think that these systems do not have synergistic information sharing. However, it can be shown that a multivariate Gaussian is the maximum entropy distribution for a given covariance matrix Σ. Hence, the discussion provided in Section 5.1 suggests that these distributions can indeed have non-zero information synergy, depending on the structure of the pairwise distributions or, equivalently, on the properties of Σ.
Moreover, it has been reported that synergistic phenomena are rather common among multivariate Gaussian variables [41]. As a simple example, consider
where A and B are independent Gaussians. Intuitively, it can be seen that although is useless by itself for predicting , it can be used jointly with to remove the noise term B and provide a perfect prediction. For refining this intuition, let us consider a case where the variables have equal variances and and are independent (i.e., ). Then, the optimal predictor of given is ; the optimal predictor given is ; and the optimal predictor given both and is [52]
Therefore, although is useless to predict by itself, it can be used for further improving the prediction given by . Hence, all of the information provided by is synergistic, as is useful only when combined with the information provided by . Note that all of these examples fall in the category of the systems considered in Section 4.
6.2. Understanding the Shared Information
Let us start studying the information shared between two Gaussians. For this, let us consider a pair of zero-mean variables with unit variance and correlation α. A suggestive way of expressing these variables is given by
where , and are independent centered Gaussian variables with variances and , respectively. Note that the signs in Equation (79) can be set in order to achieve any desired sign for the covariance (as ). The mutual information is given by (see Appendix D)
showing that it is directly related to the variance of the common term .
For studying the shared information between three Gaussian variables, let us start considering a case where and . It can be seen that (cf. Appendix D)
A direct evaluation shows that Equation (81) is non-positive for all ρ with (note that cannot be larger that because of Equation (76)). This is consistent with the fact that and are pairwise independent, and hence, due to Equation (37), one has that . Therefore, from Equations (19) and (34) is clear that this system has no shared information for all ρ and has zero synergistic information only for .
In contrast, let us now consider a case where , for which
A direct evaluation shows that, in contrast to Equation (81), the co-information in this case is non-negative, showing that the system is dominated by shared information for all .
The previous discussion suggests that the shared information depends on the smallest of the correlation coefficients. An interesting approach to understand this fact can be found in [41], where the predictability among Gaussians is discussed. In this work, the author note that from the point of view of , both and are able to decompose the target in a predictable and an unpredictable portion: . In this sense, both predictors achieve the same effect, although with a different efficiency, which is determined by their correlation coefficient. As a consequence of this, the predictor that is less correlated with the target does not provide unique predictability, and hence, its contribution is entirely redundant. This motivates using , as defined in Equation (14), as an adequate measure for the redundant predictability among Gaussians. Moreover, in [41], it is shown that is the only consistent definition of redundant predictability that only depends on the pairwise distributions of and .
6.3. Shared, Private and Synergistic Information for Gaussian Variables
Based on the previous discussion, the unique definition of shared information among Gaussians that corresponds to a canonical symmetrization of a redundant predictability measure (as discussed in Lemma 3) is given by
In contrast with , Equation (85) states that there cannot be information shared by the three components of the system if two of them are pairwise independent. Therefore, the magnitude of the shared information is governed by the lowest correlation coefficient of the whole system, being upper-bounded by any of the redundant predictability terms. An intuitive understanding of this definition can be built over a subclass of multivariate Gaussians using the following lemma (whose proof is presented in Appendix E).
Lemma 5.
Let follow a multivariate Gaussian distribution with zero mean and covariance matrix Σ, as given in Equation (75). Let us further assume that and . Then,
where and are independent standard Gaussians and and are given by
It is natural to relate to the shared information, and to the private information and , and to the exclusive terms. Moreover, if do not hold, then , which is consistent with what Equations (79) and (80) state for the case of two variables. Note that the coefficients determined in Equation (89) are unique, as they correspond to the six degrees of freedom of the variables . Finally, note also that the decomposition presented in Lemma 5 does not require a private component between the least correlated variables, i.e., a term .
Based on Equation (85), the remaining elements of a symmetric information decomposition for Gaussians can be found as
According to Equation (91), the two less correlated Gaussians share no private information, which is consistent with the absence of in Lemma 5. Moreover, by comparing Equations (93) and (D5), it can be seen that if and are the less correlated variables, then the synergistic information can be expressed as , which, for the particular case of , confirms Equation (37). This, in turn, also shows that, for the particular case of Gaussians variables, forming a Markov chain is a necessary and sufficient condition for having zero information synergy (for the case of , a direct calculation shows that is equivalent to ).
To close this section, let us note that Equation (84) corresponds to the upper bound provided by Equation (15), which means that multivariate Gaussians have a maximal shared information. This is complementary to the fact that, because of being a maximum entropy distribution, they also have the smallest amount of synergy that is compatible with the corresponding second order statistics.
7. Applications to Network Information Theory
In this section, we use the framework presented in Section 3 to analyze four fundamental scenarios in network information theory [53]. Our goal is to illustrate how the framework can be used to build new intuitions over these well-known optimal information-theoretic strategies. The application of the framework to scenarios with open problems is left for future work.
In the following, Section 7.1 uses the general framework to analyze the Slepian–Wolf coding for three sources, which is a fundamental result in the literature of distributed source compression. Then, Section 7.2 applies the results of Section 4 to the multiple access channel, which is one of the fundamental settings in multiuser information theory. Section 7.3 uses the results related to Markov chains from Section 5 to the wiretap channel, which constitutes one of the main models of information-theoretic secrecy. Finally, Section 7.4 uses results from Section 6 to study fundamental limits of public or private broadcast transmissions over Gaussian channels.
7.1. Slepian–Wolf Coding
The Slepian–Wolf coding gives lower bounds for the data rates that are required in order to transfer the information contained in various data sources. Let us denote as the data rate of the k-th source and define as the extra data rate that each source has above its own exclusive information (cf. Section 2.2). Then, in the case of two sources and , the well-known Slepian–Wolf bounds can be re-written as , , and ([53], Section 10.3). The last inequality states that corresponds to shared information that can be transmitted by any of the two sources.
Let us consider now the case of three sources, and denote . The Slepian–Wolf bounds provide seven inequalities ([53], Section 10.5), which can be re-written as
Above, Equation (96) states that the DTC needs to be accounted for by the extra rate of the sources and Equation (95) that every pair needs to take care of its private information. Interestingly, due to Equation (29), the shared information needs to be included in only one of the rates, while the synergistic information needs to be included in at least two. For example, one possible solution that is consistent with these bounds is , and . This can be interpreted as follows: it is sufficient if just one of the three sources provides the information shared among all sources and if for each pair of sources, exactly one transfers their private information . Additionally, the constraints on synergistic information require that exactly two of the three sources transfer it. This brings some light to the factor of two required in Equation (29).
7.2.Multiple Access Channel
Let us consider a multiple access channel, where two pairwise independent transmitters send and and a receiver gets , as shown in Figure 3. It is well known that, for a given distribution , the achievable transmission rates and satisfy the constrains given by ([53], Section 4.5)
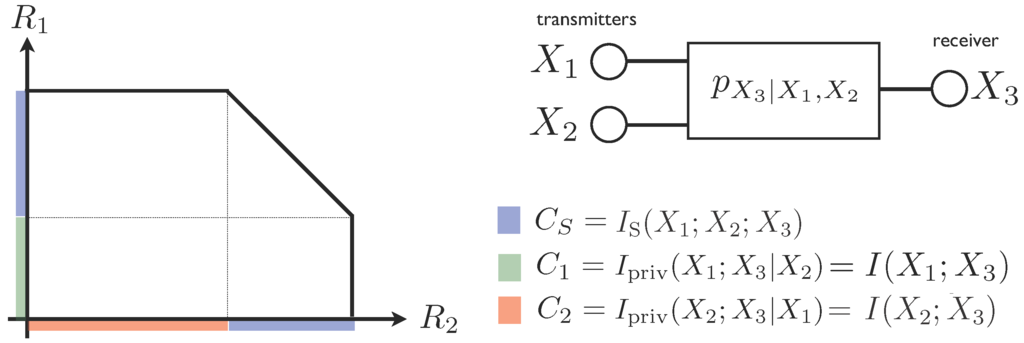
Figure 3.
Capacity region of the multiple access channel, which represents the possible data rates that two transmitters can use for transferring information to one receiver.
As the transmitted random variables are pairwise independent, one can apply the results of Section 4. Therefore, there is no shared information, and . Let us introduce a shorthand notation for the remaining terms: , and . Then, one can re-write the bounds for the transmission rates as
From this, it is clear that while each transmitter has a private portion of the channel with capacity or , their interaction creates synergistically extra capacity that corresponds to what can be actually shared.
7.3. Degraded Wiretap Channel
Consider a communication system with an eavesdropper (shown in Figure 4), where the transmitter sends , the intended receiver gets and the eavesdropper receives . For simplicity of the exposition, let us consider the case where the eavesdropper gets only a degraded copy of the signal received by the intended receiver, i.e., that form a Markov chain. Using the results of Section 5.2, one can see that in this case, there is no synergistic, but only shared and private information between , and .
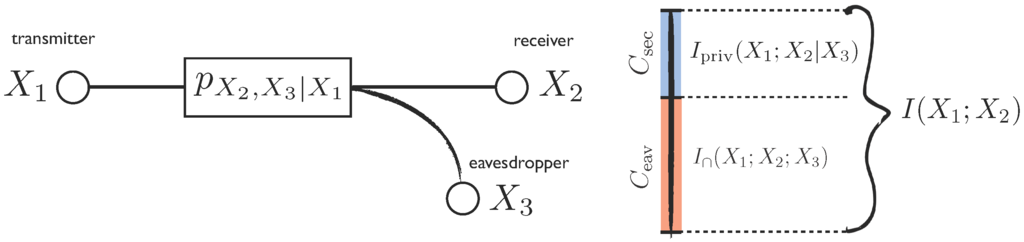
Figure 4.
The rate of secure information transfer, , is the portion of the mutual information that can be used while providing perfect confidentiality with respect to the eavesdropper.
In this scenario, it is known that for a given input distribution , the rate of secure communication that can be achieved is upper bounded by ([44], Section 3.4)
which is precisely the private information sharing between and . Furthermore, as intuition would suggest, the eavesdropping capacity is equal to the shared information between the three variables:
7.4. Gaussian Broadcast Channel
Let us consider a Gaussian broadcast channel, where a transmitter sends a Gaussian signal that is received as and by two receivers. Assuming that all of these variables are jointly Gaussian with a zero mean and covariance matrix given by Equation (75), the transmitter can broadcast a public message, intended for both users, at a maximum rate given by ([44], Section 5.1)
where, following the discussion presented in Section 6.2, the MMI redundant predictability is as defined in Equation (14). On the other hand, if the transmitter wants to send a private (confidential) message to Receiver 1, the corresponding maximum rate that can be achieved in this case is given by
where the last equality follows from Axiom (2).
Interestingly, the predictability measures prove to be better suited to describing the communication limits in the above scenario than their symmetrical counterparts. In effect, the shared information, as defined in Section 6.3, underestimates the public capacity. This opens the question of whether or not directed measures could be better suited for studying certain communication systems, compared to their symmetrized counterparts. Unfortunately, one cannot explore this issue in the previous cases, as although the symmetric decomposition is uniquely defined, there is no unique predictability decomposition to compare. Therefore, a definite answer to this question is not straightforward at this stage. We hope that future research will provide more evidence and a better understanding of this issue.
8. Conclusions
In this work, we propose an axiomatic framework for studying the interdependencies that can exist between multiple random variables as different modes of information sharing. The framework is based on a symmetric notion of information that refers to properties of the system as a whole. We showed that, in contrast to predictability-based decompositions, all of the information terms of the proposed decomposition have unique expressions for Markov chains and for the case where two variables are pairwise independent. We also analyzed the cases of pairwise maximum entropy (PME) distributions and multivariate Gaussian variables. Finally, we illustrated the application of the framework by using it to develop a more intuitive understanding of the optimal information-theoretic strategies in several fundamental communication scenarios. These results are focused on the case of three variables, as their generalization to a larger number of variables is not straightforward. One of the main difficulties for such a generalization is the increasing complexity of the decompositions, caused by the exponential growth of the number of information-sharing modes [11]).
The key insight that this framework provides is that although there is only one way in which information can be shared between two random variables, there are two essentially different ways of sharing between three. One of these ways is a simple extension of the pairwise dependency, where information is shared redundantly, and hence, any of the variables can be used to predict any other. The second way leads to the counter-intuitive notion of synergistic information sharing, where the information is shared in a way that the statistical dependency is destroyed if any of the variables is removed; hence, the structure exists in the whole, but not in any of the parts.
The synergistic information has been commonly related to statistical structures that exist only in the joint pdf and not in low-order marginals. Interestingly, although we showed that indeed, PME distributions posses the minimal information synergy that is allowed by their pairwise marginals, this minimum can be strictly positive. Therefore, there exists a connection between pairwise marginals and synergistic information sharing that is still to be further clarified. In fact, this phenomenon is related to the difference between the TC and the DTC, which is rooted in the fact that the information sharing modes and the marginal structure of the pdf are, although somehow related, intrinsically different. This important distinction has been represented in our framework by the sequence of internal and external entropies. This new unifying picture for the entropy, negentropy, TC and DTC has shed new light on the understanding of high-order interdependencies, whose consequences have only begun to be explored.
Acknowledgments
We want to thank David Krakauer and Jessica Flack for providing support and inspiration for this research. We also thank Bryan Daniels, Michael Gastpar, Bernhard Geiger, Vigil Griffith and Martin Ugarte for helpful discussions. This work was partially supported by a grant to the Santa Fe Institute for the study of complexity and by the U.S. Army Research Laboratory and the U.S. Army Research Office under Contract Number W911NF-13-1-0340. Fernando Rosas would also like to acknowledge the support of the F+ fellowship from KU Leuven and the project “SINS: Sound INterfacing through the Swarm”, funded by the Agency for Innovation by Science and Technology (IWT), Belgium.
Author Contributions
The research was initiated by Fernando Rosas and carried out by all of the authors. The manuscript was initially written by Fernando Rosas and then edited by the other authors. All authors have read and approved the final manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix
A. Proof of Lemma 1
Proof.
Let us assume that and satisfy Axioms (1)–(3). Then,
where the inequalities are a consequence of the non-negativity of and the third equality is due to the weak symmetry of the redundant predictability. To verify the lower bound, first notice that Axiom (3) can be re-written as
The lower bound follows considering the non-negativity of and by noting that .
The proof of the converse is direct and left as an exercise to the reader. ☐
B. Proof of the Consistency of Axiom (3)
Let us show that , showing that the bounds defined by Axiom (3) always can be satisfied. For this, let us assume that the variables are ordered in a way such that holds. Then, as one can express , it is direct to show that
from where the desired result follows.
C. Proof of Lemma 2
Proof.
The symmetry of with respect to and can be directly verified from its definition and Axiom (4). The symmetry with respect to and is proved using Axiom (2) and the weak symmetry of as follows:
The strong symmetry of is proved directly using (19) and the strong symmetry of the shared information and the co-information.
The bounds for , and follow directly from the definition of these quantities and Axiom (3). ☐
D. Useful Facts about Gaussians
Here, we list some useful expressions for Gaussian variables:
where is a matrix determinant, and
E. Proof of Lemma 5
Proof.
Consider the following random variables:
where and are independent standard Gaussians and the parameters and as defined in (89). Then, it is direct to check that is a multivariate Gaussian variable with zero mean and covariance matrix equal to (75). Therefore, and have the same statistics, which proves the desired result. ☐
References
- Kaneko, K. Life: An Introduction to Complex Systems Biology; Springer-Verlag: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Perrings, C. Economy and Environment: A Theoretical Essay on the Interdependence of Economic and Environmental Systems; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Martignon, L.; Deco, G.; Laskey, K.; Diamond, M.; Freiwald, W.; Vaadia, E. Neural coding: Higher-order temporal patterns in the neurostatistics of cell assemblies. Neural Comput. 2000, 12, 2621–2653. [Google Scholar] [CrossRef] [PubMed]
- Deutscher, D.; Meilijson, I.; Schuster, S.; Ruppin, E. Can single knockouts accurately single out gene functions? BMC Syst. Biol. 2008, 2, 50. [Google Scholar] [CrossRef] [PubMed]
- Anand, K.; Bianconi, G. Entropy measures for networks: Toward an information theory of complex topologies. Phys. Rev. E 2009, 80, 045102. [Google Scholar] [CrossRef] [PubMed]
- Gastpar, M.; Vetterli, M.; Dragotti, P.L. Sensing reality and communicating bits: A dangerous liaison. IEEE Signal Process. Mag. 2006, 23, 70–83. [Google Scholar] [CrossRef]
- Casella, G.; Berger, R.L. Statistical Inference; Duxbury Press: Pacific Grove, CA, USA, 2002. [Google Scholar]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory; John Wiley: Hoboken, NJ, USA, 1991. [Google Scholar]
- Senge, P.M.; Smith, B.; Kruschwitz, N.; Laur, J.; Schley, S. The Necessary Revolution: How Individuals and Organizations Are Working Together to Create a Sustainable World; Crown Business: New York, NY, USA, 2008. [Google Scholar]
- Amari, S.I. Information geometry on hierarchy of probability distributions. IEEE Trans. Inf. Theory 2001, 47, 1701–1711. [Google Scholar] [CrossRef]
- Williams, P.L.; Beer, R.D. Nonnegative decomposition of multivariate information. 2010; arXiv:1004.2515. [Google Scholar]
- Olbrich, E.; Bertschinger, N.; Rauh, J. Information Decomposition and Synergy. Entropy 2015, 17, 3501–3517. [Google Scholar] [CrossRef]
- Li, W. Mutual information functions versus correlation functions. J. Stat. Phys. 1990, 60, 823–837. [Google Scholar] [CrossRef]
- Jaynes, E.T. Probability Theory: The Logic of Science; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Brillouin, L. The negentropy principle of information. J. Appl. Phys. 1953, 24, 1152–1163. [Google Scholar] [CrossRef]
- Watanabe, S. Information theoretical analysis of multivariate correlation. IBM J. Res. Dev. 1960, 4, 66–82. [Google Scholar] [CrossRef]
- Studenỳ, M.; Vejnarová, J. The multiinformation function as a tool for measuring stochastic dependence. In Learning in Graphical Models; Springer Netherlands: Amsterdam, The Netherlands, 1998; pp. 261–297. [Google Scholar]
- Schneidman, E.; Still, S.; Berry, M.J.; Bialek, W. Network information and connected correlations. Phys. Rev. Lett. 2003, 91, 238701. [Google Scholar] [CrossRef] [PubMed]
- Schneidman, E.; Berry, M.J.; Segev, R.; Bialek, W. Weak pairwise correlations imply strongly correlated network states in a neural population. Nature 2006, 440, 1007–1012. [Google Scholar] [CrossRef] [PubMed]
- Roudi, Y.; Nirenberg, S.; Latham, P.E. Pairwise Maximum Entropy Models for Studying Large Biological Systems: When They Can Work and When They Can’t. PLoS Comput. Biol. 2009, 5, e1000380. [Google Scholar] [CrossRef] [PubMed]
- Bialek, W.; Cavagna, A.; Giardina, I.; Mora, T.; Silvestri, E.; Viale, M.; Walczak, A.M. Statistical mechanics for natural flocks of birds. Proc. Natl. Acad. Sci. USA 2012, 109, 4786–4791. [Google Scholar] [CrossRef] [PubMed]
- Merchan, L.; Nemenman, I. On the sufficiency of pairwise interactions in maximum entropy models of biological networks. 2015; arXiv:1505.02831. [Google Scholar]
- Daniels, B.C.; Krakauer, D.C.; Flack, J.C. Sparse code of conflict in a primate society. Proc. Natl. Acad. Sci. USA 2012, 109, 14259–14264. [Google Scholar] [CrossRef] [PubMed]
- Lee, E.D.; Broedersz, C.P.; Bialek, W. Statistical mechanics of the US Supreme Court. J. Stat. Phys. 2013, 160, 275–301. [Google Scholar] [CrossRef]
- Sun, H.T. Nonnegative entropy measures of multivariate symmetric correlations. Inf. Control 1978, 36, 133–156. [Google Scholar]
- Olbrich, E.; Bertschinger, N.; Ay, N.; Jost, J. How should complexity scale with system size? Eur. Phys. J. B 2008, 63, 407–415. [Google Scholar] [CrossRef]
- Crutchfield, J.P.; Feldman, D.P. Regularities unseen, randomness observed: Levels of entropy convergence. Chaos 2003, 13, 25–54. [Google Scholar] [CrossRef] [PubMed]
- Rosas, F.; Ntranos, V.; Ellison, C.J.; Verhelst, M.; Pollin, S. Understanding high-order correlations using a synergy-based decomposition of the total entropy. In Proceedings of the 5th Joint WIC/IEEE Symposium on Information Theory and Signal Processing in the Benelux, Brussels, Belgium, 6–7 May 2015; pp. 146–153.
- Yeung, R.W. A new outlook on Shannon’s information measures. IEEE Trans. Inf. Theory 1991, 37, 466–474. [Google Scholar] [CrossRef]
- Bar-Yam, Y. Multiscale complexity/entropy. Adv. Complex Syst. 2004, 7, 47–63. [Google Scholar] [CrossRef]
- Bell, A.J. The co-information lattice. In Proceedings of the 4th International Symposium on Independent Component Analysis and Blind Signal Separation (ICA 2003), Nara, Japan, 1–4 April 2003; pp. 921–926.
- McGill, W.J. Multivariate information transmission. Psychometrika 1954, 19, 97–116. [Google Scholar] [CrossRef]
- James, R.G.; Ellison, C.J.; Crutchfield, J.P. Anatomy of a bit: Information in a time series observation. Chaos Interdiscip. J Nonlinear Sci. 2011, 21, 037109. [Google Scholar] [CrossRef] [PubMed]
- Griffith, V.; Koch, C. Quantifying Synergistic Mutual Information. In Guided Self-Organization: Inception; Prokopenko, M., Ed.; Springer-Verlag: Berlin/Heidelberg, Germany, 2014; Volume 9, pp. 159–190. [Google Scholar]
- Griffith, V. Quantifying synergistic information. Ph.D. Thesis, California Institute of Technology, Pasadena, CA, USA, 2014. [Google Scholar]
- Jiao, J.; Courtade, T.; Venkat, K.; Weissman, T. Justification of Logarithmic Loss via the Benefit of Side Information. IEEE Trans. Inf. Theory 2015, 61, 5357–5365. [Google Scholar] [CrossRef]
- Harder, M.; Salge, C.; Polani, D. Bivariate measure of redundant information. Phys. Rev. E 2013, 87, 012130. [Google Scholar] [CrossRef] [PubMed]
- Griffith, V.; Chong, E.K.; James, R.G.; Ellison, C.J.; Crutchfield, J.P. Intersection information based on common randomness. Entropy 2014, 16, 1985–2000. [Google Scholar] [CrossRef]
- Bertschinger, N.; Rauh, J.; Olbrich, E.; Jost, J.; Ay, N. Quantifying unique information. Entropy 2014, 16, 2161–2183. [Google Scholar] [CrossRef]
- Bertschinger, N.; Rauh, J.; Olbrich, E.; Jost, J. Shared information—New insights and problems in decomposing information in complex systems. In Proceedings of the European Conference on Complex Systems 2012, Brussels, Belgium, 3–7 September 2012; pp. 251–269.
- Barrett, A.B. Exploration of synergistic and redundant information sharing in static and dynamical Gaussian systems. Phys. Rev. E 2015, 91, 052802. [Google Scholar] [CrossRef] [PubMed]
- Berkson, J. Limitations of the application of fourfold table analysis to hospital data. Biom. Bull. 1946, 2, 47–53. [Google Scholar] [CrossRef]
- Kim, J.; Pearl, J. A computational model for causal and diagnostic reasoning in inference systems. In Proceedings of the Eighth International Joint Conference on Artificial Intelligence (IJCAI), Karlsruhe, Germany, 8–12 August 1983; pp. 190–193.
- Bloch, M.; Barros, J. Physical-Layer Security: From Information Theory to Security Engineering; Cambridge University Press: Cambrige, UK, 2011. [Google Scholar]
- Shannon, C.E. Communication theory of secrecy systems*. Bell Syst. Tech. J. 1949, 28, 656–715. [Google Scholar] [CrossRef]
- Ahlswede, R.; Cai, N.; Li, S.Y.R.; Yeung, R.W. Network information flow. IEEE Trans. Inf. Theory 2000, 46, 1204–1216. [Google Scholar] [CrossRef]
- Li, S.Y.R.; Yeung, R.W.; Cai, N. Linear network coding. IEEE Trans. Inf. Theory 2003, 49, 371–381. [Google Scholar] [CrossRef]
- Katti, S.; Rahul, H.; Hu, W.; Katabi, D.; Médard, M.; Crowcroft, J. XORs in the air: Practical wireless network coding. IEEE/ACM Trans. Netw. 2008, 16, 497–510. [Google Scholar] [CrossRef]
- Landau, L.; Lifshitz, E. Statistical Physics, 2nd ed.; Pergamon Press: Oxford, UK, 1970; Volume 5. [Google Scholar]
- Wainwright, M.J.; Jordan, M.I. Graphical models, exponential families, and variational inference. Found. Trends Mach. Learn. 2008, 1, 1–305. [Google Scholar] [CrossRef]
- Cipra, B.A. An introduction to the Ising model. Am. Math. Mon. 1987, 94, 937–959. [Google Scholar] [CrossRef]
- Sayed, A.H. Adaptive Filters; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- El Gamal, A.; Kim, Y.H. Network Information Theory; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).