Abstract
Information-theoretic measures, such as the entropy, the cross-entropy and the Kullback–Leibler divergence between two mixture models, are core primitives in many signal processing tasks. Since the Kullback–Leibler divergence of mixtures provably does not admit a closed-form formula, it is in practice either estimated using costly Monte Carlo stochastic integration, approximated or bounded using various techniques. We present a fast and generic method that builds algorithmically closed-form lower and upper bounds on the entropy, the cross-entropy, the Kullback–Leibler and the α-divergences of mixtures. We illustrate the versatile method by reporting our experiments for approximating the Kullback–Leibler and the α-divergences between univariate exponential mixtures, Gaussian mixtures, Rayleigh mixtures and Gamma mixtures.
1. Introduction
Mixture models are commonly used in signal processing. A typical scenario is to use mixture models [1,2,3] to smoothly model histograms. For example, Gaussian Mixture Models (GMMs) can be used to convert grey-valued images into binary images by building a GMM fitting the image intensity histogram and then choosing the binarization threshold as the average of the Gaussian means [1]. Similarly, Rayleigh Mixture Models (RMMs) are often used in ultrasound imagery [2] to model histograms, and perform segmentation by classification. When using mixtures, a fundamental primitive is to define a proper statistical distance between them. The Kullback–Leibler (KL) divergence [4], also called relative entropy or information discrimination, is the most commonly used distance. Hence the main target of this paper is to faithfully measure the KL divergence. Let and be two finite statistical density mixtures of k and components, respectively. Notice that the Cumulative Density Function (CDF) of a mixture is like its density also a convex combinations of the component CDFs. However, beware that a mixture is not a sum of random variables (RVs). Indeed, sums of RVs have convolutional densities. In statistics, the mixture components are often parametric: , where is a vector of parameters. For example, a mixture of Gaussians (MoG also used as a shortcut instead of GMM) has each component distribution parameterized by its mean and its covariance matrix (so that the parameter vector is ). Let be the support of the component distributions. Denote by the cross-entropy [4] between two continuous mixtures of densities m and , and denote by the Shannon entropy [4]. Then the Kullback–Leibler divergence between m and is given by:
The notation “:” is used instead of the usual comma “,” notation to emphasize that the distance is not a metric distance since neither is it symmetric (), nor does it satisfy the triangular inequality [4] of metric distances (). When the natural base of the logarithm is chosen, we get a differential entropy measure expressed in nat units. Alternatively, we can also use the base-2 logarithm () and get the entropy expressed in bit units. Although the KL divergence is available in closed-form for many distributions (in particular as equivalent Bregman divergences for exponential families [5], see Appendix C), it was proven that the Kullback–Leibler divergence between two (univariate) GMMs is not analytic [6] (see also the particular case of a GMM of two components with the same variance that was analyzed in [7]). See Appendix A for an analysis. Note that the differential entropy may be negative. For example, the differential entropy of a univariate Gaussian distribution is , and is therefore negative when the standard variance . We consider continuous distributions with entropies well-defined (entropy may be undefined for singular distributions like Cantor’s distribution [8]).
1.1. Prior Work
Many approximation techniques have been designed to beat the computationally intensive Monte Carlo (MC) stochastic estimation: with (s independently and identically distributed (i.i.d.) samples ). The MC estimator is asymptotically consistent, , so that the “true value” of the KL of mixtures is estimated in practice by taking a very large sample (say, ). However, we point out that the MC estimator gives as output a stochastic approximation, and therefore does not guarantee deterministic bounds (confidence intervals may be used). Deterministic lower and upper bounds of the integral can be obtained by various numerical integration techniques using quadrature rules. We refer to [9,10,11,12] for the current state-of-the-art approximation techniques and bounds on the KL of GMMs. The latest work for computing the entropy of GMMs is [13]. It considers arbitrary finely tuned bounds of the entropy of isotropic Gaussian mixtures (a case encountered when dealing with KDEs, kernel density estimators). However, there is a catch in the technique of [13]: It relies on solving the unique roots of some log-sum-exp equations (See Theorem 1 of [13], p. 3342) that do not admit a closed-form solution. Thus it is a hybrid method that contrasts with our combinatorial approach. Bounds of the KL divergence between mixture models can be generalized to bounds of the likelihood function of mixture models [14], because log-likelihood is just the KL between the empirical distribution and the mixture model up to a constant shift.
In information geometry [15], a mixture family of linearly independent probability distributions is defined by the convex combination of those non-parametric component distributions: with and . A mixture family induces a dually flat space where the Kullback–Leibler divergence is equivalent to a Bregman divergence [5,15] defined on the η-parameters. However, in that case, the Bregman convex generator (the Shannon information) is not available in closed-form. Except for the family of multinomial distributions that is both a mixture family (with closed-form , the discrete KL [4]) and an exponential family [15].
1.2. Contributions
In this work, we present a simple and efficient method that builds algorithmically a closed-form formula that guarantees both deterministic lower and upper bounds on the KL divergence within an additive factor of . We then further refine our technique to get improved adaptive bounds. For univariate GMMs, we get the non-adaptive bounds in time, and the adaptive bounds in time. To illustrate our generic technique, we demonstrate it based on Exponential Mixture Models (EMMs), Gamma mixtures, RMMs and GMMs. We extend our preliminary results on KL divergence [16] to other information theoretical measures such as the differential entropy and α-divergences.
1.3. Paper Outline
The paper is organized as follows. Section 2 describes the algorithmic construction of the formula using piecewise log-sum-exp inequalities for the cross-entropy and the Kullback–Leibler divergence. Section 3 instantiates this algorithmic principle to the entropy and discusses related works. Section 4 extends the proposed bounds to the family of alpha divergences. Section 5 discusses an extension of the lower bound to f-divergences. Section 6 reports our experimental results on several mixture families. Finally, Section 7 concludes this work by discussing extensions to other statistical distances. Appendix A proves that the Kullback–Leibler divergence of mixture models is not analytic [6]. Appendix B reports the closed-form formula for the KL divergence between scaled and truncated distributions of the same exponential family [17] (that include Rayleigh, Gaussian and Gamma distributions among others). Appendix C shows that the KL divergence between two mixtures can be approximated by a Bregman divergence.
2. A Generic Combinatorial Bounding Algorithm Based on Density Envelopes
Let us bound the cross-entropy by deterministic lower and upper bounds, , so that the bounds on the Kullback–Leibler divergence follows as:
Since the cross-entropy of two mixtures and :
has a log-sum term of positive arguments, we shall use bounds on the log-sum-exp (lse) function [18,19]:
We have the following basic inequalities:
The left-hand-side (LHS) strict inequality holds because since . The right-hand-side (RHS) inequality follows from the fact that , and equality holds if and only if . The lse function is convex but not strictly convex, see exercise 7.9 [20]. It is known [21] that the conjugate of the lse function is the negative entropy restricted to the probability simplex. The lse function enjoys the following translation identity property: , . Similarly, we can also lower bound the lse function by . We write equivalently that for l positive numbers ,
In practice, we seek matching lower and upper bounds that minimize the bound gap. The gap of that ham-sandwich inequality in Equation (5) is , which is upper bounded by .
A mixture model must satisfy
point-wisely for any . Therefore we shall bound the integral term in Equation (3) using piecewise lse inequalities where the min and max are kept unchanged. We get
In order to calculate and efficiently using closed-form formula, let us compute the upper and lower envelopes of the real-valued functions defined on the support , that is, and . These envelopes can be computed exactly using techniques of computational geometry [22,23] provided that we can calculate the roots of the equation , where and are a pair of weighted components. (Although this amounts to solve quadratic equations for Gaussian or Rayleigh distributions, the roots may not always be available in closed form, e.g. in the case of Weibull distributions.)
Let the envelopes be combinatorially described by ℓ elementary interval pieces in the form partitioning the support (with and ). Observe that on each interval , the maximum of the functions is given by , where indicates the weighted component dominating all the others, i.e., the arg max of for any , and the minimum of is given by .
To fix ideas, when mixture components are univariate Gaussians, the upper envelope amounts to find equivalently the lower envelope of parabolas (see Figure 1) which has linear complexity, and can be computed in -time [24], or in output-sensitive time [25], where ℓ denotes the number of parabola segments in the envelope. When the Gaussian mixture components have all the same weight and variance (e.g., kernel density estimators), the upper envelope amounts to find a lower envelope of cones: (a Voronoi diagram in arbitrary dimension).

Figure 1.
Lower envelope of parabolas corresponding to the upper envelope of weighted components of a Gaussian mixture with components.
To proceed once the envelopes have been built, we need to calculate two types of definite integrals on those elementary intervals: (i) the probability mass in an interval where Φ denotes the Cumulative Distribution Function (CDF); and (ii) the partial cross-entropy [26]. Thus let us define these two quantities:
By Equations (7) and (8), we get the bounds of as
The size of the lower/upper bound formula depends on the envelope complexity ℓ, the number k of mixture components, and the closed-form expressions of the integral terms and . In general, when a pair of weighted component densities intersect in at most p points, the envelope complexity is related to the Davenport–Schinzel sequences [27]. It is quasi-linear for bounded , see [27].
Note that in symbolic computing, the Risch semi-algorithm [28] solves the problem of computing indefinite integration in terms of elementary functions provided that there exists an oracle (hence the term “semi-algorithm”) for checking whether an expression is equivalent to zero or not (however it is unknown whether there exists an algorithm implementing the oracle or not).
We presented the technique by bounding the cross-entropy (and entropy) to deliver lower/upper bounds on the KL divergence. When only the KL divergence needs to be bounded, we rather consider the ratio term . This requires to partition the support into elementary intervals by overlaying the critical points of both the lower and upper envelopes of and , which can be done in linear time. In a given elementary interval, since , we then consider the inequalities:
We now need to compute definite integrals of the form (see Appendix B for explicit formulas when considering scaled and truncated exponential families [17]). (Thus for exponential families, the ratio of densities removes the auxiliary carrier measure term.)
We call these bounds CELB and CEUB for Combinatorial Envelope Lower and Upper Bounds, respectively.
2.1. Tighter Adaptive Bounds
We shall now consider shape-dependent bounds improving over the additive non-adaptive bounds. This is made possible by a decomposition of the lse function explained as follows. Let . By translation identity of the lse function,
for all . Since if , and , we have necessarily for any . Since Equation (13) is an identity for all , we minimize the residual by maximizing . Denoting by the sequence of numbers sorted in non-decreasing order, the decomposition
yields the smallest residual. Since for all , we have
This shows the bounds introduced earlier can indeed be improved by a more accurate computation of the residual term .
When considering 1D GMMs, let us now bound in a combinatorial range . Let denote the index of the dominating weighted component in this range. Then,
Thus we have:
Now consider the ratio term:
It is maximized in by maximizing equivalently the following quadratic equation:
Setting the derivative to zero (), we get the root (when )
If , the ratio can be bounded in the slab by considering the extreme values of the three element set . Otherwise is monotonic in , its bounds in are given by . In any case, let and represent the resulting lower and upper bounds of in . Then is bounded in the range by:
In practice, we always get better bounds using the shape-dependent technique at the expense of computing overall intersection points of the pairwise densities. We call those bounds CEALB and CEAUB for Combinatorial Envelope Adaptive Lower Bound and Combinatorial Envelope Adaptive Upper Bound.
Let us illustrate one scenario where this adaptive technique yields very good approximations. Consider a GMM with all variance tending to zero (a mixture of k Diracs). Then in a combinatorial slab , we have for all , and therefore we get tight bounds.
As a related technique, we could also upper bound by where denotes the maximal value of the mixture density in the range . This maximal value is either found at the slab extremities, or is a mode of the GMM. It then requires to find the modes of a GMM [29,30], for which no analytical solution is known in general.
2.2. Another Derivation Using the Arithmetic-Geometric Mean Inequality
Let us start by considering the inequality of arithmetic and geometric weighted means (AGI, Arithmetic-Geometric Inequality) applied to the mixture component distributions:
with equality holds iff. .
To get a tractable formula with a positive remainder of the log-sum term , we need to have the log argument greater or equal to 1, and thus we shall write the positive remainder:
Therefore, we can decompose the log-sum into a tractable part and a remainder as:
For exponential families, the first term can be integrated accurately. For the second term, we notice that is a distribution in the same exponential family. We denote . Then
As the ratio can be bounded above and below using techniques in Section 2.1, can be correspondingly bounded. Notice the similarity between Equations (14) and (15). The key difference with the adaptive bounds is that, here we choose instead of the dominating component in as the “reference distribution” in the decomposition. This subtle difference is not presented in detail in our experimental studies but discussed here for completeness. Essentially, the gap of the bounds is up to the difference between the geometric average and the arithmetic average. In the extreme case that all mixture components are identical, this gap will reach zero. Therefore we expect good quality bounds with a small gap when the mixture components are similar as measured by KL divergence.
2.3. Case Studies
In the following, we instantiate the proposed method for several prominent cases on the mixture of exponential family distributions.
2.3.1. The Case of Exponential Mixture Models
An exponential distribution has density defined on for . Its CDF is . Any two components and (with ) have a unique intersection point
if ; otherwise they do not intersect. The basic formulas to evaluate the bounds are
2.3.2. The Case of Rayleigh Mixture Models
A Rayleigh distribution has density , defined on for . Its CDF is . Any two components and (with ) must intersect at and can have at most one other intersection point
if the square root is well defined and . We have
The last term in Equation (20) does not have a simple closed form (it requires the exponential integral, Ei). One need a numerical integrator to compute it.
2.3.3. The Case of Gaussian Mixture Models
The Gaussian density has support and parameters and . Its CDF is , where is the Gauss error function. The intersection point of two components and can be obtained by solving the quadratic equation , which gives at most two solutions. As shown in Figure 1, the upper envelope of Gaussian densities corresponds to the lower envelope of parabolas. We have
2.3.4. The Case of Gamma Distributions
For simplicity, we only consider gamma distributions with the shape parameter fixed and the scale varying. The density is defined on as , where is the gamma function. Its CDF is , where is the lower incomplete gamma function. Two weighted gamma densities and (with ) intersect at a unique point
if ; otherwise they do not intersect. From straightforward derivations,
Similar to the case of Rayleigh mixtures, the last term in Equation (25) relies on numerical integration.
3. Upper-Bounding the Differential Entropy of a Mixture
First, consider a finite parametric mixture model . Using the chain rule of the entropy, we end up with the well-known lemma:
Lemma 1.
The entropy of a d-variate mixture is upper bounded by the sum of the entropy of its marginal mixtures: , where is the 1D marginal mixture with respect to variable .
Since the 1D marginals of a multivariate GMM are univariate GMMs, we thus get a loose upper bound. A generic sample-based probabilistic bound is reported for the entropies of distributions with given support [31]: The method builds probabilistic upper and lower piecewisely linear CDFs based on an i.i.d. finite sample set of size n and a given deviation probability threshold. It then builds algorithmically between those two bounds the maximum entropy distribution [31] with a so-called string-tightening algorithm.
Instead, we proceed as follows: Consider finite mixtures of component distributions defined on the full support that have finite component means and variances (like exponential families). Then we shall use the fact that the maximum entropy distribution with prescribed mean and variance is a Gaussian distribution, and conclude the upper bound by plugging the mixture mean and variance in the differential entropy formula of the Gaussian distribution. In general, the maximum entropy with moment constraints yields as a solution an exponential family.
Without loss of generality, consider GMMs in the form ( for univariate Gaussians). The mean of the mixture is and the variance is . Since , we deduce that
The entropy of a random variable with a prescribed variance is maximal for the Gaussian distribution with the same variance , see [4]. Since the differential entropy of a Gaussian is , we deduce that the entropy of the GMM is upper bounded by
This upper bound can be easily generalized to arbitrary dimensionality. We get the following lemma:
Lemma 2.
The entropy of a d-variate GMM is upper bounded by , where .
In general, exponential families have finite moments of any order [17]: In particular, we have and . For Gaussian distribution, we have the sufficient statistics so that yields the mean and variance from the log-normalizer. It is easy to generalize Lemma 2 to mixtures of exponential family distributions.
Note that this bound (called the Maximum Entropy Upper Bound in [13], MEUB) is tight when the GMM approximates a single Gaussian. It is fast to compute compared to the bound reported in [9] that uses Taylor’ s expansion of the log-sum of the mixture density.
A similar argument cannot be applied for a lower bound since a GMM with a given variance may have entropy tending to . For example, assume the 2-component mixture’s mean is zero, and that the variance approximates 1 by taking where G denotes the Gaussian density. Letting , we get the entropy tending to .
We remark that our log-sum-exp inequality technique yields a additive approximation range in the case of a Gaussian mixture with two components. It thus generalizes the bounds reported in [7] to GMMs with arbitrary variances that are not necessarily equal.
To see the bound gap, we have
Therefore the gap is at most
Thus to compute the gap error bound of the differential entropy, we need to integrate terms in the form
See Appendix B for a closed-form formula when dealing with exponential family components.
4. Bounding the α-Divergence
The α-divergence [15,32,33,34] between and is defined as
which clearly satisfies . The α-divergence is a family of information divergences parametrized by . Let , we get the KL divergence (see [35] for a proof):
and gives the reverse KL divergence:
Other interesting values [33] include (squared Hellinger distance), (Pearson Chi-square distance), (Neyman Chi-square distance), etc. Notably, the Hellinger distance is a valid distance metric which satisfies non-negativity, symmetry, and the triangle inequality. In general, only satisfies non-negativity so that for any and . It is neither symmetric nor admitting the triangle inequality. Minimization of α-divergences allows one to choose a trade-off between mode fitting and support fitting of the minimizer [36]. The minimizer of α-divergences including MLE as a special case has interesting connections with transcendental number theory [37].
To compute for given and reduces to evaluate the Hellinger integral [38,39]:
which in general does not have a closed form, as it was known that the α-divergence of mixture models is not analytic [6]. Moreover, may diverge making the α-divergence unbounded. Once can be solved, the Rényi and Tsallis divergences [35] and in general Sharma–Mittal divergences [40] can be easily computed. Therefore the results presented here directly extend to those divergence families.
Similar to the case of KL divergence, the Monte Carlo stochastic estimation of can be computed either as
where are i.i.d. samples, or as
where are i.i.d. In either case, it is consistent so that . However, MC estimation requires a large sample and does not guarantee deterministic bounds. The techniques described in [41] work in practice for very close distributions, and do not apply between mixture models. We will therefore derive combinatorial bounds for . The structure of this Section is parallel with Section 2 with necessary reformulations for a clear presentation.
4.1. Basic Bounds
For a pair of given and , we only need to derive bounds of in Equation (31) so that . Then the α-divergence can be bounded by a linear transformation of the range . In the following we always assume without loss of generality . Otherwise we can bound by considering equivalently the bounds of .
Recall that in each elementary slab , we have
Notice that , , and are all single component distributions up to a scaling coefficient. The general thinking is to bound the multi-component mixture by single component distributions in each elementary interval, so that the integral in Equation (31) can be computed in a piecewise manner.
If , then both and are monotonically increasing on . Therefore we have
where
and I denotes an interval . The other case is similar by noting that and are monotonically increasing and decreasing on , respectively. In conclusion, we obtain the following bounds of :
The remaining problem is to compute the definite integral in the above equations. Here we assume all mixture components are in the same exponential family so that , where is a base measure, is a vector of sufficient statistics, and the function F is known as the cumulant generating function. Then it is straightforward from Equation (37) that
If , then belongs to the natural parameter space . Therefore is bounded and can be computed from the CDF of as
The other case is more difficult: if still lies in , then can be computed by Equation (41). Otherwise we try to solve it by a numerical integrator. This is not ideal as the integral may diverge, or our approximation may be too loose to conclude. We point the reader to [42] and Equations (61)–(69) in [35] for related analysis with more details. As computing only requires time, the overall computational complexity (without considering the envelope computation) is .
4.2. Adaptive Bounds
This section derives the shape-dependent bounds which improve the basic bounds in Section 4.1. We can rewrite a mixture model in a slab as
where is a weighted component in serving as a reference. We only discuss the case that the reference is chosen as the dominating component, i.e., . However it is worth to note that the proposed bounds do not depend on this particular choice. Therefore the ratio
can be bounded in a sub-range of by analyzing the extreme values of in the slab . This can be done because usually consists of polynomial functions with finite critical points which can be solved easily. Correspondingly the function in can be bounded in a subrange of , denoted as . Hence
This forms better bounds of than Equation (32) because each component in the slab is analyzed more accurately. Therefore, we refine the fundamental bounds of by replacing the Equations (34) and (35) with
Then, the improved bounds of are given by Equations (38) and (39) according to the above replaced definition of and .
To evaluate and requires iterating through all components in each slab. Therefore the computational complexity is increased to .
4.3. Variance-Reduced Bounds
This section further improves the proposed bounds based on variance reduction [43]. By assumption, , then is more similar to rather than . The ratio is likely to have a small variance when x varies inside a slab , especially when α is close to 1. We will therefore bound this ratio term in
No matter or , the function must be monotonic on . In each slab , ranges between these two functions:
where , , and are defined in Equations (45) and (46). Similar to the definition of in Equation (37), we define
Therefore we have,
The remaining problem is to evaluate in Equation (49). Similar to Section 4.1, assuming the components are in the same exponential family with respect to the natural parameters θ, we get
If is in the natural parameter space, can be computed from the CDF of ; otherwise can be numerically integrated by its definition in Equation (49). The computational complexity is the same as the bounds in Section 4.2, i.e., .
We have introduced three pairs of deterministic lower and upper bounds that enclose the true value of α-divergence between univariate mixture models. Thus the gap between the upper and lower bounds provides the additive approximation factor of the bounds. We conclude by emphasizing that the presented methodology can be easily generalized to other divergences [35,40] relying on Hellinger-type integrals like the γ-divergence [44] as well as entropy measures [45].
5. Lower Bounds of the -Divergence
The f-divergence between two distributions and (not necessarily mixtures) is defined for a convex generator f by:
If , then .
Let us partition the support arbitrarily into elementary ranges, which do not necessarily correspond to the envelopes. Denote by the probability mass of a mixture in the range I: . Then
Note that in range , is a unit weight distribution. Thus by Jensen’s inequality , we get
Notice that the RHS of Equation (52) is the f-divergence between and , denoted by . In the special case that and , the above Equation (52) turns out to be the usual Gibbs’ inequality: , and Csiszár generator is chosen so that . In conclusion, for a fixed (coarse-grained) countable partition of , we recover the well-know information monotonicity [46] of the f-divergences:
In practice, we get closed-form lower bounds when is available in closed-form, where denote the CDF. In particular, if is a mixture model, then its CDF can be computed by linearly combining the CDFs of its components.
To wrap up, we have proved that coarse-graining by making a finite partition of the support yields a lower bound on the f-divergence by virtue of the information monotonicity. Therefore, instead of doing Monte Carlo stochastic integration:
with , it could be better to sort those n samples and consider the coarse-grained partition:
to get a guaranteed lower bound on the f-divergence. We will call this bound CGQLB for Coarse Graining Quantization Lower Bound.
Given a budget of n splitting points on the range , it would be interesting to find the best n points that maximize the lower bound . This is ongoing research.
6. Experiments
We perform an empirical study to verify our theoretical bounds. We simulate four pairs of mixture models as the test subjects. The component type is implied by the model name, where stands for Gamma mixtures. The components of each mixture model are given as follows.
- ’s components, in the form , are given by , , ; ’s components are , , .
- ’s components, in the form , are given by , , ; consists of , , .
- ’s components, in the form , are , , , , , , ; consists of , , , , , , , , .
- ’s components, in the form , are , , ; consists of , , .
We compare the proposed bounds with Monte Carlo estimation with different sample sizes in the range . For each sample size configuration, we report the 0.95 confidence interval by Monte Carlo estimation using the corresponding number of samples. Figure 2a–d shows the input signals as well as the estimation results, where the proposed bounds CELB, CEUB, CEALB, CEAUB, CGQLB are presented as horizontal lines, and the Monte Carlo estimations over different sample sizes are presented as error bars. We can loosely consider the average Monte Carlo output with the largest sample size () as the underlying truth, which is clearly inside our bounds. This serves as an empirical justification on the correctness of the bounds.
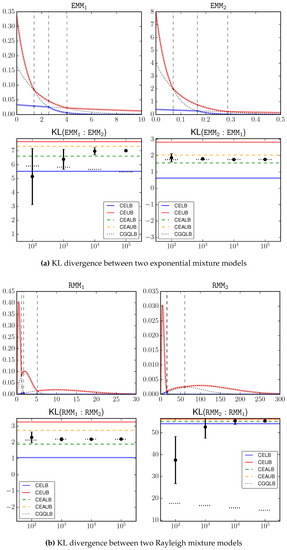
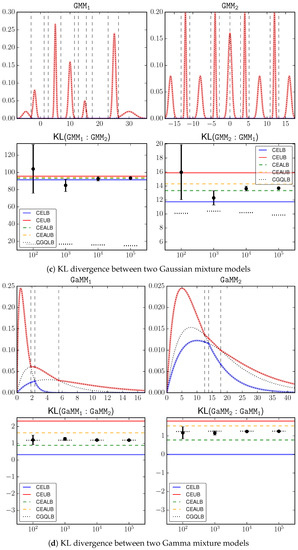
Figure 2.
Lower and upper bounds on the KL divergence between mixture models. The y-axis means KL divergence. Solid/dashed lines represent the combinatorial/adaptive bounds, respectively. The error-bars show the 0.95 confidence interval by Monte Carlo estimation using the corresponding sample size (x-axis). The narrow dotted bars show the CGQLB estimation w.r.t. the sample size.
A key observation is that the bounds can be very tight, especially when the underlying KL divergence has a large magnitude, e.g., . This is because the gap between the lower and upper bounds is always guaranteed to be within . Because KL is unbounded [4], in the general case two mixture models may have a large KL. Then our approximation gap is relatively very small. On the other hand, we also observed that the bounds in certain cases, e.g., , are not as tight as the other cases. When the underlying KL is small, the bounds are not as informative as the general case.
Comparatively, there is a significant improvement of the shape-dependent bounds (CEALB and CEAUB) over the combinatorial bounds (CELB and CEUB). In all investigated cases, the adaptive bounds can roughly shrink the gap by half of its original size at the cost of additional computation.
Note that, the bounds are accurate and must contain the true value. Monte Carlo estimation gives no guarantee on where the true value is. For example, in estimating , Monte Carlo estimation based on samples can go beyond our bounds! It therefore suffers from a larger estimation error.
CGQLB as a simple-to-implement technique shows surprising good performance in several cases, e.g., . Although it requires a large number of samples, we can observe that increasing sample size has limited effect on improving this bound. Therefore, in practice, one may intersect the range defined by CEALB and CEAUB with the range defined by CGQLB with a small sample size (e.g., 100) to get better bounds.
We simulates a set of Gaussian mixture models besides the above and . Figure 3 shows the GMM densities as well as their differential entropy. A detailed explanation of the components of each GMM model is omitted for brevity.
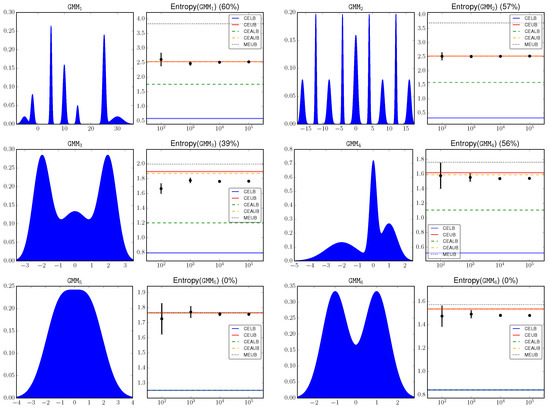
Figure 3.
Lower and upper bounds on the differential entropy of Gaussian mixture models. On the left of each subfigure is the simulated GMM signal. On the right of each subfigure is the estimation of its differential entropy. Note that a subset of the bounds coincide with each other in several cases.
The key observation is that CEUB (CEAUB) is very tight in most of the investigated cases. This is because that the upper envelope that is used to compute CEUB (CEAUB) gives a very good estimation of the input signal.
Notice that MEUB only gives an upper bound of the differential entropy as discussed in Section 3. In general the proposed bounds are tighter than MEUB. However, this is not the case when the mixture components are merged together and approximate one single Gaussian (and therefore its entropy can be well approximated by the Gaussian entropy), as shown in the last line of Figure 3.
For α-divergence, the bounds introduced in Section 4.1, Section 4.2 and Section 4.3 are denoted as “Basic”, “Adaptive” and “VR”, respectively. Figure 4 visualizes these GMMs and plots the estimations of their α-divergences against α. The red lines mean the upper envelope. The dashed vertical lines mean the elementary intervals. The components of and are more separated than and . Therefore these two pairs present different cases. For a clear presentation, only VR (which is expected to be better than Basic and Adaptive) is shown. We can see that, visually in the big scale, VR tightly surrounds the true value.
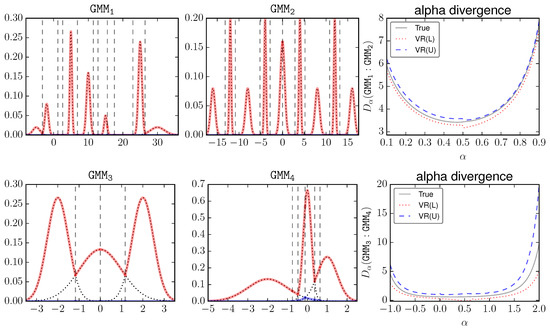
Figure 4.
Two pairs of Gaussian Mixture Models and their α-divergences against different values of α. The “true” value of is estimated by MC using random samples. VR(L) and VR(U) denote the variation reduced lower and upper bounds, respectively. The range of α is selected for each pair for a clear visualization.
For a more quantitative comparison, Table 1 shows the estimated α-divergence by MC, Basic, Adaptive, and VR. As is defined on , the KL bounds CE(A)LB and CE(A)UB are presented for or 1. Overall, we have the following order of gap size: Basic > Adaptive > VR, and VR is recommended in general for bounding α-divergences. There are certain cases that the upper VR bound is looser than Adaptive. In practice one can compute the intersection of these bounds as well as the trivial bound to get the best estimation.

Table 1.
The estimated and its bounds. The 95% confidence interval is shown for MC.
Note the similarity between KL in Equation (30) and the expression in Equation (47). We give without a formal analysis that: CEAL(U)B is equivalent to VR at the limit or . Experimentally as we slowly set , we can see that VR is consistent with CEAL(U)B.
7. Concluding Remarks and Perspectives
We have presented a fast versatile method to compute bounds on the Kullback–Leibler divergence between mixtures by building algorithmic formulae. We reported on our experiments for various mixture models in the exponential family. For univariate GMMs, we get a guaranteed bound of the KL divergence of two mixtures m and with k and components within an additive approximation factor of in -time. Therefore, the larger the KL divergence, the better the bound when considering a multiplicative -approximation factor, since . The adaptive bounds are guaranteed to yield better bounds at the expense of computing potentially intersection points of pairwise weighted components.
Our technique also yields the bound for the Jeffreys divergence (the symmetrized KL divergence: ) and the Jensen–Shannon divergence [47] (JS):
since is a mixture model with components. One advantage of this statistical distance is that it is symmetric, always bounded by , and its square root yields a metric distance [48]. The log-sum-exp inequalities may also be used to compute some Rényi divergences [35]:
when α is an integer, a mixture and a single (component) distribution. Getting fast guaranteed tight bounds on statistical distances between mixtures opens many avenues. For example, we may consider building hierarchical mixture models by merging iteratively two mixture components so that those pairs of components are chosen so that the KL distance between the full mixture and the simplified mixture is minimized.
In order to be useful, our technique is unfortunately limited to univariate mixtures: indeed, in higher dimensions, we can still compute the maximization diagram of weighted components (an additively weighted Bregman–Voronoi diagram [49,50] for components belonging to the same exponential family). However, it becomes more complex to compute in the elementary Voronoi cells V, the functions and (in 1D, the Voronoi cells are segments). We may obtain hybrid algorithms by approximating or estimating these functions. In 2D, it is thus possible to obtain lower and upper bounds on the Mutual Information [51] (MI) when the joint distribution is a 2D mixture of Gaussians:
Indeed, the marginal distributions and are univariate Gaussian mixtures.
A Python code implementing those computational-geometric methods for reproducible research is available online [52].
Acknowledgments
The authors gratefully thank the referees for their comments. This work was carried out while Ke Sun was visiting Frank Nielsen at Ecole Polytechnique, Palaiseau, France.
Author Contributions
Frank Nielsen and Ke Sun contributed to the theoretical results as well as to the writing of the article. Ke Sun implemented the methods and performed the numerical experiments. All authors have read and approved the final manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. The Kullback–Leibler Divergence of Mixture Models Is Not Analytic [6]
Ideally, we aim at getting a finite length closed-form formula to compute the KL divergence of finite mixture models. However, this is provably mathematically intractable [6] because of the log-sum term in the integral, as we shall prove below.
Analytic expressions encompass closed-form formula and may include special functions (e.g., Gamma function) but do not allow to use limits or integrals. An analytic function is a function (infinitely differentiable) such that around any point the k-order Taylor series converges to : for x belonging to a neighborhood of , where r is called the radius of convergence. The analytic property of a function is equivalent to the condition that for each , there exists a constant c such that .
To prove that the KL of mixtures is not analytic (hence does not admit a closed-form formula), we shall adapt the proof reported in [6] (in Japanese, we thank Professor Aoyagi for sending us his paper [6]). We shall prove that is not analytic for and , where , and is the density of a univariate Gaussian of mean μ and standard deviation σ. Let denote the KL divergence between these two mixtures (p has a single component and q has two components).
We have
Therefore
Let be the root of the equation so that for , we have . It follows that:
with . When , we have . Consider such that . Then the radius of convergence r is such that:
Thus the convergence radius is , and therefore the KL divergence is not an analytic function of the parameter w. The KL of mixtures is an example of a non-analytic smooth function. (Notice that the absolute value is not analytic at 0.)
Appendix B. Closed-Form Formula for the Kullback–Leibler Divergence between Scaled and Truncated Exponential Families
When computing approximation bounds for the KL divergence between two mixtures and , we end up with the task of computing where is a subset of the full support . We report a generic formula for computing these formula when the mixture (scaled and truncated) components belong to the same exponential family [17]. An exponential family has canonical log-density written as , where denotes the sufficient statistics, the log-normalizer (also called cumulant function or partition function), and an auxiliary carrier term.
Let . Since it is a difference of two cross-entropies, we get for three distributions belonging to the same exponential family [26] the following formula:
Furthermore, when the support is restricted, say to support range , let denote the mass and the normalized distribution. Then we have:
When is strictly convex and differentiable then is an exponential family and the closed-form formula follows straightforwardly. Otherwise, we still get a closed-form but need more derivations. For univariate distributions, we write and where denotes the cumulative distribution function.
The usual formula for truncated and scaled Kullback–Leibler divergence is:
where is a Bregman divergence [5]:
This formula extends the classic formula [5] for full regular exponential families (by setting and with ).
Similar formulæ are available for the cross-entropy and entropy of exponential families [26].
Appendix C. On the Approximation of KL between Smooth Mixtures by a Bregman Divergence [5]
Clearly, since Bregman divergences are always finite while KL divergences may diverge, we need extra conditions to assert that the KL between mixtures can be approximated by Bregman divergences. We require that the Jeffreys divergence between mixtures be finite in order to approximate the KL between mixtures by a Bregman divergence. We loosely derive this observation (Careful derivations will be reported elsewhere) using two different approaches:
- First, continuous mixture distributions have smooth densities that can be arbitrarily closely approximated using a single distribution (potentially multi-modal) belonging to the Polynomial Exponential Families [53,54] (PEFs). A polynomial exponential family of order D has log-likelihood : Therefore, a PEF is an exponential family with polynomial sufficient statistics . However, the log-normalizer of a D-order PEF is not available in closed-form: It is computationally intractable. Nevertheless, the KL between two mixtures and can be theoretically approximated closely by a Bregman divergence between the two corresponding PEFs: :, where θ and are the natural parameters of the PEF family approximating and , respectively (i.e., and ). Notice that the Bregman divergence of PEFs has necessarily finite value but the KL of two smooth mixtures can potentially diverge (infinite value), hence the conditions on Jeffreys divergence to be finite.
- Second, consider two finite mixtures and of k and components (possibly with heterogeneous components ’s and ’s), respectively. In information geometry, a mixture family is the set of convex combination of fixed component densities. Thus in statistics, a mixture is understood as a convex combination of parametric components while in information geometry a mixture family is the set of convex combination of fixed components. Let us consider the mixture families generated by the fixed components :We can approximate arbitrarily finely (with respect to total variation) mixture for any by with (so that ) and with (and ). Therefore , where is the Shannon information (negative Shannon entropy) for the composite mixture family. Again, the Bregman divergence is necessarily finite but between mixtures may be potentially infinite when the KL integral diverges (hence, the condition on Jeffreys divergence finiteness). Interestingly, this Shannon information can be arbitrarily closely approximated when considering isotropic Gaussians [13]. Notice that the convex conjugate of the continuous Shannon neg-entropy is the log-sum-exp function on the inverse soft map.
References
- Huang, Z.K.; Chau, K.W. A new image thresholding method based on Gaussian mixture model. Appl. Math. Comput. 2008, 205, 899–907. [Google Scholar] [CrossRef]
- Seabra, J.; Ciompi, F.; Pujol, O.; Mauri, J.; Radeva, P.; Sanches, J. Rayleigh mixture model for plaque characterization in intravascular ultrasound. IEEE Trans. Biomed. Eng. 2011, 58, 1314–1324. [Google Scholar] [CrossRef] [PubMed]
- Julier, S.J.; Bailey, T.; Uhlmann, J.K. Using Exponential Mixture Models for Suboptimal Distributed Data Fusion. In Proceedings of the 2006 IEEE Nonlinear Statistical Signal Processing Workshop, Cambridge, UK, 13–15 September 2006; IEEE: New York, NY, USA, 2006; pp. 160–163. [Google Scholar]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Banerjee, A.; Merugu, S.; Dhillon, I.S.; Ghosh, J. Clustering with Bregman divergences. J. Mach. Learn. Res. 2005, 6, 1705–1749. [Google Scholar]
- Watanabe, S.; Yamazaki, K.; Aoyagi, M. Kullback Information of Normal Mixture is Not an Analytic Function; Technical Report of IEICE Neurocomputing; The Institute of Electronics, Information and Communication Engineers: Tokyo, Japan, 2004; pp. 41–46. (In Japanese) [Google Scholar]
- Michalowicz, J.V.; Nichols, J.M.; Bucholtz, F. Calculation of differential entropy for a mixed Gaussian distribution. Entropy 2008, 10, 200–206. [Google Scholar] [CrossRef]
- Pichler, G.; Koliander, G.; Riegler, E.; Hlawatsch, F. Entropy for singular distributions. In Proceedings of the IEEE International Symposium on Information Theory (ISIT), Honolulu, HI, USA, 29 June–4 July 2014; pp. 2484–2488.
- Huber, M.F.; Bailey, T.; Durrant-Whyte, H.; Hanebeck, U.D. On entropy approximation for Gaussian mixture random vectors. In Proceedings of the IEEE International Conference on Multisensor Fusion and Integration for Intelligent Systems, Seoul, Korea, 20–22 August 2008; IEEE: New York, NY, USA, 2008; pp. 181–188. [Google Scholar]
- Yamada, M.; Sugiyama, M. Direct importance estimation with Gaussian mixture models. IEICE Trans. Inf. Syst. 2009, 92, 2159–2162. [Google Scholar] [CrossRef]
- Durrieu, J.L.; Thiran, J.P.; Kelly, F. Lower and upper bounds for approximation of the Kullback-Leibler divergence between Gaussian Mixture Models. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Kyoto, Japan, 25–30 March 2012; IEEE: New York, NY, USA, 2012; pp. 4833–4836. [Google Scholar]
- Schwander, O.; Marchand-Maillet, S.; Nielsen, F. Comix: Joint estimation and lightspeed comparison of mixture models. In Proceedings of the 2016 IEEE International Conference on Acoustics, Speech and Signal Processing, ICASSP 2016, Shanghai, China, 20–25 March 2016; pp. 2449–2453.
- Moshksar, K.; Khandani, A.K. Arbitrarily Tight Bounds on Differential Entropy of Gaussian Mixtures. IEEE Trans. Inf. Theory 2016, 62, 3340–3354. [Google Scholar] [CrossRef]
- Mezuman, E.; Weiss, Y. A Tight Convex Upper Bound on the Likelihood of a Finite Mixture. arXiv 2016. [Google Scholar]
- Amari, S.-I. Information Geometry and Its Applications; Springer: Tokyo, Japan, 2016; Volume 194. [Google Scholar]
- Nielsen, F.; Sun, K. Guaranteed Bounds on the Kullback–Leibler Divergence of Univariate Mixtures. IEEE Signal Process. Lett. 2016, 23, 1543–1546. [Google Scholar] [CrossRef]
- Nielsen, F.; Garcia, V. Statistical exponential families: A digest with flash cards. arXiv 2009. [Google Scholar]
- Calafiore, G.C.; El Ghaoui, L. Optimization Models; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- Shen, C.; Li, H. On the dual formulation of boosting algorithms. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 32, 2216–2231. [Google Scholar] [CrossRef] [PubMed]
- Beck, A. Introduction to Nonlinear Optimization: Theory, Algorithms, and Applications with MATLAB; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2014. [Google Scholar]
- Boyd, S.; Vandenberghe, L. Convex Optimization; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- De Berg, M.; van Kreveld, M.; Overmars, M.; Schwarzkopf, O.C. Computational Geometry; Springer: Heidelberg, Germany, 2000. [Google Scholar]
- Setter, O.; Sharir, M.; Halperin, D. Constructing Two-Dimensional Voronoi Diagrams via Divide-and-Conquer of Envelopes in Space; Springer: Heidelberg, Germany, 2010. [Google Scholar]
- Devillers, O.; Golin, M.J. Incremental algorithms for finding the convex hulls of circles and the lower envelopes of parabolas. Inf. Process. Lett. 1995, 56, 157–164. [Google Scholar] [CrossRef]
- Nielsen, F.; Yvinec, M. An output-sensitive convex hull algorithm for planar objects. Int. J. Comput. Geom. Appl. 1998, 8, 39–65. [Google Scholar] [CrossRef]
- Nielsen, F.; Nock, R. Entropies and cross-entropies of exponential families. In Proceedings of the 17th IEEE International Conference on Image Processing (ICIP), Hong Kong, China, 26–29 September 2010; IEEE: New York, NY, USA, 2010; pp. 3621–3624. [Google Scholar]
- Sharir, M.; Agarwal, P.K. Davenport-Schinzel Sequences and Their Geometric Applications; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Bronstein, M. Algorithms and computation in mathematics. In Symbolic Integration. I. Transcendental Functions; Springer: Berlin, Germany, 2005. [Google Scholar]
- Carreira-Perpinan, M.A. Mode-finding for mixtures of Gaussian distributions. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 1318–1323. [Google Scholar] [CrossRef]
- Aprausheva, N.N.; Sorokin, S.V. Exact equation of the boundary of unimodal and bimodal domains of a two-component Gaussian mixture. Pattern Recognit. Image Anal. 2013, 23, 341–347. [Google Scholar] [CrossRef]
- Learned-Miller, E.; DeStefano, J. A probabilistic upper bound on differential entropy. IEEE Trans. Inf. Theory 2008, 54, 5223–5230. [Google Scholar] [CrossRef]
- Amari, S.-I. α-Divergence Is Unique, Belonging to Both f-Divergence and Bregman Divergence Classes. IEEE Trans. Inf. Theory 2009, 55, 4925–4931. [Google Scholar] [CrossRef]
- Cichocki, A.; Amari, S.I. Families of Alpha- Beta- and Gamma-Divergences: Flexible and Robust Measures of Similarities. Entropy 2010, 12, 1532–1568. [Google Scholar] [CrossRef]
- Póczos, B.; Schneider, J. On the Estimation of α-Divergences. In Proceedings of the 14th International Conference on Artificial Intelligence and Statistics, Ft. Lauderdale, FL, USA, 11–13 April 2011; pp. 609–617.
- Nielsen, F.; Nock, R. On Rényi and Tsallis entropies and divergences for exponential families. arXiv 2011. [Google Scholar]
- Minka, T. Divergence Measures and Message Passing; Technical Report MSR-TR-2005-173; Microsoft Research: Cambridge, UK, 2005. [Google Scholar]
- Améndola, C.; Drton, M.; Sturmfels, B. Maximum Likelihood Estimates for Gaussian Mixtures Are Transcendental. arXiv 2015. [Google Scholar]
- Hellinger, E. Neue Begründung der Theorie quadratischer Formen von unendlichvielen Veränderlichen. J. Reine Angew. Math. 1909, 136, 210–271. (In German) [Google Scholar]
- Van Erven, T.; Harremos, P. Rényi divergence and Kullback-Leibler divergence. IEEE Trans. Inf. Theory 2014, 60, 3797–3820. [Google Scholar] [CrossRef]
- Nielsen, F.; Nock, R. A closed-form expression for the Sharma-Mittal entropy of exponential families. J. Phys. A Math. Theor. 2012, 45, 032003. [Google Scholar] [CrossRef]
- Nielsen, F.; Nock, R. On the Chi Square and Higher-Order Chi Distances for Approximating f-Divergences. IEEE Signal Process. Lett. 2014, 21, 10–13. [Google Scholar] [CrossRef]
- Nielsen, F.; Boltz, S. The Burbea-Rao and Bhattacharyya centroids. IEEE Trans. Inf. Theory 2011, 57, 5455–5466. [Google Scholar] [CrossRef]
- Jarosz, W. Efficient Monte Carlo Methods for Light Transport in Scattering Media. Ph.D. Thesis, University of California, San Diego, CA, USA, 2008. [Google Scholar]
- Fujisawa, H.; Eguchi, S. Robust parameter estimation with a small bias against heavy contamination. J. Multivar. Anal. 2008, 99, 2053–2081. [Google Scholar] [CrossRef]
- Havrda, J.; Charvát, F. Quantification method of classification processes. Concept of structural α-entropy. Kybernetika 1967, 3, 30–35. [Google Scholar]
- Liang, X. A Note on Divergences. Neural Comput. 2016, 28, 2045–2062. [Google Scholar] [CrossRef] [PubMed]
- Lin, J. Divergence measures based on the Shannon entropy. IEEE Trans. Inf. Theory 1991, 37, 145–151. [Google Scholar] [CrossRef]
- Endres, D.M.; Schindelin, J.E. A new metric for probability distributions. IEEE Trans. Inf. Theory 2003, 49, 1858–1860. [Google Scholar] [CrossRef]
- Nielsen, F.; Boissonnat, J.D.; Nock, R. On Bregman Voronoi diagrams. In Proceedings of the Eighteenth Annual ACM-SIAM Symposium on Discrete Algorithms, New Orleans, LA, USA, 7–9 January 2007; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2007; pp. 746–755. [Google Scholar]
- Boissonnat, J.D.; Nielsen, F.; Nock, R. Bregman Voronoi diagrams. Discret. Comput. Geom. 2010, 44, 281–307. [Google Scholar] [CrossRef]
- Foster, D.V.; Grassberger, P. Lower bounds on mutual information. Phys. Rev. E 2011, 83, 010101. [Google Scholar] [CrossRef] [PubMed]
- Nielsen, F.; Sun, K. PyKLGMM: Python Software for Computing Bounds on the Kullback-Leibler Divergence between Mixture Models. 2016. Available online: https://www.lix.polytechnique.fr/~nielsen/KLGMM/ (accessed on 6 December 2016).
- Cobb, L.; Koppstein, P.; Chen, N.H. Estimation and moment recursion relations for multimodal distributions of the exponential family. J. Am. Stat. Assoc. 1983, 78, 124–130. [Google Scholar] [CrossRef]
- Nielsen, F.; Nock, R. Patch matching with polynomial exponential families and projective divergences. In Proceedings of the 9th International Conference Similarity Search and Applications (SISAP), Tokyo, Japan, 24–26 October 2016.
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).