Static Einstein–Maxwell Magnetic Solitons and Black Holes in an Odd Dimensional AdS Spacetime
Abstract
:1. Introduction
2. Magnetic Fields in an Odd-Dimensional AdS Spacetime
3. Einstein–Maxwell Solutions: the Formalism
3.1. The ansatz and Equations
3.2. The Asymptotics
3.3. The Mass Computation
3.4. Other Quantities
4. Einstein–Maxwell Solutions: The Results
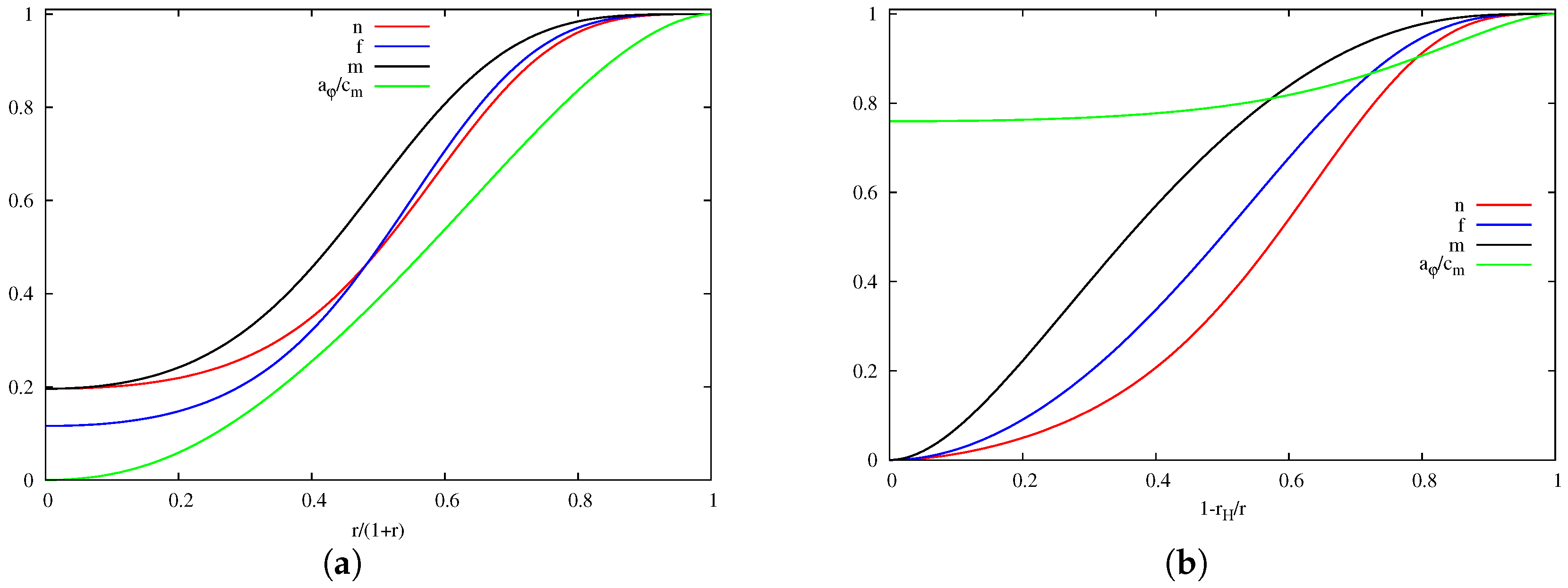
4.1. The Solitons
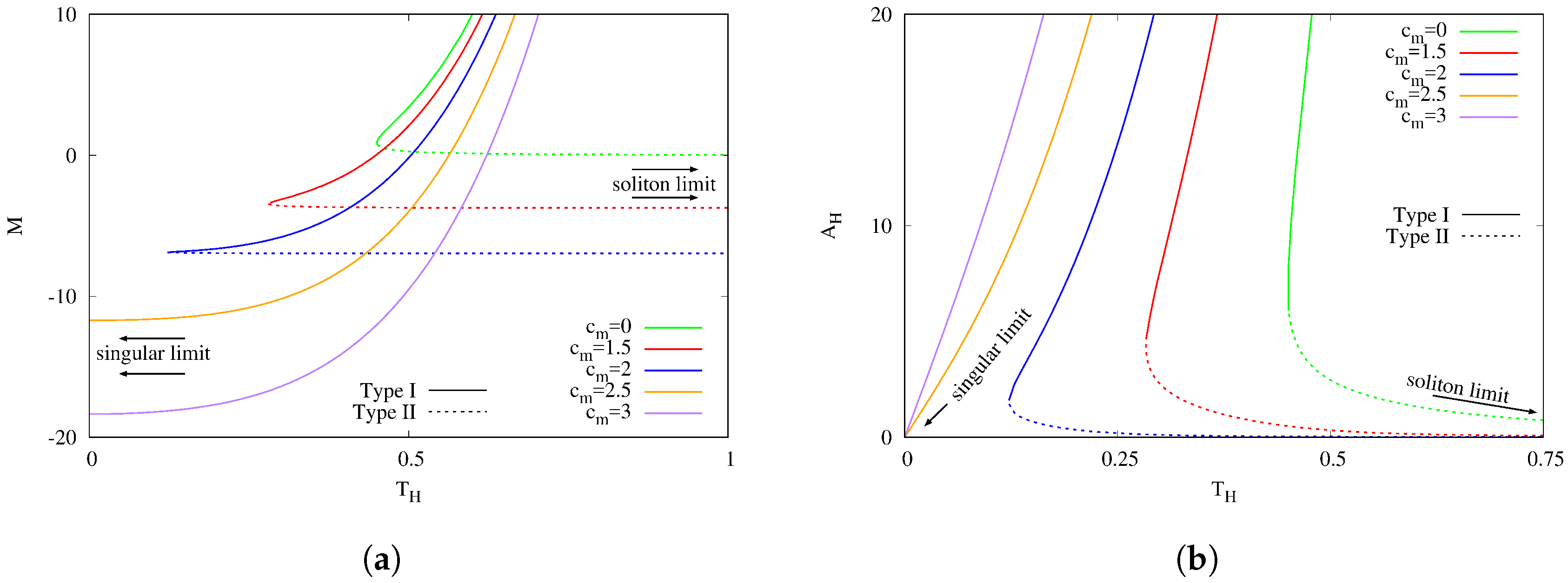
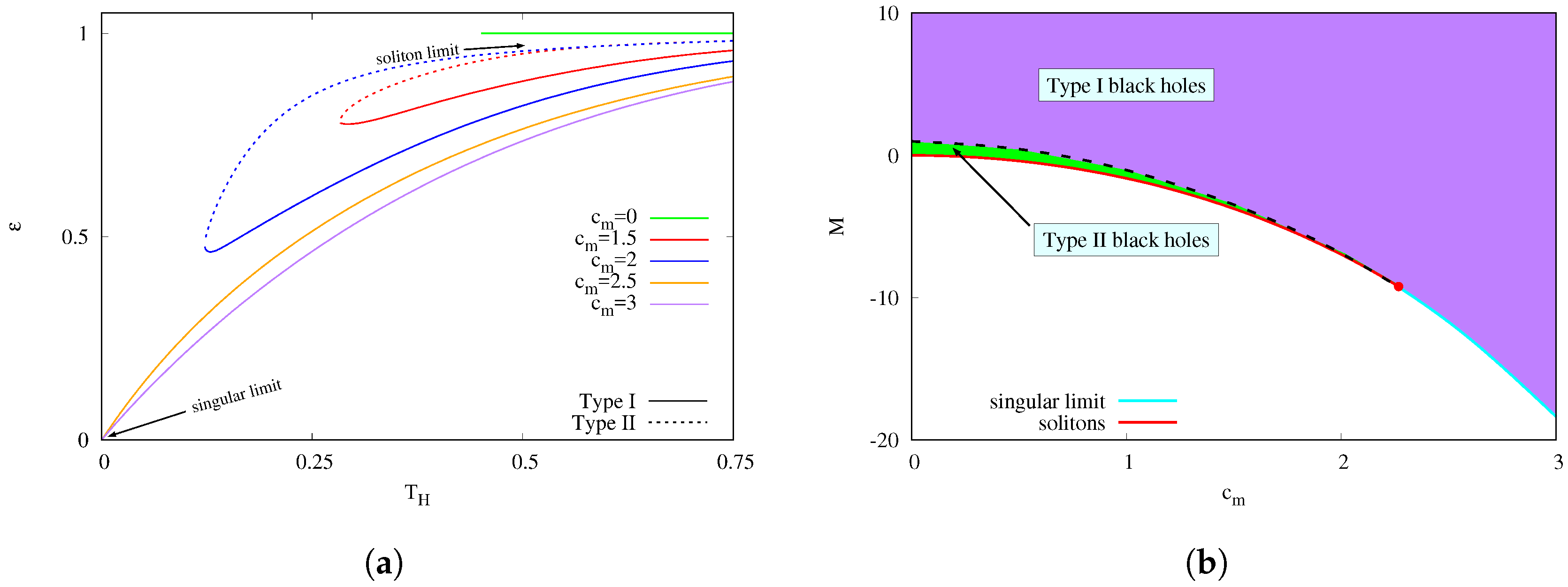
4.2. The Black Holes
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Coleman, S.R. There are no classical glueballs. Commun. Math. Phys. 1977, 55, 113–116. [Google Scholar] [CrossRef]
- Deser, S. Absence of static Einstein-Yang-Mills excitations in three-dimensions. Class. Quant. Grav. 1984, 1, L1. [Google Scholar] [CrossRef]
- Shiromizu, T.; Ohashi, S.; Suzuki, R. A no-go on strictly stationary spacetimes in four/higher dimensions. Phys. Rev. D 2012, 86, 064041. [Google Scholar] [CrossRef]
- Boutaleb-Joutei, H.; Chakrabarti, A.; Comtet, A. Gauge field configurations in curved space-times. Phys. Rev. D 1979, 20, 1884. [Google Scholar] [CrossRef]
- Van der Bij, J.J.; Radu, E. Gravitating sphalerons and sphaleron black holes in asymptotically anti-de Sitter space-time. Phys. Rev. D 2001, 64, 064020. [Google Scholar] [CrossRef]
- Hooft, G. Magnetic monopoles in unified gauge theories. Nucl. Phys. B 1974, 79, 276–284. [Google Scholar] [CrossRef]
- Polyakov, A.M. Particle spectrum in the quantum field theory. JETP Lett. 1974, 20, 430–433. [Google Scholar]
- Hosotani, Y. Scaling behavior in the Einstein-Yang-Mills monopoles and dyons. J. Math. Phys. 2002, 43, 597. [Google Scholar] [CrossRef]
- Bjoraker, J.; Hosotani, Y. Monopoles, dyons and black holes in the four-dimensional Einstein-Yang-Mills theory. Phys. Rev. D 2000, 62, 043513. [Google Scholar] [CrossRef]
- Winstanley, E. Existence of stable hairy black holes in SU(2) Einstein-Yang-Mills theory with a negative cosmological constant. Class. Quant. Grav. 1999, 16, 1963. [Google Scholar] [CrossRef]
- Volkov, M.S.; Gal’tsov, D.V. Non-Abelian Einstein-Yang-Mills black holes. JETP Lett. 1989, 50, 346–350. [Google Scholar]
- Kuenzle, H.P.; Masood-ul-Alam, A.K.M. Spherically symmetric static SU(2) Einstein Yang–Mills fields. J. Math. Phys. 1990, 31, 928. [Google Scholar] [CrossRef]
- Bizon, P. Colored black holes. Phys. Rev. Lett. 1990, 64, 2844. [Google Scholar] [CrossRef] [PubMed]
- Volkov, M.S.; Gal’tsov, D.V. Gravitating non-Abelian solitons and black holes with Yang-Mills fields. Phys. Rep. 1999, 319, 1–83. [Google Scholar] [CrossRef]
- Winstanley, E. Classical Yang-Mills black hole hair in anti-de Sitter space. Lect. Notes Phys. 2009, 769, 49–87. [Google Scholar]
- Herdeiro, C.; Radu, E. Anti-de-Sitter regular electric multipoles: Towards Einstein–Maxwell-AdS solitons. Phys. Lett. B 2015, 749, 393. [Google Scholar] [CrossRef]
- Costa, M.S.; Greenspan, L.; Oliveira, M.; Penedones, J.; Santos, J.E. Polarised Black Holes in AdS. Class. Quant. Grav. 2016, 33, 115011. [Google Scholar] [CrossRef]
- Herdeiro, C.; Radu, E. Einstein–Maxwell-Anti-de-Sitter spinning solitons. Phys. Lett. B 2016, 757, 268. [Google Scholar] [CrossRef]
- Herdeiro, C.A.R.; Radu, E. Static black holes with no spatial isometries in AdS-electrovacuum. Phys. Rev. Lett. 2016, 117, 221102. [Google Scholar] [CrossRef]
- Okuyama, N.; Maeda, K.I. Five-dimensional black hole and particle solution with non-Abelian gauge field. Phys. Rev. D 2003, 67, 104012. [Google Scholar] [CrossRef]
- Radu, E.; Tchrakian, D.H. No hair conjecture, nonAbelian hierarchies and Anti-de Sitter spacetime. Phys. Rev. D 2006, 73, 024006. [Google Scholar] [CrossRef]
- Stotyn, S.; Leonard, C.D.; Oltean, M.; Henderson, L.J.; Mann, R.B. Numerical Boson Stars with a Single Killing Vector I: The D ≥ 5 Case. Phys. Rev. D 2014, 89, 044017. [Google Scholar] [CrossRef]
- Kunz, J.; Navarro-Lérida, F.; Viebahn, J. Charged rotating black holes in odd dimensions. Phys. Lett. B 2006, 639, 362–367. [Google Scholar] [CrossRef]
- Kunz, J.; Navarro-Lérida, F.; Radu, E. Higher dimensional rotating black holes in Einstein–Maxwell theory with negative cosmological constant. Phys. Lett. B 2007, 649, 463–471. [Google Scholar] [CrossRef]
- Clement, G. Classical solutions in three-dimensional Einstein–Maxwell cosmological gravity. Class. Quant. Grav. 1993, 10, L49. [Google Scholar] [CrossRef]
- Hirschmann, E.W.; Welch, D.L. Magnetic solutions to 2+1 gravity. Phys. Rev. D 1996, 53, 5579–5582. [Google Scholar] [CrossRef]
- Cataldo, M.; Salgado, P. Static Einstein–Maxwell solutions in (2+1)-dimensions. Phys. Rev. D 1996, 54, 2971. [Google Scholar] [CrossRef]
- Dias, O.J.C.; Lemos, J.P.S. Rotating magnetic solution in three dimensional Einstein gravity. J. High Energy Phys. 2002. [Google Scholar] [CrossRef]
- Cataldo, M.; Crisostomo, J.; del Campo, S.; Salgado, P. On magnetic solution to 2+1 Einstein–Maxwell gravity. Phys. Lett. B 2004, 584, 123–126. [Google Scholar] [CrossRef]
- Balasubramanian, V.; Kraus, P. A stress tensor for anti-de Sitter gravity. Commun. Math. Phys. 1999, 208, 413–428. [Google Scholar] [CrossRef]
- Das, S.; Mann, R.B. Conserved quantities in Kerr-anti-de Sitter spacetimes in various dimensions. arXiv, 2000; arXiv:hep-th/0008028. [Google Scholar]
- Emparan, R.; Johnson, C.V.; Myers, R.C. Surface terms as counterterms in the AdS/CFT correspondence. Phys. Rev. D 1999, 60, 104001. [Google Scholar] [CrossRef]
- Skenderis, K. Asymptotically Anti-de Sitter space-times and their stress energy tensor. Int. J. Mod. Phys. A 2001, 16, 740–749. [Google Scholar] [CrossRef]
- Taylor, M. More on counterterms in the gravitational action and anomalies. arXiv, arXiv:hep-th/0002125.
- Blázquez-Salcedo, J.L.; Kunz, J.; Navarro-Lérida, F.; Radu, E. Radially excited rotating black holes in Einstein–Maxwell–Chern–Simons theory. Phys. Rev. D 2015, 92, 044025. [Google Scholar] [CrossRef]
- Blázquez-Salcedo, J.L.; Kunz, J.; Navarro-Lérida, F.; Radu, E. Charged rotating black holes in Einstein–Maxwell–Chern–Simons theory with negative cosmological constant. arXiv, 2016; arXiv:1610.05282. [Google Scholar]
- Ascher, U.; Christiansen, J.; Russell, R.D. A collocation solver for mixed order systems of boundary value problems. Math. Comput. 1979, 33, 659–679. [Google Scholar] [CrossRef]
- Ascher, U.; Christiansen, J.; Russell, R.D. Collocation software for boundary-value ODEs. ACM Trans. 1981, 7, 209–222. [Google Scholar] [CrossRef]
- D’Hoker, E.; Kraus, P. Magnetic Brane Solutions in AdS. arXiv, 2009; arXiv:0908.3875. [Google Scholar]
- D’Hoker, E.; Kraus, P. Charged Magnetic Brane Solutions in AdS5 and the fate of the third law of thermodynamics. arXiv, 2010; arXiv:0911.4518. [Google Scholar]
- Ammon, M.; Leiber, J.; Macedo, R.P. Phase diagram of 4D field theories with chiral anomaly from holography. J. High Energy Phys. 2016, 1603, 164. [Google Scholar] [CrossRef]

© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Blázquez-Salcedo, J.L.; Kunz, J.; Navarro-Lérida, F.; Radu, E. Static Einstein–Maxwell Magnetic Solitons and Black Holes in an Odd Dimensional AdS Spacetime. Entropy 2016, 18, 438. https://doi.org/10.3390/e18120438
Blázquez-Salcedo JL, Kunz J, Navarro-Lérida F, Radu E. Static Einstein–Maxwell Magnetic Solitons and Black Holes in an Odd Dimensional AdS Spacetime. Entropy. 2016; 18(12):438. https://doi.org/10.3390/e18120438
Chicago/Turabian StyleBlázquez-Salcedo, Jose Luis, Jutta Kunz, Francisco Navarro-Lérida, and Eugen Radu. 2016. "Static Einstein–Maxwell Magnetic Solitons and Black Holes in an Odd Dimensional AdS Spacetime" Entropy 18, no. 12: 438. https://doi.org/10.3390/e18120438
APA StyleBlázquez-Salcedo, J. L., Kunz, J., Navarro-Lérida, F., & Radu, E. (2016). Static Einstein–Maxwell Magnetic Solitons and Black Holes in an Odd Dimensional AdS Spacetime. Entropy, 18(12), 438. https://doi.org/10.3390/e18120438





