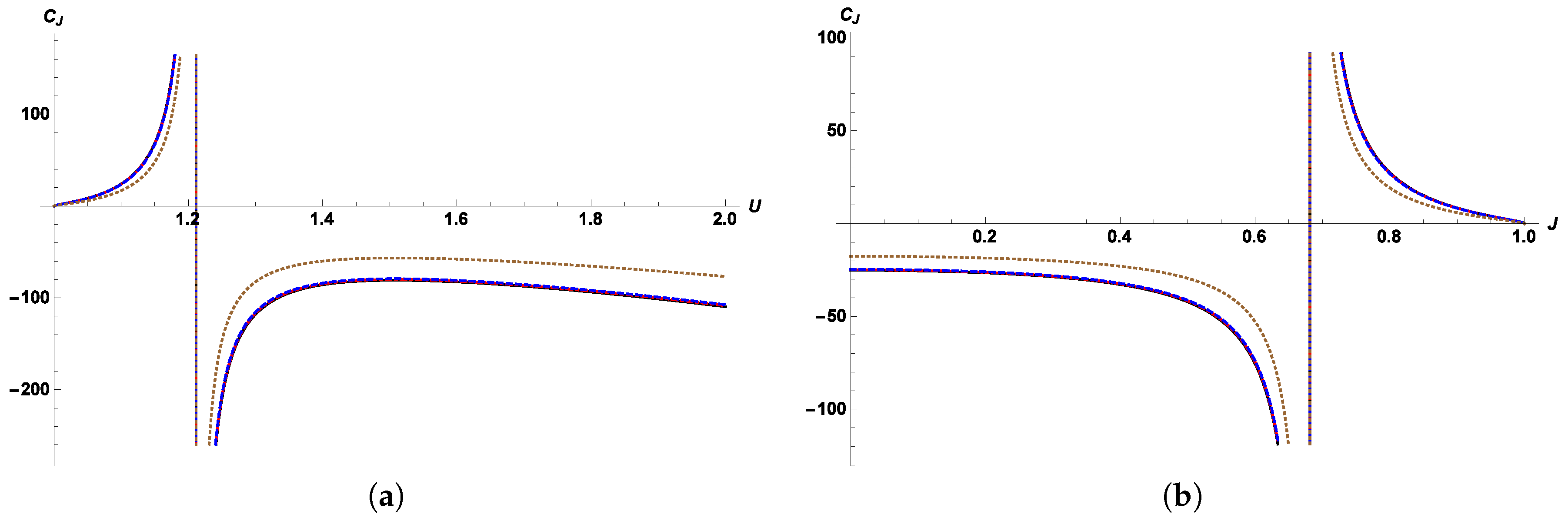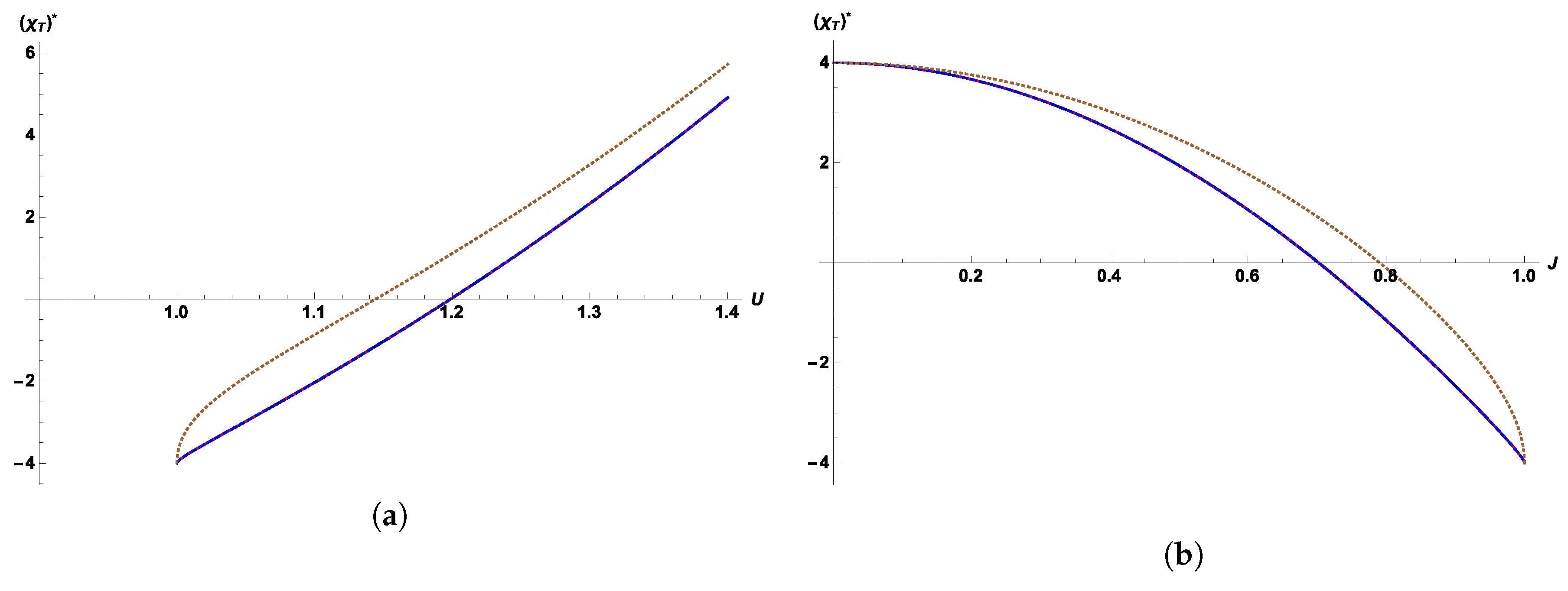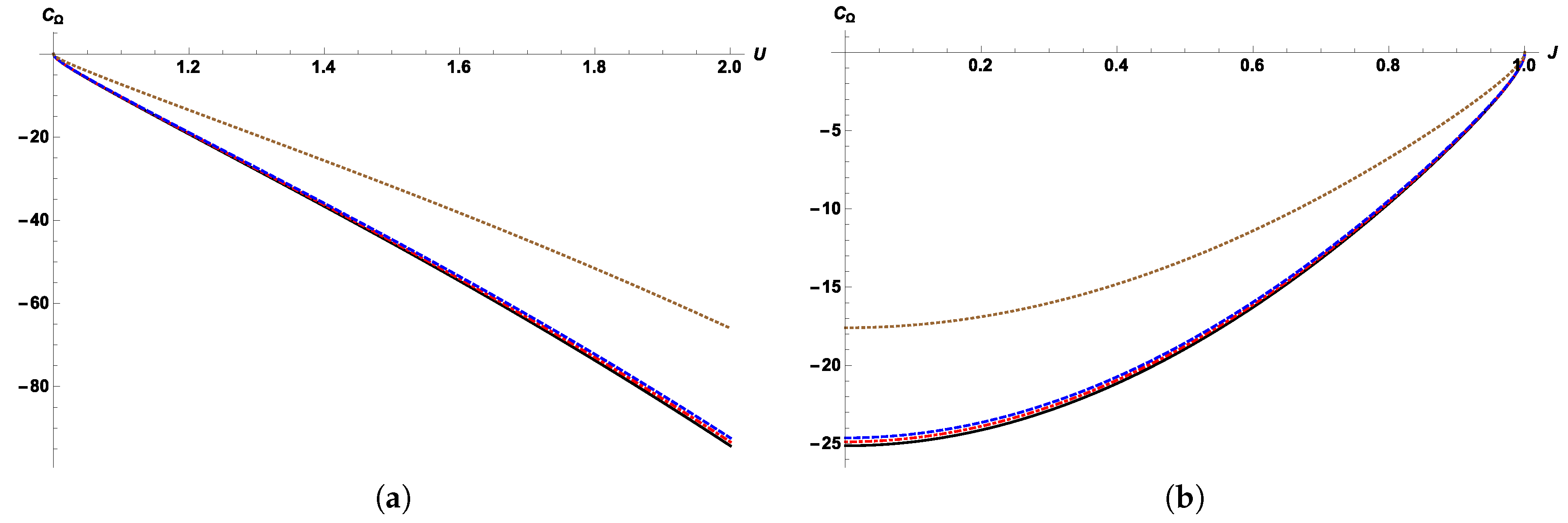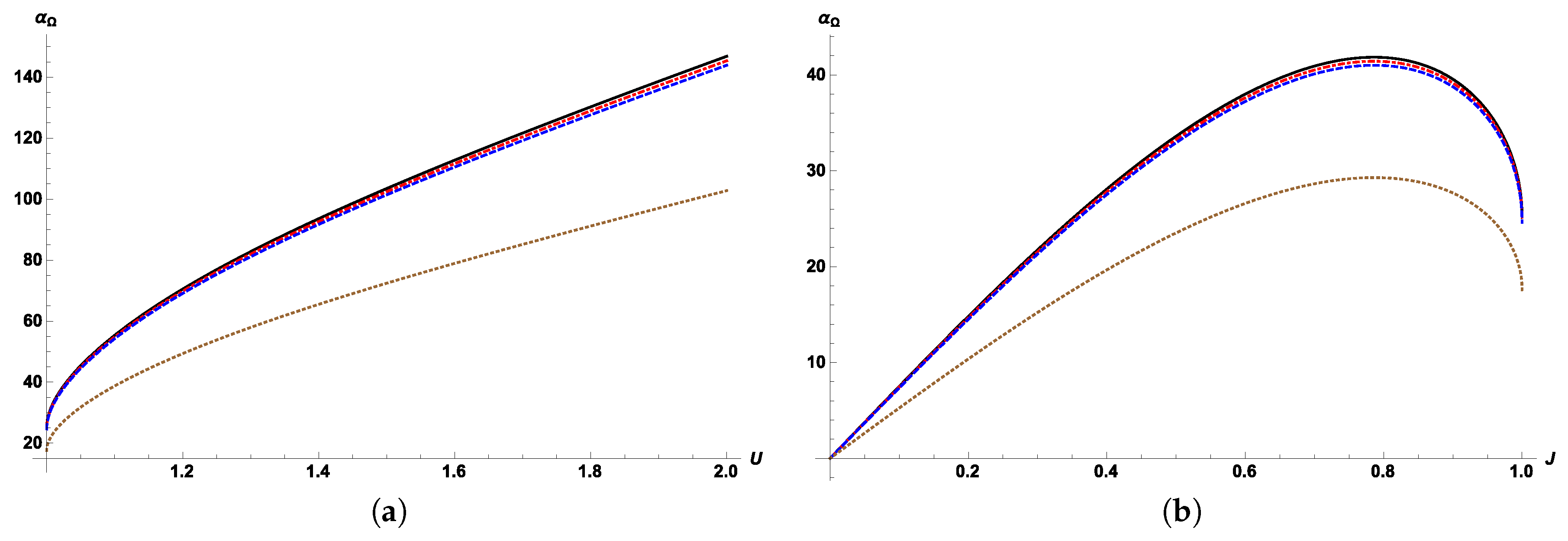1. Introduction
It is known that the classical thermodynamics formalism can be applied to explore the physical entropy of a black hole, using semiclassical approaches to general relativity. The best known of these approximations was proposed by Bekenstein and Hawking in order to solve the so-called information problem [
1,
2,
3,
4]. They found that the area
A of the event horizon of black holes, in an asymptotically-flat spacetime, obeys a simple relation, which is the mathematical analogue of the corresponding entropy for a black hole
(
, Bekenstein–Hawking). The results obtained by Bekenstein and Hawking are supported by quantum field theory in the curved spacetime formalism. This formalism is not able to give a bound for the precision with which distance measurements are made; such a bound presumably must exist, given by the Planck length. One possible way to introduce this bound is by means of the noncommutativity of spacetime. In the context of gravity, noncommutativity is usually introduced using the Seiberg–Witten map, gauging some appropriate group [
5]. More recently, a new proposal to introduce an effective noncommutativity was considered, deforming the minisuperspace in cosmological models instead of the spacetime manifold, in such a way that its coordinates do not commute [
6]. In this work, the latter formalism will be considered in order to take into account noncommutativity for black holes.
The thermodynamics of black holes has a long history, in particular related to the problem of thermodynamic stability. Since the seminal work of Gibbons and Hawking [
7], it is known that this problem can be extended to black holes in non-asymptotically-flat spacetimes. They found that the thermodynamic information of de Sitter black holes exhibits important differences with respect to black holes on an asymptotically-flat spacetime, which was later corroborated in different works [
8,
9]. They found that such black holes emit radiation with a perfect blackbody spectrum. The temperature of these black holes is determined by their surface gravity, which is the same result obtained for the asymptotically-flat space case. However, in a de Sitter space, a cosmological event horizon also exists, which also emits particles with a temperature proportional to its surface gravity. Therefore, the only way that thermal equilibrium can be achieved is when both surface gravities are equal, which only occurs in a degenerate case of extreme solutions [
10,
11].
Regarding black holes in an AdS (Anti de Sitter) manifold, Hawking and Page [
12] found that thermodynamic stability can be achieved. For this manifold, the gravitational potential produces a confinement for particles with nonzero mass, acting effectively as a cavity of finite volume, where the black hole is contained. Moreover, their heat capacity is positive, which also allows a canonical description of the system. Another motivation to study the thermodynamic stability of black holes is the known relation with the dynamical stability of those systems. For an asymptotically-flat spacetime, Schwarzschild black holes are thermodynamically unstable, but have dynamical stability [
13]. On the other hand, for AdS spacetimes, it is known that thermodynamic and dynamical stability are closely related [
14,
15].
Since we are considering black holes in asymptotically-flat spacetime, it seems legitimate to ask if corrections like the noncommutativity or semiclassical ones are capable of modifying the thermodynamics of black holes in order to have thermodynamically-stable systems.
In [
16,
17,
18], this is postulated to be the fundamental thermodynamic relation for black holes, which contains all thermodynamic information of the system. Under this assumption, its classical thermodynamic formalism is constructed finding that for black holes, the thermodynamic structure of the theory resembles magnetic systems instead of fluids.
As mentioned above, it is well known that for an asymptotically-flat spacetime, the temperature of black holes is proportional to its surface gravity
κ, as
[
1]; this semiclassical result was the key that led to the Bekenstein–Hawking entropy, which is related to the area of its event horizon,
The appropriated metric to describe a rotating black hole is the Kerr one, which can be written as,
where
,
,
and
. The area of the event horizon of a black hole is given by
. Applying the elements of the metric tensor given in Equation (2), the resulting area is:
Substituting in Equation (1), the resulting expression is assumed to be a thermodynamic fundamental relation for Kerr black holes; with
, the internal energy of the system and
J its angular momentum. This relation can be written as [
16],
where
G is the universal gravitational constant,
ℏ is the reduced Planck constant,
c is the speed of light in vacuum and
is the Boltzmann constant. We are interested in the thermodynamic implications of quantum correction to Bekenstein–Hawking (BH) entropy
that have arisen in recent years, in the search for suitable candidates of quantum gravity, namely the quest for understanding microscopic states of black holes [
19,
20]; and the inclusion to black hole entropy of noncommutativity. This is given considering that the coordinates of minisuperspace are noncommutative [
21]. Different corrections to Bekenstein–Hawking entropy have emerged from a variety of approaches in recent years, logarithmic ones are a popular choice among those; arising from quantum corrections to the string theory partition function [
22]. They are related to the low energy or infrared properties of gravity and are also independent of high energy or ultraviolet properties of the theory [
19,
22,
23,
24]. In this work, the selected expression for quantum and noncommutative corrected entropy to work with, which will be denoted as
, is obtained according to the ideas presented in [
21]. Starting from a diffeomorphism between the Kantowski–Sachs cosmological model, which describes a homogeneous, but anisotropic universe [
25], and the Schwarzschild solution, whose line element inside the event horizon
is given by:
where the temporal
t and the spatial
r coordinates swap their role, producing a change on the causal structure of spacetime, i.e., the transformation
is performed and considering the Misner parametrization of the Kantowski–Sachs metric, it follows,
In this parametrization, λ and γ play the role of the Cartesian coordinates in the Kantowski–Sachs minisuperspace. Comparing Equations (5) and (6), it is straightforward to note the correspondence between the components of the metric tensor, in order to identify the functions N, γ and λ. The following step is to obtain the Wheeler–DeWitt (WDW) equation for the Kantowski–Sachs metric given in (6), whose parametrization is related with the Schwarzschild solution given in Equation (5), finding the corresponding Hamiltonian of the system H through the Arnowitt–Deser–Misner (ADM) formalism, to introduce it into the quantum wave equation , where is the wave function. This process leads to the WDW equation whose solution can be found by the separation of the variables.
We are interested in the solution that can be obtained when the symplectic structure of minisuperspace is modified, making the coordinates
λ and
γ obey the commutation relation
, where
θ is the noncommutative parameter; this relation strongly resembles noncommutative quantum mechanics. The aforementioned deformation can be introduced in terms of a Moyal product, modifying the original phase space, similarly to noncommutative quantum mechanics [
26]:
These modifications allow us to redefine the coordinates of minisuperspace in order to obtain a noncommutative version of the WDW equation,
where
is the momentum on coordinate
γ. The above equation can be solved by the separation of the variables to obtain the corresponding wave function [
6]:
where
ν is the separation constant and
are the modified Bessel functions. It can be noticed that in Equation (8), the wave function has the form
; therefore, the dependence on the coordinate
γ is the one of a plane wave. It is worth mentioning that this contribution vanishes when thermodynamic observables are calculated.
With the above wave equation for the noncommutative Kantowski–Sachs cosmological model, we are able to derive a modified noncommutative version of the entropy. For that purpose, the Feynman–Hibbs procedure is considered in order to calculate the partition function of the system [
27]. In this approach, the separated differential equation for
λ,
is considered, and the exponential in the potential term
of this equation is expanded up to second order in
λ; with a change of variables, the resulting differential equation can be compared with the corresponding equation for a quantum harmonic oscillator in one dimension, which is a non-degenerate quantum system. In the Feynman–Hibbs procedure, the potential is modified by the quantum effects, which in the case of the harmonic oscillator is given by:
where
is the mean value of
x and
stands for the second derivative of the potential. For the considered changes of variables, the noncommutative quantum corrected potential can be written as,
The above potential allows us to calculate the canonical partition function of the system,
where
is proportional to the Bekenstein–Hawking temperature and
is a constant. Substituting
into (11) and performing the integral over
x, the partition function is given by:
through this partition function, it is possible to calculate any thermodynamic observable, by means of the usual thermodynamic relations for the internal energy and the Legendre transformation for Helmholtz free energy,
With the equation for internal energy, it is possible to determine the value of
β as a function of the Hawking temperature
, obtaining:
and with the aid of this relation and the Legendre transformation for Helmholtz free energy along with the partition function
, the entropy for the noncommutative quantum corrected black hole can be found:
The functional form of noncommutative quantum black hole entropy
is basically the same as the quantum corrected one, besides the addition of multiplicative factor
to Bekenstein–Hawking entropy. For the sake of simplicity, we denote the noncommutative term in this expression as:
Through the rest of this paper, natural units will be considered.
In this work, the previous result found for the Schwarzschild noncommutative black hole will be extended to the rotating black hole case. This extension is not straightforward, since it requires obtaining an analog expression for the noncommutative entropy of the rotating black hole, through the application of a diffeomorphism between the Kerr metric and some appropriated cosmological model, and (for instance) for the procedure presented in [
21], to our knowledge, the implementation of this procedure has not been reported. However, it would be interesting to have an expression to study the effect of angular momentum on the physical properties of the system. Therefore, in order to have an approximated relation for the extended Kerr black hole entropy, the usual Bekenstein–Hawking entropy for rotating black holes, presented in Equation (4), and the generalized one found in Equation (14) will be used to obtain an entropy for rotating black holes including quantum and noncommutative effects. Starting from the fact that Equation (14) is correct, whatever be the expression for the non-approximated entropy for the quantum noncommutative Kerr black hole, it is clear that our proposed entropy will be a good approximation for small values of
J when compared to the values of
. Therefore, in this approximation in the vicinity of small values of angular momentum, the coordinates of the minisuperspace, namely
λ and
γ, are the same as in the Schwarzschild case. Hence, the corrected entropy that we will analyze is:
It is important to clarify that Equation (15) is not the only possible valid generalization for the corrected entropy of the Kerr black hole in the neighborhood of small
J. We claim that this is the most natural one, since this is the natural extension from the Schwarzschild case to the rotating one. To our knowledge, there is not a general argument to claim that Equation (14) remains valid for any black hole, other than the Schwarzschild one. However, there is some evidence (not yet published) that for the case of charged black holes with quantum corrections, the functional form of Equation (14) is maintained. In the following, all of the thermodynamic expressions with super-index ★ will stand up for the noncommutative quantum corrected quantities derived from corresponding
entropy, and quantities without sub-indexes or super-indexes will represent their noncommutative Bekenstein–Hawking counterparts. It is known from observational data that the noncommutative parameter in spacetime is small [
28,
29]; however, for entropy
, noncommutativity on the coordinates of minisuperspace is considered instead. It is expected that such parameter will be small, as well [
30]; nonetheless, the actual bounds of
θ are not well known yet.
In this work, the parameter Γ will be considered to be bounded in the interval given by
. As mentioned above, Equation (15) will be assumed as a fundamental thermodynamic relation for Kerr black holes when noncommutative and quantum corrections are considered. It is well known from classical thermodynamics that fundamental thermodynamic relations contain all thermodynamic information of the system under study [
31]; as a consequence, modifications on thermodynamic information originated by the introduced corrections to entropy are carried through all thermodynamic quantities.
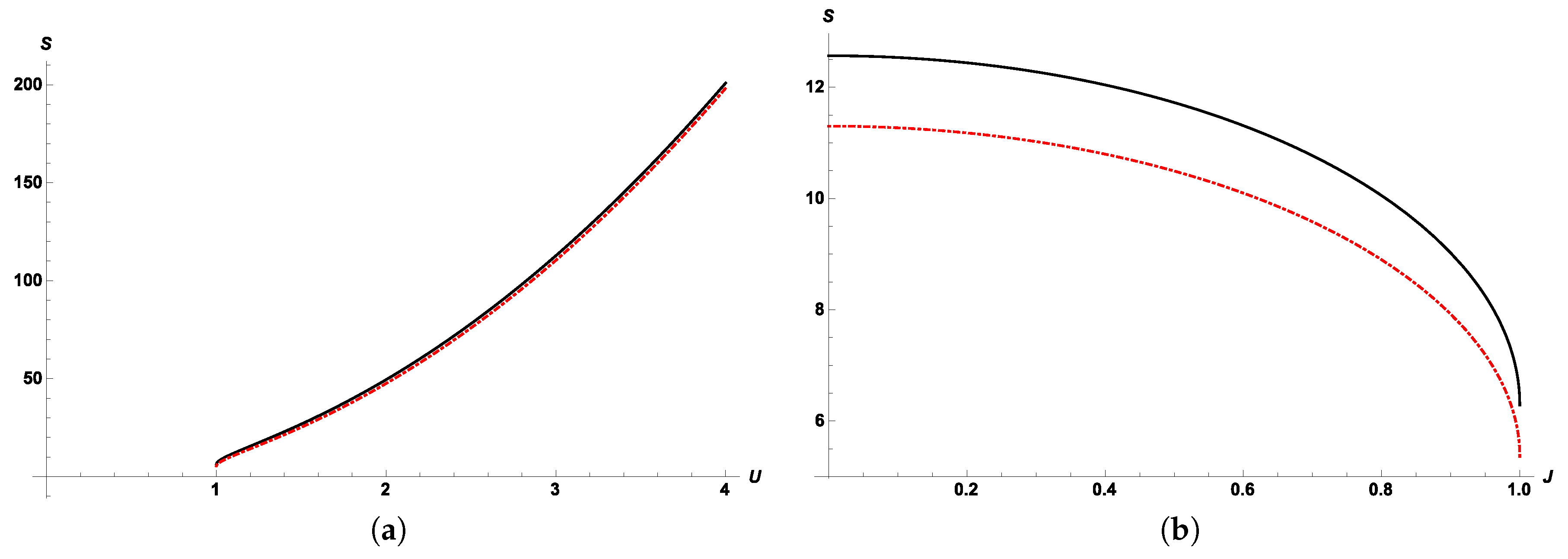
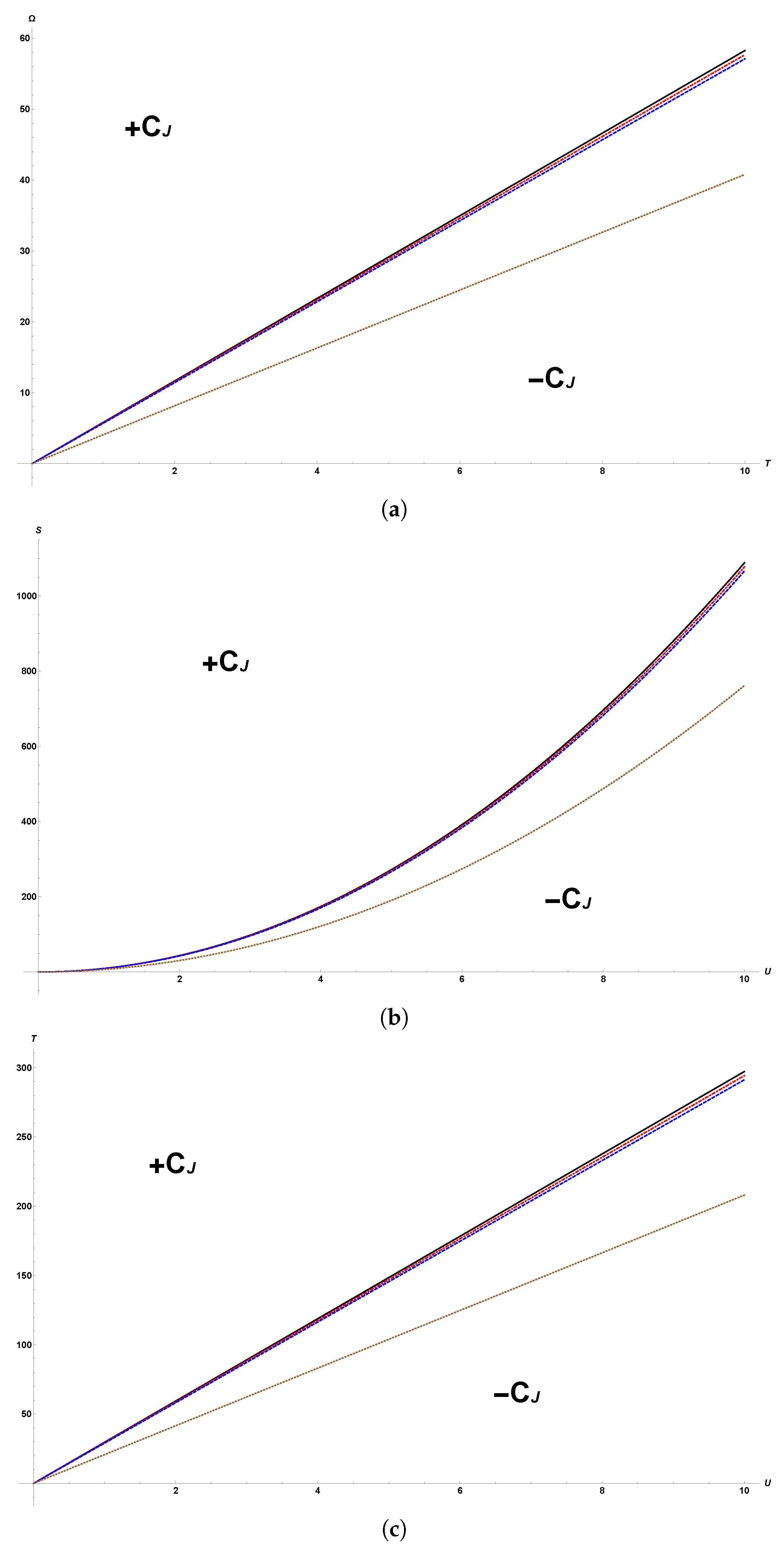
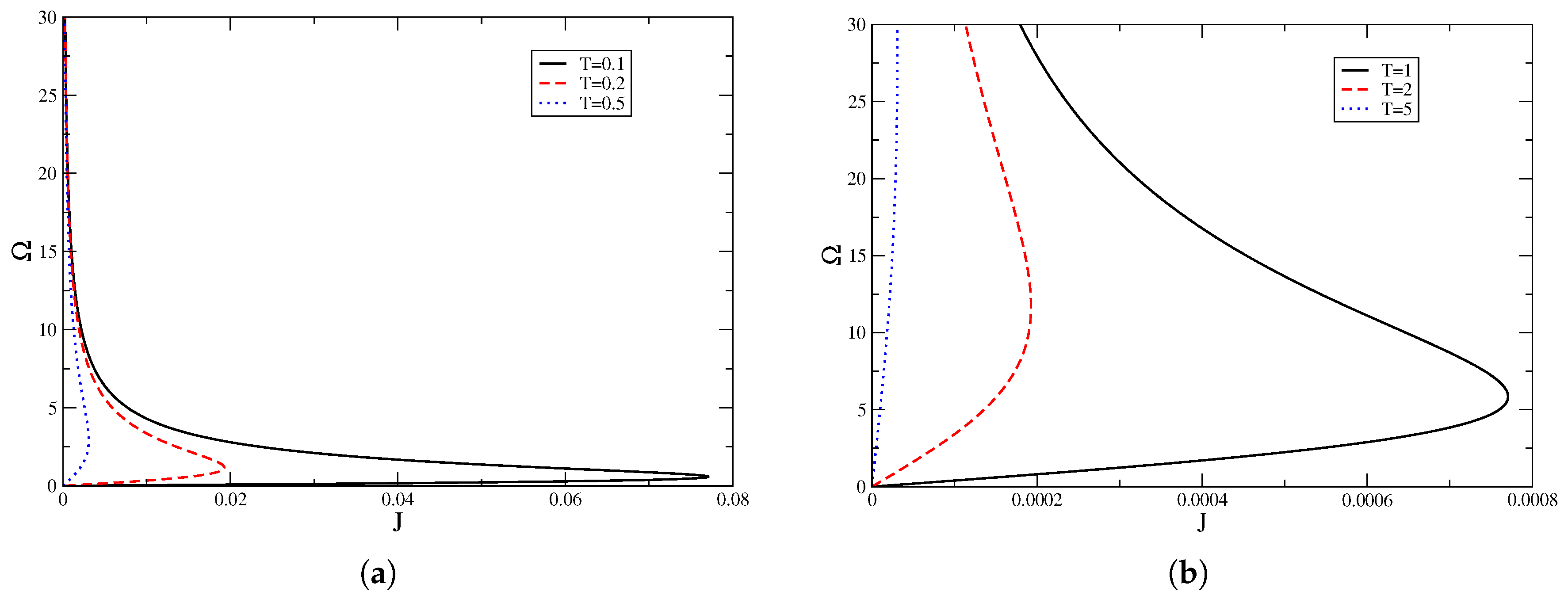
In
Figure 1, curves for Bekenstein–Hawking and quantum corrected entropy are presented considering only commutative relations (
).
Figure 1a considers plots for
and
. Bekenstein–Hawking entropy is above the quantum correction one, including the region of small energy where entropy is thermodynamically stable [
18].
Figure 1b shows the same entropy as a function of angular momentum instead, for fixed values of
U; it can be noticed that Bekenstein–Hawking entropy is above
in all of the considered dominion, as well. A similar analysis can be performed over noncommutativity, finding that for small values of
θ, variations over
S and
are negligible.
The goal of this manuscript is to explore how these considerations introduced into Bekenstein–Hawking entropy change the thermodynamic information contained in this new fundamental relation, in particular thermodynamic stability and the existence of thermodynamic phase transition for these systems. In the following, an outline of this work is presented.
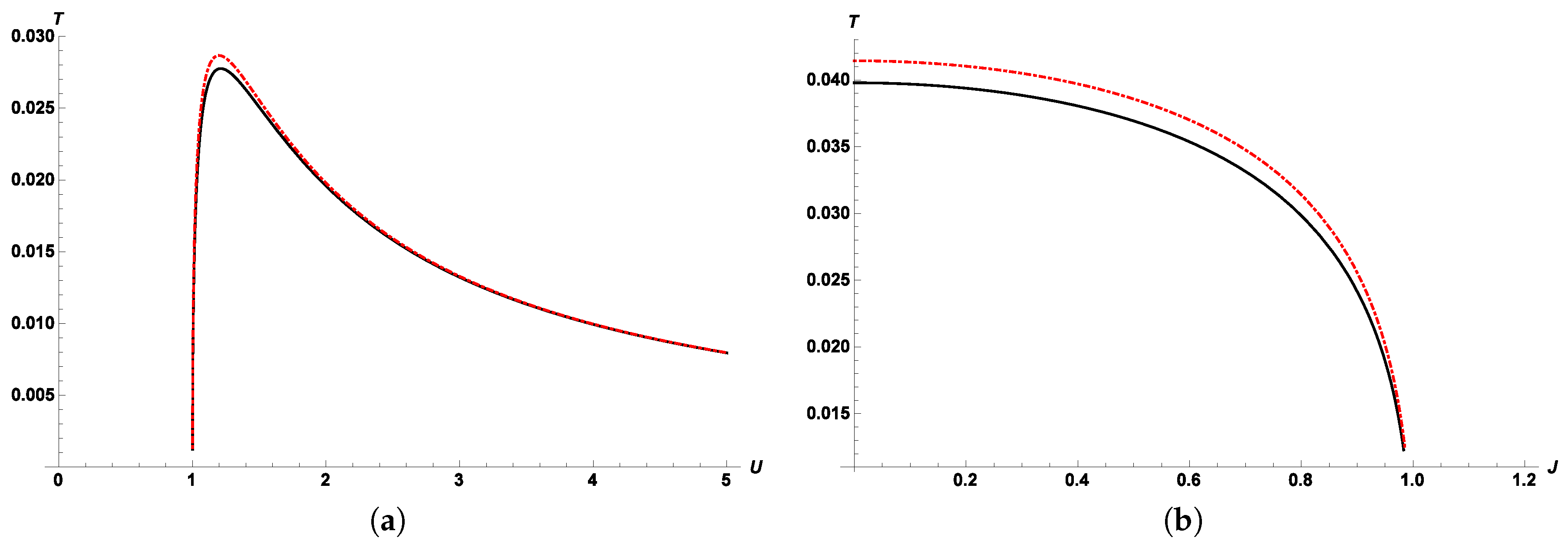
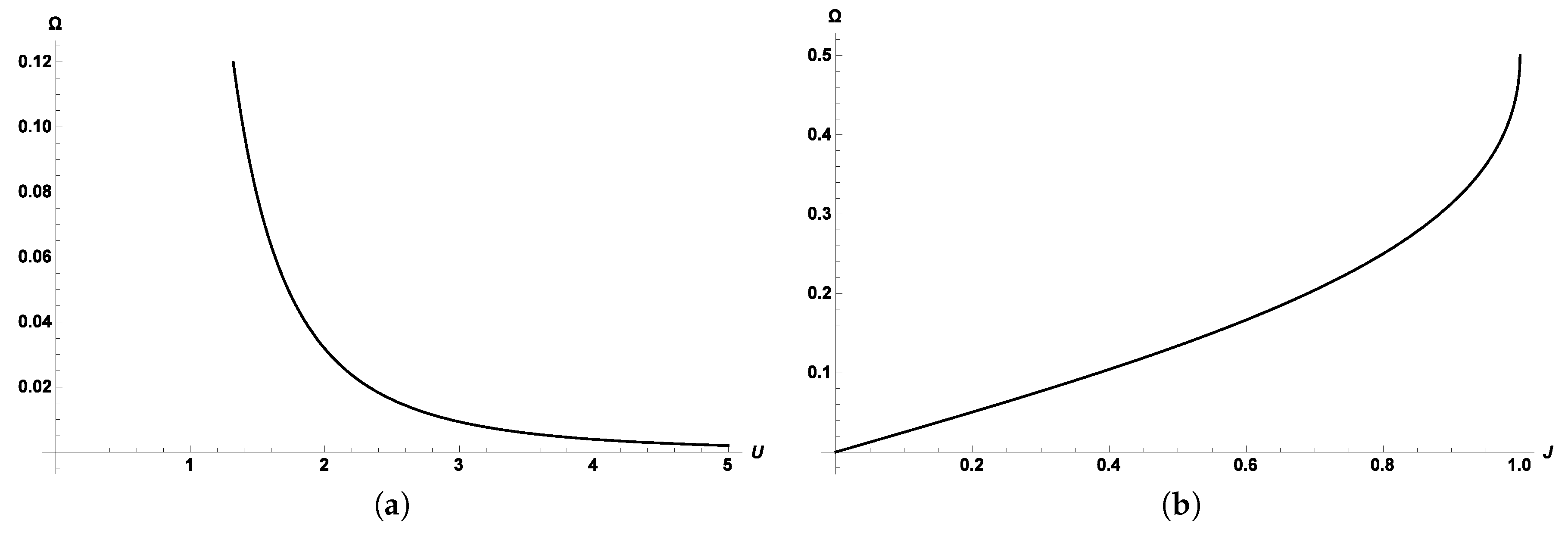
Section 2 examines the different thermodynamic equations of state and their behavior when considering the aforementioned modifications to entropy. The same analysis is carried out in
Section 3.1, considering thermodynamic response functions instead. In
Section 3.2, a discussion of thermodynamic stability and phase transitions for Kerr black holes is presented. Some conclusions of this work are given in
Section 4.