Texture Segmentation Using Laplace Distribution-Based Wavelet-Domain Hidden Markov Tree Models
Abstract
:1. Introduction
2. Previous Works
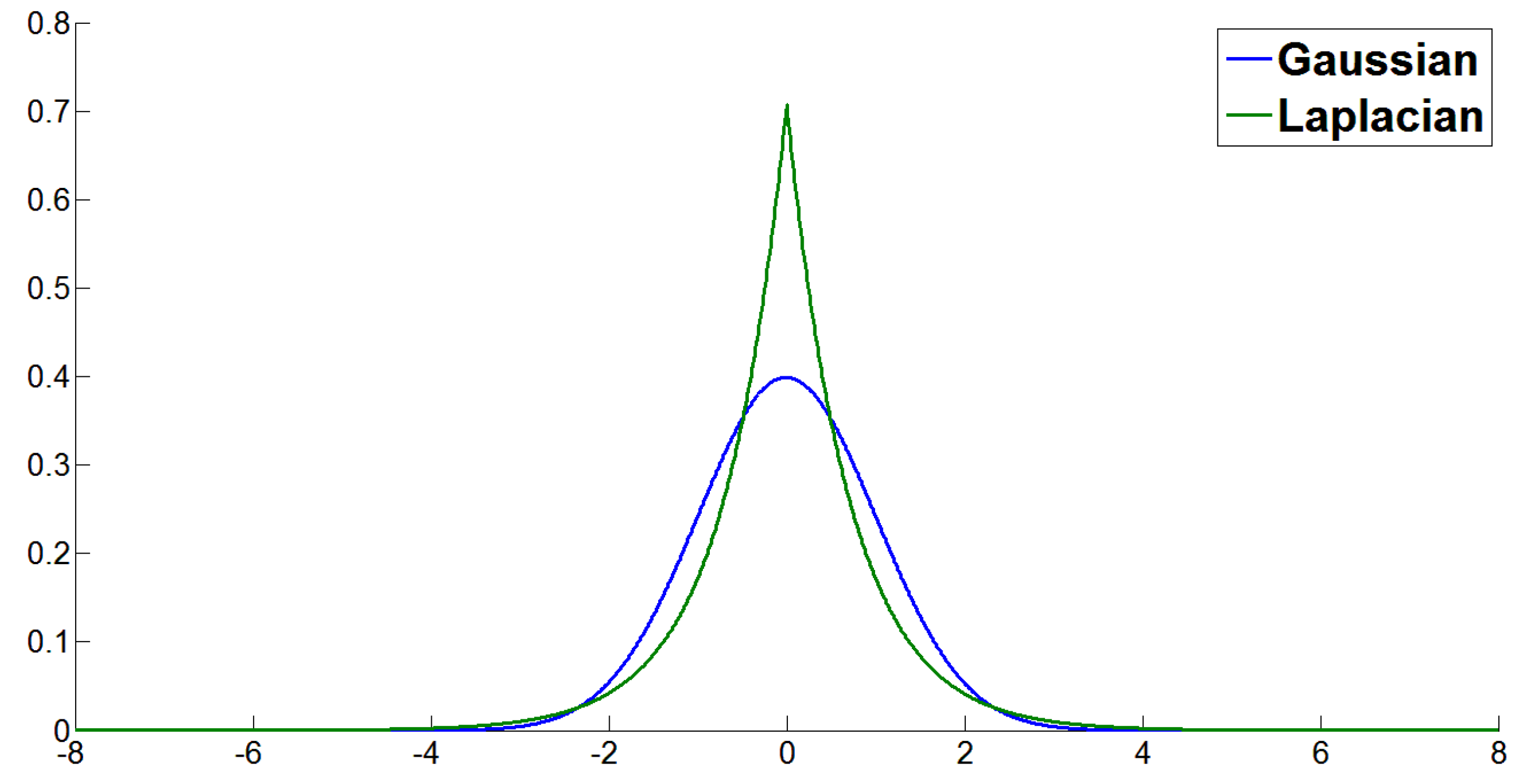
2.1. Laplacian Distribution
2.2. HMT Models
2.3. EM Algorithm
- E step: Computes the conditional expectation of the complete log-likelihood, given the observed data and the current estimate as follows:
- M step: Update the parameters by maximizing the function:
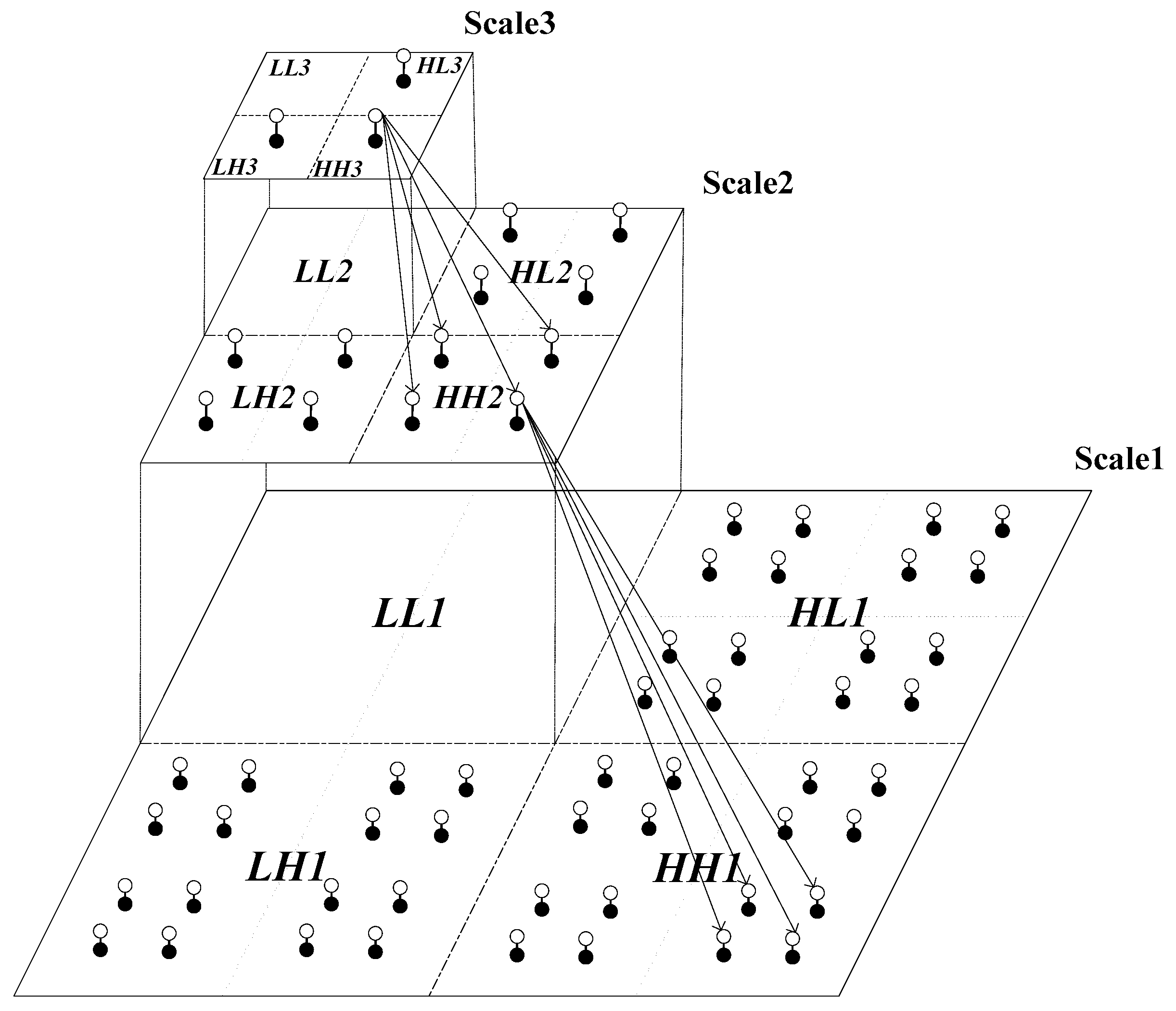
2.4. HMT Based Texture Segmentation
2.4.1. Raw Maximum Likelihood Segmentation
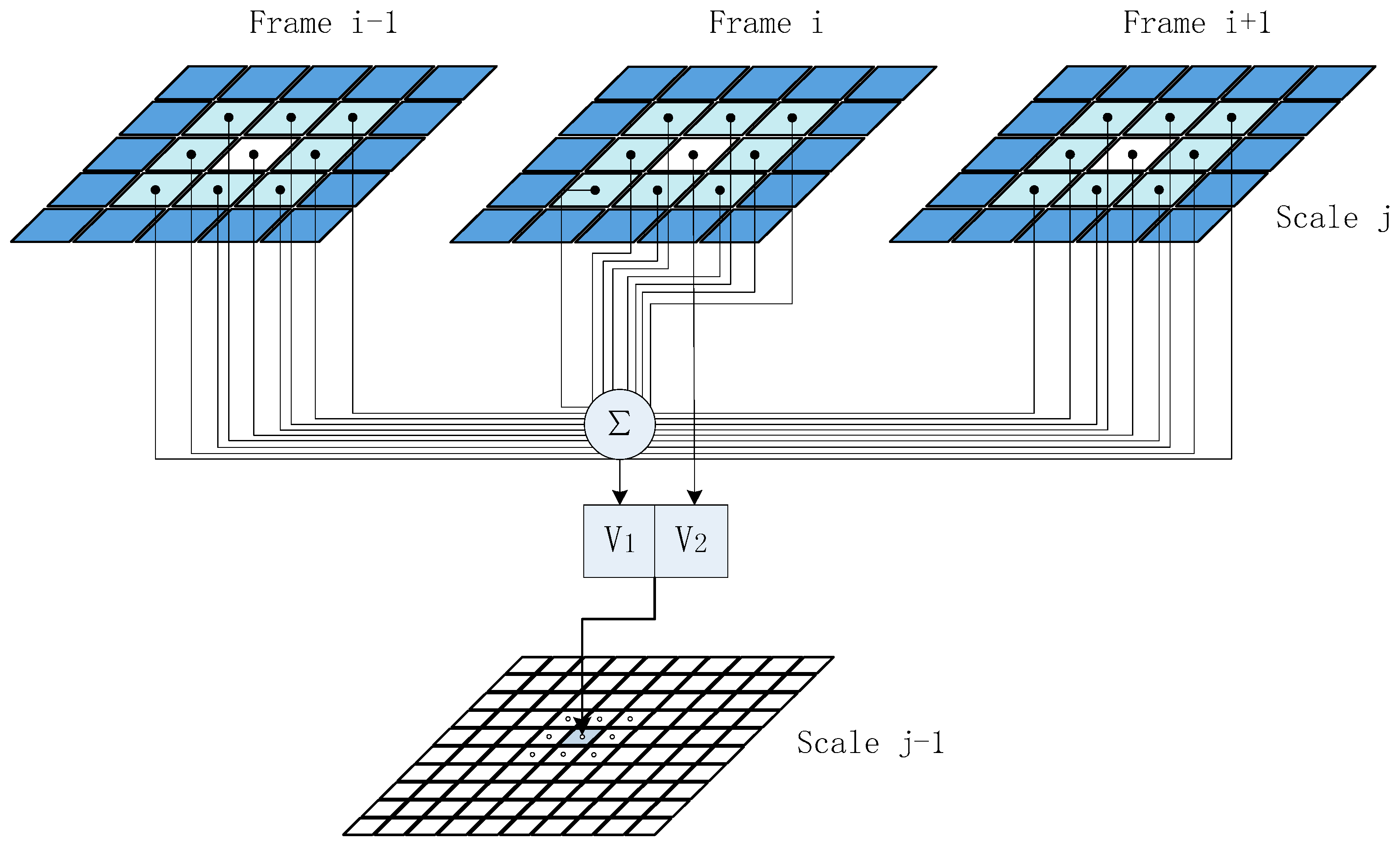
2.4.2. Context-Based Multiscale Fusion
2.4.3. Pixel-Level Segmentation
3. LMM-HMT Based Description of Texture
3.1. LMM Based HMT Model
- The probability of the state at the root node in the coarsest scale
- The state transition probability is:It is the conditional probability that is in state given state variable is the parent state of ;
- The scale parameter , given .
3.2. Parameter Estimation
3.3. Pixel-Level Texture Description
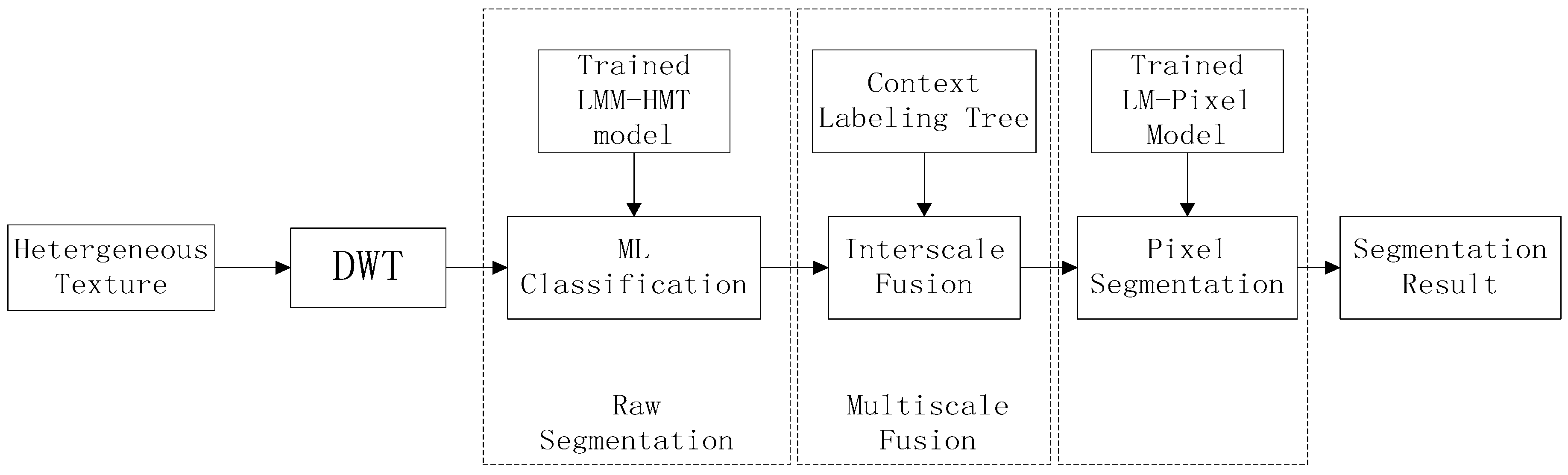
4. Texture Segmentation
- (1)
- Model training. For each texture class, we train the wavelet domain LMM-HMT model with the homogeneous texture samples by using EM algorithm as the Section 3.2, and obtain the model parameters , in which c denotes the cth texture class. Meanwhile, the pixel-level multivariate Laplace mixture model parameters are gotten with Equations (19)–(24).
- (2)
- Raw maximum likelihood segmentation. For a heterogeneous texture to be segmented, the likelihood of each subtree at different scale can be computed by using the HMT likelihood computation method and the Equation (7). The raw segmentation at the coarest scale is accomplished by using Equation (5) with the trained LMM-HMT model parameters .
- (3)
- Context-based multiscale fusion. At the scale j, the context vectors s are constructed from the segmentation label at scale j + 1. The segmentation result is obtained by using EM algorithm and maximizing the contextual posterior distribution as the work [13].
- (4)
- Pixel-level segmentation. Compute the likelihood of each pixel with the trained pixel-level multivariate Laplace mixture models. Perform the context-based fusion scheme from the scale j = 1 to the pixel-level as the step (3). The output is the final segmentation result.
4.1. Image Texture Segmentation
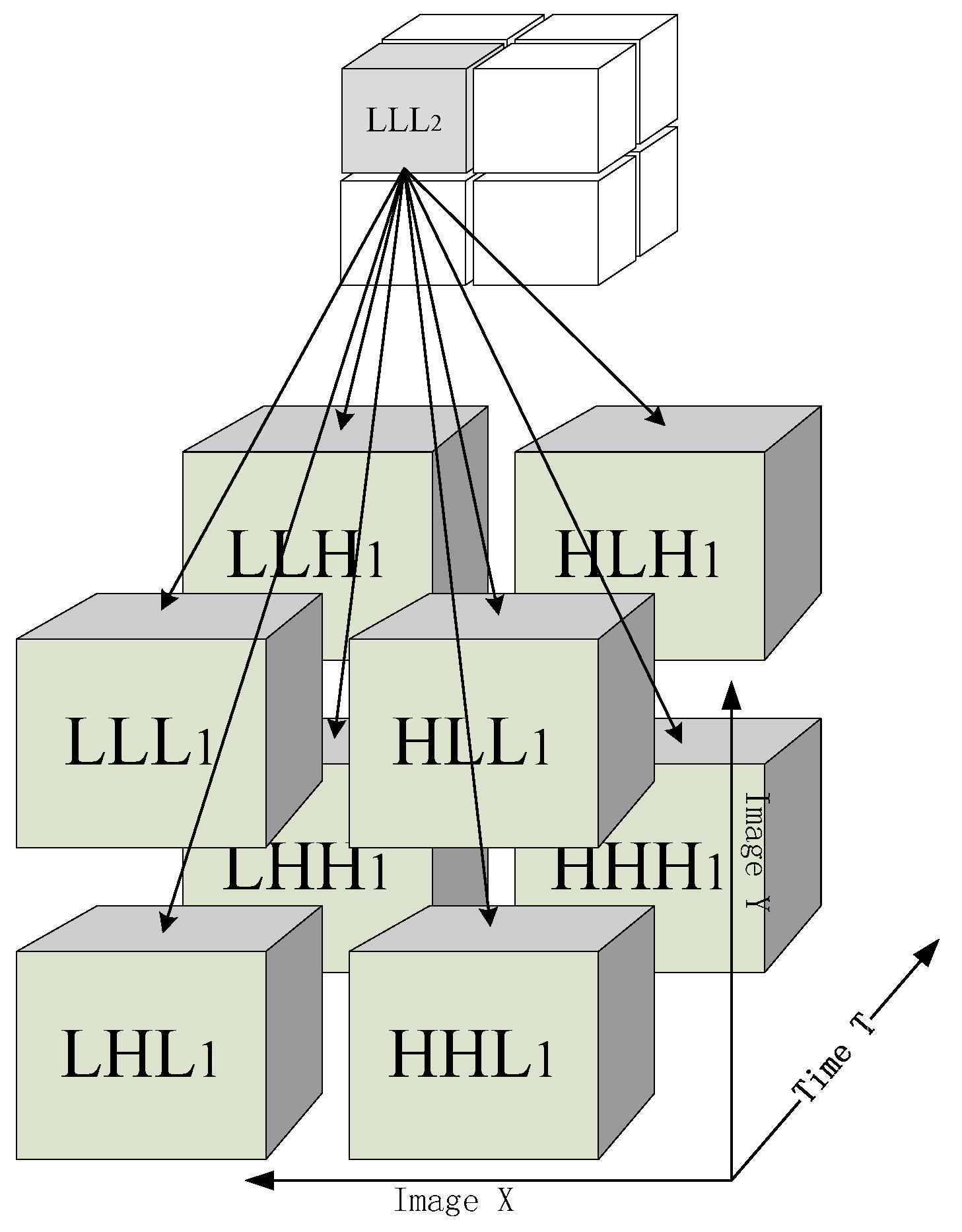
4.2. Dynamic Texture Segmentation
5. Experimental Results
5.1. Image Texture Segmentation
5.2. Dynamic Texture Segmentation
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Chen, J.; Zhao, G.Y.; Salo, M.; Rahtu, E.; Pietikainen, M. Automatic dynamic texture segmentation using local descriptors and optical flow. IEEE Trans. Image Proc. 2013, 22, 326–339. [Google Scholar] [CrossRef] [PubMed]
- Qiao, Y.L.; Weng, L.X. Hidden Markov model based dynamic texture classification. IEEE Signal Proc. Lett. 2015, 22, 509–512. [Google Scholar] [CrossRef]
- Wang, L.; Liu, J. Texture classification using multiresolution Markov random field models. Pattern Recognit. Lett. 1999, 20, 171–182. [Google Scholar] [CrossRef]
- Qiao, Y.L.; Wang, F.S. Wavelet-based dynamic texture classification using Gumbel distribution. Math. Probl. Eng. 2013, 2013, 762472. [Google Scholar] [CrossRef]
- Nelson, J.D.B.; Nafornta, C.; Isar, A. Semi-local scaling exponent estimation with box-penalty constraints and total-variation regularization. IEEE Trans. Image Proc. 2016, 25, 3167–3181. [Google Scholar] [CrossRef] [PubMed]
- Pustelnik, N.; Wendt, H.; Abry, P.; Dobigeon, N. Combining Local Regularity Estimation and Total Variation Optimization for Scale-Free Texture Segmentation. 2015; arXiv:1504.05776. [Google Scholar]
- Arbelaez, P.; Maire, M.; Fowlkes, C.; Malik, J. Contour detection and hierarchical image segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2011, 33, 898–916. [Google Scholar] [CrossRef] [PubMed]
- Yuan, J.; Wang, D.; Cheriyadat, A.M. Factorization-based texture segmentation. IEEE Trans. Image Proc. 2015, 24, 3488–3496. [Google Scholar] [CrossRef] [PubMed]
- Sasidharan, R.; Menaka, D. Dynamic texture segmentation of video using texture descriptors and optical flow of pixels for automating monitoring in different environments. In Proceedings of the International Conference on Communication and Signal Processing, Melmaruvathur, India, 3–5 April 2013; pp. 841–846.
- Crouse, M.S.; Nowak, R.D.; Baraniuk, R.G. Wavelet-based statistical signal processing using hidden Markov models. IEEE Trans. Signal Proc. 1998, 46, 886–902. [Google Scholar] [CrossRef]
- Romberg, J.K.; Choi, H.; Baraniuk, R.G. Bayesian tree-structured image modeling using wavelet-domain hidden Markov models. IEEE Trans. Signal Proc. 2001, 10, 1056–1068. [Google Scholar] [CrossRef] [PubMed]
- Durand, J.B. Computational methods for hidden Markov tree models—An application to wavelet trees. IEEE Trans. Signal Proc. 2004, 52, 2551–2560. [Google Scholar] [CrossRef]
- Choi, H.; Baraniuk, R.G. Multiscale image segmentation using wavelet-domain hidden Markov Models. IEEE Trans. Signal Proc. 2001, 10, 1309–1321. [Google Scholar] [CrossRef] [PubMed]
- Ye, W.; Zhao, J.H.; Wang, S.; Wang, Y.; Zhang, D.Y.; Yuan, Z.Y. Dynamic texture based smoke detection using Surfacelet transform and HMT model. Fire Saf. J. 2015, 73, 91–101. [Google Scholar] [CrossRef]
- Wang, X.Y.; Sun, W.W.; Wu, Z.F.; Yang, H.Y.; Wang, Q.Y. Color image segmentation using PDTDFB domain hidden Markov tree model. Appl. Soft Comput. 2015, 29, 138–152. [Google Scholar] [CrossRef]
- Teodoro, A.; Bioucas-Dias, J.; Figueiredo, M. Image Restoration and Reconstruction Using Variable Splitting and Class-Adapted Image Priors. 2016; arXiv.1602.04052. [Google Scholar]
- Hajri, H.; Ilea, I.; Said, S.; Bombrun, L.; Berthoumieu, Y. Riemannian Laplace distribution on the space of symmetric positive definite matrices. Entropy 2016, 18, 98. [Google Scholar] [CrossRef]
- Nath, V.K.; Mahanta, A. Image denoising based on Laplace distribution with local parameters in Lapped transform domain. In Proceedings of the International Conference on Signal Processing and Multimedia Applications, Seville, Spain, 18–21 July 2011; pp. 1–6.
- Figueiredo, M.; Bioucas-Dias, J.; Nowak, R. Majorization-minimization algorithms for wavelet-based image restoration. IEEE Trans. Image Proc. 2007, 16, 2980–2991. [Google Scholar] [CrossRef]
- Huda, A.R.; Nadia, J.A. Some Bayes’ estimators for Laplace distribution under different loss functions. J. Babylon Univ. 2014, 22, 975–983. [Google Scholar]
- Bishop, C.M. Pattern Recognition and Machine Learning; Springer: New York, NY, USA, 2006. [Google Scholar]
- Dempster, A.P.; Laird, N.M.; Rubin, D.B. Maximum-likelihood from incomplete data via the EM algorithm. J. R. Stat. Soc. Ser. B 1977, 39, 1–38. [Google Scholar]
- Song, X.M.; Fan, G.L. Unsupervised Bayesian image segmentation using wavelet-domain hidden Markov models. In Proceedings of the International Conference on Image Processing, Barcelona, Spain, 14–17 September 2003; pp. 423–426.
- Brauer, S. A Probabilistic Expectation Maximization Algorithm for Multivariate Laplacian Mixtures. Master’s Thesis, Paderborn University, Paderborn, Germany, 2014. [Google Scholar]
- Brodatz, P. Textures: A Photographic Album for Artists & Designers; Dover: New York, NY, USA, 1966. [Google Scholar]
- Péteri, R.; Fazekas, S.; Huiskes, M.J. DynTex: A comprehensive database of dynamic textures. Pattern Recognit. Lett. 2010, 31, 1627–1632. [Google Scholar] [CrossRef]
- The DynTex Database. Available online: http://dyntex.univ-lr.fr/index.html (accessed on 26 October 2016).
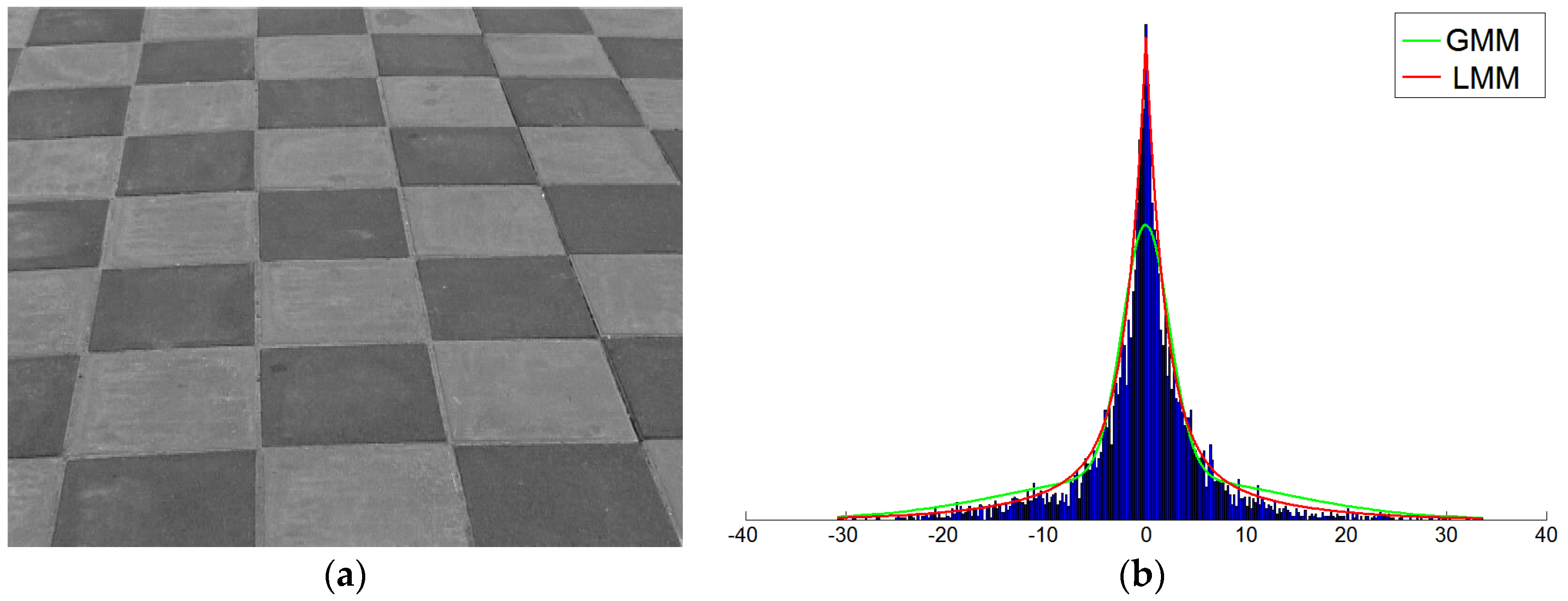










| Texture | GMM-HMT | LMM-HMT | Factorization [8] | LMM-HMT with LM-Pixel |
|---|---|---|---|---|
| IT1 | 95.17 | 95.34 | 97.52 | 96.21 |
| IT2 | 96.56 | 97.29 | 96.80 | 97.42 |
| IT3 | 94.32 | 94.65 | 92.43 | 95.04 |
| IT4 | 96.01 | 96.23 | 95.23 | 96.37 |
| Texture | GMM-HMT | LMM-HMT with LM-Pixel |
|---|---|---|
| IT5 | 93.55 | 94.74 |
| IT6 | 93.64 | 93.82 |
| IT7 | 93.37 | 93.56 |
| IT8 | 95.44 | 94.79 |
| IT9 | 90.28 | 89.14 |
| IT10 | 65.29 | 66.73 |
| Texture | GMM-HMT | LMM-HMT | |||||||
|---|---|---|---|---|---|---|---|---|---|
| GM-Pixel | LM-Pixel | ||||||||
| Max | Min | Avg | Max | Min | Avg | Max | Min | Avg | |
| DT1 | 97.41 | 92.97 | 94.92 | 97.29 | 91.52 | 96.11 | 97.45 | 93.56 | 96.43 |
| DT2 | 97.33 | 90.31 | 95.23 | 96.57 | 95.43 | 95.96 | 96.85 | 96.24 | 96.31 |
| DT3 | 98.14 | 94.98 | 97.19 | 98.92 | 94.85 | 97.06 | 98.78 | 95.80 | 97.63 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qiao, Y.; Zhao, G. Texture Segmentation Using Laplace Distribution-Based Wavelet-Domain Hidden Markov Tree Models. Entropy 2016, 18, 384. https://doi.org/10.3390/e18110384
Qiao Y, Zhao G. Texture Segmentation Using Laplace Distribution-Based Wavelet-Domain Hidden Markov Tree Models. Entropy. 2016; 18(11):384. https://doi.org/10.3390/e18110384
Chicago/Turabian StyleQiao, Yulong, and Ganchao Zhao. 2016. "Texture Segmentation Using Laplace Distribution-Based Wavelet-Domain Hidden Markov Tree Models" Entropy 18, no. 11: 384. https://doi.org/10.3390/e18110384
APA StyleQiao, Y., & Zhao, G. (2016). Texture Segmentation Using Laplace Distribution-Based Wavelet-Domain Hidden Markov Tree Models. Entropy, 18(11), 384. https://doi.org/10.3390/e18110384





