1. Introduction
In most equipment faults gradually aggravate. It is very important to achieve equipment fault trend prediction by analyzing the equipment vibration signals, in order to perform early fault diagnosis and provide timely maintenance which can avoid catastrophic failures. This paper applies the FBM random model to study the prediction of the bearing slow faults.
At present the ways of predicting equipment faults are mainly of two types: one is based on statistics and has some knowledge about faults. Then the fault information is extracted from the vibration noise and a prediction model is built by setting a fault threshold [
1,
2]. In [
3,
4,
5], the authors extracted feature information from faults, then used neural networks, fuzzy algorithms and SVM to make fault predictions. However, using these methods it is probably difficult to extract the weak faults, and any improvement of the prediction precision always needs a large number of samples, which is hard to achieve in practice. The main idea of this paper is to achieve the self-similarity between the random signal and the actual signal by a stochastic model used to predict the random vibration signals which contain the fault information.
Many years ago, scholars had put forward the concept of self-similarity and LRD characteristics of network traffic [
6,
7], but traditional models such as the Poisson process, Markov modulated Poisson process (MMPP) can only handle the problem with short-range dependence (SRD). Therefore, some LRD models, such as fractional Gaussian noise (FGN), fractional Brown motion (FBM) and fractional auto-regressive integrated moving average (FARIMA) models are presented as the network business model [
8]. In recent year, the scholars have predicted the traffic trends and optimized the network configuration by an LRD model, so that we can further evaluate the network performance and improve the utilization of network resources. Thence, the research on LRD properties and models has become a key challenge in various technical fields.
Rolling element bearings are one of the most critical components to determine machinery health and its remaining lifetime in modern production equipment, so bearing incipient weak fault diagnosis and health condition trend prediction should be the emphasis [
9]. In early weak faults, the vibration signal is not only generally very weak, and typically non-linear and non-stationary, but also the implied impulse components are weaker and often submerged in strong noise, so the traditional analysis methods such as Fast Fourier Transform (FFT), envelope detection, wavelet analysis, etc. cannot meet the requirements of incipient fault diagnosis [
10,
11,
12]. Thence, the improved minimum entropy deconvolution technique is proposed to search for an optimal set of filter coefficients to highlight the impulse component signal. For fault condition trend prediction, LRD models can describe their slow progress and better reflect the operation conditions of the equipment to realize weak fault trend predictions [
13,
14]. An LRD model−FBM stochastic model is not only applied to network traffic, but also in financial field problems with long memory. In the financial field, scholars have simulated the change process of return of assets based on the stochastic differential equations (SDE) driven by FBM [
15,
16]. Brownian motion (BM) has been applied to the bearing fault prediction [
17], but since FBM is more flexible than BM, which is a special case of FBM for
H = 0.5, our method based on FBM may be more flexible than the BM one. This is a novel approach. Therefore, the paper presents the FBM stochastic model which achieves good results applied in other fields to predict the equipment condition trends and estimate the remaining useful lifetime of bearings.
Most mechanical equipment generates random vibrations and the vibration signals take on the characteristics of stationarity and self−similarity in normal operation, but once a weak fault exists in the equipment, the vibration signals take on non-stationary, non-self−similarity and LRD characteristics. This paper studies the prediction of the bearing fault development by using a FBM stochastic model.
The paper is organized as follows: in
Section 2, we present a method based on MED and envelope spectrum analysis to detect the early weak faults.
Section 3 discusses briefly the LRD properties and analyzes the six methods of Hurst parameter estimation. An algorithm is provided for generating the FBM time series, and the properties and application of the FBM stochastic model are also outlined.
Section 4 gives a case study and verifies the prediction performance of the FBM model. Finally,
Section 5 concludes the paper.
2. Incipient Fault Prediction for Bearings
When early faults appear in rotating machinery, the weak fault information is often submerged in strong noise, so the traditional spectrum analysis is powerless. This has made feature extraction and diagnosis of early weak faults in rotating machinery a difficult topic and hotspot in research. The rolling bearing is regarded as the main research object. For mechanical fault feature extraction and diagnosis, the minimum entropy deconvolution (MED) analysis method is proposed to detect weak faults [
18], and the diagnosis results are verified through the vibration intensity and sample entropy feature parameters. The whole ideas and procedures for the weak fault diagnosis of rotating machinery are shown in the following
Figure 1.
2.1. Minimum Entropy Deconvolution
Minimum entropy deconvolution theory was first used by scholars in the study of seismic waves, and achieved good results. MED is a time-domain blind deconvolution method, that can approximately restore the true signals and improve the SNR of signals.
The basic idea of the MED method is that we need to find a filter to restore the original signal and highlight the impulse components, so that the entropy becomes the smallest. If the system input is
x(
k), through a linear system
h(
n), the output is
z(
k):
Through the surrounding environment and path transmission, it is actually a process of increasing entropy, and we need to find an inverse filter
g(
L). Through filter
g(
L), the output
y(
k) can restore the original input signal
x(
k), this process can be described as given in [
19]:
To restore the original system input x(k), the key is that the filtered signal can restore the original input signal “simple features”, this process minimizes the entropy, so we also call this minimum entropy deconvolution. In the process of the realization of the MED method, the K order cumulant is used as the objective function of the blind deconvolution.
In practical application, we usually set
K for 4 order, which makes the filtered signal’s entropy minimum, and the first derivative of the objective function of the blind deconvolution is zero, so we can obtain:
The k order cumulant is used as the objective function of the blind deconvolution, and the optimal filter is found to minimize the entropy of the filtered signal and to highlight the characteristic signal.
2.2. Extracting Fault Feature in Frequency Domain
To evaluate the performance of the MED method for weak fault diagnosis, it was tested using data from CWRU. Bearing data were collected at 12,000 samples per second, bearing rotation frequency
fr = 29.95 Hz, the inner ring fault’s characteristic frequency
fi = 162 Hz, the outer race’s characteristic frequency
fo = 107 Hz, the rolling element’s characteristic frequency
frs = 141 Hz. Then, the MED maximum cycle number is set to 30, the error is 0.01, FIR filter points is 40, so that we can verify the weak fault diagnostic effect by the MED method.
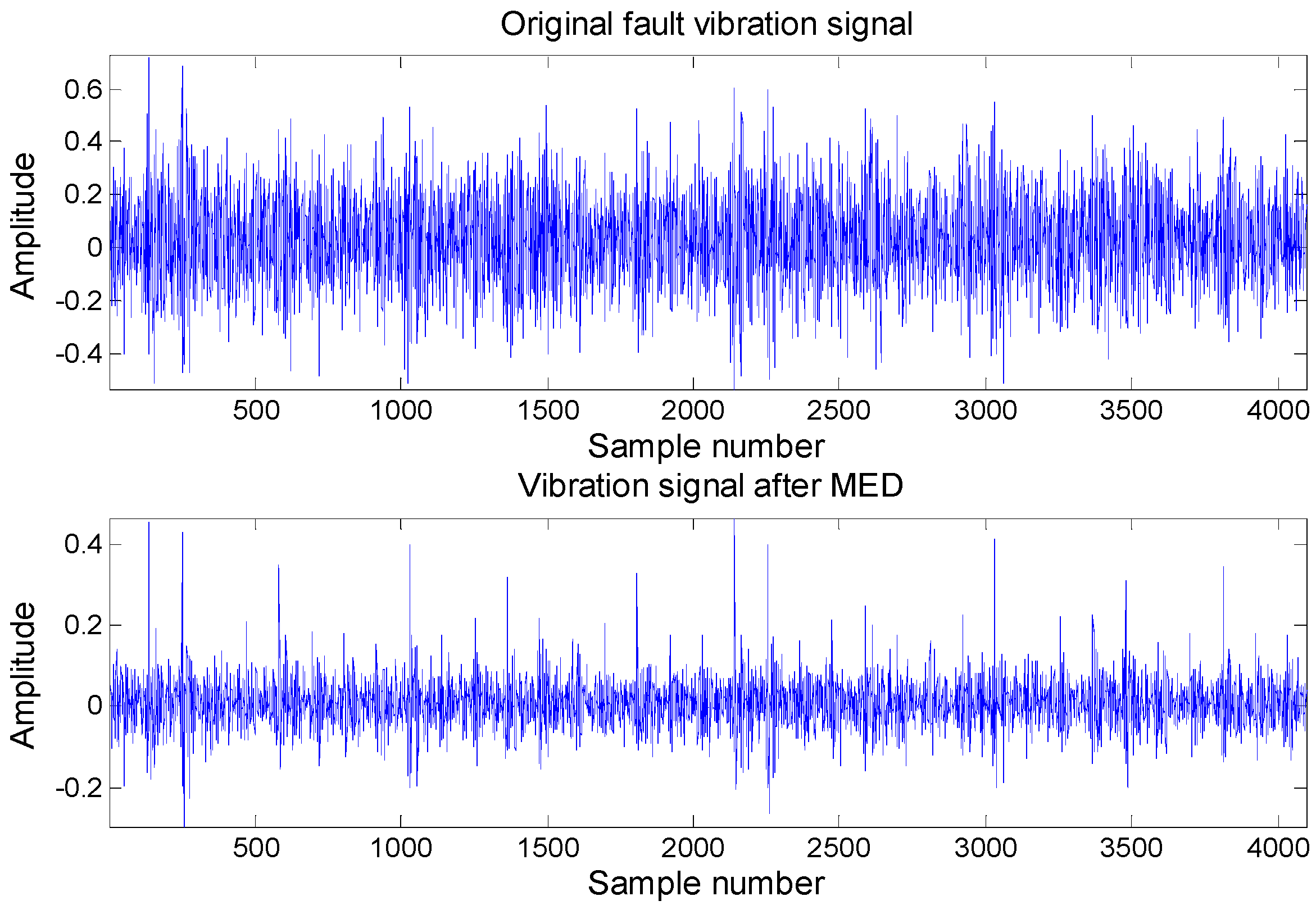
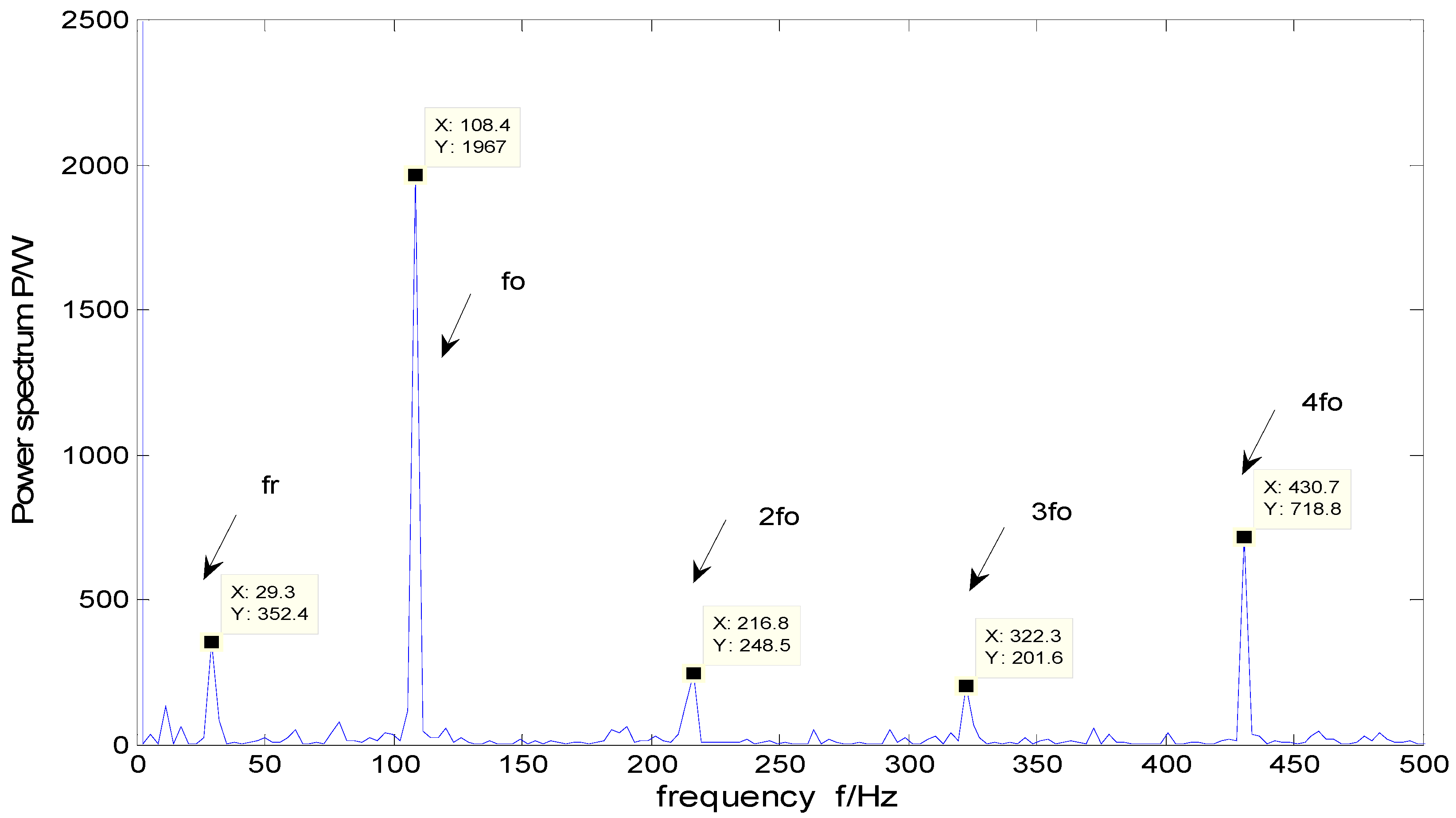
Figure 2 shows the time-domain vibration signal and filtered signal with MED. Combined with the envelope spectrum, the filtered vibration signal envelope spectrum is shown in
Figure 3, from which it can be seen that the envelope spectrum exists at the rotation frequency
fr = 29.95 Hz, outer race fault’s characteristic frequency
fo = 107 Hz, and its twice frequency, triple frequency, four times frequency components. After filtering, the fault characteristic frequency of the signal is more obvious, the rest of the frequency components are almost entirely eliminated, which can accurately realize the fault feature extraction of the outer race.
2.3. Experimental Confirmation
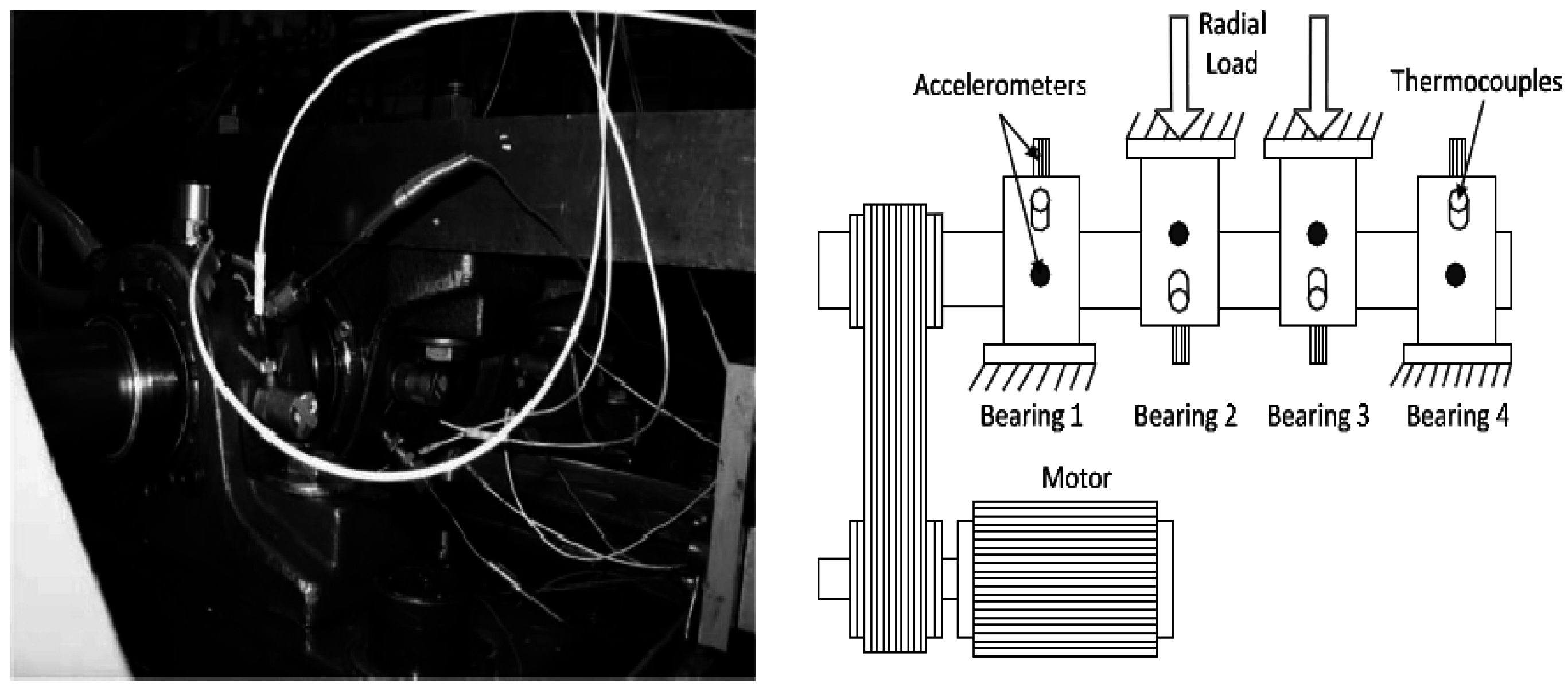
In order to prove the feasibility and validity in weak fault diagnosis and condition monitoring of utilizing the MED, the actual data from accelerated life tests of rolling bearings generated by the NSF I/UCR Center for Intelligent Maintenance Systems with support from Rexnord Corp. (Milwaukee, WI, USA) is used. Four Rexnord ZA-2115 double row bearings were installed on the shaft as shown in
Figure 4. The shaft is driven by an AC motor and coupled by rub belts. Accelerometers were installed on the bearing housing. Four thermocouples were attached to the outer race of each bearing to record the temperature for the purpose of monitoring the lubrication. The sampling rate set at 20 kHz and the data length is 204,800 points. At the end of the test-to-failure experiment, outer race failure occurred in bearing 1. The whole period lasted about 8 days, which is divided into eight representative stages.
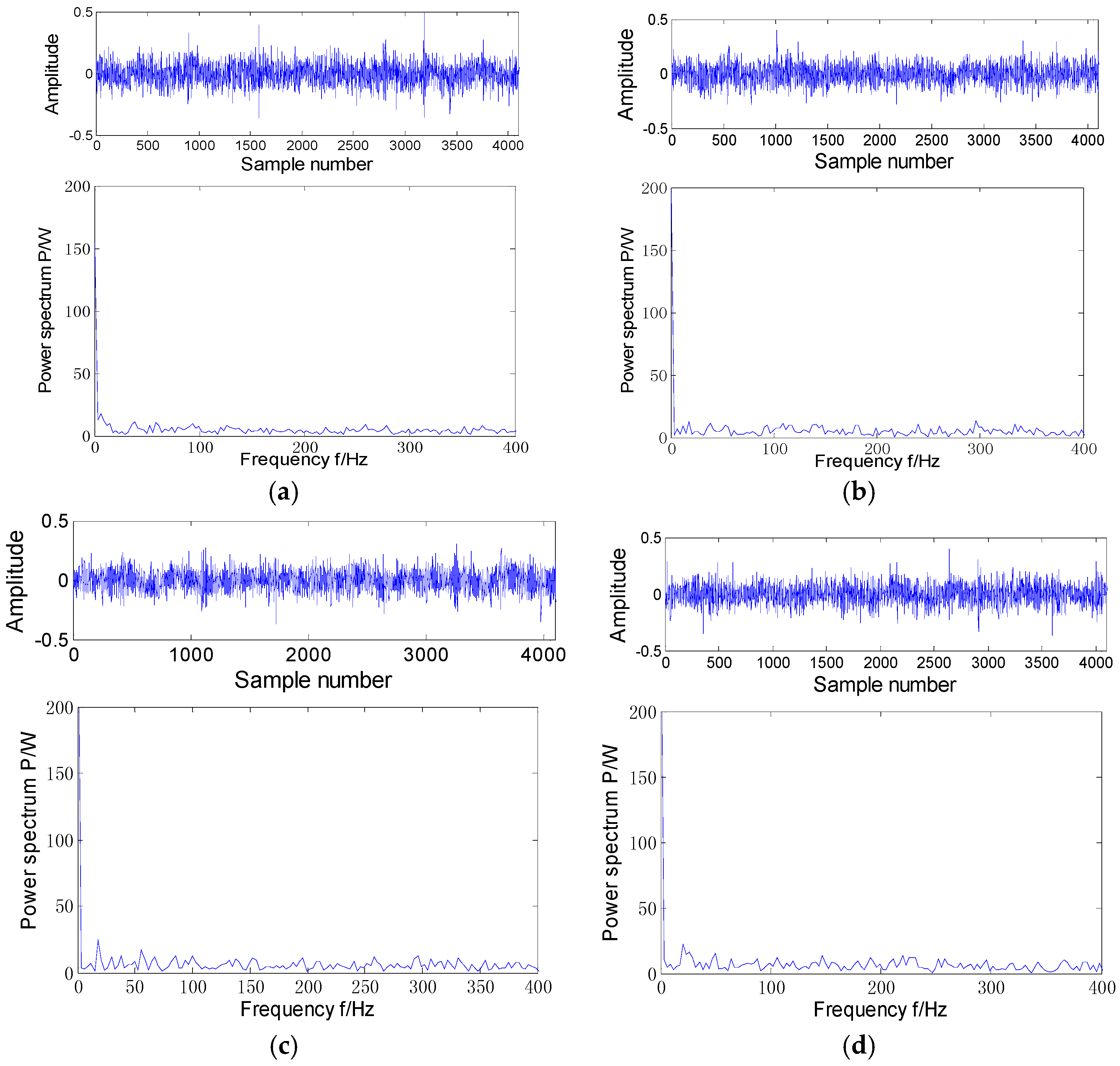
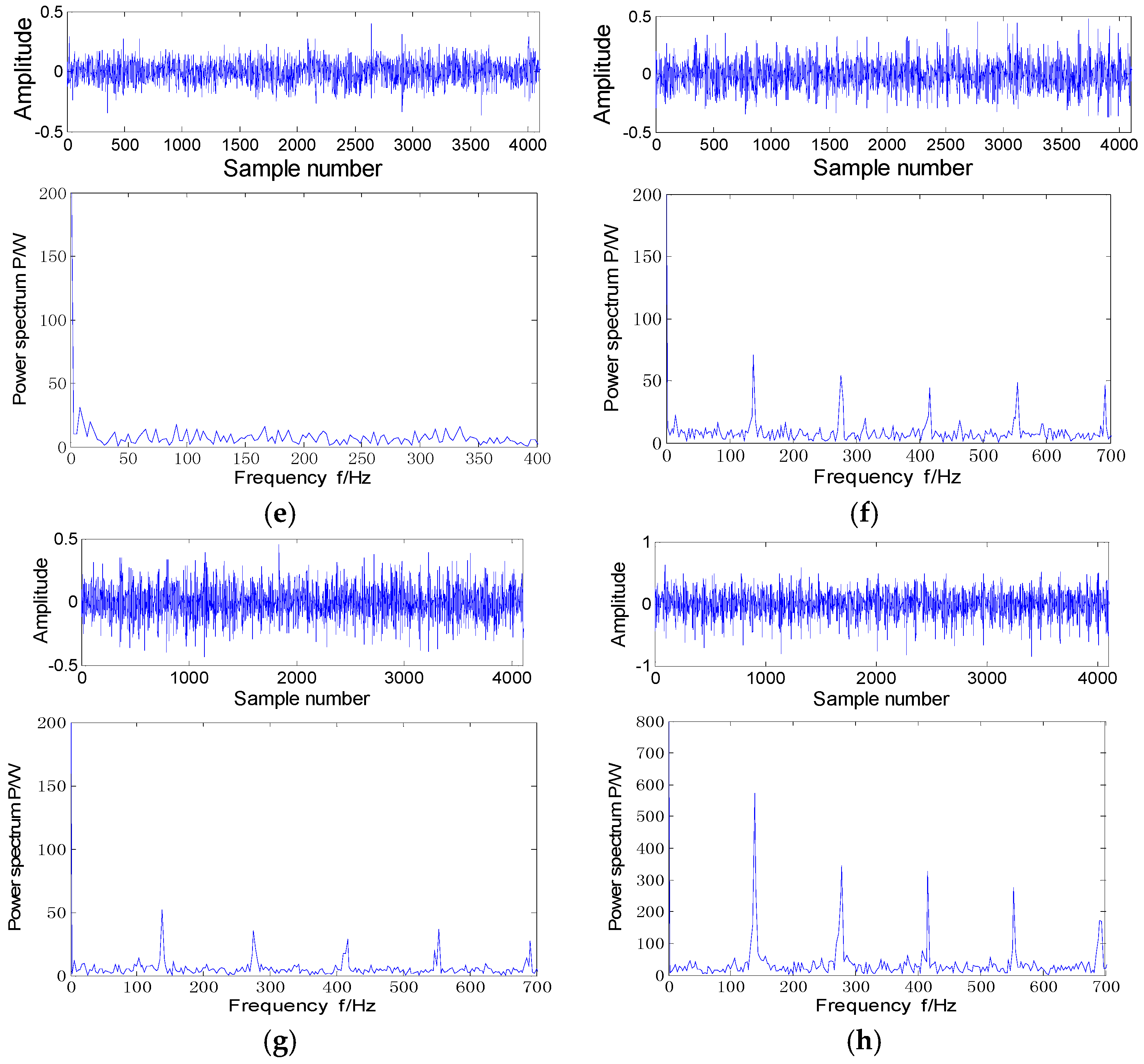
Figure 5 shows the whole accelerated life data and the diagnosis results by envelope spectrum combined with MED in this paper. According to the
Figure 5a–e, we can see that from the first day to the fifth day, the envelope spectrum’s energy of vibration data by the MED algorithm is evenly distributed, from which we can conclude the bearing is in a normal health state. After the sixth day, the energy distribution is regular, which mainly focuses on the fault frequency and its time frequency, so we can judge that bearing has begun to wear.
2.4. Distinguishing Equipment Weak Faults
In order to precisely position when and where a weak fault occurs, the final vibration data of the fifth day were analyzed with the same principle, and we can find that a faint outer race fault has already appeared at the end of the fifth day.
Here, the diagnosis results are verified through the vibration intensity and sample entropy feature parameter [
20,
21]. In the calculation of bearing vibration intensity, according to the definition in the time domain, calculus is needed to deal with complex methods such as signal type conversion and filtering. Therefore, in the calculation of vibration intensity, we need to remove the signal trend in order to improve the accuracy of the calculation [
22,
23].
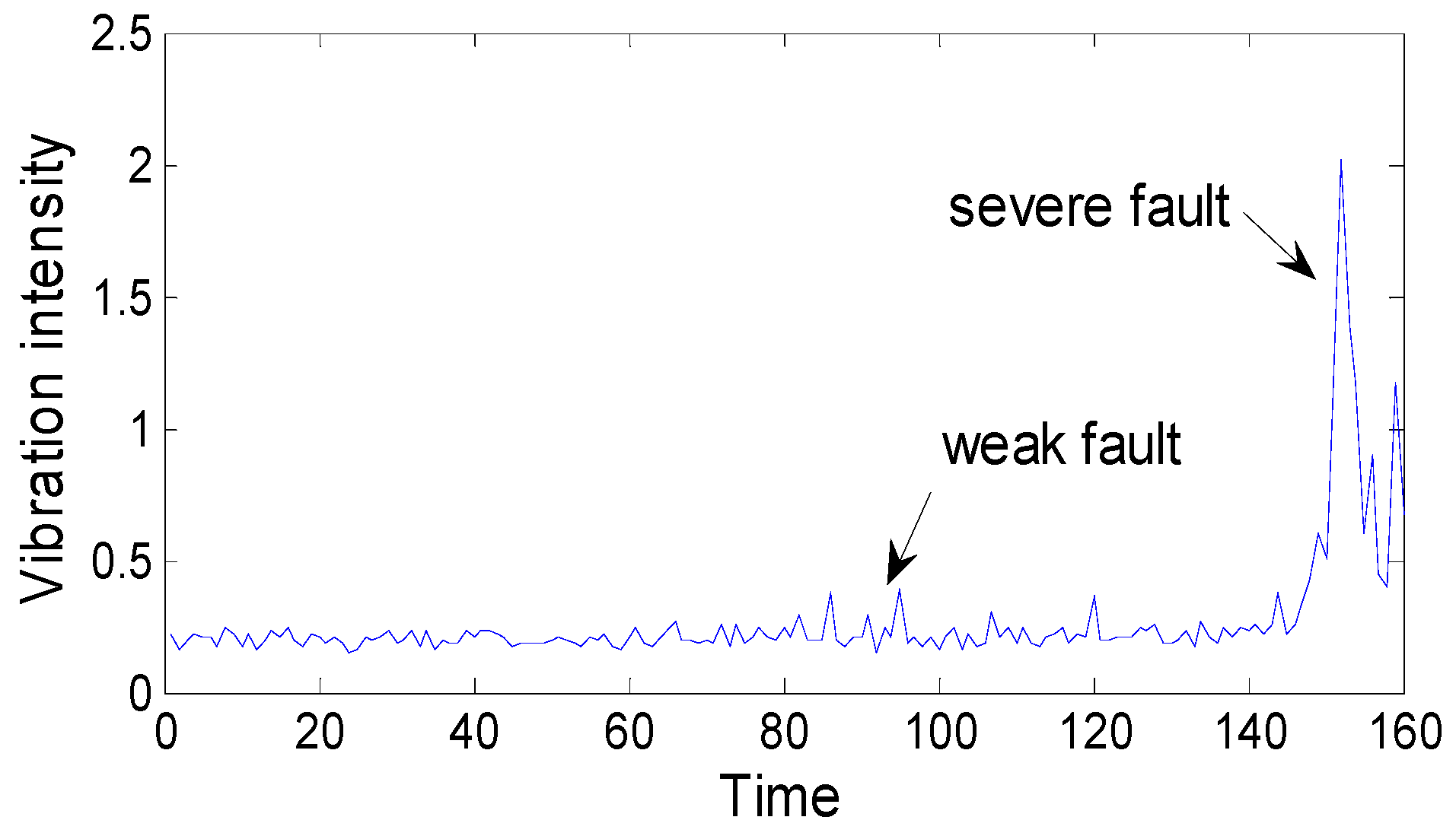
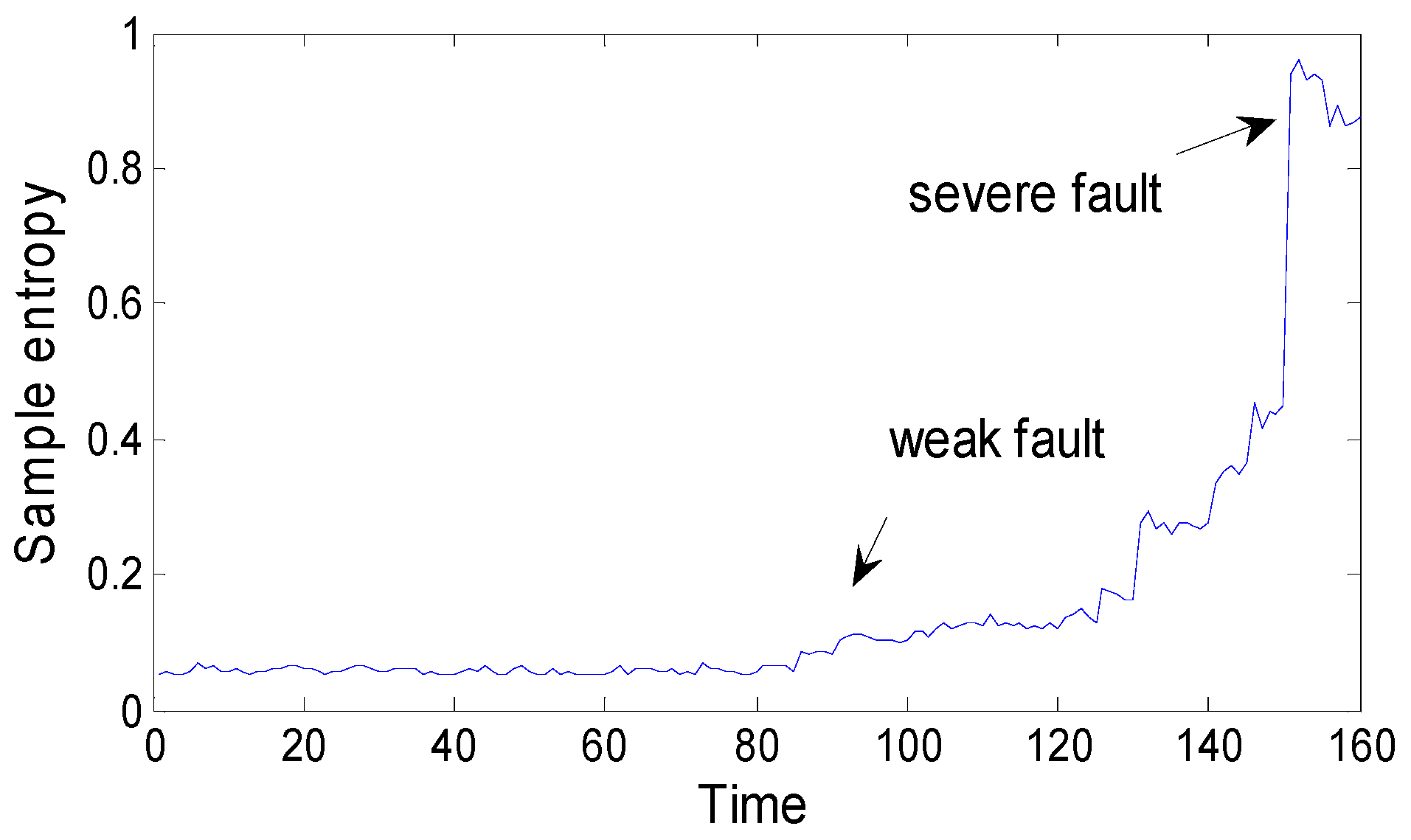
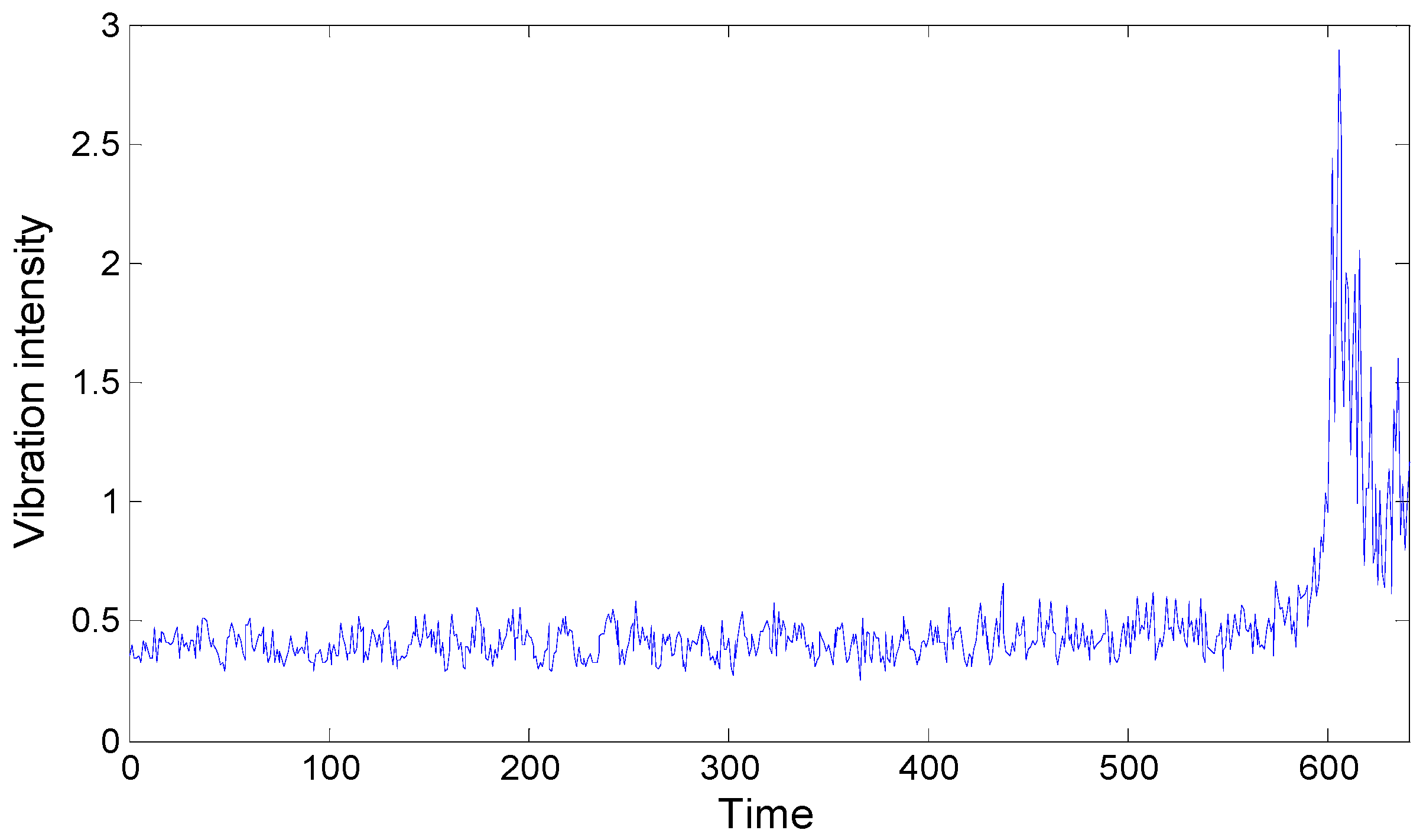
One vibration intensity and sample entropy point are calculated by every 1024 points in 204,800 sampling points. The intensity series and the sample entropy series are composed of 200 datapoints, respectively, as
Figure 6 and
Figure 7 show, the vibration intensity and sample entropy change in the whole life cycle.
As we can see, before sample time 85, there is no too large fluctuations, but after that point, there are changes, and these continue to aggravate, which verifies the appearance of a weak fault at the end of the fifth day. This corresponds to the MED method’s diagnosis result and further verifies the effectiveness and accuracy of the MED method for fault diagnosis.
3. The Fault Trend Prediction of Mechanical Equipment by FBM
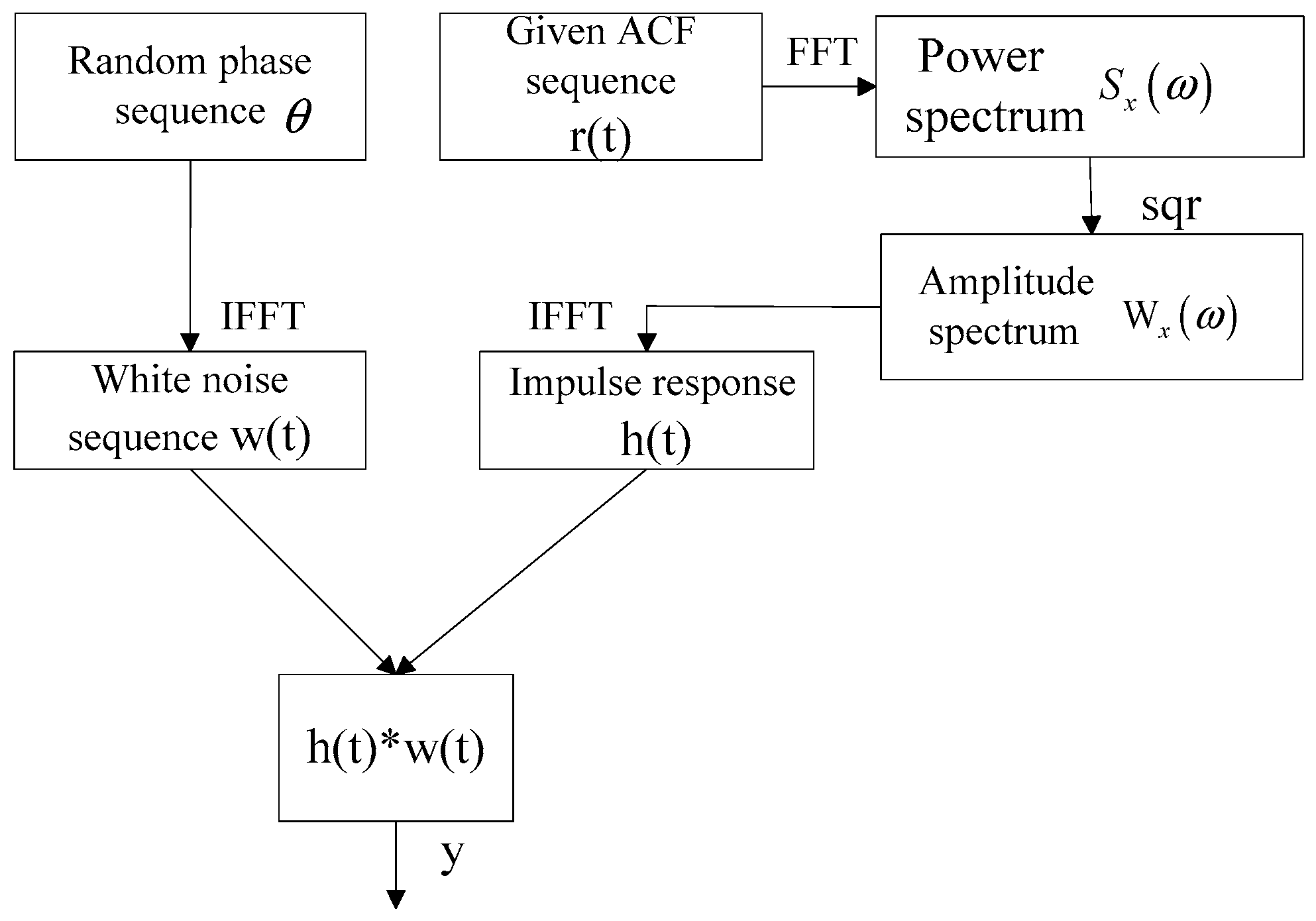
The bearing vibration intensity is chosen as the criterion to measure the health status of mechanical equipment, and the fractional Brown motion (FBM) model is applied to predict the weak fault trend. The whole idea and steps of the weak fault trend prediction for the mechanical equipment are shown in
Figure 8.
3.1. Calculate the Hurst Index of Vibration Intensity by R/S Method
The term of LRD series is usually introduced as follows: Let
X(
t) be a stationary process and
R(
τ) the autocorrelation function (ACF) of
X(
t). Then:
where
τ denotes the time lag,
E is the mean operator. The function
X(
t) is termed LRD if its autocorrelation function
R(
τ) is non-summable [
24], that is:
The Hurst parameter is the only parameter to measure the self-similarity property. When the Hurst parameter H ranges from 0 to 0.5, it is an SRD process; when the Hurst parameter H ranges from 0.5 to 1, it is an LRD process.
For time series, we need to calculate the Hurst parameter to estimate whether the sequence has an LRD property. There are many methods to estimate the Hurst value in the time domain and frequency domain way [
25].
It can be seen from
Table 1 that all these algorithms are able to judge accurately whether the sequence has an LRD property, but the different methods for estimating the Hurst values are not the same. We select the R/S estimation method to estimate the Hurst parameters of an LRD time series after an in depth evaluation.
3.2. FBM Model
Analysis and research on an LRD model is the key and core of the application of an LRD model. In the process of monitoring the condition of rotating equipment, the weak faults of equipment present a gradually aggravation and take on an LRD property. However, traditional models such as the Poisson process, compound Poisson process, Markov modulated Poisson process (MMPP) can only handle the problem with short-range dependence. For time series with LRD, traditional models can’t solve it. Therefore, it is more suitable to describe the real problem with a model which has LRD properties, such as fractional Brown motion, fractional Gauss noise and FARIMA model. From a large number of actual data analysis, we find that bearing vibration intensity of the slowly varying fault process not only has a random non-stationarity, but also has long-range dependence characteristics. Therefore, the stochastic model with long-range dependence (LRD)−fractional Brownian motion (FBM) model is proposed to evaluate and predict the condition of bearing slowly varying faults which is a long-running gradual process from weak fault occurrence to severity. The FBM model can more fully express and describe the actual problems with an LRD property for bearing fault prediction. The remainder of this paper focuses on the fractional Brown motion (FBM) model.
3.2.1. Characteristic Analysis of FBM
FBM was originally proposed to describe the actual 1/
f process. In a 1/
f process, its power spectrum satisfies
when
[
26,
27,
28], so the most intuitive way of getting the 1/
f process is that using a Gaussian white noise puts through a suitable linear time invariant system. In fact, such the definition of a 1/
f process is not appropriate. To avoid the problem, Mandelbrot scholars summed this up with the following definition: let 0 <
H < 1, and let
b0 be an arbitrary real number, Let
BH(
t) be fractional Brownian motion (FBM), so
BH(
t) is defined by [
29]:
From the point of view of filter theory, furthermore, we say that BH(t) is a filtered B(t) under the operation of Equation (6) and Brownian motion can be regarded as a special case of FBM.
3.2.2. Stochastic Differential Equations (SDE) Based on FBM
For the application of fractional Brown movement in the financial field, scholars have done a lot of research. In 1996, Heyde and Dai researched the issues related to the fractional Brownian motion, and introduced the relationship with short-term dependence (SRD) and long-range dependence (LRD), and got the SDE definition driven by the fractional Brownian motion [
30,
31,
32,
33]. In 2002, Necula simulated the change process of asset returns based on the SDE driven by FBM. According to the theory of FBM, assuming the asset in the financial market satisfies the following fractional stochastic differential equation (FSDE) [
34]:
where
μ is the return rate,
σ is the fluctuation rate of gain,
λ is the interference term of gain,
BH(
t) is FBM. Therefore, the methods and ideas based on FBM in the financial field with the long memory are applied to the time series with LRD characteristics and can predict the time series changes in future time.
3.3. Generating FBM Series
In order to study an LRD property, an LRD time series is important to be generated. Let a Gaussian white noise through the linear system which has a LRD property, and the output response is the fractional stochastic sequence of LRD property. Therefore, the acquisition of LRD data can be divided into two parts, one is the generation of the impulse response
h(
t) with a LRD structure. Let
X(
t) be a stationary process. Let
R(
τ) =
E[
X(
t)
X(
t +
τ)] be the autocorrelation function (ACF) of
X(
t). According to the definitions, the ACF can be given by [
35,
36]:
According to the Wiener–Khinchine relation
, the relationship between impulse response and ACF can be derived [
37]:
Another part is the generation of the white Gaussian noise
w(
t). We define Gauss white noise as follows:
where
,
is a real random function with arbitrary distribution.
Therefore, LRD data
y(
t) can be expressed as:
where
means the operation of convolution.
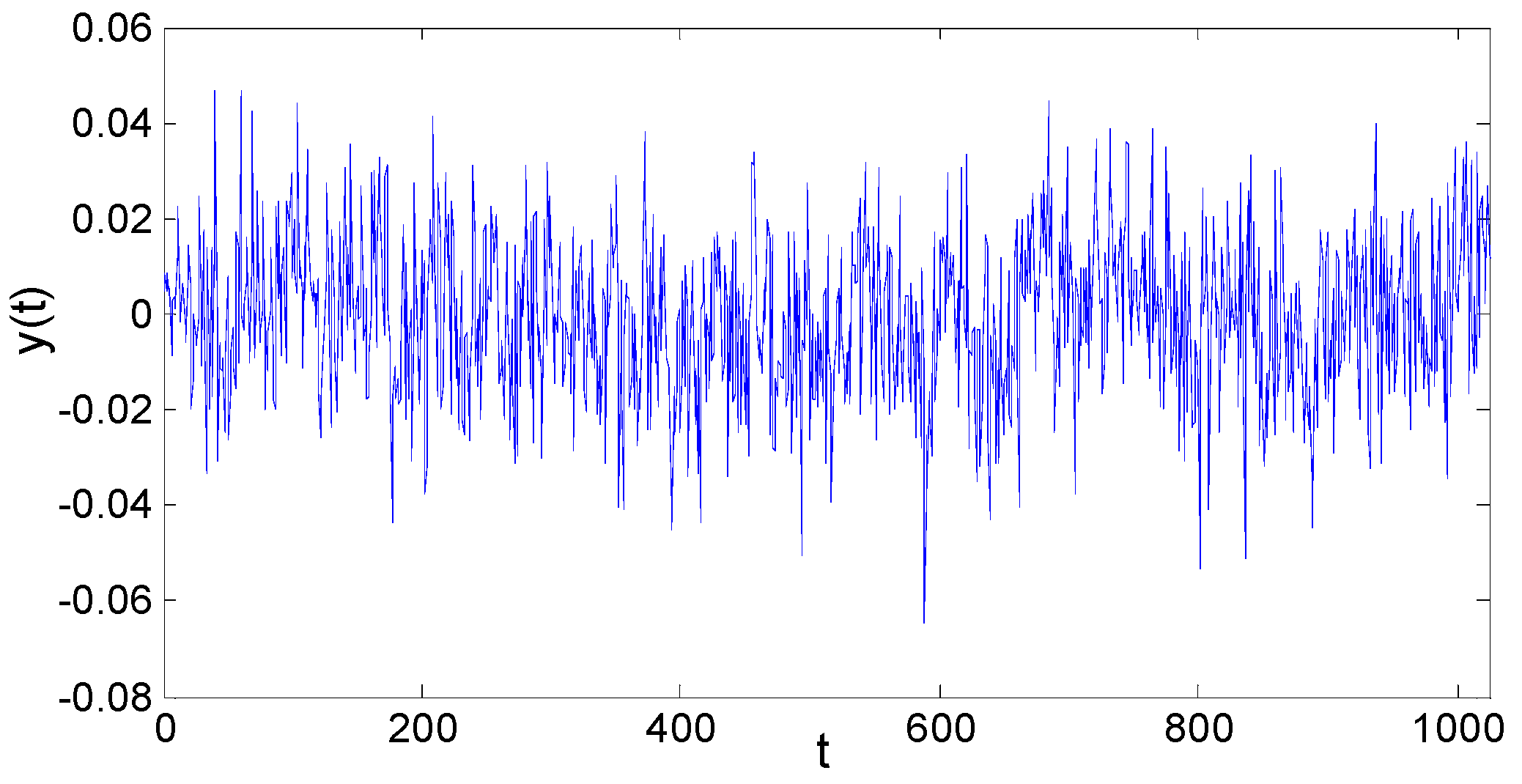
According to the Equation (11) and the ACF sequence of
H = 0.8, the corresponding LRD sequence of
y(
t) is shown in
Figure 9.
Based on the derivation of the Equation (11), the flow chart of LRD algorithm can be shown in
Figure 10.
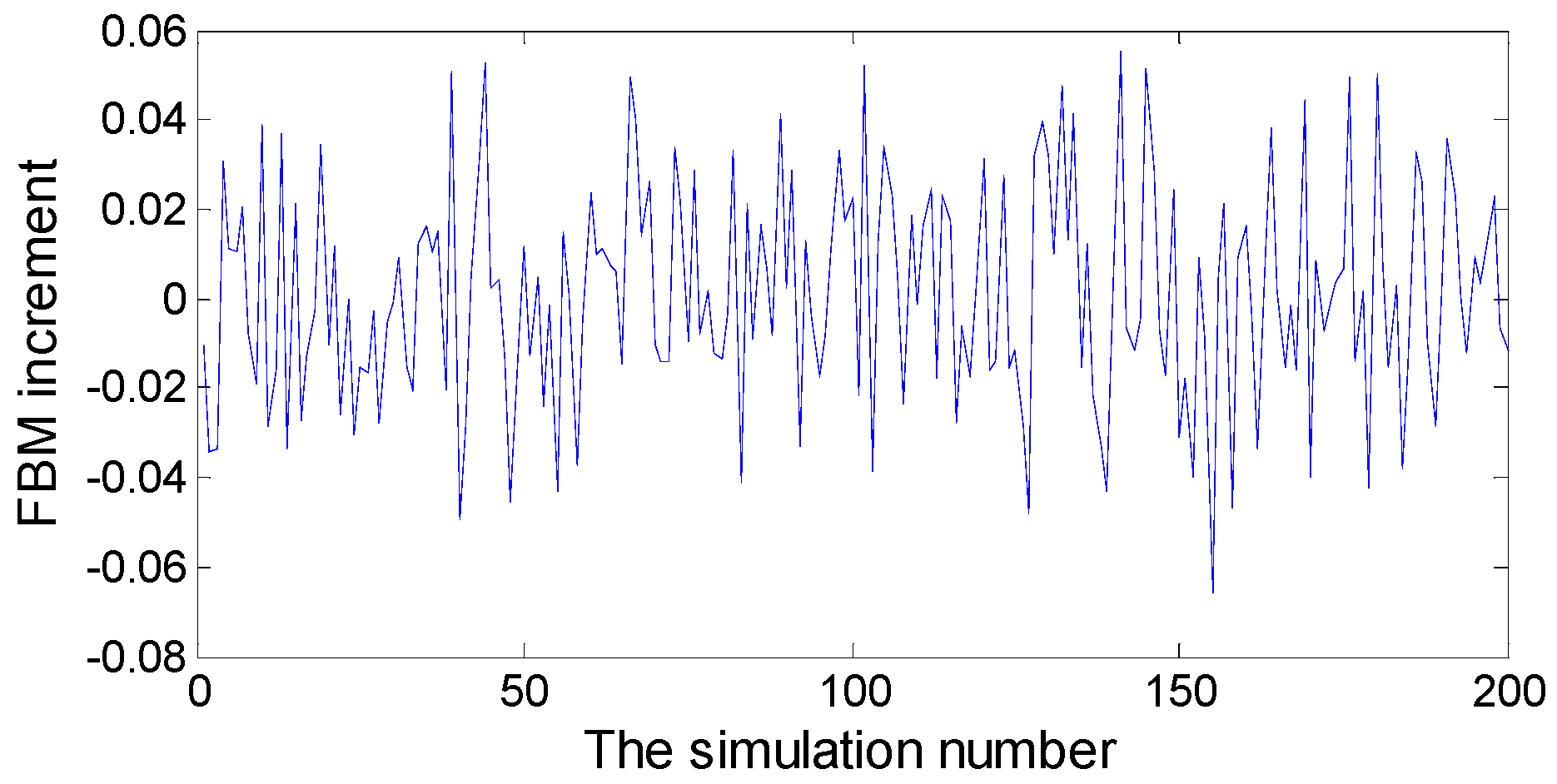
There have been some theoretical results on the financial problems in FBM environment, but it is more important to solve the practical problem which is how to simulate the process. From the Equation (7), it is known that the increment of FBM and the incremental need to be simulated first. In this paper, a simple method of the extended form of Maruyama symbols dB(t,H) = w(t)(dt)H is used to simulate the increment of FBM.
If the time interval [0, T] is divided into N equal parts, then each length is Δ
t =
T/
N. For each interval of time
tj (
j = 0, 1, 2, …,
N), the increment of the FBM is discretized:
If
T = 1,
N = 200,
H = 0.65, then we get incremental simulation curve of FBM, as shown in
Figure 11.
Combined with the Equation (2), the FSDE can be discretized:
where
w1(
t),
w2(
t) are independent and are standard normal distributions.
Using Monte Carlo simulation, though multiple approximation curves of the time sequence that can be obtained through several simulations, the average value of all the approximate curve amplitudes at each time point can be obtained, then one can obtain time series at each time point approximation, which is the most likely change path.
3.4. Parameters Estimation of FBM
Assuming time interval of the gain data is Δ
t, the
N + 1 data of observation vector consist of
y = (
y0,
yΔt, …,
yNΔt), time vector is
t = (0, Δ
t, …,
NΔ
t), fractional Brown motion vector is
BH(
t) = [
BH(0),
BH (Δ
t), …,
BH(
NΔ
t)], so the parameters
μ and
σ by the maximum likelihood estimation are determined as follows [
37,
38]:
Parameter
λ can be obtained by fourth-order matrix describing the extreme phenomenon:
where:
4. Predicting Fault Trends
After research and analysis, due to working conditions, strong noise, external interference and other factors, equipment state trends are very difficult to predict. As we all know, it is difficult to establish accurate prediction models with the traditional methods and the prediction accuracy is low. Therefore, the earlier a bearing fault is detected, the better important mechanical equipment operates.
4.1. Property of Vibration Intensity
By the vibration intensity of the whole life cycle is known, calculating the vibration intensity of the different interval lengths will affect their own LRD characteristics. Therefore, we need to find the appropriate point number to calculate the intensity value. For this we select the vibration intensity V1 in each stage that has a better LRD characteristic (2560 points to calculate an intensity value), as shown in
Figure 12.
Table 2 shows that the distribution of the Hurst values corresponds to different sections of the vibration intensity sequence V1. From
Table 2 it can be found that an LRD characteristic of vibration intensity is relatively weak and accounts for 25% before the fault point, and the vibration intensity after the fault point shows LRD characteristics and accounts for 90%.
4.2. Experiment Result Validation
According to an LRD characteristics, the vibration intensity of rolling bearing faults in the time period before and after the weak fault is analyzed. First, by calculating the value of the Hurst parameter we judge whether the intensity value sequence has an LRD characteristic. If the H value ranges from 0.5 to 1, it is indicated that the sequence has an LRD characteristic. The parameters of the model are calculated according to the rolling bearing intensity value as sample corresponding to the weak fault. Then, multiple approximation curves of intensity values are obtained through multiple simulations. One can get rolling bearing intensity approximate values at each time point, which is the most likely change path.
Because of an LRD characteristic randomness of vibration intensity and the influence of the prediction length on model prediction accuracy, we need to find the best prediction sample interval. Through analysis, it is found that the error is relatively small with 3.7% and the forecast effect is better when the prediction step size is 50.
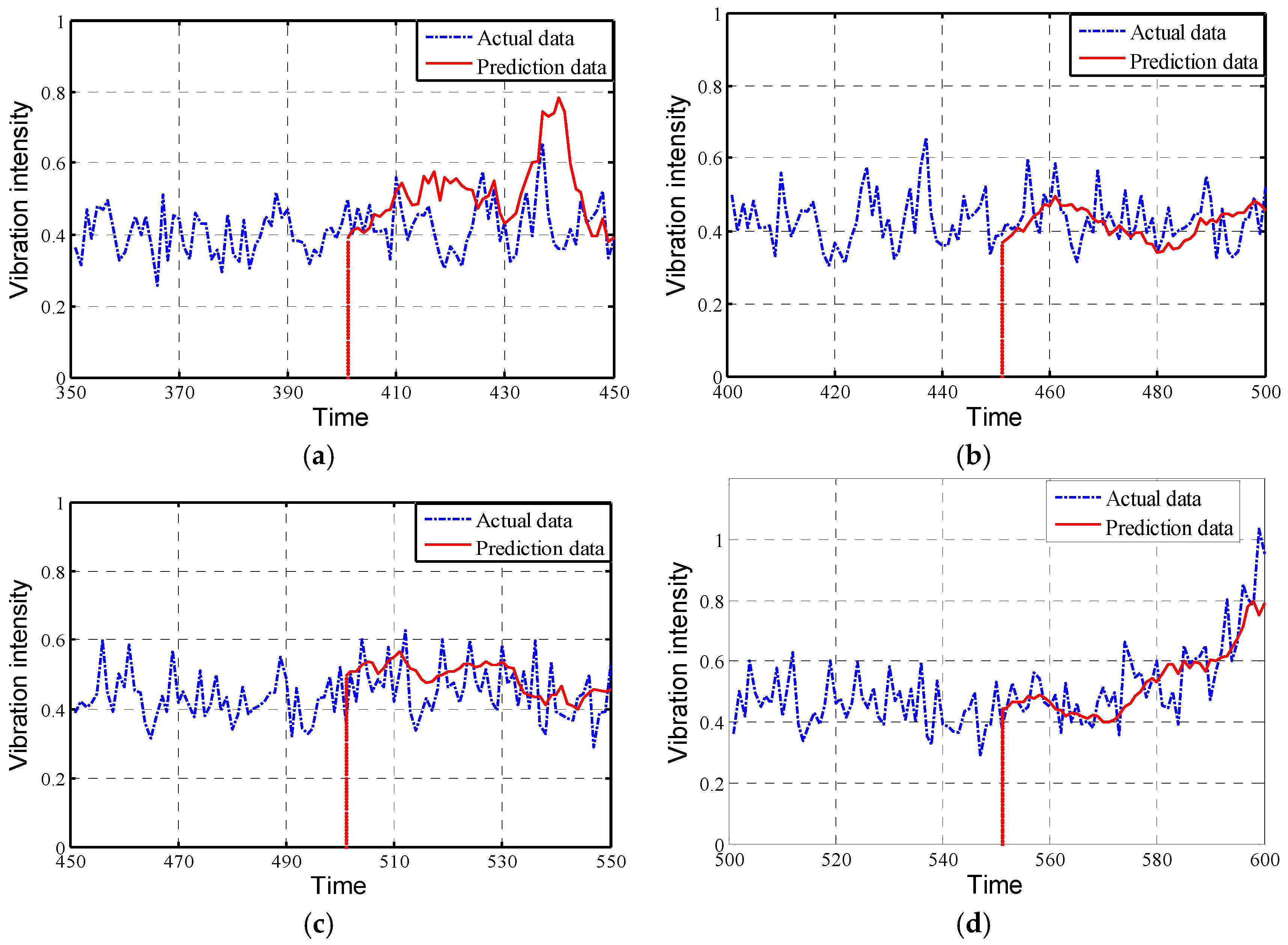
Therefore, based on the FBM model, the prediction data after the fault point is divided into
A to
E stage, the prediction results of the next stage are as shown in
Figure 13.
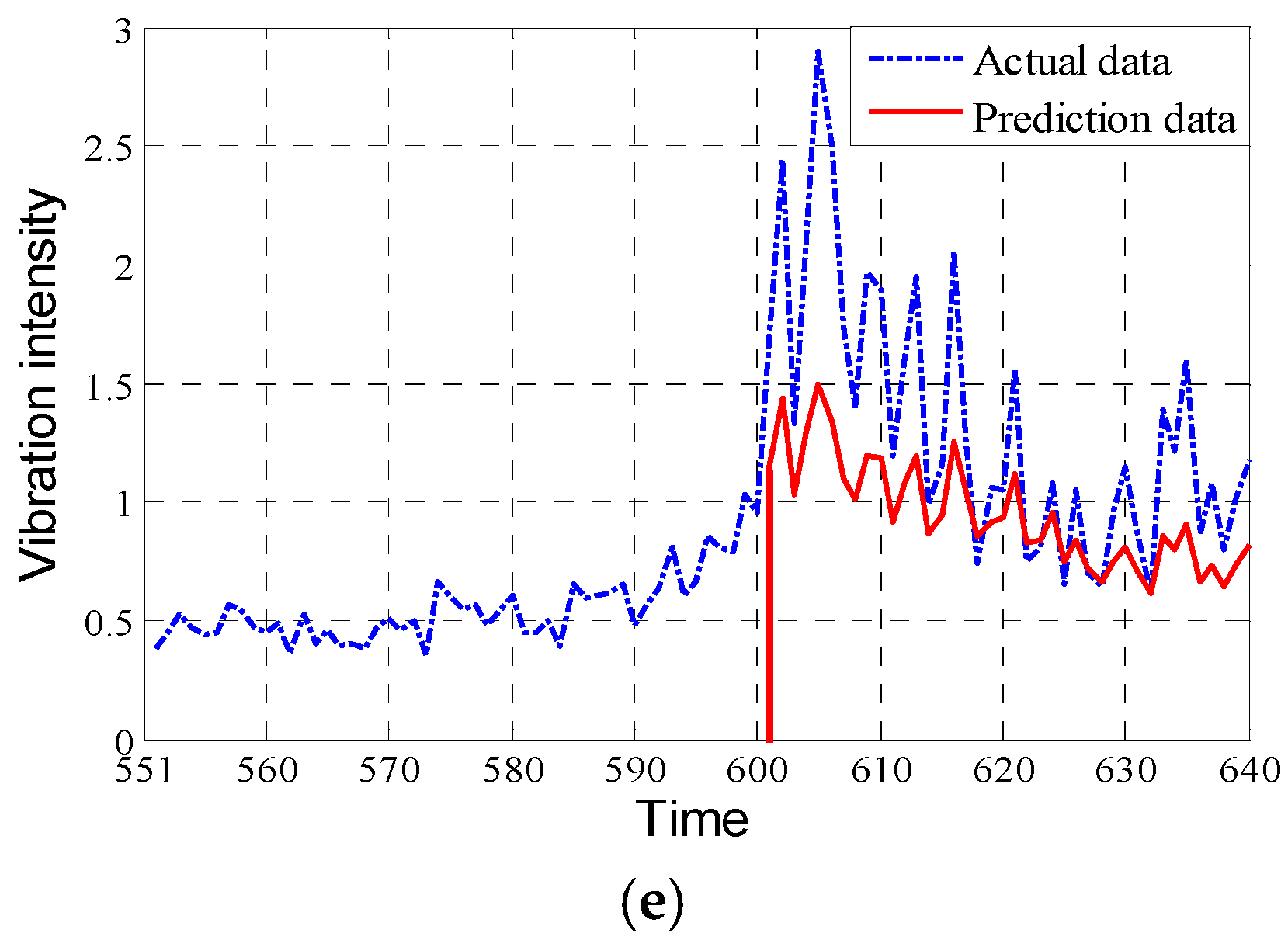
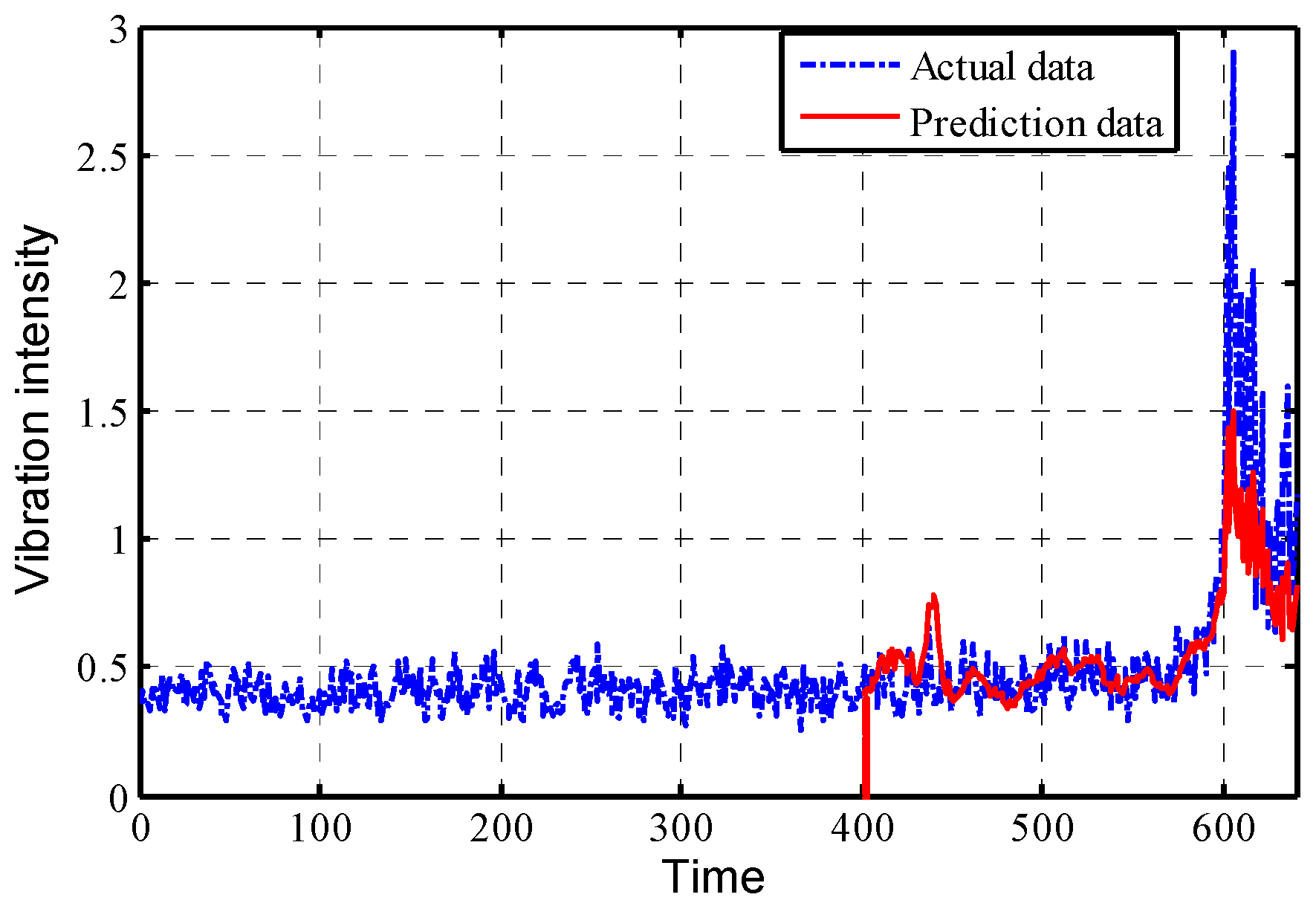
The prediction data of different stages are integrated and compared with the original vibration data of the whole cycle, the overall prediction results are shown in
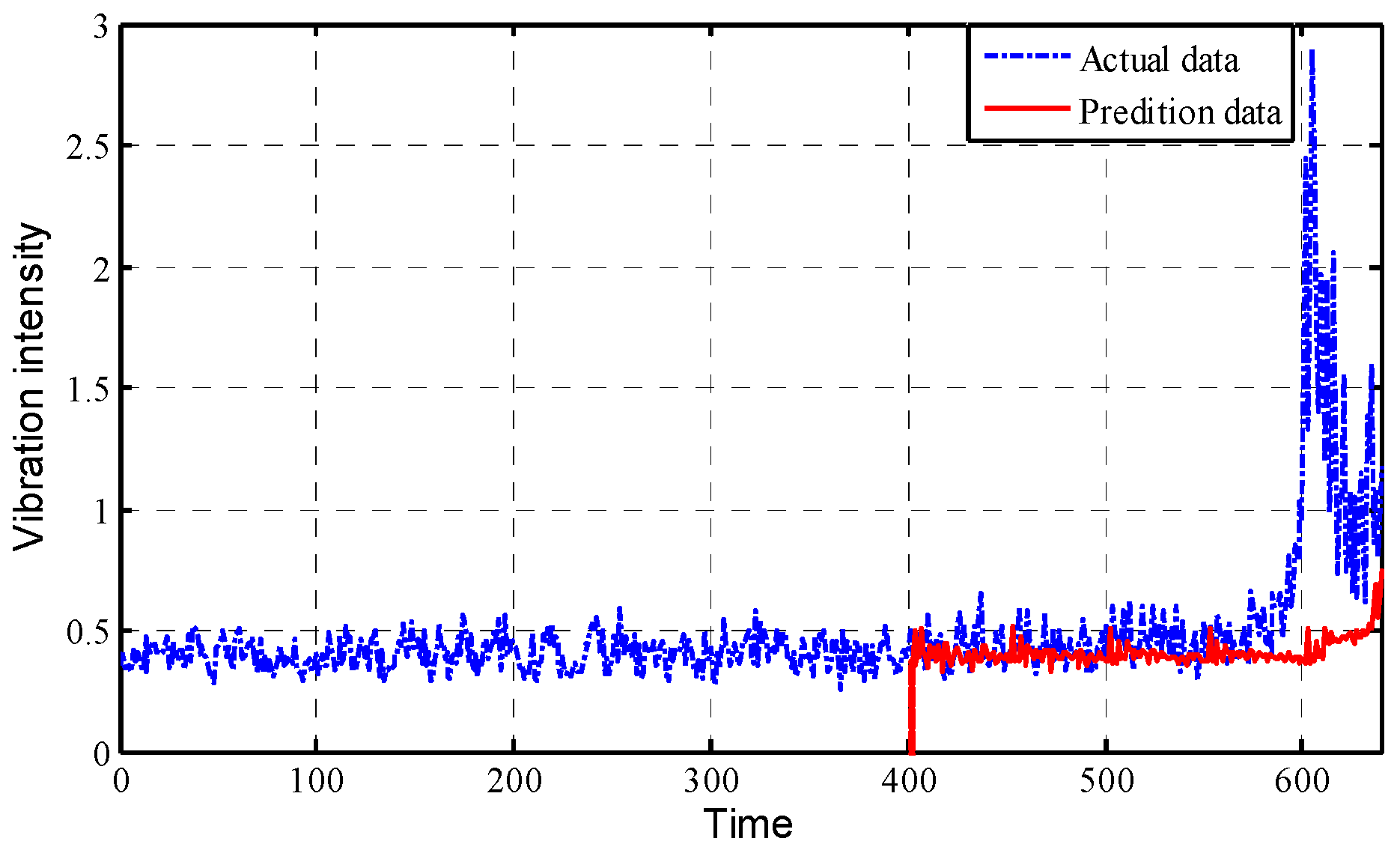
Figure 14. Then, the traditional ARMA model predicts the change trend of vibration intensity, as shown in
Figure 15.
As can be seen from
Figure 14 and
Figure 15, the prediction effect of the FBM model on the bearing vibration intensity sequence is more satisfactory than the traditional ARMA model, which provides a new method and idea for the real-time monitoring and prediction of the bearing condition.
Furthermore, in order to quantitatively determine the better model, the mean absolute error (MAE) criterion is employed for a comprehensive model comparison. Compared with the real values, the MAE obtained with the FBM model is more within 10% for the medium and long-term trend prediction than 22% of the other traditional models.
5. Conclusions
This paper has presented the algorithm and model for the detection of rotating machinery weak faults in the early stage and condition trend prediction. For the weak fault diagnosis, the implied impulse components of vibration signals when early faults occur are relatively weak and often submerged in strong noise. The method based on MED and envelope spectrum analysis is proposed to detect the early weak faults and the diagnosis results are very accurate.
In regard to predicting the equipment condition, an LRD model is introduced which previous applications are in the study of network traffic and return of assets. In order to research the property of LRD, an algorithm based on the ACF is provided for generating an LRD time series. Then, a FBM stochastic model with LRD property is derived to predict the condition trend of rotating machinery and it is more accurate than traditional models. In further study, the medium and long term prediction will be taken into consideration as the key of an LRD model application.