1. Introduction
Fractional calculus is a vital branch of mathematical analysis which deals with derivatives and integrals to an arbitrary order (real or complex). There are intensive studies of fractional calculus from both theoretical and practical points of view. The applications of fractional calculus in many fields such as physics, economics, probability theory and statistics are numerous. For example, many physical and engineering models are described by fractional differential equations. For some applications of fractional calculus, one can refer to [
1].
Due to the great importance of fractional differential equations (FDEs) and their applications in various disciplines, many researchers have shown considerable interest in developing numerical algorithms for solving these types of equations. Numerical solutions for various types of FDEs by applying several techniques were proposed, for instance, Adomian’s decomposition method [
2,
3], the Taylor collocation method [
4], the variational iteration method [
5], the finite difference method [
6,
7] and the ultraspherical wavelets method [
8,
9]. In addition, orthogonal polynomials have been widely used for obtaining numerical solutions for different types of FDEs. For example, Chebyshev polynomials of the second kind were employed by Sweilam et al. for solving space fractional-order diffusion equations [
10]. Moreover, Chebyshev polynomials of the first kind were used for solving some fractional differential equations in Khader and Sweilam [
11].
The three well-known versions of spectral methods; namely collocation, tau and Galerkin methods play pivotal roles in the numerical solutions of various types of differential equations. The spectral solutions are expressed in terms of truncated series of various polynomials. Actually, this solution is written as
∑akφk, where {
φk} is a set of polynomials, which is often orthogonal. The expansion coefficients
ak can be determined by applying an appropriate spectral method. The collocation approach is performed by enforcing the differential equation to be satisfied exactly at some selected points called nodes or collocation points. The tau method is a synonym for expanding the residual function as a series of orthogonal polynomials and then, applying the boundary conditions as constraints. The Galerkin method is basically based on selecting some combinations satisfying the underlying boundary (initial) conditions as basis functions, and then, enforcing the residual to be orthogonal with the basis functions. This approach is fruitfully applied in many studies to solve two point linear boundary value problems (BVPs), in one and two dimensions [
12,
13,
14,
15].
The utilization of operational matrices of derivatives of different orthogonal polynomials is very effective for treating almost all types of differential equations. To be more precise, several operational matrices are employed for obtaining numerical solutions of ordinary differential equations. In this regard, Abd-Elhameed in [
16] has developed a novel harmonic numbers operational matrix of derivatives to solve linear and nonlinear sixth-order BVPs. Likewise, Abd-Elhameed [
17] and Doha et al. [
18] used tau and Galerkin operational matrices of derivatives, respectively, to solve the singular Lane-Emden differential equations. The approach of employing the operational matrices is not limited to application in ordinary differential equations, but it can be also followed to handle FDEs. In this respect, a number of articles were devoted to introducing numerical solutions for these equations. In this respect, a Legendre operational matrix of fractional derivatives were constructed and employed for solving some types of FDEs in [
19]. As well, Rostamy et al. [
20] handled these equations with the aid of a Bernstein operational matrix of fractional derivatives. Other articles were interested in using the operational matrices of fractional integration to solve FDEs, i.e., Kazem [
21].
The Fibonacci polynomials with their generalizations, and Fibonacci numbers and the golden ratio, are key elements in number theory. They have enormous applications in various disciplines such as computer science, statistics, physics, biology and graph theory [
22]. Several studies were peformed to theoretically discuss Fibonacci polynomials and generalized Fibonacci polynomials (see [
23,
24,
25]). However, as far we know, articles interested in using these polynomials in different applications are scarce. For example, a collocation procedure for treating BVPs based on using the Fibonacci operational matrix of derivatives has been developed in [
26,
27].
The principal objective of the present article is to present and implement new numerical spectral solutions of some types of FDEs. For this purpose, the operational matrix of fractional derivatives of Fibonacci polynomials are constructed, and then employed along with the tau and collocation spectral methods for obtaining numerical solutions of FDEs.
The paper is organized as follows: first, in
Section 2, some preliminaries including some fundamental definitions of the fractional calculus theory are presented. This section also includes an overview on Fibonacci polynomials and their relevant properties.
Section 3 is interested in constructing Fibonacci operational matrix of the fractional derivatives in the Caputo sense.
Section 4 is devoted to implementing and presenting two numerical algorithms for solving two-term FDEs.
Section 5 is interested in investigating the convergence and error analysis of the suggested expansion of Fibonacci polynomials. Some numerical examples and discussions are presented in
Section 6, hoping to illustrate the efficiency, simplicity and applicability of the two proposed algorithms. Finally, some conclusions are reported in
Section 7.
4. Two New Matrix Algorithms for Solving Fractional-Order Differential Equations
This section is devoted to analyzing and presenting two numerical algorithms for solving fractional-order linear and nonlinear differential equations based on using the constructed Fibonacci operational matrix. The two algorithms, namely, the tau Fibonacci matrix method (TFMM) and the collocation Fibonacci matrix method (CFMM) are employed for solving linear and nonlinear multi-term orders fractional differential equations, respectively.
4.1. Use of TFMM for Handling Linear Fractional Differential Equations
Consider the linear fractional differential equation ([
31,
32]):
subject to the initial conditions:
or the boundary conditions:
Now, assume that
u(
x) can be approximated as:
In virtue of Theorem 1,
Dαu(
x) and
Dβu(
x) can be approximated as:
and
Making use of the approximations in (15)–(17), the residual of (12) can be calculated by the formula:
and accordingly the application of tau method (see [
18]) yields:
Moreover, the initial conditions (13) yield:
while the boundary conditions (14) yield:
From Equation (18) with (19) or (20), a linear system of equations in the unknown expansion coefficients ci of dimension (n + 1) can be generated. Thanks to the Gaussian elimination technique or any suitable technique, this system can be solved, and consequently, the approximate solution (15) can be found.
4.2. Use of CFMM for Handling Nonlinear Fractional Differential Equations
Consider the following nonlinear fractional-order differential equation:
subject to the initial conditions (13) or the boundary conditions (14).
We approximate
u(
x),
Dαu(
x) and
Dβu(
x) as in the previous section, hence the residual
of Equation (21) is given by:
The application of the spectral collocation method requires that
must vanish at certain collocation points. We select the collocation points to be:
and therefore:
Equations (22) with (19) or (20) generate a nonlinear system of equations in the unknown expansion coefficients ci of dimension (n + 1). Newton’s iterative technique can be employed for solving this system, and consequently, the approximate solution is obtained from (15).
Remark 1. It is worthy to mention here that the CFMM, which described above, can be also applied to linear fractional differential equations.
5. Convergence and Error Analysis
In this section, a comprehensive study of the convergence and error analysis of the suggested expansion of Fibonacci polynomials is performed. For this purpose, the following Lemmas are needed.
Lemma 1 (Byrd [33]). If f(x) is an infinitely differentiable function at the origin, then f(x) can be expanded in terms of Fibonacci polynomials as:
where
Lemma 2 (Abramowitz et al. [34]). Let Iv(x) denote the modified Bessel function of order v of the first kind. The following identity holds: Lemma 3 (Luke [35]). The modified Bessel function of the first kind Iv(x) satisfies the following inequality: Lemma 4. If denotes the golden ratio, then the following inequality is valid: The following two theorems discuss the convergence and error analysis of the Fibonacci expansion.
Theorem 2. If f(x) is defined on [0, 1]
with is a positive constant and , then we have: Proof. Starting from Lemma 1, we have:
and therefore the application of Lemma 2 implies that:
The inequality in (23) along with Lemma 3 leads to the inequality in the first part.
Now, to prove that the series converges absolutely, the comparison test is applied. Making use of the first part along with Lemma 4, yields but and therefore the series converges absolutely. □
Theorem 3. If f(x) satisfies the hypothesis of Theorem 2, and then we have the following error estimate: Proof. By Theorem 2, we can write:
which can be written as:
where Γ(
n + 1) and Γ(
n + 1,
μ) denote the well-known gamma function and the incomplete gamma function, respectively (see [
36]).
Now, we have but since Therefore we have which completes the proof of the theorem. □
6. Numerical Tests
This section presents some numerical experiments and comparisons to illustrate the efficiency and applicability of the two proposed algorithms in this paper.
Example 1 (Doha et al. [37]). Consider the following linear fractional initial value problem We apply TFMM for the case n = 2. The residual of Equation (24) can be calculated by the formula:where the operational matrices M(2) and M(½) are given explicitly as follows: If we apply the method which described in Section 4.1 to Equation (24), then we get: Moreover, the initial conditions (25) yield: Equations (26) and (27) can be immediately solved to give c1 = −1, c2 =0, c3 = 1, and consequently u(x) = x2 which is the exact solution.
Example 2 (Doha et al. [38]). Consider the following inhomogeneous Bagley–Trovik equation:where f(x) is chosen such that the exact solution of Equation (28) is u(x) = sin(αx). We apply the two methods, namely, TFMM, CFMM for different values of α and n. In Table 1, we display a comparison between the results obtained if the two methods TFMM, CFMM are applied with the results obtained by applying Chebyshev spectral method (CSM) which developed in [
38]
. The displayed results in this table show that our algorithm gives a lesser error in almost all cases. Example 3 ([32,39]). Consider the following linear boundary value problem: The exact solution of (29) in the case corresponds to
q1 = 2 and
q2 = 1 is
u(
x) =
x(1 −
ex–1). In
Table 2, we compare our results with those obtained in [
32,
39].
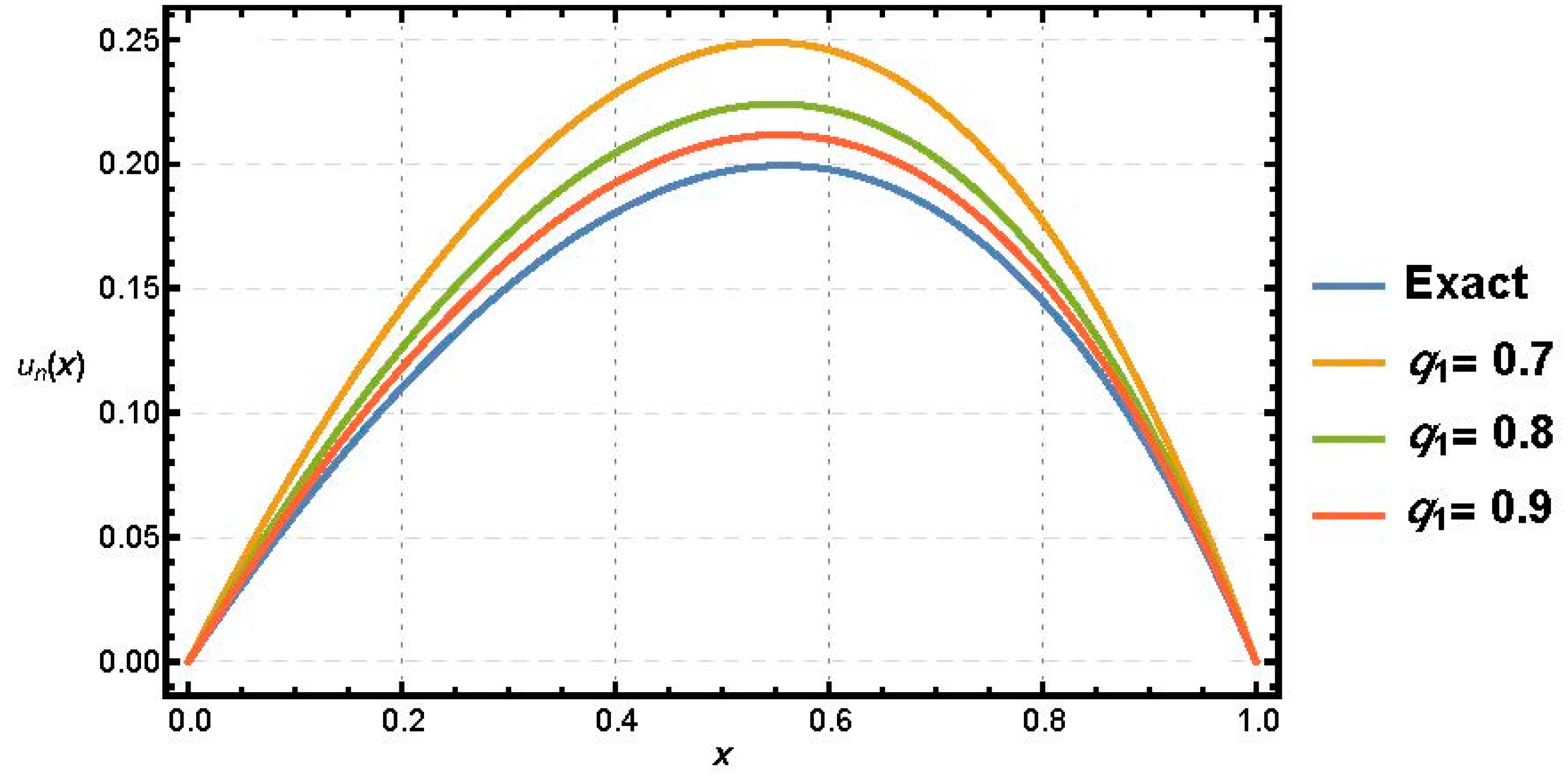
Figure 1 illustrates that the approximate solutions in the case corresponds to
q2 = 2 and for various values of
q1 near the value 1, have similar behavior.
Example 4 ([32,39]). Consider the following nonlinear boundary value problem:subject to the homogenous boundary conditions: The exact solution of Equation (30) for the case
q = 2 is
u(
x) = sin
2(
πx) We apply CFMM.
Table 3 lists the maximum pointwise error of Equation (30) for the case
q = 2 and different values of
n.
Figure 2 illustrates that the behavior of the approximate solution for values of
q near 2 is somehow close to the behavior of the exact solution.
Example 5 ([40]). Consider the fractional Van der Pol equation with fractional damping:subject to the homogenous initial conditions: We solve Equation (31) for the case corresponds to
a = 1.31,
ω = 0.5. In
Table 4, we compare our results with the numerical solution obtained in [
40] and the solution obtained from
Mathematica 9 by applying the fourth-order Runge–Kutta method. In
Table 5, we compare our results with the results obtained in [
40] in case with no damping
η = 0.
Remark 2. The results of Table 5 indicate that the numerical spectral solutions obtained by CFMM are in high agreement with the solutions of the fourth order Runge-Kutta method, also it is more accurate than the results obtained in Maleknejad [
40]
with the same number of retained modes. Example 6 ([40]). Consider the fractional Rayleigh equation with fractional damping:subject to the initial conditions: We solve Equation (32) for the case corresponds to
γ = 0.1, 0.5. In
Table 6 we give a comparison between CFMM and the operational matrix method developed in Maleknejad [
40] for the case corresponds to
α = 1,
γ = 0.1, 0.5.
Remark 3. From the numerical results of Table 6, we conclude that CFMM with fewer number of terms is compared favorably with the fourth-order Runge-Kutta solution obtained from Mathematica. Example 7. Consider the following fractional differential equation:subject to the initial conditions:where, .
The exact solution of Equation (33) is
u(
x) =
ex. To illustrate the advantages of our method if compared with methods which employ orthogonal polynomials, We solve Equation (33) by our proposed algorithm namely, TFMM, and also by using Legendre spectral tau method (LSTM).
Table 7 presents a comparison between the maximum pointwise errors which resulted from the application of TFMM and LSTM for different values of
n. In addition, a comparison between the running times (in seconds) if the two methods are applied is also displayed in
Table 7. The results of this table indicate the advantages of our method if compared with LSTM. Moreover, they ensure that TFMM is efficient for higher order fractional differential equations.
Remark 4: From the obtained numerical results in Table 1, Table 2, Table 3, Table 4, Table 5, Table 6 and Table 7 and the obtained estimates in Theorems 2 and 3, we list here the advantages of the current work:- (1)
The generation of Fibonacci Polynomials is very easy either from the recurrence relation or from the direct definition.
- (2)
The implementation of Fibonacci polynomials is efficient compared to the orthogonal polynomials in other words. The running time of the “Mathematica” code is very short compared with using the orthogonal polynomials.
- (3)
The speed of convergence of Fibonacci polynomials (inverse factorial rate of convergence) is very efficient. Theorem 2 ensures this result.