Fuzzy Shannon Entropy: A Hybrid GIS-Based Landslide Susceptibility Mapping Method
Abstract
:1. Introduction
2. Description of the Study Region
3. Materials and Methods
3.1. Landslide Influencing Data Layers
3.2. Proposed Methodology
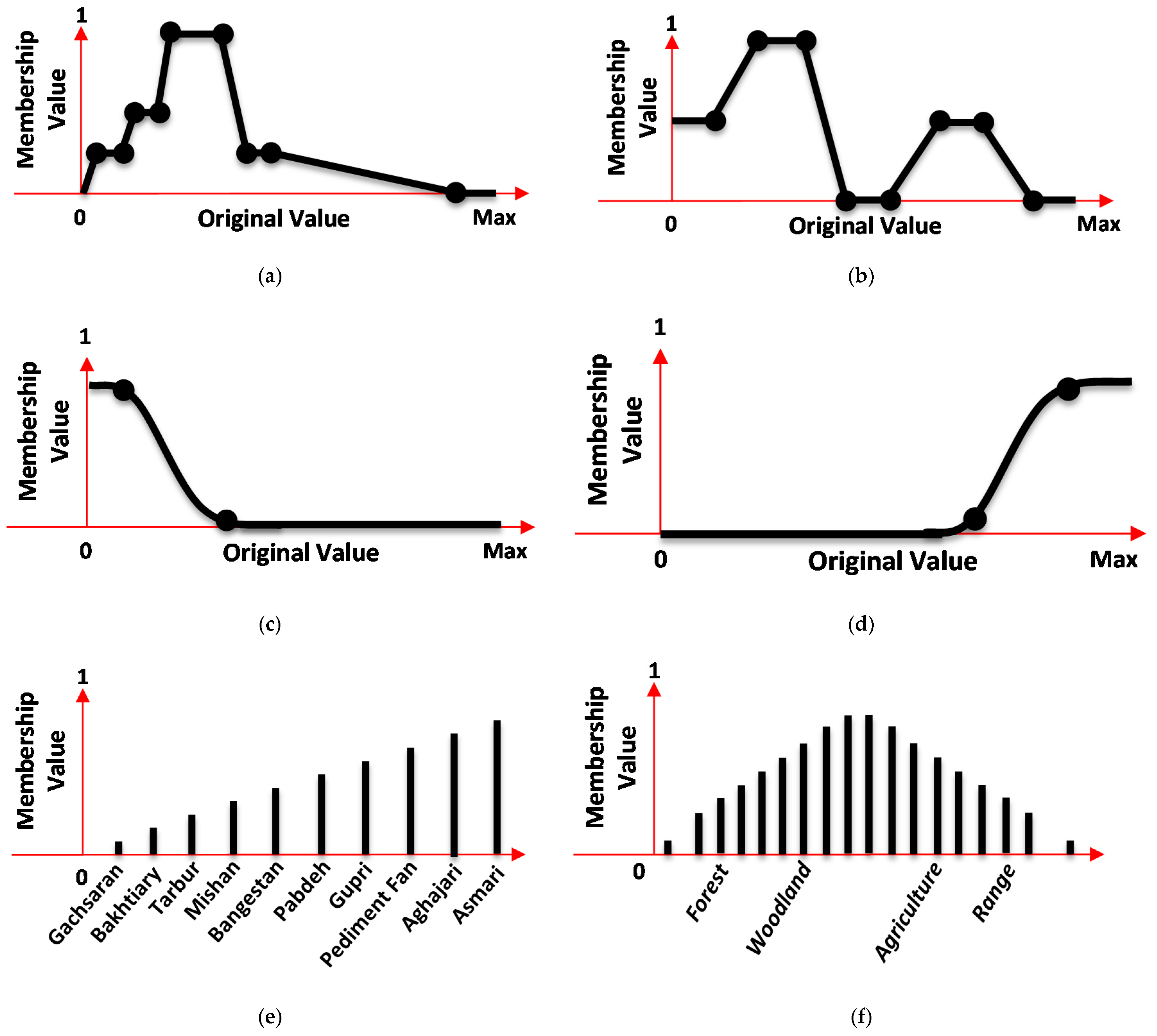
3.2.1. Fuzzy Membership Function (FMF)
3.2.2. Shannon Entropy
3.2.3. Hybrid Landslide Susceptibility Mapping Model
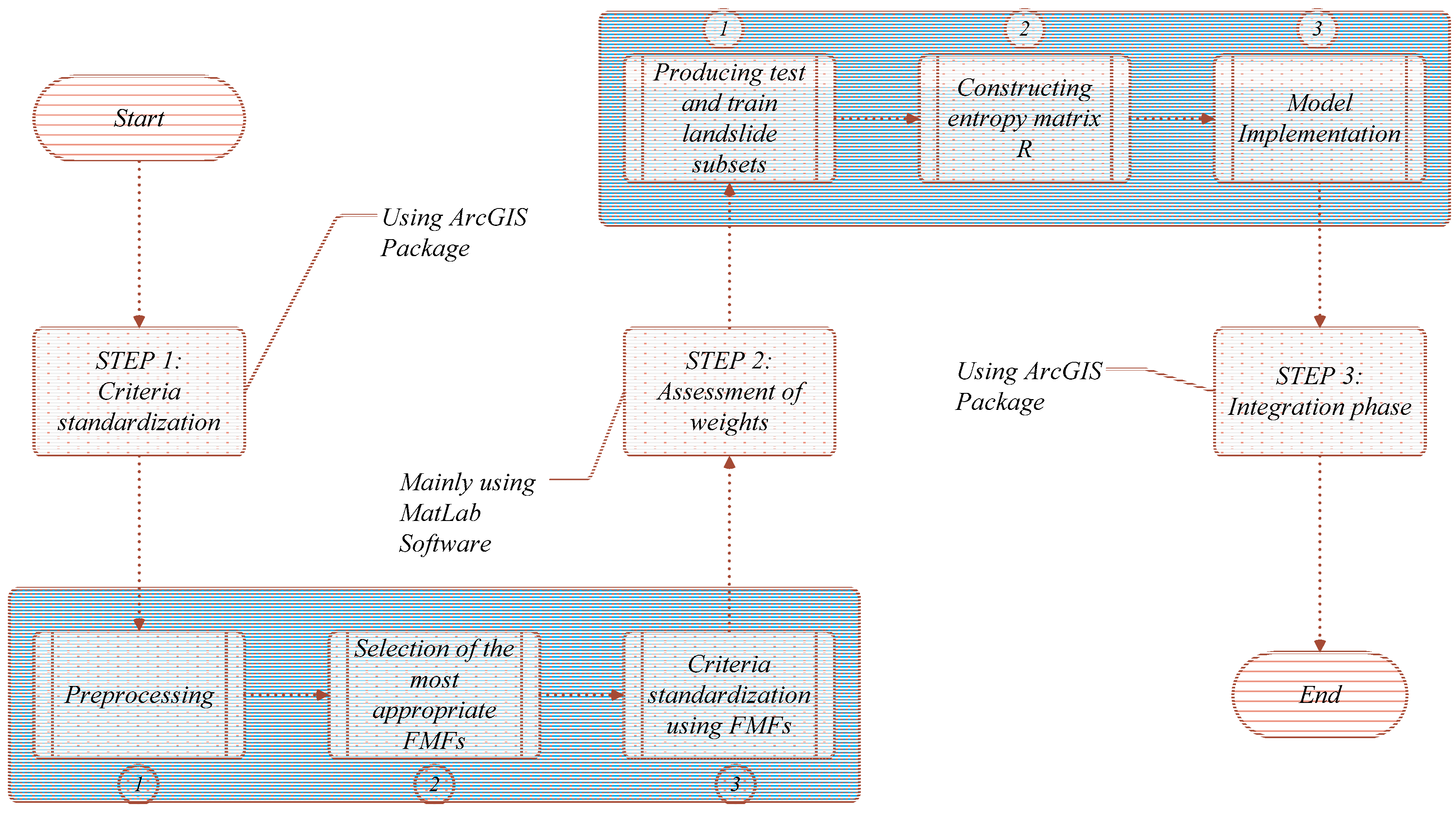
3.3. Methodology Implementation
3.3.1. Step 1: Data Standardisation Using FMFs
3.3.2. Step 2: Assessment of Weights with Shannon Entropy
3.3.3. Step 3: Integration Phase
4. Results
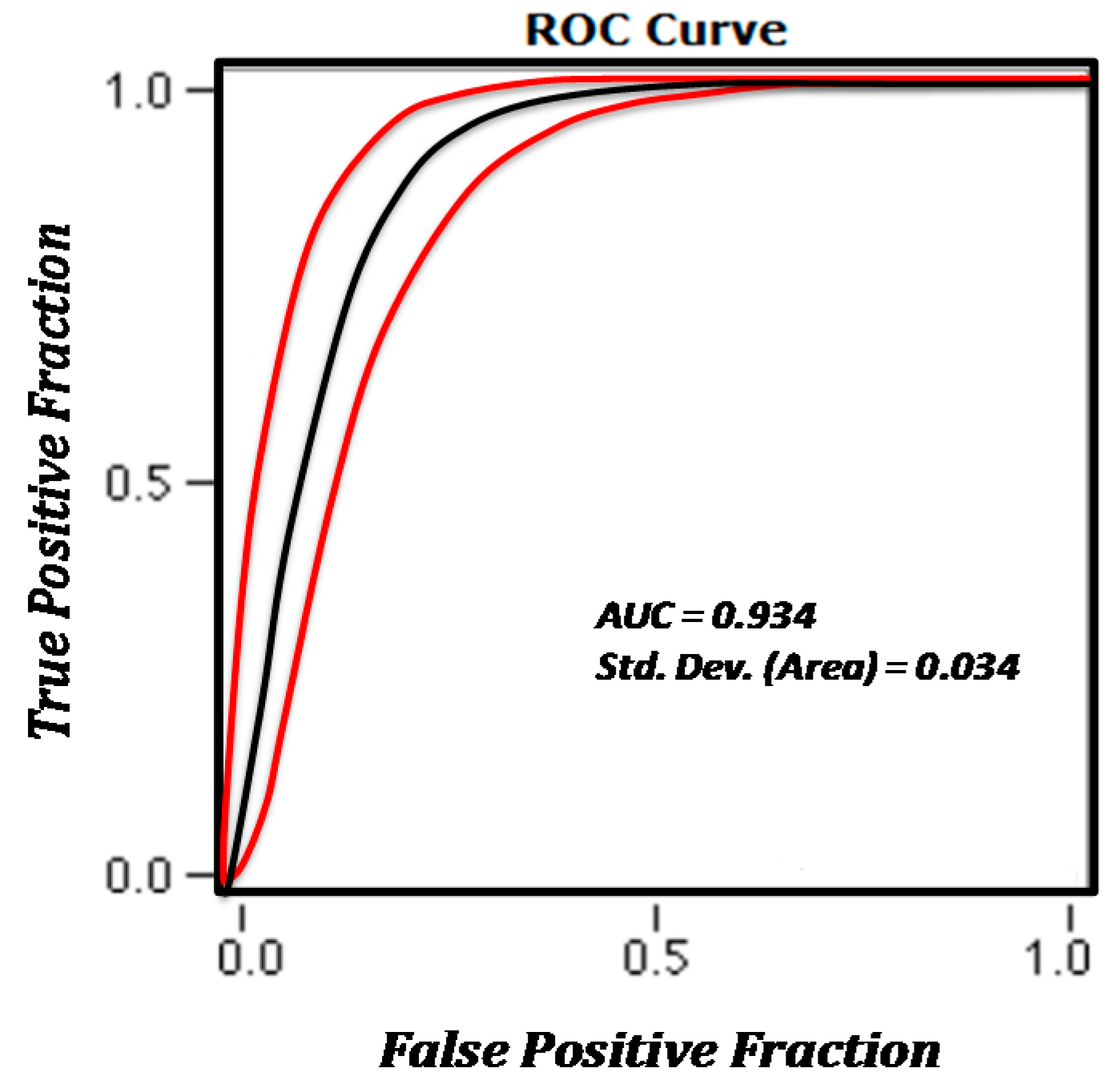
4.1. Validation of the Results Using ROC Curve
4.2. Validation of the Results Using Simple Overlay
5. Discussion
5.1. Obtained Results and Relevance to the Previous Studies
5.2. Spatial Information Extraction and Prediction
5.3. Decision Aiding and Planning
5.4. Limitation of the Proposed Methodology in LSM
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Varnes, D.J. Slope movement types and processes. Transp. Res. Board Spec. Res. 1978, 176, 11–33. [Google Scholar]
- Brabb, E.E. Innovative approaches to landslide hazard and risk mapping. In Proceedings of the Fourth International Symposium on Landslides; Canadian Geotechnical Society: Torento, Canada, 1984; Volume 1, pp. 307–324. [Google Scholar]
- Ercanoglu, M.; Gokceoglu, C. Use of fuzzy relations to produce landslide susceptibility map of a landslide prone area (West Black Sea Region, Turkey). Eng. Geol. 2004, 75, 229–250. [Google Scholar] [CrossRef]
- Bui, D.T.; Pradhan, B.; Lofman, O.; Revhaug, I.; Dick, O.B. Spatial prediction of landslide hazards in Hoa Binh province (Vietnam): A comparative assessment of the efficacy of evidential belief functions and fuzzy logic models. Catena 2012, 96, 28–40. [Google Scholar]
- Atkinson, P.M.; Massari, R. Autologistic modelling of susceptibility to landsliding in the Central Apennines, Italy. Geomorphol. 2011, 130, 55–64. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- De Luca, A.; Termini, S. A definition of a nonprobabilistic entropy in the setting of fuzzy sets theory. Inf. Control 1972, 20, 301–312. [Google Scholar] [CrossRef]
- Kosko, B. Fuzzy entropy and conditioning. Inf. Sci. 1986, 40, 165–174. [Google Scholar] [CrossRef]
- Majerník, V. Entropy—A universal concept in sciences. Nat. Sci. 2014, 6, 552–564. [Google Scholar] [CrossRef]
- Xu, C.; Dai, F.; Xu, X.; Lee, Y.H. GIS-based support vector machine modeling of earthquake-triggered landslide susceptibility in the Jianjiang River watershed, China. Geomorphology 2012, 145, 70–80. [Google Scholar] [CrossRef]
- Shahabi, H.; Hashim, M.; Ahmad, B.B. Remote sensing and GIS-based landslide susceptibility mapping using frequency ratio, logistic regression, and fuzzy logic methods at the central Zab basin, Iran. Environ. Earth Sci. 2015, 73, 8647–8668. [Google Scholar] [CrossRef]
- Wang, W.D.; Guo, J.; Fang, L.G.; Chang, X.S. A subjective and objective integrated weighting method for landslides susceptibility mapping based on GIS. Environ. Earth Sci. 2012, 65, 1705–1714. [Google Scholar] [CrossRef]
- Feizizadeh, B.; Blaschke, T. GIS-multicriteria decision analysis for landslide susceptibility mapping: Comparing three methods for the Urmia lake basin, Iran. Nat. Hazards 2013, 65, 2105–2128. [Google Scholar] [CrossRef]
- Ayalew, L.; Yamagishi, H.; Ugawa, N. Landslide susceptibility mapping using GIS-based weighted linear combination, the case in Tsugawa area of Agano River, Niigata Prefecture, Japan. Landslides 2004, 1, 73–81. [Google Scholar] [CrossRef]
- Yalcin, A. GIS-based landslide susceptibility mapping using analytical hierarchy process and bivariate statistics in Ardesen (Turkey): Comparisons of results and confirmations. Catena 2008, 72, 1–12. [Google Scholar] [CrossRef]
- Neaupane, K.M.; Piantanakulchai, M. Analytic network process model for landslide hazard zonation. Eng. Geol. 2006, 85, 281–294. [Google Scholar] [CrossRef]
- Roodposhti, M.S.; Rahimi, S.; Beglou, M.J. PROMETHEE II and fuzzy AHP: An enhanced GIS-based landslide susceptibility mapping. Nat. Hazards 2014, 73, 77–95. [Google Scholar] [CrossRef]
- Barredo, J.; Benavides, A.; Hervás, J.; van Westen, C. J. Comparing heuristic landslide hazard assessment techniques using GIS in the Tirajana basin, Gran Canaria Island, Spain. Int. J. Appl. Earth Obs. Geoinf. 2000, 2, 9–23. [Google Scholar] [CrossRef]
- Van Westen, C.J.; Getahun, F.L. Analyzing the evolution of the Tessina landslide using aerial photographs and digital elevation models. Geomorphology 2003, 54, 77–89. [Google Scholar] [CrossRef]
- Ruff, M.; Czurda, K. Landslide susceptibility analysis with a heuristic approach in the Eastern Alps (Vorarlberg, Austria). Geomorphology 2008, 94, 314–324. [Google Scholar] [CrossRef]
- Lee, S.; Min, K. Statistical analysis of landslide susceptibility at Yongin, Korea. Environ. Geol. 2001, 40, 1095–1113. [Google Scholar] [CrossRef]
- Havenith, H.B.; Strom, A.; Caceres, F.; Pirard, E. Analysis of landslide susceptibility in the Suusamyr region, Tien Shan: Statistical and geotechnical approach. Landslides 2006, 3, 39–50. [Google Scholar] [CrossRef]
- Greco, R.; Sorriso-Valvo, M.; Catalano, E. Logistic regression analysis in the evaluation of mass movements susceptibility: The Aspromonte case study, Calabria, Italy. Eng. Geol. 2007, 89, 47–66. [Google Scholar] [CrossRef]
- Nandi, A.; Shakoor, A. A GIS-based landslide susceptibility evaluation using bivariate and multivariate statistical analyses. Eng. Geol. 2010, 110, 11–20. [Google Scholar] [CrossRef]
- Ozdemir, A. Landslide susceptibility mapping using Bayesian approach in the Sultan Mountains (Akşehir, Turkey). Nat. Hazards 2011, 59, 1573–1607. [Google Scholar] [CrossRef]
- Budimir, M.E.A.; Atkinson, P.M.; Lewis, H.G. A systematic review of landslide probability mapping using logistic regression. Landslides 2015, 12, 419–436. [Google Scholar] [CrossRef]
- Shahabi, H.; Hashim, M. Landslide susceptibility mapping using GIS-based statistical models and Remote sensing data in tropical environment. Sci. Rep. 2015, 5, 9899. [Google Scholar] [CrossRef] [PubMed]
- Lee, S.; Ryu, J.H.; Won, J.S.; Park, H.J. Determination and application of the weights for landslide susceptibility mapping using an artificial neural network. Eng. Geol. 2004, 71, 289–302. [Google Scholar] [CrossRef]
- Pradhan, B.; Lee, S. Regional landslide susceptibility analysis using back-propagation neural network model at Cameron Highland, Malaysia. Landslides 2010, 7, 13–30. [Google Scholar] [CrossRef]
- Carrara, A. Multivariate models for landslide hazard evaluation. J. Int. Assoc. Math. Geol. 1983, 15, 403–426. [Google Scholar] [CrossRef]
- Pradhan, B. A comparative study on the predictive ability of the decision tree, support vector machine and neuro-fuzzy models in landslide susceptibility mapping using GIS. Comput. Geosci. 2013, 51, 350–365. [Google Scholar] [CrossRef]
- Bui, D.T.; Tuan, T.A.; Klempe, H.; Pradhan, B.; Revhaug, I. Spatial prediction models for shallow landslide hazards: A comparative assessment of the efficacy of support vector machines, artificial neural networks, kernel logistic regression, and logistic model tree. Landslides 2016, 13, 361–378. [Google Scholar]
- Conforti, M.; Pascale, S.; Robustelli, G.; Sdao, F. Evaluation of prediction capability of the artificial neural networks for mapping landslide susceptibility in the Turbolo River catchment (northern Calabria, Italy). Catena 2014, 113, 236–250. [Google Scholar] [CrossRef]
- Dou, J.; Yamagishi, H.; Pourghasemi, H.R.; Yunus, A.P.; Song, X.; Xu, Y.; Zhu, Z. An integrated artificial neural network model for the landslide susceptibility assessment of Osado Island, Japan. Nat. Hazards 2015, 78, 1749–1776. [Google Scholar] [CrossRef]
- Yeon, Y.K.; Han, J.G.; Ryu, K.H. Landslide susceptibility mapping in Injae, Korea, using a decision tree. Eng. Geol. 2010, 116, 274–283. [Google Scholar] [CrossRef]
- Hong, H.; Pradhan, B.; Xu, C.; Bui, D.T. Spatial prediction of landslide hazard at the Yihuang area (China) using two-class kernel logistic regression, alternating decision tree and support vector machines. Catena 2015, 133, 266–281. [Google Scholar] [CrossRef]
- Youssef, A.M.; Pourghasemi, H.R.; El-Haddad, B.A.; Dhahry, B.K. Landslide susceptibility maps using different probabilistic and bivariate statistical models and comparison of their performance at Wadi Itwad Basin, Asir Region, Saudi Arabia. Bull. Eng. Geol. Environ. 2016, 75, 63–87. [Google Scholar] [CrossRef]
- Pourghasemi, H.R.; Mohammady, M.; Pradhan, B. Landslide susceptibility mapping using index of entropy and conditional probability models in GIS: Safarood Basin, Iran. Catena 2012, 97, 71–84. [Google Scholar] [CrossRef]
- Constantin, M.; Bednarik, M.; Jurchescu, M.C.; Vlaicu, M. Landslide susceptibility assessment using the bivariate statistical analysis and the index of entropy in the Sibiciu Basin (Romania). Environ. Earth Sci. 2011, 63, 397–406. [Google Scholar] [CrossRef]
- Devkota, K.C.; Regmi, A.D.; Pourghasemi, H.R.; Yoshida, K.; Pradhan, B.; Ryu, I.C.; Dhital, M.R.; Althuwaynee, O.F. Landslide susceptibility mapping using certainty factor, index of entropy and logistic regression models in GIS and their comparison at Mugling–Narayanghat road section in Nepal Himalaya. Nat. Hazards 2013, 65, 135–165. [Google Scholar] [CrossRef]
- Tsangaratos, P.; Ilia, I. Combining fuzzy logic and information theory for producing a landslide susceptibility model. In Proceedings of the 14th International Congress of the Geological Society of Greece, Thessaloniki, Greece, 25–27 May 2016; Volume 50, pp. 34–46.
- Zongji, Y.; Jianping, Q.; Xiaogang, Z. Regional landslide zonation based on entropy method in Three Gorges area, China. In Proceedings of the Fuzzy Systems and Knowledge Discovery (FSKD), Yantai, China, 10–12 August 2010; pp. 1336–1339.
- Davis, J.; Blesius, L. A hybrid physical and maximum-entropy landslide susceptibility model. Entropy 2015, 17, 4271–4292. [Google Scholar] [CrossRef]
- Feizizadeh, B.; Roodposhti, M.S.; Jankowski, P.; Blaschke, T. A GIS-based extended fuzzy multi-criteria evaluation for landslide susceptibility mapping. Comput. Geosci. 2014, 73, 208–221. [Google Scholar] [CrossRef] [PubMed]
- Ministry of Natural Resources. Landslide Event Report; Ministry of Natural Resources: Khuzestan, Iran, 2010.
- Komac, M. A landslide susceptibility model using the analytical hierarchy process method and multivariate statistics in perialpine Slovenia. Geomorphology 2006, 74, 17–28. [Google Scholar] [CrossRef]
- Conoscenti, C.; Di Maggio, C.; Rotigliano, E. GIS analysis to assess landslide susceptibility in a fluvial basin of NW Sicily (Italy). Geomorphology 2008, 94, 325–339. [Google Scholar] [CrossRef]
- Thiery, Y.; Malet, J.P.; Sterlacchini, S.; Puissant, A.; Maquaire, O. Landslide susceptibility assessment by bivariate methods at large scales: Application to a complex mountainous environment. Geomorphology 2007, 92, 38–59. [Google Scholar] [CrossRef]
- Kayastha, P.; Dhital, M.R.; De Smedt, F. Landslide susceptibility mapping using the weight of evidence method in the Tinau watershed, Nepal. Nat. Hazards 2012, 63, 479–498. [Google Scholar] [CrossRef]
- Bennett, N.D.; Croke, B.F.; Guariso, G.; Guillaume, J.H.; Hamilton, S. H.; Jakeman, A.J.; Marsili-Libelli, S.; Newham, L.T.; Norton, J.P.; Perrin, C.; et al. Characterising performance of environmental models. Environ. Model. Softw. 2013, 40, 1–20. [Google Scholar] [CrossRef]
- Kritikos, T.; Robinson, T.R.; Davies, T.R. Regional coseismic landslide hazard assessment without historical landslide inventories: A new approach. J. Geophys. Res. Earth Surf. 2015, 120, 711–729. [Google Scholar] [CrossRef]
- Ayalew, L.; Yamagishi, H. The application of GIS-based logistic regression for landslide susceptibility mapping in the Kakuda-Yahiko Mountains, Central Japan. Geomorphology 2005, 65, 15–31. [Google Scholar] [CrossRef]
- Guzzetti, F.; Reichenbach, P.; Ardizzone, F.; Cardinali, M.; Galli, M. Estimating the quality of landslide susceptibility models. Geomorphology 2006, 81, 166–184. [Google Scholar] [CrossRef]
- Lotfi, F.H.; Fallahnejad, R. Imprecise Shannon’s entropy and multi attribute decision making. Entropy 2010, 12, 53–62. [Google Scholar] [CrossRef]
- Sabokbar, H.F.; Roodposhti, M.S.; Tazik, E. Landslide susceptibility mapping using geographically-weighted principal component analysis. Geomorphology 2014, 226, 15–24. [Google Scholar] [CrossRef]
- Pareek, N.; Sharma, M.L.; Arora, M.K. Impact of seismic factors on landslide susceptibility zonation: A case study in part of Indian Himalayas. Landslides 2010, 7, 191–201. [Google Scholar] [CrossRef]
- Kanungo, D.P.; Arora, M.K.; Sarkar, S.; Gupta, R.P. A comparative study of conventional, ANN black box, fuzzy and combined neural and fuzzy weighting procedures for landslide susceptibility zonation in Darjeeling Himalayas. Eng. Geol. 2006, 85, 347–366. [Google Scholar] [CrossRef]
- Lee, S.; Pradhan, B. Landslide hazard mapping at Selangor, Malaysia using frequency ratio and logistic regression models. Landslides 2007, 4, 33–41. [Google Scholar] [CrossRef]
- Marjanović, M.; Kovačević, M.; Bajat, B.; Voženílek, V. Landslide susceptibility assessment using SVM machine learning algorithm. Eng. Geol. 2011, 123, 225–234. [Google Scholar] [CrossRef]
- Shahabi, H.; Ahmad, B.B.; Khezri, S. Evaluation and comparison of bivariate and multivariate statistical methods for landslide susceptibility mapping (case study: Zab basin). Arab. J. Geosci. 2013, 6, 3885–3907. [Google Scholar] [CrossRef]
- Hong, Y.; Hiura, H.; Shino, K.; Sassa, K.; Suemine, A.; Fukuoka, H.; Wang, G. The influence of intense rainfall on the activity of large-scale crystalline schist landslides in Shikoku Island, Japan. Landslides 2005, 2, 97–105. [Google Scholar] [CrossRef]
- Guzzetti, F.; Peruccacci, S.; Rossi, M.; Stark, C.P. Rainfall thresholds for the initiation of landslides in central and southern Europe. Meteorol. Atmos. Phys. 2007, 98, 239–267. [Google Scholar] [CrossRef]
- Youssef, A.M.; Maerz, N.H.; Hassan, A.M. Remote sensing applications to geological problems in Egypt: Case study, slope instability investigation, Sharm El-Sheikh/Ras-Nasrani Area, Southern Sinai. Landslides 2009, 6, 353–360. [Google Scholar] [CrossRef]
- Bathrellos, G.D.; Kalivas, D.P.; Skilodimou, H.D. GIS-based landslide susceptibility mapping models applied to natural and urban planning in Trikala, Central Greece. Estud. Geol. 2009, 65, 49–65. [Google Scholar] [CrossRef]
- Akgun, A.; Sezer, E.A.; Nefeslioglu, H.A.; Gokceoglu, C.; Pradhan, B. An easy-to-use MATLAB program (MamLand) for the assessment of landslide susceptibility using a Mamdani fuzzy algorithm. Comput. Geosci. 2012, 38, 23–34. [Google Scholar] [CrossRef]
- Günlü, A.; Sivrikaya, F.; Baskent, E.Z.; Keles, S.; Çakir, G.; Kadiogullari, A.I. Estimation of stand type parameters and land cover using landsat-7 ETM image: A case study from Turkey. Sensors 2008, 8, 2509–2525. [Google Scholar] [CrossRef]
- Shi, Y.F.; Jin, F.X. Landslide stability analysis based on generalized information entropy. In Proceedings of the International Conference on Environmental Science and Information Application Technology (ESIAT 2009), Los Alamitos, CA, USA, 4–5 July 2009; pp. 83–85.
- Sujatha, E.R. Geoinformatics based landslide susceptibility mapping using probabilistic analysis and entropy index of Tevankarai stream sub-watershed, India. Disaster Adv. 2012, 5, 26–33. [Google Scholar]
- Mon, D.L.; Cheng, C.H.; Lin, J.C. Evaluating weapon system using fuzzy analytic hierarchy process based on entropy weight. Fuzzy Sets Syst. 1994, 62, 127–134. [Google Scholar] [CrossRef]
- Wang, F.; Cao, Y.; Liu, M. Risk early-Warning method for natural disasters based on integration of entropy and DEA model. Appl. Math. 2011, 2, 23–32. [Google Scholar] [CrossRef]
- Akgun, A.; Türk, N. Landslide susceptibility mapping for Ayvalik (Western Turkey) and its vicinity by multicriteria decision analysis. Environ. Earth Sci. 2010, 61, 595–611. [Google Scholar] [CrossRef]
- Liu, J.G.; Mason, P.J.; Hilton, F.; Lee, H. Detection of rapid erosion in SE Spain: A GIS approach based on ERS SAR coherence imagery: InSAR Application. Photogramm. Eng. Remote Sens. 2004, 70, 1179–1185. [Google Scholar] [CrossRef]
- Mason, P.J.; Rosenbaum, M. Geohazard mapping for predicting landslides: An example from the Langhe Hills in Piemonte, NW Italy. Q. J. Eng. Geol. Hydrogeol. 2002, 35, 317–326. [Google Scholar] [CrossRef]
- Gemitzi, A.; Petalas, C.; Tsihrintzis, V.A.; Pisinaras, V. Assessment of groundwater vulnerability to pollution: A combination of GIS, fuzzy logic and decision making techniques. Environ. Geol. 2006, 49, 653–673. [Google Scholar] [CrossRef]
- Rojas-Mora, J.; Josselin, D.; Aryal, J.; Mangiavillano, A.; Ellerkamp, P. The weighted fuzzy barycenter: Definition and application to forest fire control in the PACA region. Int. J. Agric. Environ. Inf. Syst. 2013, 4, 48–67. [Google Scholar] [CrossRef]
- Eastman, J.R. IDRISI Kilimanjaro: Guide to GIS and Image Processing; Clark University: Worcester, MA, USA, 2003. [Google Scholar]
- Galang, J.S. A Comparison of GIS Approaches to Slope Instability Zonation in the Central Blue Ridge Mountains of Virginia. Master‘s Thesis, Virginia Polytechnic Institute and State University, Blacksburg, VA, USA, 21 December 2004. [Google Scholar]
- Fawcett, T. An introduction to ROC analysis. Pattern Recognit. Lett. 2006, 27, 861–874. [Google Scholar] [CrossRef]
- Stein, A.; Aryal, J.; Gort, G. Use of the Bradley-Terry model to quantify association in remotely sensed images. IEEE Trans. Geosci. Remote Sens. 2005, 43, 852–856. [Google Scholar] [CrossRef]
- Lerner, J.S.; Li, Y.; Valdesolo, P.; Kassam, K.S. Emotion and decision making. Annu. Rev. Psychol. 2015, 66, 799–823. [Google Scholar] [CrossRef] [PubMed]
- Castellan, N.J. Individual and Group Decision Making: Current Issues; Psychology Press: Hove, UK, 2013. [Google Scholar]
- Wang, C.; Shen, H.-W. Information theory in scientific visualization. Entropy 2011, 13, 254–273. [Google Scholar] [CrossRef]
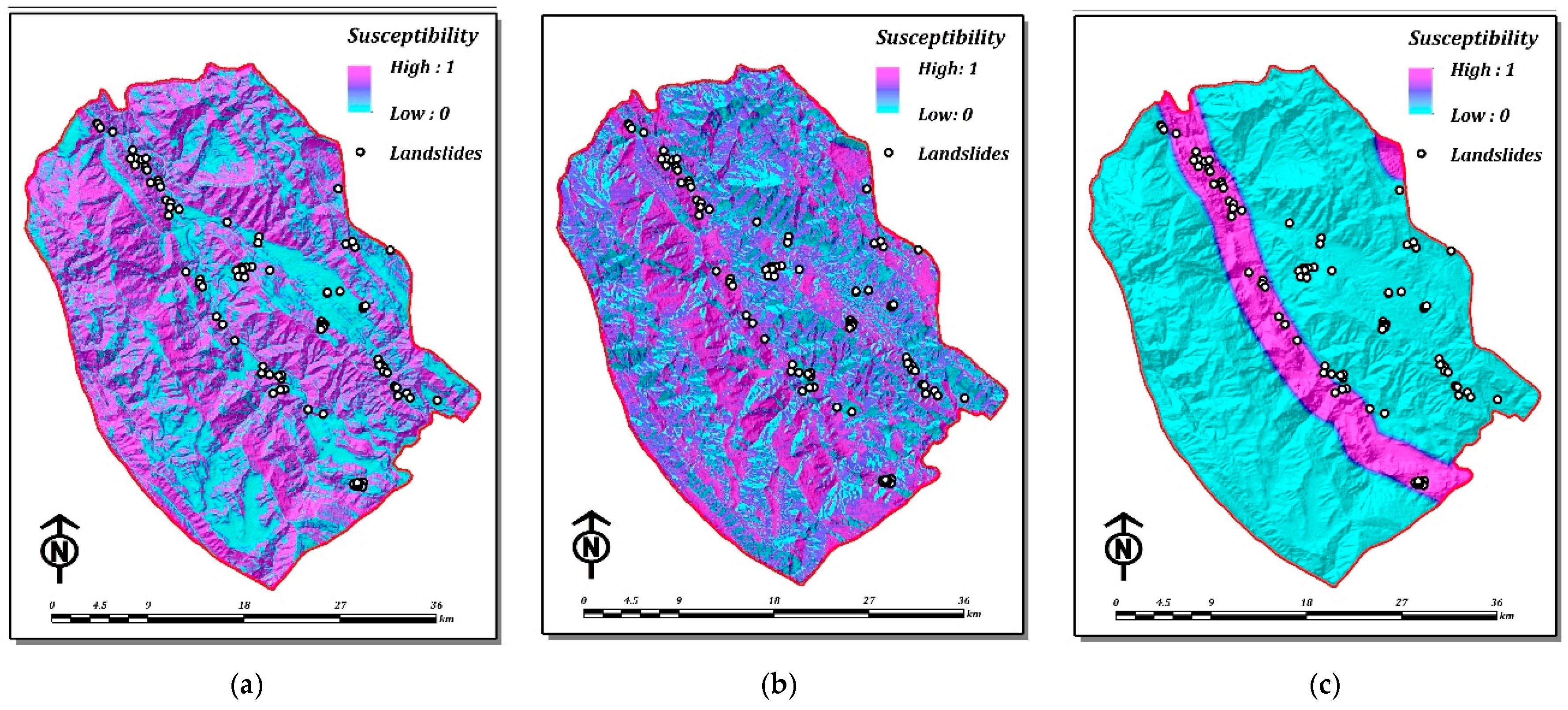
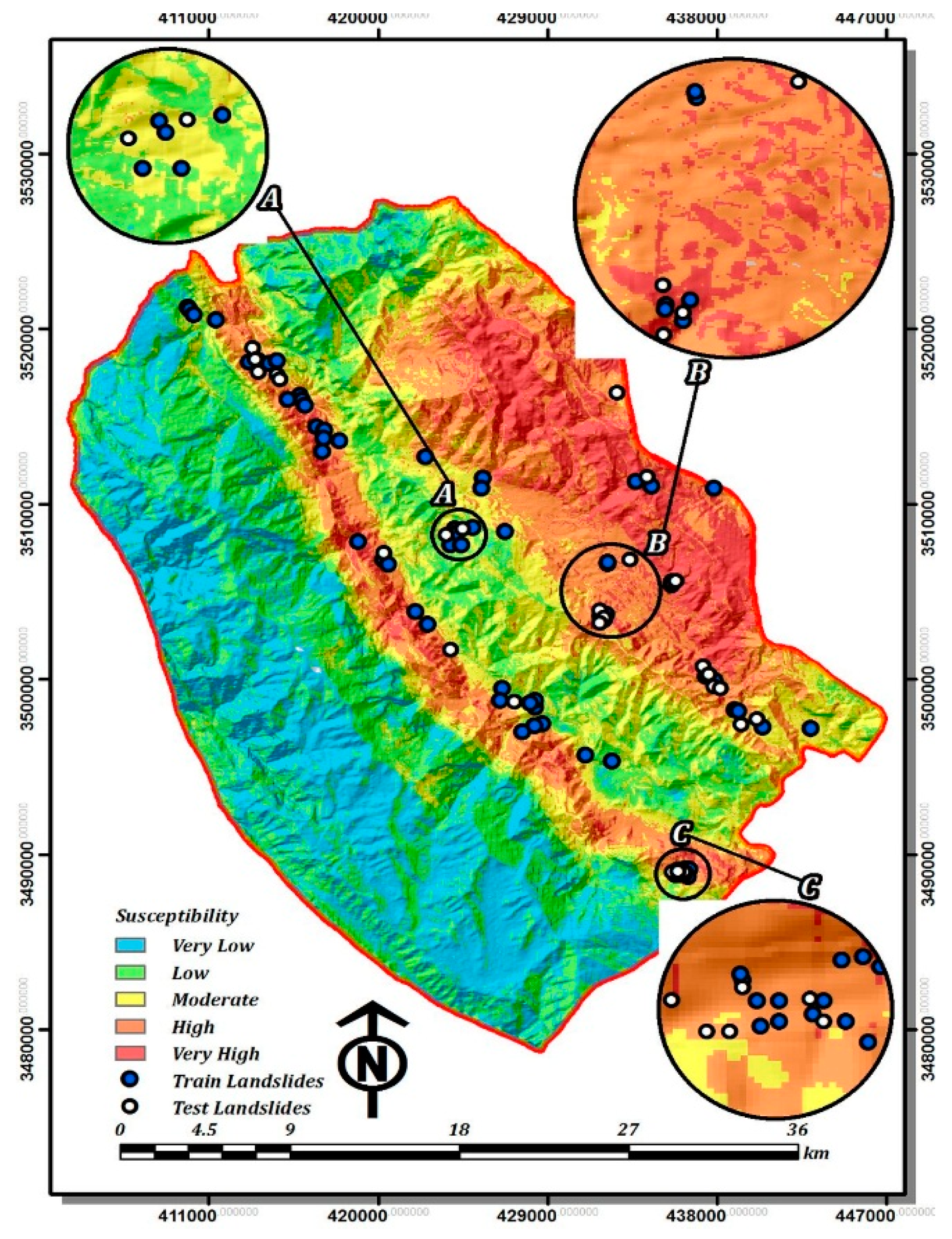
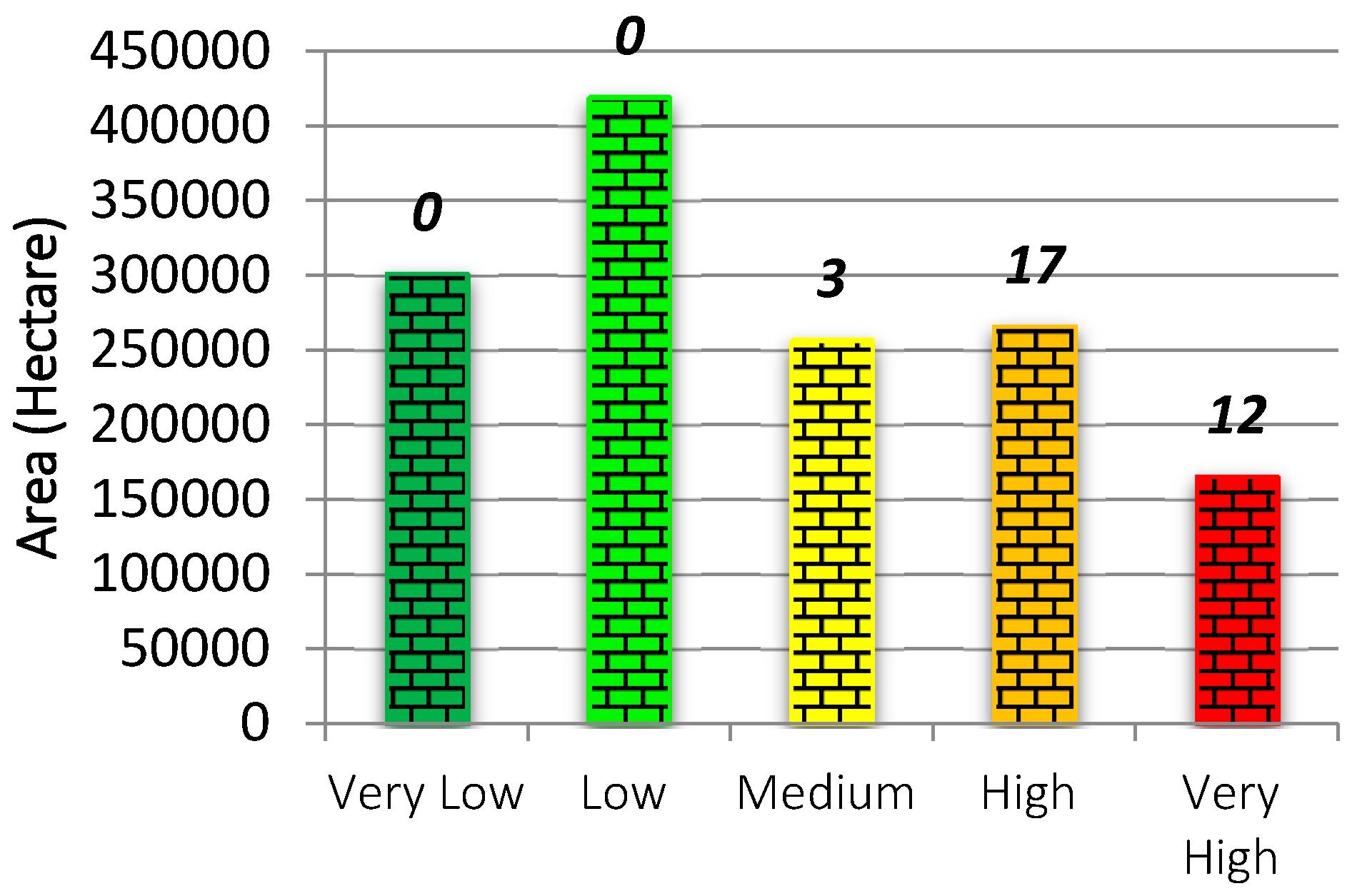
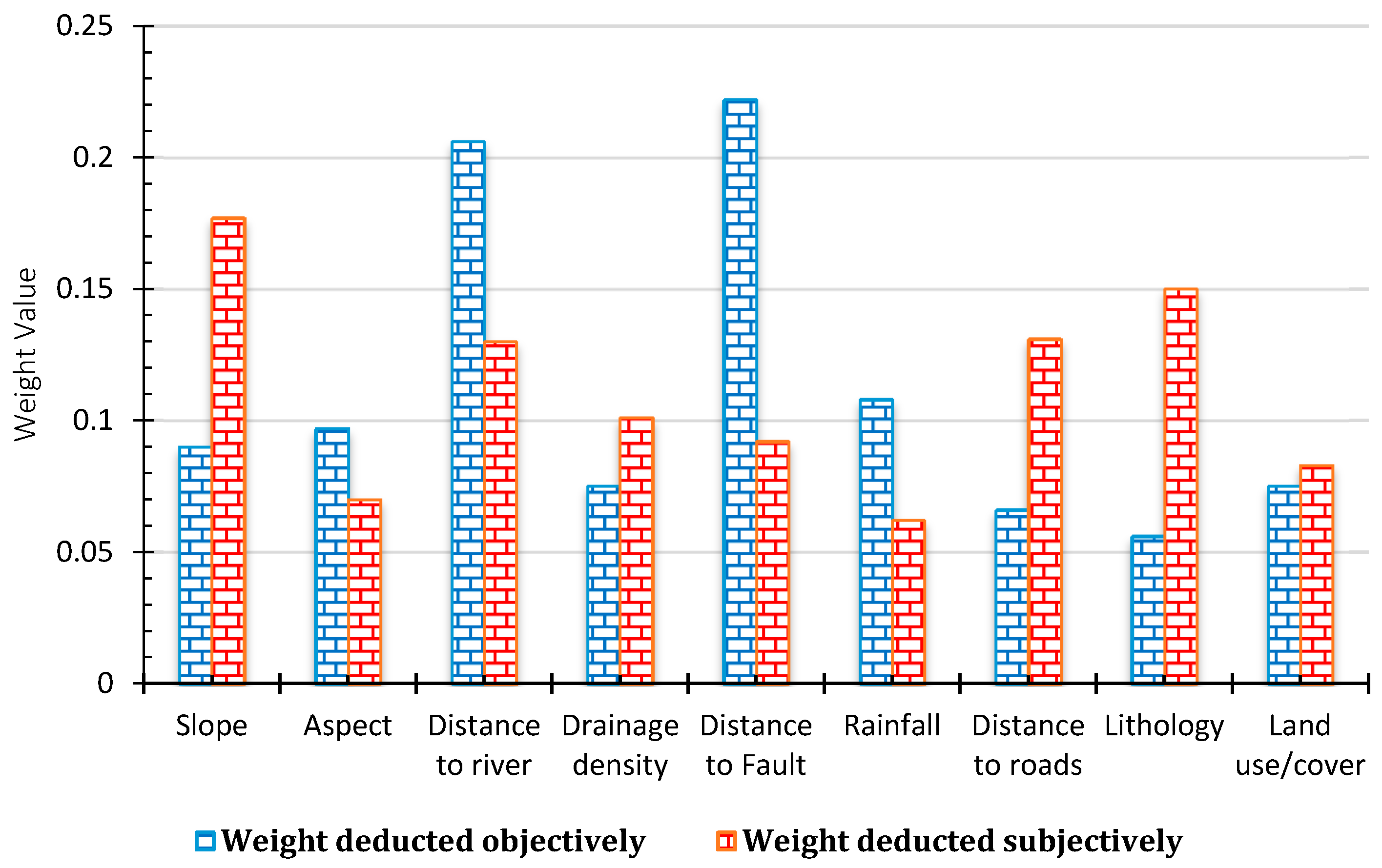
| Criteria | Data Source | Former Studies Using the Same Criterion for GIS-Based LSM |
|---|---|---|
| Slope | 30 m, STRM DEM | Lee and Min [21]; Komac [46]; Ayalew et al. [14]; Conoscenti et al. [47]; Thiery et al. [48]; Yalcin [15]; Kayastha et al. [49]; Bennett et al. [50]; Kritikos et al. [51] |
| Aspect | 30 m, STRM DEM | Ayalew and Yamagishi [52]; Komac [46]; Guzzetti et al. [53]; Thiery et al. [48]; Yalcin [15]; Lotfi et al. [54] |
| River | 1:50,000, Topo-map | Yalcin [15]; Feizizadeh et al. [44]; Faraji Sabokbar et al. [55] |
| Drainage | 1:50,000, Topo-map | Yalcin [15]; Pareek et al. [56]; Shadman et al. [17]; Feizizadeh et al. [44] |
| Fault | 1:100,000, Geo-map | Havenith et al. [22]; Kanungo et al. [57]; Lee and Pradhan [58]; Marjanović et al. [59]; Shahabi et al. [60] |
| Rainfall | 30 years, IMO data | Hong et al. [61]; Guzzetti et al. [62]; Feizizadeh et al. [44] |
| Road | 1:50,000, Topo-map | Ayalew and Yamagishi [52]; Yalcin [15]; Youssef et al. [63]; Bathrellos et al. [64]; Pradhan [31] |
| Lithology | 1:100,000, Geo-map | Ercanoglu and Gokceoglu [3]; Ayalew and Yamagishi [52]; Thiery et al. [48]; Akgun et al. [65]; Davis and Blesius [43] |
| Land use | 30 m, Landsat image | Lee and Pradhan [58]; Bathrellos et al. [64]; Feizizadeh et al. [44] |
| Criteria | Weight |
|---|---|
| Slope | 0.090 |
| Aspect | 0.097 |
| Distance to river | 0.206 |
| Drainage density | 0.075 |
| Distance to Fault | 0.222 |
| Rainfall | 0.108 |
| Distance to roads | 0.066 |
| Lithology | 0.056 |
| Land use/cover | 0.075 |
| Metric | Objective Weighting Approach | Subjective Weighting Approach |
|---|---|---|
| Number of Cases | 64 | 212 |
| Number Correct | 56 (76% of total) | 173 (81% of total) |
| AUC | 0.93 | 0.89 |
| Std. Dev. (Area) | 0.01 | 0.02 |
| Accuracy | 76.6% | 81.6% |
| Sensitivity | 100.0% | 98.1% |
| Specificity | 53.1% | 65.1% |
| Pos Cases Missed | 0 | 2 |
| Neg Cases Missed | 15 | 37 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shadman Roodposhti, M.; Aryal, J.; Shahabi, H.; Safarrad, T. Fuzzy Shannon Entropy: A Hybrid GIS-Based Landslide Susceptibility Mapping Method. Entropy 2016, 18, 343. https://doi.org/10.3390/e18100343
Shadman Roodposhti M, Aryal J, Shahabi H, Safarrad T. Fuzzy Shannon Entropy: A Hybrid GIS-Based Landslide Susceptibility Mapping Method. Entropy. 2016; 18(10):343. https://doi.org/10.3390/e18100343
Chicago/Turabian StyleShadman Roodposhti, Majid, Jagannath Aryal, Himan Shahabi, and Taher Safarrad. 2016. "Fuzzy Shannon Entropy: A Hybrid GIS-Based Landslide Susceptibility Mapping Method" Entropy 18, no. 10: 343. https://doi.org/10.3390/e18100343
APA StyleShadman Roodposhti, M., Aryal, J., Shahabi, H., & Safarrad, T. (2016). Fuzzy Shannon Entropy: A Hybrid GIS-Based Landslide Susceptibility Mapping Method. Entropy, 18(10), 343. https://doi.org/10.3390/e18100343









