Trusted Noise in Continuous-Variable Quantum Key Distribution: A Threat and a Defense
Abstract
:1. Introduction
2. Gaussian Continuous-Variable Quantum Key Distribution Protocols
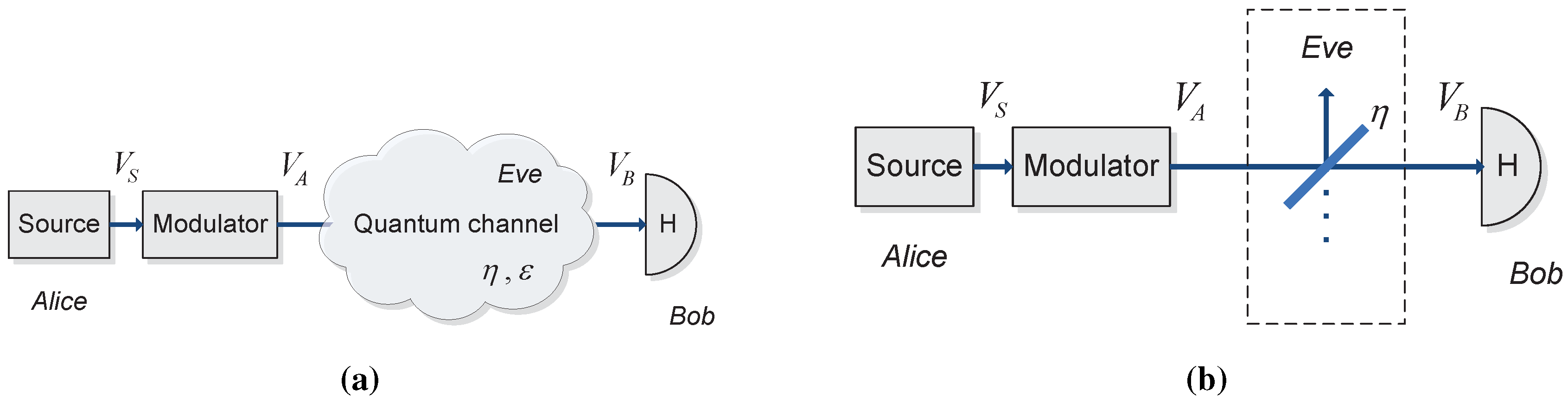
3. Trusted Preparation and Detection Noise in CV QKD
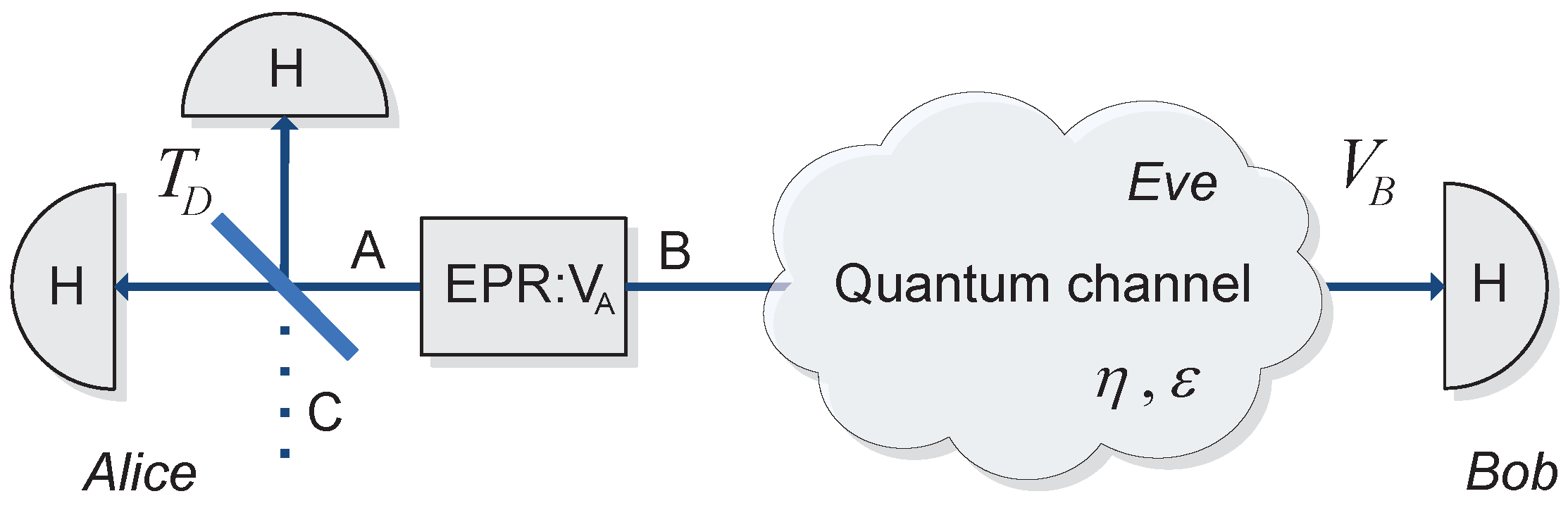
4. Trusted Noise as a Threat
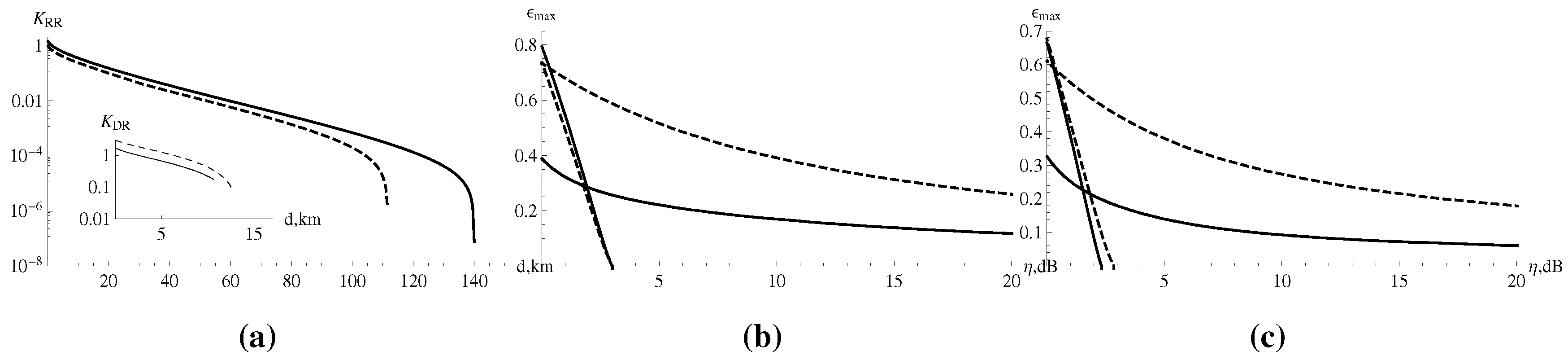
4.1. Preparation Noise and Reverse Reconciliation
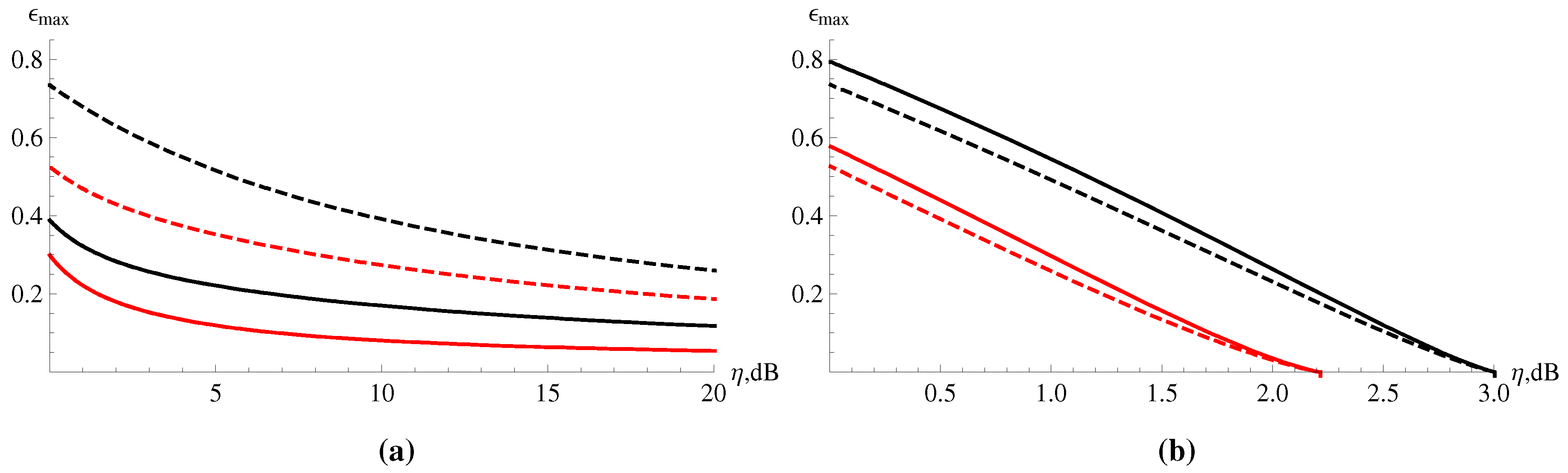
4.2. Detection Noise and Direct Reconciliation
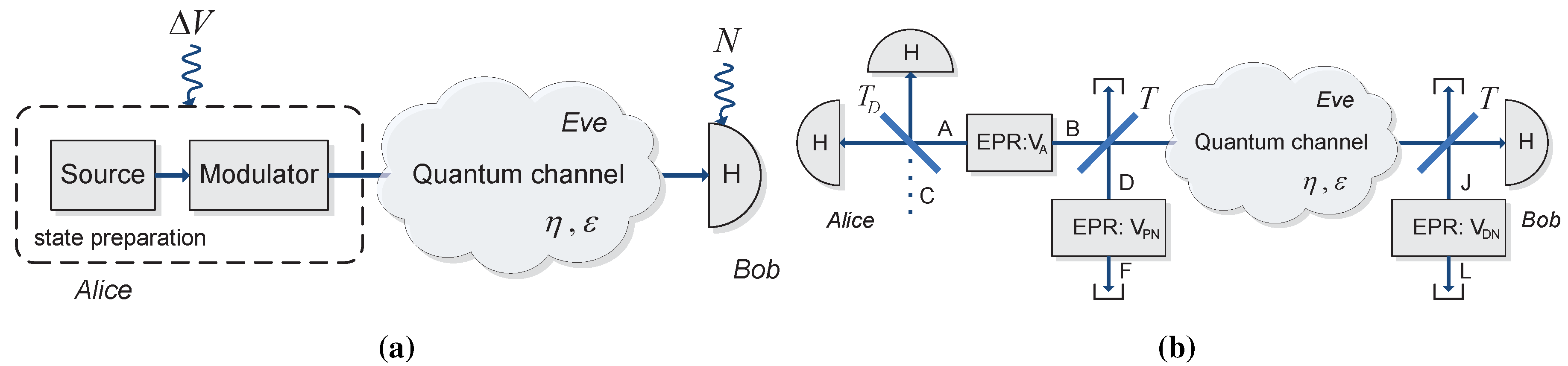
5. Trusted Noise as a Defense
5.1. Preparation Noise and Direct Reconciliation
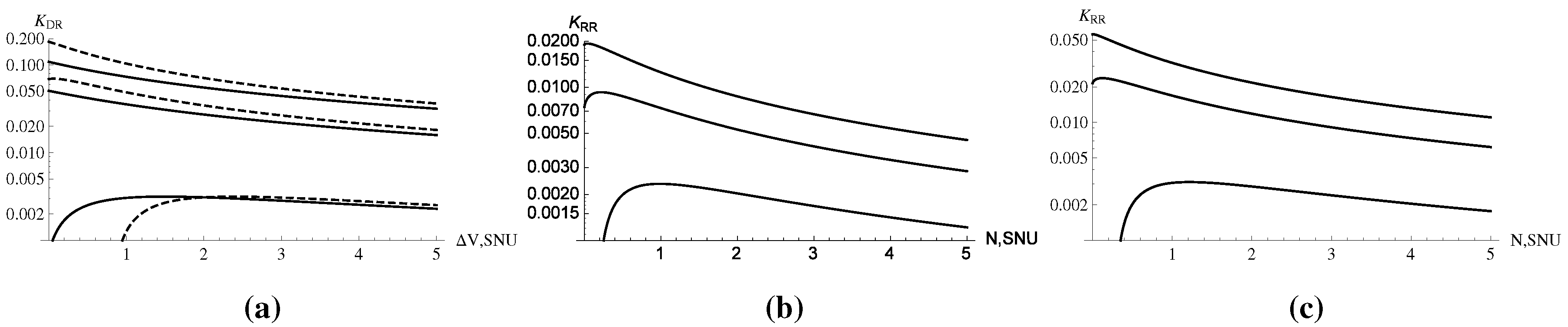
5.2. Detection Noise and Reverse Reconciliation
6. Combined Trusted Noise Effects on Security
6.1. Trusted Noise and Imperfect Post-Processing
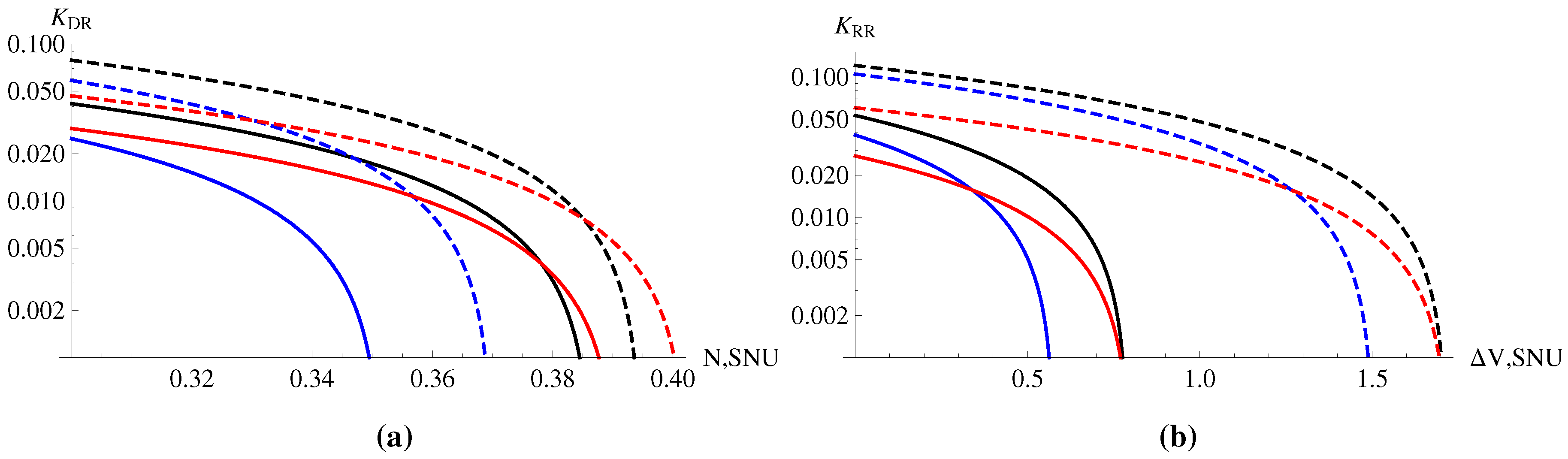
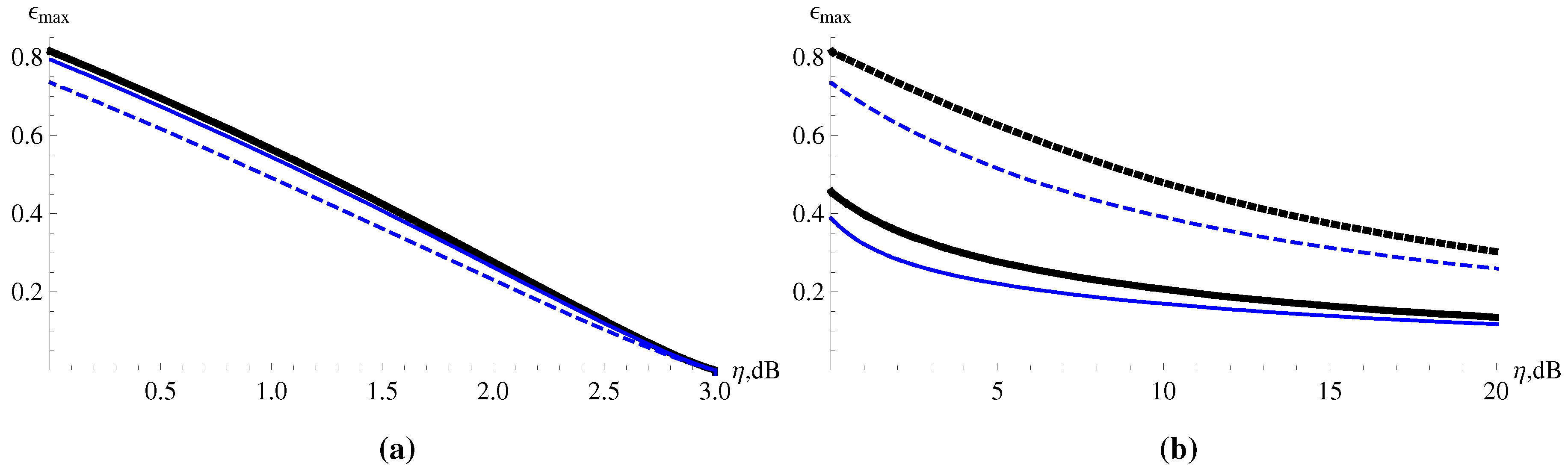
6.2. Combination of Preparation and Detection Noise

7. Summary and Discussion
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Gisin, N.; Ribordy, G.; Tittel, W.; Zbinden, H. Quantum cryptography. Rev. Mod. Phys. 2002, 74, 145–195. [Google Scholar] [CrossRef]
- Scarani, V.; Bechmann-Pasquinucci, H.; Cerf, N.J.; Dušek, M.; Lütkenhaus, N.; Peev, M. The security of practical quantum key distribution. Rev. Mod. Phys. 2009, 81, 1301–1350. [Google Scholar] [CrossRef]
- Vernam, G.S. Cipher printing telegraph systems: For secret wire and radio telegraphic communications. J. AIEE 1926, 45, 109–115. [Google Scholar]
- Shannon, C.E. Communication theory of secrecy systems. Bell Syst. Tech. J. 1949, 28, 656–715. [Google Scholar] [CrossRef]
- Bennett, C.H.; Brassard, G. Quantum cryptography: Public Key Distribution and Coin Tossing. In Proceedings of the International Conference on Computers, Systems and Signal Processing, Bangalore, India, 10–19 December 1984.
- Bennett, C.H. Quantum cryptography using any two nonorthogonal states. Phys. Rev. Lett. 1992, 68, 3121–3124. [Google Scholar] [CrossRef] [PubMed]
- Scarani, V.; Acin, A.; Ribordy, G.; Gisin, N. Quantum cryptography protocols robust against photon number splitting attacks for weak laser pulse implementations. Phys. Rev. Lett. 2004, 92, 057901. [Google Scholar] [CrossRef] [PubMed]
- Brendel, J.; Gisin, N.; Tittel, W.; Zbinden, H. Pulsed energy-time entangled twin-photon source for quantum communication. Phys. Rev. Lett. 1999, 82, 2594–2597. [Google Scholar] [CrossRef]
- Lo, H.K.; Ma, X.; Chen, K. Decoy state quantum key distribution. Phys. Rev. Lett. 2005, 94, 230504. [Google Scholar] [CrossRef] [PubMed]
- Einstein, A.; Podolsky, B.; Rosen, N. Can quantum-mechanical description of physical reality be considered complete? Phys. Rev. 1935, 47, 777–780. [Google Scholar] [CrossRef]
- Ekert, A.K. Quantum cryptography based on Bell’s theorem. Phys. Rev. Lett. 1991, 67, 661–663. [Google Scholar] [CrossRef] [PubMed]
- Bell, J.S. On the Einstein Podolsky Rosen paradox. Physics 1964, 1, 195–200. [Google Scholar]
- Clauser, J.F.; Horne, M.A.; Shimony, A.; Holt, R.A. Proposed experiment to test local hidden-variable theories. Phys. Rev. Lett. 1969, 23, 880–884. [Google Scholar] [CrossRef]
- Bennett, C.H.; Brassard, G.; Mermin, N.D. Quantum cryptography without Bell’s theorem. Phys. Rev. Lett. 1992, 68, 557–559. [Google Scholar] [CrossRef] [PubMed]
- Devetak, I.; Winter, A. Distillation of secret key and entanglement from quantum states. Proc. R. Soc. A 2005, 461, 207–235. [Google Scholar] [CrossRef]
- Kraus, B.; Gisin, N.; Renner, R. Lower and upper bounds on the secret-key rate for quantum key distribution protocols using one-way classical communication. Phys. Rev. Lett. 2005, 95, 080501. [Google Scholar] [CrossRef] [PubMed]
- Müller-Quade, J.; Renner, R. Composability in quantum cryptography. New J. Phys. 2009, 11, 085006. [Google Scholar] [CrossRef]
- Renner, R. Symmetry of large physical systems implies independence of subsystems. Nat. Phys. 2007, 3, 645–649. [Google Scholar] [CrossRef]
- Christandl, M.; König, R.; Renner, R. Postselection technique for quantum channels with applications to quantum cryptography. Phys. Rev. Lett. 2009, 102, 020504. [Google Scholar] [CrossRef] [PubMed]
- Tomamichel, M.; Lim, C.C.W.; Gisin, N.; Renner, R. Tight finite-key analysis for quantum cryptography. Nat. Commun. 2012, 3, 634. [Google Scholar] [CrossRef] [PubMed]
- Braunstein, S.L.; van Loock, P. Quantum information with continuous variables. Rev. Mod. Phys. 2005, 77, 513–577. [Google Scholar] [CrossRef]
- Weedbrook, C.; Pirandola, S.; García-Patrón, R.; Cerf, N.J.; Ralph, T.C.; Shapiro, J.H.; Lloyd, S. Gaussian quantum information. Rev. Mod. Phys. 2012, 84. [Google Scholar] [CrossRef]
- Lorenz, S.; Korolkova, N.; Leuchs, G. Continuous-variable quantum key distribution using polarization encoding and post selection. Appl. Phys. B 2004, 79, 273–277. [Google Scholar] [CrossRef] [Green Version]
- Funk, A.; Raymer, M. Quantum key distribution using nonclassical photon-number correlations in macroscopic light pulses. Phys. Rev. A 2002, 65, 042307. [Google Scholar] [CrossRef]
- Zhang, Y.; Kasai, K.; Hayasaka, K. Quantum channel using photon number correlated twin beams. Opt. Express 2003, 11, 3592–3597. [Google Scholar] [CrossRef] [PubMed]
- Usenko, V.C.; Lev, B.I. Large-alphabet quantum key distribution with two-mode coherently correlated beams. Phys. Lett. A 2005, 348, 17–23. [Google Scholar] [CrossRef] [Green Version]
- Usenko, V.C.; Paris, M.G. Multiphoton communication in lossy channels with photon-number entangled states. Phys. Rev. A 2007, 75, 043812. [Google Scholar] [CrossRef]
- Usenko, V.C.; Paris, M.G. Quantum communication with photon-number entangled states and realistic photodetection. Phys. Lett. A 2010, 374, 1342–1345. [Google Scholar] [CrossRef]
- Ralph, T.C. Continuous variable quantum cryptography. Phys. Rev. A 1999, 61, 010303. [Google Scholar] [CrossRef]
- Ralph, T.C. Security of continuous-variable quantum cryptography. Phys. Rev. A 2000, 62, 062306. [Google Scholar] [CrossRef]
- Hillery, M. Quantum cryptography with squeezed states. Phys. Rev. A 2000, 61, 022309. [Google Scholar] [CrossRef]
- Gottesman, D.; Preskill, J. Secure quantum key distribution using squeezed states. Phys. Rev. A 2001, 63, 022309. [Google Scholar] [CrossRef]
- Reid, M.D. Quantum cryptography with a predetermined key, using continuous-variable Einstein–Podolsky–Rosen correlations. Phys. Rev. A 2000, 62, 062308. [Google Scholar] [CrossRef]
- Silberhorn, C.; Korolkova, N.; Leuchs, G. Quantum key distribution with bright entangled beams. Phys. Rev. Lett. 2002, 88, 167902. [Google Scholar] [CrossRef] [PubMed]
- Cerf, N.J.; Levy, M.; van Assche, G. Quantum distribution of Gaussian keys using squeezed states. Phys. Rev. A 2001, 63, 052311. [Google Scholar] [CrossRef]
- Grosshans, F.; Grangier, P. Continuous variable quantum cryptography using coherent states. Phys. Rev. Lett. 2002, 88, 057902. [Google Scholar] [CrossRef] [PubMed]
- Silberhorn, C.; Ralph, T.C.; Lütkenhaus, N.; Leuchs, G. Continuous variable quantum cryptography: Beating the 3 dB loss limit. Phys. Rev. Lett. 2002, 89, 167901. [Google Scholar] [CrossRef] [PubMed]
- Grosshans, F.; van Assche, G.; Wenger, J.; Brouri, R.; Cerf, N.J.; Grangier, P. Quantum key distribution using Gaussian-modulated coherent states. Nature 2003, 421, 238–241. [Google Scholar] [CrossRef] [PubMed]
- Weedbrook, C.; Lance, A.M.; Bowen, W.P.; Symul, T.; Ralph, T.C.; Lam, P.K. Quantum cryptography without switching. Phys. Rev. Lett. 2004, 93, 170504. [Google Scholar] [CrossRef] [PubMed]
- Usenko, V.C.; Grosshans, F. Unidimensional continuous-variable quantum key distribution. Phys. Rev. A 2015, 92, 062337. [Google Scholar] [CrossRef]
- Grosshans, F.; Cerf, N.J. Continuous-variable quantum cryptography is secure against non-Gaussian attacks. Phys. Rev. Lett. 2004, 92, 047905. [Google Scholar] [CrossRef] [PubMed]
- Navascués, M.; Grosshans, F.; Acin, A. Optimality of Gaussian attacks in continuous-variable quantum cryptography. Phys. Rev. Lett. 2006, 97, 190502. [Google Scholar] [CrossRef] [PubMed]
- García-Patrón, R.; Cerf, N.J. Unconditional optimality of Gaussian attacks against continuous-variable quantum key distribution. Phys. Rev. Lett. 2006, 97, 190503. [Google Scholar] [CrossRef] [PubMed]
- Wolf, M.M.; Giedke, G.; Cirac, J.I. Extremality of Gaussian quantum states. Phys. Rev. Lett. 2006, 96, 080502. [Google Scholar] [CrossRef] [PubMed]
- Pirandola, S.; Braunstein, S.L.; Lloyd, S. Characterization of collective Gaussian attacks and security of coherent-state quantum cryptography. Phys. Rev. Lett. 2008, 101, 200504. [Google Scholar] [CrossRef] [PubMed]
- Pirandola, S.; García-Patrón, R.; Braunstein, S.L.; Lloyd, S. Direct and reverse secret-key capacities of a quantum channel. Phys. Rev. Lett. 2009, 102, 050503. [Google Scholar] [CrossRef] [PubMed]
- Renner, R.; Cirac, J.I. de Finetti representation theorem for infinite-dimensional quantum systems and applications to quantum cryptography. Phys. Rev. Lett. 2009, 102, 110504. [Google Scholar] [CrossRef] [PubMed]
- Braunstein, S.L.; Kimble, H.J. Teleportation of continuous quantum variables. Phys. Rev. Lett. 1998, 80, 869–872. [Google Scholar] [CrossRef]
- Chizhov, A.; Knöll, L.; Welsch, D.G. Continuous-variable quantum teleportation through lossy channels. Phys. Rev. A 2002, 65, 022310. [Google Scholar] [CrossRef]
- Fiurášek, J. Improving the fidelity of continuous-variable teleportation via local operations. Phys. Rev. A 2002, 66, 012304. [Google Scholar] [CrossRef]
- Pirandola, S.; Mancini, S. Quantum teleportation with continuous variables: A survey. Laser Phys. 2006, 16, 1418–1438. [Google Scholar] [CrossRef]
- Cerf, N.J.; Iblisdir, S. Optimal N-to-M cloning of conjugate quantum variables. Phys. Rev. A 2000, 62, 040301. [Google Scholar] [CrossRef]
- Braunstein, S.L.; Cerf, N.J.; Iblisdir, S.; van Loock, P.; Massar, S. Optimal cloning of coherent states with a linear amplifier and beam splitters. Phys. Rev. Lett. 2001, 86, 4938–4941. [Google Scholar] [CrossRef] [PubMed]
- Fiurášek, J. Optical implementation of continuous-variable quantum cloning machines. Phys. Rev. Lett. 2001, 86, 4942–4945. [Google Scholar] [CrossRef] [PubMed]
- Leverrier, A.; Grosshans, F.; Grangier, P. Finite-size analysis of a continuous-variable quantum key distribution. Phys. Rev. A 2010, 81, 062343. [Google Scholar] [CrossRef]
- Ruppert, L.; Usenko, V.C.; Filip, R. Long-distance continuous-variable quantum key distribution with efficient channel estimation. Phys. Rev. A 2014, 90, 062310. [Google Scholar] [CrossRef]
- Leverrier, A.; Grangier, P. Simple proof that Gaussian attacks are optimal among collective attacks against continuous-variable quantum key distribution with a Gaussian modulation. Phys. Rev. A 2010, 81, 062314. [Google Scholar] [CrossRef]
- Walk, N.; Ralph, T.C.; Symul, T.; Lam, P.K. Security of continuous-variable quantum cryptography with Gaussian postselection. Phys. Rev. A 2013, 87, 020303. [Google Scholar] [CrossRef]
- Fiurášek, J.; Cerf, N.J. Gaussian postselection and virtual noiseless amplification in continuous-variable quantum key distribution. Phys. Rev. A 2012, 86, 060302. [Google Scholar] [CrossRef]
- Furrer, F.; Franz, T.; Berta, M.; Leverrier, A.; Scholz, V.B.; Tomamichel, M.; Werner, R.F. Continuous variable quantum key distribution: Finite-key analysis of composable security against coherent attacks. Phys. Rev. Lett. 2012, 109, 100502. [Google Scholar] [CrossRef] [PubMed]
- Furrer, F. Reverse-reconciliation continuous-variable quantum key distribution based on the uncertainty principle. Phys. Rev. A 2014, 90, 042325. [Google Scholar] [CrossRef]
- Leverrier, A.; García-Patrón, R.; Renner, R.; Cerf, N.J. Security of continuous-variable quantum key distribution against general attacks. Phys. Rev. Lett. 2013, 110, 030502. [Google Scholar] [CrossRef] [PubMed]
- Leverrier, A. Composable security proof for continuous-variable quantum key distribution with coherent states. Phys. Rev. Lett. 2015, 114, 070501. [Google Scholar] [CrossRef] [PubMed]
- Heid, M.; Lütkenhaus, N. Efficiency of coherent-state quantum cryptography in the presence of loss: Influence of realistic error correction. Phys. Rev. A 2006, 73, 052316. [Google Scholar] [CrossRef]
- Lodewyck, J.; Bloch, M.; García-Patrón, R.; Fossier, S.; Karpov, E.; Diamanti, E.; Debuisschert, T.; Cerf, N.J.; Tualle-Brouri, R.; McLaughlin, S.W.; et al. Quantum key distribution over 25 km with an all-fiber continuous-variable system. Phys. Rev. A 2007, 76, 042305. [Google Scholar] [CrossRef]
- Fossier, S.; Diamanti, E.; Debuisschert, T.; Villing, A.; Tualle-Brouri, R.; Grangier, P. Field test of a continuous-variable quantum key distribution prototype. New J. Phys. 2009, 11, 045023. [Google Scholar] [CrossRef]
- Leverrier, A.; Alléaume, R.; Boutros, J.; Zémor, G.; Grangier, P. Multidimensional reconciliation for a continuous-variable quantum key distribution. Phys. Rev. A 2008, 77, 042325. [Google Scholar] [CrossRef]
- Jouguet, P.; Kunz-Jacques, S.; Leverrier, A. Long-distance continuous-variable quantum key distribution with a Gaussian modulation. Phys. Rev. A 2011, 84, 062317. [Google Scholar] [CrossRef]
- Jouguet, P.; Kunz-Jacques, S. High performance error correction for quantum key distribution using polar codes. Quantum Inf. Comput. 2014, 14, 329–338. [Google Scholar]
- Jouguet, P.; Kunz-Jacques, S.; Leverrier, A.; Grangier, P.; Diamanti, E. Experimental demonstration of long-distance continuous-variable quantum key distribution. Nat. Photonics 2013, 7, 378–381. [Google Scholar] [CrossRef]
- Usenko, V.C.; Filip, R. Squeezed-state quantum key distribution upon imperfect reconciliation. New J. Phys. 2011, 13, 113007. [Google Scholar] [CrossRef]
- Grosshans, F. Collective attacks and unconditional security in continuous variable quantum key distribution. Phys. Rev. Lett. 2005, 94, 020504. [Google Scholar] [CrossRef] [PubMed]
- Grosshans, F.; Cerf, N.J.; Wenger, J.; Tualle-Brouri, R.; Grangier, P. Virtual entanglement and reconciliation protocols for quantum cryptography with continuous variables. Quantum Inf. Comput. 2003, 3, 535–552. [Google Scholar]
- Navascués, M.; Acín, A. Security bounds for continuous variables quantum key distribution. Phys. Rev. Lett. 2005, 94, 020505. [Google Scholar] [CrossRef] [PubMed]
- Heid, M.; Lütkenhaus, N. Security of coherent-state quantum cryptography in the presence of Gaussian noise. Phys. Rev. A 2007, 76, 022313. [Google Scholar] [CrossRef]
- Blandino, R.; Leverrier, A.; Barbieri, M.; Etesse, J.; Grangier, P.; Tualle-Brouri, R. Improving the maximum transmission distance of continuous-variable quantum key distribution using a noiseless amplifier. Phys. Rev. A 2012, 86, 012327. [Google Scholar] [CrossRef]
- Mayers, D.; Yao, A. Quantum Cryptography with Imperfect Apparatus. In Proceedings of the 39th Annual Symposium on Foundations of Computer Science (FOCS ‘98), Palo Alto, CA, USA, 8–11 November 1998.
- Barrett, J.; Hardy, L.; Kent, A. No signaling and quantum key distribution. Phys. Rev. Lett. 2005, 95, 010503. [Google Scholar] [CrossRef] [PubMed]
- Acín, A.; Gisin, N.; Masanes, L. From Bell’s Theorem to Secure Quantum Key Distribution. Phys. Rev. Lett. 2006, 97, 120405. [Google Scholar] [CrossRef] [PubMed]
- Acín, A.; Brunner, N.; Gisin, N.; Massar, S.; Pironio, S.; Scarani, V. Device-independent security of quantum cryptography against collective attacks. Phys. Rev. Lett. 2007, 98, 230501. [Google Scholar] [CrossRef] [PubMed]
- Gisin, N.; Pironio, S.; Sangouard, N. Proposal for implementing device-independent quantum key distribution based on a heralded qubit amplifier. Phys. Rev. Lett. 2010, 105, 070501. [Google Scholar] [CrossRef] [PubMed]
- Vazirani, U.; Vidick, T. Fully device-independent quantum key distribution. Phys. Rev. Lett. 2014, 113, 140501. [Google Scholar] [CrossRef] [PubMed]
- Grangier, P.; Potasek, M.; Yurke, B. Probing the phase coherence of parametrically generated photon pairs: A new test of Bell’s inequalities. Phys. Rev. A 1988, 38, 3132. [Google Scholar] [CrossRef] [PubMed]
- Banaszek, K.; Wódkiewicz, K. Nonlocality of the Einstein–Podolsky–Rosen state in the Wigner representation. Phys. Rev. A 1998, 58, 4345–4347. [Google Scholar] [CrossRef]
- Banaszek, K.; Wódkiewicz, K. Testing quantum nonlocality in phase space. Phys. Rev. Lett. 1999, 82, 2009–2013. [Google Scholar] [CrossRef]
- Marshall, K.; Weedbrook, C. Device-independent quantum cryptography for continuous variables. Phys. Rev. A 2014, 90, 042311. [Google Scholar] [CrossRef]
- Gottesman, D.; Kitaev, A.; Preskill, J. Encoding a qubit in an oscillator. Phys. Rev. A 2001, 64, 012310. [Google Scholar] [CrossRef]
- Braunstein, S.L.; Pirandola, S. Side-channel-free quantum key distribution. Phys. Rev. Lett. 2012, 108, 130502. [Google Scholar] [CrossRef] [PubMed]
- Lo, H.K.; Curty, M.; Qi, B. Measurement-device-independent quantum key distribution. Phys. Rev. Lett. 2012, 108, 130503. [Google Scholar] [CrossRef] [PubMed]
- Pirandola, S.; Ottaviani, C.; Spedalieri, G.; Weedbrook, C.; Braunstein, S.L.; Lloyd, S.; Gehring, T.; Jacobsen, C.S.; Andersen, U.L. High-rate quantum cryptography in untrusted networks. 2014; arXiv:1312.4104. [Google Scholar]
- Pirandola, S.; Ottaviani, C.; Spedalieri, G.; Weedbrook, C.; Braunstein, S.L.; Lloyd, S.; Gehring, T.; Jacobsen, C.S.; Andersen, U.L. High-rate measurement-device-independent quantum cryptography. Nat. Photonics 2015, 9, 397–402. [Google Scholar] [CrossRef]
- Zhang, Y.C.; Li, Z.; Yu, S.; Gu, W.; Peng, X.; Guo, H. Continuous-variable measurement-device-independent quantum key distribution using squeezed states. Phys. Rev. A 2014, 90, 052325. [Google Scholar] [CrossRef]
- Li, Z.; Zhang, Y.C.; Xu, F.; Peng, X.; Guo, H. Continuous-variable measurement-device-independent quantum key distribution. Phys. Rev. A 2014, 89, 052301. [Google Scholar] [CrossRef]
- Pirandola, S. Quantum discord as a resource for quantum cryptography. Sci. Rep. 2014, 4. [Google Scholar] [CrossRef] [PubMed]
- Csiszár, I.; Körner, J. Broadcast channels with confidential messages. IEEE Trans. Inf. Theory 1978, 24, 339–348. [Google Scholar] [CrossRef]
- Holevo, A.S.; Werner, R.F. Evaluating capacities of bosonic Gaussian channels. Phys. Rev. A 2001, 63, 032312. [Google Scholar] [CrossRef]
- Serafini, A.; Paris, M.G.A.; Illuminati, F.; de Siena, S. Quantifying decoherence in continuous variable systems. J. Opt. B: Quantum Semiclass. Opt. 2005, 7. [Google Scholar] [CrossRef]
- Penrose, R. A Generalized Inverse for Matrices. In Mathematical Proceedings of the Cambridge Philosophical Society; Cambridge University Press: Cambridge, UK, 1955; pp. 406–413. [Google Scholar]
- Serafini, A.; Illuminati, F.; de Siena, S. Symplectic invariants, entropic measures and correlations of Gaussian states. J. Phys. B 2004, 37, L21–L28. [Google Scholar] [CrossRef]
- Araki, H.; Lieb, E.H. Entropy Inequalities. In Inequalities; Springer: Berlin/Heidelberg, Germany, 2002; pp. 47–57. [Google Scholar]
- Lance, A.M.; Symul, T.; Sharma, V.; Weedbrook, C.; Ralph, T.C.; Lam, P.K. No-switching quantum key distribution using broadband modulated coherent light. Phys. Rev. Lett. 2005, 95, 180503. [Google Scholar] [CrossRef] [PubMed]
- Usenko, V.C.; Heim, B.; Peuntinger, C.; Wittmann, C.; Marquardt, C.; Leuchs, G.; Filip, R. Entanglement of Gaussian states and the applicability to quantum key distribution over fading channels. New J. Phys. 2012, 14, 093048. [Google Scholar] [CrossRef]
- García-Patrón, R.; Cerf, N.J. Continuous-variable quantum key distribution protocols over noisy channels. Phys. Rev. Lett. 2009, 102, 130501. [Google Scholar] [CrossRef] [PubMed]
- Fossier, S.; Diamanti, E.; Debuisschert, T.; Tualle-Brouri, R.; Grangier, P. Improvement of continuous-variable quantum key distribution systems by using optical preamplifiers. J. Phys. B 2009, 42, 114014. [Google Scholar] [CrossRef]
- Filip, R. Continuous-variable quantum key distribution with noisy coherent states. Phys. Rev. A 2008, 77, 022310. [Google Scholar] [CrossRef]
- Usenko, V.C.; Filip, R. Feasibility of continuous-variable quantum key distribution with noisy coherent states. Phys. Rev. A 2010, 81, 022318. [Google Scholar] [CrossRef]
- Weedbrook, C.; Pirandola, S.; Lloyd, S.; Ralph, T.C. Quantum cryptography approaching the classical limit. Phys. Rev. Lett. 2010, 105, 110501. [Google Scholar] [CrossRef] [PubMed]
- Weedbrook, C.; Pirandola, S.; Ralph, T.C. Continuous-variable quantum key distribution using thermal states. Phys. Rev. A 2012, 86, 022318. [Google Scholar] [CrossRef]
- Jouguet, P.; Kunz-Jacques, S.; Diamanti, E.; Leverrier, A. Analysis of imperfections in practical continuous-variable quantum key distribution. Phys. Rev. A 2012, 86, 032309. [Google Scholar] [CrossRef]
- Huang, J.Z.; Weedbrook, C.; Yin, Z.Q.; Wang, S.; Li, H.W.; Chen, W.; Guo, G.C.; Han, Z.F. Quantum hacking of a continuous-variable quantum-key-distribution system using a wavelength attack. Phys. Rev. A 2013, 87, 062329. [Google Scholar] [CrossRef]
- Ma, X.C.; Sun, S.H.; Jiang, M.S.; Liang, L.M. Wavelength attack on practical continuous-variable quantum-key-distribution system with a heterodyne protocol. Phys. Rev. A 2013, 87, 052309. [Google Scholar] [CrossRef]
- Huang, J.Z.; Kunz-Jacques, S.; Jouguet, P.; Weedbrook, C.; Yin, Z.Q.; Wang, S.; Chen, W.; Guo, G.C.; Han, Z.F. Quantum hacking on quantum key distribution using homodyne detection. Phys. Rev. A 2014, 89, 032304. [Google Scholar] [CrossRef]
- Kunz-Jacques, S.; Jouguet, P. Robust shot-noise measurement for continuous-variable quantum key distribution. Phys. Rev. A 2015, 91, 022307. [Google Scholar] [CrossRef]
- Jouguet, P.; Kunz-Jacques, S.; Diamanti, E. Preventing calibration attacks on the local oscillator in continuous-variable quantum key distribution. Phys. Rev. A 2013, 87, 062313. [Google Scholar] [CrossRef]
- Ma, X.C.; Sun, S.H.; Jiang, M.S.; Liang, L.M. Local oscillator fluctuation opens a loophole for Eve in practical continuous-variable quantum-key-distribution systems. Phys. Rev. A 2013, 88, 022339. [Google Scholar] [CrossRef]
- Ma, X.C.; Sun, S.H.; Jiang, M.S.; Gui, M.; Zhou, Y.L.; Liang, L.M. Enhancement of the security of a practical continuous-variable quantum-key-distribution system by manipulating the intensity of the local oscillator. Phys. Rev. A 2014, 89, 032310. [Google Scholar] [CrossRef]
- Shen, Y.; Peng, X.; Yang, J.; Guo, H. Continuous-variable quantum key distribution with Gaussian source noise. Phys. Rev. A 2011, 83, 052304. [Google Scholar] [CrossRef]
- Huang, P.; He, G.Q.; Zeng, G.H. Bound on Noise of Coherent Source for Secure Continuous-Variable Quantum Key Distribution. Int. J. Theor. Phys. 2013, 52, 1572–1582. [Google Scholar] [CrossRef]
- Yang, J.; Xu, B.; Guo, H. Source monitoring for continuous-variable quantum key distribution. Phys. Rev. A 2012, 86, 042314. [Google Scholar] [CrossRef]
- Wang, T.; Yu, S.; Zhang, Y.C.; Gu, W.; Guo, H. Improving the maximum transmission distance of continuous-variable quantum key distribution with noisy coherent states using a noiseless amplifier. Phys. Lett. A 2014, 378, 2808–2812. [Google Scholar] [CrossRef]
- Madsen, L.S.; Usenko, V.C.; Lassen, M.; Filip, R.; Andersen, U.L. Continuous variable quantum key distribution with modulated entangled states. Nat. Commun. 2012, 3. [Google Scholar] [CrossRef] [PubMed]
- Weedbrook, C. Continuous-variable quantum key distribution with entanglement in the middle. Phys. Rev. A 2013, 87, 022308. [Google Scholar] [CrossRef]
- Su, X.; Wang, W.; Wang, Y.; Jia, X.; Xie, C.; Peng, K. Continuous variable quantum key distribution based on optical entangled states without signal modulation. Europhys. Lett. 2009, 87, 20005. [Google Scholar] [CrossRef]
- Usenko, V.C.; Ruppert, L.; Filip, R. Entanglement-based continuous-variable quantum key distribution with multimode states and detectors. Phys. Rev. A 2014, 90, 062326. [Google Scholar] [CrossRef]
- Usenko, V.C.; Ruppert, L.; Filip, R. Quantum communication with macroscopically bright nonclassical states. Opt. Express 2015, 23, 31534–31543. [Google Scholar] [CrossRef] [PubMed]
- Peřina, J.; Křepelka, J.; Peřina, J.; Bondani, M.; Allevi, A.; Andreoni, A. Experimental joint signal-idler quasidistributions and photon-number statistics for mesoscopic twin beams. Phys. Rev. A 2007, 76, 043806. [Google Scholar] [CrossRef]
- Iskhakov, T.; Chekhova, M.V.; Leuchs, G. Generation and direct detection of broadband mesoscopic polarization-squeezed vacuum. Phys. Rev. Lett. 2009, 102, 183602. [Google Scholar] [CrossRef] [PubMed]
- Pirandola, S.; Mancini, S.; Lloyd, S.; Braunstein, S.L. Continuous-variable quantum cryptography using two-way quantum communication. Nat. Phys. 2008, 4, 726–730. [Google Scholar] [CrossRef]
- Weedbrook, C.; Ottaviani, C.; Pirandola, S. Two-way quantum cryptography at different wavelengths. Phys. Rev. A 2014, 89, 012309. [Google Scholar] [CrossRef]
- Wang, T.; Yu, S.; Zhang, Y.C.; Gu, W.; Guo, H. Security of two-way continuous-variable quantum key distribution with source noise. J. Phys. B 2014, 47, 215504. [Google Scholar] [CrossRef]
- Da Silva, M.P.; Bozyigit, D.; Wallraff, A.; Blais, A. Schemes for the observation of photon correlation functions in circuit QED with linear detectors. Phys. Rev. A 2010, 82, 043804. [Google Scholar] [CrossRef]
- Bozyigit, D.; Lang, C.; Steffen, L.; Fink, J.; Eichler, C.; Baur, M.; Bianchetti, R.; Leek, P.; Filipp, S.; da Silva, M.; et al. Antibunching of microwave-frequency photons observed in correlation measurements using linear detectors. Nat. Phys. 2011, 7, 154–158. [Google Scholar] [CrossRef]
- Eichler, C.; Bozyigit, D.; Lang, C.; Baur, M.; Steffen, L.; Fink, J.; Filipp, S.; Wallraff, A. Observation of two-mode squeezing in the microwave frequency domain. Phys. Rev. Lett. 2011, 107, 113601. [Google Scholar] [CrossRef] [PubMed]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Usenko, V.C.; Filip, R. Trusted Noise in Continuous-Variable Quantum Key Distribution: A Threat and a Defense. Entropy 2016, 18, 20. https://doi.org/10.3390/e18010020
Usenko VC, Filip R. Trusted Noise in Continuous-Variable Quantum Key Distribution: A Threat and a Defense. Entropy. 2016; 18(1):20. https://doi.org/10.3390/e18010020
Chicago/Turabian StyleUsenko, Vladyslav C., and Radim Filip. 2016. "Trusted Noise in Continuous-Variable Quantum Key Distribution: A Threat and a Defense" Entropy 18, no. 1: 20. https://doi.org/10.3390/e18010020
APA StyleUsenko, V. C., & Filip, R. (2016). Trusted Noise in Continuous-Variable Quantum Key Distribution: A Threat and a Defense. Entropy, 18(1), 20. https://doi.org/10.3390/e18010020






