1. Introduction
To improve product quality, system safety and reliability, advanced methods of process monitoring and fault detection become increasingly important in many manufacturing processes. As the rapid development of sensing and computing technology, numerous process data can be collected to reflect the variation of different process parameters, in which a large number of various waveform signals are included. Examples of these waveform signals include tonnage signals in the stamping process [
1], acoustic data for squirrel cage induction motor fault diagnosis [
2] and vibration signals for ball bearing defect diagnostics [
3]. These waveform signals contain much process information of the process conditions. Usually, in the area of statistical process control (SPC), these waveform signals can be called profile data.
Many researchers focus on analyzing the profile data and numerous methods and techniques have been developed for process monitoring in literature. A comprehensive review of the process monitoring approaches based on the profile data can be found in William [
4]. Depending on the characteristics of the profile data, process monitoring can be divided into two categories which are linear profile monitoring and nonlinear profile monitoring. Extensive research has been reported on linear profile monitoring in literature. For example, see the work in Kang and Albin [
5], Mahmoud
et al. [
6], Zhu and Lin [
7]. However, in these research papers, there is an assumption associated with linear profile monitoring methods that the underlying curves of the profile data are simple straight lines, whereas the process data is almost nonlinear profiles in most practical situations.
To address this problem, increasing research for process monitoring by using nonlinear profile monitoring methods can be found in literature. Colosimo
et al. [
8] developed a regression model with spatial autoregressive errors for monitoring the bidimensional profiles of manufactured products. Williams
et al. [
9] proposed to monitor the dose-response profiles by developing a four-parameter logistic regression model. However, these approaches are parametric with an assumption that the profile data should follow a specified functional form. There is a limitation of the parametric model that the parameters may remain the same when the profile data has a small change. Thus, the parametric model could not represent the profile data change well [
9].
In order to overcome these issues, nonparametric modeling approaches have been developed. One of the widely used nonparametric methods is smoothing approach, such as kernel smoothing and spline smoothing. For example, Kwon
et al. [
10] used adaptive support vector regression to investigate the relationship of the closed-loop measurement error between different inspection techniques. Lim and Mba [
11] employed the switching Kalman filter for model estimation and life prediction based on the condition monitoring data of gearbox bearings. However, the smoothing approaches assume that the profile data cannot contain unsmooth characteristics. Another widely used nonparametric method is a wavelet to analyze the profile data. For example, Sang
et al. [
12] proposed a novel noise reduction method for time series data based on wavelet by applying information entropy theories. Lu and Hsu [
13] employed the wavelet transform to analyze the vibration signal for the detection of structural damage. However, as pointed out by Woodall
et al. [
4], monitoring only a subgroup of the most significant wavelet coefficients based on in-control profile data can be dangerous in the sense that some out-of-control process changes will be ignored. Other nonparametric modeling approaches still have been investigated. For example, Tan and Hammond [
14] applied principal component analysis to develop a nonparametric approach for linear system identification. However, it assumes that the profile data under a specific process condition follow a multivariate normal distribution when using the principal component analysis method.
Recently, recurrence plot (RP) method has emerged as an effective tool to analyze the nonlinear profile data [
15]. The RP method has been widely used in various fields such as geography and physiology, which was first introduced by Eckmann
et al. [
16] as a diagnostic tool to detect the recurrences of trajectories of a dynamic system. The main idea of this method is to transform waveform signals into a two-dimensional matrix, which can be visualized as an image named as recurrence plot. In order to differentiate the concepts of the recurrence plot method and the visualization of the two-dimensional matrix, we use the “RP method” to represent the recurrence plot method and use the “RP plot” to represent the image visualized from the two-dimensional matrix in this paper. There are several advantages when using the RP method to analyze the nonlinear profile data. First, it doesn’t require any assumptions on profile data distribution, data stationarity and data size [
15]. Second, the RP plot which derives from the process profile data contains rich information of process conditions and can interpret the process characteristics easily. The recurrence quantification analysis (RQA) method has been developed to aim at quantifying the RP plot by a few summary statistics [
17]. For example, Syta
et al. [
18] adopted the RQA method to analyze the acceleration time series of a gear transmission system for mechanical diagnosis. Tykierko [
19,
20] integrated the RP method and the exponentially weighted moving average (EWMA) control chart technique to detect changes in the complex system. However, the RQA method loses much information compared with the RP plot when describing the characteristics of the process profile data. Zhou and Zhang [
21] developed a bootstrap
control chart based on the recurrence quantification measures to monitor vibration signals. However, this method did not consider the correlation between different signals.
In this paper, we develop a generic scheme for process monitoring by integrating the RP method and the control chart technique. A new feature extraction method based on the RP plot is proposed to better preserve the characteristic features from the original profile data than the existing method. Then a control chart will be constructed based on the new features to detect the changes of profiles data. Since the RP method has several advantages to analyze the nonlinear profile data, our proposed process monitoring scheme does not make any assumption on the functional form or characteristics of the profiles data. In addition, the RP method has the potential to be used for fault diagnosis based on the relationship between the RP plot and the process profile data.
The remainder of this paper is organized as follows. The concepts of the RP method are introduced in
Section 2. Then, a novel process monitoring scheme by integrating the RP method and the control chart technique is proposed in
Section 3. Next, in
Section 4, a simulation study is showed to evaluate the performance of our proposed method by comparing with the existing RQA-based control chart methods. In
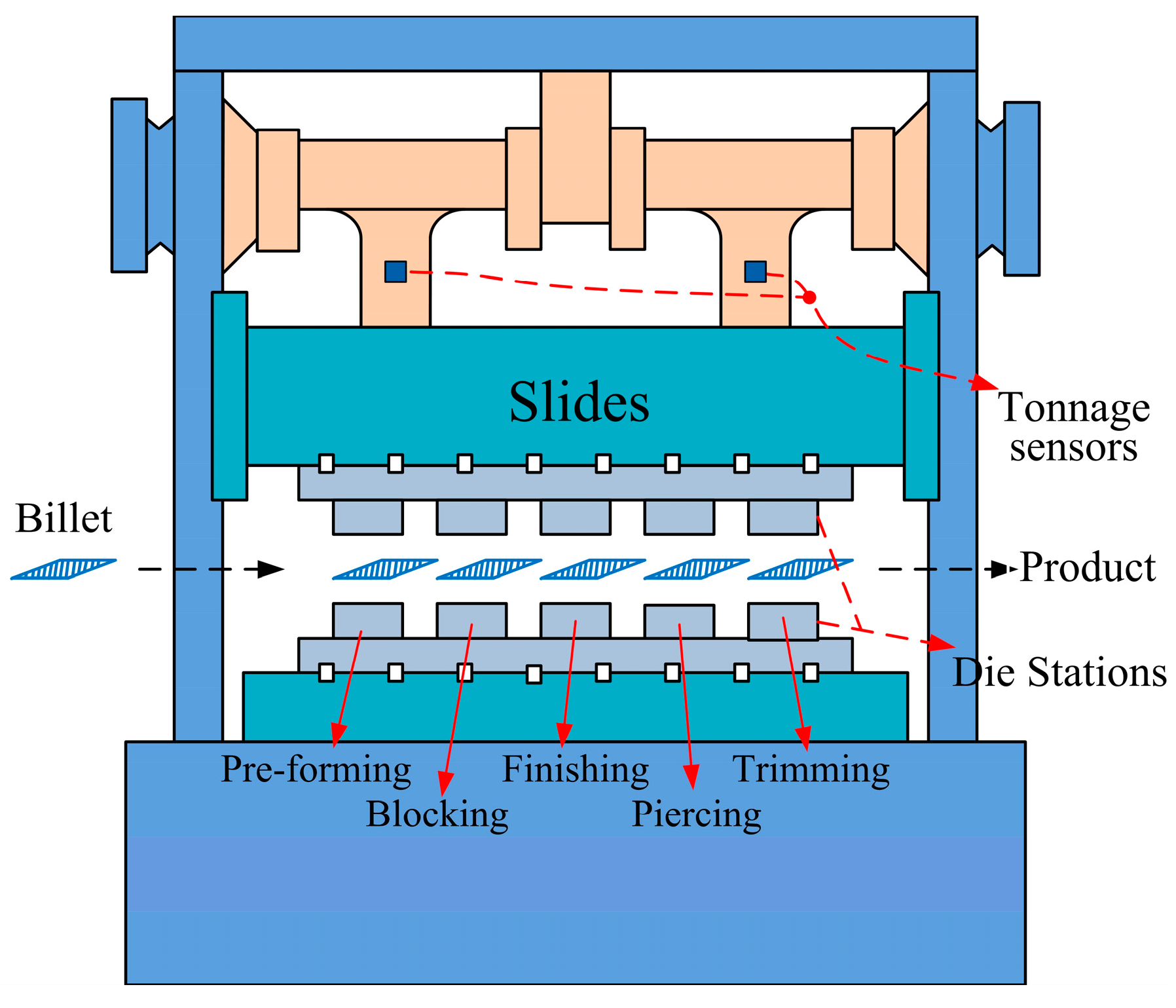
Section 5, a real progressive stamping process is illustrated to demonstrate our proposed process monitoring scheme. Finally, conclusions and discussions are given.
2. Recurrence Plot Method
In this section, we will introduce the concepts of the RP method. Then, the relationship between the recurrence plot and the profile data is discussed. The RQA method will be introduced at last.
Denote
is a series of nonlinear profile data with
points each. Then, a series of
-dimensional vectors
can be constructed from the one-dimensional signal
by Equation (1).
where
and
are called embedding dimension and time delay,
. The vectors
represent the signal trajectories in the
-dimensional space. If we define a threshold
, then a two-dimensional matrix can be obtained by comparing the distance between the vectors in
with
as showed in Equation (2).
where
is a norm function and
is the Heaviside function.
is called recurrence matrix with
columns and
rows.
represents the element with row
and column
. If the distance between
and
is less than the threshold
,
, otherwise
. If we plot the element “1” as black dot and plot the element “0” as white dot, then the matrix
can be visualized as a binary image, which is named RP plot in this paper.
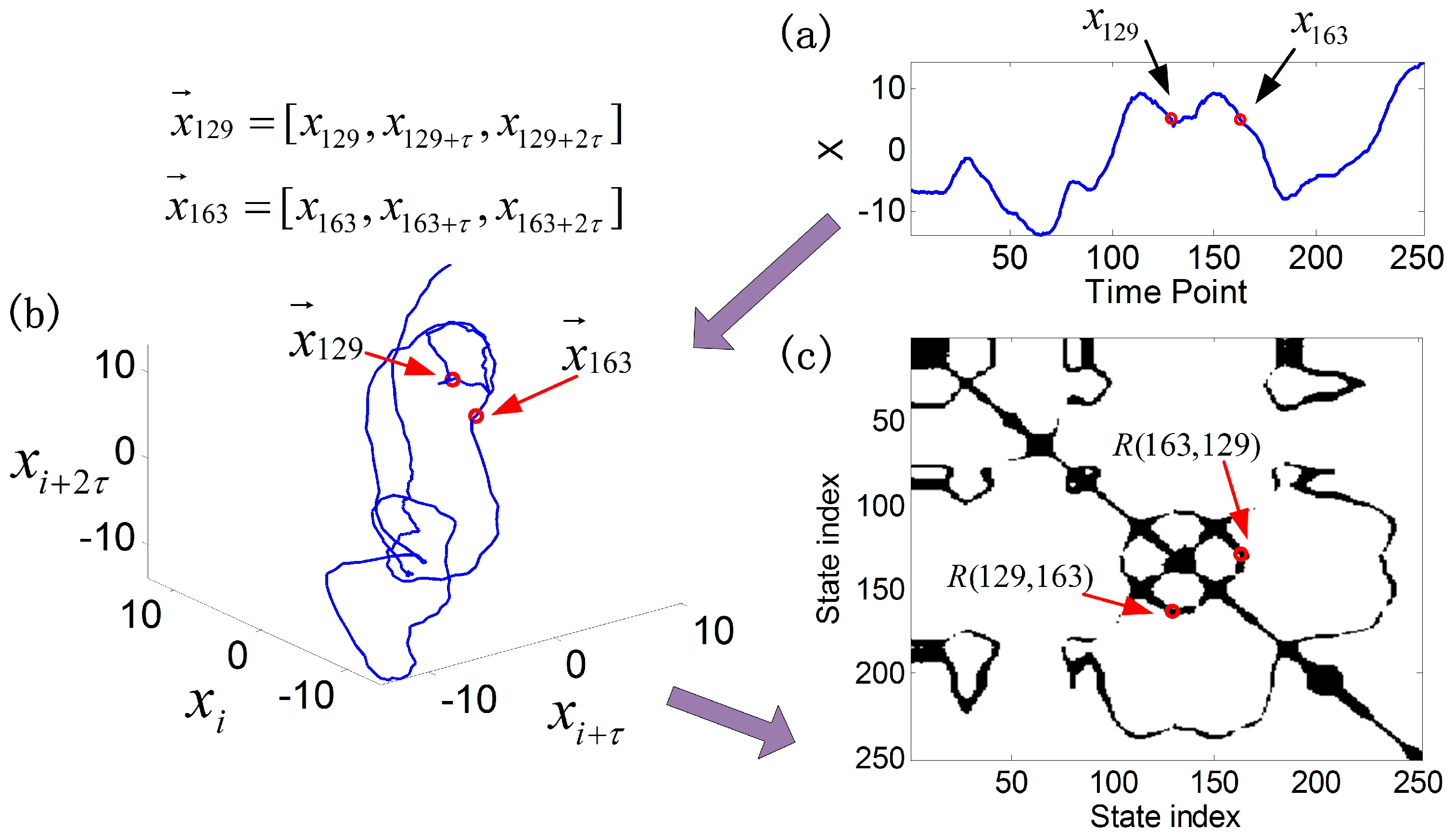
Figure 1 is an example to show the RP method with the parameters
,
,
.
Figure 1a shows a segment of tonnage signal collected from a progressive stamping process, and
Figure 1b shows the trajectory of the tonnage signal in a three dimensional space.
Figure 1c represents the RP plot of the tonnage signal. According to the definition of the RP method, the vectors
and
in the three-dimensional space (
Figure 1b) represent the trajectories of the tonnage signal around the points
and
. The relationship between the vectors
and
can be reflected as the points
and
in the RP plot (
Figure 1c), which also represent the correlation of the tonnage signal around the points
and
.
Figure 1.
An example of the recurrence plot method: (a) a segment of a tonnage signal collected from progressive stamping process, (b) the trajectory of the tonnage signal in a three dimensional space, and (c) the corresponding RP plot of the tonnage signal.
Figure 1.
An example of the recurrence plot method: (a) a segment of a tonnage signal collected from progressive stamping process, (b) the trajectory of the tonnage signal in a three dimensional space, and (c) the corresponding RP plot of the tonnage signal.
According to the introduction above, the RP plot contains single points, horizontal lines, vertical lines and diagonal lines. The RQA was proposed to characterize the patterns based on these points and lines in the RP plot [
22,
23]. There are five most commonly used features by RQA method which are recurrence rate (RR), determinism (DET), entropy (ENT), laminarity (LAM) and trapping time (TT). RR is a feature to measure the density of the black dots in the RP plot. DET presents the proportion of the black dots forming the diagonal lines. According to Marwan
et al. [
15], the diagonal lines mean the repeat of the signal patterns in the original signal. Thus, the DET characterizes the signal recurrence behaviors. ENT represents the Shannon information entropy of selected diagonal lines. LAM measures the proportion of the black dots forming the vertical lines. TT measures the average length of the vertical lines.
There are three important parameters in RP method, which are the embedding dimension
, the time delay
and the threshold
. Many researchers have already developed some rules to determine them. In this paper, we used the FNNs [
24] and the mutual information method [
25] to determine the embedding dimension
and time delay
. Schinkel
et al. [
26] explored the relationship between the threshold
and each RQA measure, and compared the area under the curve (AUC) in receiver operating characteristic (ROC) curve of each RQA measure. We chose Schinkel’s method to train the threshold
to get the optimal value based on industry process data.
3. Process Monitoring Scheme
In this section, a novel process monitoring scheme is proposed by integrating the RP method with the control chart technique. Although the RQA method can well characterize the patterns in the RP plot and has been widely used in different applications, there is a limitation when it is used to detect the small changes in profile data. Since the RQA characterizes the RP plot as several quantitative features, each of which can only detect one specific type of changes in the RP plot. For example, using the feature RR can detect a significant change in the density of recurrent points of the RP plots. However, in some cases, the RR could remain the same when there is a small change in the process signals. In order to overcome this limitation, we propose a novel process monitoring scheme to directly monitor the changes in the RP plot instead of using the RQA features by integrating with control chart technique for process monitoring. Since the RP plot preserves much information about the original process signals [
15], we expect this novel process monitoring scheme can lead to a more sensitive and robust monitoring performance.
3.1. Template Recurrence Plot
As pointed out by Woodall
et al. [
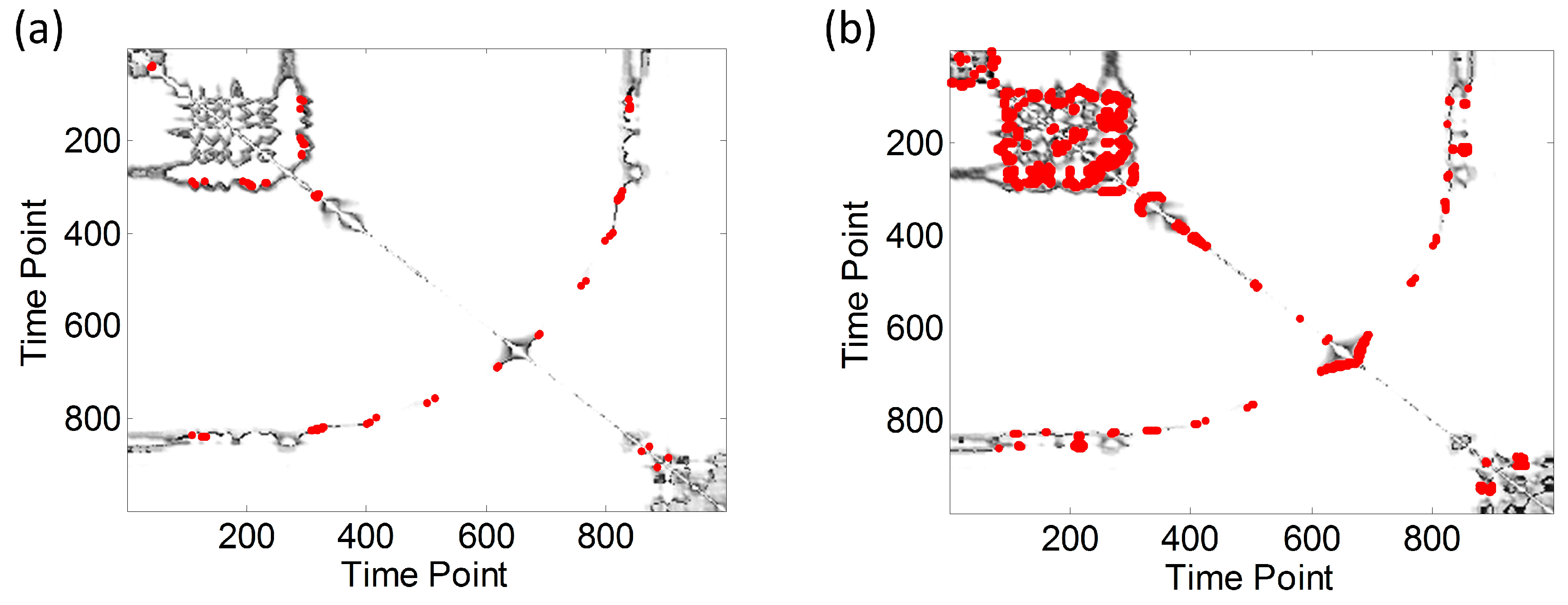
4], we need to consider Phase I and Phase II methods when developing the monitoring scheme. In Phase I, we need to collect a group of in-control historical data to analyze the underlying process variation. Since it is difficult to estimate the process in-control variation directly, we propose a new approach to estimate the profile data based on the RP plot, which is named as “Template RP plot” in this paper.
Assume
is a series of recurrence plot matrices obtained from
in-control process signals. The template RP plot can be estimated by
Denote the
as an element at the
th row and
th column in
. Then, we can conclude that each element
) is varying in [0, 1] and the value of the element
can represent the probability that the point appears at coordinate
. Recall that
in the RP plot represents a black dot at the coordinate
. Thus, a large value of the element
indicates that there is a high probability to find a black point at the element
in the recurrence matrices
. We can conclude that the points with large (close to 1) or low (close to 0) values in
can be considered as a common effect at the coordinate
in these recurrence matrices. In addition, if all profile data is obtained in an ideal in-control condition, all the elements in the template RP plot should be only 0 or 1.
3.2. Continuous-Scale Recurrence Plot and Monitoring Statistics
Given an observed profile data
, we can then calculate the standardized amount of discrepancies between the RP plot of the observed profile data
and the template RP plot
at each coordinate
:
According to the interpretation of the template RP plot
, we can conclude that the element in
varying in [0, 1].
is called continuous-scale RP plot in this paper. There are two advantages of using the template RP and the continuous-scale RP:
- (1)
More information of process data has been preserved in the template RP and the continuous-scale RP. The values in the template RP and the continuous-scale RP are varying in [0, 1]. These values can be considered as the probabilities that the corresponding elements are equal to 1. More methods can be used to analyze the process data with the new proposed concepts.
- (2)
The relationship between a new process data and the in-control data can be directly represented in the continuous-scale RP. The values have directly meanings to represent the differences between the new process data and the in-control data. A large value in continuous-scale RP means the largest difference while a small value means little difference.
As the value of the element
represents the difference between
and
at the coordinate
, the term
should be small when the observed profile data is collected under in-control condition; otherwise,
will become large. Based on this observation, there are many approaches can be developed to monitor the process based on the local statistics
.
One approach is to use the sum of all
local statistics to construct a new monitoring statistics which is showed in Equation (5):
where
is a suitable constant that corresponds to a pre-specified false alarm rate
. This procedure is most effective when the signal changes result in different values in all elements of the corresponding RP plot. However, in most cases, different process conditions may only result in a small segment of signal changes, which corresponds to a change of part of elements in the RP plot. In order to address this issue, we consider the top-
approach to develop the monitoring statistics [
27]. Specifically, we construct a monitoring statistic as showed in Equation (6):
where
is an indicator function that
;
is the monitoring statistic of the new RP plot
of the new profile data; and
is a threshold value to select a number of elements whose values are larger than
. Based on whether
is a constant, we propose the hard threshold and soft threshold methods as showed in the following Equations:
- (i)
- (ii)
Soft threshold:
where
is a constant value as the hard threshold method; and
is the soft threshold method where
is a matrix and each element
in
has its own threshold value
.
This proposed approach has several advantages: (1) It does not require any prior information to monitor the process condition. Any fault occurring in the process will be reflected as signal changes and the changes can be reserved in the continuous-scale RP plot
. We can detect the process condition changes by monitoring the proposed monitoring statistics
. (2) This proposed approach is easy to conduct. It does not need to estimate a parametric model for characterizing the profile data. (3) It can not only detect a wide range of possible process faults with no prior knowledge but also can localize the coordinates in the RP plot. This unique feature also can be used for identifying the exact segment of changes in the process signals for future research.
3.3. Parameter Settings
The optimal values for the hard threshold
or soft threshold
can be determined by the information of the profile changes. The threshold is related to the number of changed elements in the RP plot. Generally speaking, the monitoring statistics constructed via the top-
approach should contain all changed elements in the RP plot. Thus, we consider the following two rules to determine the appropriate value of the threshold
:
- (1)
When the information related to the process condition changes is unavailable, the hard threshold approach is preferred to use. We can determine the appropriate value of
based on the empirical distribution of
, which can be estimated from a set of in-control profile data.
- (2)
When we have enough in-control and out-of-control profile data, the soft threshold is preferred to use. Here, we should notice that it is difficult to use the soft threshold in practice due to information and data limitation. The prerequisite of using the soft threshold to derive the monitoring statistics is that we should have numerous in-control and out-of-control process data. If we have enough in-control and out-of-control profile data, we can calculate the probability of the element value distribution in
as:
If we set the value of
according to the process requirements, then we can obtain the value of the
of each elements in
. Thus, we can set the soft threshold
.
3.4. RP-Based Bootstrap Control Chart
In this section, we will develop a control chart based on the monitoring statistic
and the control limit will be estimated. Many control chart techniques, such as
chart, cumulative sum (CUSUM) control chart and EWMA chart, require the observations following a normal distribution. However, the distribution of the proposed monitoring statistic
is very difficult to obtain. The bootstrap method, which was originally proposed by Efron [
28], is a random sampling with replacement method that can be used to estimate the sampling distribution of a statistic by assuming that the observations are independent and identically distributed. Jones and Woodall [
29] have provided a comprehensive investigation of several bootstrap control charts and compared their performance, which shows that the bootstrap method can significantly improve the performance of the control chart technique when the monitoring statistics do not satisfy the assumption of following the normal distribution. Here, we employ the bootstrap method proposed by Bajgier [
30] to build a RP-based bootstrap control chart based on the constructed monitoring statistic
. The detailed introduction of the bootstrap method can be seen in Bajgier [
30].
The control chart technique, which has been widely used in manufacturing processes, is an important tool in the field of statistic quality control to determine whether a process is in-control or out-of-control. For more information about the control chart technique, one can refer to Woodall
et al. [
4]. There are two phases when implement the control chart technique in practice: Phase I and Phase II. The parameters of the control chart will be estimated based on monitoring statistics in Phase I. The new derived monitoring statistics will be test in Phase II to determine the process conditions.
According to the bootstrap control chart method in Bajgier [
30] and Teyarachakul
et al. [
31], the procedures of building the proposed RP-based bootstrap control chart are below:
Obtain
in-control profile data, and calculate the corresponding monitoring statistics
.
Draw a random sample of size
with replacement from the monitoring statistics
, and obtain a bootstrap sample
, here
should be much smaller than
.
Compute the mean of the bootstrap sample
.
Repeat the step 2 and step 3 a large amount of times, say
times (e.g.,
=1000). Then we can derive
bootstrap sample means as
.
Sort the
bootstrap sample means in an increasing order to obtain a new
bootstrap sample means denoted as
.
Define a constant
to represent the false alarm rate of the bootstrap control chart. Then, find the upper control limit (UCL) and the lower control limit (LCL) based on the formulae
and
.
3.5. Monitoring Scheme
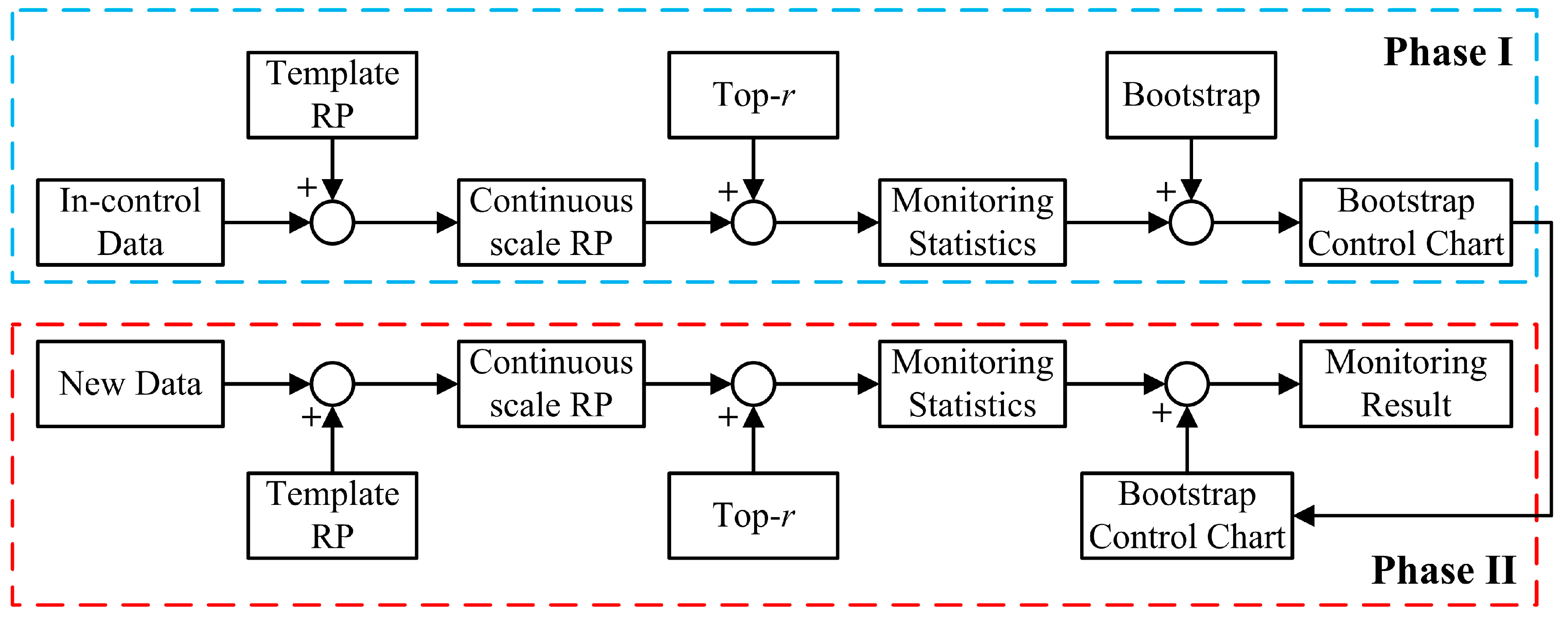
Based on the proposed RP-based bootstrap control chart, we further summarize the procedures of the monitoring scheme as below. An overview of the proposed monitoring scheme can be found in
Figure 2.
Obtain two groups of in-control profile data. One group data is used to estimate the template RP plot
by using Equation (3).
Calculate the continuous-scale RP plot
by using Equation (4) based on the other group of in-control data and derive the monitoring statistics by using Equation (6) via the top-r approach.
Estimate the control limit of the proposed bootstrap control chart following the procedures introduced in Subsection 3.4.
When a new profile is obtained, calculate the continuous-scale RP plot
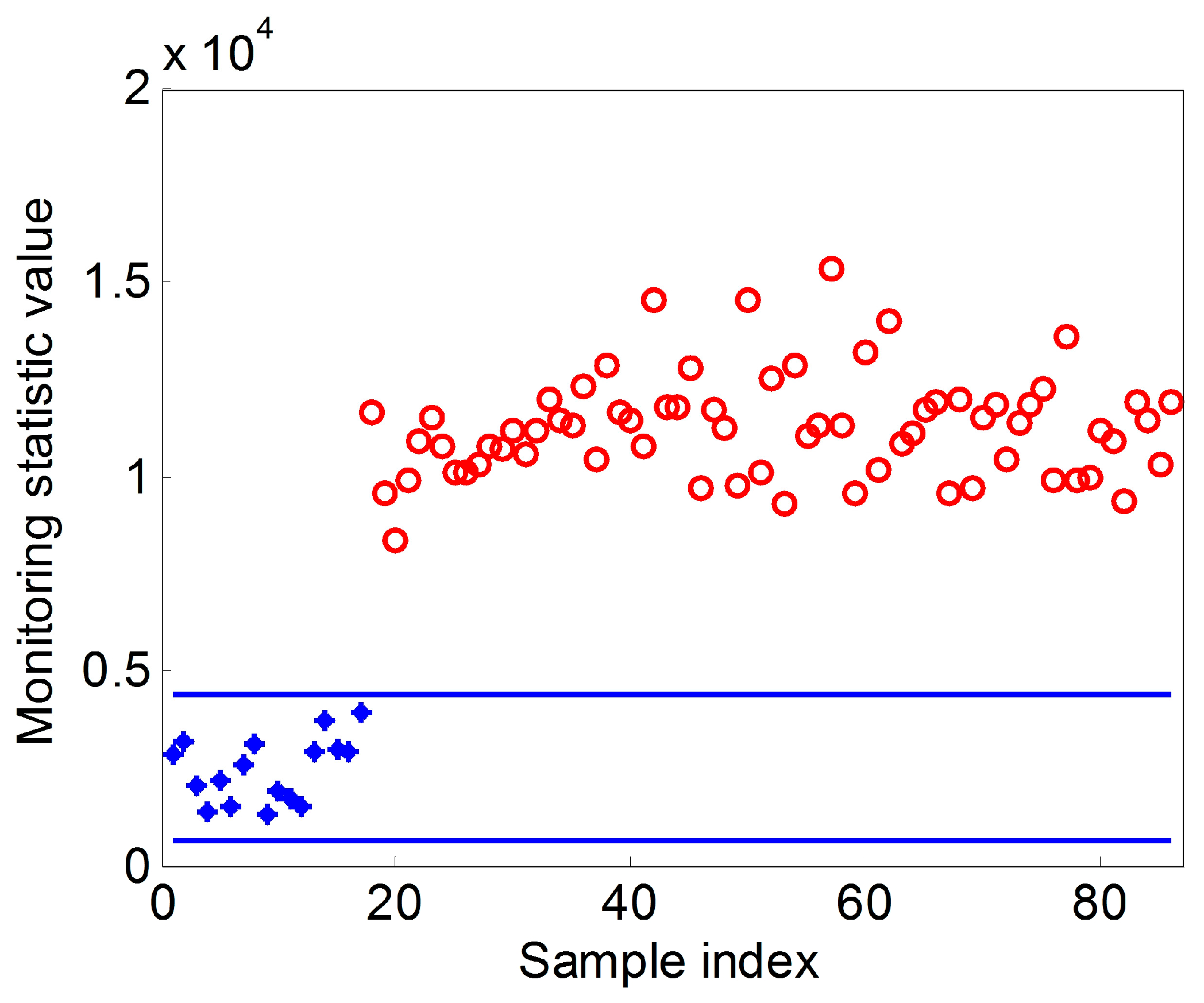
and the monitoring statistic of this profile. Then, test the monitoring statistic by the constructed bootstrap control chart. If this statistic falls outside the control limit estimated from step 3, we can conclude that the process is out-of-control. Otherwise, the process is in-control.
Figure 2.
The framework of the monitoring scheme.
Figure 2.
The framework of the monitoring scheme.
4. Performance Comparisons
In this section, we will conduct comprehensive simulation studies to evaluate and compare the performance of our proposed RP-based bootstrap control chart with other RP-based control chart method in literature. Tykierko [
19,
20] developed an EWMA control chart to detect changes in the complex system based on RQA method. However, one limitation exists in his method that is the distributions of the RQA features may not follow normal distribution. Hence, improved RQA-based bootstrap control charts are developed based on these five RQA features to compare with our proposed method. These five features are RR, DET, ENT, LAM and TT which are mentioned in
Section 2. For clarification, the RQA-based bootstrap control charts built on these features are named as RR-based control chart, DET-based control chart, ENT-based control chart, LAM-based control chart and TT-based control chart. Specifically, a variety of change scenarios, including mean shift and frequency change with different magnitudes will be considered. Out-of-control average run length (ARL) will be computed and compared under each change scenario to measure the performance of our proposed RP-based bootstrap control chart and the RQA-based bootstrap control charts.
Recall the steps of building the proposed RP-based bootstrap control chart in
Section 3, the procedures of building the RQA-based bootstrap control charts are similar to the RP-based bootstrap control chart but need to replace the monitoring statistics by the five features. Our proposed RP-based bootstrap control chart monitors the changes in the RP plot directly while the RQA-based bootstrap control charts require obtaining five features for characterizing the RP plot. Thus, this case study also can demonstrate the effectiveness of the proposed monitoring statistics over the existing measures of RP plots when used for nonlinear profile monitoring.
Denote the in-control profile data as
and the out-of-control profile data as
, where
represents the common effect under normal condition,
represents the change segments and
represents the process noise. Without loss of generality, we assume the process noise
follows a normal distribution. Denote
is as the amplitude of
. Then,
to measures the signal magnitude change. For simplicity, we denote
= 0.5, 1.0 and 1.5 to represent the small, medium and large changes, respectively.
In this simulation study, we use the sinusoidal functions to simulate the in-control and the out-of-control profile data. Shinozuka [
32] pointed out that the components of multivariate and multidimensional processes can be simulated as the sum of sinusoidal functions with random frequencies and random phase angles. Due to the limitation of the computation ability, we choose three frequencies and phases to generate three sinusoidal functions. Then, we combine these three sinusoidal functions together to generate the in-control simulation signals with noise
. In particular, we generate a group of in-control signals by the function
+
, where
= 15,
= 10,
= 12,
= 12,
= 20,
= 38,
= 100,
= 50,
= 25,
= 1. The parameter
represents the time point of the in-control profile data and is defined as
= [1, 500]. Similarly, a group of out-of-control signals are generated by
, where
. The parameter
denotes the segment which the change occurs in the profile data. For simplicity, we will consider
in this case study.
Before implementing the proposed monitoring scheme, the threshold of the top-r approach must be determined. As mentioned above, the hard threshold is preferred when the information related to the out-of-control is unavailable, while the soft threshold is preferred when we have prior information about the out-of-condition. In this simulation study, the out-of-control condition includes a variety of fault scenarios. As a result, we assume that no prior knowledge of the potential failure patterns is available and the hard threshold is chosen to obtain the monitoring statistic. To study the uncertainties of the hard threshold parameter on the out-of-control ARL performance, we will consider different values
= 0.9, 0.8, 0.7, and 0.6. In addition, the number of samples used to estimate the template RP plot is set to be
= 1000. The false alarm rate and the number of samples used to estimate the control limit are
= 0.027 and
= 5000, respectively.
In this simulation study, our proposed RP-based bootstrap control chart will be evaluated by detecting the mean shift and frequency change to compare with other RQA-based bootstrap control charts. Hence,
represents the component of the signal mean shift or frequency change respectively and
measures the magnitude of the component
. For mean shift case,
and
. For frequency change case,
and
.
Table 1 and
Table 2 show the comparison results of our proposed RP-based bootstrap control chart and other RQA-based bootstrap control charts in detecting the mean shift and frequency change cases. In
Table 1 and
Table 2, the RR, DET, ENT, LAM and TT represent the corresponding RQA-based bootstrap control chart. The values under our method, RR, DET, ENT, LAM and TT are the out-of-control ARL with the defined
and
. The out-of-control ARL is defined as the average number of the samples located within the control limits of a control chart when the control chart is detecting the out-of-control samples. The out-of-control ARL means detection ability and speed of a control chart to find the process abnormal condition and is a widely used indicator to evaluate the performance of control charts. The smaller value of the out-of-control ARL means the better performance of the control chart. According to
Table 1 and
Table 2, the out-of-control ARLs of our method are significantly smaller than other RQA-based control charts under all conditions. Thus, we can conclude that the proposed RP-based bootstrap control chart uniformly outperforms the RQA-based bootstrap control charts in all cases. This indicates that the constructed monitoring statistics can better characterize the changes in nonlinear profiles. Moreover, comparing the out-of-control ARLs in
Table 1 and
Table 2 under the conditions when
= 0.5, we can see that the values in
Table 2 are significantly smaller than in
Table 1. Thus, we can conclude that our proposed RP-based bootstrap control chart is more effective when detecting the signals with frequency changes. At last, comparing the out-of-control ARLs either in
Table 1 or in
Table 2 under different settings of
, the values are smaller than others when
. Hence, a better performance can be achieved if we can choose an optimal threshold
as
.
Table 1.
Out-of-control average run length (ARL) comparisons with mean shift.
Table 1.
Out-of-control average run length (ARL) comparisons with mean shift.
| | Our method | Recurrence Rate (RR) | Determinism (DET) | Entropy (ENT) | Laminarity (LAM) | Trapping Time (TT) |
|---|
| 0.9 | 0.5 | 66.31 | 165.43 | 183.21 | 178.32 | 185.26 | 183.61 |
| 1.0 | 1 | 12.27 | 35.57 | 116.21 | 41.23 | 27.13 |
| 1.5 | 1 | 1.348 | 4.513 | 11.32 | 4.39 | 2.752 |
| 0.8 | 0.5 | 102.35 | 171.83 | 191.23 | 184.85 | 186.93 | 172.97 |
| 1.0 | 1 | 11.28 | 37.87 | 110.32 | 43.94 | 25.98 |
| 1.5 | 1 | 1.043 | 4.832 | 12.12 | 4.231 | 2.793 |
| 0.7 | 0.5 | 67.25 | 167.85 | 180.23 | 175.92 | 187.63 | 188.76 |
| 1.0 | 1 | 12.87 | 34.51 | 115.81 | 41.53 | 32.08 |
| 1.5 | 1 | 1.287 | 4.639 | 11.84 | 4.372 | 2.873 |
| 0.6 | 0.5 | 68.78 | 163.86 | 197.35 | 177.38 | 193.23 | 185.34 |
| 1.0 | 1 | 11.65 | 35.82 | 115.73 | 42.85 | 27.62 |
| 1.5 | 1 | 1.493 | 4.892 | 11.76 | 2.38 | 2.87 |
Table 2.
Out-of-control average run length (ARL) comparisons with frequency change.
Table 2.
Out-of-control average run length (ARL) comparisons with frequency change.
| | Our method | Recurrence Rate (RR) | Determinism (DET) | Entropy (ENT) | Laminarity (LAM) | Trapping Time (TT) |
|---|
| 0.9 | 0.5 | 8.763 | 188.92 | 189.32 | 187.32 | 185.43 | 147.87 |
| 1.0 | 1.342 | 168.83 | 126.28 | 183.98 | 118.23 | 66.25 |
| 1.5 | 1 | 153.21 | 62.32 | 173.52 | 67.42 | 28.09 |
| 0.8 | 0.5 | 13.87 | 187.76 | 188.21 | 198.12 | 193.87 | 152.54 |
| 1.0 | 1.212 | 172.12 | 131.23 | 185.91 | 123.32 | 72.89 |
| 1.5 | 1 | 163.31 | 69.89 | 180.19 | 69.72 | 34.42 |
| 0.7 | 0.5 | 16.87 | 182.2 | 183.24 | 188.53 | 173.19 | 150.32 |
| 1.0 | 1.19 | 164.83 | 121.92 | 176.59 | 121.73 | 63.13 |
| 1.5 | 1 | 157.37 | 58.24 | 163.73 | 59.39 | 30.28 |
| 0.6 | 0.5 | 18.73 | 182.82 | 179.31 | 178.73 | 176.48 | 156.36 |
| 1.0 | 1.142 | 165.76 | 125.65 | 170.12 | 118.86 | 65.62 |
| 1.5 | 1 | 154.83 | 53.32 | 161.28 | 57.39 | 30.83 |
6. Conclusions
Industrial process monitoring based on nonlinear profile analysis is an important research area. In this paper, a RP-based bootstrap control chart is proposed to analyze the nonlinear profile for process monitoring. Although the RP plot has been shown as an effective tool to analyze the nonlinear profile data, the existing approaches heavily rely on the RQA method to develop quantitate measures for the RP plot. Instead, we propose to develop a concept called continuous-scale RP plot to preserve the variation of the original profile data. Then, the top-
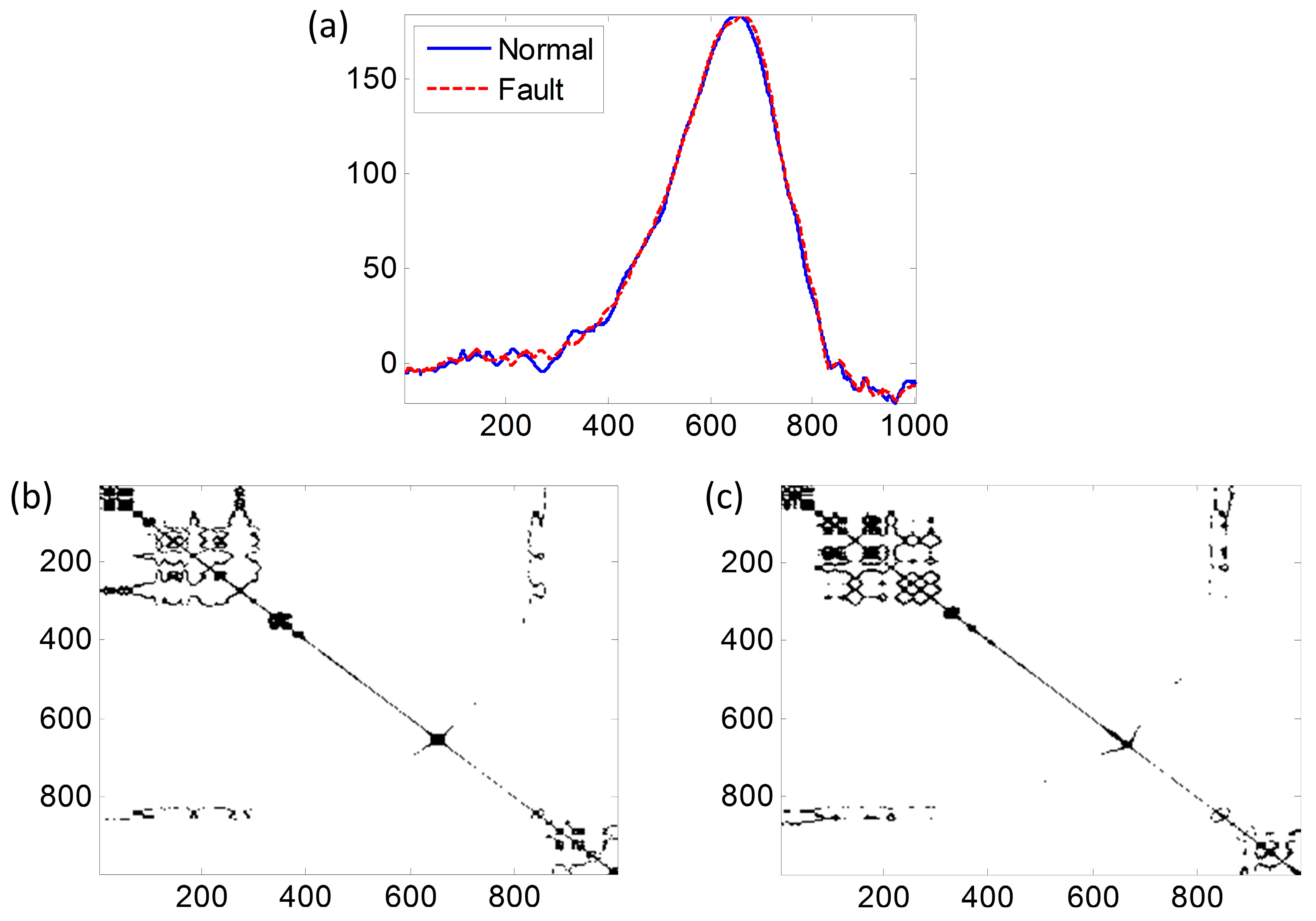
approach is employed to adaptively screen out a set of local statistics whose values are significantly large and sum them together to construct a monitoring statistic. This monitoring scheme is able to detect a wide range of possible changes in the nonlinear profile data without any prior information about the potential fault patterns. The simulation study shows that the proposed RP-based bootstrap control chart performs uniformly better than the RQA-based bootstrap control charts to detect different kinds of profile changes. The real case study demonstrates that the proposed method can successfully monitor the profile changes when the process fault occurred in progressive stamping processes.
Once an out-of-control alarm is raised, our future research will focus on developing a fault diagnosis method based on the continuous-scale RP plot to identify the location at which the change occurs. Our proposed method provides the fundamental research method for analyzing the waveform signals, which can be collected in many areas such as biophysics, seismology, mechanics and manufacture. Further research can be done based on our proposed method, such as fault detection, fault diagnosis, process prognostic and risk analysis. Therefore, the proposed nonlinear profile monitoring scheme can be widely used in many areas.