Nonlinear Predictive Control of a Hydropower System Model
Abstract
:1. Introduction
2. Nonlinear Predictive Control
2.1. System Model
2.2. Nonlinear Predictive Control Theory
3. The Model of a Hydropower Plant

4. Main Results


| Elapsed CPU Time (ms) | |
|---|---|
| Offline part | 5370 |
| Online part | 11569 |
| Number of Step | Performance Index | Number of Step | Performance Index |
|---|---|---|---|
| 1 | 0.117856 | 101 | 0.0022 |
| 11 | 0.039339 | 111 | 0.012638 |
| 21 | 0.030683 | 121 | 0.006103 |
| 31 | 0.050499 | 131 | 0.001474 |
| 41 | 0.077429 | 141 | 0.000687 |
| 51 | 0.119509 | 151 | 0.001066 |
| 61 | 0.016413 | 161 | 0.00026 |
| 71 | 0.005165 | 171 | 0.000517 |
| 81 | 0.010286 | 181 | 0.001085 |
| 91 | 0.002602 | 191 | 0.000607 |




5. Discussion and Conclusions
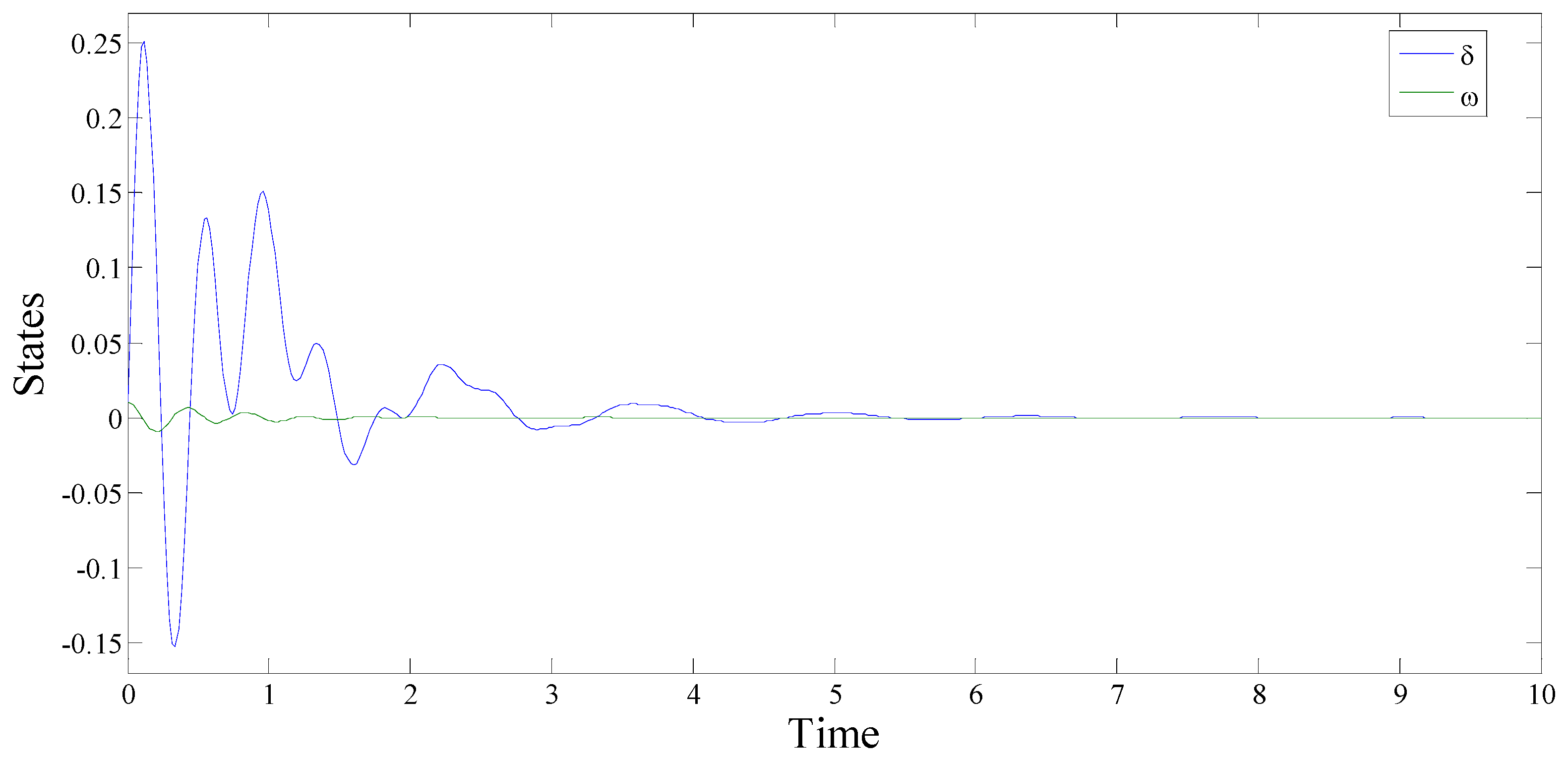
5.1. Discussion
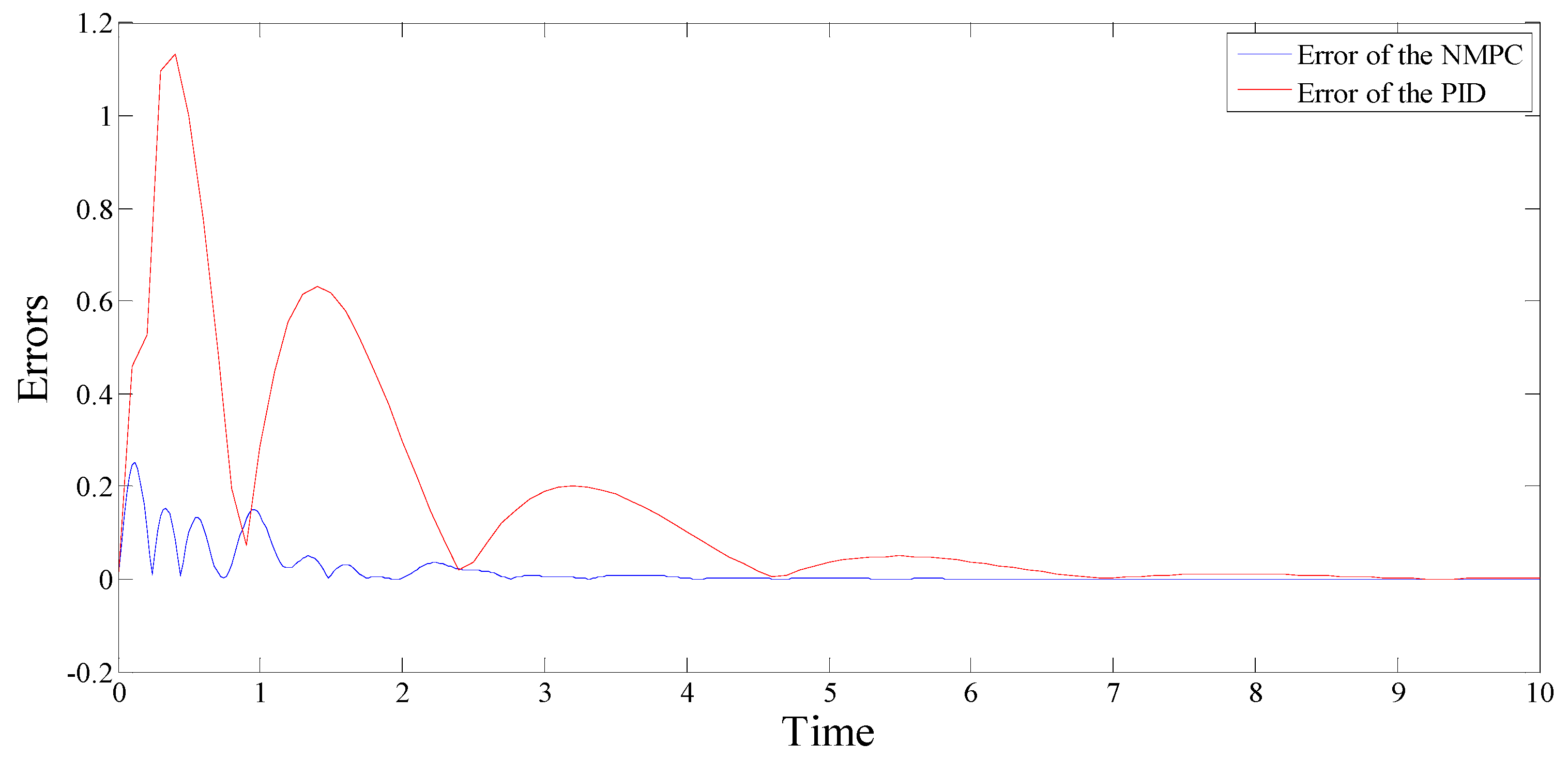
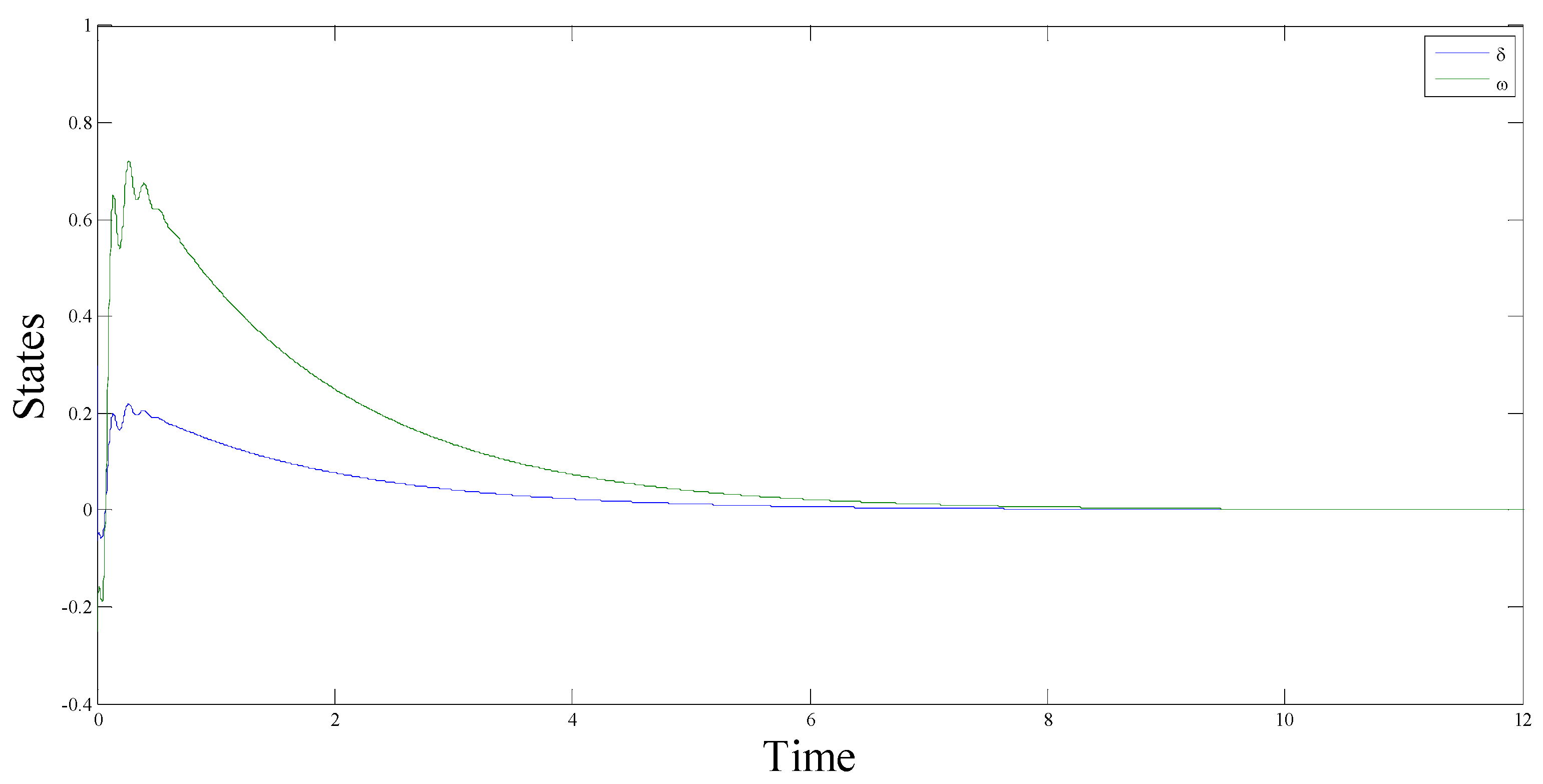
5.2. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Edward, G.R.; Xu, J.C. Mekong hydropower development. Science 2011, 332, 178–179. [Google Scholar]
- Mahmoud, M.; Dutton, K.; Denman, M. Design and simulation of a nonlinear fuzzy controller for a hydropower plant. Electr. Power Syst. Res. 2005, 73, 87–99. [Google Scholar] [CrossRef]
- Li, C.L.; Zhou, J.Z.; Ouyang, S.; Ding, X.L.; Chen, L. Improved decomposition-coordination and discrete differential dynamic programming for optimization of large-scale hydropower system. Energ. Convers. Manag. 2014, 84, 363–373. [Google Scholar] [CrossRef]
- Martínez-Lucas, G.; Sarasúa, J.I.; Sánchez-Fernández, J.Á.; Wilhelmi, J.R. Power-frequency control of hydropower plants with long penstocks in isolated systems with wind generation. Renew. Energy 2015, 83, 245–255. [Google Scholar] [CrossRef]
- Márquez, J.L.; Molina, M.G.; Pacas, J.M. Dynamic modeling, simulation and control design of an advanced micro-hydro power plant for distributed generation applications. Int. J. Hydrog. Energy 2010, 35, 5772–5777. [Google Scholar] [CrossRef]
- Mahmoud, M.; Dutton, K.; Denman, M. Dynamical modelling and simulation of a cascaded reserevoirs hydropower plant. Electr. Power Syst. Res. 2004, 70, 129–139. [Google Scholar] [CrossRef]
- Zoby, M.R.G.; Yanagihara, J.I. Primary control system and stability analysis of a hydropower plant. In Power Plants and Power Systems Control 2006; Westwick, D., Ed.; Elsevier: Kidlington, UK; Burlington, MA, USA, 2007; pp. 165–170. [Google Scholar]
- Ren, M.; Wu, D.; Zhang, J.; Jiang, M. Minimum entropy-based cascade control for governing hydroelectric turbines. Entropy 2014, 16, 3136–3148. [Google Scholar] [CrossRef]
- Ying, H. Theory and application of a novel fuzzy PID controller using a simplified Takagi-Sugeno rule scheme. Inf. Sci. 2000, 123, 281–293. [Google Scholar] [CrossRef]
- Clarke, D.W. Adaptive predictive control. Annu. Rev. Control 1996, 20, 83–94. [Google Scholar] [CrossRef]
- Miller, D.E. A new approach to adaptive control: No nonlinearities. Syst. Control Lett. 2003, 49, 67–79. [Google Scholar] [CrossRef]
- Mei, R.; Chen, M.; Guo, W.W. Robust adaptive control scheme for optical tracking telescopes with unknown disturbances. Opt. Int. J. Light Electron Opt. 2015, 126, 1185–1190. [Google Scholar] [CrossRef]
- Ren, M.; Zhang, J.; Jiang, M.; Tian, Y.; Hou, G. Statistical information based single neuron adaptive control for non-gaussian stochastic systems. Entropy 2012, 14, 1154–1164. [Google Scholar] [CrossRef]
- Hu, B.; Michel, A.N. Robustness analysis of digital feedback control systems with time-varying sampling periods. J. Franklin Inst. 2000, 337, 117–130. [Google Scholar] [CrossRef]
- Stich, M.; Beta, C. Control of pattern formation by time-delay feedback with global and local contributions. Physica D 2010, 239, 1681–1691. [Google Scholar] [CrossRef]
- Xin, B.G.; Wu, Z.H. Projective synchronization of chaotic discrete dynamical systems via linear state error feedback control. Entropy 2015, 17, 2677–2687. [Google Scholar] [CrossRef]
- Bidarvatan, M.; Shahbakhti, M.; Jazayeri, S.A.; Koch, C.R. Cycle-to-cycle modeling and sliding mode control of blended-fuel HCCI engine. Control Eng. Pract. 2014, 24, 79–91. [Google Scholar] [CrossRef]
- Tian, X.M.; Fei, S.M. Robust control of a class of uncertain fractional-order chaotic systems with input nonlinearity via an adaptive sliding mode technique. Entropy 2014, 16, 729–746. [Google Scholar] [CrossRef]
- Yashar, T.; Wang, J.D. Chaos control and synchronization of a hyperchaotic Zhou system by integral sliding mode control. Entropy 2014, 16, 6539–6552. [Google Scholar]
- Chen, D.Y.; Zhao, W.L.; Ma, X.Y.; Zhang, R.F. No-chattering sliding mode control chaos in Hindmarsh—Rose neurons with uncertain parameters. Comput. Math. Appl. 2011, 61, 3161–3171. [Google Scholar] [CrossRef]
- Long, L.J.; Zhao, J. Adaptive fuzzy tracking control of switched uncertain nonlinear systems with unstable. Fuzzy Sets Syst. 2015, 273, 49–67. [Google Scholar] [CrossRef]
- Huang, H.; Chen, L.; Hu, E. A neural network-based multi-zone modelling approach for predictive control system design in commercial buildings. Energy Build. 2015, 97, 86–97. [Google Scholar] [CrossRef]
- Chen, H.Y.; Liu, M.Q.; Zhang, S.L. Robust H∞ finite-time control for discrete Markovian jump systems with disturbances of probabilistic distributions. Entropy 2015, 17, 346–367. [Google Scholar] [CrossRef]
- Grüne, L.; Pannek, J. Nonlinear Model Predictive Control; Springer: London, UK, 2011. [Google Scholar]
- Chen, H.; Allgower, F. A quasi-infnite horizon nonlinear model predictive control scheme with guaranteed stability. Automatica 1998, 34, 1205–1217. [Google Scholar] [CrossRef]
- Chen, C.C.; Shaw, L. On receding horizon feedback control. Automatica 1982, 18, 349–352. [Google Scholar] [CrossRef]
- Mayne, D.Q. Model predictive control: Recent developments and future promise. Automatica 2014, 50, 2967–2986. [Google Scholar] [CrossRef]
- Xu, J.; Huang, X.L.; Mu, X.M.; Wang, S.L. Model predictive control based on adaptive hinging hyperplanes mode. J. Process Control 2012, 22, 1821–1831. [Google Scholar] [CrossRef]
- Martí, R.; Lucia, S.; Sarabia, D.; Paulen, R.; Engell, S.; de Prada, C. Improving scenario decomposition algorithms for robust nonlinear model predictive control. Comput. Chem. Eng. 2015, 79, 30–45. [Google Scholar] [CrossRef]
- Zeng, X.H.; Yang, N.N.; Wang, J.N.; Song, D.F.; Zhang, N.; Shang, M.L.; Liu, J.X. Predictive-model-based dynamic coordination control strategy for power-split hybrid electric bus. Mech. Syst. Signal Process. 2015, 60, 785–798. [Google Scholar] [CrossRef]
- Li, S.Y.; Zhang, Y.; Zhu, Q.M. Nash-optimization enhanced distributed model predictive control applied to the Shell benchmark problem. Inf. Sci. 2005, 170, 329–349. [Google Scholar] [CrossRef]
- Yang, J.; Li, X.; Mou, H.G.; Jian, L. Predictive control of solid oxide fuel cell based on an improved Takagi-Sugeno fuzzy model. J. Power Sources 2009, 93, 699–705. [Google Scholar] [CrossRef]
- Roubos, J.A.; Mollov, S.; Babuska, R.; Verbruggen, H.B. Fuzzy model-based predictive control using Takagi-Sugeno models. Int. J. Approx. Reason. 1999, 22, 3–30. [Google Scholar] [CrossRef]
- Sarimveis, H.; Bafas, G. Fuzzy model predictive control of non-linear processes using genetic algorithms. Fuzzy Sets Syst. 2003, 139, 59–80. [Google Scholar] [CrossRef]
- Jiang, Z.P.; Wang, Y. Input-to-state stability for discrete time nonlinear systems. Automatica 2001, 37, 875–867. [Google Scholar] [CrossRef]
- Xu, B.B.; Chen, D.Y.; Zhang, H.; Wang, F.F. Modeling and stability analysis of a fractional-order Francis hydro-turbine governing system. Chaos Soliton. Fract. 2015, 75, 50–61. [Google Scholar] [CrossRef]
- Shen, Z.Y. Hydraulic Turbine Reglation, 3rd ed.; China Water Press: Beijing, China, 1998. (In Chinese) [Google Scholar]
- Chen, D.Y.; Ding, C.; Do, Y.H.; Ma, X.Y.; Zhao, H.; Wang, Y.C. Nonlinear dynamic analysis for a Francis hydro-turbine governing system and its control. J. Franklin Inst. 2014, 351, 4596–4618. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, R.; Chen, D.; Ma, X. Nonlinear Predictive Control of a Hydropower System Model. Entropy 2015, 17, 6129-6149. https://doi.org/10.3390/e17096129
Zhang R, Chen D, Ma X. Nonlinear Predictive Control of a Hydropower System Model. Entropy. 2015; 17(9):6129-6149. https://doi.org/10.3390/e17096129
Chicago/Turabian StyleZhang, Runfan, Diyi Chen, and Xiaoyi Ma. 2015. "Nonlinear Predictive Control of a Hydropower System Model" Entropy 17, no. 9: 6129-6149. https://doi.org/10.3390/e17096129
APA StyleZhang, R., Chen, D., & Ma, X. (2015). Nonlinear Predictive Control of a Hydropower System Model. Entropy, 17(9), 6129-6149. https://doi.org/10.3390/e17096129






