1. Introduction
Modeling texts in natural language by a stochastic process is a frequent approach in computational linguistics. Classes of stochastic processes, such as hidden Markov processes, constitute state-of-the-art models in natural language processing tasks, such as speech recognition [
1] or parts-of-speech tagging [
2]. Whereas these kinds of statistical models have the advantages of being easily trained and adapted to the modeled data, they do not capture long-distance dependence in texts, which are connected to coherence of narration, transmission of knowledge or intentionality of language communication. Therefore, state-of-the-art models in natural language processing overestimate the actual amount of randomness in texts.
In contrast, in this article, we would like to present some novel theoretical and experimental results concerning fundamental properties of texts in natural language as modeled by a stochastic process. These results suggest that the amount of randomness in natural language texts may be much smaller than generally supposed. Briefly speaking, there are two disjoint classes of stochastic processes: finite energy processes (
cf. [
3]), with a strictly positive entropy rate, and Hilberg processes (
cf. [
4]), with a vanishing entropy rate. Experimentally-measuring maximal repetition in some empirical data, we may decide whether the data have been generated by a finite energy processes or by a Hilberg process. Following this idea, in a preliminary study by Dębowski [
5], it was discovered that texts in English are not typical of a finite energy process. In the present article, we would like, first, to extend this study by providing empirical data also for French and German and, second, to show that the natural language data may be typical of Hilberg processes.
The further organization of the article is as follows. In
Section 2, we present the relevant mathematical models.
Section 3 concerns the empirical investigations of natural language.
Section 4 contains the conclusion. Finally, in
Appendix A and
Appendix B, we prove two theorems stated in
Section 2.
2. Mathematical Models
Let
be a probability space,
i.e., Ω is the event space,
is the set of events on which the probability measure is defined and
P is the probability measure [
6]. A discrete (nonstationary) stochastic process
is a sequence of random variables
on probability space
, where the indices
i vary across the set of integers
and the alphabet
is a finite or countably infinite set of values of
. Let
be blocks of consecutive random variables. A discrete stationary stochastic process
is such a discrete stochastic process that the distribution of blocks
does not depend on the index
t.
There are various classifications of particular stochastic processes. The first class we want to discuss are finite energy processes. The defining feature of a finite energy process is that the conditional probability of any block drawn from the process decreases exponentially with the block length. By
, we denote the length of a fixed string
, that is the number of symbols in it. Formally, a discrete process
is called a finite energy process if conditional probabilities of blocks satisfy:
for all indices
, all strings
and certain constants
and
[
3]. (Finite energy processes have nothing to do with the concept of energy in physics. This is just some name coined by a mathematician.)
An important example of finite energy processes is uniformly-dithered processes;
cf. a formally unproven remark by Shields [
3]. Let us recall that i.i.d. processes, called also sequences of independent identically distributed random variables or unigram models in computational linguistics, are processes for which the probability of a block is the product of probabilities of the individual random variables,
. Now, let
be a group. A group
is a pair of a set
and a binary operation
, which is associative, that is
has an identity element
, that is
, and for each
, there exists the inverse element
, that is
. A discrete stochastic process
is called uniformly dithered if it satisfies:
where
is an arbitrary discrete process and
is an independent i.i.d. process with
. We have this result:
Theorem 1. Any uniformly-dithered process is a finite energy process.
Uniformly-dithered processes are processes that are contaminated by random noise in quite a general way. Dębowski [
7] supposed that texts in natural language may be contaminated in this way, and so, the appropriate model for the generation of texts in natural language is finite energy. As we will see, this hypothesis is false. Given some data typical of a stochastic process, we can check whether the process is finite energy and, in particular, show for texts in natural language that this is not the case.
The pivotal statistics for our consideration is so-called maximal repetition. For a string of symbols (a text)
, we define the maximal repetition as:
where
s,
and
range over all admissible substring partitions of text
w [
8]. In the above definition, strings
s,
and
may be empty, and overlapping repeats are admitted on purpose. For example,
for text
w being “Then burst forth the unending argument between the believers and the unbelievers in the societies of the wise and the scientific journals.” because string “believers_” contains 10 characters (nine letters and a space) and appears in the text twice, whereas there is no longer a repeat. The properties of maximal repetition have been studied by both computer scientists [
8,
9,
10,
11] and probabilists [
3,
7,
12,
13,
14]. An efficient algorithm was found for computing the maximal repetition in linear time, so we can compute maximal repetition efficiently for relatively long texts [
10].
The object of our interest is how fast the maximal repetition grows with the length of text . In particular, for a finite energy process, the maximal repetition cannot grow faster than logarithmically, i.e., proportionally to the logarithm of the text length.
Theorem 2 (Shields [
3])
. For a finite energy process ,
there exists a constant ,
such that maximal repetition satisfies:for sufficiently large text lengths m with probability one.
Law (
4) has been studied in mathematics for some time. It was first proven for independent identically distributed (i.i.d.) processes [
12,
13]. Later, Shields [
3] formulated Law (
4) under the assumption that the process is stationary finite energy over a finite alphabet. In fact, his proof does not make use of the stationarity or finiteness of the alphabet, so these two conditions may be omitted as above. However, when the process fails to be finite energy, Law (
4) need not be satisfied. Shields [
14] demonstrated that there exist stationary stochastic processes for which maximal repetition
grows faster than an arbitrary sublinear function of the text length
n.
Now, we may return to the question of whether texts in natural language are typical of a finite energy process. A short empirical study conducted by Dębowski [
5] has shown that in printed texts in English, the maximal repetition grows faster than for a finite energy process. The observed growth is hyperlogarithmic,
i.e., faster than the logarithm of the text length raised to a certain power
. That is, the maximal repetition for texts in English satisfies:
The further question arises then what kind of a stochastic process can be responsible for the generation of texts in natural language. As we are going to show, this question can be related to a hypothesis by Hilberg [
4] concerning natural language. This hypothesis involves the entropy of the hypothetical text generation process.
The relevant mathematical background is as follows. The Rényi entropy of order
of a random variable
X is defined as:
for
[
15]. The limiting cases, the topological entropy
and the Shannon entropy
, can be equivalently defined as:
and:
It can be shown that the so-extended Rényi entropy is a decreasing function of
. In particular,
. Subsequently, for a discrete stationary stochastic process
, we define block entropy
and entropy rate:
if the limit exists. In particular, Limit (
9) exists for
[
16] and
[
17,
18].
We will say that a discrete stationary stochastic process
is a strong Hilberg process of order
and exponent
β if:
for some
and
. In contrast, we will say that a discrete stationary stochastic process
is a relaxed Hilberg process of order
and exponent
β if:
for some
,
and
. That is, the entropy rate
equals zero for a strong Hilberg process, whereas it can be greater than zero for a relaxed Hilberg process. In particular, if
, then the process is asymptotically deterministic,
i.e., there exist functions
, such that
holds with probability one for all
(Lemma 4 in [
19]).
Let us come back to natural language modeling. Reinterpreting the estimates of entropy for printed English by Shannon [
20], Hilberg [
4] supposed that texts in natural language can be generated by a strong Hilberg process of order one and exponent
. However, any strong Hilberg process of order one has entropy rate
, so this condition would imply asymptotic determinism of human utterances. Therefore, in some later works [
7,
21,
22,
23,
24], it was expected that texts in natural language are rather generated by a relaxed Hilberg process of order one with a strictly positive entropy rate
.
Now, we want to suggest that a much stronger hypothesis might be true for natural language. In the following, we will observe that for a strong Hilberg process of order zero, the maximal repetition cannot grow slower than hyperlogarithmically.
Theorem 3. For a strong Hilberg process of order zero and exponent β, there exist constants ,
such that the maximal repetition satisfies Condition (5) with probability one for and .
Theorem 3 does not preclude the possibility that a relaxed Hilberg processes (or some other processes) may also satisfy Condition (
5). Whereas finding such processes is an interesting open problem, at this moment, let us remark that the empirical observation of the hyperlogarithmic growth of maximal repetition (
5) might be explained by a hypothesis that texts in natural language are generated by a strong Hilberg process of order zero. This hypothesis will be called the strong Hilberg conjecture. Since
, the strong Hilberg conjecture implies that natural language production is also asymptotically deterministic.
Immediately, we would like also to remark that the strong Hilberg conjecture does not imply that texts in natural language are easy to predict or to compress. If we do not know the exact probability distribution of the process, all we can do is universal coding or universal prediction, done for example via the Lempel–Ziv code [
25]. It is known that, for a stationary process, the length of the Lempel–Ziv code
divided by the block length
n is a consistent estimator of the Shannon entropy rate
. However, the convergence rate of
to
is very slow, since by Theorem 3 of Dębowski [
26], we have:
where
is the maximal repetition. Therefore, if the maximal repetition grows slower than a power law and the process is a strong Hilberg process, then the length of the Lempel–Ziv code
is orders of magnitude larger than block entropy
! Consequently, we cannot estimate block entropy
by the length of the Lempel–Ziv code
.
3. Empirical Data
In this section, we check empirically how fast the maximal repetition grows for texts in natural language. Resuming the previous section, if we observe that the maximal repetition in a sample of texts grows faster than the logarithm of the text length, we may infer that the generating process is not finite energy, whereas the strong Hilberg conjecture becomes more likely if we observe hyperlogarithmic growth (
5). As we will see, this happens to be the case of natural language.
Let us observe that it is possible to investigate the concerned probabilistic hypotheses on two levels. In the first case, we assume that random variables are consecutive characters of the text, whereas, in the second case, we assume that random variables are consecutive words of the text. Respectively, we have to compute the repetitions in texts as repeated strings of characters or as repeated strings of words. We will test both levels. Moreover, we will show that the maximal repetitions in texts in natural language scale quite differently than for i.i.d. processes, that is the unigram models of the text.
For the experiment, we have downloaded 14 texts in English, 10 texts in German and 11 texts in French from the Project Gutenberg (
http://www.gutenberg.org/). To make the finite energy hypothesis more plausible, we have removed legal notices, tables of contents and strings of repeated spaces from the considered text, since they contain long repeats, which dominate repeats in the proper text;
cf. Dębowski [
5]. However, we have not excluded prefaces and afterwords, which sometimes also contain long quotations, but otherwise seem to be non-singular parts of the text. Moreover, using the statistics for the English texts, we have generated four-character-based unigram texts and four-word-based unigram texts (the texts have been generated via sampling with replacement rather than as random permutations). All so prepared texts are presented in
Table 1,
Table 2,
Table 3 and
Table 4.
Table 1.
The selection of texts in German.
Table 1.
The selection of texts in German.
| Text | Maximal Repeated Substring |
|---|
| Mark Twain, Die Abenteuer Tom Sawyers | “selig sind, die da arm sind im Geiste, denn” (9 words, close) |
| Lewis Carroll, Alice’s Abenteuer im Wunderland | “Edwin und Morcar, Grafen von Mercia und” (7 words) |
| Friedrich Nietzsche, Also sprach Zarathustra | “stiftete mehr Leid, als die Thorheiten der Mitleidigen? Wehe allen Liebenden, die nicht noch eine Höhe haben, welche über ihrem Mitleiden ist! Also sprach der Teufel einst zu mir: «auch Gott hat seine Hölle: das ist seine Liebe zu den Menschen.» Und jüngst hörte ich ihn diess Wort sagen: «Gott ist todt; an seinem Mitleiden mit den Menschen ist Gott gestorben.»” (61 words) |
| Thomas Mann, Buddenbrooks | “Mit raschen Schritten, die Arme ausgebreitet und den Kopf zur Seite geneigt, in der Haltung eines Mannes, welcher sagen will: Hier bin ich! Töte mich, wenn du willst!” (28 words) |
| Goethe, Faust | “Kühn ist das Mühen, Herrlich der Lohn! Und die” (9 words) |
| Dante Alighieri, Die Göttliche Komödie | “Da kehrt er sich zu mir” (6 words) |
| Immanuel Kant, Kritik der reinen Vernunft | “als solche, selbst ein von ihnen unterschiedenes Beharrliches, worauf in Beziehung der Wechsel derselben, mithin mein Dasein in der Zeit, darin sie wechseln, bestimmt werden” (25 words, in quotes) |
| Thomas Mann, Der Tod in Venedig | “diesem Augenblick dachte er an” (6 words) |
| Sigmund Freud, Die Traumdeutung | “ich muß auch auf einen anderen im sprachlichen Ausdruck enthaltenen Zusammenhang hinweisen. In unseren Landen existiert eine unfeine Bezeichnung für den masturbatorischen Akt: sich einen ausreißen oder sich einen” (29 words, in footnote) |
| Franz Kafka, Die Verwandlung | “daß sein Körper zu breit war, um” (7 words) |
In the proper experiment, for each text, we have considered initial blocks of the text of exponentially-growing length, and the maximal repetition was computed for each block. We report the results in terms of figures and examples of maximal repeats. First, also in
Table 1,
Table 2,
Table 3 and
Table 4, we have presented the maximal repeated substring in each whole text. For each maximal repeated substring, we give its length and sometimes short comments about its location: “close” means that the repeat was observed within a few paragraphs; “in quotes” means that the repeat was located within quotes one or more times. Further analysis of these repeats is left to more linguistically-oriented researchers.
Table 2.
The selection of texts in French.
Table 2.
The selection of texts in French.
| Text | Maximal Repeated Substring |
|---|
| Voltaire, Candide ou l’optimisme | “voyez, tome XXI, le chapitre XXXI du Précis du Siècle de Louis XV. B.” (14 words, in footnote) |
| Alexandre Dumas, Le comte de Monte-Cristo, Tome I | “le procureur du roi est prévenu, par un ami du trône et de la religion, que le nommé Edmond Dantès, second du navire le Pharaon, arrivé ce matin de Smyrne, après avoir touché à Naples et à Porto-Ferrajo, a été chargé, par Murat, d’une lettre pour l’usurpateur, et, par” (49 words, in quotes) |
| Victor Hugo, L’homme qui rit | “trois hommes d’équipage, le patron ayant été enlevé par un coup de mer, il ne reste que” (17 words, in quotes) |
| Gustave Flaubert, Madame Bovary | “et madame Tuvache, la femme du maire,” (7 words) |
| Victor Hugo, Les miserables, Tome I | “livres Pour la société de charité maternelle” (7 words, close) |
| Descartes, Oeuvres. Tome Premier | “que toutes les choses que nous concevons fort clairement et fort distinctement sont toutes” (14 words, many times in paraphrases) |
| François Villon, Oeuvres completes | “mes lubres sentemens, Esguisez comme une pelote, M’ouvrist plus que tous les Commens D’Averroys sur” (15 words, in quotes in footnote in preface) |
| Stendhal, Le Rouge et le Noir | “Which now shows all the beauty of the sun And by and by a cloud takes all away!” (18 words, in quotes) |
| Alexandre Dumas, Les trois mousquetaires | “murmura Mme Bonacieux. «Silence!» dit d’Artagnan en lui” (9 words, close) |
| Jules Verne, Vingt mille lieues sous les mers | “à la partie supérieure de la coque du «Nautilus», et” (10 words) |
| Jules Verne, Voyage au centre de la terre | “D0 E6 B3 C5 BC D0 B4 B3 A2 BC BC C5 EF «Arne” (14 words, in quotes) |
Table 3.
The selection of texts in English.
Table 3.
The selection of texts in English.
| Text | Maximal Repeated Substring |
|---|
| Jacques Casanova de Seingalt, Complete Memoirs | “but not deaf. I am come from the Rhone to bathe you. The hour of Oromasis has begun.»” (18 words, in quotes) |
| Thomas Babington Macaulay, Critical and Historical Essays, Volume II | “therefore there must be attached to this agency, as that without which none of our responsibilities can be met, a religion. And this religion must be that of the conscience of the” (32 words, in quotes, close) |
| Charles Darwin, The Descent of Man and Selection in Relation to Sex | “Variability of body and mind in man-Inheritance-Causes of variability-Laws of variation the same in man as in the lower animals–Direct action of the conditions of life-Effects of the increased use and disuse of parts-Arrested development-Reversion-Correlated variation-Rate of increase-Checks to increase-Natural selection-Man the most dominant animal in the world-Importance of his corporeal structure-The causes which have led to his becoming erect-Consequent changes of structure-Decrease in size of the canine teeth-Increased size and altered shape of the skull-Nakedness-Absence of a tail-Defenceless condition of man.” (86 words, in the table of contents, undeleted by omission) |
| Jules Verne, Eight Hundred Leagues on the Amazon | “After catching a glimpse of the hamlet of Tahua-Miri, mounted on its piles as on stilts, as a protection against inundation from the floods, which often sweep up” (28 words, close, probably by mistake) |
| William Shakespeare, First Folio/35 Plays | “And so am I for Phebe Phe. And I for Ganimed Orl. And I for Rosalind Ros. And I for no woman Sil. It is to be all made of” (30 words, close) |
| Jules Verne, Five Weeks in a Balloon | “forty-four thousand eight hundred and forty-seven cubic feet of” (9 words, close) |
| Jonathan Swift, Gulliver’s Travels | “of meat and drink sufficient for the support of 1724” (10 words, in quotes, close) |
| Jonathan Swift, The Journal to Stella | “chocolate is a present, madam, for Stella. Don’t read this, you little rogue, with your little eyes; but give it to Dingley, pray now; and I will write as plain as the” (32 words, in quotes in preface) |
| George Smith, The Life of William Carey, Shoemaker & Missionary | “I would not go, that I was determined to stay and see the murder, and that I should certainly bear witness of it at the tribunal of” (27 words, in quotes) |
| Albert Bigelow Paine, Mark Twain. A Biography | “going to kill the church thus with bad smells I will have nothing to do with this work of” (19 words, in quotes, close) |
| Etienne Leon Lamothe-Langon, Memoirs of the Comtesse du Barry | “M. de Maupeou, the duc de la Vrilliere, and the” (10 words) |
| Jules Verne, The Mysterious Island | “we will try to get out of the scrape” (9 words, in the same sentence) |
| Willa Cather, One of Ours | “big type on the front page of the” (8 words, close) |
| Jules Verne, Twenty Thousand Leagues under the Sea | “variety of sites and landscapes along these sandbanks and” (9 words, close) |
Table 4.
The selection of unigram texts.
Table 4.
The selection of unigram texts.
| Text | Maximal Repeated Substring |
|---|
| Character-based unigram Text 1 | “ u ti t r ” |
| Character-based unigram Text 2 | “e t tloeu ” |
| Character-based unigram Text 3 | “o d t eie” |
| Character-based unigram Text 4 | “s ei er e” |
| Word-based unigram Text 1 | “of that A for” |
| Word-based unigram Text 2 | “was the of in” |
| Word-based unigram Text 3 | “in of of the” |
| Word-based unigram Text 4 | “of of of of a” |
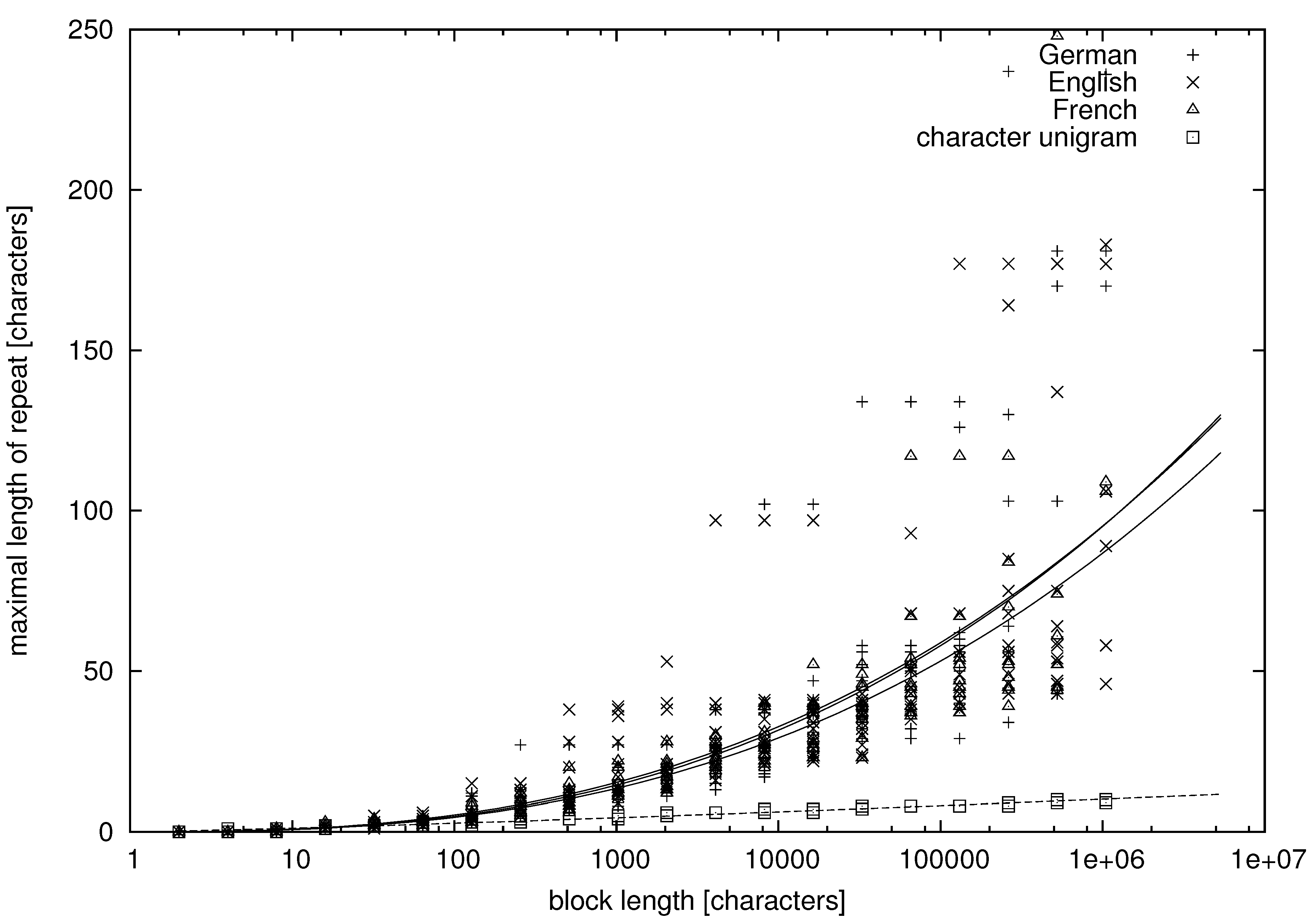
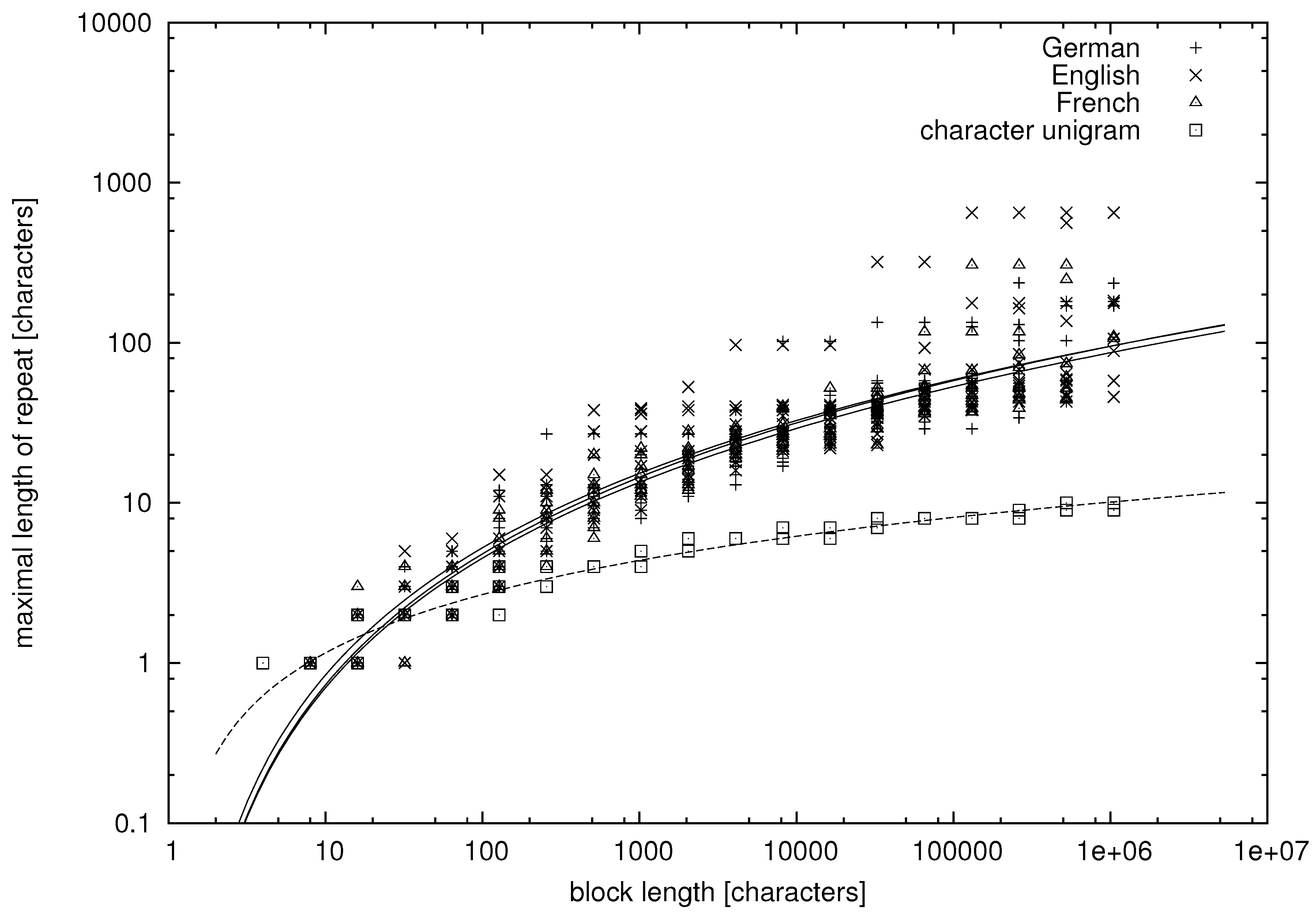
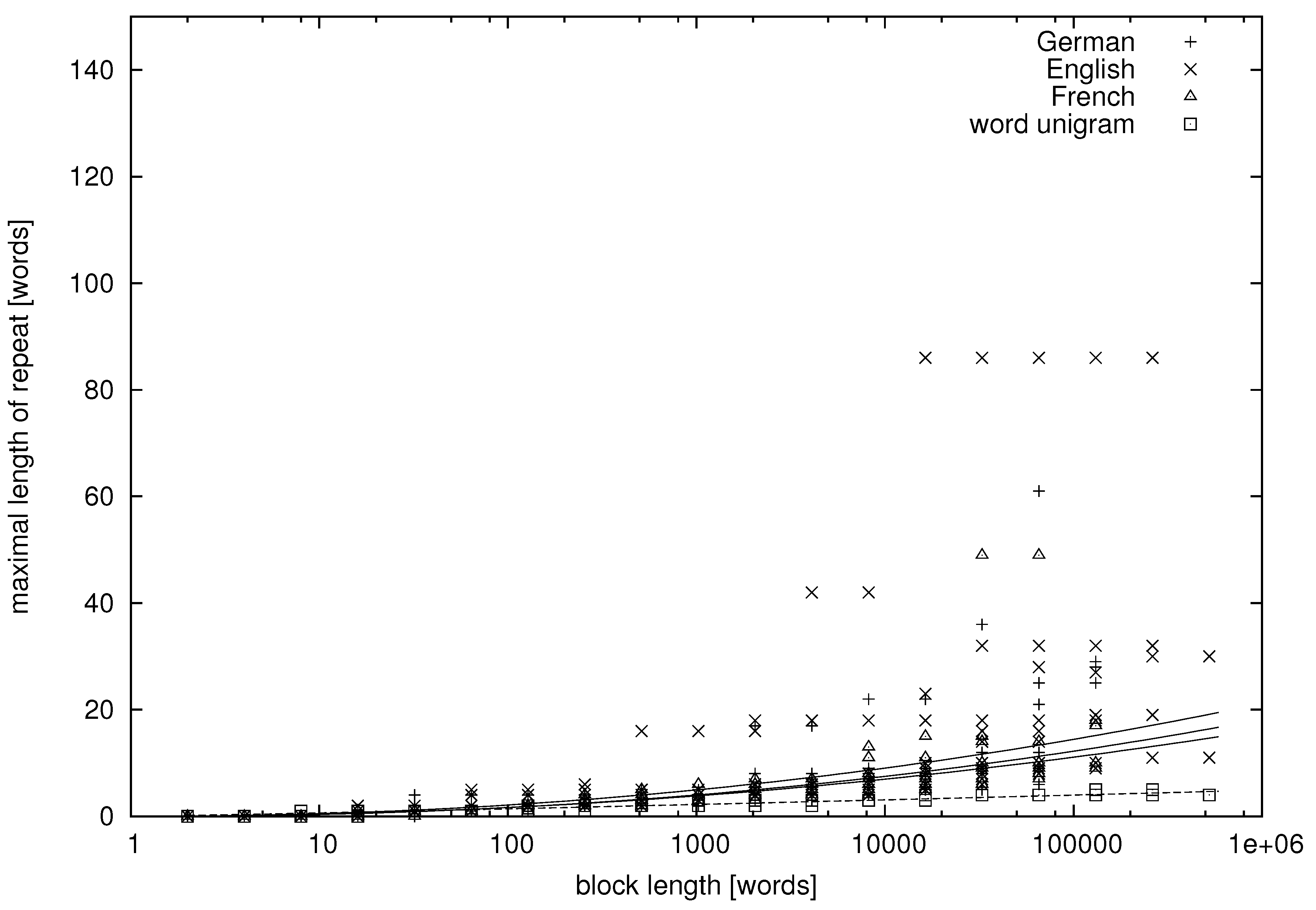
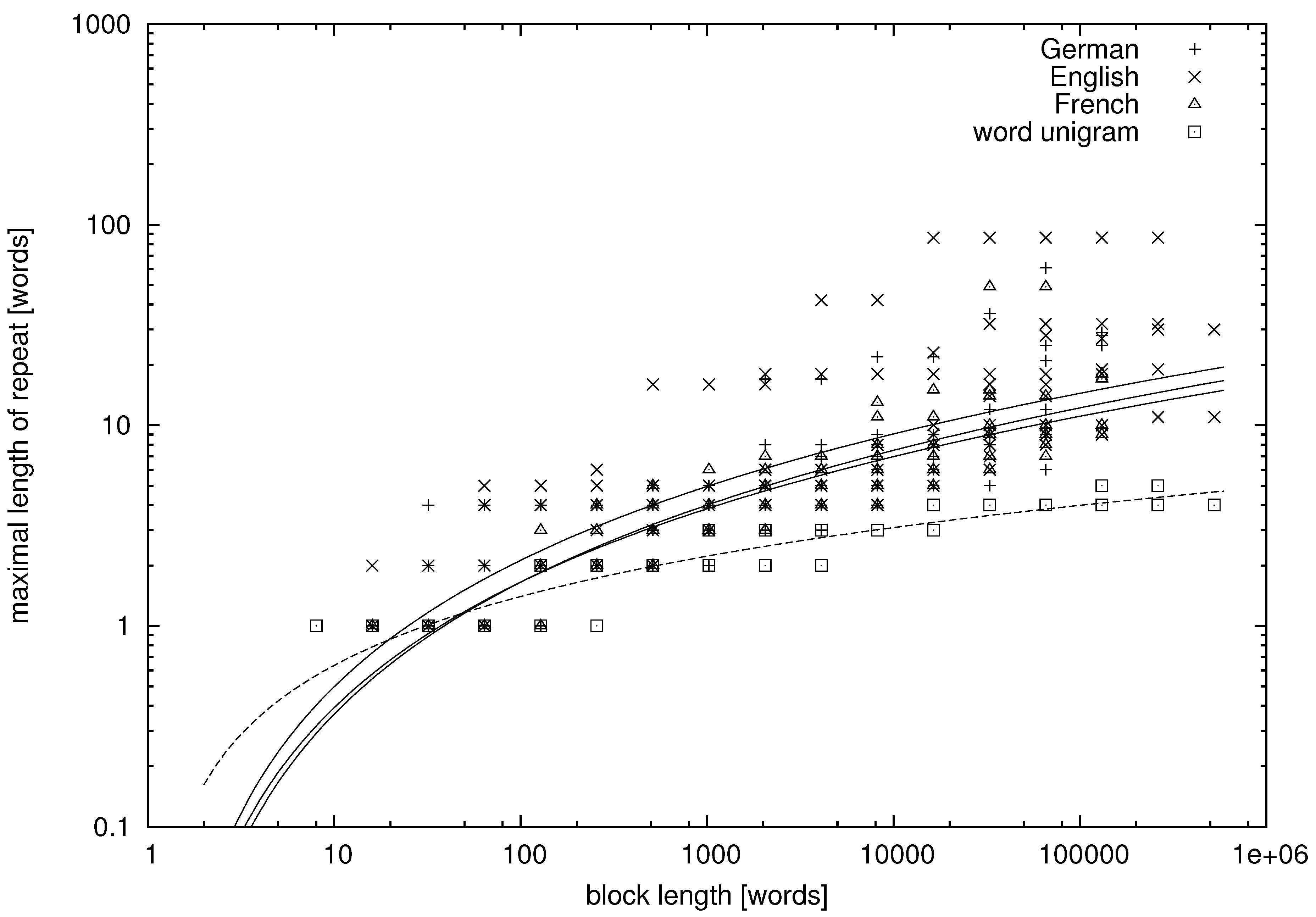
From the tables, we can learn that there appear repeats in texts in natural language whose lengths exceed a dozen of words. More quantitative data are presented in
Figure 1,
Figure 2,
Figure 3 and
Figure 4, where we study the dependence between the block length and the maximal repetition within the block for both natural language and unigram models.
Figure 1 and
Figure 2 concern variables
being characters, whereas
Figure 3 and
Figure 4 concern variables
being words. It can be seen that there is much variation in the data, but let us try to fit some functional dependence to the data points.
Figure 1.
Character-based maximal repetition on the logarithmic-linear scale. The lines are the regression lines.
Figure 1.
Character-based maximal repetition on the logarithmic-linear scale. The lines are the regression lines.
Figure 2.
Character-based maximal repetition on the doubly-logarithmic scale. The lines are the regression lines.
Figure 2.
Character-based maximal repetition on the doubly-logarithmic scale. The lines are the regression lines.
Figure 3.
Word-based maximal repetition on the logarithmic linear scale. The lines are the regression lines.
Figure 3.
Word-based maximal repetition on the logarithmic linear scale. The lines are the regression lines.
Figure 4.
Word-based maximal repetition on the doubly-logarithmic scale. The lines are the regression lines.
Figure 4.
Word-based maximal repetition on the doubly-logarithmic scale. The lines are the regression lines.
In
Figure 1 and
Figure 3, the abscissa is on the logarithmic scale, and the cloud of points forms a convex (∪) shape. Thus, on average, the maximal repetition grows faster than logarithmically. On the other hand, the clouds of points are concave (∩) in
Figure 2 and
Figure 4, where both the abscissa and the ordinate are on the logarithmic scale. Hence, on average, the maximal repetition grows slower than a power law. Therefore, let us try to fit the hyperlogarithmic function:
where
A and
α are free parameters. If we obtain
α significantly larger than one, the investigated process cannot be finite energy. Since the distributions of
for fixed
n are skewed towards large values, to make the finite energy hypothesis more plausible, we fit parameters
A and
α using the least squares method in the doubly-logarithmic scale. In this way, we obtain smaller values of parameters
A and
α than when applying the least squares method in the linear scale.
It can be seen in the figures that the maximal repetition behaves quite comparably for texts in English, German and French, whereas it is strikingly different for the unigram texts, for which the mean and variance of
are much lower. The fitted parameters of Model (
13) and their standard errors are presented in
Table 5. They were obtained using the standard fitting procedure of the Gnuplot program.
The unigram texts are in theory a finite energy process, so parameter
α should not exceed one in that case. In
Table 5, we see however that
on the level of characters and
on the level of words, where the second digit is significant. This observation needs a definite explanation, which we cannot provide at the moment. The reviewers of this paper suggested that our simple fitting procedure may overestimate parameter
α and underestimate its error, analogically as in using the least squares method to fit power law distributions [
27]. However, here, we cannot use the improved method of fitting power law distributions by Clauset
et al. [
27], since we are not fitting a probability distribution. As an alternative explanation, let us note that our observation of
for the unigram texts might be due to generating these texts using an imperfect pseudorandom number generator, which does not satisfy the finite energy property. In fact, to generate the unigram texts, we have used the pseudorandom number generator built in the Perl programming language, which need not be the best choice.
Table 5.
The fitted parameters of Model (
13). The values after the sign ± are the standard errors.
Table 5.
The fitted parameters of Model (13). The values after the sign ± are the standard errors.
| Level of Description | Class of Texts | A | α |
|---|
| characters | German | | |
| characters | English | | |
| characters | French | | |
| characters | unigram | | |
| words | German | | |
| words | English | | |
| words | French | | |
| words | unigram | | |
Having made this remark, let us note that it is obvious by looking at the plots that texts in natural language are of a different class than the unigram texts. The value of
α is twice larger,
on the level of characters and
on the level of words, for texts in natural language. Hence, we may conclude that texts in natural language, as far as we can trust the estimated parameters and extrapolate the data, are not generated by a finite energy process on the level of characters or on the level of words. Repeats as long as 20 words are expected if they appear in samples of one million word tokens, which is close to the observed maximal length of a text. That the repeats can be so long may seem surprising, but the empirical data, such as the examples in
Table 1,
Table 2,
Table 3 and
Table 4, confirm this claim. This behavior is strikingly different than for the unigram texts.
4. Conclusions
In this article, we have studied two hypotheses about a possible probabilistic mechanism of generating texts in natural language. According to the first hypothesis, texts are in a certain sense uniformly contaminated by random noise. As we have shown, this conjecture implies that the stochastic process of generating texts is finite energy. According to the second hypothesis, the strong Hilberg conjecture, the number of different admissible texts of a given length is severely restricted, namely the logarithm of it grows as a power law. In other words, the strong Hilberg conjecture assumes some mechanism of intense and very selective replication of texts. According to the presented mathematical results, the finite energy hypothesis and the strong Hilberg conjecture are mutually incompatible and can be tested by investigating the growth rate of the maximal repetition: the maximal length of a repeated substring in a text.
The empirical study performed in this article confirms that in written texts, the maximal repetition grows hyperlogarithmically, i.e., the maximal repetition grows as a power of the logarithm of the text length. As far as we can trust our fitting procedure and extrapolate the empirical data, this falsifies the finite energy hypothesis and partly corroborates the strong Hilberg conjecture. Rejection of the finite energy hypothesis implies that texts written in natural language cannot be formed by transmission through a specific noisy channel without any correction after the transmission. Thus, some mechanism of reducing randomness must be at work during the composition of texts written in natural language.
Although the strong Hilberg conjecture implies the asymptotic determinism of human utterances, it should not be discarded on a purely rational basis. For the further evaluation of the strong Hilberg conjecture, it might be useful to exhibit some abstract examples of strong Hilberg processes. So far, we have constructed some processes, so-called Santa Fe processes and some hidden Markov processes, which are relaxed Hilberg processes with entropy rate
[
7,
28,
29]. There are also known some stationary processes, such as the Thue–Morse process, for which
and
[
30,
31]. We are now on the way to construct a strong Hilberg process, but this is a topic for a separate paper.
The present study, although extending the previous study by Dębowski [
5], covers still a narrow selection of Indo-European languages, for which we obtain very similar results. In future research, it may be interesting to extend the scope to some non-Indo-European languages, especially Chinese or Japanese, which use a very different script, featuring a very large alphabet. However, we suppose that the results may be comparable. The reason is that the strong Hilberg conjecture appears to be not a hypothesis about a particular ethnic language, but rather a hypothesis about fundamental limitations of human memory and attention. On this ground, let us claim that we may have discovered a new language universal. This claim should be thoroughly verified.
In future research, it may be also illuminating to contrast our observation for natural language with genetics, as suggested by Shields [
3]. DNA sequences are certain sequences that have been generated by the process of biological evolution, which, like human communication, may be conceptualized as a complicated stochastic process combining randomness and computational mechanisms that decrease the observed disorder. According to Chandrasekaran and Betrán [
32], imperfect copying of very long sequences is the main mechanism of creating new genes. Hence, we suppose that repeated strings in DNA are much longer than in texts in natural language. Although we have not found any article concerning the maximal repetition as a function of DNA sequence length, there are publications that concern tools for computing repetitions in DNA [
33], topological entropy of DNA [
34] and a power law for frequencies of repeated strings in DNA, which resembles Zipf’s law for natural language [
35].
Finally, let us recall the idea of memetic cultural evolution, an analogue of biological evolution [
36]. The principle of that theory is that the human mind tends to select and imitate previously-encountered strings of symbols or ideas, according to their utility, regardless of whether being produced on their own or provided by the environment. It may be obvious that this process occurs heavily in music at the level of melodies or during language acquisition at the level of single words or grammatical constructions;
cf. Bloom
et al. [
37]. However, the empirical data we provide show that the self-imitation process operates on many length scales of text composition and leads to surprisingly long literal repeats in spite of a conscious intention of not repeating long phrases too often. Moreover, according to the strong Hilberg conjecture, the number of different admissible texts of a given length is severely restricted, that is there must exist some mechanism of intense and very selective replication of texts. Thus, we suppose that the strong Hilberg conjecture may describe a certain idealized equilibrium state in the cultural/biological evolution. This idea may deserve further research. Let us note that a completely different approach to mathematics of cultural/biological evolution has been proposed by Chaitin [
38]. In the research of the strong Hilberg conjecture, it might be fruitful to use his ideas.