1. Introduction
The light storage effect (LSE) has become a powerful technique that offers storing and restoring quantum information [
1,
2,
3,
4,
5,
6,
7]. Quantum repeaters [
8,
9,
10,
11], as well as quantum-information networks [
12,
13,
14,
15,
16,
17,
18,
19,
20,
21,
22,
23,
24,
25] have been facilitated through the LSE technique. According to electromagnetically-induced transparency (EIT) [
26,
27,
28], LSE is prominent when two fields that have a common excited state interact on different transitions. Ground states of hyperfine
and
transitions in alkali atoms [
29] have long radiative decay and form memory nodes for quantum communication. In EIT experiments, the coupling field is known as the write field. In order to reveal information about the mutual interaction of EIT pulses, coupling and probe, a delayed pulse in the coupling channel is applied. It is known as the read field. The read and write sequence have been exploited in remote quantum memories, as well as in the Duan, Lukin, Cirac and Zoller scheme for a quantum repeater [
12]. As the read field propagates, the generated field in the probe channel, at the time section of the read field, gradually grows. Recently, EIT-based four-wave mixing has been studied in a four-level system of a
line transition with circularly-polarized fields [
30]. The propagation in a duplicated two-level atom using irreducible tensorial representation of the bases for fine structure transition in sodium atoms has been reported for circularly-polarized fields [
31].
The aim of this paper is to present an alternative view of the light restoring phenomenon. Our issue is based on entropy. The notion of entropy seems to be useful, since it is a measure of the lack of information about the so-called restoring field. Thus, entropy should be maximal at the entrance boundary for probe and coupling fields. As the read field propagates, the generated restoring field in the probe channel increases with entropy production. The entropy associated with light scattering is discussed, as well.
This paper is organized as follows.
Section 2 depicts the energy diagram for the
line in sodium, where the single-, as well as double-excitation are indicated. In addition,
Section 2, presents the atomic basis operators and relative units adopted in this work.
Section 3 is devoted to entropy associated with light scattering for single excitation.
Section 4 is devoted to Shannon entropy associated with light storage and its retrieval for the lower Λ excitation of the four-level atom configuration.
Section 5 presents conclusions. Finally,
Appendix A presents the time evolution of the density matrix components. The maximal density matrix components that are accessible to the
atomic configuration are given. Therefore, we can easily study triple-color, four-color, as well as different V configurations with the same set of equations. The first (second) V configuration corresponds to the transitions between the excited hyperfine levels and lower (upper) ground hyperfine level.
2. The Theoretical Description
This paper is an attempt to analyze coherent excitation of
transition
in sodium. The field with Rabi frequency
couples the lower hyperfine (hf) state
to the upper hf states
and
. In addition, the field
couples the second lower hf state
to upper hf states, where
F stands for total angular momentum with
indicating the lower (upper) hf state. The coupling fields in a double-Λ excitation are shown in
Figure 1.
For one-color excitation, its frequency
is tuned to the line center of the fine structure transition. In arrival time distribution analysis, it is preferable to deal with the
line in sodium atoms. This is because sodium has a smaller upper hyperfine splitting
than that of rubidium. Therefore, the influence of phase modulations produced by upper hyperfine splitting will be smaller in sodium. The propagation dynamics of linearly-polarized and co-propagating fields will be investigated. The state of the atom is described by the Liouville–von Neumann equation for the density matrix of the dressed atom as
, where
,
and
stand for the system Liouvillian, Hamiltonian, and the relaxation superoperators, respectively [
32,
33,
34]. The relaxation superoperator contains both radiation and collisional contributions. In this paper, we have followed the notations of Fiutak and Van Kranendonk for the representation of the density matrix components, the atom-laser interaction and the radiation damping operator [
32], where
. The atomic basis operators using the irreducible set
have been presented in [
35]. The indices
i and
k numerate hyperfine states from one to four. In this paper, the bases operators
are written in flattened form as
and
, instead of the tensor double and lower indices form
. The basis operators are orthogonal in difference space; in a sense, the trace of the metric tensor vanishes:
, where
for
and zero for
. In terms of basis operators, the density matrix
ρ can be expanded as
. The density matrix is normalized as
. The normalization condition provides the completeness of the basis operators. The components of the density matrix operators are as follows. There are four components with zero rank tensors:
,
,
and
. The populations of hf levels are given by
,
,
and
. There are eight complex coherences:
,
,
and
and their adjoint. We have alignment components for lower and upper hyperfine states, such as:
,
,
and
. The lower and upper Raman coherences of the second rank are:
and
. The components that are of third rank are
,
and
. Finally, we have the hexadecapole moment components
and
.
Figure 1.
Excitation of the sodium line. The dashed arrow shows the excitation with one beam, which is tuned to the fine structure transition. is the detuning. The solid arrows show the double-Λ configuration excitation with and fields. and are the detuning of the fields with and from the transitions and , respectively. and are lower and upper hyperfine splitting, respectively.
Figure 1.
Excitation of the sodium line. The dashed arrow shows the excitation with one beam, which is tuned to the fine structure transition. is the detuning. The solid arrows show the double-Λ configuration excitation with and fields. and are the detuning of the fields with and from the transitions and , respectively. and are lower and upper hyperfine splitting, respectively.
The present work describes, mainly, two cases for entropy considerations. The first one is to study the stationary illumination of the
line with hyperfine structure to reveal the associated spectral entropy. The light is tuned to the fine structure transition as shown in
Figure 1. The second case is devoted to the dual-pulsed light excitation to investigate the entropy associated with the quantum interference within the double-Λ excitation. Special attention is paid to the entropy associated with the light storage effect. In what follows, and irrespective of the strength of the fields, we shall associate the fields
and
with the transitions
and
, respectively. To reduce absorption, the pulses are detuned from the third level, as indicated in
Figure 1. The detuning of the pulses is within the upper hyperfine splitting. In addition, the coupling pulses
and
also couple the fourth hyperfine level with detuned coherences of the first and third rank. The second rank Raman coherence for the lower hyperfine levels seems to be the most important in light storage principles, since it has a long radiative decay. However, ignoring components of the same rank or higher will produce the reduction of dissipation, and loss of the information will be revealed. Thus, we have considered the maximal bases.
The flattened form of the density matrix components seems to be convenient in our description, especially for numerical computations. In addition, as concerns the time evolution of the density matrix, one can easily find the connection between the flattened form and the explicit form, which shows the rank of the density matrix component and the levels. The connection can be made in terms of the collisional relaxation rates. As an example in Equation (A5), one can see that the collisional relaxation rate of is . The superscript (1) is the rank of the coherence , and the lower index indicates the connected levels by the field.
To reduce our computation, we use the same absorption coefficient
for the
p and
c channels as an approximation. The atom-field coupling constant is given as
, where
is the reduced value of the dipole moment and
E stands for the electric field amplitude [
32]. The Rabi frequency is related to the atom-field coupling constant through the relation
by inspection of the eigenvalues of the matrix
. The relation between Rabi frequency and the laser intensity
I is given as
where
is the saturation intensity [
29,
36,
37].
In our calculations, we make use of relative units, where detuning, relaxation rates and Rabi frequencies are in γ units, and γ is the spontaneous decay rate of the state. The time t is presented as normalized and retarded where with c is the velocity of light and z is the prolonged distance. The distance z is normalized to the Beer’s length cm, as or .
3. Spectral Dependence of Entropies Associated with Light Scattering for Single Color Excitation of Line
In this section, we aim to describe steady-state illumination of the
line in the sodium atom. For stationary illumination, we use a light with frequency
ω. The detuning
stands for light detuning from the fine structure transition with frequency
. When
, we have four off-resonant transitions. Our main concern is basically for the entropy and its decomposition. Shannon entropy [
38] is denoted here by
, which is an entropy measure on the probability distribution
as:
where
stands for the occupation probability densities of the respective levels at frequency
ω. We have constructed the occupation probability density
in terms of subdividing the occupation probability
by the frequency window
, which covers the lower hyperfine splitting. This ensures that:
over the selected frequency window under consideration.
The former procedure is to be extended to produce spectral entropy analysis for other variables, such as the dipole operator
with emphasis on its real and imaginary parts. Its real part is important for slow and fast light indications. The imaginary part gives the absorption profile. For simplicity, the case of one-color excitation in this section is considered. The dipole operator
μ becomes:
with the trace metric normalization condition:
. In terms of the density matrix components, the dipole operator
μ is given as:
Let
J denotes the total mean number of photons scattered per unit time. The spectral dependence of the total scattered light intensity is defined in terms of the dipole operator
μ, and the left
, as well as right
eigenvectors of the Liouvillian
as:
and:
where
and
are the right and left eigensystems. These eigensystems satisfy the completeness relation
, with
the identity operator. If we retain the exponential time series dependence, such as
, we clearly obtain a Lyapunov function for
that depends on time. The case when
is of special importance. In this case,
and
. The index
means the stationary value. Thereafter:
Generally,
gives the spectral dependence of the coherent part of the scattered light. Turning to the incoherent part of the spectrum, by removing the partition of unity in Equation (
6), one obtains:
Using the expansions
and
, one can operate
on
ρ and uses the orthogonality of the bases to obtain:
We set
in our dimensionless analysis. The spectral entropy associated with the scattered light over a frequency window
Ω can be investigated in terms of cross-section as:
For the coherent (Rayleigh) part of the scattered photons, we have:
The Rayleigh scattered light and the redistribution of radiation have been studied in [
32,
39,
40,
41] and the references therein. Let us construct the spectral entropy associated with the coherent part of the scattered photons from:
In the same manner, we define the spectral entropy associated with the total
π polarized light in terms of:
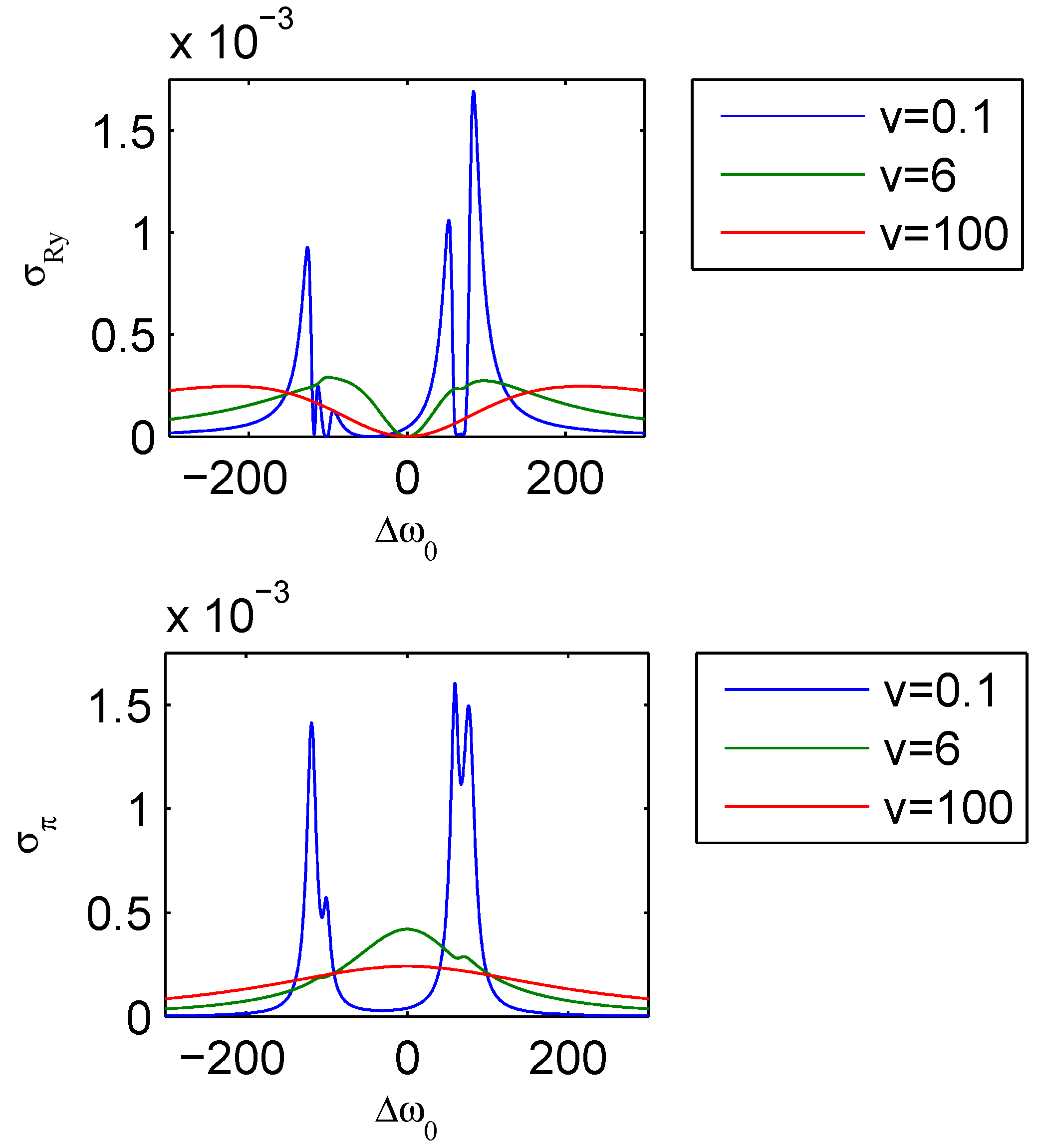
The remarkable features of spectrum are available in the treatment of entropy. It is to be noted that Shannon entropy is composed of four terms that interfere with each other. We presented in
Figure 2 the probability cross-section associated with the Rayleigh scattered light
and the probability for
π scattered light
at different atom-field coupling values. In
Figure 3, we presented the relative Shannon entropy
, the relative entropy due to Rayleigh
and the relative entropy due to the total
π scattered light
. The relative entropy for
and
is an entropy that is measured with respect to that entropy where all of the frequency window components are equally probable. However, we choose relative entropy for Shannon entropy
as an entropy that is measured with respect to that entropy where all of the hyperfine levels are equally populated by one fourth for all components of the frequency window. The frequency window
with discrete values at step
.
Figure 2.
Spectral dependence of the probability cross-sections for the Rayleigh and π scattered light at different atom-field couplings: weak, moderate and strong.
Figure 2.
Spectral dependence of the probability cross-sections for the Rayleigh and π scattered light at different atom-field couplings: weak, moderate and strong.
Figure 3.
The dependence of relative entropy on the atom-field coupling v for: the scattered π polarized light , Rayleigh scattering and Shannon entropy, based on populations of the hyperfine levels .
Figure 3.
The dependence of relative entropy on the atom-field coupling v for: the scattered π polarized light , Rayleigh scattering and Shannon entropy, based on populations of the hyperfine levels .
In
Figure 2, the hyperfine structure is exposed, and
has a resemblance to the stationary spectrum. The probability associated with Rayleigh light for negative frequency detuning does not show the doublet structure, as shown by
. In addition,
shows more peaks due to the interference effect at nearby wings. The reduction of the total dipole moment is shown by the positions
, which indicate slow light. The relative Shannon entropy
shows the minimum at moderate fields
to
, in
Figure 3. The upper hf structure is destroyed at moderate field excitation. The hf line structure reduces to two lines separated by the lower hf splitting, resulting in a three-level structure. For a stronger field, the structure reduces to the two-level atom, where the lower hf splitting is destroyed. We distinguish the last case by considering that
approaches zero and
approaches unity at the upper-ground hf level. For the three-level case,
and
have values less than unity and greater than zero. Therefore, a three-level atom corresponds to the case when the upper hf structure is smeared in width, but the height is not higher than that of the weak field case. The presence of a structure for weak fields increases entropy. However, the wide broadening of spectral line and the continuous distribution of populations increases the entropy for strong fields.
Our calculations of spectral entropy are good candidates for parallel processing, as we did, where the time of the calculations was considerably reduced. By spectral, we mean that the probability distribution depends on frequency, and the corresponding entropy depends on the chosen frequency window. In this paper, we have considered the entropy associated with
π polarized light. For a different polarization, the difference space can be constructed by spherically-polarized fields [
33,
42], and the corresponding spectral entropy can be obtained.
4. Time-Dependent Entropy Associated with Light Storage and Light Restoring
This section focuses on entropy associated with light storage and light retrieval within the traditional framework of EIT. It is important to obtain an entropy signature about maximum correlations in some parts of the total system. For this reason, the two-fold excitation of the double-Λ system is considered. The p-field is tuned to the transition, whilst the c-field is tuned to the transition. The time-delayed pulse in the c-channel is used to check the presence of the light storage effect, while the pulses and form the EIT structure.
The time dependences of the coupling fields are:
where the amplitudes
and
. The initial and finial times are
and
, respectively. The positions of the fields maxima are
and
for the delayed component of the field
. The other parameters take the values as
,
and
, where
is the Heaviside function. The initial pulses have dimensionless energies as
, where
, respectively. Thermal equilibrium among lower hf states is assumed. Therefore, at the entrance boundary
, the density matrix components satisfy
,
and
. It is also assumed that the fields detuning are
and
. The propagation of the radiation fields are governed by the reduced Maxwell equations as:
The time evolution of the density matrix equations is listed in
Appendix. The energies of the propagated fields are defined by the following relations:
where
. The time section of the fields is determined by
. The
and
fields overlap on the same period
. In addition, the restoring field has a time section
. Thus,
gives the efficiency of restoring.
Shannon entropy at instant
t, over the whole time
, can be formulated with
representing the weighed populations over the whole time section
T. It is instructive to look at the probability for a specific transition as:
In terms of these weighed probabilities, one can obtain Shannon entropy with explicit dependence on the transition probability branching. Decomposing the double-Λ system into
and
subsystems, the first subsystem contains the
p pulses with the transitions
. The second one contains the
c pulses with the transitions
. The population at instant
t within
and
subsystems are given by combinations of
; therefore:
and:
Thus, the probability distribution within each subsystem has been constructed. The basic functions associated with
and
subsystems read:
One can choose
and
’s of different lengths, but the functions
and
should satisfy the normalization condition:
Thus, one can define the entropy for the two V subsystems as:
It will be instructive to expose the interrelation between the entropies associated with the storage and the retrieval periods. The constructed
and
corresponding to the storage and the retrieval periods are formulated by
and
, where:
and
. In addition,
and
time sections are of equal lengths,
i.e., subdivisions. The constructed entropies for
and
systems to obtain differential entropy are given by:
The continuous and dashed lines in
Figure 4 represent
and
, respectively, where the inset shows
with a slight entropy reduction. At small and moderate distances,
is bigger than
. This is because the first period
includes the first coupling and probe fields. In addition, the second period
includes the second coupling and a small restoring field. Therefore, the reason
is accounted for by the excitation done by the probe and first coupling pulses, lifting populations
and
at a value that is slightly different from equality on the storage period and, so, in the reading period. The entropy transfer (
Figure 4) is associated with population transfer among the two sectional periods
and
, as well as due to the light storage effect. The drop of
at
is attributed to the drop in
leading to a storage level, after the excitation period, with higher populations in
and
. The process is reversed in the reading period where
is increased.
Let the time-dependent energy
be the energy distributed in time and associated with the p-transitions
, where
is the generated restoring field in the p-transition. Similarly, the energy
is the energy contained in the c-transition
. The probability of finding energy in each transition can be obtained as
and
:
The entropy associated with the probability distribution of energy in each transition can be written as:
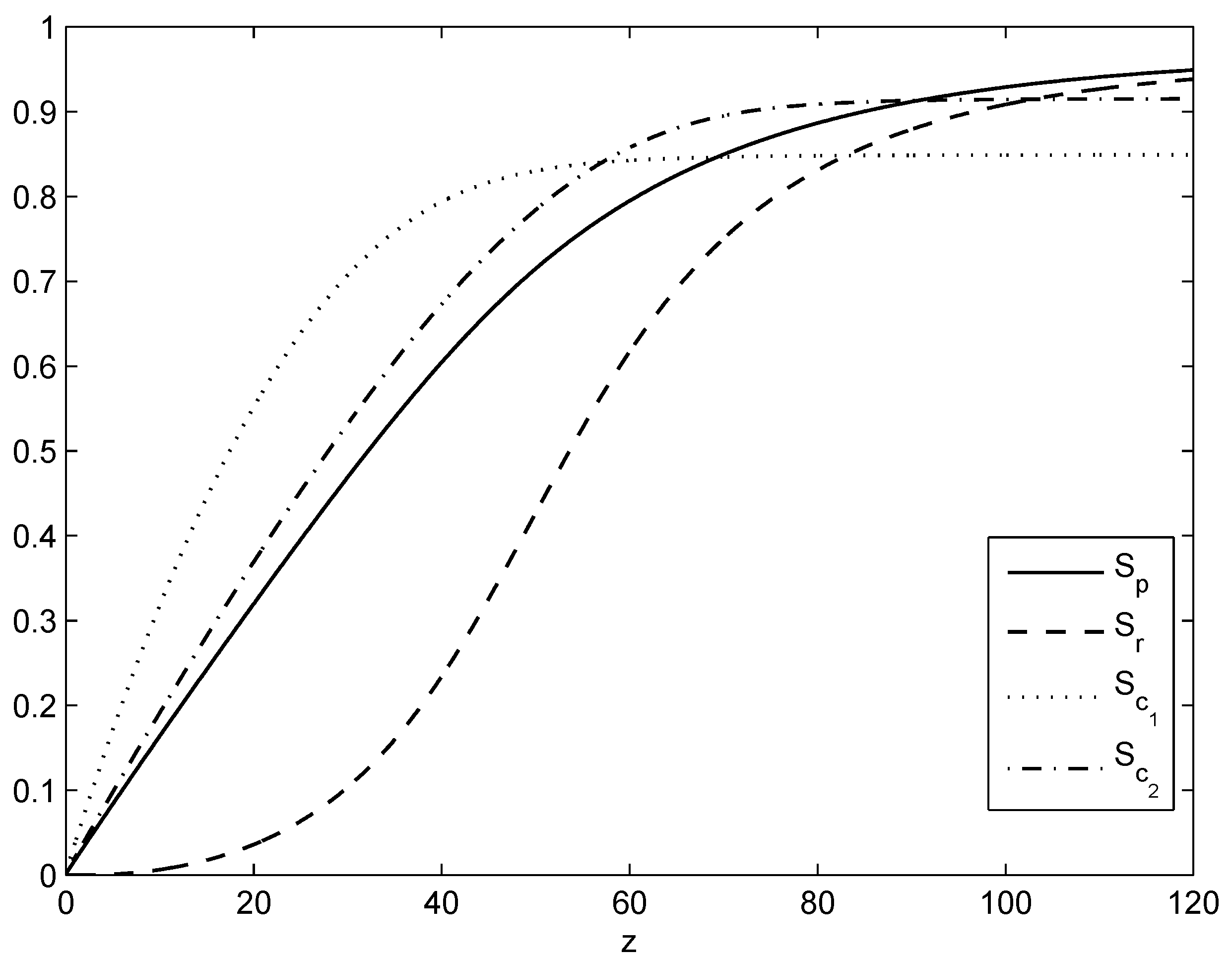
Figure 4.
Space dependence of the relative Shannon entropy associated with and subsystems. The inset shows the space dependence of relative Shannon entropy for the period .
Figure 4.
Space dependence of the relative Shannon entropy associated with and subsystems. The inset shows the space dependence of relative Shannon entropy for the period .
Figure 5 shows an entropy exchange among the two transitions in the course of distance. The increase of
for a moderate distance manifests the generation of the restoring field and the depletion of the coupling fields. For a big distance, the second coupling field entropy rises where the first coupling has been diminished. In order to confirm that, let us consider the space-dependent pulse entropy in what follows. Let us construct the probability distribution at a fixed position
z from:
where
L is the space length,
is the time period for every field and:
The cumulative sum
of Shannon entropy
associated with the probability distribution
is given as:
Figure 5.
The space dependence of the relative entropies and . The probability is defined as the ratio of energy of the fields in the transitions and to the corresponding total field energy in each transition, respectively.
Figure 5.
The space dependence of the relative entropies and . The probability is defined as the ratio of energy of the fields in the transitions and to the corresponding total field energy in each transition, respectively.
The cumulative sums
,
,
and
are shown in
Figure 6. The light storage effect is shown as an entropy production in the time section
revealed by the restoring field
.
Figure 6 shows that the production of entropy is accounted for by the entropy reduction for the first coupling. The first coupling approaches its asymptotic value of relative entropy quicker than that of other fields, showing the high gradation flow [
44] of its entropy.
Our aim is to study the entropy as an identifier for quantum interferences in multilevel systems. It seems to us that one could use the maximum or the minimum entropy [
45] value reached in the atomic system as a critical value for the breakup of the local stabilization of short optical pulses in the double-Λ system. This is important, since the area theorem [
46,
47,
48,
49,
50] does not hold in multilevel systems with soliton-like solutions of the reduced Maxwell–Bloch equations [
51]. In terms of entropy, we would be able to find when the pulses in the multilevel system stabilize or collapse to fractional
pulses in area. Finally, it is worth mentioning that the entropy of a system of solitons has been considered in [
52].
Figure 6.
The space dependence of the cumulative sum of the relative Shannon entropy associated with the probability distribution , where stand for the p-field, restoring field, the first coupling field and the second coupling field, respectively.
Figure 6.
The space dependence of the cumulative sum of the relative Shannon entropy associated with the probability distribution , where stand for the p-field, restoring field, the first coupling field and the second coupling field, respectively.
5. Conclusions
A dynamical entropy approach is adopted to describe atomic entropy by irreducible tensor components of the statistical operator. The constructed dynamical entropy for stationary illumination is based on populations of hf levels, as well as the dipole operator. The projection of the dipole operator on eigenvectors of the Liouvillian describes different processes. We introduced with zero eigenvalue to obtain an entropy associated with the Rayleigh scattered light. For a coherent scattering process in ω-space, we have used the imaginary part of the dipole operator as the generator for the entropy . In addition, we introduced as a generator for entropy associated with different eigenvalues in ω-space. Generally, we express entropy as a relative entropy, i.e., with respect to the entropy where all of the frequency window components are equally probable.
The notion of entropy and its probability distribution functions seems to be useful in describing light scattering, as well as quantum interference generated within the hyperfine structure. For weak fields, the probability cross-section
for
shows good resemblance to the stationary spectrum with exposed peaks due to the four resonances. The relative Shannon entropy
shows the minimum for moderate fields, indicating destructive interference where the upper hf is smeared out (
Figure 3).
For two-color excitation, we have shown that the system division into subsystems seems to be hard, since the atomic populations are continuously distributed over the hyperfine levels at the same instant. Therefore, we have constructed three types of partitions that are based on the probability branching of upper hf levels. The first one of these partitions is defined on the population of the whole interaction period with two probability distributions that are complementary to each other. Its corresponding entropy is
. It is shown to be reduced in the course of propagation (
Figure 4).
We have constructed entropy associated with and subsystems corresponding to the storage and the retrieval periods, respectively as and . Both of them are less than unity, with reduction up to moderate distances and enhancement at big distances. The two time sections and clearly identify two two-level atom equivalents for the four-level system. The first of these two-level atoms is based on and the mixing of and . The second two-level atom is based on , as well as the mixing of hf upper levels.
In the forging analysis, the diversity function of entropy depended on the population. We have constructed entropy with diversity functions depending on the local energy of the time-dependent pulse.
Figure 5 shows an entropy exchange among the two optical transitions in the course of propagation. Finally, we have considered the commutative sum of the Shannon entropy (
Figure 6) for the energy distribution in space, which emphasizes the entropy flow and its attenuation, as well as its generation.
In summary, we have described quantum correlations generated by or within the manifold of sodium atoms. Multilevel structures result in information channelization, which is characterized by entropy transfer within and out of the total system by relaxations.