Fruit Classification by Wavelet-Entropy and Feedforward Neural Network Trained by Fitness-Scaled Chaotic ABC and Biogeography-Based Optimization
Abstract
:1. Introduction
2. State-of-the-Art
3. Methodology
3.1. Materials

3.2. Four-Step Preprocessing
3.3. Discrete Wavelet Transform
3.4. Wavelet-Entropy
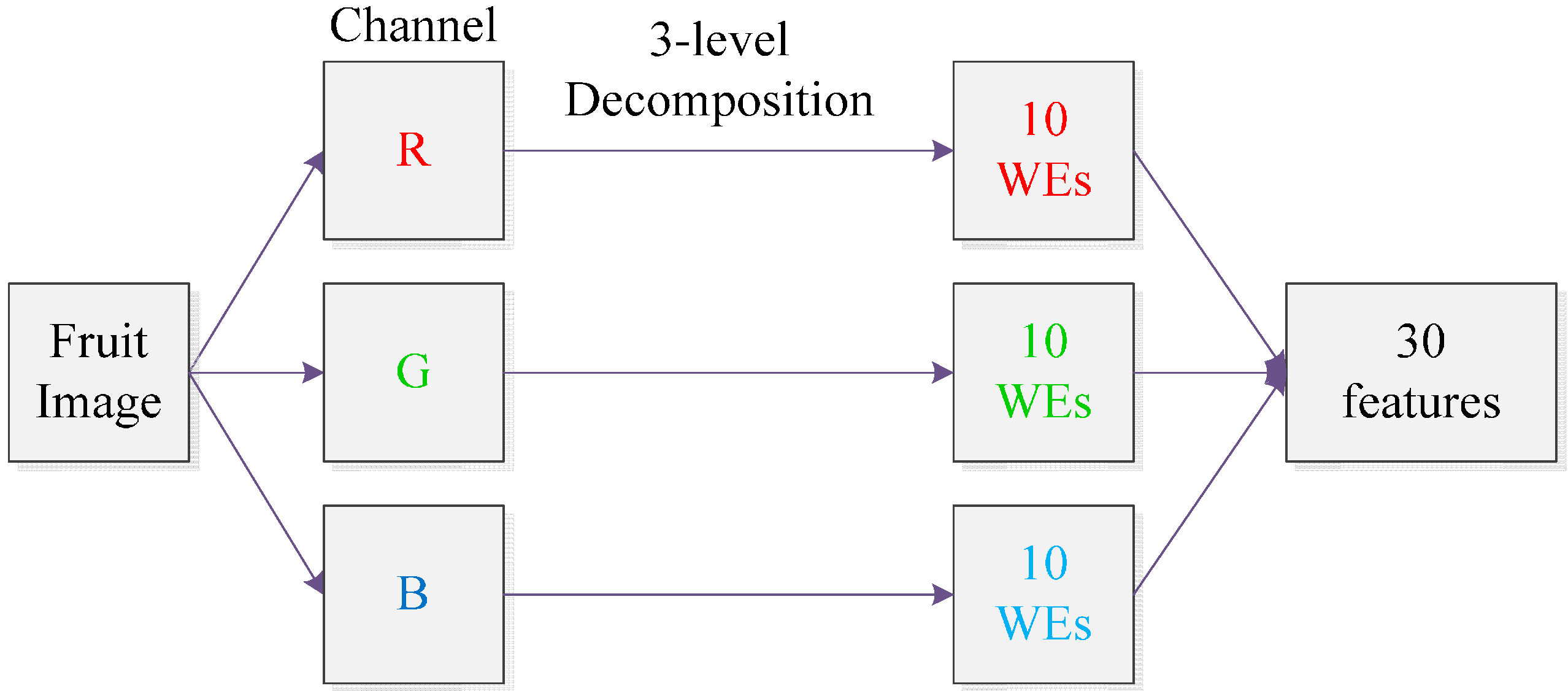
3.5. Principal Component Analysis
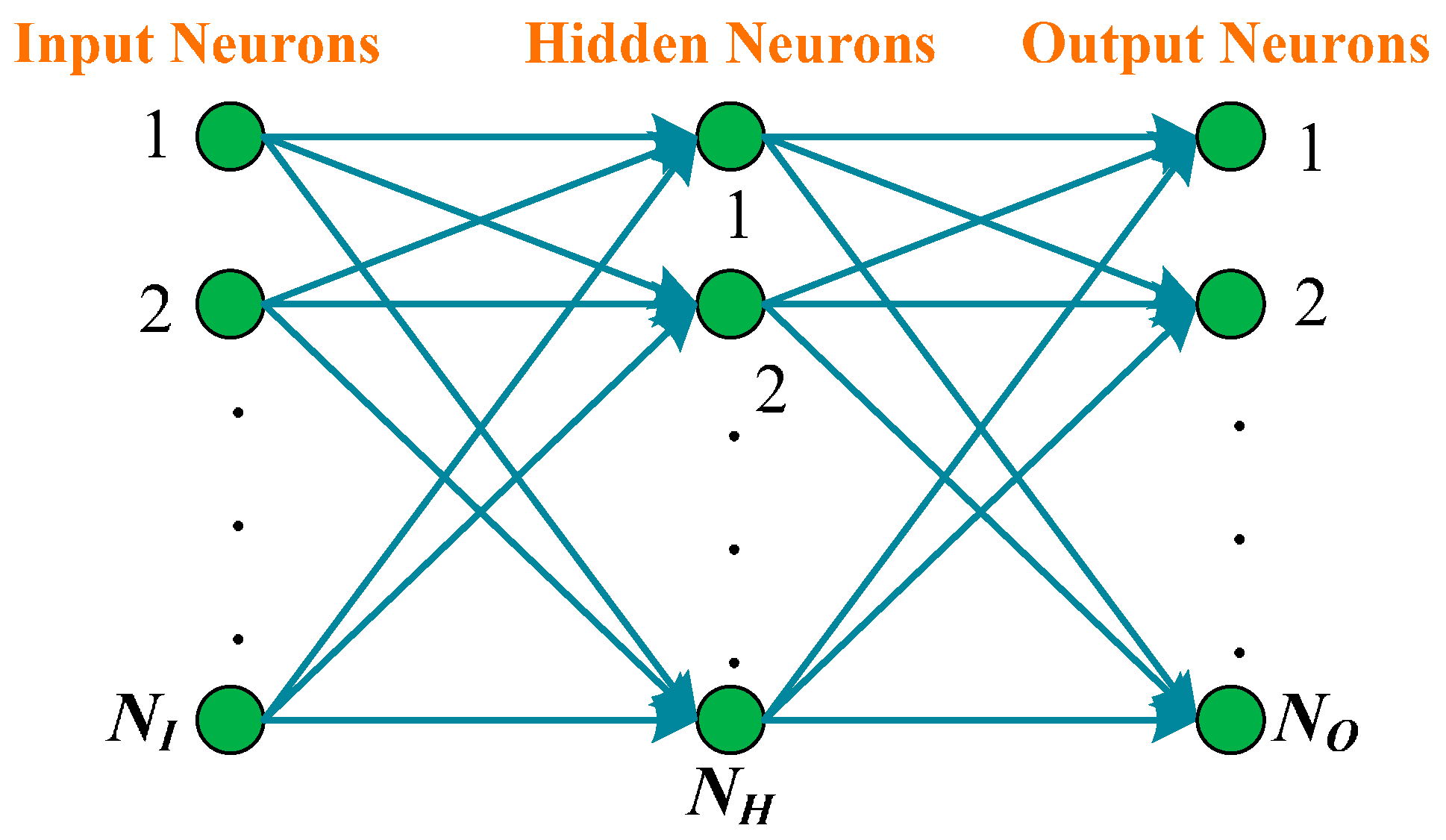
3.6. Feed-Forward Neural Network
3.7. Training Methods
3.7.1. Fitness-Scaled Chaotic Artificial Bee Colony
| Algorithm 1: Fitness-Scaled Chaotic Artificial Bee Colony (FSCABC) | |
| Step 1 | Initialization: Initialize the population (solution candidates) within the lower & upper bounds. Evaluation and initial population |
| Step 2 | Produce new food sources: Produce new solutions in the neighborhood of last solution for the employed bees. The random number is replaced with a chaotic number generator. Implement the greedy selection to select the best solutions. |
| Step 3 | Produce new onlookers: Generate new solutions for the onlookers based on population group of last step, selecting the best depending on the probability of scaled fitness values. |
| Step 4 | Produce new scouts: Produce the discarded solution, i.e., the worst candidate, which is replaced with a novel randomly generated solution. Here the random number generator is replaced with a chaotic number generator. |
| Step 5 | If the termination criterion is met, output the final results, otherwise jump to the second step. |
3.7.2. Biogeography-Based Optimization
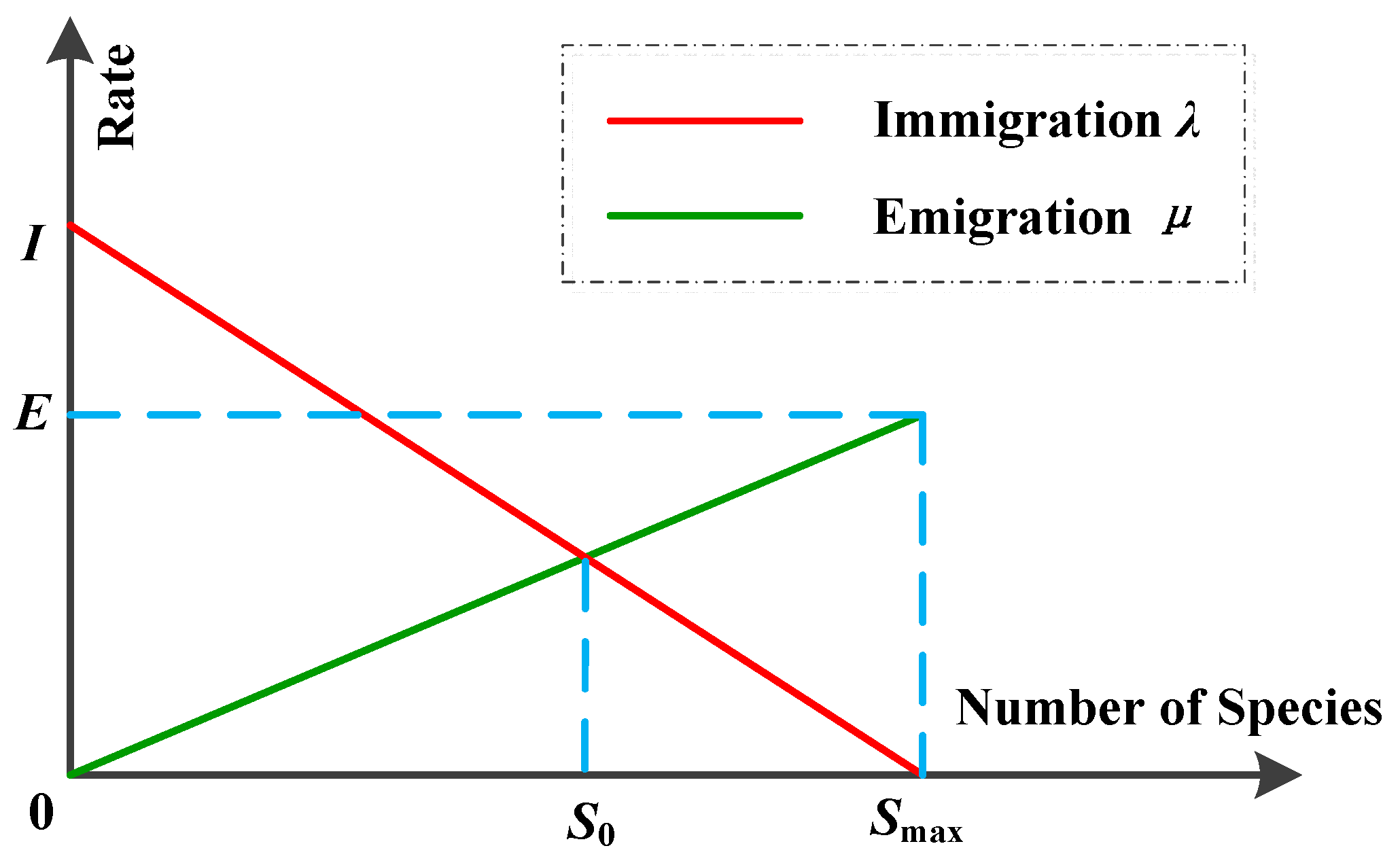
| Algorithm 2: Biogeography-Based Optimization (BBO) | |
| Step 1 | Initialize BBO parameters, which include a problem-dependent method of mapping problem solutions to SIVs and habitats, the modification probability Pd, the maximum species count Smax, the maximum mutation rate Wmax, the maximum migration rates E and I, and elite number e. |
| Step 2 | Initialize the population by generating a random set of habitats. |
| Step 3 | Compute HSI for each habitat. |
| Step 4 | For each habitat, computer S, μ, and λ. |
| Step 5 | Modify the whole ecosystem by migration based on Pd, λ and μ. |
| Step 6 | Mutate the ecosystem based on mutate probabilities. |
| Step 7 | Implement elitism. |
| Step 8 | If termination criterion was met, output the best habitat, otherwise jump to Step 3. |
3.8. Statistical Analysis
| Algorithm 3: 5-Fold Stratified Cross Validation | |
| Step 1 | Divide the fruit images into five equally distributed folds. |
| Step 2 | Let i-th fold be test set, and the rest four folds as training set. |
| Step 3 | Feed the training and test set to the classifiers. |
| Step 4 | Record the accuracy Ai of test set of i-th fold. |
| Step 5 | Let i = i + 1. If i ≤ 5, then jump to Step 2, otherwise jump to Step 6. |
| Step 6 | Output the average accuracy A = (A1 + … + A5)/5. |
3.9. Implementation
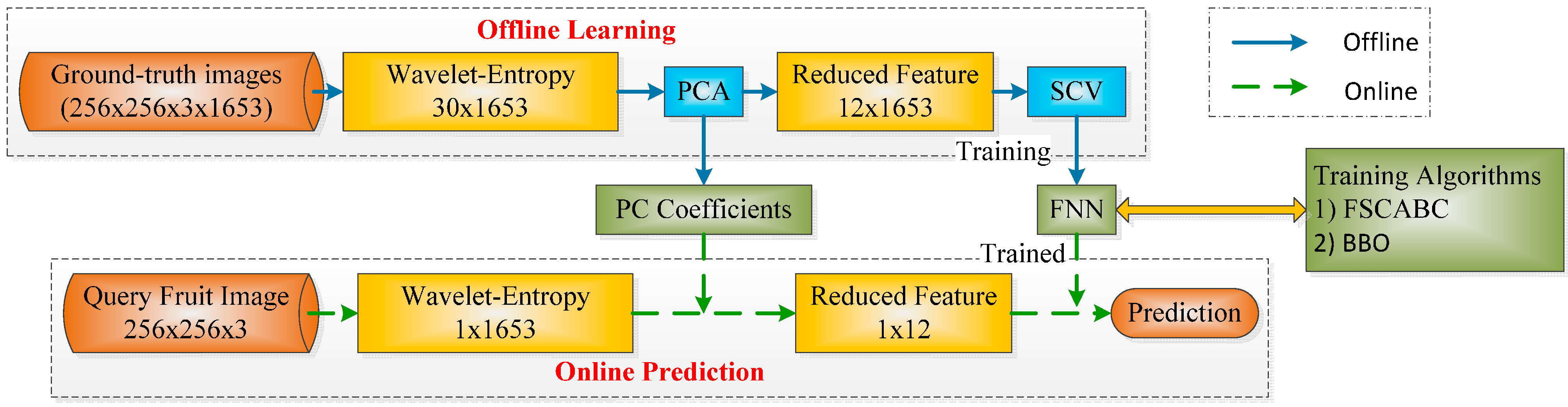
| Algorithm 4: Proposed System | |
| Phase I: Offline Learning | |
| Step 1 | Database. 1653 color images containing 18 categories of fruits are obtained. Their sizes are of 1024 × 768 × 3 (Length × Width × Color Channel). |
| Step 2 | Preprocessing and Feature Extraction. Remove background by split-and-merge algorithm [19]. Crop and resize each image to 256 × 256 × 3. Center the fruits. For each image, 30 features are obtained that contain WEs of three color channels. |
| Step 3 | Feature Reduction. The number of features are decreased by PCA, and the criterion is to cover more than 95% of total variance. PC coefficient matrix was generated. |
| Step 4 | Classifier Training. The training set is fed into feed-forward neural network. The weights and biases of the FNN are adjusted to make minimal the average MSE of FNN. BBO and FSCABC are set as the training algorithms, respectively. |
| Step 5 | Evaluation. A K-fold SCV is employed for statistical evaluation. |
| Phase II: Online Prediction | |
| Step 1 | Query Image. Generate the query image by a digital camera. |
| Step 2 | Preprocessing and Feature Extraction. The same as Phase I. |
| Step 3 | Feature Reduction. Reduced feature is obtained by multiplying extracted features with PC coefficient matrix generated in Phase I. |
| Step 4 | Prediction. The reduced feature is sent into the classifier trained in Phase I to predict the fruit category. |
4. Experiments and Results
4.1. DWT Results
| Fruit | R-Channel | G-Channel | B-Channel |
|---|---|---|---|
| Black Grapes |  | 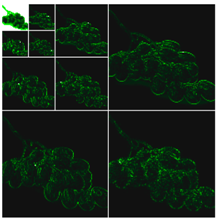 | 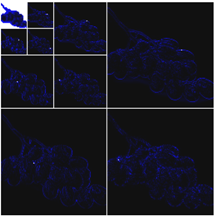 |
| Tangerines |  | 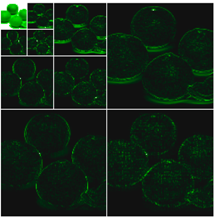 | 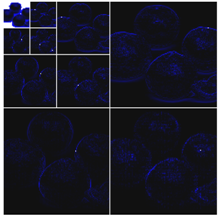 |
4.2. Feature Reduction
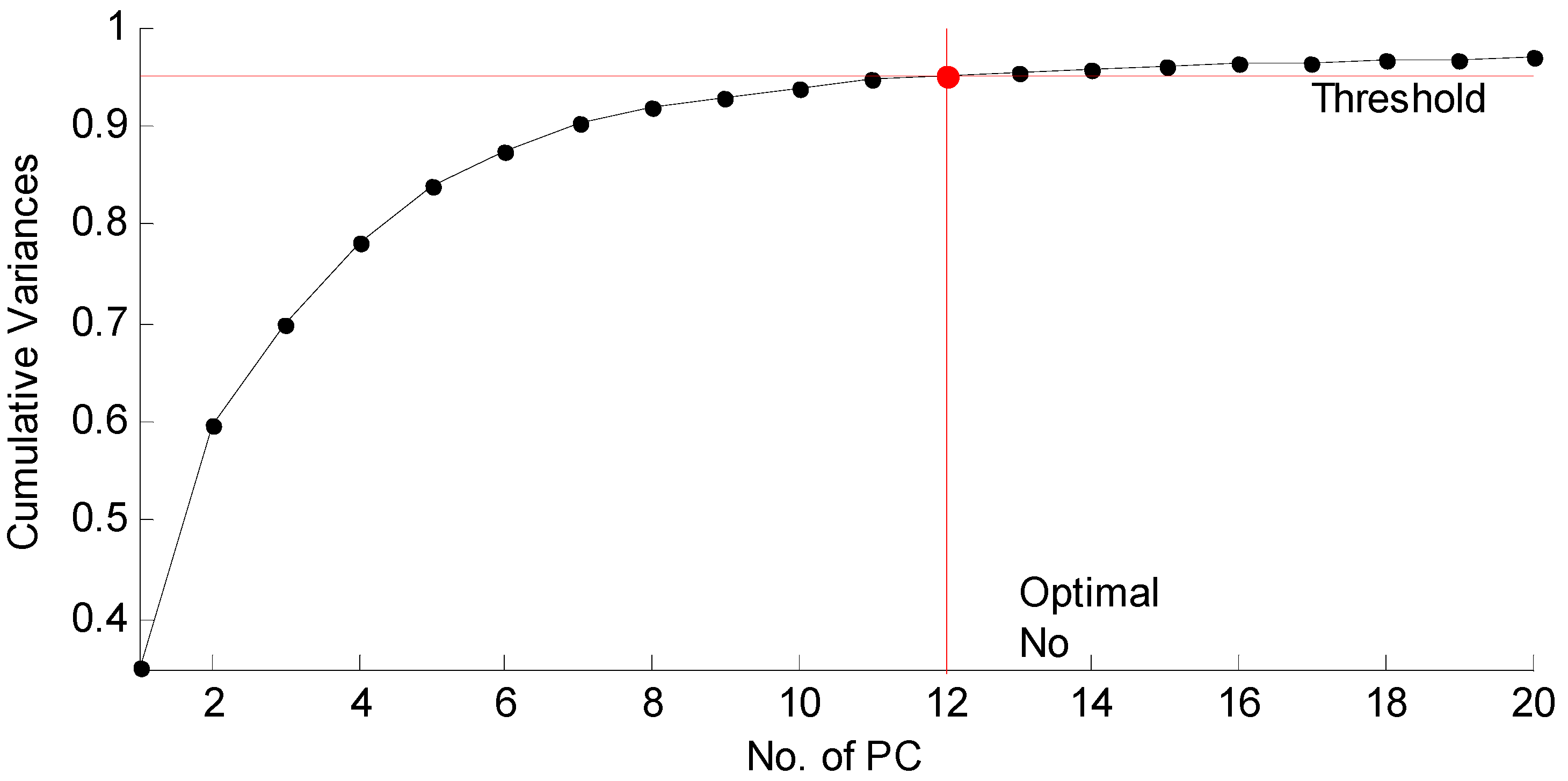
4.3. Algorithm Comparison
| Algorithm | Parameter/Value |
|---|---|
| GA | SP = 20, Mutation Probability = 0.1, Crossover Probability = 0.8 |
| PSO | SP = 20, Initial Weight = 0.5, Maximal Velocity = 1, Acceleration Factor = 1 |
| ABC | SP = 20, (10 employed bees and 10 onlooker bees) |
| FSCABC | SP = 20, (10 employed bees and 10 onlooker bees) |
| BBO | SP = 20, Modification Probability = 0.95, maximum immigration rate = maximum emigration rate = 1, Wmax = 0.1, e = 2 |
| # of Reduced Features | Accuracy | ||
|---|---|---|---|
| Existing Algorithms * | (CH + MP + US) + PCA + GA-FNN Chandwani, Agrawal and Nagar (2015) [18] | 14 | 84.8% |
| (CH + MP + US) + PCA + PSO-FNN Momeni, et al. (2015) [16] | 14 | 87.9% | |
| (CH + MP + US) + PCA + ABC-FNN Awan, et al. (2014) [31] | 14 | 85.4% | |
| (CH + MP + US) + PCA + kSVM Wu (2012) [6] | 14 | 88.2% | |
| (CH + MP + US) + PCA + FSCABC-FNN Zhang, et al. (2014) [12] | 14 | 89.1% | |
| Proposed Algorithms | WE + PCA + FSCABC-FNN | 12 | 89.5% |
| WE + PCA + BBO-FNN | 12 | 89.5% | |
5. Discussions
6. Conclusions and Future Research
Acknowledgment
Author Contributions
Conflicts of Interest
Nomenclature
| (FSC)ABC | (Fitness-scaled Chaotic) Artificial Bee Colony |
| BBO | Biogeography-based Optimization |
| BP | Back-Propagation |
| CH | Color-histogram |
| FNN | Feed-forward Neural Network |
| FT-NIR | Fourier transform near infrared |
| GA | Genetic Algorithm |
| HCA | Hierarchical cluster analysis |
| kSVM | kernel Support Vector Machine |
| MP | Morphology-based features |
| MSE | Mean-Squared Error |
| PC(A) | Principal Component (Analysis) |
| PSO | Particle Swarm Optimization |
| ReLU | Rectified Linear Unit |
| SA | Simulating Annealing |
| SCV | Stratified Cross Validation |
| US | Unser’s features |
References
- Zhang, B.H.; Huang, W.; Li, J.; Zhao, C.; Fan, S.; Wu, J.; Liu, C. Principles, developments and applications of computer vision for external quality inspection of fruits and vegetables: A review. Food Res. Int. 2014, 62, 326–343. [Google Scholar] [CrossRef]
- Zhang, Y.D.; Wu, L.; Wang, S.; Ji, G. Comment on “Principles, developments and applications of computer vision for external quality inspection of fruits and vegetables: A review (Food Research International; 2014, 62: 326–343)”. Food Res. Int. 2015, 70, 142–142. [Google Scholar] [CrossRef]
- Pennington, J.A.T.; Fisher, R.A. Classification of fruits and vegetables. J. Food Compos. Anal. 2009, 22 (Suppl. 1), S23–S31. [Google Scholar] [CrossRef]
- Pholpho, T.; Pathaveerat, S.; Sirisomboon, P. Classification of longan fruit bruising using visible spectroscopy. J. Food Eng. 2011, 104, 169–172. [Google Scholar] [CrossRef]
- Yang, C.; Lee, W.S.; Williamson, J.G. Classification of blueberry fruit and leaves based on spectral signatures. Biosyst. Eng. 2012, 113, 351–362. [Google Scholar] [CrossRef]
- Wu, L.; Zhang, Y. Classification of Fruits Using Computer Vision and a Multiclass Support Vector Machine. Sensors 2012, 12, 12489–12505. [Google Scholar]
- Feng, X.W.; Zhang, Q.H.; Zhu, Z.L. Rapid Classification of Citrus Fruits Based on Raman Spectroscopy and Pattern Recognition Techniques. Food Sci. Technol. Res. 2013, 19, 1077–1084. [Google Scholar] [CrossRef]
- Cano Marchal, P.; Gila, D.M.; García, J.G.; Ortega, J.G. Expert system based on computer vision to estimate the content of impurities in olive oil samples. J. Food Eng. 2013, 119, 220–228. [Google Scholar] [CrossRef]
- Breijo, E.G.; Guarrasi, V.; Peris, R.M.; Fillol, M.A.; Pinatti, C.O. Odour sampling system with modifiable parameters applied to fruit classification. J. Food Eng. 2013, 116, 277–285. [Google Scholar] [CrossRef]
- Fan, F.H.; Ma, Q.; Ge, J.; Peng, Q.Y.; Riley, W.W.; Tang, S.Z. Prediction of texture characteristics from extrusion food surface images using a computer vision system and artificial neural networks. J. Food Eng. 2013, 118, 426–433. [Google Scholar] [CrossRef]
- Omid, M.; Soltani, M.; Dehrouyeh, M.H.; Mohtasebi, S.S.; Ahmadi, H. An expert egg grading system based on machine vision and artificial intelligence techniques. J. Food Eng. 2013, 118, 70–77. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, S.; Ji, G.; Phillips, P. Fruit classification using computer vision and feedforward neural network. J. Food Eng. 2014, 143, 167–177. [Google Scholar] [CrossRef]
- Khanmohammadi, M.; Karami, F.; Mir-Marqués, A.; Garmarudi, A.B.; Garrigues, S.; de la Guardia, M. Classification of persimmon fruit origin by near infrared spectrometry and least squares-support vector machines. J. Food Eng. 2014, 142, 17–22. [Google Scholar] [CrossRef]
- Chaivivatrakul, S.; Dailey, M.N. Texture-based fruit detection. Precis. Agric. 2014, 15, 662–683. [Google Scholar] [CrossRef]
- Muhammad, G. Date fruits classification using texture descriptors and shape-size features. Eng. Appl. Artif. Intell. 2015, 37, 361–367. [Google Scholar] [CrossRef]
- Momeni, E.; Armaghani, D.J.; Hajihassani, M.; Amin, M.F.M. Prediction of uniaxial compressive strength of rock samples using hybrid particle swarm optimization-based artificial neural networks. Measurement 2015, 60, 50–63. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, Y.; Dong, Z.; Du, S.; Ji, G.; Yan, J.; Yang, J.; Wang, Q.; Feng, C.; Phillips, P. Feed-forward neural network optimized by hybridization of PSO and ABC for abnormal brain detection. Int. J. Imaging Syst. Technol. 2015, 25, 153–164. [Google Scholar] [CrossRef]
- Chandwani, V.; Agrawal, V.; Nagar, R. Modeling slump of ready mix concrete using genetic algorithms assisted training of Artificial Neural Networks. Expert Syst. Appl. 2015, 42, 885–893. [Google Scholar] [CrossRef]
- Damiand, G.; Resch, P. Split-and-merge algorithms defined on topological maps for 3D image segmentation. Graph. Models 2003, 65, 149–167. [Google Scholar] [CrossRef]
- Fang, L.; Wu, L.; Zhang, Y. A Novel Demodulation System Based on Continuous Wavelet Transform. Math. Probl. Eng. 2015, 2015, 9. [Google Scholar] [CrossRef]
- Zhou, R.; Bao, W.; Li, N.; Huang, X.; Yu, D. Mechanical equipment fault diagnosis based on redundant second generation wavelet packet transform. Digit. Signal Process. 2010, 20, 276–288. [Google Scholar] [CrossRef]
- Zhang, Y.; Dong, Z.; Wang, S.; Ji, G.; Yang, J. Preclinical Diagnosis of Magnetic Resonance (MR) Brain Images via Discrete Wavelet Packet Transform with Tsallis Entropy and Generalized Eigenvalue Proximal Support Vector Machine (GEPSVM). Entropy 2015, 17, 1795–1813. [Google Scholar] [CrossRef]
- Zhang, Y.; Wu, L. An Mr Brain Images Classifier via Principal Component Analysis and Kernel Support Vector Machine. Prog. Electromagn. Res. 2012, 130, 369–388. [Google Scholar] [CrossRef]
- Fuangkhon, P. An incremental learning preprocessor for feed-forward neural network. Artif. Intell. Rev. 2014, 41, 183–210. [Google Scholar] [CrossRef]
- Llave, Y.A.; Hagiwara, T.; Sakiyama, T. Artificial neural network model for prediction of cold spot temperature in retort sterilization of starch-based foods. J. Food Eng. 2012, 109, 553–560. [Google Scholar] [CrossRef]
- Shojaee, S.A.; Wang, S.; Dong, Z.; Phillip, P.; Ji, G.; Yang, J. rediction of the binary density of the ILs+ water using back-propagated feed forward artificial neural network. Chem. Ind. Chem. Eng. Q. 2014, 20, 325–338. [Google Scholar] [CrossRef]
- Karmakar, S.; Shrivastava, G.; Kowar, M.K. Impact of learning rate and momentum factor in the performance of back-propagation neural network to identify internal dynamics of chaotic motion. Kuwait J. Sci. 2014, 41, 151–174. [Google Scholar]
- Holzinger, K.; Palade, V.; Rabadan, R.; Holzinger, A. Darwin or Lamarck? Future Challenges in Evolutionary Algorithms for Knowledge Discovery and Data Mining. In Interactive Knowledge Discovery and Data Mining in Biomedical Informatics; Holzinger, A., Jurisica, I., Eds.; Springer: Berlin/Heidelberg, Germany, 2014; pp. 35–56. [Google Scholar]
- Holzinger, A.; Blanchard, D.; Bloice, M.; Holzinger, K.; Palade, V.; Rabadan, R. Darwin, Lamarck, or Baldwin: Applying Evolutionary Algorithms to Machine Learning Techniques. In Proceedings of the 2014 IEEE/WIC/ACM International Joint Conferences on Web Intelligence (WI) and Intelligent Agent Technologies (IAT), Warsaw, Poland, 11–14 August 2014; pp. 449–453.
- Manoochehri, M.; Kolahan, F. Integration of artificial neural network and simulated annealing algorithm to optimize deep drawing process. Int. J. Adv. Manuf. Technol. 2014, 73, 241–249. [Google Scholar] [CrossRef]
- Awan, S.M.; Aslam, M.; Khan, Z.A.; Saeed, H. An efficient model based on artificial bee colony optimization algorithm with Neural Networks for electric load forecasting. Neural Comput. Appl. 2014, 25, 1967–1978. [Google Scholar] [CrossRef]
- Zhang, Y.; Wu, L.; Wang, S. UCAV path planning based on FSCABC. Inf. Int. Interdiscip. J. 2011, 14, 687–692. [Google Scholar]
- Christy, A.A.; Raj, P. Adaptive biogeography based predator-prey optimization technique for optimal power flow. Int. J. Electr. Power Energy Syst. 2014, 62, 344–352. [Google Scholar] [CrossRef]
- Guo, W.A.; Li, W.; Zhang, Q.; Wang, L.; Wu, Q.; Ren, H. Biogeography-based particle swarm optimization with fuzzy elitism and its applications to constrained engineering problems. Eng. Optim. 2014, 46, 1465–1484. [Google Scholar] [CrossRef]
- Simon, D. A Probabilistic Analysis of a Simplified Biogeography-Based Optimization Algorithm. Evolut. Comput. 2011, 19, 167–188. [Google Scholar] [CrossRef] [PubMed]
- Ludwig, O., Jr.; Nunes, U.; Araújo, R.; Schnitman, L.; Lepikson, H.A. Applications of information theory, genetic algorithms, and neural models to predict oil flow. Commun. Nonlinear Sci. Numer. Simul. 2009, 14, 2870–2885. [Google Scholar] [CrossRef]
- Toulis, P.; Airoldi, E.M. Scalable estimation strategies based on stochastic approximations: Classical results and new insights. Stat. Comput. 2015, 25, 781–795. [Google Scholar] [CrossRef] [PubMed]
- Indurkhya, N. Emerging directions in predictive text mining. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2015, 5, 155–164. [Google Scholar] [CrossRef]
- Zeiler, M.D.; Ranzato, M.; Monga, R.; Mao, M.; Yang, K.; Le, Q.V.; Nguyen, P.; Senior, A.; Vanhoucke, V.; Dean, J.; et al. On rectified linear units for speech processing. In Proceedings of the 2013 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Vancouver, BC, Canada, 26–31 May 2013; pp. 3517–3521.
- Han, S.; Vasconcelos, N. Object recognition with hierarchical discriminant saliency networks. Front. Comput. Neurosci. 2014, 8. [Google Scholar] [CrossRef] [PubMed]
- Yang, G.; Zhang, Y.; Yang, J.; Ji, G.; Dong, Z.; Wang, S.; Feng, C.; Wang, W. Automated classification of brain images using wavelet-energy and biogeography-based optimization. Multimed. Tools Appl. 2015. [Google Scholar] [CrossRef]
- Zhang, Y.; Dong, Z.; Ji, G.; Wang, S. Effect of spider-web-plot in MR brain image classification. Pattern Recognit. Lett. 2015, 62, 14–16. [Google Scholar] [CrossRef]
- Holzinger, A.; Dehmer, M.; Jurisica, I. Knowledge Discovery and interactive Data Mining in Bioinformatics - State-of-the-Art, future challenges and research directions. BMC Bioinform. 2014, 15. [Google Scholar] [CrossRef] [PubMed]
- Holzinger, A.; Jurisica, I. Knowledge Discovery and Data Mining in Biomedical Informatics: The Future is in Integrative, Interactive Machine Learning Solutions. In Interactive Knowledge Discovery and Data Mining in Biomedical Informatics; Holzinger, A., Jurisica, I., Eds.; Springer: Berlin/Heidelberg, Germany, 2014; pp. 1–18. [Google Scholar]
- Zhang, Y.; Dong, Z.; Phillips, P.; Wang, S.; Ji, G.; Yang, J. Exponential Wavelet Iterative Shrinkage Thresholding Algorithm for compressed sensing magnetic resonance imaging. Inf. Sci. 2015, 322, 115–132. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, S.; Ji, G.; Dong, Z. Exponential wavelet iterative shrinkage thresholding algorithm with random shift for compressed sensing magnetic resonance imaging. IEEJ Trans. Electr. Electron. Eng. 2015, 10, 116–117. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, S.; Zhang, Y.; Ji, G.; Yang, J.; Wu, J.; Wei, L. Fruit Classification by Wavelet-Entropy and Feedforward Neural Network Trained by Fitness-Scaled Chaotic ABC and Biogeography-Based Optimization. Entropy 2015, 17, 5711-5728. https://doi.org/10.3390/e17085711
Wang S, Zhang Y, Ji G, Yang J, Wu J, Wei L. Fruit Classification by Wavelet-Entropy and Feedforward Neural Network Trained by Fitness-Scaled Chaotic ABC and Biogeography-Based Optimization. Entropy. 2015; 17(8):5711-5728. https://doi.org/10.3390/e17085711
Chicago/Turabian StyleWang, Shuihua, Yudong Zhang, Genlin Ji, Jiquan Yang, Jianguo Wu, and Ling Wei. 2015. "Fruit Classification by Wavelet-Entropy and Feedforward Neural Network Trained by Fitness-Scaled Chaotic ABC and Biogeography-Based Optimization" Entropy 17, no. 8: 5711-5728. https://doi.org/10.3390/e17085711
APA StyleWang, S., Zhang, Y., Ji, G., Yang, J., Wu, J., & Wei, L. (2015). Fruit Classification by Wavelet-Entropy and Feedforward Neural Network Trained by Fitness-Scaled Chaotic ABC and Biogeography-Based Optimization. Entropy, 17(8), 5711-5728. https://doi.org/10.3390/e17085711







