Abstract
Identity authentication is the process of verifying users’ validity. Unlike classical key-based authentications, which are built on noiseless channels, this paper introduces a general analysis and design framework for identity authentication over noisy channels. Specifically, the authentication scenarios of single time and multiple times are investigated. For each scenario, the lower bound on the opponent’s success probability is derived, and it is smaller than the classical identity authentication’s. In addition, it can remain the same, even if the secret key is reused. Remarkably, the Cartesian authentication code proves to be helpful for hiding the secret key to maximize the secrecy performance. Finally, we show a potential application of this authentication technique.
1. Introduction
Identity authentication (also known as identification or entity authentication) verifies users’ identities to prevent potential losses caused by fraudsters [1,2]. The failure to properly authenticate users will result in serious damage, since the opponent can forge the valid identity to do anything [3].
The most common identity authentication is the challenge-response authentication [1]. As is illustrated in Figure 1, Alice and Bob share a secret key K for identity authentication. In case of potential frauds, Alice initiates a challenge X when an access request is received (even if with the identity declaration). Upon receiving the challenge X, the access requester shall make a response Y. The correctness of Y can be verified by the secret key K. If Y is correct, it demonstrates that the access requester matches the declared identity; otherwise, the access request will be rejected.

Figure 1.
The challenge-response authentication model.
In conventional investigations (e.g., [4–6]), the channels are assumed to be noiseless, because the authentication model is designed on top of the channel coding, which converts the physical noisy channels into noiseless ones. Following this, as is depicted in Figure 2, an attacker, Eve, can completely eavesdrop on the authentication between the legitimate users Alice and Bob and then initiates an impersonation attack by forging a response message Y′ before Bob replies. Eve’s attack is successful if Alice accepts Y′ as a correct response message (i.e., Y′ = Y). We use P to denote the success probability of this attack; then, we have P ≥ 2−I(K;X,Y) (the rigorous proof will be given in Section 3.1). One can easily find out that this lower bound reduces to P ≥ 2−H(K) when H(K|X, Y) = 0, since I(K; X, Y) = H(K) − H(K|X, Y). In this case, all information of the secret key is used to protect Eve’s attack one time. That is, the secret key K needs to be changed in every round of authentication, because Eve is aware of K after eavesdropping on X and Y.
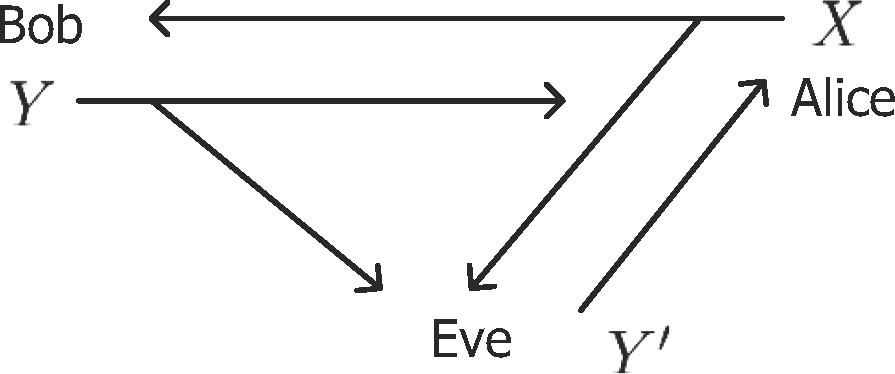
Figure 2.
The challenge-response authentication over noiseless channels.
Unfortunately, the open-air nature of wireless communications makes it difficult to distribute, refresh and revoke the secret key K, especially in ad hoc networks [7]. Therefore, reusing the same secret key to authenticate several times is considered in practice. In this scenario, the success probability of Eve’s attack in the i-th (1 ≤ i ≤ n, where n represents to use the same secret key n-times) round of authentication is lower bounded by
(the rigorous proof will be given in Section 4.1), where Xn and Yn respectively denote the n-length sequences of X and Y. This lower bound suggests that after eavesdropping on several rounds of authentication, Eve can be aware of almost all of the information about the secret key K. Then, she can initiate an attack successfully with a high probability. That is, reusing the secret key will cause the secret key’s information leakage. However, recent research [8,9] about the message authentication (also known as data-origin authentication, which validates a message’s integrity and originator [1,2,10,11]) showed that channel noise can help prevent the secret key’s information leakage based on Wyner’s wiretap channel.
According to the results of Wyner’s wiretap channel [12], perfectly secure transmission of a message is possible by using a codebook whose codeword rate is higher than the channel capacity between the source and the opponent. In this way, [8] introduced noisy channels into the classical Simmons’s authentication model. By jointly designing the channel and authentication coding, Eve’s success probability can reduce from P ≥ 2−H(K)/2 to P = 2−H(K), since the secret key can be hidden from her by channel noise. Furthermore, our previous work [9] introduced noisy channels into the systematic authentication code and proved that it is more robust and flexible than Simmons’s authentication to protect against Eve’s attacks.
There are two primary differences between message authentication and identity authentication [1,2]: (1) message authentication might not happen in real time, but identity authentication does; and (2) message authentication simply authenticates one message, and the process needs to be repeated for each new message. However, identity authentication authenticates the claimant for the entire duration of a session. Unlike the previous works [8,9], which focused on the message authentication over noisy channels, this paper develops the classical identity authentication over noisy channels and makes the following contributions.
- We present a general analysis and design framework of the challenge-response authentication, and investigate the authentication scenarios of single time and multiple times. For each scenario, we respectively derive an information-theoretic lower bound on the opponent’s success probability in the classical model and our new one. This shows that after introducing channel noise into the classical authentication model, the opponent’s success probability is significantly reduced.
- We find out that the Cartesian authentication code satisfies the optimal strategy to maximize the security performance. Then, with a slight improvement of the classical authentication, the security performance can be dramatically promoted.
- In the multiple-time authentication scenario, with the Cartesian authentication code, we show that the noise spreading over two separate channels can together hide the secret key from the opponent. In this way, the opponent’s success probability can be effectively reduced.
- We show the potential applications of our work in wireless communications, such as cooperating with the secret key agreement from wireless channels [13,14] to prevent the information leakage of both the original and fresh secret key.
The rest of this paper is organized as follows. Section 2 provides various aspects of our authentication scheme in the given scenarios. Sections 3 and 4 compare the security performance between the classical challenge-response authentication and our proposed authentication in the authentication scenarios of single time and multiple times, respectively. Section 5 introduces a potential application of our work. Section 6 concludes the paper.
Notation: Throughout this paper, the random variables are denoted by upper case letters (e.g., X), and the corresponding finite alphabets are denoted by calligraphic letters (e.g.,
). The n-length sequence of X is denoted by Xn (e.g., Xn = X1, X2, …, Xn).
2. Proposed Authentication Scheme
2.1. Scenario
This paper considers the scenario depicted in Figure 3, where Alice, Bob and Eve share a wireless noisy medium. Alice is a critical node that has sensitive information. Suppose that Bob has the legitimate rights to access Alice, while Eve is a malicious attacker who covets Bob’s authority. Additionally, Alice and Bob are assumed to be honest with each other. In this context, Bob and Alice agree on the challenge-response authentication scheme that allows Alice to verify whether the access requester is valid or not.
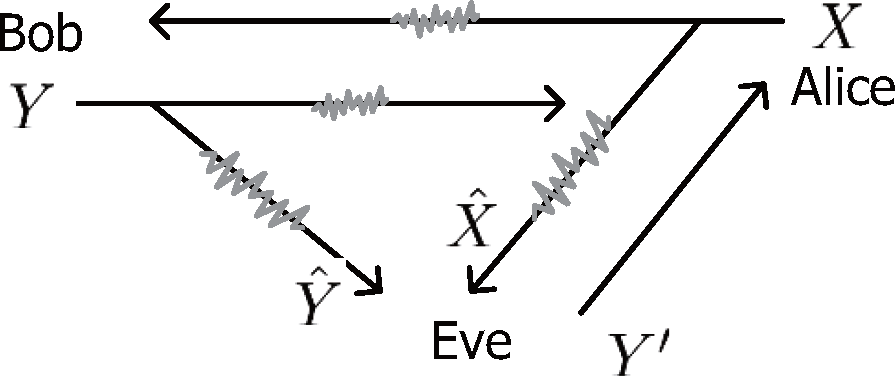
Figure 3.
The challenge-response authentication over noisy channels.
2.2. Channel Model
Wyner’s wiretap channel [12] is introduced in our scenario. The wiretap channel is defined by two discrete memoryless channels
, where
is the input alphabet of the transmitter and
and
are the output alphabets at the legitimate receiver and the wiretapper, respectively. It is proven in [15] that the secrecy capacity is given by:
where U is an auxiliary random variable [16] satisfying the Markov chain U → X → (YZ).
According to the following Definition 1, if a wiretap channel is less noisy, there must exist a U satisfying I(U; Y) ≥ I(U; Z), then the secrecy capacity is positive. Actually, the selection U = X is optimal for the entire rate-equivocation region [15,16], which results in:
Definition 1 ([15,16]). A wiretap channel is less noisy if the main channel is less noisy than the wiretapper’s channel, i.e., for all possible U → X → (Y, Z), I(U; Y) ≥ I(U; Z).
In Figure 3, we assume that the channels between every two nodes among Alice, Bob and Eve are noisy, except that the one-way channel Eve → Alice is noiseless. This Eve’s advantage does not incur any loss of generality, since a stronger opponent can lead to more general bounds. Then, it is able to construct two wiretap channels Alice → (Bob, Eve) and Bob → (Alice, Eve). Moreover, we firstly assume that they are both less noisy (the case that one of them is not less noisy is considered in Section 4.3), so the secrecy capacity of these two wiretap channels is positive. Then, there must exist a codebook (whose codeword rate is higher than the channel capacity between the source and the opponent) satisfying that Alice and Bob can obtain perfect transmitted messages, while Eve only receives completely equivocal observations [8,12,17].
Take the wiretap channel Alice → (Bob, Eve) in Figure 3 for example, I(X; Y) and
respectively denote the codeword rate of channels Alice → Bob and Alice → Eve. When this wiretap channel is less noisy, we have
. Then, by a codebook whose codeword rate is R ≤ I(X; Y), Bob can perfectly receive Alice’s message X, while Eve obtains an observation
with the equivocation
. According to Equation (2), we have Cs = max Re. Additionally, there are several technologies (e.g., beamforming and artificial noise [18–20]) to ensure that a wiretap channel is less noisy (i.e., Cs > 0). Thus, we can make the above assumption.
2.3. Authentication Model
Alice and Bob share a secret key K for authentication. The secret key K is only known to Alice and Bob, and it has been allocated beforehand. Let
,
and
respectively denote the finite alphabets of the challenge message, the secret key and the response message. The challenge message X and the secret key K are statistically independent, and they are uniformly distributed on
and
, respectively.
Similar to the classical model (as is illustrated in Figure 1), in case of Eve’s attack, when Alice receives an access request with an identity declaration (maybe true or false), she sends a challenge message X to the access requester. In this way, the access requester shall correctly make a response:
where f(·) encapsulates any prospective coding or modulation. Additionally, splitting code is not considered in this paper, i.e., H(Y|X, K) = 0.
Upon receiving a response message Ỹ, which may come from either Bob or Eve, Alice firstly generates the correct response message Y by the secret key K she owns, then compares it with Ỹ. If Ỹ = Y, this demonstrates that the access requester matches the declared identity; otherwise, the access request will be rejected.
Eve listens to the authentication between Alice and Bob. Since the wiretap channels are less noisy, by an appropriate codebook [21–24], Bob and Alice perfectly receive X and Y respectively, while Eve only obtains equivocal observations of X and Y, which are denoted by
and Ŷ.
Since Bob owns the secret key K, he is able to give response Y correctly whenever he wants to access Alice. That is, the authentication model can ensure the accessibility of a legitimate user. Eve, a potential attacker, also wants to access Alice. However, she is not aware of the secret key K a priori. Therefore, she listens to the authentications between Alice and Bob, observes
and Ŷ and tries to extract the information about the secret key K from the observations. Then, she requires access to Alice by disguising herself as Bob, which is known as the impersonation attack. Without loss of generality, we assume that Eve has infinite computation power and knows the authentication scheme.
This paper focuses on the success probability of the impersonation attack. Specifically, we hope to minimize Eve’s success probability.
3. Single-Time Authentication
3.1. Noiseless Channels Model
The classical challenge-response authentication model assumes that channels are noiseless, because the authentication model is designed after the channel coding converts the noisy channels into noiseless ones. In this way, Eve can eavesdrop on the complete challenge message X to impersonate Bob’s response. We denote the success probability of Eve’s impersonation attack as P. In the single-time authentication (e.g., the initial authentication), it has been shown that:
To simplify the analysis, we have the following lemma.
Lemma 1. In the classical authentication model, Eve’s success probability is lower bounded by:
with equality iff. Note that means a constant δ that satisfies 0 < δ ≤ 1 and the same hereinafter.
Proof. This result is derived because:
and:
In Equation (6), inequality (a) comes from Jensen’s inequality, and (a) with equality iff
are equal for all
; (b) with equality iff there exists a subset of
to satisfy p(y|x) = δ(x) (0 < δ(·) ≤ 1). Thus, Equation (5) with equality iff p(y|x) ∈ {δ, 0} (0 < δ ≤ 1).
In Equation (7), equality (c) holds because the secret key K and the challenge message X are statistically independent (i.e., H(X) = H(X|K)), and the splitting code is not considered (i.e., H(Y|K, X) = 0).
3.2. Noisy Channels Model
Consider the noisy channels. Since the wiretap channels are less noisy, Eve only obtains an equivocal observation of the challenge message, which is denoted by
. We denote the success probability of Eve’s impersonation attack as
. Following the same steps as those used in Equation (6),
is lower bounded by:
and
achieves its lower bound iff
.
To simplify the analysis, we draw the following lemma to show our scheme’s advantage to protect against Eve’s attack.
Lemma 2. In our new authentication model, Eve’s success probability is lower bounded by:
Proof. Please refer to Appendix A for technical details. □
According to Lemma 1 and Lemma 2, we have the following Theorem 1 and Example 1 to show the optimal strategy of our new scheme to protect against Eve’s attack. We firstly declare the concepts of the Cartesian authentication code and the systematic Cartesian authentication code (the simplest Cartesian authentication code) and then present the theorem and the example.
Definition 2 ([25,26]). If the authentication code satisfies that given any message y, there exists a unique source state x, such that y = f(x, e) for every encoding rules e contained in y, i.e., the authentication code satisfies H(X|Y) = 0, then the code is called a Cartesian authentication code.
Definition 3 ([27,28]). If the Cartesian authentication code satisfies that the message y is formed by its source state x and an authenticator t (e.g., y = (x, t) = (x, g(x, e)) where e represents the encoding rule), then the code is called a systematic Cartesian authentication code.
Theorem 1. In our new authentication model, to promote the security performance maximally, the optimal strategy for f(·) is the Cartesian authentication code.
Proof. The authentication’s security performance is indicated by the achievable lower bound on Eve’s success probability [4,5,8]. The lower the achievable bound is, the more secure the authentication is. Thus, according to Equation (5) and Equation (9), we use
to represent the achievable lower bound of P (in Equation (5)) and denote the promoted performance as:
where inequality (d) comes from Equation (9); inequality (e) holds since:
and
increases with the increase of
equivocation; and inequality (f) follows from H(X|Y) ≥ 0.
Obviously, in Equation (10), (f) with equality iff the Cartesian authentication code is used (i.e., H(X|Y) = 0). Moreover, since
maximum equivocation is H(X), (e) with equality iff
, i.e.,
because x is uniformly chosen from
. In addition, with the Cartesian authentication code, we have
because k is uniformly chosen from
. Thus, we have:
Then, according to the conditions for quality of Equation (5) (in Lemma 1) and Equation (9) (the same with Equation (8)’s), P and
can simultaneously achieve their lower bounds. Therefore, we have equality in (d).
Then, we can draw Theorem 1 because H(X|Y) = 0 is a sufficient and necessary condition to achieve ΔP = H(K).
Remark 1. Theorem 1 demonstrates that a slight improvement (e.g., Example 1) can significantly promote the security performance. Specifically, since the wiretap channel Alice → (Bob, Eve) is less noisy (i.e., the secrecy capacity is positive), Eve only obtains an equivocal challenge message. When using the Cartesian authentication code, the response message Y contains all of the information of the challenge message X. Then, the transmitting process of the challenge message X is equal to a secret key agreement, which generates new secret key information.
Example 1. In practical classical authentication, the response message Y is a short data block, which comes from the challenge message X and the secret key K, i.e., Y = f(X, K) where f(·) encapsulates a compressive function. However, in our new authentication model, if we improve the response message to Y = (X, g(X, K)) (i.e., the systematic Cartesian authentication code, where g(·) is the compressive function in f(·)), Eve’s success probability will reduce to:
according to Equation (9).
4. Multiple-Time Authentication
In practical networks, the secret key K is reused to authenticate Bob’s identity for several rounds. In each round, Eve can choose to initiate an attack. She attacks in the i-th round authentication based on the information of the previous i − 1 rounds of authentication. The attack is successful if her fake response message passes Alice’s authentication.
4.1. Noiseless Channels Model
Compared with the single-time authentication, Eve obtains additional i − 1 challenge messages and response messages. We use Pi to denote the success probability of Eve’s attack in the i-th round of authentication. Following from the same steps as those used in the proof of Lemma 1, the lower bound on Pi is derived as:
with equality iff
.
Since (Xi−1, Yi−1) → K → (Xi, Yi) forms a Markov chain, we have I(K; Xi, Yi|Xi−1, Yi−1) ≤ I(K; Xi, Yi). Obviously, reusing the secret key K results in the increase of Eve’s success probability.
Moreover, Eve will choose the attack that maximizes her success probability, i.e.,
Consequently, we have the following lemma.
Lemma 3. In the classical authentication model, Eve’s success probability is lower bounded by:
where n represents that the secret key is used n times.
Proof. This result is derived due to:
and the maximum must be greater than or equal to the average, i.e.,
Remark 2. This lower bound demonstrates that if Eve initiates an attack at any round i (1 ≤ i ≤ n), no authentication strategy can prevent her from being successful with probability at least. A secret key K is used optimally when all of these success probabilities are (roughly) equal [5,6]. Thus, in an optimal scheme, the secret key is split into n nearly equal parts, each of which is allocated to protect against an attack at the i-th round of authentication. Then, after eavesdropping on n rounds of authentication, Eve may be aware of almost all of the information about the secret key and able to attack successfully with a high probability.
4.2. Noisy Channels Model
Consider the noisy channels. Since the wiretap channels are less noisy, Eve obtains i − 1 rounds of equivocal challenge messages
and response messages Ŷi−1 and an equivocal challenge message
in the i-th round. We use
to denote the success probability of Eve’s attack in the i-th round of authentication. Following the same steps as those used in Equation (6), the lower bounded on
is derived as:
with equality iff
. Further, we have the following lemma.
Lemma 4. In our new authentication model, Eve’s success probability at the i-th round of authentication is lower bounded by:
Proof. Please refer to Appendix B for technical details.
According to Equation (14) and Equation (20), in multiple-time authentication, we still can deduce that the Cartesian authentication code is optimal to promote the security performance (i.e., Theorem 1). By the following Theorem 2, we demonstrate this inference in Remark 4.
Theorem 2. If there are no information leaks to Eve in the wiretap channels (i.e.,
and), Eve’s success probability is lower bounded by:
Proof. As is explained in Section 2.2, since the wiretap channels Alice → (Bob, Eve) and Bob → (Alice, Eve) are less noisy, there must exist a codebook, such that the transmitted messages can be perfectly obtained by Alice and Bob, but completely hidden from Eve [8,12,17], i.e.,
and I(Yi; Ŷi) = 0. Then, Equation (20) becomes:
Since X and K are respectively uniformly distributed on
and
, we have H(Yi) = H(Y). Then, similar to the proof of Lemma 3, we have:
Remark 3. In the classical authentication model, after Eve eavesdrops on several rounds of authentication, the knowledge of the challenge messages and response messages enable the information of the secret key to be determined (i.e., Lemma 3). In contrast, in our new authentication model, Eve’s success probability can remain the same even if she continues eavesdropping (i.e., Theorem 2).
Remark 4. H(X, Y ) is constant, since X and K are uniformly distributed, and:
Then, with the Cartesian authentication code,
lower bound reduces to:
4.3. Single-Wiretap Channel and Double-Wiretap Channels
As is depicted in Figure 3, the channels Bob → Alice and Alice → Bob are approximately the same if the response message is replied to in the coherence time, but the channels Bob → Eve and Alice → Eve are not equivalent. Therefore, it is possible that only one wiretap channel in Figure 3 satisfies the less noisy wiretap channel (i.e., Cs > 0). If a wiretap channel is not less noisy, it cannot ensure that Equation (1) remains positive under the optimal selection U = X for less noisy wiretap channels [16]. Without loss of generality, if a wiretap channel in Figure 3 is not less noisy, we assume that Eve can obtain what legitimate users receive.
As is shown in Table 1, to show the distinctions, we use
instead of
to denote the success probability of Eve’s attack when the wiretap channels Bob → (Alice, Eve) and Alice → (Bob, Eve) are both less noisy. Furthermore, similar to the analysis in the proof of Theorem 1, we introduce
to denote the promoted performance in the corresponding wiretap channels, i.e.,
where
and
respectively represent the achievable lower bounds on
and
.

Table 1.
Terminologies of Eve’s success probability and the promoted performance.
In the same way, we respectively use
and
to represent Eve’s success probability when only the Alice → (Bob, Eve) channel is less noisy and only the Bob → (Alice, Eve) channel is less noisy. In addition, we introduce
and
to respectively denote the promoted performance in the corresponding wiretap channels (note that
and
are two special cases of
), i.e.,
where
and
respectively represent the achievable lower bounds on
and
.
Furthermore, with the Cartesian authentication code, we respectively have:
To simplify the analysis, we draw the following Theorem 3 to show our scheme’s advantage to protect against Eve’s attack.
Theorem 3. With the Cartesian authentication code, we have:
Proof. Specifically, when i = 1, Xi−1,
, Yi−1 and Ŷi−1 do not exist. At this time, Equation (29a) is same with Equation (29b), and Equation (29c) is equal to zero. Hence, Equation (30) is satisfied.
When i ≥ 2, we have:
Then, Equation (30) is proven.
Additionally, without the Cartesian authentication code, Equation (30) does not certainly hold. Because according to Equation (28) and Equation (31), we have:
where
and
.
Remark 5. Theorem 3 demonstrates that with the Cartesian authentication code, the noise of two separate wiretap channels can together hide the secret key information from Eve. Therefore, though the secret key information is all contained in the response message Y, by securely transmitting the challenge message X, we can further reduce Eve’s success probability from P ≥ 2−H(Y) to P ≥ 2−H(X,Y) (i.e., Remark 4).
5. Application
Since the physical channels are noisy and the challenge-response authentication is widely applied in existing communication systems, our authentication scheme has significant potential foreground. By our work, the existing systems can be smoothly upgraded with great promotion of the security performance. In the sequel, we present an application of protecting the secret key agreement in wireless communications by an improved authentication scheme (i.e., Example 1).
Since wireless channels are reciprocal in space and varied in time [7], extracting secret keys through channel characteristics is considered as one of the most developed solutions for the secret key renewal [13,14]. As is depicted in Figure 4a, Alice wants to negotiate secret keys with her legitimate user Bob. If Alice and Bob exchange a sequence of known pilots in the coherence time Δt, they can have almost the same channel characteristic to generate the same secret key [13,14]. Unfortunately, this secret key agreement may incur the following risks, which can be prevented by our new authentication model.
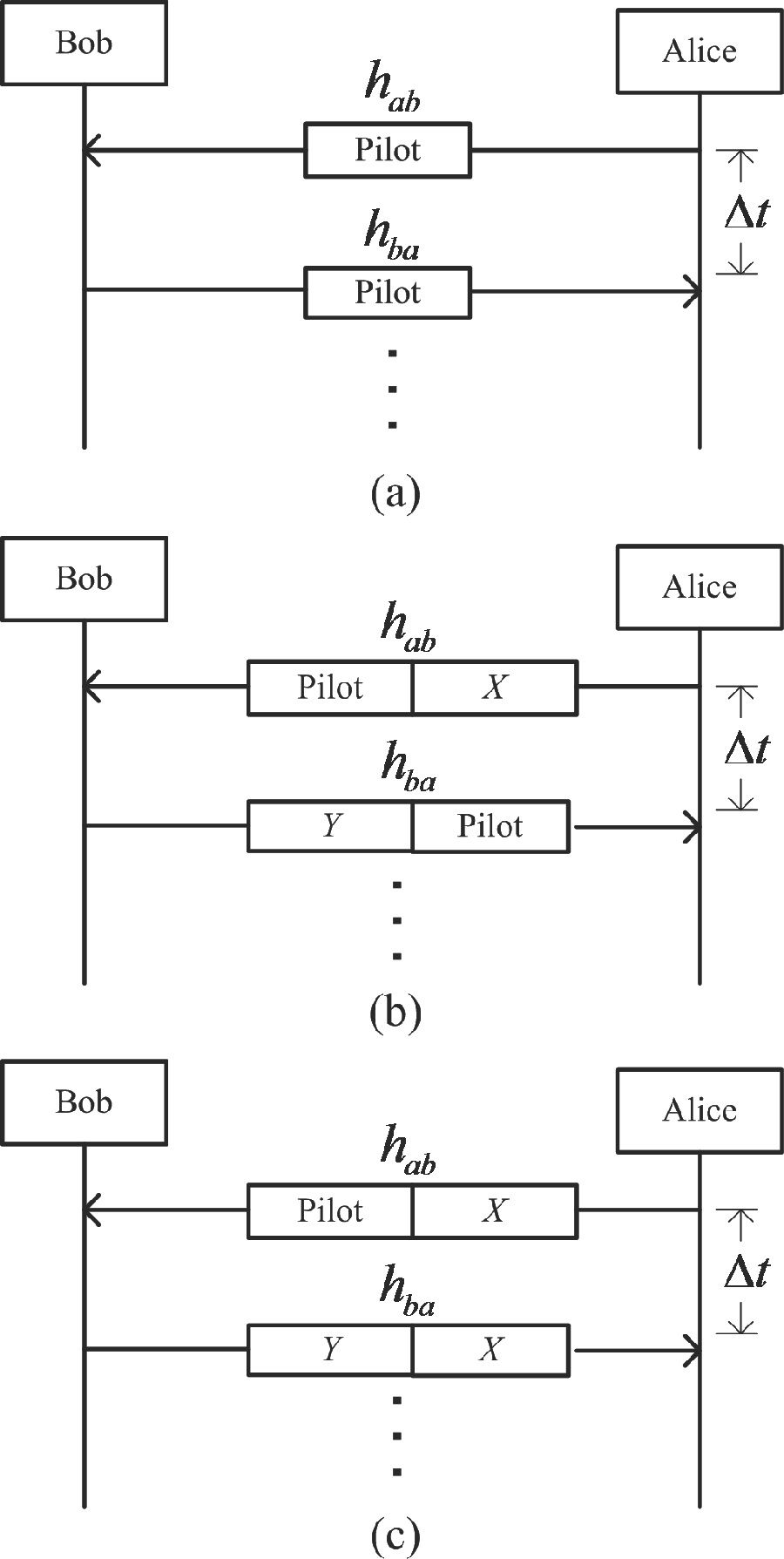
Figure 4.
(a) Example of the secret key agreement from wireless channels. (b) The secret key agreement is protected by the challenge-response authentication. (c) The secret key agreement is improved by our proposed authentication model.
Firstly, when there exists potential opponents (e.g., Eve proactively responds to the pilot sequence before Bob sends anything), the secret key agreement should be protected by the identity authentication (e.g., as is depicted in Figure 4b, the secret key agreement is protected by the challenge-response authentication).
Secondly, the amount of new secret key information generated once is too little to replace the original one. Thus, by the classical challenge-response authentication, several times of secret key agreement will cause the information leakage of the original secret key. Under this circumstance, Eve’s success probability will increase before the renewal of the original secret key. However, in our new authentication model, Eve’s success probability is significantly reduced and can remain the same even if the secret key is reused (i.e., Equation (21)). Then, the original secret key’s renewal can be ensured to be completed with high security performance.
Thirdly, without loss of generality, the pilot sequence is public. Then, Eve can respectively have the channel characteristics of Alice → Eve and Bob → Eve. Moreover, if she is aware of the distribution of the scatters in the environment, she can estimate the channel characteristics of Alice ↔ Bob with high probability [29–31]. Then, she can filch the new secret keys. However, as is depicted in Figure 4c, if we use the challenge message X to replace the public pilot sequence for Alice’s channel estimation, the information leakage of the new secret key can be effectively reduced.
Actually, the improved secret key agreement (i.e., Figure 4c) is similar to Example 1. Then, according to Equations (5) and (13), Eve’s success probability of obtaining the new secret key will reduce to
times of its original when the wiretap channel Alice → (Bob, Eve) is less noisy.
6. Conclusion
In this paper, we have built the challenge-response authentication model over noisy channels. Towards this end, we have respectively derived the information-theoretic lower bounds on the opponent’s success probability in the authentication scenarios of single time and multiple times. In comparison with the classical authentication model, analysis results have shown that our new authentication model is more secure. Remarkably, it has been proven that the Cartesian authentication code can maximize the security performance. In addition, with the Cartesian authentication code, it has been proven that the noise spreading over two separate wiretap channels can together hide the secret key. Finally, we have proposed an improved challenge-response authentication and applied it to the secret key agreement from wireless channels. Thus, we have established the utility of channel noise in identity authentication applications.
Appendix
A. Proof of Lemma 2
We have the facts that:
and:
Hence, according to the equality (h) in Equation (33) and the equality (j) in Equation (34), we have:
The derivation reasons of Equation (33) and Equation (34) are listed in the following.
In Equation (33), equality (g) holds due to the fact that K and
are statistically independent. Equality (h) comes from:
where equality (k) follows from the Markov chain
and H(Y|X, K) = 0.
In Equation (34), equality (i) comes from:
and equality (j) follows from I(K; X, Y) = H(K) − H(K|X, Y).
B. Proof of Lemma 4
Firstly, following the same steps as those used in the proof of Lemma 2, we have:
Furthermore, we have:
where equality (l) comes from:
and:
Thus, Equation (20) is derived by putting Equation (39) into Equation (38). This completes our proof.
Acknowledgments
The authors would like to thank Xianglin Yan for her language revision on this paper.
This work was supported in part by the National High Technology Research and Development Program (ss2015AA011306), the National Basic Research Program of China (2013CB329002), the National Natural Science Foundation of China (61440002), the National Science and Technology Major Project (2014ZX03004003-006), the Keygrant Project of Chinese Ministry of Education (313005), the International Science and Technology Cooperation Program (2012DFG12010), the Open Research Fund of National Mobile Communications Research Laboratory, Southeast University (2012D02), the Natural Science Foundation of Fujian Province of China (2014J01250) and the Tsinghua-Qualcomm Joint Research Program.
Author Contributions
Fanfan Zheng conceived of this work, derived all involved conclusions and wrote this paper. Zhiqing Xiao participated in the derivation of some conclusions and contributed valuable suggestions to develop the composition. Shidong Zhou, Jing Wang and Lianfen Huang conducted the theoretical analyses of this work and contributed valuable suggestions to consummate this paper. All authors have read and approved the final manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Menezes, A.J.; Vanstone, S.A.; Oorschot, P.C.V. Handbook of Applied Cryptography; CRC Press: Boca Raton, FL, USA, 1997. [Google Scholar]
- Yang, L. Course Notes: Biometrics and Cryptography. Available online: http://web2.utc.edu/~Li-Yang/cpsc4600/08_Entity-Authentication14.ppt accessed on 10 July 2015.
- Yu, P.; Baras, J.; Sadler, B. An Implementation of Physical Layer Authentication Using Software Radio; Technical report, DTIC Document, ARL-TR-4888; Army Research Laboratory: Adelphi, MD, USA, July 2009. [Google Scholar]
- Simmons, G.J. Authentication theory/coding theory. In Advances in Cryptology; Blakley, G.R., Chaum, D., Eds.; Springer: Berlin/Heidelberg, Germany, 1985; pp. 411–431. [Google Scholar]
- Maurer, U.M. Authentication theory and hypothesis testing. IEEE Trans. Inf. Theory. 2000, 46, 1350–1356. [Google Scholar]
- Rosenbaum, U. A lower bound on authentication after having observed a sequence of messages. J. Cryptol. 1993, 6, 135–156. [Google Scholar]
- Zeng, K.; Govindan, K.; Mohapatra, P. Non-cryptographic authentication and identification in wireless networks. IEEE Trans. Wirel. Commun. 2010, 17, 56–62. [Google Scholar]
- Lai, L.; El Gamal, H.; Poor, H.V. Authentication over noisy channels. IEEE Trans. Inf. Theory. 2009, 55, 906–916. [Google Scholar]
- Zheng, F.; Xiao, Z.; Zhou, S.; Wang, J.; Huang, L. Message authentication over noisy channels. Entropy 2015, 17, 368–383. [Google Scholar]
- Bellare, M. Course Notes: Modern Cryptography. Available online: http://cseweb.ucsd.edu/~mihir/cse207/w-mac.pdf accessed on 10 July 2015.
- Koç, Ç.K. Course Notes: Explorations in Cryptography. Available online: http://cs.ucsb.edu/~koc/ccs130h/notes/mac2.pdf accessed on 10 July 2015.
- Wyner, A.D. The wire-tap channel. Bell Syst. Tech. J 1975, 54, 1355–1387. [Google Scholar]
- Ren, K.; Su, H.; Wang, Q. Secret key generation exploiting channel characteristics in wireless communications. IEEE Trans. Wirel. Commun. 2011, 18, 6–12. [Google Scholar]
- Chen, C.; Jensen, M.A. Improved channel quantization for secret key establishment in wireless systems, Proceedings of 2010 IEEE International Conference on Wireless Information Technology and Systems (ICWITS), Honolulu, HI, USA, 28 August–3 September 2010; pp. 1–4.
- Csiszár, I.; Korner, J. Broadcast channels with confidential messages. IEEE Trans. Inf. Theory. 1978, 24, 339–348. [Google Scholar]
- Ozel, O.; Ulukus, S. Wiretap channels: Roles of rate splitting and channel prefixing, Proceedings of 2011 IEEE International Symposium on Information Theory Proceedings (ISIT), St. Petersburg, Russia, 31 July–5 August 2011; pp. 628–632.
- Bloch, M.; Barros, J. Physical-Layer Security; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Qin, H.; Chen, X.; Sun, Y.; Zhao, M.; Wang, J. Optimal power allocation for joint beamforming and artificial noise design in secure wireless communications, Proceedings of 2011 IEEE International Conference on Communications Workshops (ICC), Kyoto, Japan, 5–9 June 2011; pp. 1–5.
- Liao, W.C.; Chang, T.H.; Ma, W.K.; Chi, C.Y. Joint transmit beamforming and artificial noise design for QoS discrimination inwireless downlink, Proceedings of 2010 IEEE International Conference on Acoustics Speech and Signal Processing (ICASSP), Dallas, TX, USA, 14–19 March 2010; pp. 2562–2565.
- Goel, S.; Negi, R. Guaranteeing secrecy using artificial noise. IEEE Trans. Wirel. Commun. 2008, 7, 2180–2189. [Google Scholar]
- Thangaraj, A.; Dihidar, S.; Calderbank, A.R.; McLaughlin, S.W.; Merolla, J.M. Applications of LDPC codes to the wiretap channel. IEEE Trans. Inf. Theory. 2007, 53, 2933–2945. [Google Scholar]
- Klinc, D.; Ha, J.; McLaughlin, S.W.; Barros, J.A.; Kwak, B.J. LDPC codes for the Gaussian wiretap channel. IEEE Trans. Inf. Forensics Secur. 2011, 6, 532–540. [Google Scholar]
- Richardson, T.J.; Shokrollahi, M.A.; Urbanke, R.L. Design of capacity-approaching irregular low-density parity-check codes. IEEE Trans. Inf. Theory. 2001, 47, 619–637. [Google Scholar]
- Subramanian, A.; Thangaraj, A.; Bloch, M.; McLaughlin, S.W. Strong secrecy on the binary erasure wiretap channel using large-girth LDPC codes. IEEE Trans. Inf. Forensics Secur. 2011, 6, 585–594. [Google Scholar]
- Ding, C.; Helleseth, T.; Klove, T.; Wang, X. A generic construction of Cartesian authentication codes. IEEE Trans. Inf. Theory. 2007, 53, 2229–2235. [Google Scholar]
- Li, Z.; Gao, S.; Wang, Z.; Thuraisingham, B.M.; Wu, W. A construction of Cartesian authentication code from orthogonal spaces over a finite field of odd characteristic. Discrete Math., Alg. Appl. 2009, 1, 105–114. [Google Scholar]
- Sze, T.; Chanson, S.; Ding, C.; Helleseth, T.; Parker, M. Logarithm cartesian authentication codes. Inf. Compu. 2003, 184, 93–108. [Google Scholar]
- Chanson, S.; Ding, C.; Salomaa, A. Cartesian authentication codes from functions with optimal nonlinearity. Theor. Comput. Sci. 2003, 290, 1737–1752. [Google Scholar]
- Chen, G.; Zhang, Y.; Luan, F.; Xiao, L. Optimization of AP placement in indoor fingerprint positioning, Proceedings of 2013 International Conference on ICT Convergence (ICTC), Jeju, South Korea, 14–16 October 2013; pp. 98–100.
- Luan, F.; Zhang, Y.; Xiao, L.; Zhou, C.; Zhou, S. Fading characteristics of wireless channel on high-speed railway in hilly terrain scenario. Int. J. Antennas Propag. 2013, 12, 188–192. [Google Scholar]
- Zhang, Y.; Li, Z.; Luan, F.; Xiao, L.; Zhou, S.; Wang, J. Measurement-based analysis of transmit antenna selection for in-cabin distributed MIMO system. Int. J. Antennas Propag. 2012, 16, 104–107. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).