Generalized Boundary Conditions for the Time-Fractional Advection Diffusion Equation
Abstract
:1. Introduction
2. Different Kinds of Boundary Conditions
2.1. The Classical Diffusion Equation
2.2. The Standard Advection Diffusion Equation
2.3. The Time-Fractional Diffusion-Wave Equation
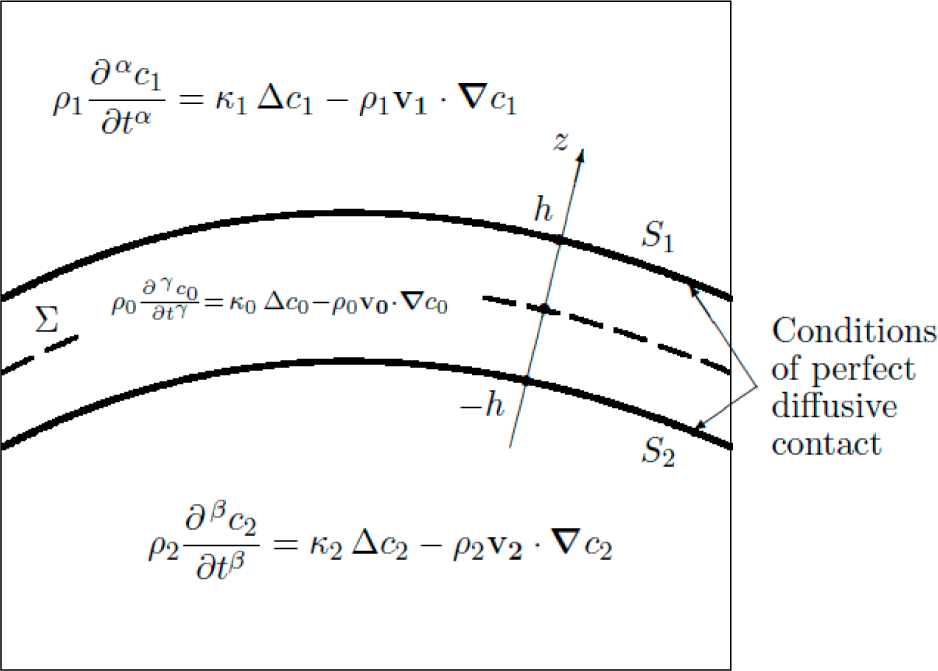
2.4. The Time-Fractional Advection Diffusion Equation
3. Generalized Conditions of Nonperfect Contact
4. Conclusions
Conflict of Interest
References
- Metzler, R.; Klafter, J. The random walk’s guide to anomalous diffusion: A fractional dynamics approach. Phys. Rep. 2000, 339, 1–77. [Google Scholar]
- Metzler, R.; Klafter, J. The restaurant at the end of the random walk: recent developments in the description of anomalous transport by fractional dynamics. J. Phys. A Math. Gen. 2004, 37, R161–R208. [Google Scholar]
- Zaslavsky, G.M. Chaos, fractional kinetics, and anomalous transport. Phys. Rep. 2002, 371, 461–580. [Google Scholar]
- Magin, R.L. Fractional Calculus in Bioengineering; Begell House Publishers: Redding, CT, USA, 2006. [Google Scholar]
- Gafiychuk, V.; Datsko, B. Mathematical modeling of different types of instabilities in time fractional reaction-diffusion systems. Comput. Math. Appl. 2010, 59, 1101–1107. [Google Scholar]
- Uchaikin, V.V. Fractional Derivatives for Physicists and Engineers; Springer: Berlin, Germany, 2013. [Google Scholar]
- Povstenko, Y. Fractional Thermoelasticity; Springer: New York, NY, USA, 2015. [Google Scholar]
- Hoffmann, K.H.; Essex, C.; Schulzky, C. Fractional diffusion and entropy production. J. Non-Equilibr. Thermodyn. 1998, 23, 166–175. [Google Scholar]
- Essex, C.; Schulzky, C.; Franz, A.; Hoffmann, K.H. Tsallis and Rényi entropies in fractional diffusion and entropy production. Physica A 2000, 284, 299–308. [Google Scholar]
- Li, X.; Essex, C.; Davison, M.; Hoffmann, K.H.; Schulzky, C. Fractional diffusion, irreversibility and entropy. J. Non-Equilibr. Thermodyn 2003, 28, 279–291. [Google Scholar]
- Cifani, S.; Jakobsen, E.R. Entropy solution theory for fractional degenerate convection-diffusion equations. Annales de l’Institut Henri Poincare (C) Nonlinear Anal 2011, 28, 413–441. [Google Scholar]
- Magin, R.; Ingo, C. Entropy and information in a fractional order model of anomalous diffusion, Proceedings of the 16th IFAC Symposium on System Identification, Brussels, Belgium, 11–13 July 2011; pp. 428–433.
- Magin, R.; Ingo, C. Spectral entropy in a fractional order model of anomalous diffusion, Proceedings of the 13th International Carpathian Control Conference, High Tatras, Slovakia, 28–31 May 2012; pp. 458–463.
- Prehl, J.; Essex, C.; Hoffmann, K.H. Tsallis relative entropy and anomalous diffusion. Entropy 2012, 14, 701–706. [Google Scholar]
- Prehl, J.; Boldt, F.; Essex, C.; Hoffmann, K.H. Time evolution of relative entropies for anomalous diffusion. Entropy 2013, 15, 2989–3006. [Google Scholar]
- Magin, R.L.; Ingo, C.; Colon-Perez, L.; Triplett, W.; Mareci, T.H. Characterization of anomalous diffusion in porous biological tissues using fractional order derivatives and entropy. Microporous Mesoporous Mater 2013, 178, 39–43. [Google Scholar]
- Ingo, C.; Magin, R.L.; Colon-Perez, L.; Triplett, W.; Mareci, T.H. On random walks and entropy in diffusion-weighted magnetic resonance imaging studies of neural tissue. Magn. Reson. Med. 2014, 71, 617–627. [Google Scholar]
- Ingo, C.; Magin, R.L.; Parrish, T.B. New insight into the fractional order diffusion equation using entropy and kurtosis. Entropy 2014, 16, 5838–5852. [Google Scholar]
- Zhuang, P.; Liu, F.; Anh, V.; Turner, I. Numerical treatment for the fractional Fokker-Planck equation. ANZIAM J 2007, 48, C759–C774. [Google Scholar]
- Chen, C.; Liu, F.; Turner, I.; Anh, V. Implicit difference approximation of the Galilei invariant fractional advection diffusion equation. ANZIAM J 2007, 48, C775–C789. [Google Scholar]
- Liu, F.; Zhuang, P.; Anh, V.; Turner, I.; Burrage, K. Stability and convergence of the difference methods for the space-time fractional advection-diffusion equation. Appl. Math. Comput. 2007, 191, 12–20. [Google Scholar]
- Liu, F.; Zhuang, P.; Burrage, K. Numerical methods and analysis for a class of fractional advection-dispersion models. Comp. Math. Appl. 2012, 64, 2990–3007. [Google Scholar]
- El-Sayed, A.M.A.; Behiry, S.H.; Raslan, W.E. Adomian’s decomposition method for solving an intermediate fractional advection-dispersion equation. Comp. Math. Appl. 2010, 59, 1759–1765. [Google Scholar]
- Golbabai, A.; Sayevand, K. Analytical modelling of fractional advection-dispersion equation defined in a bounded space domain. Math. Comp. Model. 2011, 53, 1708–1718. [Google Scholar]
- Panday, R.K.; Singh, O.P.; Baranwal, V.K. An analytic algorithm for the space-time fractional advection-dispersion equation. Comp. Phys. Commun. 2011, 182, 1134–1144. [Google Scholar]
- Saadatmandi, A.; Dehghan, M.; Azizi, M.-R. The Sinc-Legendre collocation method for a class of fractional convection-diffusion equations with variable coefficients. Commun. Nonlinear Sci. Numer. Simulat. 2012, 17, 4125–4136. [Google Scholar]
- Parvizi, M.; Eslahchi, M.R.; Dehghan, M. Numerical solution of fractional advection-diffusion equation with a nonlinear source term. Numer. Algor. 2015, 68, 601–629. [Google Scholar]
- Zhang, X.; Huang, P.; Feng, X.; Wei, L. Finite element method for two-dimensional time-fractional Tricomi-type equations. Numer. Methods Partial Differ. Equ. 2013, 29, 1081–1096. [Google Scholar]
- Yang, Q.; Moroney, T.; Burrage, K.; Turner, I.; Liu, F. Novel numerical methods for time-space fractional reaction diffusion equation in two dimensions. ANZIAM J 2011, 52, C395–C409. [Google Scholar]
- Jiang, W.; Lin, Y. Approximate solution of the fractional advection-dispersion equation. Comp. Phys. Commun. 2010, 181, 557–561. [Google Scholar]
- Fu, Z.-J.; Chen, W.; Yang, H.-T. Boundary particle method for Laplace transformed time-fractional diffusion equations. J. Comput. Phys. 2013, 235, 52–66. [Google Scholar]
- Sun, H.G.; Zhang, Y.; Chen, W.; Reeves, D.M. Use of a variable-index fractional-derivative model to capture transient dispersion in heterogeneous media. J. Contaminant Hydrol 2014, 157, 47–58. [Google Scholar]
- Chen, W.; Sun, H.; Zhang, X.; Korošak, D. Anomalous diffusion modeling by fractal and fractional derivatives. Comp. Math. Appl. 2010, 59, 1754–1758. [Google Scholar]
- Gafiychuk, V.; Datsko, B.; Meleshko, V.; Blackmore, D. Analysis of the solutions of coupled nonlinear fractional reaction-diffusion equations. Chaos Solitons Fractals 2009, 41, 1095–1104. [Google Scholar]
- Povstenko, Y. Different kinds of boundary conditions for time-fractional heat conduction equation, Proceedings of the 13th International Carpathian Control Conference, High Tatras, Slovakia, 28–31 May 2012; pp. 588–591.
- Povstenko, Y.Z. Fractional heat conduction in infinite one-dimensional composite medium. J. Therm. Stresses 2013, 36, 351–363. [Google Scholar]
- Povstenko, Y. Fractional heat conduction in an infinite medium with a spherical inclusion. Entropy 2013, 15, 4122–4133. [Google Scholar]
- Podstrigach, Y.S.; Povstenko, Y.Z. Introduction to the Mechanics of Surface Phenomena in Deformable Solids; Naukova Dumka: Kiev, Ukraine, 1985; In Russian. [Google Scholar]
- Kaviany, M. Principles of Heat Transfer in Porous Media; Springer: NewYork, NY, USA, 1995. [Google Scholar]
- Feller, W. An Introduction to Probability Theory and Its Applications; John Wiley & Sons: New York, NY, USA, 1971. [Google Scholar]
- Scheidegger, A.E. The Physics of Flow through Porous Media; University of Toronto Press: Toronto, Canada, 1974. [Google Scholar]
- Van Kampen, N.G. Stochastic Processes in Physics and Chemistry; North-Holland: Amsterdam, The Netherlands, 1981. [Google Scholar]
- Risken, H. The Fokker-Planck Equation; Springer: Berlin, Germany, 1989. [Google Scholar]
- Nield, D.A.; Bejan, A. Convection in Porous Media; Springer: New York, NY, USA, 2006. [Google Scholar]
- Povstenko, Y.Z. Fractional heat conduction equation and associated thermal stresses. J. Therm. Stresses 2005, 28, 83–102. [Google Scholar]
- Povstenko, Y.Z. Thermoelasticity which uses fractional heat conduction equation. J Math. Sci 2009, 162, 296–305. [Google Scholar]
- Povstenko, Y.Z. Theory of thermoelasticity based on the space-time-fractional heat conduction equation. Phys. Scr. 2009, 136, 014017. [Google Scholar]
- Povstenko, Y.Z. Fractional Cattaneo-type equations and generalized thermoelasticity. J. Therm. Stresses 2011, 34, 97–114. [Google Scholar]
- Povstenko, Y. Non-axisymmetric solutions to time-fractional diffusion-wave equation in an infinite cylinder. Fract. Calc. Appl. Anal. 2011, 14, 418–435. [Google Scholar]
- Gorenflo, R.; Mainardi, F. Fractional calculus: integral and differential equations of fractional order. In Fractals and Fractional Calculus in Continuum Mechanics; Carpinteri, A., Mainardi, F., Eds.; Springer: New York, NY, USA, 1997; pp. 223–276. [Google Scholar]
- Podlubny, I. Fractional Differential Equations; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Povstenko, Y. Theory of diffusive stresses based on the fractional advection-diffusion equation. In Fractional Calculus: Applications; Abi Zeid Daou, R., Moreau, X., Eds.; NOVA Science Publishers: New York, NY, USA, 2015; pp. 227–241. [Google Scholar]
- Goldenveiser, A.L. Theory of Thin Shells; Pergamon Press: Oxford, UK, 1961. [Google Scholar]
- Naghdi, P.M. The theory of shells and plates. In Handbuch der Physik; Truesdell, C., Ed.; Springer: Berlin, Germany, 1972; pp. 425–640. [Google Scholar]
- Vekua, I.N. Some General Methods of Constructing Different Variants of Shell Theory; Nauka: Moscow, Russia, 1982; In Russian. [Google Scholar]
- Ventsel, E.; Krauthammer, T. Thin Plates and Shells: Theory, Analysis, and Applications; Marcel Dekker: New York, NY, USA, 2001. [Google Scholar]
- Podstrigach, Ya.S. Temperature field in a system of solids conjugated by a thin intermediate layer. Inzh.-Fiz. Zhurn 1963, 6, 129–136, In Russian. [Google Scholar]
- Podstrigach, Ya.S.; Shvetz, R.N. Thermoelasicity of Thin Shells; Naukova Dumka: Kiev, Ukraine, 1978; In Russian. [Google Scholar]

© 2015 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Povstenko, Y. Generalized Boundary Conditions for the Time-Fractional Advection Diffusion Equation. Entropy 2015, 17, 4028-4039. https://doi.org/10.3390/e17064028
Povstenko Y. Generalized Boundary Conditions for the Time-Fractional Advection Diffusion Equation. Entropy. 2015; 17(6):4028-4039. https://doi.org/10.3390/e17064028
Chicago/Turabian StylePovstenko, Yuriy. 2015. "Generalized Boundary Conditions for the Time-Fractional Advection Diffusion Equation" Entropy 17, no. 6: 4028-4039. https://doi.org/10.3390/e17064028
APA StylePovstenko, Y. (2015). Generalized Boundary Conditions for the Time-Fractional Advection Diffusion Equation. Entropy, 17(6), 4028-4039. https://doi.org/10.3390/e17064028





