Abstract
The paper proposes a new non-parametric density estimator from region-censored observations with application in the context of population studies, where standard maximum likelihood is affected by over-fitting and non-uniqueness problems. It is a maximum entropy estimator that satisfies a set of constraints imposing a close fit to the empirical distributions associated with the set of censoring regions. The degree of relaxation of the data-fit constraints is chosen, such that the likelihood of the inferred model is maximal. In this manner, the estimator is able to overcome the singularity of the non-parametric maximum likelihood estimator and, at the same time, maintains a good fit to the observations. The behavior of the estimator is studied in a simulation, demonstrating its superior performance with respect to the non-parametric maximum likelihood and the importance of carefully choosing the degree of relaxation of the data-fit constraints. In particular, the predictive performance of the resulting estimator is better, which is important when the population analysis is done in the context of risk assessment. We also apply the estimator to real data in the context of the prevention of hyperbaric decompression sickness, where the available observations are formally equivalent to region-censored versions of the variables of interest, confirming that it is a superior alternative to non-parametric maximum likelihood in realistic situations.
1. Introduction
1.1. Motivation
The paper presents a new density estimator motivated by problems of population modeling, where the interest is in estimating the probability distribution πθ, θ ∈ Θ, of the parameters of a mathematical model M(·|θ) characterizing the response y(t|θ) of individuals to applied stimuli x(t). The ultimate goal is in general to be able to predict the dispersion of the response of the population to an arbitrary future stimulus x(t), rather than to make a “tomography” of the population itself. These types of problems are frequent in domains like biomedical engineering, insurance studies or environmental management.
If the parameter θ can be estimated from each observation y(t|θ) and each individual’s parameter is chosen independently from πθ, the problem of estimating πθ from a collection of responses
is formally equivalent to the usual density estimation problem from a set of independent and identically distributed samples
and can be solved using standard parametric or non-parametric methods; see the abundant literature on non-linear mixed-effects models. The situation considered in this paper is more complex, in that the response y(·|θ) of the model not observable, and we only have access to the result of the classification of its assignment to a finite number (L + 1) of possible labels by a known classifier C(·). Figure 1 illustrates the structural modeling/observation framework that we consider.
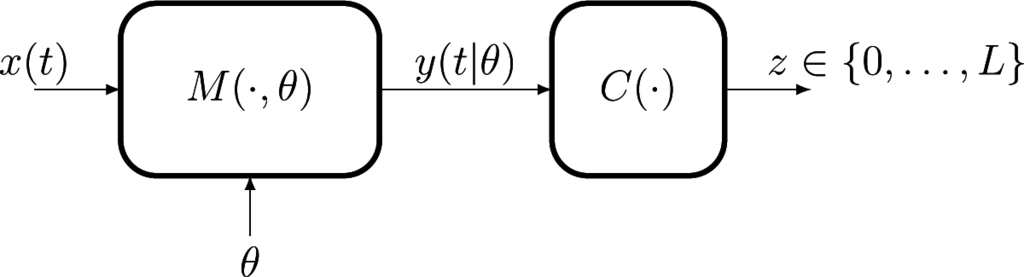
Figure 1.
Partial response observation: z is the classification of the response to stimulus x(t) in a finite set.
In this setup, each observation can no longer be related to a single point θ ∈ Θ, the same label z being assigned, for the same stimulus x(t), to all responses inside a subset R ⊂ Θ. The set R is completely determined by the pair (z, x(t)) together with knowledge of the model M(·|θ) and of the classifier rule C(·). This situation, when a single observation does not give information with respect to the individual value θ, but only the indication that it belongs to a set, is commonly known in the statistical literature as “censored observations”. While in general studies of the density estimation under censored observations have assumed that the censoring sets R are intervals, the geometry of our censoring regions is determined by the structure of the (possibly highly non-linear) operators M(·|θ) and C(·) and can have an arbitrary morphology, requiring modification of the existing methods.
In Section 4, we detail a particular instance of the problem formally presented above, relevant in the context of the prevention of decompression sickness in hyperbaric diving. Readers may want to read the material in Section 4.1 to have a concrete instantiation of the generic stimuli and operators used in the presentation above.
1.2. Notation and Problem Formulation
Consider the notation introduced in Section 1.1 (see also Figure 1), and let
denote the available set of observations, where label zn ∈ {0, …, L} has been observed for input X(n) = {xn(t), t ∈ Tn}, where Tn is the duration of the stimulus. Denote by Rn ⊂ Θ the set of all individual parameters whose response to X(n) receives label zn:
We assume that for all possible stimuli X(n), the composition C(M(X(n)|·)) (of the model and the classifier) is a measurable function from Θ to {0, …, L} with respect to the restriction of the Lebesgue measure to the set Θ. Under this assumption, the probability of the sets
is well defined for all 0 ≤ ℓ ≤ L and all stimuli for any distribution absolutely continuous with respect to the Lebesgue measure.
Usually, in population studies, the same stimulus is applied to several individuals. We assume here that stimuli X(j) are chosen in a finite set
Each possible input function X(j) in
determines a partition of Θ in L + 1 sets, that we denote by
:
The top row of Figure 2 illustrates schematically partitions that correspond to classification in two (L1 = 1) and three (L2 = 2) classes of the response to two distinct stimuli.

Figure 2.
Two partitions associated with distinct stimuli,
(top left) and
(top right) and the resulting partition
(bottom); see Definition 1.
Let nj be the number of times that stimulus X(j) has been used in the N observations and
the number of times label ℓ occurred in these nj experiences. The observed dataset determines J empirical laws
, each one associated with a distinct partition
:
When we want to emphasize the number of observations on which these empirical laws are based, we will call
an nj-type. With the notation defined above, we can finally state the problem addressed in this paper with full generality.
Problem 1. (Density estimation from region-censored data)
Find the non-parametric estimate of πθ from the set of J nj-types, j = 1, …, J (see Equation (1)) of the discrete random variables associated with the known partitions (see Equation (4)).
Before initiating the study of this estimation problem, we show below how a set of constraints can be related to the observations (1) leading to an alternative problem formulation.
Let 1A(θ) be the indicator function of set A ⊂ Θ and
the (non-observed) empirical distribution:
where
, i = 1, …, nj, is the parameter of the i-th individual to whom stimulus X(j) has been applied. It is immediate that
in Equation (1) can be written as the statistical expectation of the indicator function of
with respect to
:
We stress that in our context, the (virtual) datasets
are distinct for different values of j ∈ {1, …, J}, since they correspond to statistically-independent samples from πθ.
The remarks above allow us to relate Problem 1 to two alternative problems: Problem 2 formulated below and Problem 3 presented in the next subsection.
Problem 2. (Density estimation under moment constraints)
Consider a set of partitions (j), j ∈ {0 … L} all of size L+1, and let, with M = (L+1) J, be the set of indicator functions. Denote by, m = 1, …, M, the corresponding empirical moments as in (2). Find the non-parametric estimate of πθ that satisfies the set of constraints:
Note that the existence and unicity of the solution to this problem is not guaranteed: depending on the set of partitions and empirical moments, the problem may have no solution or admit a solution (possibly non-unique).
The next subsection summarizes the present background on the two problems formulated above. Prior to that, we present three definitions that will be useful in the sequel.
Definition 1. Let be the smallest partition of Θ whose generated σ-algebra,
, contains all partitions (elements of are the minimal elements of the closure of the union of all partitions with respect to set intersection). The size is necessarily finite. We denote by Em, m ∈ {1, …, Q} a generic element of.
The bottom row of Figure 2 shows the partition
generated by the two partitions in the top.
Definition 2.
is the set of elements of that intersect, such that:
Definition 3. Let πθ be a probability distribution over Θ and a finite partition of Θ. We denote byπθ,Q the probability law induced by πθ over the elements of:
1.3. Background
1.3.1. Density Estimation from Region-Censored Data
Determination of
, the NPMLE (non-parametric maximum likelihood estimate) of πθ from censored observations, i.e., the solution of Problem 1, has been studied by many authors, starting with the pioneering formulation of the Kaplan–Meier product-limit estimator [1]. Several types of censoring (one-sided, interval, etc.) have been considered since, first for scalar and more recently for multivariate distributions.
The problem assessed here departs from previous studies in that our (multi-dimensional) censoring regions
⊂ Θ can have arbitrary geometry. To emphasize this, we speak of “region-censoring”, instead of the more common term “interval-censoring.” Another important difference concerns the fact that our regions are elements of a known set of partitions, being in general observed several times, while in general, no relation between the censoring intervals is assumed in the literature, each one being usually applied once.
Several facts are known about the NPMLE for censored observations.
Proposition 1.
- The support of, is confined to a finite number K ≤ Q of elements of, the so-called “elementary regions”:This set necessarily has a non-empty intersection with all observed lists, i.e.,
- all distributions that put the same probability mass wk = {πθ(Ek)}, k = 1, …, K in the elementary regions have the same likelihood;
- there is in general no unique assignment of probabilities that maximizes the likelihood.
Turnbull [2] has first demonstrated (i) giving an algorithm to find the pairs
for the scalar case. Gentleman and Vandal [3] addressed the multivariate interval-censored case, showing that the Ek’s are the intersections of the elements of the maximal cliques of the intersection graph of the set of observed intervals; see Figure 3a for a bi-dimensional example. We have shown elsewhere [4] that (i) also holds when the censoring sets have arbitrary geometry, but that some elementary regions are now associated with non-maximal cliques of the intersection graph, as shown in Figure 3b, requiring a slightly more complex identification of the sets Ek, which we do not detail here.
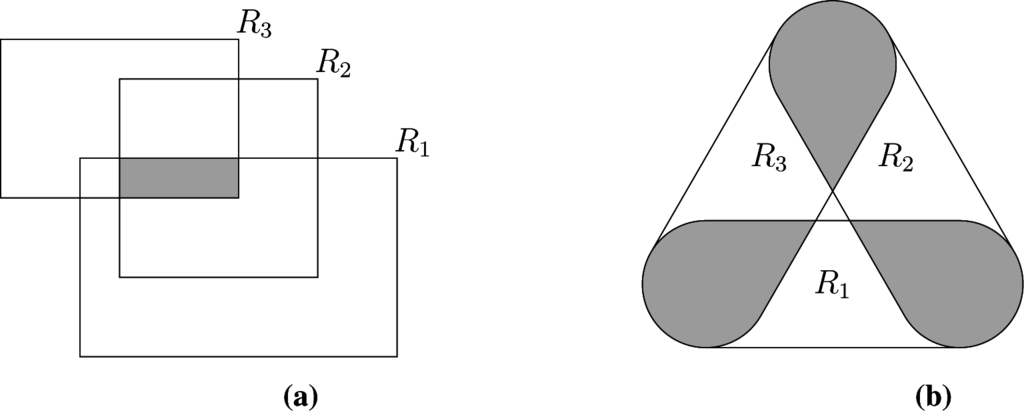
Figure 3.
Definition of elementary regions from the cliques of the intersection graph. (a) Three intervals: maximal clique and corresponding elementary region Ek (shaded region); (b) three regions with empty intersection resulting in three disjoint elementary regions Ek (the shaded regions).
Facts (i) and (ii) together imply that the NPMLE problem can be studied in the K-dimensional probability simplex
, since
is determined only up to the probability vector ŵ = {ŵ1, …, ŵK}. The two types of “non-uniqueness” of the NPMLE, (ii) and (iii), have been first pointed out by Turnbull [2]. More recently, they were studied in detail for the multi-variate case in [3], where the authors coined the terms representational (ii) and mixture (iii) non-uniqueness, further showing that the set of probability laws
defining NPMLEs is a polytope.
The NPMLE under censored observations retains the typical consistency properties of the maximum likelihood estimates, in particular
tends to πθ,(j) (ℓ) (see Equation (4)) when nj → ∞. It is not possible to guarantee the consistency of the estimate of the distribution of
over the finer partition
. However, the simulations studies presented in Section 3 show that as the number of partitions J tends to infinity and this σ-algebra gets finer, while keeping fixed each nj (and thus, n → ∞ with J), the distance between the true and estimated probability laws decreases to zero.
Facts (i)–(iii) seriously hinder application of NPMLEs in many domains, in particular when, as is the case in our study, they provide a model of the diversity of the population under analysis that will be used for subsequent risk assessment. Besides being affected by some degree of arbitrariness (Facts (ii) and (iii)), the concentration of the probability mass in a small number of bounded regions reveals a tendency to underestimate population diversity, which may result in strong biases when estimating risk under unobserved stresses. The simulation studies that will be presented in Section 4 illustrates to what extent a lack of identifiability and a tendency to concentrate its support compromise the ability to predict the empirical laws corresponding to stimuli that were not used in the available dataset.
1.3.2. Density Estimation under Moment Constraints
Eventual non-unicity problems in density estimation under constraints on moments, like Problem 2, have been most often solved by relying on the maximum entropy (MaxEnt) principle [5] to select the most un-informative density that can match the observed moments
. Several information entropies have been considered in this context, the original Shannon entropy H1(·) remaining the most commonly used due to its simple interpretation in terms of coding theory and its intimate link to fundamental results in estimation theory, while amongst generalized entropies, the Rényi entropy Hα(·), coinciding with Shannon when α → 1, is often chosen due to its appealing numerical and analytical tractability for α = 2:
Problem 3. (H-MaxEnt density estimator)
Let H(·) be a generalized entropy. The H-MaxEnt estimate of Problem 2 is the solution of:
When
is non-empty (i.e., the constraints are compatible) the MaxEnt density can be analytically determined for some choices of H(·).
Proposition 2. (Equivalence to ML estimation in the exponential family)
Assume that the constraints of Problem 2 are statistical averages with respect to the empirical distribution of a common dataset, i.e.,
in Equation (2), such that:
Then:
- (Boltzmann theorem [6]) the H1-MaxEnt estimate maximizes the likelihood of the observations in the exponential family,where Zλ is a normalizing constant (the partition function), and the are determined such that the M constraints are satisfied.In short, the MaxEnt (non-parametric) estimate coincides with the maximum likelihood parametric estimate inside the exponential distributions.
- the H2-MaxEnt estimate [7] is:where [·]+ = max (·,0) and the are such that the M constraints are satisfied.
Note that the H1-MaxEnt/ML equivalence is lost when the empirical averages
are not all obtained from the same dataset, as is the case in our problem, where (see Equation (2)) constraints associated with distinct stimuli are being derived from distinct empirical distributions.
When the constraints are not compatible, i.e.,
and Problem 2 has no solution,
is not defined, and only a relaxed version of the original problem can be solved.
Problem 4. (Relaxed H–MaxEnt density estimator)
Let H be a generalized entropy, and ϵ ∈ ℝ+M. The -relaxed H-MaxEnt density estimate is the solution of:
where g is the M-dimensional vector function with m-th component gm(·),
is the M-dimensional vector of empirical expectations of g, ║·║π is a vector of norms depending on π and inequality is understood component-wise.
This estimator has been studied in detail in [8,9] for the Shannon entropy and moment constraints derived from a single empirical distribution, where the authors fully exploit the equivalence between regularized MaxEnt as formulated above and ℓ1-penalized maximum likelihood in the exponential family, showing that Proposition 2 holds in a more generic sense.
Proposition 3. (Equivalence of ℓ1-regularized H1-MaxEnt and penalized log-likelihood [9])
Problem 4 with H = H1 (Shannon entropy) and ║·║π the ℓ1 norm for the expected value:
where the constraintsare empirical averages computed using a dataset Θ, is equivalent to the maximization of the sum of the log-likelihood of Θ for the exponential family (6) penalized by the term, where ϵm is the m-th element of ϵ.
By linking the relaxation level (the parameter in Problem 4) to the expected level of accuracy of the empirical averages
, in [8,9], the authors are able to establish performance guarantees for the resulting density estimate, in terms of log-likelihood loss.
As before, this regularized-MaxEnt/penalized-ML equivalence only holds when all constraints are on the empirical moments with respect to the same underlying empirical distribution. This is not true in population analysis, where an individual is observed only through one of the partitions, and we cannot invoke the properties of maximum likelihood estimators to characterize the properties of regularized MaxEnt estimators, as is done in [8].
We remark that the regularized MaxEnt estimates are unique for strictly concave entropy functionals and always exist for sufficiently large ϵ. They do not suffer from neither representational non-unicity, the optimal continuous distribution being constant inside each element of
, nor from mixture non-uniqueness, being the solution of a concave criterion under linear inequality constraints.
1.4. Contributions
As largely documented in the literature, the NPMLE using censored data frequently exhibits a singular behavior. By concentrating probability mass in a subset of Θ of a small Lebesgue measure, they favor “over-homogenous” population models that may lead to dangerous biases in the context of risk assessment, by masking the existence of individuals for which risk can be large. As shown above, the problem of density estimation from censored observations addressed in the paper can be recast as the problem of density estimation under a set of constraints derived from the censored observations, each constraint being associated with one of the censoring regions.
While MaxEnt has been frequently used for density estimation from the joint observation of empirical moments of a set of features, its use for region-censored data arising from strongly quantified data, as we consider in this paper, violates the conditions under which previous equivalence to maximum likelihood estimation in the Gibbs family can be established. In these circumstances, guarantees on the likelihood of the original data can be no longer given.
We propose a novel estimator that explicitly relies on the two criteria, the most likely maximum entropy estimator (MLME), where the degree of regularization of a MaxEnt estimate (i.e., of the solutions to Problem 4) is chosen such that the resulting estimate has maximum likelihood. The duality of the two criteria is exploited to allow suppression of singularities that are due to inconsistent or small datasets, and the resulting solution converges to the non-parametric maximum likelihood solution as the size of the datasets associated with each constraint (censoring region) grows. By using the Rényi entropy of order two instead of the Shannon entropy, we are led to a quadratic optimization problem with linear inequality constraints that has an efficient numerical implementation.
While no theoretical performance guarantees are given, the paper presents numerical studies of the performance of the proposed MLME estimator in real and simulated data, comparing it to the NPMLE and to the best fitting MaxEnt solutions. The results of cross-validation on a real dataset show that our novel estimator is better than the NPMLE or the minimally-regularized MaxEnt estimator, leading to better predictions of the population risk under unobserved stress conditions.
The paper is organized as follows. Section 2 illustrates the poor behavior of the NPMLE using simulated data. We show (Section 2.4) that even the most uncertain of the NPMLEs still presents singularities that are unlikely to occur in a natural population. The section starts by presenting the likelihood function and defining the polytope of NPMLE solutions. It also addresses the numerical determination of the NPMLE, and two optimization algorithms are presented.
Section 3 presents the main contribution of the paper, introducing the most likely Rényi MaxEnt estimator (MLME; see Definition 4). We compare our estimator to the NPMLE, demonstrating using simulated datasets that it performs better. We also present numerical studies of its asymptotic behavior as the number J of different stimuli becomes large, revealing a remarkably better behavior.
In Section 4, the proposed estimator is applied to the real problem that motivated this study, in the context of the prevention of decompression sickness in hyperbaric deep sea diving. The new estimator is compared to classical maximum likelihood and maximum entropy estimators on real and simulated data, illustrating the superior performance of the new estimator in a realistic situation.
2. The NPMLE
2.1. Simulated Data Generation Mechanism
Before presenting the NPMLE and discussing its determination, we present the data generation mechanism that will be used to illustrate the different estimators presented in this and the next sections. The simulated population distribution πθ is the restriction of the joint distribution of two independent and identically distributed normal variables of mean µ = 0.5 and variance σ2 = 0.2 to the unit square Θ = [0, 1]2.
Partitions (j) are randomly generated by considering random unions of the elements of the Voronoi tessellation of S = 50 points uniformly drawn in Θ; see Figure 4. The partition
induced by 10 random binary splits of Θ is shown in Figure 5a, and Figure 5b is a color-coded representation of the probability law
, where the fine partition
is easily recognizable (black delimited polygonal regions). We remark that the size of the elements of the partitions generated by our simulation mechanism tends have low dispersion, following approximately a gamma distribution with both parameters equal to (7/2)λ−2, where λ is the intensity of the homogenous Poisson process [10] (λ = 1/50 in our simulations). In Section 4, we will see that this may not be the case in practical applications.

Figure 4.
Two randomly-generated partitions of the unit square.
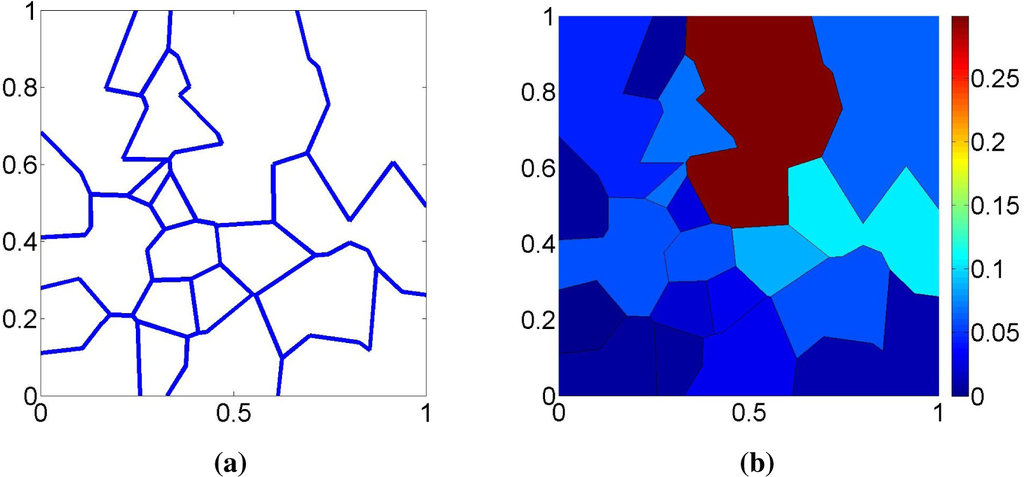
Figure 5.
(a) Partition
determined by J = 10 random binary partitions of Θ. (b) Probability law
induced over the elements of the partition
.
Observations are then generated by independently sampling nj times from each of the probability laws associated with the individual partitions (j), for j = 1, …, J. In the numerical studies presented in this section, J = 10. To simulate the situation when some stimuli are seldom applied (for instance, if they may have compromised the safety of the individual to which they are applied), the partitions are divided into two groups, representing “safe” and “dangerous” stimuli, of sizes seven and three, respectively. The probability that a dangerous partition is chosen is 10−3, and inside each group, partitions are chosen uniformly. Except when indicated otherwise, we will consider a total of N = 104 observations.
2.2. Likelihood Function
The log-likelihood function for Problem 1 is:
Consider the partition
, with
the complement of set A, and where SNPMLE is the union of the elementary regions
in Proposition 1 (i), such that
.
Note that since the elementary regions
are elements of
, notation
introduced in Definition 2 is well defined.
From Proposition 1 (i)
and, thus, using (3):
where
. is the ℓ-th row of B(j), the (L + 1) × K binary matrix, with
, and
is the vector of probabilities of the elementary regions Ek: wk = πθ(Ek), k = 1, …, K, with
the K-dimensional probability simplex:
Equations (7) and (8) show that (Proposition 1 (iii)) all πθ leading to the same w have the same likelihood.
Proposition 4. There is in general no single w maximizing (7) and all elements of:
where ŵ is a NPMLE are also NPMLEs. We call the NPMLE polytope.
Note that the non-unicity statement above concerns w the probabilities of the elementary regions Ek, but that the probability of the censoring regions
is uniquely estimated, all w ∈
assigning the same probabilities to the elements of the partitions
. It is obvious that the estimator is consistent for these, but no stronger statement seems to be possible.
2.3. Optimizing the Likelihood
Several algorithms have been proposed to maximize (7); see e.g., [11]. Gentleman and Vandal [3] discussed several methods and summarized them in two categories: those based on convex optimization and those based on finite mixture estimation. Two algorithms are compared in [11]: the iterative convex minorant (ICM), initially presented by Groeneboom and Wellner [12], and the vertex exchange method [13].
We show below that a multiplicative algorithm, known as the Richardson–Lucy algorithm [14] in the framework of image deconvolution, can be used to maximize
. This follows from the fact that maximization of
is equivalent to an optimal design problem, enabling application of a vast collection of efficient algorithms originating from optimal design theory. As far as we know, this link of NPMLE estimation using censored observations to a D-optimal design problem has not been remarked on before.
Consider the nj(L + 1) × K matrices B(j)′, obtained from the ((L + 1) × K) matrix B(j) by repeating
times line ℓ, the N × K matrix B′ that stacks all B(j)′, j = 1, …, J, the N × N diagonal matrix
and the matrix
. Then, it is easy to show that
can be written as:
demonstrating that the determination of ŵ maximizing
with respect to w ∈
corresponds to a D-optimal design problem for the matrix M(w), with w considered as a design measure allocating weight wk to the elementary design matrix Hk (see, e.g., [15]). A number of important properties follow from this equivalence with a D-optimal design problem. In particular, see [16,17], the iterations:
initialized at some strictly positive w(0) converge to a maximizer of (7). This multiplicative algorithm is easy to implement, but the following vertex exchange method (VEM) [13] ensures a faster convergence to the optimum. The VEM updating rule is:
where:
and α is chosen to maximize a quadratic approximation of the log-likelihood evaluated at w(t+1). In the multiplicative and VEM algorithms, we use the stopping condition
.
Our numerical studies show that the VEM Algorithm (11) is faster than the multiplicative Algorithm (10) requiring on average three-times less iterations to converge. We stress that these optimization algorithms can be applied to all Q elements of the complete partition
and automatically sets to zero the entries of w that do not correspond to the elementary sets
(in particular, when using the result in [18] to detect the entries of w that can be set to zero), so that the computationally-expensive analysis of the intersection graph presented in [4] is not required.
Figure 6a shows one of the NPMLE estimates (i.e., one element of the NPMLE polytope) for a simulated dataset produced, as we explained in the beginning of the section. This example clearly displays the NPMLE singularities that have been mentioned before: while πθ is strictly positive inside the complete unit square, significant regions of Θ are assigned zero probability mass (the white regions in the figure), and the support of
is strictly contained in Θ.
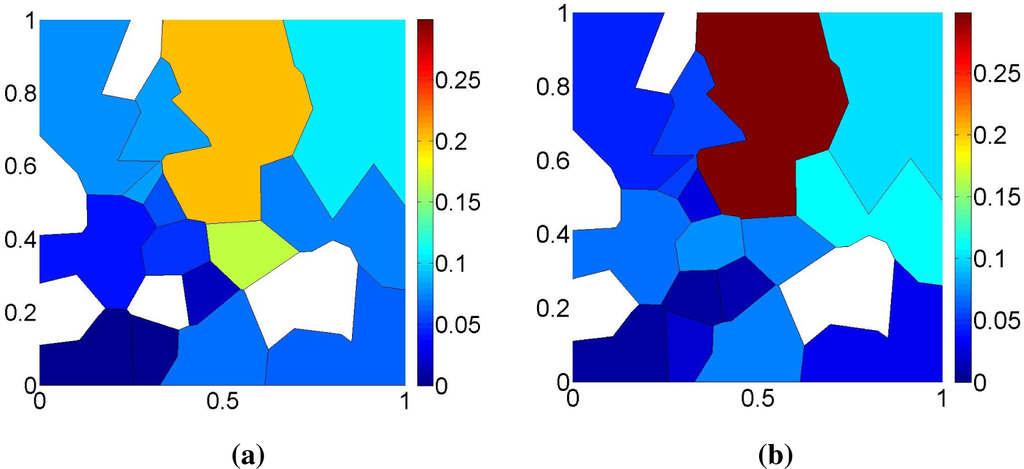
Figure 6.
(a)
, one non-parametric maximum likelihood estimate (NPMLE) solution found by (10). (b)
, the Rényi-MaxEnt NPMLE. The white regions have zero probability mass.
2.4. Least Informative NPMLE
As stated in Proposition 1 (iii), the NPMLE is not unique, and we have seen (Proposition (4)) that the set of solutions is the polytope
defined in Equation (9), associated with the matrix B,
Motivated by the ultimate goal of capturing the largest possible diversity of the underlying population, we select from the NPMLE polytope
the distribution that is least informative, i.e., that has maximum entropy.
Let ŵ be an NPMLE, and define
, with ŵ the vector of probabilities
, k = 1, …, K. We denote by
the distribution in
maximizing the entropy H; it satisfies:
Determining
for the Shannon entropy, i.e., for H = H1, is a non-trivial non-linear constrained optimization problem. However, for H = H2, the Rényi-MaxEnt NPMLE probability vector
is the solution to the following quadratic program with linear equality constraints:
with ν(Ek) the volume of Ek, for which efficient solutions exist.
The Rényi-MaxEnt NPMLE for the same dataset that leads to the NPMLE in Figure 6a is displayed in Figure 6b. We can see that the restriction to the NPMLE polytope still forces the density to be concentrated in a strict subset of Θ, with areas of zero measure (white zones in Figures 6a,b). This is inherent to the likelihood criterion, which favors the most concentrated densities that are able to explain the observed data.
Indeed, it is easy to see that the support of a NPMLE density may importantly shrink when a stimulus that is applied only once is added to the dataset, confirming the ill-conditioning of the NPMLE for small datasets. Suppose a new stimulus X(J+1) applied only once with resulting label ℓ⋆ is added to a dataset already containing J stimuli:
Let
be the partition of Θ corresponding to “old” stimuli j ≤ J and
the new partition, which also integrates (X(J+1), n(J+1)). If
intersects an elementary set Ek ∈
, such that:
then
will no longer be an elementary set, showing that the support of the NPMLE will shrink. Note that we may have
, with ν(·) the Lebesgue measure.
3. Most Likely Rényi-MaxEnt
To avoid the singular behavior of the NPMLE, we must estimate πθ with a criterion other than maximum likelihood. Relying on the link of our problem with density estimation under constraints, we propose to estimate πθ through the maximum entropy principle.
If there exists a π that can satisfy all constraints, i.e., if there exists a solution to Problem 2, the corresponding w belongs to the NPMLE polytope
. However, being derived from J distinct empirical distributions, the J constraints are in general inconsistent, and as in [9], we consider entropy maximization under relaxed constraints, i.e., Problem 4. For reasons of numerical efficiency, we consider the Rényi entropy H2.
Problem 5. (Relaxed ME estimator)
For ϵ ∈ ℝ+, define the -relaxed MaxEnt estimator as:
where ∑(j) is the covariance of the empirical estimate and is obtained from f(j) by retaining all but one of its non-zero elements.
We remark that the constraints in Problem 5, the relaxed MaxEnt problem that we solve, take into account the correlation between the observed frequencies, contrary to what is done in [9], where the degrees of relaxation of each constraint are fixed independently, as in Problem 4. As we will verify in Section 4 (see also the discussion around Figure 8), use of an inappropriate metric in the constraints directs the estimator towards sets of solutions that have have lower likelihood, resulting in a poor ability to reproduce the observed empirical moments.
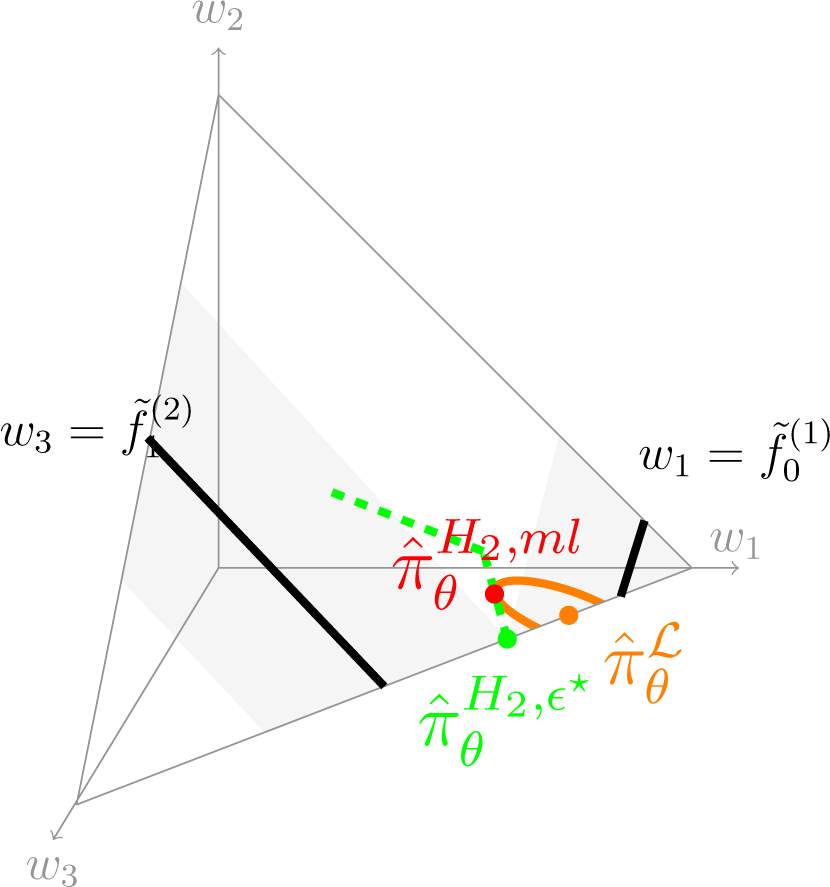
Figure 8.
Illustration of the three proposed estimators in a simple example.
Denote by ϵ⋆ ≥ 0 the smallest value of ϵ for which there exists a solution to Problem 5. Since in (13) we use the ℓ∞ metric to evaluate the deviation of a model π with respect to the empirical moments and ℓ∞ is not equivalent to the (Riemannian) metric induced by maximum likelihood in the simplex
, we cannot guarantee that likelihood is monotonically decreasing with the degree of relaxation, i.e., that
, for ϵ > ϵ⋆. In fact, as the plot of the log-likelihood of
as a function of ϵ/ϵ⋆ in Figure 7 shows, this is not necessarily true for values of ϵ close to ϵ⋆. More importantly, this figure shows that a suitable choice of the relaxation term can lead to a likelihood loss with respect to the NPMLE that is minimal, improving the fit to the data. These remarks motivate the definition of the new estimator proposed in this paper.
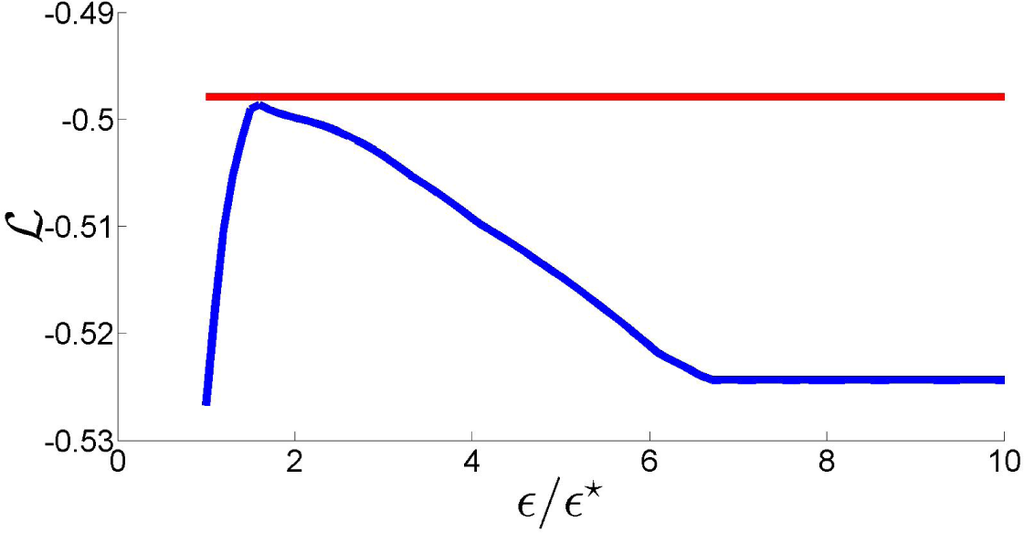
Figure 7.
Log likelihood variation of
as a function of ϵ/ϵ⋆. Red line:
.
Definition 4. (MLME: the most likely MaxEnt estimator)
Let denote the solution of Problem 5 for a generic ϵ ≥ ϵ⋆. The most likely Rényi-MaxEnt estimator is:
Proposition 5. (ϵ⋆ = 0)
If ϵ⋆ = 0, then the feasible set of the constrained optimization Problem 5 coincides with the NPMLE polytope. Since the likelihood of all solutions with ϵ > 0 will be smaller, the MLME estimate coincides in this case with the MaxEnt NPMLE:.
Since the probability that ϵ⋆ = 0 is small for finite datasets, the solution space of our constrained optimization problem is in general larger than the NPMLE polytope
. We illustrate now the geometry of the NLME
using the following simple example for which L = 1, J = 2, K = 3 and:
This choice allows us to represent graphically the elements of
; see Figure 8. The empirical moments (
,
,
,
) have been chosen such that the constraints are incompatible, avoiding the trivial case where
,
and
all coincide.
Figure 8 illustrates in
the geometry behind the MLME. Black lines
and
correspond to the constraints, which do not intersect since they are incompatible. For this example, the NPMLE (orange dot on the boundary of
, its second component being zero) is unique. All distributions that satisfy the minimally-relaxed constraints (i.e., with ϵ = ϵ⋆) belong to the two gray areas, their intersection defining
(the green dot, also on the boundary of
). The dashed green line is the curve defined by
in
for ϵ ≥ ϵ⋆, which has an accumulation point in the uniform distribution
as ϵ becomes sufficiently large for the uniform distribution to satisfy the constraints. Our estimator MLME is the point in this green curve at which the value of the likelihood is the largest, that is the highest level set of the likelihood function over
whose intersection with the green curve is a single point. The orange curve shows this level set, the contact point (red dot) being the MLME
.
The MLME estimator
corresponds in general to an ϵ > ϵ⋆ in the constraints (13). In terms of vector w of probabilities of the elementary regions Ek, this set is a polytope
, defined by its linear boundaries, which characterizes all solutions compatible with the data. One may notice that although the determination of its vertices is a difficult task, approximation of
by the maximum-volume interior ellipsoid is feasible at a reasonable computational cost [19], providing directly a lower bound on the volume of
.
Figure 9 shows the proposed estimator
for the same dataset as in Figure 6. Note that the distribution of the probability mass is much smoother than in Figure 6 and that the support of
is now the entire Θ. This example shows that the new estimator
is able to exploit the dual characteristics of the ML and MaxEnt criteria to produce an estimate that is not too informative while still fitting the observed data reasonably well.
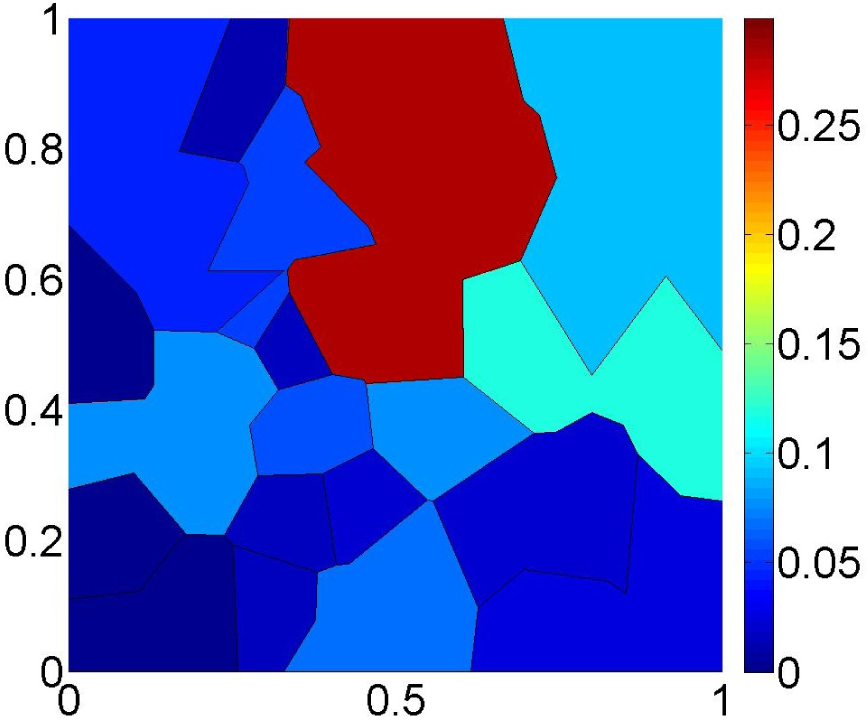
Figure 9.
.
Two common measures of the difference between two distributions are the Kolmogorov and the total variation distances. The Kolmogorov distance dK is the maximum value of the absolute difference between the two cumulative distributions, while the total variation distance dTV is the sum of all absolute differences [20]. Figure 10 addresses the performance of the estimation of the true probability law over
, showing box-plots of the Kolmogorov–Smirnov (left) and total variation (right) distances between
and the NPMLE and the MLME estimates observed in 200 simulations, each for N = 103 observations. In each plot, the box in the left corresponds to the MaxEnt-NPMLE estimator
and the one on the right to the the proposed estimator
. This clearly demonstrates the superiority of the estimator proposed in the paper. Note that the difference is more pronounced for the total variation, which is the criterion that best indicates the predictive power of the identified population model.
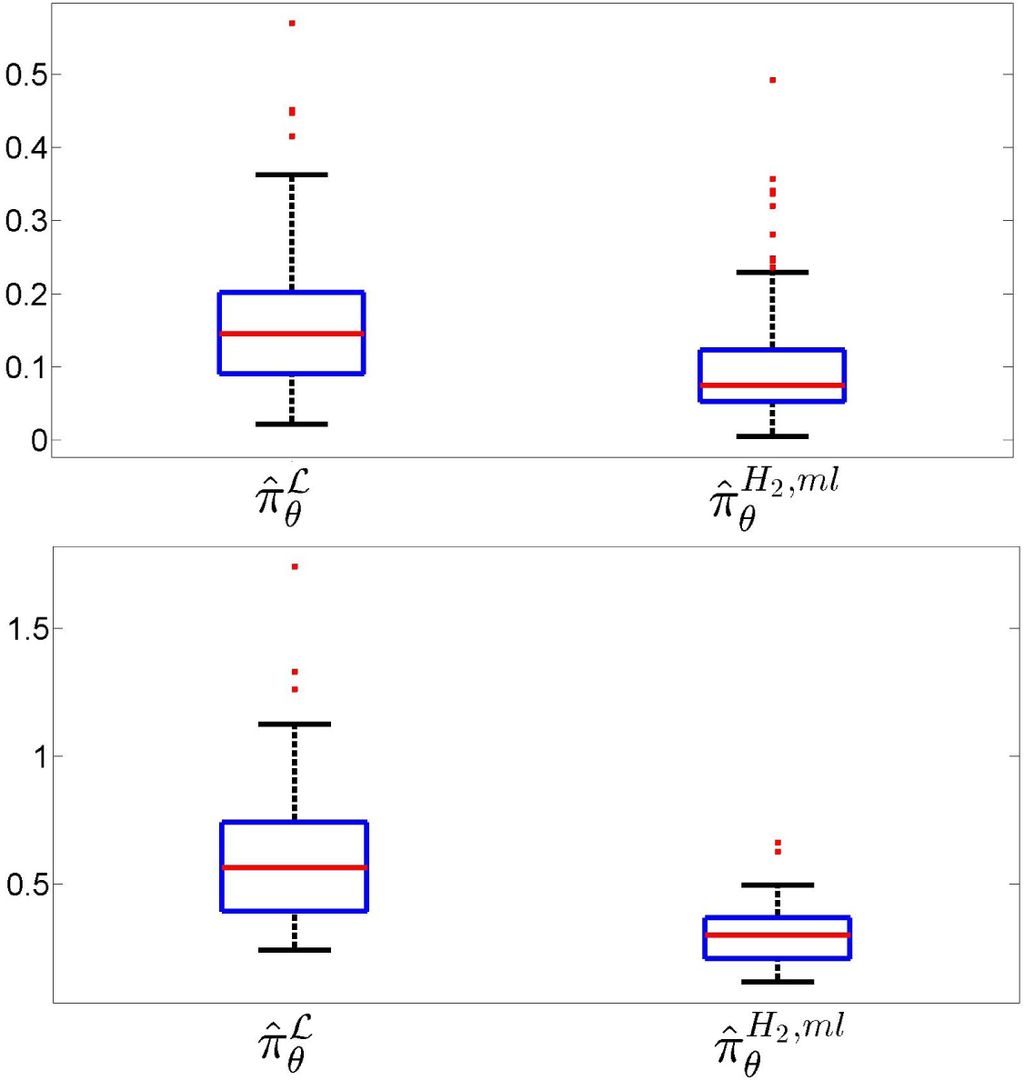
Figure 10.
Box-plots of the Kolmogorov–Smirnov (Top) and total variation (Bottom) distances between
and estimates
and
observed in 200 simulations.
Finally, Figure 11 shows the behavior under an increasing number of randomly-generated binary partitions. The total number of observations grows with J: N = 100J. The plots show the empirical average of the two Kullback–Leibler divergences D(·║πθ) (Figure 11a) and D(πθ║·) (Figure 11b) over 100 randomly-generated datasets for each value of J, with J varying from 10 to 100 in steps of 10. Here, the probability of “dangerous” partitions has been increased to 10−2, to guarantee a sufficient number of samples censored by them. Figure 11a suggests that
may be consistent, which is strongly contradicted by the behavior observed for the NPMLE. The divergence
was infinite in all simulations (due to
for some Ek ∈
) and, thus, cannot be presented in Figure 11b.
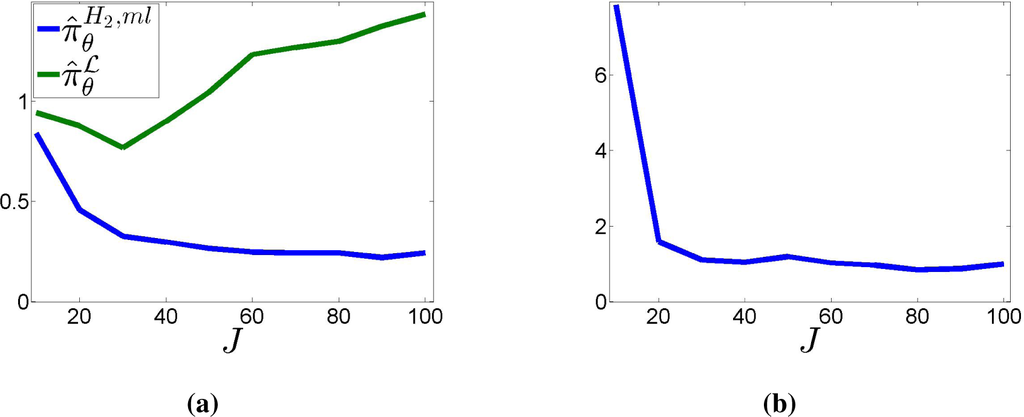
Figure 11.
Kullback–Leibler divergence for an increasing number J of partitions. (a) Empirical average of
and
; (b) empirical average of
.
4. Numerical Results
4.1. Application to a Real Problem: Modeling Decompression Sickness
The density estimation problem studied in this paper has been motivated by a problem of population analysis in the context of the prevention of decompression sickness (DCS) in deep sea diving, which is known to be highly correlated with the presence of gas bubbles in the diver’s blood. The ability to correctly predict the probability that this volume becomes exceedingly high can thus be exploited to establish safe diving rules, avoiding diving profiles (duration/depth) that may be dangerous for a non-negligible part of the population.
More precisely, we are interested in estimating the distribution πθ of the biophysical parameters θ of a mathematical model [21] for the instantaneous volume B(t) of micro-bubbles flowing through the right ventricle of a diver’s heart when executing a decompression profile P (t) (see Figure 12a):
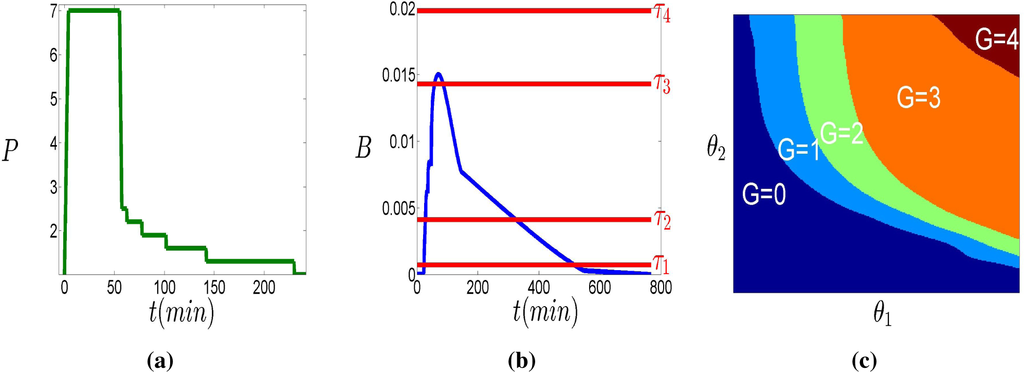
Figure 12.
Definition of bubble grades G and regions
. (a) Diving profile P (t); (b) blue: gas volume B; red: thresholds τℓ; (c) regions corresponding to the L+1 = 5 bubble grades G.
Gas presence in the diver’s circulatory system is only observed through “bubble grades”, which are strongly quantified samples of B(t) (the red horizontal lines in Figure 12b indicate the quantification levels
applied to B(t), represented by the blue curve). In our case L = 4, as shown in Figure 12b, and thresholds τ0 = 0 < τ1 < ⋯ < τL < τL+1 = ∞ are assumed known. Since it is usually accepted that DCS is related to the maximum observed grade, only the grade corresponding to the peak volume:
is retained, such that for each executed dive Dn where (the known) profile Pn has been followed by a diver with (unknown) bio-physical parameter θn, a single grade measure Gn is recorded:
In Figure 12, a simplified model with θ ∈ Θ ⊂ ℝ2, with Θ the rectangular colored region in Figure 12c, has been used, all other parameters of model (15) being held fixed. Note that all biophysical parameters θ in region Rn:
yield the same grade Gn for all dives that use profile Pn. Each diving profile P induces in this manner a partition
of Θ:
Figure 12c displays the regions corresponding to the L + 1 = 5 possible grade values for the profile P in Figure 12a. In this example, observation of a grade G = 3 indicates that the diver’s biophysical parameters θ belong to the orange region.
The dataset available for this study contains records of the bubble grades observed over a total of J = 19 distinct profiles, repeated a number nj of times ranging from 12 to 41 (see Table 1; the most dangerous profiles have been executed less often) and leads to the partition
shown in Figure 13. We remark on the strong dispersion of the sizes of the elements of
in this case, in particular the presence of very narrow regions that are contained in the elements of several partitions. The elements of
have in this case strongly elongated shapes, markedly different from the partitions built from Voronoi cells used in the simulations of the previous sections.

Table 1.
Number of experiments by profile in a real dataset.

Figure 13.
Partition induced by the 19 profiles in the real diving dataset.
4.1.1. Simulated Data
Before showing the results obtained in the real dataset of grade measures for the set of profiles available, we study the performance of the method proposed on the set of partitions corresponding to the set of observed profiles using simulated data. We considered the simulation of two normally and independent random variables restricted to a (biologically motivated) rectangular domain Θ. We kept the same nj as shown in Table 1 and, thus, the same total N = 433.
Figures 14 and 15 show the results obtained with a total of N = 104 observations. The singularity of both
and
, represented in Figure 14, is very strong in this case, the probability mass being concentrated in a subset of Θ of small Lebesgue measure. On the contrary, even for a partition of complex geometry like this one, the proposed MLME estimator (see Figure 15b) is able to overcome the shortcomings of the maximum-likelihood based estimates, producing an estimate that resembles the simulated law (in Figure 15a). The resulting population model has limited complexity while still retaining a superior predictive power, as is obvious from these plots.
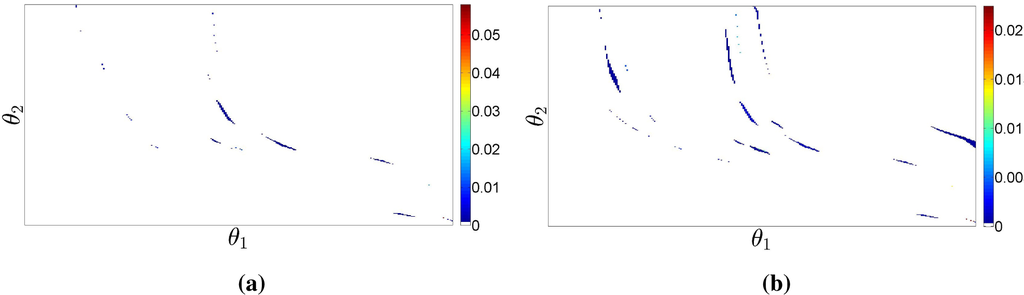
Figure 14.
(a) Rényi-MaxEnt NPMLE
. (b) Rényi-MaxEnt
. White regions have zero probability mass.
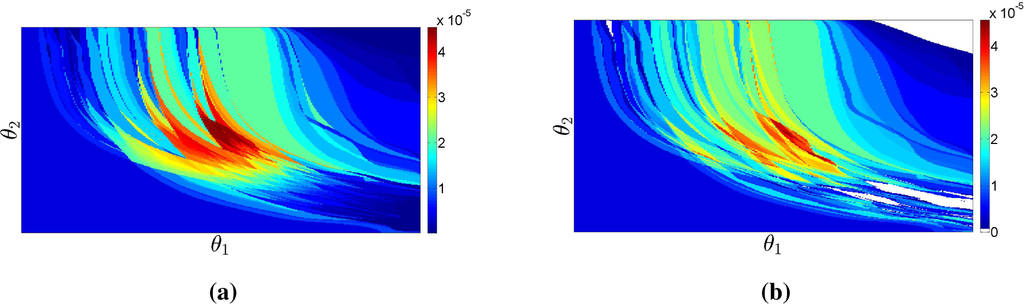
Figure 15.
(a) Simulated distribution
. (b) MLME estimate
. White regions have zero probability mass.
Figure 16 shows the evolution of the likelihood along the curve
, ϵ > ϵ⋆. We can see that the likelihood loss is larger than for the random partitions and that
is obtained for ϵ ≃ ϵ⋆. The larger likelihood loss can be explained by a smaller number of observations (N = 433 here, while for the previous simulation study N = 104) and also by the more irregular geometry of the partition
, with a large number of small elongated sets, which can produce over-optimistic values of the likelihood by concentrating mass over those sets.
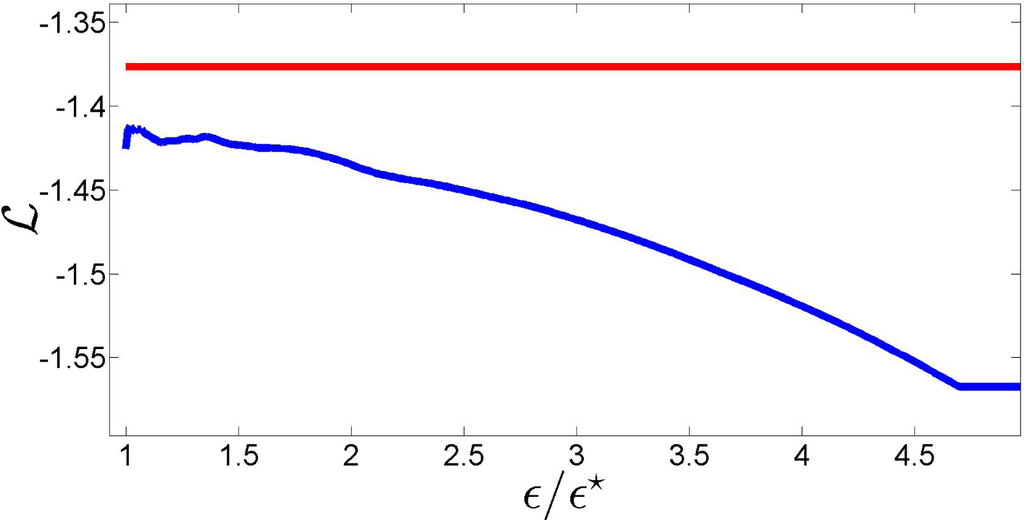
Figure 16.
Variation of
with ϵ/ϵ⋆ Red line:
.
4.1.2. Real Data (Part of the Material in this Section Has Been Previously Presented in [22])
Figure 17 shows the densities obtained for the real dataset by the three different estimators discussed in the previous sections: the least informative NPMLE
, the minimally-regularized MaxEnt estimate
and the new most likely MaxEnt estimate
. Analysis of this figure reveals the marked singularity of the first two estimates, which are highly concentrated in regions of small Lebesgue measure. The estimator proposed in the paper,
, leads to a much smoother solution, resembling
and covering nearly all of the domain, which seems to provide a more natural model of a biological population than the solution found by the two other estimators.
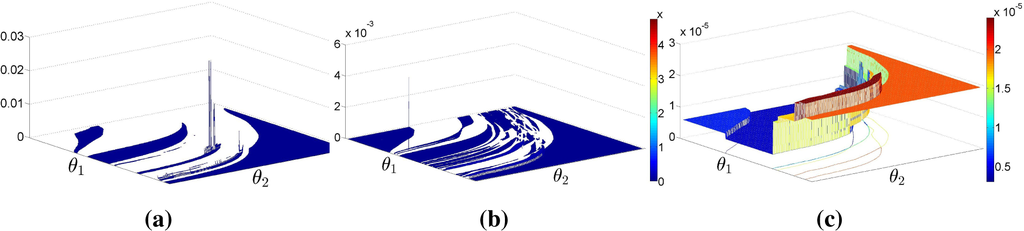
Figure 17.
Estimates of πθ with real dataset. (a) Least informative NPMLE
. (b) Rényi-MaxEnt
. (c) MLME
. White regions have zero probability mass.
For the dataset sizes of our study with Q = 665, we observed very fast convergence of (11) for the complete
(35 iterations for δ = 10−4), confirming the applicability of the proposed algorithm.
We now assess the likelihood loss of our solution. Figure 18 shows the variation of
with ϵ/ϵ⋆ for this real dataset. Compared to what we observed with random partitions in Figure 7, there is now a significant likelihood loss, the blue curve staying well below the maximum likelihood value for all values of the regularization parameter. This is natural, being an expected consequence of eventual misfits of the biophysical/classification model, which induce errors in the definition of the partitions
associated with the distinct profiles P(j) and, thus, compromise the ability to closely fit the data.
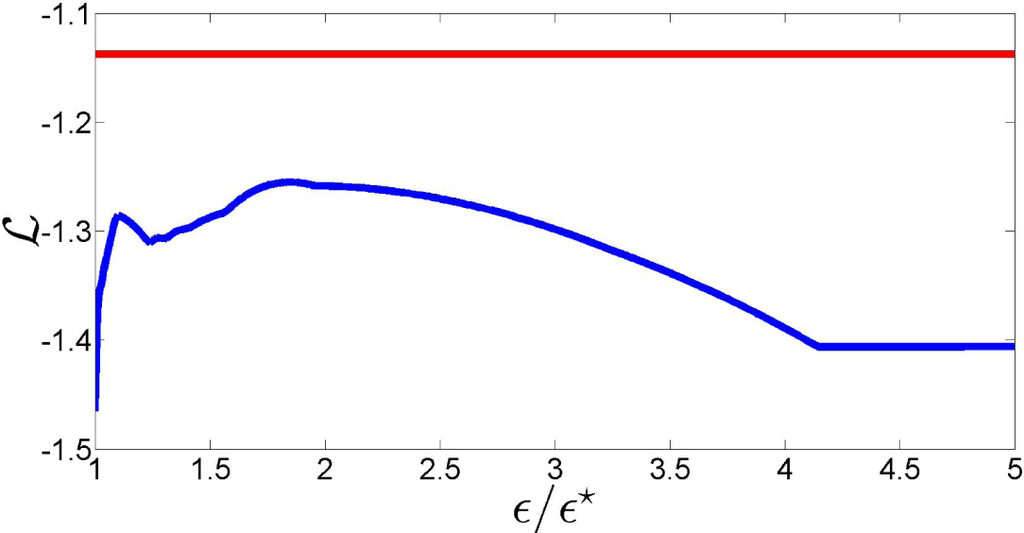
Figure 18.
Variation of
with ϵ/ϵ⋆ Red line:
.
Finally, we show, for this real dataset, the importance of accounting for the correlation of the empirical distributions in the constrained optimization problem. Figure 19 shows the estimates
(top) and
(bottom) obtained using the entire matrix Σ (left) or just its diagonal elements (right). We can see that simple independent relaxation of the empirical laws is not able to prevent the estimates from becoming highly concentrated, indicating an over-homogeneous population.
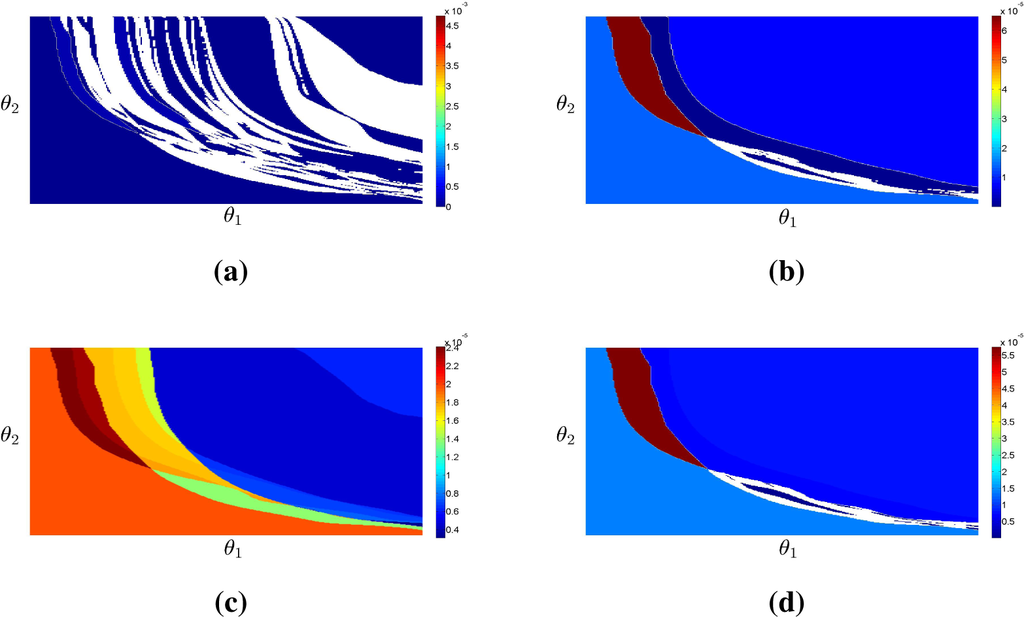
Figure 19.
(a)
, full
; (b)
; (c)
; full
; (d)
,
.
4.2. Assessing Predictive Power
To assess the predictive power of the three estimators
,
and
, we performed leave-one-out cross-validation, removing at each time all observations relative to one profile P(j) and computing the three estimators using the data for the remaining 18 profiles. We then compare the estimated and observed grades’ frequencies
for the retained profile.
Figure 20 represents boxplots of the total variation distance for each of the 19 profiles in the dataset, confirming the superiority of the estimator proposed for prediction purposes. In the sense of the total variation distance,
is on average the closest distribution to the empirical frequencies in the dataset.
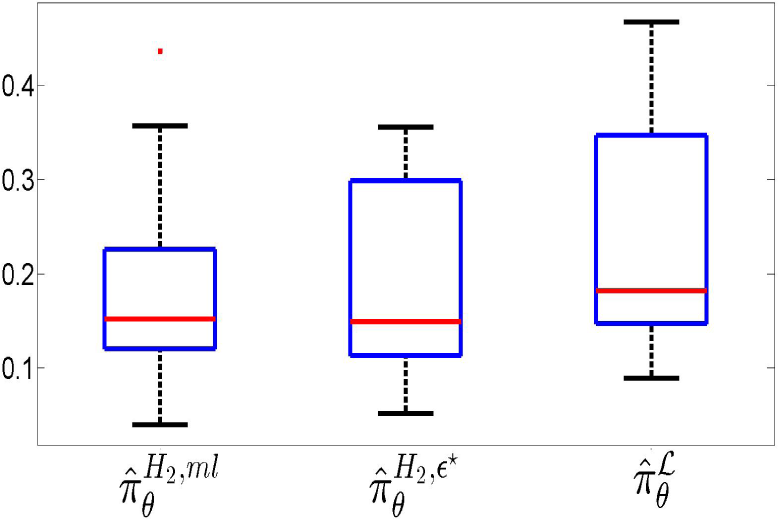
Figure 20.
Boxplots of the total variation distance dTV for the 19 datasets in the leave-on-out cross-validation study.
5. Conclusions
The paper studied the estimation of a probability density from region-censored observations, with application to the prevention of decompression sickness during hyperbaric diving. We show that the NPMLE is intrinsically ill-posed, leading to unstable solutions that are biologically implausible. Expressing counts of the censored observations as empirical means of a set of features, we derive the MaxEnt solution that best approximates the empirical distributions. The degree of fitting to the observed frequencies is chosen by selecting the MaxEnt solution that has the largest likelihood. The tests conducted show that the proposed most likely Rényi-MaxEnt estimator has superior behavior compared to the minimally-relaxed MaxEnt estimator, being able to approximate the observed dataset while at the same time being plausible as a description of a natural population. In particular, our numerical experiments show that our construction leads to a distribution estimate with good generalization properties, being able to predict grade probabilities for unseen profiles well, and can thus be used to detect profiles with a high risk of decompression sickness.
Acknowledgments
This work has been partially funded by contract SAFE-DIVE (Rapid, DGA/DGCIS) 122906109 EJThe authors acknowledge the support of Julien Hugon and Axel Barbaud (BF Systèmes, France) on the biophysical modeling of hyperbaric diving, as well as providing the dataset used for the study. They also thank the anonymous reviewers for their careful reading and constructive comments, which helped us to improve the quality of the manuscript.
Author Contributions
The work presented in this paper is carried out as part of the Ph.D. Thesis of Youssef Bennani, supervised by Luc Pronzato and Maria João Rendas. All authors have read and approved the final manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kaplan, E.L.; Meier, P. Nonparametric estimation from incomplete observations. J. Am. Stat. Assos. 1958, 53, 457–481. [Google Scholar]
- Turnbull, B.W. The empirical distribution function with arbitrarily grouped, censored and truncated data. J. R. Stat. Soc. Ser. B (Methodol.) 1976, 38, 290–295. [Google Scholar]
- Gentleman, R.; Vandal, A.C. Computational algorithms for censored-data problems using intersection graphs. J. Comput. Graph. Stat. 2001, 10, 403–421. [Google Scholar]
- Bennani, Y. Intersection Graph for Region-Censored Data; Rapport de recherche I3S; I3S: Sophia-Antipolis, France, 2013. [Google Scholar]
- Jaynes, E.T. Information theory and statistical mechanics. Phys. Rev. 1957, 106, 620–630. [Google Scholar]
- Della Pietra, S.; Della Pietra, V.; Lafferty, J. Inducing features of random fields. IEEE Trans. Pattern Anal. Mach. Intell. 1997, 19, 380–393. [Google Scholar]
- Grechuk, B.; Molyboha, A.; Zabarankin, M. Maximum entropy principle with general deviation measures. Math. Oper. Res. 2009, 34, 445–467. [Google Scholar]
- Dudik, M. Maximum Entropy Density Estimation and Modeling of Geographic Distributions of Species. Ph.D. Thesis, Princeton University, Princeton, NJ, USA, 2007. [Google Scholar]
- Dudik, M.; Phillips, M.; Schapire, R. Performance guarantees for regularized maximum entropy density estimation. Proceedings of the 17th Annual Conference on Computational Learning Theory, Banff, AL, Canada, 1–4 July 2004.
- Járai-Szabó, F.; Néda, Z. On the size-distribution of Poisson Voronoi cells. Physica A 2007, 385, 518–526. [Google Scholar]
- Liu, X. Nonparametric Estimation With Censored Data: A Discrete Approach. Ph.D. Thesis, McGill University, Montreal, QC, Canada, 2005. [Google Scholar]
- Groeneboom, P.; Wellner, J.A. Information Bounds and Nonparametric Maximum Likelihood Estimation; Birkhauser Verlag: Basel, Switzerland, 1992. [Google Scholar]
- Böhning, D.; Schlattmann, P.; Dietz, E. Interval censored data: A note on the nonparametric maximum likelihood estimator of the distribution function. Biometrika 1996, 83, 462–466. [Google Scholar]
- Fish, D.; Brinicombe, A.; Pike, E.; Walker, J. Blind deconvolution by means of the Richardson–Lucy algorithm. JOSA A 1995, 12, 58–65. [Google Scholar]
- Fedorov, V.V. Theory of Optimal Experiments; Academic Press: New York, NY, USA, 1972. [Google Scholar]
- Silvey, S.D.; Titterington, D.H.; Torsney, B. An algorithm for optimal designs on a finite design space. Commun. Stat.-Theor. M. 1978, 7, 1379–1389. [Google Scholar]
- Torsney, B. A moment inequality and monotonicity of an algorithm. In Semi-Infinite Programming and Applications; Springer: Berlin, Germany, 1983; pp. 249–260. [Google Scholar]
- Harman, R.; Pronzato, L. Improvements on removing nonoptimal support points in D-optimum design algorithms. Stat. Probab. Lett. 2007, 77, 90–94. [Google Scholar]
- Khachiyan, L.G.; Todd, M.J. On the complexity of approximating the maximal inscribed ellipsoid for a polytope. Math. Program 1993, 61, 137–159. [Google Scholar]
- Strassen, V. The existence of probability measures with given marginals. Ann. Math. Stat. 1965, 36, 423–439. [Google Scholar]
- Hugon, J. Vers Une Modélisation Biophysique De La Décompression. Ph.D. Thesis, Université Aix Marseille, Aix-en-Provence, France, 22 November 2010. [Google Scholar]
- Bennani, Y.; Pronzato, L.; Rendas, M.J. Nonparametric density estimation with region-censored data, Proceedings of the 22nd European Signal Processing Conference (EUSIPCO), Lisbon, Portugal, 1–5 September 2014; pp. 1098–1102.
© 2015 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).