Entropy-Based Privacy against Profiling of User Mobility
Abstract
:1. Introduction
- Jaynes’ rationale on maximum entropy methods [4,5] enables us [6] to measure the privacy of confidential data modeled by a probability distribution by means of its Shannon entropy. In particular, one may measure the anonymity of a user’s behavioral profile as the entropy of a relative histogram of online activity along predefined categories of interest. Inspired by this principle, we propose the use of Shannon’s entropy to measure the privacy of a sequence of places of interest visited by a user (which we will refer to as the user’s locations profile), with the caveat that this may only be appropriate for a series of statistically-independent, identically-distributed outcomes.
- Taking this a step further, we tackle the case in which a sequence of location data is more adequately modeled as a stochastic process with memory, representing the (entire or recent) history of a user moving across predefined, discretized locations. We propose extending the more traditional measure of privacy by means of Shannon’s entropy, to the more general information-theoretic quantity known as the entropy rate, which quantifies the amount of uncertainty contained in a process with memory. In other words, we put forth the notion of entropy rates as the natural extension of Jaynes’ rationale from independent outcomes to time series. Concordantly, we propose the entropy rate as a novel, more adequate measurement of privacy of what we will call user mobility profiles: profiles capturing sequential behavior in which current activity is statistically dependent on the past, as is commonly the case for location data.
- The extension from location to mobility profiles requires a reconsideration of the privacy preserving mechanisms. We propose two simple perturbative methods, previously used for web search applications, looking for their suitability in these two profiling scenarios.
- Finally, we compare the results of calculating the privacy metrics proposed for different theoretical processes of increasing memory, to finally analyze a real location and mobility profile, made up of cell-based locations, which shows the usefulness of the proposed privacy metric. The work ends up with a discussion of different aspects impacting the privacy level obtained and further considerations to improve it in mobility profiling scenarios.
2. Related Work
2.1. User Mobility Profiles
2.2. Privacy-Enhancing Technologies for LBSs
2.3. Privacy Metrics for Data Perturbation against User Profiling
3. Entropic Measures of User Privacy, the Adversary Model and Perturbative Mechanisms
3.1. User Mobility Profiling and the Adversary Model
3.1.1. Location Profile
- Definition (location profile): Let L be a random variable (r.v.) representing the location of a given user, from an alphabet of predefined location categories . The time of the location referred to is chosen uniformly at random. We model the location profile of said user as the probability distribution of L; precisely, the probability mass function (PMF) pL of the discrete r.v. L. Thus, pL(l) is the probability that the user is at location at any given time. In other words, pL(l) represents the relative frequency with which the user visits this location.
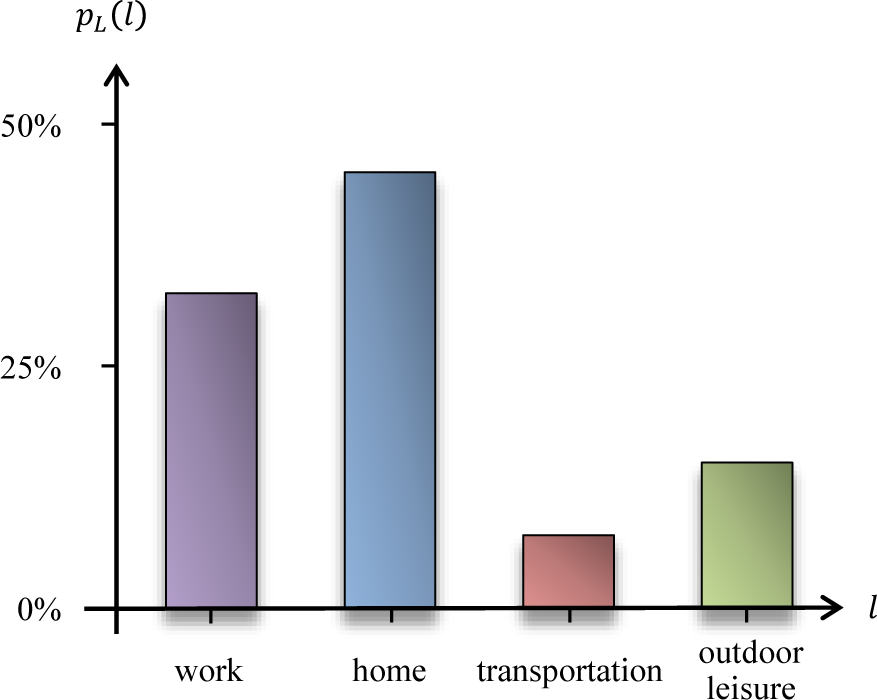
- Example: Examples of location categories that may characterize the behavioral profile of a user include categories, such as “work”, “home”, “car”, “subway”, “restaurant”, “movie theater” and “out of town”. These could be inferred from geographical locations with the help of an appropriate map. Figure 2 depicts a simple example of a location profile on a location alphabet with a few categories.
- Adversary model: The adversary model for the location profile is, in this case, estimating the visit probability distribution as accurately as possible, by inspecting the locations attached to the LBS requests. To this end, the adversary could utilize a maximum likelihood estimate of the distribution, directly as the histogram of relative frequencies, simply by counting observed locations, or any other well-known statistical techniques for the estimation of probability distributions, such as additive or Laplace smoothing.
3.1.2. Mobility Profile
- Definition (mobility profile): More precisely, for each user, we define a stochastic process (Lt)t=1,2,… representing the sequence of categorized locations over discretized time instants t = 1, 2, … Concordantly, the corresponding location Lt at time t is a discrete r.v. on the alphabet of predefined location categories introduced earlier. We define the mobility profile of the user as the joint probability distribution of locations over time,which may be equivalently expressed, by the chain rule of probabilities, as the sequence of conditional PMFs of the current location Lt given the past location history Lt−1, Lt−2, …, i.e.,Discretized times could be defined in terms of fixed time intervals, such as hours or fractions thereof, or more simply, but less informatively, as times relative to a change in activity of the user, so that the actual logged data are the order of the given locations in time, but not their duration.
- Example: Following up with the simple example of Figure 2, with location alphabet , the mobility profile now incorporates time information, in the form of fixed time intervals, say 15 min. In this manner, one could record the average time spent at work, at home, on the road or at various types of outdoor leisure activities and also the mobility patterns involving said locations. With a more detailed location alphabet, one may detect that a user predictably goes to work directly from home, or to the movies, or to a restaurant after work on a given day of the week.
- Adversary model: The mobility profile, characterized by the probability distribution of categorized locations across time, serves to effectively model the knowledge of an adversary about the future locations of a user and raises the concern that motivates our contribution. Since predictability is directly linked to the entropy rate of the mobility profile as a stochastic process, rather than the entropy (the higher the entropy rate, the lower the predictability, as shown in [3]), we could use this information theory concept in order to quantify the privacy of the user mobility profile in such a way that the less predictable a user is (the higher her entropy rate is), the higher her mobility profile privacy will be.
3.2. Privacy Model and Additional Discussion on Entropy and the Entropy Rate as Privacy Measures
3.3. Perturbative Mechanisms
4. Theoretical Analysis of Perturbative Methods and the Entropy-Based Privacy Metric
4.1. Notation and Information-Theoretic Preliminaries
4.2. Perturbative Mechanisms
- Uniform replacement: is drawn uniformly from .
- Improved replacement: is drawn according to the distribution obtained as the solution to the maximum-entropy problem of [38].
4.2.1. Uniform Replacement
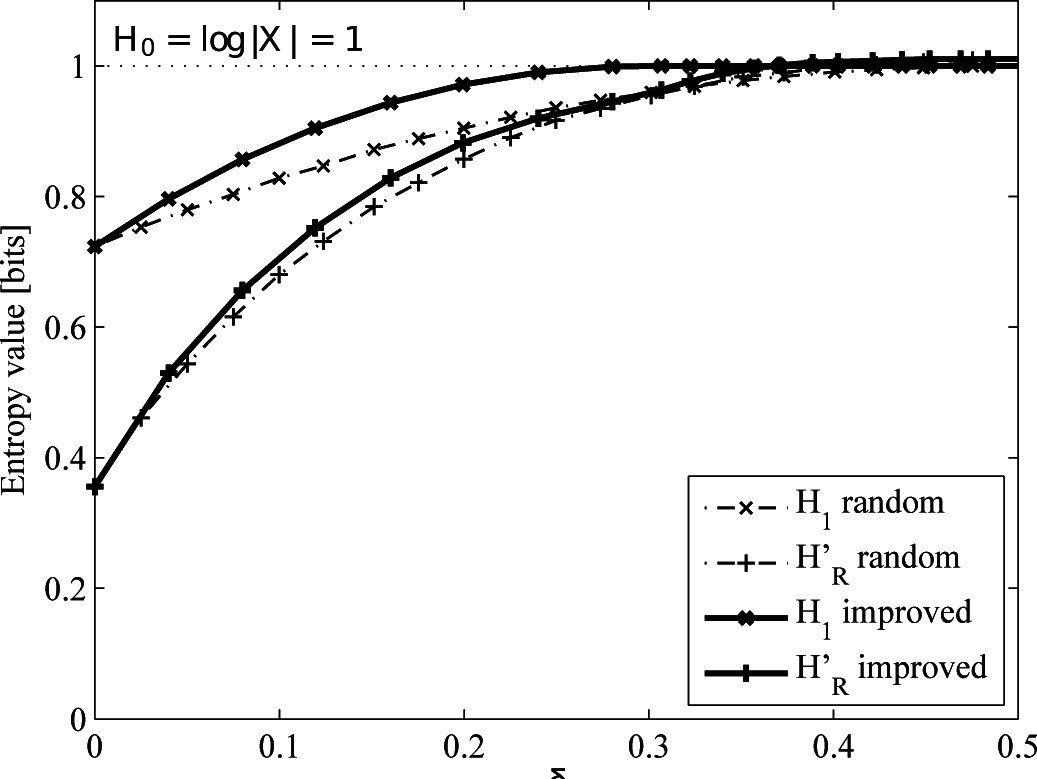
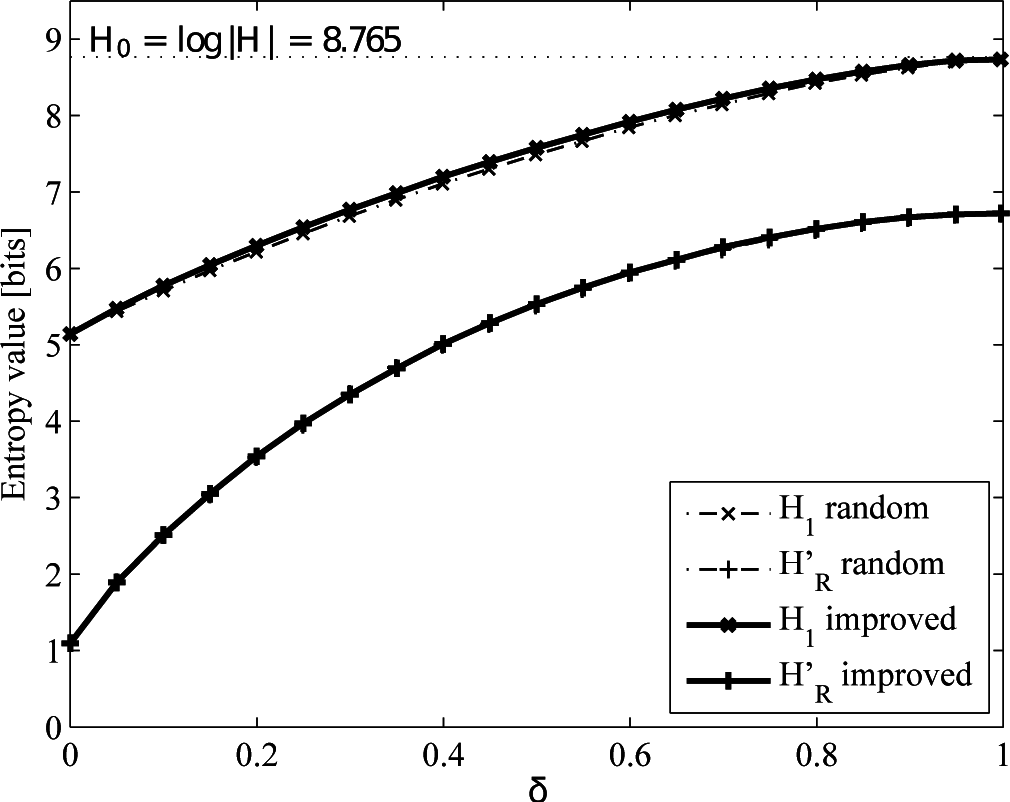
4.2.2. Uniform versus Improved Replacement
4.3. Entropy Estimation
- Hartley entropy, H0(X), is the maximum attainable entropy value. We should recall that entropy is maximized for the uniform distribution and for this distribution only and that the maximum attained is the logarithm of the cardinality of the alphabet. Put mathematically:with equality if and only if X is drawn from the uniform distribution. Applied to our case, it would be calculated considering the probability mass function of the locations trace (since no temporal dependencies are considered) to be a uniform distribution of different symbols (locations). This entropy represents the highest possible uncertainty, as it does not take into account temporal aspects nor the number of visits accumulated by each location.
- Shannon entropy, H1(X), is calculated as:In our scenario, pX(xi) is the probability of visiting location xi, which can be computed as , where is the number of visits received by location xi, and N is the total number of visits (i.e., the length of the movement history). Shannon entropy considers the correlations in the location visits frequencies, thus being lower (or equal if the probability to visit each location is the same) than H0(X). Actually, this entropy would be lower than H0(X), such a PMF being less uniform (i.e., as some locations receive many more visits than other ones). Location profiles (because no temporal dependencies are considered) behave precisely like this: some locations corresponding to home or work unite the majority of visits, whilst the rest of the locations are much less visited.
- Entropy rate, HR(X), comes to the scene when dealing with stationary processes, as pointed out in Section 4.1. It takes into account temporal dependencies between samples of the mobility profile (in this case, we consider the mobility instead of the locations profile, because the time dependencies must be considered). Since HR(X) takes into account more correlations of the profile, the resulting value is lower than the previous ones (there is less uncertainty regarding the next symbol of the profile) or equal if there are no temporal dependencies.Applied to our case, we have a finite number of samples of the profile. Therefore, in order to obtain a good estimate of HR(X), we should choose the optimal block size, n. This block size should be large enough so that the blocks include important long-term temporal dependencies among location samples. However, since the length of the process (i.e., mobility profile) is limited and the cardinality of the alphabet (i.e., the number of different locations) is high, there are not many samples of long blocks. Thus, choosing a block size too large leads to a poor estimate of pX(X1, …, Xn). In order to use an appropriate value of n, we could use a well-known entropy rate estimator based on Lempel–Ziv compression algorithms [3,57]. This way, the estimate of the entropy rate can be calculated as:where Δi is the shortest substring starting at position i, which has not been seen before from Position 1 to i − 1, N being the number of samples of the profile.
5. Experimental Study: Results and Discussion
5.1. Results
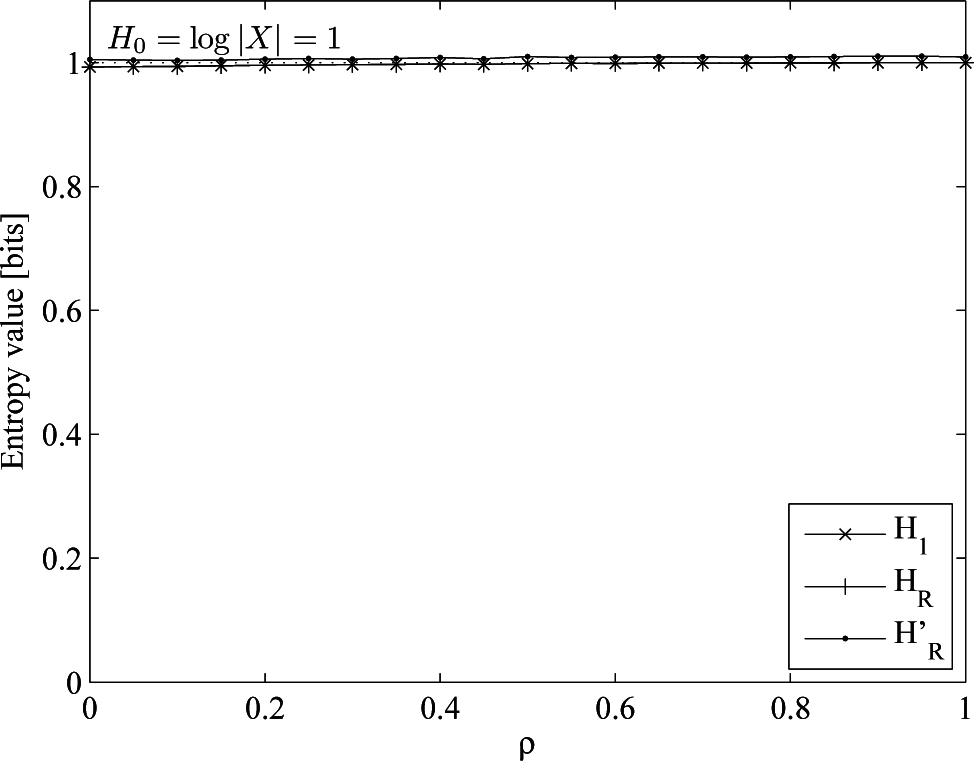
- An almost uniform distribution, drawn from an order-one Markov process with p(1|0) = 0.45, p(0|1) = 0.55, p(1) = 0.55, H0 = H1 = HR = 0.993. This is the base case.
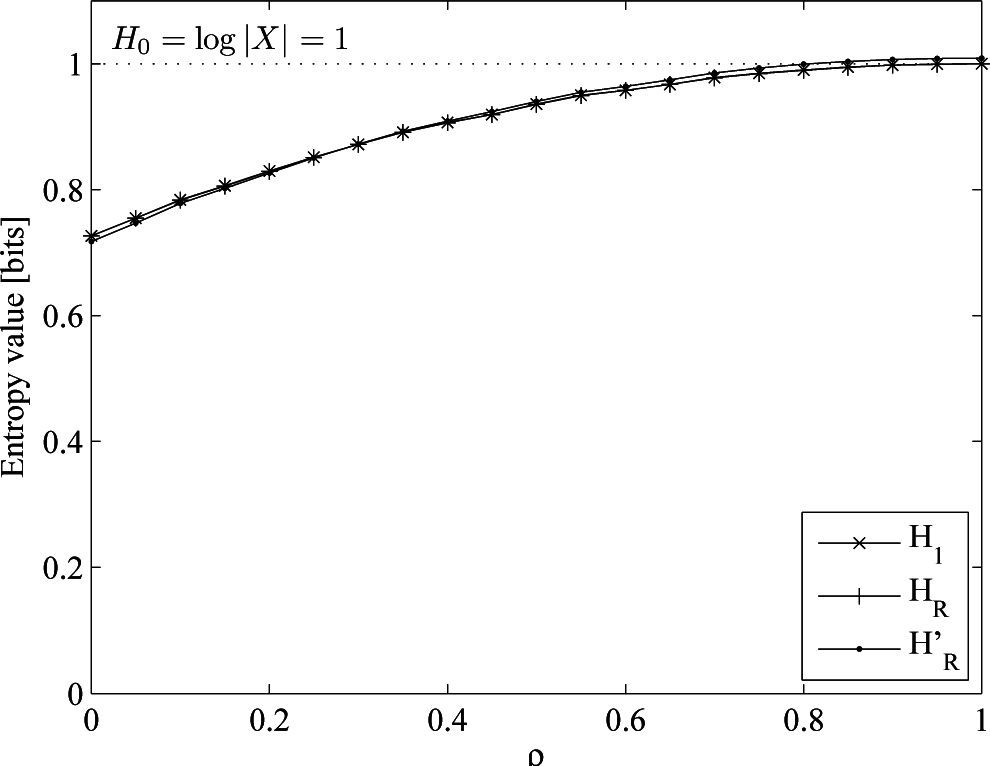
- An i.i.d. (not uniform) process, drawn from an order-one Markov process with p(1|0) = 0.8, p(0|1) = 0.2, p(1) = 0.8, H0 = 1, H1 = HR = 0.772. Here, we keep the process memoryless and change the probability distribution, such that there is a bias towards one of the two symbols of the alphabet.
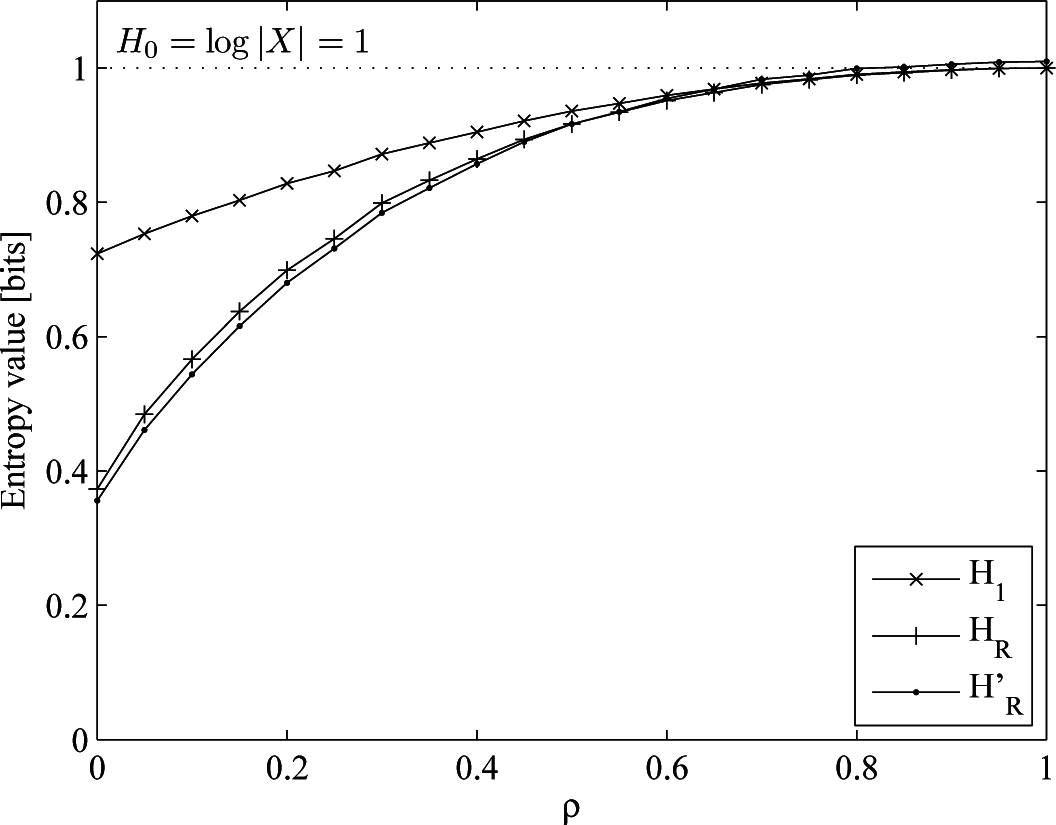
- A Markov process with p(1|0) = 0.2, p(0|1) = 0.05, p(1) = 0.8, H0 = 1, H1 = 0.772, HR = 0.374. In this case, we increase the memory of the process, keeping the cardinality and probability distribution with respect to the second case.
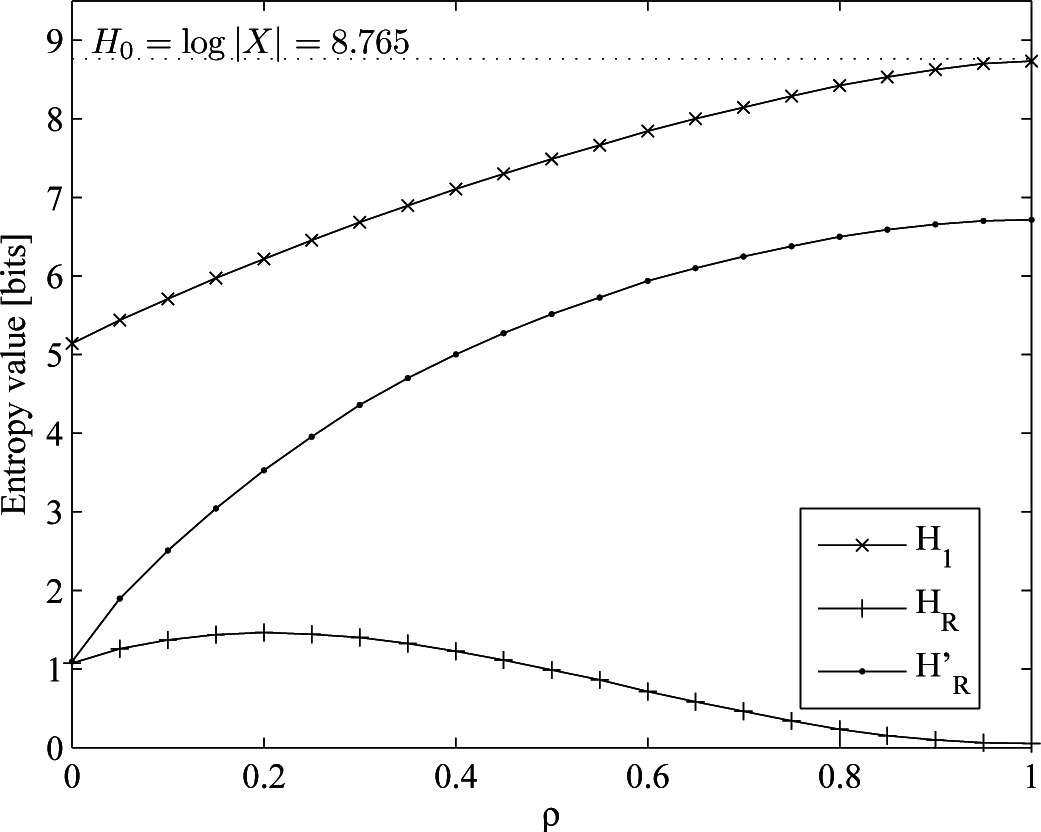
- A real mobility trace taken from the dataset provided by the Reality Mining Project [58]. We can only theoretically know H0 = 8.765 (drawn from the cardinality of the alphabet, i.e., the number of different symbols representing the locations visited by the user), since the underlying probability distribution is unknown. This means an increase both in the cardinality and the memory of the process, due to the long-range dependencies of human mobility.
5.2. Discussion
6. Conclusions and Future Work
Author Contributions
Conflicts of Interest
Appendix
A. Proof of Lemma 1
B. Proof of Theorem 1
C. Proof of Theorem 2
Acknowledgments
References
- Danezis, G. Introduction to Privacy Technology; Katholieke University Leuven, COSIC: Leuven, Belgium, 2007. [Google Scholar]
- Dingledine, R. Free Haven’s Anonymity Bibliography; Free Haven Project; Massachusetts Institute of Technology: Massachusetts, MA, USA, 2009. [Google Scholar]
- Song, C.; Qu, Z.; Blumm, N.; Barabási, A.L. Limits of Predictability in Human Mobility. Science 2010, 327, 1018–1021. [Google Scholar]
- Jaynes, E.T. On the Rationale of Maximum-Entropy Methods. Proc. IEEE 1982, 70, 939–952. [Google Scholar]
- Jaynes, E.T. Information Theory Statistical Mechanics II. Phys. Rev. 1957, 108, 171–190. [Google Scholar]
- Parra-Arnau, J.; Rebollo-Monedero, D.; Forné, J. Measuring the privacy of user profiles in personalized information systems. Future Gen. Comput. Syst. 2014, 53–63. [Google Scholar]
- Wicker, S.B. The Loss of Location Privacy in the Cellular Age. Commun. ACM 2012, 55, 60–68. [Google Scholar]
- De Mulder, Y.; Danezis, G.; Batina, L.; Preneel, B. Identification via Location-profiling in GSM Networks, Proceedings of the 7th ACM Workshop on Privacy in the Electronic Society (WPES ’08), Alexandria, VA, USA, 27 October 2008; ACM: New York, NY, USA, 2008; pp. 23–32.
- Freudiger, J.; Shokri, R.; Hubaux, J.P. Evaluating the Privacy Risk of Location-based Services, Proceedings of the 15th International Conference on Financial Cryptography and Data Security, Gros Islet, St. Lucia, 28 February–4 March 2011; Springer-Verlag: Berlin, Germany, 2012; pp. 31–46.
- Shokri, R.; Theodorakopoulos, G.; Le Boudec, J.Y.; Hubaux, J.P. Quantifying Location Privacy, Proceedings of the 2011 IEEE Symposium on Security and Privacy (SP), Berkeley, CA, USA, 22–25 May 2011; pp. 247–262.
- Hsu, W.j.; Dutta, D.; Helmy, A. Structural analysis of user association patterns in university campus wireless lans. IEEE Trans. Mobile Comput. 2012, 11, 1734–1748. [Google Scholar]
- Gonzalez, M.C.; Hidalgo, C.A.; Barabasi, A.L. Understanding individual human mobility patterns. Nature 2008, 453, 779–782. [Google Scholar]
- Sricharan, M.; Vaidehi, V. User Classification Using Mobility Patterns in Macrocellular Wireless Networks, Proceedings of the 2011 International Symposium on Ad Hoc and Ubiquitous Computing, 2006 (ISAUHC ’06), Surathkal, India, 20–23 December 2006; pp. 132–137.
- Sun, B.; Yu, F.; Wu, K.; Xiao, Y.; Leung, V. Enhancing security using mobility-based anomaly detection in cellular mobile networks. IEEE Trans. Veh. Technol. 2006, 55, 1385–1396. [Google Scholar]
- Rallapalli, S.; Dong, W.; Lee, G.M.; Chen, Y.C.; Qiu, L. Analysis and applications of smartphone user mobility, In Proceedings of the 2013 IEEE Conference on Computer Communications Workshops (INFOCOM WKSHPS), Turin, Italy, 14–19 April 2013; pp. 235–240.
- Chen, X.; Pang, J.; Xue, R. Constructing and comparing user mobility profiles. ACM Trans. Web (TWEB) 2014, 8, 21. [Google Scholar]
- Pham, N.; Cao, T. A. Spatio-Temporal Profiling Model for Person Identification. In Knowledge and Systems Engineering; Springer: Berlin, Germany, 2014; pp. 363–373. [Google Scholar]
- Samarati, P.; Sweeney, L. Protecting privacy when disclosing information: k-Anonymity and its enforcement through generalization and suppression, Proceedings of the IEEE Symposium on Research in Security and Privacy, Oakland, CA, USA, 3–6 May 1998.
- Samarati, P. Protecting respondents’ identities in microdata release. IEEE Trans. Knowl. Data Eng. 2001, 13, 1010–1027. [Google Scholar]
- Truta, T.M.; Vinay, B. Privacy protection: p-Sensitive k-anonymity property, Proceedings of the IEEE 22nd International Conference on Data Engineering Workshops (ICDEW), Atlanta, GA, USA, 3–7 April 2006; p. 94.
- Sun, X.; Wang, H.; Li, J.; Truta, T.M. Enhanced p-sensitive k-anonymity models for privacy preserving data publishing. Trans. Data Priv. 2008, 1, 53–66. [Google Scholar]
- Machanavajjhala, A.; Gehrke, J.; Kiefer, D.; Venkitasubramanian, M. l-Diversity: Privacy beyond k-anonymity, Proceedings of the IEEE 22nd International Conference on Data Engineering (ICDE), Atlanta, GA, USA, 3–7 April 2006; p. 24.
- Dwork, C. Differential privacy. In Encyclopedia of Cryptography and Security; Springer: Berlin, Germany, 2011; pp. 338–340. [Google Scholar]
- Ho, S.S.; Ruan, S. Differential privacy for location pattern mining, Proceedings of the 4th ACM SIGSPATIAL International Workshop on Security and Privacy in GIS and LBS, Chicago, IL, USA, 1–4 November 2011; pp. 17–24.
- Chen, R.; Acs, G.; Castelluccia, C. Differentially private sequential data publication via variable-length n-grams, Proceedings of the 2012 ACM Conference on Computer and Communications Security, Raleigh, NC, USA, 16–18 October 2012; pp. 638–649.
- Bordenabe, N.E.; Chatzikokolakis, K.; Palamidessi, C. Optimal geo-indistinguishable mechanisms for location privacy, Proceedings of the 2014 ACM SIGSAC Conference on Computer and Communications Security, Scottsdale, AZ, USA, 3–7 November 2014; pp. 251–262.
- Chatzikokolakis, K.; Palamidessi, C.; Stronati, M. A predictive differentially-private mechanism for mobility traces. In Privacy Enhancing Technologies; Springer: Berlin, Germany, 2014; pp. 21–41. [Google Scholar]
- Shokri, R.; Theodorakopoulos, G.; Papadimitratos, P.; Kazemi, E.; Hubaux, J.P. Hiding in the Mobile Crowd: LocationPrivacy through Collaboration. IEEE Trans. Dependable Secur. Comput. 2014, 11, 266–279. [Google Scholar]
- Olteanu, A.M.; Huguenin, K.; Shokri, R.; Hubaux, J.P. Quantifying the effect of co-location information on location privacy. In Privacy Enhancing Technologies; Springer, 2014; pp. 184–203. [Google Scholar]
- Deng, M. Privacy Preserving Content Protection. Ph.D. Thesis, Department of Electrical Engineering, Katholieke Univivresity Leuven, Leuven, Belgium, 2010. [Google Scholar]
- Duckham, M.; Mason, K.; Stell, J.; Worboys, M. A formal approach to imperfection in geographic information. Comput. Environ. Urban Syst. 2001, 25, 89–103. [Google Scholar]
- Duckham, M.; Kulit, L. A Formal Model of Obfuscation and Negotiation for Location Privacy. Proceedings of the 3rd International Conference on Pervasive Computing, Munich, Germany, 8–13 May 2005; Springer-Verlag: Berlin, Germany, 2005; 3468, pp. 152–170. [Google Scholar]
- Ardagna, C.A.; Cremonini, M.; Damiani, E.; De Capitani di Vimercati, S.; Samarati, P. Location Privacy Protection Through Obfuscation-Based Techniques, Proceedings of the Working Conference on Data and Applications Security, Redondo Beach, CA, USA, 8–11 July 2007; Springer-Verlag: Berlin, Germany, 2007; 4602, pp. 47–60.
- Yiu, M.L.; Jensen, C.S.; Huang, X.; Lu, H. SpaceTwist: Managing the trade-offs among Location Privacy, Query Performance, and Query Accuracy in Mobile Services, Proceedings of the IEEE 24th International Conference on Data Engineering, 2008,(ICDE 2008), Cancun, Mexico, 7–12 April 2008; pp. 366–375.
- Kuflik, T.; Shapira, B.; Elovici, Y.; Maschiach, A. Privacy preservation improvement by learning optimal profile generation rate. In User Modeling; Springer-Verlag: Berlin, Germany, 2003; Volume 2702, pp. 168–177. [Google Scholar]
- Elovici, Y.; Glezer, C.; Shapira, B. Enhancing customer privacy while searching for products and services on the World Wide Web. J. Med. Internet Res. 2005, 15, 378–399. [Google Scholar]
- Shapira, B.; Elovici, Y.; Meshiach, A.; Kuflik, T. PRAW—The model for PRivAte Web. J. Am. Soc. Inf. Sci. Technol. 2005, 56, 159–172. [Google Scholar]
- Rebollo-Monedero, D.; Forné, J. Optimal Query Forgery for Private Information Retrieval. IEEE Trans. Inf. Theory 2010, 56, 4631–4642. [Google Scholar]
- Parra-Arnau, J.; Rebollo-Monedero, D.; Forné, J. Optimal Forgery and Suppression of Ratings for Privacy Enhancement in Recommendation Systems. Entropy 2014, 16, 1586–1631. [Google Scholar]
- Theodorakopoulos, G.; Shokri, R.; Troncoso, C.; Hubaux, J.P.; Le Boudec, J.Y. Prolonging the Hide-and-Seek Game: Optimal Trajectory Privacy for Location-Based Services, Proceedings of the 13th Workshop on Privacy in the Electronic Society, Scottsdale, AZ, USA, 3–7 November 2014; pp. 73–82.
- Rebollo-Monedero, D.; Parra-Arnau, J.; Diaz, C.; Forné, J. On the Measurement of Privacy as an Attacker’s Estimation Error. Int. J. Inf. Secur 2013, 12, 129–149. [Google Scholar]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory, 2nd ed; Wiley: New York, NY, USA, 2006. [Google Scholar]
- Serjantov, A.; Danezis, G. Towards an Information Theoretic Metric for Anonymity, Proceedings of the 2nd International Conference on Privacy Enhancing Technologies (PET), San Francisco, CA, USA, 14–15 April 2002; Springer-Verlag: Berlin, Germany, 2002; 2482, pp. 41–53.
- Díaz, C.; Seys, S.; Claessens, J.; Preneel, B. Towards measuring anonymity, Proceedings of the 2nd International Conference on Privacy Enhancing Technologies (PET), San Francisco, CA, USA, 14–15 April 2002; Springer-Verlag: Berlin, Germnay, 2002; 2482, pp. 54–68.
- Díaz, C. Anonymity and Privacy in Electronic Services. Ph.D. Thesis, Katholieke Universiteit Leuven, Leuven, Belgium, 2005. [Google Scholar]
- Oganian, A.; Domingo Ferrer, J. A posteriori disclosure risk measure for tabular data based on conditional entropy. SORT 2003, 27, 175–190. [Google Scholar]
- Voulodimos, A.S.; Patrikakis, C.Z. Quantifying privacy in terms of entropy for context aware services. Identity Inf. Soc. 2009, 2, 155–169. [Google Scholar]
- Alfalayleh, M.; Brankovic, L. Quantifying Privacy: A Novel Entropy-Based Measure of Disclosure Risk 2014, arXiv, 1409.2112.
- Rebollo-Monedero, D.; Forné, J.; Domingo-Ferrer, J. From t-Closeness-Like Privacy to Postrandomization via Information Theory. IEEE Trans. Knowl. Data Eng. 2010, 22, 1623–1636. [Google Scholar]
- Li, N.; Li, T.; Venkatasubramanian, S. t-Closeness: Privacy beyond k-anonymity and l-diversity, Proceedings of the IEEE 23rd International Conference on Data Engineering (ICDE), Istanbul, Turkey, 15–20 April 2007; pp. 106–115.
- Parra-Arnau, J.; Rebollo-Monedero, D.; Forné, J. A Privacy-Preserving Architecture for the Semantic Web based on Tag Suppression, Proceedings of the 7th International Conference on Trust, Privacy, Security in Digital Bussiness (TRUSTBUS), Bilbao, Spain, 30 August–3 September 2010; pp. 58–68.
- Parra-Arnau, J.; Rebollo-Monedero, D.; Forné, J.; Muñoz, J.L.; Esparza, O. Optimal tag suppression for privacy protection in the semantic Web. Data Knowl. Eng. 2012, 81–82, 46–66. [Google Scholar]
- De Montjoye, Y.A.; Hidalgo, C.A.; Verleysen, M.; Blondel, V.D. Unique in the Crowd: The privacy bounds of human mobility. Sci. Rep. 2013, 3. [Google Scholar] [CrossRef]
- Hildebrandt, M.; Backhouse, J.; Andronikou, V.; Benoist, E.; Canhoto, A.; Diaz, C.; Gasson, M.; Geradts, Z.; Meints, M.; Nabeth, T.; Bendegem, J.P.V.; der Hof, S.V.; Vedder, A.; Yannopoulos, A. Descriptive Analysis and Inventory of Profiling Practices—Deliverable 7.2. Available online: http://www.fidis.net/resources/fidis-deliverables/profiling/int-d72000/doc/2/ accessed on 10 June 2015.
- Hildebrandt, M.; Gutwirth, S. (Eds.) Profiling the European Citizen: Cross-Disciplinary Perspectives; Springer-Verlag: Berlin, Germany, 2008.
- Rodriguez-Carrion, A.; Garcia-Rubio, C.; Campo, C.; Cortés-Martín, A.; Garcia-Lozano, E.; Noriega-Vivas, P. Study of LZ-Based Location Prediction and Its Application to Transportation Recommender Systems. Sensors 2012, 12, 7496–7517. [Google Scholar]
- Schurmann, T.; Grassberger, P. Entropy estimation of symbol sequences. Chaos Interdiscip. J. Nonlinear Sci. 1996, 6, 414–427. [Google Scholar]
- Eagle, N.; Pentland, A.; Lazer, D. Inferring Social Network Structure using Mobile Phone Data. PNAS 2009, 106, 15274–15278. [Google Scholar]

| Who can be the privacy attacker? | Any entity able to profile users based on their location and mobility patterns is taken into account. This includes the location-based service (LBS) provider and any entity capable of eavesdropping on users’ location data, e.g., Internet service providers, proxies, users of the same local area network, and so on. Further, we also contemplate any other entity that can collect publicly-available users’ data. This might be the case of an attacker crawling the location data that Twitter users attach to their tweets. |
| How does the attacker model location profiles? | The location profile of a user is modeled as the probability distribution of their locations within an alphabet of predefined location categories. Conceptually, a location profile is a histogram of relative frequencies of user location data across those categories. |
| How does the attacker represent mobility profiles? | The mobility profile of a user is modeled as the joint probability of visited locations over time. This model is equivalent to the sequence of conditional probabilities of the current location, given the past history of locations. |
| What is the attacker after when profiling users? | We consider the attacker wishes to individuate users on the basis of their location and mobility patterns. In other words, the adversary aims at finding users who deviate notably from the average and common profile. |
© 2015 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rodriguez-Carrion, A.; Rebollo-Monedero, D.; Forné, J.; Campo, C.; Garcia-Rubio, C.; Parra-Arnau, J.; Das, S.K. Entropy-Based Privacy against Profiling of User Mobility. Entropy 2015, 17, 3913-3946. https://doi.org/10.3390/e17063913
Rodriguez-Carrion A, Rebollo-Monedero D, Forné J, Campo C, Garcia-Rubio C, Parra-Arnau J, Das SK. Entropy-Based Privacy against Profiling of User Mobility. Entropy. 2015; 17(6):3913-3946. https://doi.org/10.3390/e17063913
Chicago/Turabian StyleRodriguez-Carrion, Alicia, David Rebollo-Monedero, Jordi Forné, Celeste Campo, Carlos Garcia-Rubio, Javier Parra-Arnau, and Sajal K. Das. 2015. "Entropy-Based Privacy against Profiling of User Mobility" Entropy 17, no. 6: 3913-3946. https://doi.org/10.3390/e17063913
APA StyleRodriguez-Carrion, A., Rebollo-Monedero, D., Forné, J., Campo, C., Garcia-Rubio, C., Parra-Arnau, J., & Das, S. K. (2015). Entropy-Based Privacy against Profiling of User Mobility. Entropy, 17(6), 3913-3946. https://doi.org/10.3390/e17063913








