1. Introduction
We consider the problem addressed in [
1,
2] about the replacement policy of low-pressure cast iron (CI) pipelines used in a metropolitan gas distribution network by the assessment of the rate of occurrence of gas escapes or leaks (denoted as failures) obtained through integration of historical data and knowledge of company experts. In the cited works, homogeneous subnetworks were identified and ranked according to their failure rates, using a methodology based on field data, experts’ qualitative judgments and Bayesian inference; the failure rate was considered as the priority index for the replacement policy (of an entire subnetwork, rather than a single section). In the current paper, we consider the same criterion for the replacement policy, presenting a sounder approach to deal with the uncertainty associated with the experts’ judgments and providing practical tools to visualize the consequences of such uncertainty and to help in making decisions through an iterative process.
The considered gas distribution network was developed in a large urban area during the last century, and thereby, it is characterized by very different technical and environmental features (material, diameter of pipelines, laying location, etc.). It consists of thousands of kilometers of pipelines of low, medium and high pressure. The main concerns about the replacement plan were related to the low-pressure network (20 mbar over atmospheric pressure). As regards the low-pressure pipelines, several materials have been used to develop the network: traditional cast iron (CI), treated cast iron (TCI), spheroidal graphite cast iron (SGCI), steel (ST) and polyethylene (PE).
Since CI pipelines have a higher failure rate than other materials, even ten-times greater (see [
2]), and cover more than a fourth of the whole network, the authors paid more attention to this material and studied its subnetworks in more detail. The low-pressure CI network consists of about 6000 different sections of pipelines whose lengths range from 3 to 250 m for a total of 320 km.
It should be noted that medium- and high-pressure steel pipelines are less critical, since automatic devices stop the gas flow if pressure decreases. Moreover, medium- and high-pressure pipelines are laid deeper in the ground, with more care about the laying procedure, so that they are less subject to accidental stress.
Using the failure rate as an index of replacement priority and taking advantage of studies developed in other similar companies and available in the literature (e.g., [
3]), factors directly involved in the failure of a low-pressure CI pipeline were identified. The preliminary data analysis highlighted three critical failure factors (laying location, diameter and laying depth) characterized by two levels each, so that eight pipeline classes were obtained; see
Table 1.
Since the structural failure of CI pipelines is a rare phenomenon, Cagno
et al. [
1] felt it appropriate to model failure events with a Poisson process. As a matter of fact, CI pipeline failures seem to be scarcely sensitive to both wear and closeness to leak points (an assumption confirmed by available data taking into account a useful life phase varying from 50 to 100 years), whereas they are mostly affected by accidental stress. Due to these considerations, a time and space homogeneous Poisson process was used for each class
i (
cf.,
Table 2), with unit intensity (or failure rate)
θi (
i.e., per km and year). Thus, the failure probability of a single section in a planning period
k is calculated as:
where
sj is the length of the
j-th section (km) and
tk is the
k-th planning period (year). In the analyzed case, the planning period
tk was taken as a year, since the planning frequency was annual. Therefore, the likelihood function of each pipeline class will be:
being
x the number of failures over the network (of length
) of pipelines characterized by the same parameter
θi.
Table 2 shows the maximum likelihood estimate (MLE) of the annual failure rate for different combinations of factors and highlights both the influence of laying location (higher failure rates in street locations) and the interactions between factors (e.g., the varying influence of laying depth as a function of diameter). Each MLE is calculated as the ratio between the total number of failures and the length multiplied by the observation period (six years).
Note that with the company’s previous method of assessing tendency to failure, the small diameter was considered the most critical factor, whereas the laying location was one of the least important factors, so that it was clearly against the historical data analysis, giving misleading results.
Maximum likelihood estimation might lead to surprising and misleading results: for the pipelines in Class 8, there were only three failures in six years over 2.81 km, and according to the MLE (see
Table 2), this class (with a large diameter, laid deeply under the street) was the one most subject to failures. The MLE is affected by the very short length of the network in Class 8 and very sensitive to the number of observed failures, whereas the conclusion is very different when we consider the experts’ judgments, as well.
In Section 2, we will consider a quantile class (a special case of generalized moment-constrained class) obtained from experts’ beliefs about failure rates. We claim that it is quite impossible to get a unique prior out of experts’ judgments, and here, we present a method, based on classes of priors, addressing the issue, which is rarely used in applications and hardly known in engineering literature. As a consequence of the choice of a class of priors, there is a set of possible values that could be taken as estimates of the failure rate in each subnetwork; this is typically described in robust Bayesian analysis as a sensitivity problem with respect to the choice of the prior. We could consider the set of all posterior means obtained when varying the prior in the class. The choice of the posterior mean corresponds, in the language of Bayesian decision analysis, to the selection of the optimal action that minimizes the posterior expected loss under a squared loss function. Under a class of priors and, possibly, of loss functions (which are the two major ingredients in the Bayesian approach along with the sampling model), the search for a class of optimal actions/estimates could lead to considering all of those actions for which there exist at least one prior and one loss, such that they minimize the corresponding posterior expected loss; this would be called the set of the Bayes actions. Another approach, fully justified from a foundational point of view, as stated, e.g., in [
4], consists of finding all of those actions for which there exists no other action performing better (dominating), in terms of not a greater posterior expected loss, when considering all possible combinations of priors and loss functions; those actions are called non-dominated. In Section 3, for each subnetwork, we will compute the set of non-dominated actions under its class of priors for a fixed, squared loss function. The goal would be to obtain disjoint non-dominated sets, implying that the subnetwork with the largest estimates (
i.e., the non-dominated actions) has a worse failure rate than the others, regardless of the choice of the prior. The subnetworks would be ranked not according to the value of a unique estimate, like in [
2], but considering if the non-dominated sets are overlapping or disjoint. Should all of the non-dominated sets be disjoint, then ranking would be obvious. If the non-dominated sets do not allow us to order the failure rates (
i.e., there is overlap between sets of different subnetwork), we propose the choice of the least sensitive action as the optimal solution of the sensitivity problem, as in [
5]. The use of non-dominated and least sensitive actions is definitely new in reliability, combining foundational justification with ease of interpretation when looking at the plots provided in the paper. The plots presented in the paper are a useful innovation in Bayesian robustness, since they allow for immediate, visual evaluation, even by non-statisticians, of the consequences of the uncertainty in specifying the prior distributions.
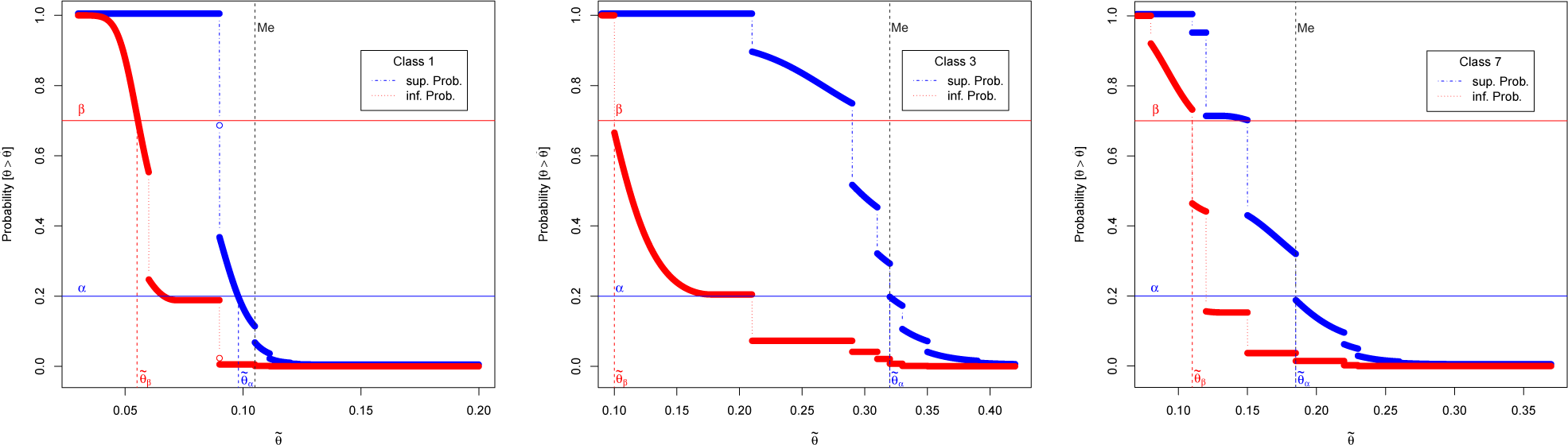
Furthermore, the paper deals not only with the comparison of different classes of pipelines to suggest a replacement order, but also with the problem of determining which classes have a failure rate
θ exceeding a given threshold
, deemed as the largest “acceptable or assumable” level with no need for replacement. Such an aspect, not considered in [
1,
2], is relevant in determining if different experts’ opinions, combined with historical data, lead to an agreement about the need or not of replacements.
Further remarks and a discussion will conclude the paper in Section 4.
Summarizing the major aspects of the paper, it is worth mentioning, first of all, that the work stems from a case study where experts are unable to express quantitative judgments on the quantity of interest (failure rates of eight subnetworks) and their qualitative assessments are transformed into a unique value for each rate, for each person. Cagno
et al. [
1] used the values assessed by the experts, like “samples” from prior distributions, conveniently chosen by the statisticians (namely gamma and lognormal ones). Other methods are possible to combine the opinion of experts; a relevant one is due to Albert
et al. [
6]. We are considering a different approach, which has roots in the Bayesian robustness literature, reviewed in [
7]. Coherently, with such an approach, we are considering a class of priors compatible with the unique information provided by the experts,
i.e., a set of values for each failure rate. This aspect is important, since we believe that in real-life applications of the Bayesian approach, it is important to be as much as possible adherent to the experts’ opinions and try to avoid (or limit) adding arbitrary assumptions. The class proposed in the paper, relying on quantiles, is definitely more realistic than the ones considered in [
2]. For the problem at hand, the use of the quantile class on the parameter of a Poisson process was a consequence of the available experts’ assessments: opinions on the failure rates. In general, we believe that experts are more keen to provide information on observable quantities, like the number of gas escapes in a given time frame and a network of known length. The generalized moment-constrained class, studied in [
8], is very powerful, since it allows considering all of the priors compatible with elicited values of moments and/or quantiles of observable quantities. There are cases in which elicitation on the parameters is possible, especially when the parameter has a physical meaning: in our case, it is the failure rate per unit of time and space and an expert (more statistically educated than the ones here) could make assessment on, say, the median and the quartiles of its distribution, just by splitting intervals with the same probability. The analysis performed in the paper can be read also in a different way with respect to how it is presented here, mimicking an actual, interactive process of the assessment of prior beliefs by just one expert and studying the consequences. We start with the assessment of upper and lower bounds on the rates (corresponding here to the largest and smallest values given by the experts), and the obtained ranks of subnetworks are unsatisfactory because of the many overlaps among ranges. The expert is asked to refine his/her assessments first by specifying three and then seven quantiles until the posterior ranges are no longer (or definitely less) overlapping. The use of the graphical tools presented in the paper would be very helpful in such a process of interactive assessment. If it is impossible to get a clear ranking using the expert’s opinions or, more simply, if point estimates are needed, then we believe an optimality criterion should be used (and two are presented here and compared).
2. Bayesian Approach
Sensitivity analysis is an important issue in Bayesian analysis and decision theory. In many fields, it is worth studying how changes in the input parameters affect the output from a model. The issue stems naturally from the difficulty in eliciting experts’ judgments, and the case at hand is typical. Experts were able neither to assess “exact” prior distributions on the parameters
θi, nor some features, like their quantiles. The experts were able to provide only qualitative judgments, which were expressed through pairwise comparison of all subnetworks about the propensity of a failure occurring in one class rather than in another. The AHP (analytic hierarchy process) methodology, proposed by [
9], was used to obtain rates of occurrence of gas escapes in each subnetwork, whereas further manipulations lead to gamma conjugate priors on
θi’s. In more detail, each expert was presented with a picture of the eight possible configurations (small/large diameter, deep/not deep in the ground, walkway/traffic) and then asked to compare them pairwise. In particular, he/she was asked if, given the occurrence of a gas escape, it was more likely in a subnetwork with respect to another. Calling
A and
B the two subnetworks, the question was if the occurrence in
A was equally/a little more/much more/clearly more/definitely more/a little less/much less/clearly less/definitely less likely than in
B. A number was associated with each answer: 1, 3, 5, 7, 9, 1/3, 1/5, 1/7, 1/9, respectively. A square matrix of size eight was obtained out of the pairwise comparisons, and the eigenvector associated with its largest eigenvalue provided the probabilities
P1,…,
P8 that the gas escape had occurred in each subnetwork (mathematical details can be found in [
9]). Given an estimate of the unit failure rate
θ∗ of the entire city network, then the guess of the
j-th expert on the failure rate of the i-th subnetwork was given by
,
i = 1,…, 8, using the coloring theorem (see [
10]). The set of all of those guesses, for each expert and each subnetwork, is the opinions used in the current paper. In [
1], they were used as a sample from a gamma prior distribution whose parameters were obtained matching mean and variance with sample mean and sample variance, respectively. The described procedure is subject to criticism, since the selected prior does not reflect the actual knowledge. Therefore, a class of priors, compatible with the prior knowledge, is entertained to solve the problem.
The consideration of classes of priors and loss functions is the starting point for much of the developments in robust Bayesian analysis; see [
11] and [
7]. Excellent surveys of sensitivity analyses with respect to the prior are [
11,
12] and [
13], whereas sensitivity with respect to the loss function has been considered in [
14–
16], among others. The main differences among works in Bayesian sensitivity are about the choice of the classes and the sensitivity measures.
2.1. Choice of Prior Distributions
In [
1], the experts’ opinions were synthesized into one value for the mean and variance of the prior distribution on each failure rate, computing the Bayes estimates (
i.e., the posterior mean) using both gamma and lognormal priors.
The work in [
2] compared two classes of gamma priors with mean and variance in intervals around the synthesized values from the experts’ opinions. The classes lead to different, but similar, ranges on the posterior mean of each class.
In [
17], other prior classes were considered. They considered, for each class i, the family of priors:
where
c is a positive constant, within the same interval for all of the classes, and
mi and
, ∀
i, are the mean and the variance, respectively, obtained in [
2]. Then, they kept the same (gamma) distribution form for priors, and they considered, for each class, the family of priors:
where each
πc has mean
mi and variance
c.
Finally, they studied, for each class
i, the family of all of the probability measures sharing the same mean
mi and variance
as in [
2]. They obtained the family of priors:
a special case of the moment-constrained class, described later. This class, unlike the previous ones, is a first attempt to use the experts’ opinions without arbitrary assumptions, like the choice of a gamma distribution. The current work goes even further, since it considers the opinions as they are (after manipulation by AHP) through quantiles of the empirical distribution of the experts’ opinions rather than summarizing measures, like mean and variance.
The generalized moments class was studied by [
8] and further explored in [
18], and it is defined as follows:
where
Hi are given
π-integrable functions and
αi (
i = 1,…,
n) are fixed real numbers. Sometimes, the moment conditions are given by equalities. In those works, the aim is to find the range of a quantity of interest
F(
π) = ∫
Θ F(
θ)
π(
θ|
x)
dθ, when
π varies over a class of prior distributions Γ.
Generalized moment classes cover a great variety of classes that are of interest for robust Bayesian analysis. For
Hi(
θ) =
θi, we have ordinary moment conditions on
π; for
, we have conditions on the prior probability of sets
Ci; and with equalities, we have the quantile class; see, e.g., [
19–
21].
In [
1,
2], the opinions from fourteen experts were collected using an “
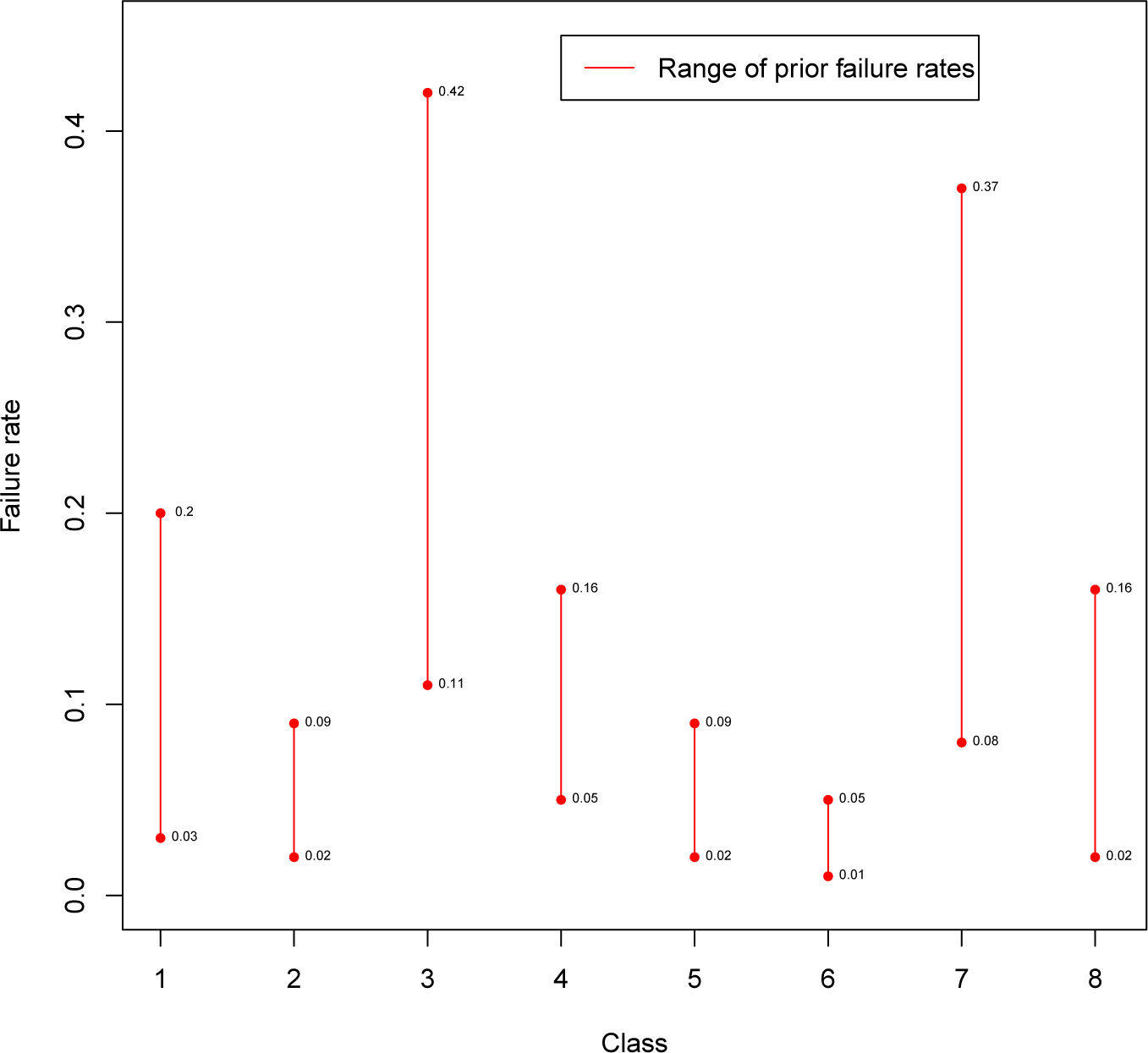
ad hoc” questionnaire, and priors were obtained. An estimate of the failure rate for the eight pipeline classes was obtained for each expert, and the sample mean and variance of those estimates were matched with the mean and variance of the entertained priors, obtaining the values of the hyperparameters. The ranges of the experts’ (prior) failure rates are shown in
Figure 1. Differences among experts can be easily detected from the plot, especially about Classes 3 and 7. Furthermore, it is worth noticing that, for all of the experts, the failure rate in Class 6 is lower than the ones in Classes 3, 4 and 7, whereas the rate of failure in Class 2 is less than in Class 3. Based just on prior opinions, there is no replacement order shared by all of the experts, although there are strong indications about the worst (3 and 7) and best (6) classes.
The previous works could raise some concerns about the proper use of experts’ judgments. The choice of a functional form for the prior (gamma or lognormal) is quite arbitrary, since it corresponds to mathematical convenience and not to actual knowledge. The classes of priors entertained in [
17] are quite simplistic, even the one determined by sample mean and variance. Here, we propose the use of sample quantiles, out of the empirical distribution of the estimates provided by experts, so that, e.g., we will consider classes of priors with the median corresponding to the sample median of the experts’ estimates. Therefore, we will consider the quantile class,
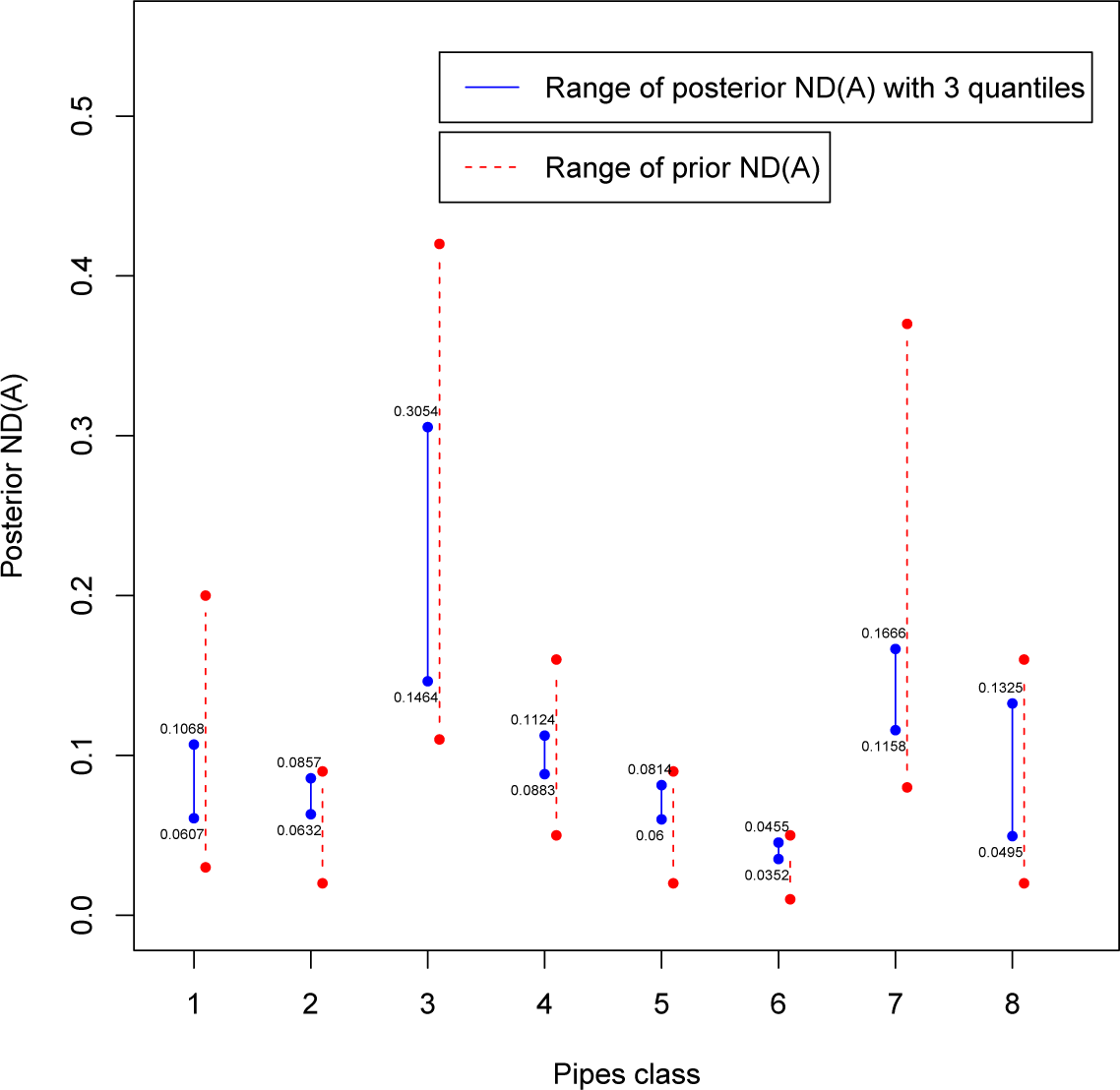
where
and {
Ci,
i=1,…,
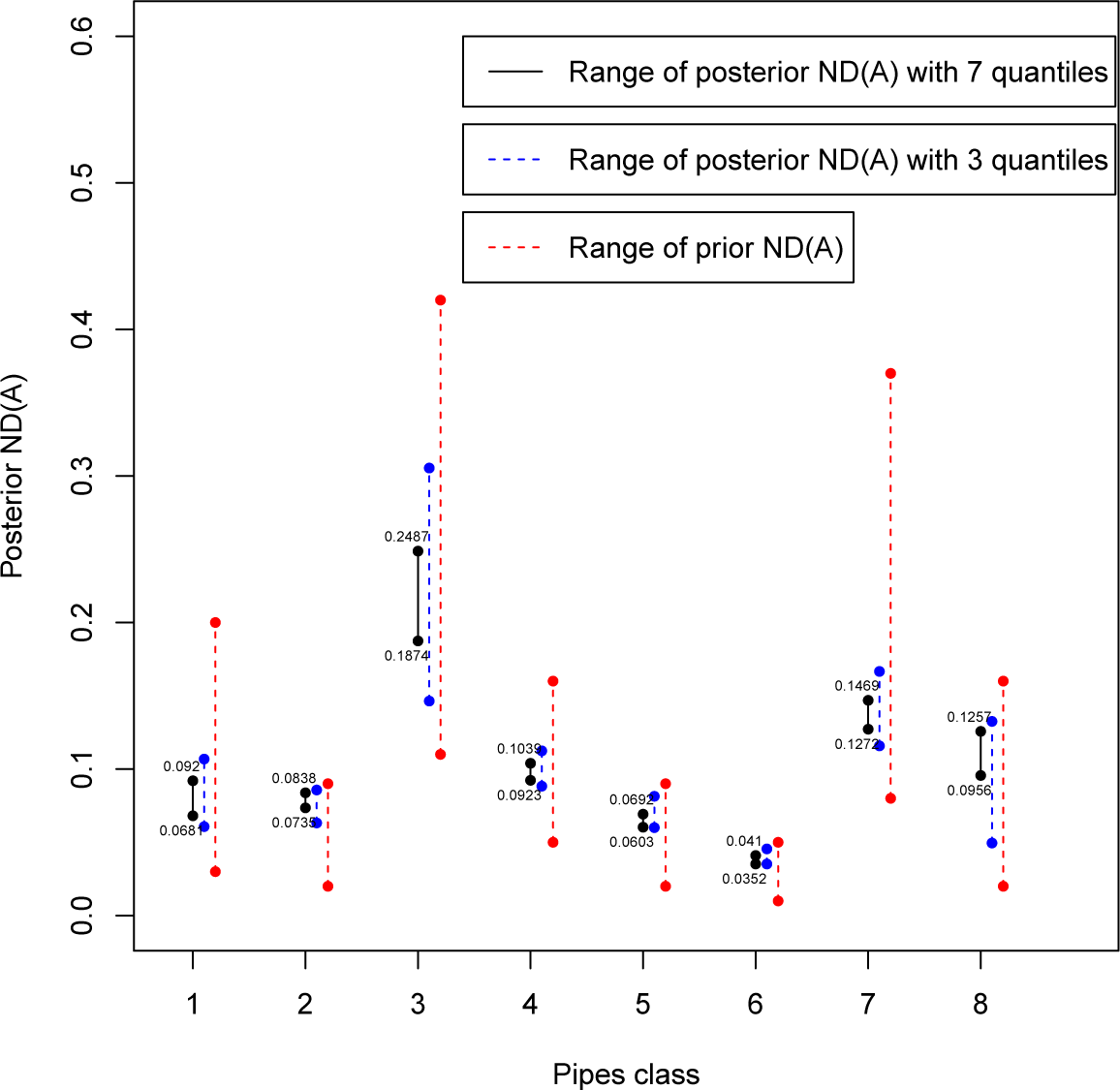
n} is a partition of the parameter space Θ. Firstly, the class is obtained considering only three sample quantiles from the distribution of experts’ assessed values. Since the range of the non-dominated sets is not “small” enough to avoid overlaps and allow us to make a clear-cut ranking of the classes, we will consider a more restricted class with seven quantiles. In that case, ranking will be more evident especially for the worst and best classes, but some overlaps will be present. Those findings could be sufficient for a decision maker (DM) about planning the replacement of the entire worst subnetwork (not just simply sections) of pipelines, whereas a precise ranking could be obtained introducing a criterion to select one representative value for each class. Here, we will consider two criteria developed in a Bayesian decision analysis framework: the posterior regret (see [
22]) and, mostly, the least sensitive action (see [
5]).
2.2. Estimation of Failure Rate
In this section, we introduce the statistical notions used to perform the estimation of the failure rates in the subnetworks and, consequently, rank them according to the need of replacements. For the readers willing to skip the necessary mathematical details of the section, we would like to point out that, among all possible values a of the failure rate in a set
(namely, the set of positive real numbers), we are using experts’ opinions and historical data to find a class of estimates (or a unique value) that satisfy some optimality criteria, aimed to reduce the incurred loss (here, more generally from a class, whereas a unique, squared loss function will be considered in the actual pipeline replacement problem). The former will lead us to the set of non-dominated actions, whereas the latter to the least sensitive action.
We consider the standard Bayesian decision theoretic framework for statistical problems; see, e.g., [
23]. Let
X be an observation from a distribution
Pθ with density
pθ(
x).
π(
θ) denotes a prior distribution belonging to a class of distributions Γ and
L a loss function belonging to a class of loss functions
, such that for all
a ∈
, there exists
θa, with
.
Let
πx(
θ) denote the posterior density when
x (possibly a sample) is observed,
mπ(
x) the marginal density,
l(
θ) the likelihood function and
ρ(
π,
L,
a) the posterior expected loss of a,
i.e.,
As a consequence of this model, the solution concept is the set of non-dominated alternatives, or actions,
.
Definition 1.
a ∈
is a non-dominated alternative if there is no other alternative b ∈
,
such that:and there is a pair (
L0,
π0),
such that: When there precision in beliefs and preferences, the solution is given by the Bayes action.
Definition 2. For any (
L,
π) ∈
× Γ,
a Bayes action corresponding to (
L,
π)
is an action minimizing ρ(
π,
L,
a)
in and will be denoted by.
Therefore, it holds: Arias-Nicolás
et al. [
24] modeled beliefs through a class of probability and preferences through a class of convex loss, showing the relation between Bayes actions and the non-dominated set. In [
21], the non-dominated set is computed for some classes of probability distributions and loss functions.
In most papers about Bayesian robustness, the range of the posterior expectation of a quantity of interest,
F(
θ), has been proposed as a measure of sensitivity. If
F(
θ) =
θ, then the range of the posterior mean is obtained, which is the Bayes alternative when the preferences are modeled by the quadratic loss function; see e.g., [
25]. If
F(
θ) =
IC(
θ), the range of the posterior probability of a credible set
C is obtained; see [
12,
26–
29], among others.
However, the use of measures based on the range can provide misleading conclusions in the sensitivity analysis with respect to the prior or loss function; see e.g., [
14]. Different approaches have been proposed, e.g., selecting the “best” (with respect to some criterion) optimal alternative. In these situations, the election of alternatives as the conditional Γ-minimax [
25,
30] and the posterior regret Γ-minimax [
22,
31] actions could be useful as a way of selecting a single robust solution.
However, these actions could lead to a huge relative increase in posterior expected loss with respect to Bayes actions. Therefore, we propose another measure [
5], which is not dependent on the unit of measurements and which generalizes the relative sensitive measure given by [
32].
From now onwards,
, for all (L, π) ∈ × Γ, and
will be a bounded closed interval.
Definition 3. Given a pair (
L,
π) ∈
× Γ,
let S(
π,
L,
a)
be the sensitivity of an alternative a with respect to the pair (
L,
π),
defined as the difference between the posterior expected losses of a
and the Bayes action,
,
with respect to the optimal expected loss, i.e.,
S(
π,
L,
a) can be viewed as the difference in the posterior expected loss when
a is used instead of the optimal action
, measured in terms of the optimal posterior expected loss. This measure is an extension of the one defined in [
32].
For this sensitivity measure, it is possible to consider the following:
Definition 4. als is the least sensitive (LS) alternative for × Γ
if:where S(
a)
will denote the sensitivity of an action a
with respect to × Γ, i.e.,
It is easy to see that the LS action (a minimax action, because of its definition) might not be Bayes for any pair (L, π) ∈ × Γ. However, it is true that the LS action must be a non-dominated alternative.
There is no general algorithm able to compute least sensitive actions in a general class. In [
5], an algorithm for classes of convex loss functions is presented. Based on [
8], the following result can help computations for some classes of distribution priors, like, for example, the generalized moment-constrained and ǫ-contaminated classes, among others.
Proposition 1.
Let Γ
be a class of prior distributions and a class of loss functions. Then, for each a ∈
,
Proof. It is easy to see that:
Conversely, let
and
, be the values where the supremum is achieved. Then,
must be a Bayes alternative for
, because for all pairs (
L,
π) ∈
× Γ, it holds:
Thus:
□
Note that the denominator in the right-hand side does not depend on a(L,π), and we do not need the calculation of mπ.
Now, we use this proposition to determine the sensitivity of the optimal action for the generalized moment-constrained class.
Proposition 2. Let Γ
be a generalized moment class defined as in (1) and a class of loss functions. Then, for each a, k ∈
,
where θ = (
θ1,…,
θn+1)′,
p = (
p1,…,
pn+1)′
and the set T ⊂ Θ
n+1 × [0, 1]
n+1 are defined by the following conditions:, i = 1,…, n, with hi = (Hi(θ1),…, Hi(θn+1))′,
.
Proof of Proposition 2. See [
8]. □
If the moments conditions of Γ are given by equalities, then Condition 1 becomes an equality, as well. A similar result can be obtained considering ϵ-contaminated classes where the contaminating class is determined by generalized moment constraints.
If we consider a quantile class (2), we have the following result:
Corollary 1. Let Γ
be a quantile class defined as in (2) and a class of loss functions. Then, for each a,
k ∈
,
Proof of Corollary 1. This result follows from the previous proposition and Theorem 1 in [
19].
4. Discussion
In this paper, we have illustrated a methodology that addresses and can overcome the major criticisms about the Bayesian approach,
i.e., arbitrariness in the choice of the prior distribution and difficulty in properly using the information provided by the experts. Taking a robust Bayesian approach, we have been able to relax the assumption about a unique prior, and we used the information gathered from the experts to build classes of priors compatible with their knowledge. We have shown how decisions can be made by managers by looking at very simple plots expressing a set of non-dominated actions or by selecting optimality criteria that provide unique values used in ranking pipelines according to their need for a replacement. The proposed methodology improves upon previous works [
1,
2,
17], since it is less dependent on the statistician’s choice on the functional form of the prior distribution (or classes of them) and closer to what the experts actually elicited. The procedure could be implemented in a more interactive way, where experts could be asked more and more information to get finer and finer classes, whose effects should be interactively presented to the experts/decision makers through the tables and the figures shown in this paper.
The proposed approach can find application in many other fields where classes of priors can be specified on parameters and quantities of interest could be compared and ranked a posteriori. Classes of priors could be the result of opinions of different experts or imprecise assessment of a unique expert, whereas the quantity of interest could be the posterior predictive probability of at least a 5% yearly gain, or the expected gain for different investments to choose from, or the expected number of failures, over a five-year period, of washing machines from different brands. The method works better when it is possible to obtain more and more information from the experts, at a relatively inexpensive price, like here, when moving from three to seven quantiles and obtaining narrower sets, with no overlap among the ones of major interest. The method is useful also in determining for which systems (here, gas subnetworks; and investments and brands in the above) is more crucial to get further information and avoid overlaps.
We have also proposed a robust Bayesian approach on the selection of pipelines to be replaced or not, regardless of their ranking, based on the exceedance of acceptable failure rate and risk. We have provided tables and figures that could be helpful in making decisions, loosening the dependence on the selected prior distributions.