Content Based Image Retrieval Using Embedded Neural Networks with Bandletized Regions
Abstract
:1. Introduction
2. Related Work
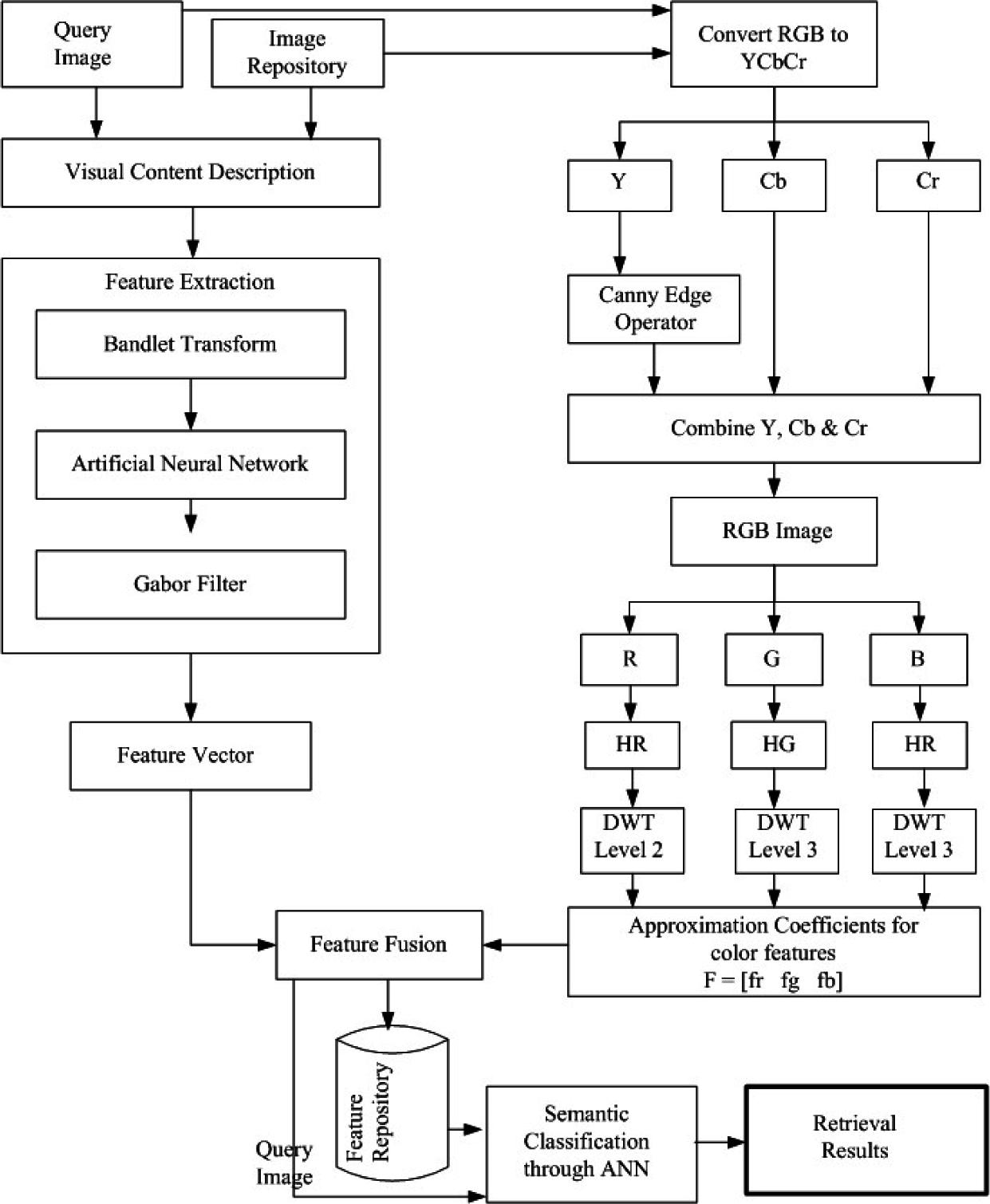
3. Proposed Method
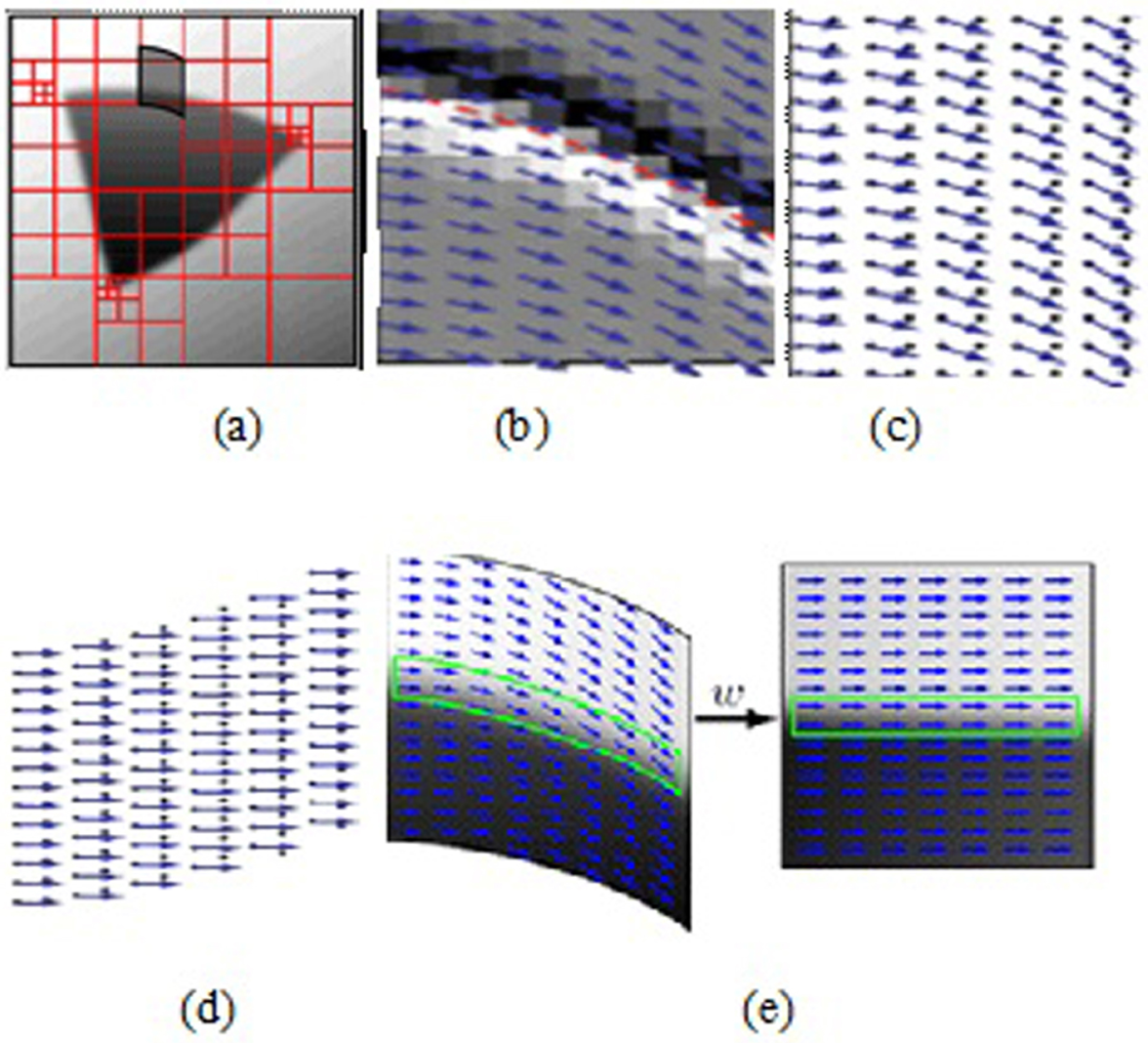
3.1. Bandelet Transform
3.1.1. Alpert bases in bandelet transform
3.1.2. Texture Feature Extraction using Bandelets
- Convert input RGB image (I) of size M × N into gray scale image.
- Apply bandelet transform to calculate the geometry of an image and obtain the directional edges.
- Artificial Neural Network is used to classify these blocks having directional edges after training on the sample edge set as described in Figure 5. Once the network is trained, every geometric shape obtained in the step 2 is classified for parameter estimation. These parameters will further be described in the Gabor filter section.
- After parameter estimation, the blocks with geometric contents are passed to the Gabor filter to estimate the texture.
- Steps 1 to 4 is repeated for whole image repository.
3.1.3. Artificial Neural Network
3.1.4. Gabor Feature
- θ = π, and λ = 0.3.
- θ = π/2, and λ = 0.4.
- θ = π/4, and λ = 0.5.
- θ = 3π/4, and λ = 0.5.
3.2. Color Feature Extraction
- RGB image (I) is converted into Y CbCr color space.
- After conversion, we separate the Y CbCr components and apply canny edge detector on Y component of the image.
- In the next step, we combine the edges obtained in the previous step with unchanged Cb and Cr.
- After step (3), convert the combined image back into single RGB image.
- Now separate the individual R, G, and B components and calculate the histogram of each component. 256 bins are obtained from HR, HG, and HB.
- To improve the feature performance, we apply wavelet transform at each histogram obtained in the previous step. We apply the discrete wavelet transform of HR at level 2, HG, and HB are applied at level 3. After this step, we have 128 bins i.e. 64 bins from HR, 32 bins from HG, and 32 bins from HB.
- Calculate feature vector for every image in the repository.
3.3. Fusion Vector
3.4. Content based image retrieval
4. Performance Evaluation
4.1. Image Datasets
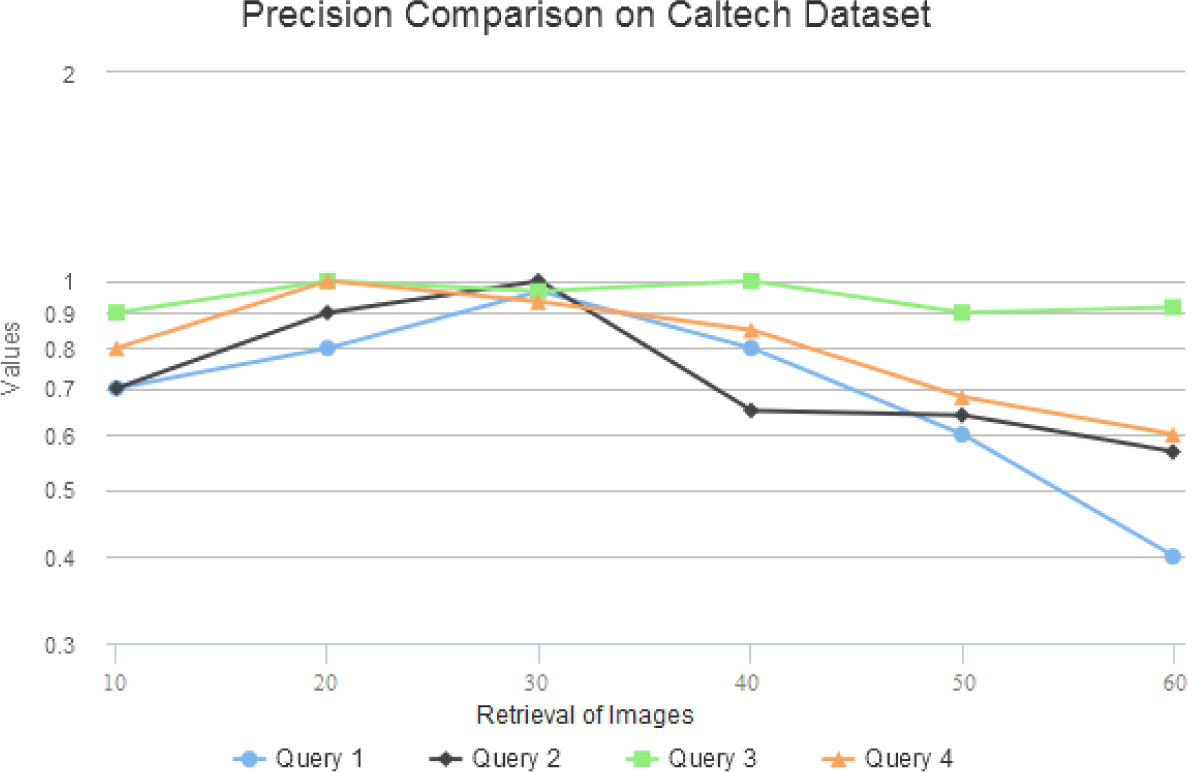
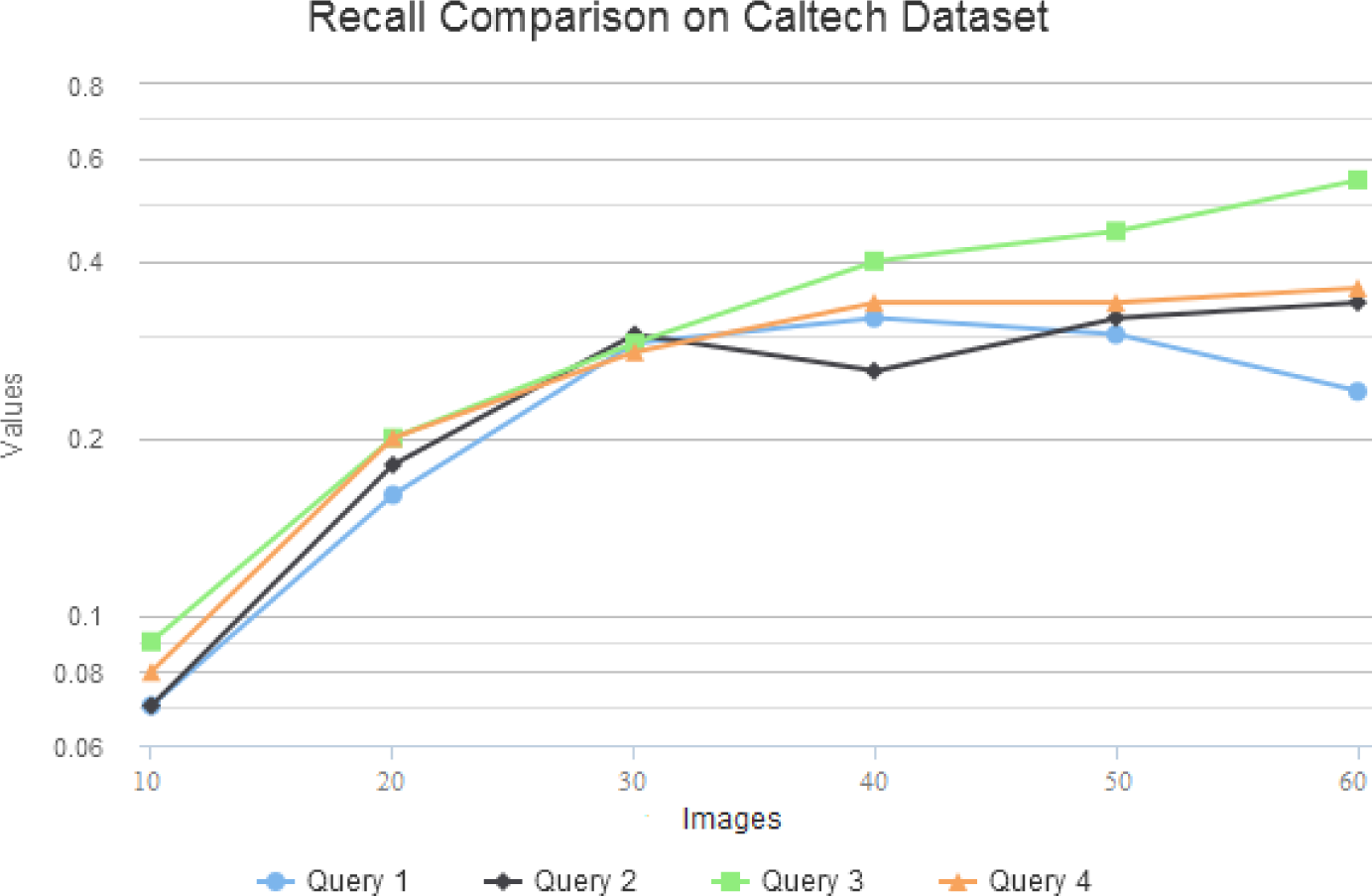
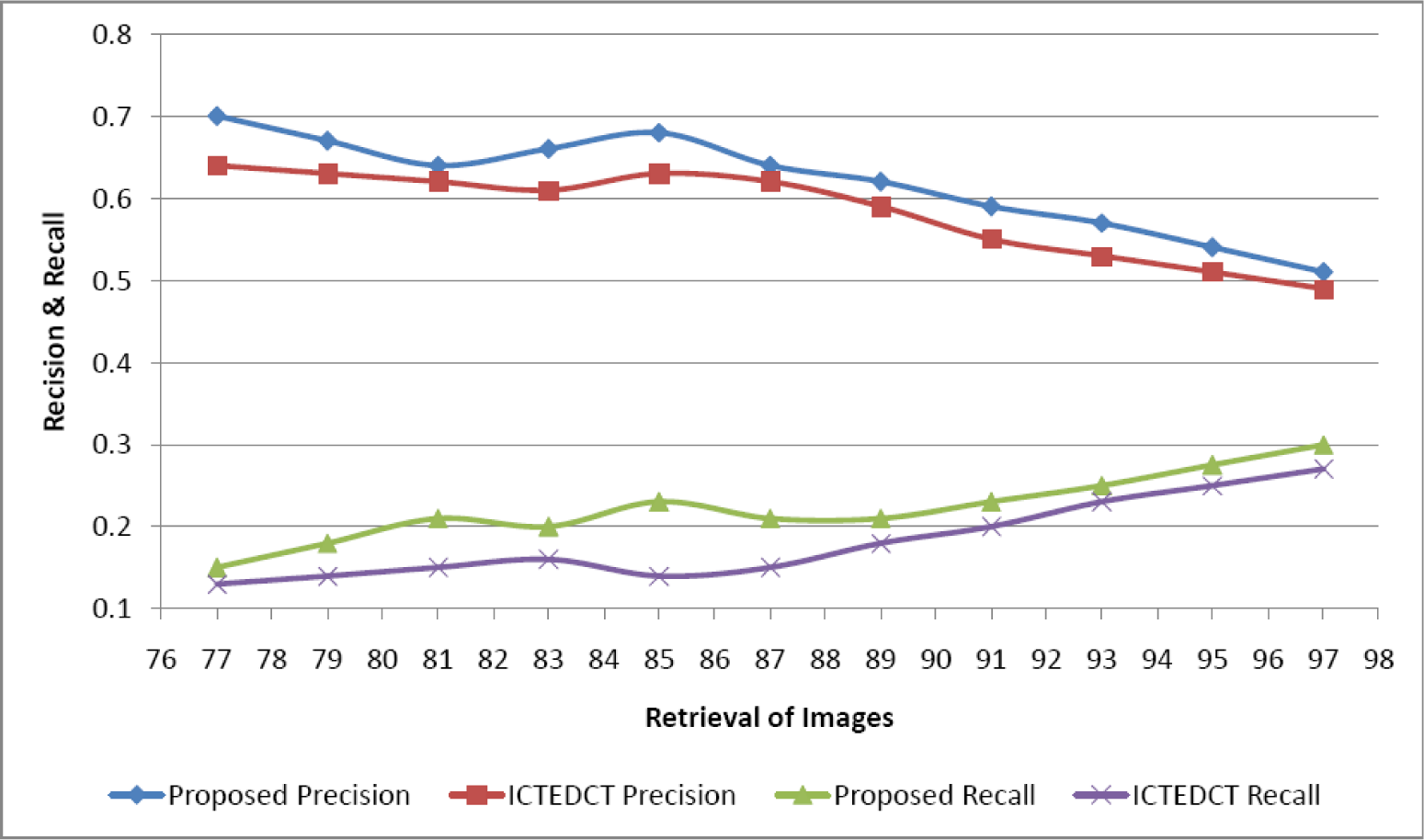
4.2. Retrieval Precision/Recall Evaluation
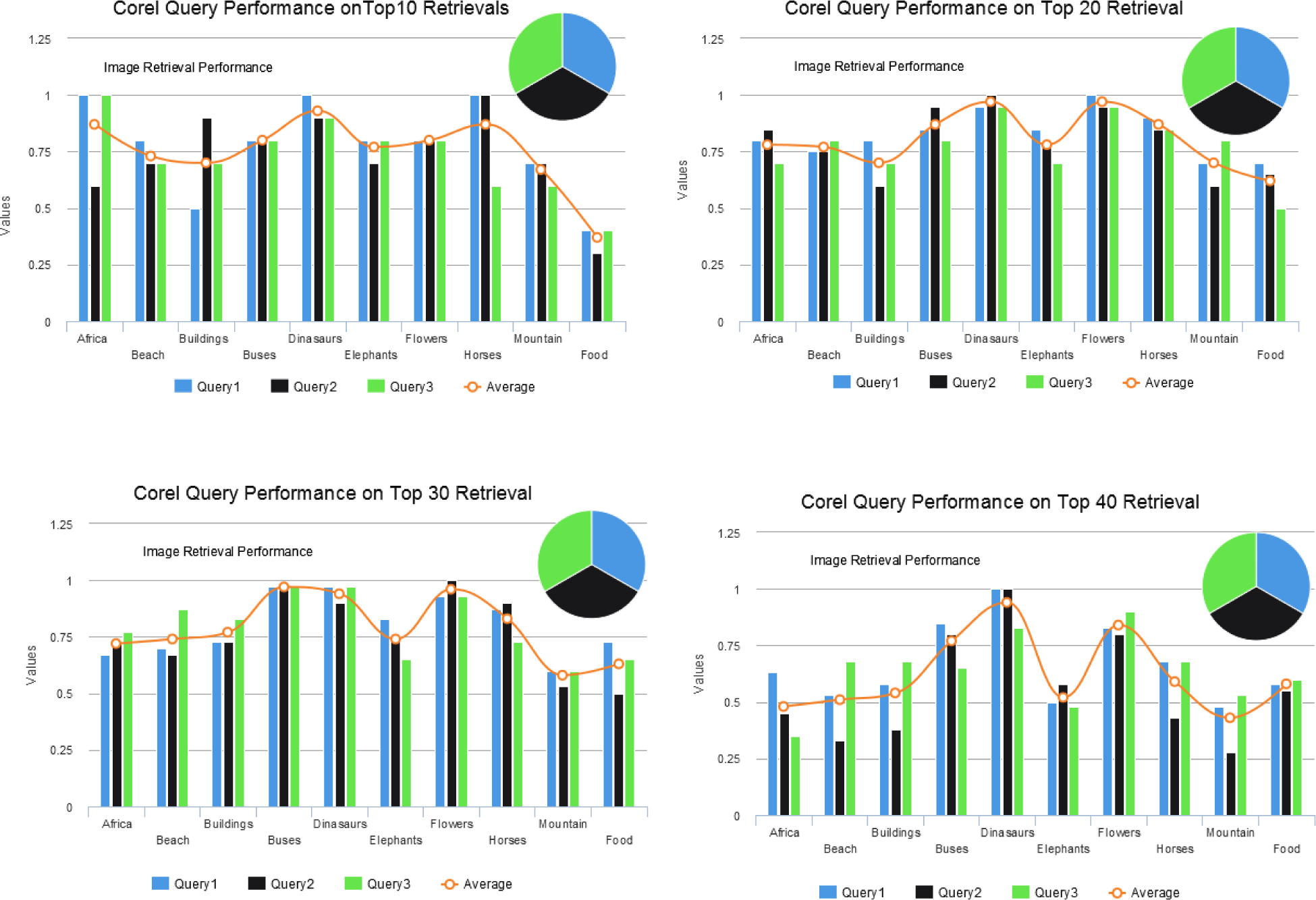
4.3. Comparison on Corel Image Set
4.4. Comparison on Coil Image Set
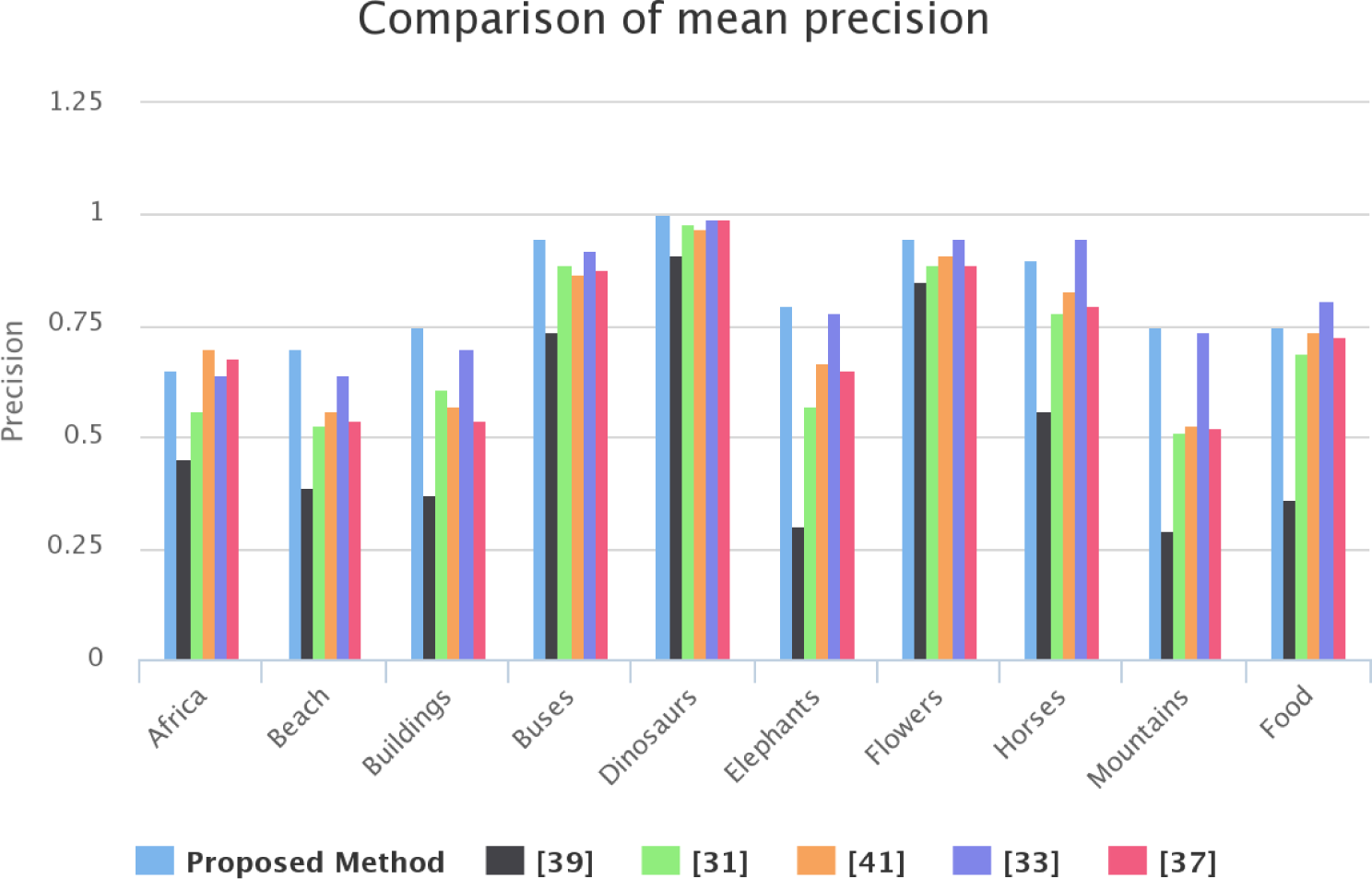
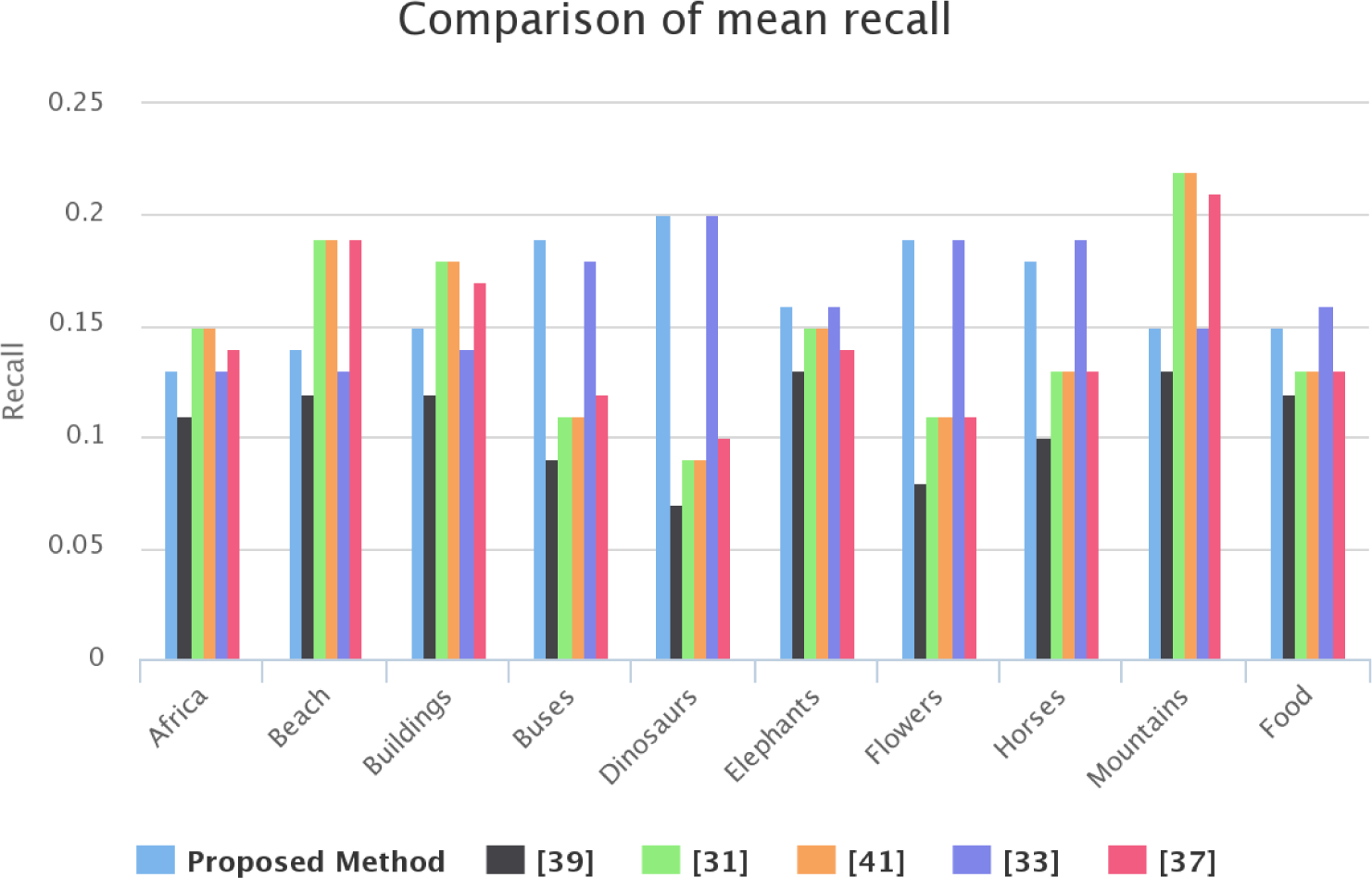
4.5. Comparison with State-of-the-Art Methods
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Gudivada, V.N.; Raghavan, V.V. Content based image retrieval systems. Computer 1995, 28, 18–22. [Google Scholar]
- Smeulders, A.W.; Worring, M.; Santini, S.; Gupta, A.; Jain, R. Content-based image retrieval at the end of the early years. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 1349–1380. [Google Scholar]
- Datta, R.; Li, J.; Wang, J.Z. Content-based image retrieval: approaches and trends of the new age, Proceedings of the 7th ACM SIGMM International Workshop on Multimedia Information Retrieval, New York, NY, USA, 1–2 August 2005; pp. 253–262.
- Lei, Z.; Fuzong, L.; Bo, Z. A. CBIR method based on color-spatial feature, Proceedings of the IEEE Region 10 Conference, Cheju Island, South Korea, 15–17 September 1999; pp. 166–169.
- Smith, J.R.; Chang, S.F. Tools and Techniques for Color Image Retrieval. Proc. SPIE. 1996, 2670, 2–7. [Google Scholar]
- Plataniotis, K.N.; Venetsanopoulos, A.N. Color Image Processing and Applications; Springer: New York, NY, USA, 2000. [Google Scholar]
- Chitaliya, N.; Trivedi, A. Comparative analysis using fast discrete Curvelet transform via wrapping and discrete Contourlet transform for feature extraction and recognition, Proceedings of 2013 International Conference on Intelligent Systems and Signal Processing (ISSP), Gujarat, India, 1–2 March 2013; pp. 154–159.
- Barley, A.; Town, C. Combinations of Feature Descriptors for Texture Image Classification. J. Data Anal. Inf. Process 2014, 2. [Google Scholar] [CrossRef]
- Sumana, I.J.; Islam, M.M.; Zhang, D.; Lu, G. Content based image retrieval using curvelet transform, Proceedings of 2008 IEEE 10th Workshop on Multimedia Signal Processing, Cairns, Australia, 8–10 October 2008; pp. 11–16.
- Zhang, J.; Tan, T. Brief review of invariant texture analysis methods. Pattern Recognit. 2002, 35, 735–747. [Google Scholar]
- Yang, M.; Kpalma, K.; Ronsin, J. A survey of shape feature extraction techniques. In Pattern Recognition Techniques, Technology and Applications; Yin, P.-Y., Ed.; InTech: Rijeka, Croatia, 2008; pp. 43–90. [Google Scholar]
- Zhang, D.; Lu, G. Shape-based image retrieval using generic Fourier descriptor. Signal Process. Image Commun. 2002, 17, 825–848. [Google Scholar]
- Vimina, E.; Jacob, K.P. Content Based Image Retrieval Using Low Level Features of Automatically Extracted Regions of Interest. J. Image Graph. 2013, 1, 7–11. [Google Scholar]
- Velmurugan, K.; Baboo, L.D.S.S. Content-based image retrieval using SURF and colour moments. Glob. J. Comput. Sci. Technol. 2011, 11, 1–4. [Google Scholar]
- Liu, Y.; Zhang, D.; Lu, G.; Ma, W.Y. A survey of content-based image retrieval with high-level semantics. Pattern Recognit. 2007, 40, 262–282. [Google Scholar]
- Liu, G.H.; Yang, J.Y. Content-based image retrieval using color difference histogram. Pattern Recognit. 2013, 46, 188–198. [Google Scholar]
- Hejazi, M.R.; Ho, Y.S. An efficient approach to texture-based image retrieval. Int. J. Imaging Syst. Technol. 2007, 17, 295–302. [Google Scholar]
- Kekre, H.; Thepade, S.D.; Sarode, T.K.; Suryawanshi, V. Image Retrieval using Texture Features extracted from GLCM, LBG and KPE. Int. J. Comput. Theory Eng. 2010, 2, 1793–8201. [Google Scholar]
- Zhang, D.; Lu, G. A comparative study on shape retrieval using Fourier descriptors with different shape signatures, Proceedings of International Conference on Intelligent Multimedia and Distance Education (ICIMADE01), Fargo, ND, USA, 1–3 June 2001; pp. 1–9.
- Prasad, B.; Biswas, K.K.; Gupta, S. Region-based image retrieval using integrated color, shape, and location index. Comput. Vis. Image Underst. 2004, 94, 193–233. [Google Scholar]
- Yuan, X.; Yu, J.; Qin, Z.; Wan, T. A. SIFT-LBP image retrieval model based on bag of features, Proceedings of 2011 18th IEEE International Conference on Image Processing, Brussels, Belgium, 11–14 September 2011.
- Wang, J.Z.; Li, J.; Wiederhold, G. SIMPLIcity: Semantics-sensitive integrated matching for picture libraries. IEEE Trans. Pattern Anal. Mach. Intell. 2001, 23, 947–963. [Google Scholar]
- Chen, Y.; Wang, J.Z.; Krovetz, R. CLUE: cluster-based retrieval of images by unsupervised learning. IEEE Trans. Image Process 2005, 14, 1187–1201. [Google Scholar]
- Irtaza, A.; Jaffar, M.A. Categorical image retrieval through genetically optimized support vector machines (GOSVM) and hybrid texture features. Signal Image Video Process 2014. [Google Scholar] [CrossRef]
- Sk. Sajidaparveen, G.; Chandramohan, B. Medical image retrieval using bandelet. Int. J. Sci. Eng. Technol. 2014, 02, 1103–1115. [Google Scholar]
- Peyré, G.; Mallat, S. Surface compression with geometric bandelets. ACM Trans. Graph. (TOG) 2005, 24, 601–608. [Google Scholar]
- Le Pennec, E.; Mallat, S. Sparse geometric image representations with bandelets. IEEE Trans. Image Process 2005, 14, 423–438. [Google Scholar]
- Alomar, F.A.; Muhammad, G.; Aboalsamh, H.; Hussain, M.; Mirza, A.M.; Bebis, G. Gender recognition from faces using bandlet and local binary patterns, Proceedings of 2013 20th International Conference onSystems, Signals and Image Processing (IWSSIP), Bucharest, Romania, 7–9 July 2013; pp. 59–62.
- Flickner, M.; Sawhney, H.; Niblack, W.; Ashley, J.; Huang, Q.; Dom, B.; Gorkani, M.; Hafner, J.; Lee, D.; Petkovic, D.; et al. Query by image and video content: The QBIC system. Computer 1995, 28, 23–32. [Google Scholar]
- Besl, P.J.; McKay, N.D. Method for registration of 3-D shapes. Proc. SPIE. 1992. [Google Scholar] [CrossRef]
- Rao, M.B.; Rao, B.P.; Govardhan, A. CTDCIRS: Content based image retrieval system based on dominant color and texture features. Int. J. Comput. Appl. 2011, 18, 40–46. [Google Scholar]
- Yue, J.; Li, Z.; Liu, L.; Fu, Z. Content-based image retrieval using color and texture fused features. Math. Comput. Model 2011, 54, 1121–1127. [Google Scholar]
- Youssef, S.M. ICTEDCT-CBIR: Integrating curvelet transform with enhanced dominant colors extraction and texture analysis for efficient content-based image retrieval. Comput. Electr. Eng. 2012, 38, 1358–1376. [Google Scholar]
- Singha, M.; Hemachandran, K. Content based image retrieval using color and texture. Signal Image Process. Int. J. 2012, 3, 39–57. [Google Scholar]
- Liu, G.H.; Li, Z.Y.; Zhang, L.; Xu, Y. Image retrieval based on micro-structure descriptor. Pattern Recognit. 2011, 44, 2123–2133. [Google Scholar]
- Wang, X.Y.; Yang, H.Y.; Li, D.M. A new content-based image retrieval technique using color and texture information. Comput. Electr. Eng. 2013, 39, 746–761. [Google Scholar]
- Lin, C.H.; Chen, R.T.; Chan, Y.K. A smart content-based image retrieval system based on color and texture feature. Image Vis. Comput. 2009, 27, 658–665. [Google Scholar]
- Ashraf, R.; Mahmood, T.; Irtaza, A.; Bajwa, K.B. A novel approach for the gender classification through trained neural networks. J. Basic Appl. Sci. Res. 2014, 4, 136–144. [Google Scholar]
- Jhanwar, N.; Chaudhuri, S.; Seetharaman, G.; Zavidovique, B. Content based image retrieval using motif cooccurrence matrix. Image Vis. Comput. 2004, 22, 1211–1220. [Google Scholar]
- Deng, Y.; Manjunath, B. Unsupervised segmentation of color-texture regions in images and video. IEEE Trans. Pattern Anal. Mach. Intell. 2001, 23, 800–810. [Google Scholar]
- ElAlami, M.E. A novel image retrieval model based on the most relevant features. Knowl.-Based Syst. 2011, 24, 23–32. [Google Scholar]
- Mallat, S.; Peyré, G. A review of bandlet methods for geometrical image representation. Numer. Algorithms 2007, 44, 205–234. [Google Scholar]
- Qu, X.; Yan, J.; Xie, G.; Zhu, Z.; Chen, B. A novel image fusion algorithm based on bandelet transform. Chin. Opt. Lett. 2007, 5, 569–572. [Google Scholar]
- Le Pennec, E.; Mallat, S. Bandelet image approximation and compression. Multiscale Model. Simul. 2005, 4, 992–1039. [Google Scholar]
- Peyré, G.; Mallat, S. Orthogonal bandelet bases for geometric images approximation. Commun. Pure Appl. Math. 2008, 61, 1173–1212. [Google Scholar]
- Weber, M.; Crilly, P.; Blass, W.E. Adaptive noise filtering using an error-backpropagation neural network. IEEE Trans. Instrum. Meas. 1991, 40, 820–825. [Google Scholar]
- Andrysiak, T.; Choraś, M. Image retrieval based on hierarchical Gabor filters. Int. J. Appl. Math. Comput. Sci. 2005, 15, 471–480. [Google Scholar]
- Lam, M.; Disney, T.; Pham, M.; Raicu, D.; Furst, J.; Susomboon, R. Content-based image retrieval for pulmonary computed tomography nodule images. Proc. SPIE. 2007. [Google Scholar] [CrossRef]
- Acharya, T.; Ray, A.K. Image Processing: Principles and Applications; John Wiley & Sons: Napoli, Italy, 2005. [Google Scholar]
- Tao, D.; Tang, X.; Li, X.; Wu, X. Asymmetric bagging and random subspace for support vector machines-based relevance feedback in image retrieval. IEEE Trans. Pattern Anal. Mach. Intell. 2006, 28, 1088–1099. [Google Scholar]
- Yildizer, E.; Balci, A.M.; Hassan, M.; Alhajj, R. Efficient content-based image retrieval using multiple support vector machines ensemble. Expert Syst. Appl. 2012, 39, 2385–2396. [Google Scholar]
- Yu, J.; Qin, Z.; Wan, T.; Zhang, X. Feature integration analysis of bag-of-features model for image retrieval. Neurocomputing 2013, 120, 355–364. [Google Scholar]
- Tian, X.; Jiao, L.; Liu, X.; Zhang, X. Feature integration of EODH and Color-SIFT: Application to image retrieval based on codebook. Signal Process. Image Commun. 2014, 29, 530–545. [Google Scholar]



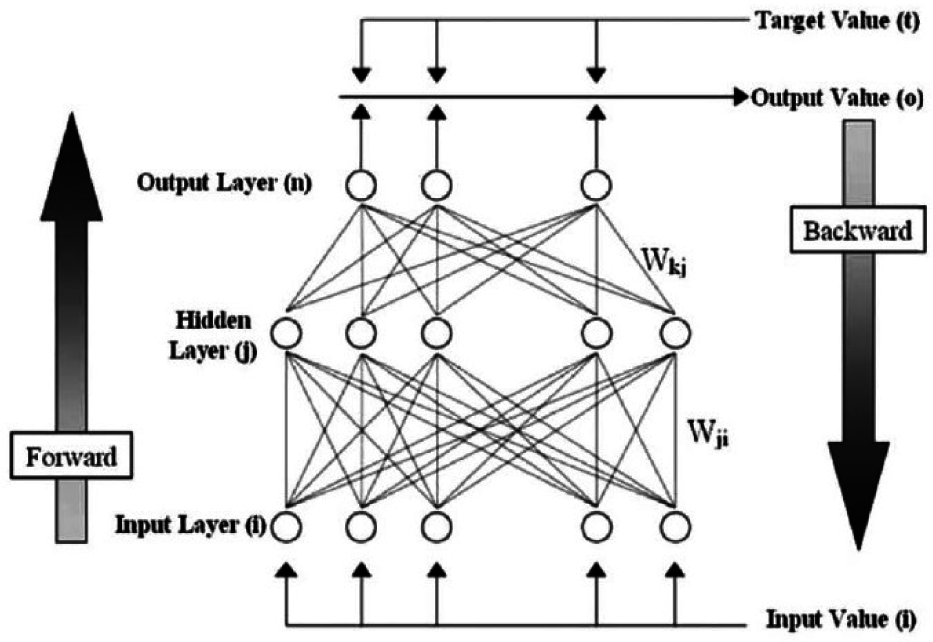

| INPUT | ||
| Input: | ||
| MIDDLE (HIDDEN) LAYER | ||
| Input: | ||
| Output: | ||
| U: | MxN weight matrix | |
| f: | hidden layer activation function | |
| thresholds | ||
| OUTPUT LAYER | ||
| Input: | ||
| Output: | ||
| W: | 1×M weight matrix | |
| g: | output layer activation function | |
| : | thresholds | |
| ERROR CORRECTION | ||
| MSE: | ||
| ΔWij | −α∂E/∂Wij= αδicj | |
| Δti | αδi | |
| ΔUji | −β∂E/∂Uji | |
| Class | Proposed Method | [39] | [31] | [41] | [33] | [37] |
|---|---|---|---|---|---|---|
| Africa | 0.65 | 0.45 | 0.56 | 0.70 | 0.64 | 0.68 |
| Beach | 0.70 | 0.39 | 0.53 | 0.56 | 0.64 | 0.54 |
| Buildings | 0.75 | 0.37 | 0.61 | 0.57 | 0.70 | 0.54 |
| Buses | 0.95 | 0.74 | 0.89 | 0.87 | 0.92 | 0.88 |
| Dinosaurs | 1.00 | 0.91 | 0.98 | 0.97 | 0.99 | 0.99 |
| Elephants | 0.80 | 0.30 | 0.57 | 0.67 | 0.78 | 0.65 |
| Flowers | 0.95 | 0.85 | 0.89 | 0.91 | 0.95 | 0.89 |
| Horses | 0.90 | 0.56 | 0.78 | 0.83 | 0.95 | 0.80 |
| Mountains | 0.75 | 0.29 | 0.51 | 0.53 | 0.74 | 0.52 |
| Food | 0.75 | 0.36 | 0.69 | 0.74 | 0.81 | 0.73 |
| Mean | 0.820 | 0.522 | 0.701 | 0.735 | 0.812 | 0.722 |
| Class | Proposed Method | [39] | [31] | [41] | [33] | [37] |
|---|---|---|---|---|---|---|
| Africa | 0.13 | 0.11 | 0.15 | 0.15 | 0.13 | 0.14 |
| Beach | 0.14 | 0.12 | 0.19 | 0.19 | 0.13 | 0.19 |
| Buildings | 0.15 | 0.12 | 0.18 | 0.18 | 0.14 | 0.17 |
| Buses | 0.19 | 0.09 | 0.11 | 0.11 | 0.18 | 0.12 |
| Dinasours | 0.20 | 0.07 | 0.09 | 0.09 | 0.20 | 0.10 |
| Elephants | 0.16 | 0.13 | 0.15 | 0.15 | 0.16 | 0.14 |
| Flowers | 0.19 | 0.08 | 0.11 | 0.11 | 0.19 | 0.11 |
| Horses | 0.18 | 0.10 | 0.13 | 0.13 | 0.19 | 0.13 |
| Mountains | 0.15 | 0.13 | 0.22 | 0.22 | 0.15 | 0.21 |
| Food | 0.15 | 0.12 | 0.13 | 0.13 | 0.16 | 0.13 |
| Mean | 0.164 | 0.107 | 0.146 | 0.146 | 0.163 | 0.144 |
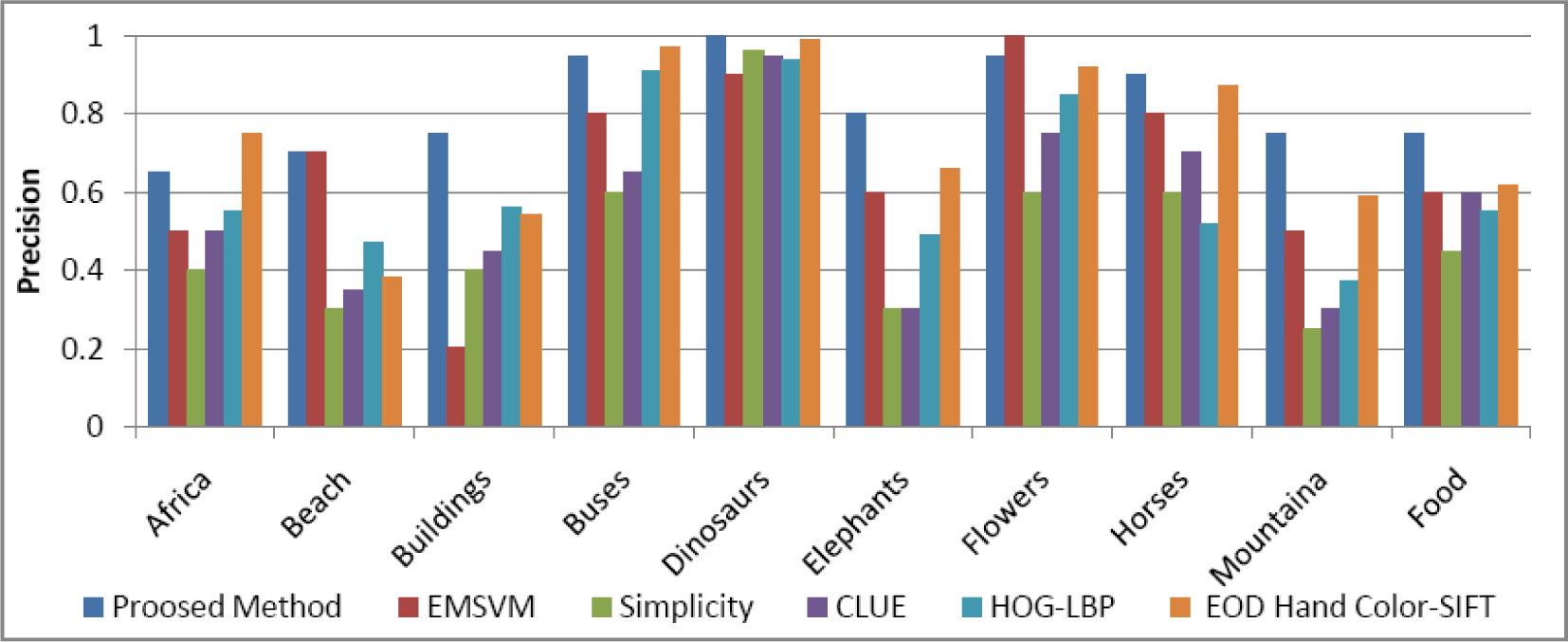
| Class | Proposed Method | EMSVM [51] | Simplicity [22] | CLUE [23] | HOG-LBP [52] | SIFT [53] |
|---|---|---|---|---|---|---|
| Africa | 0.65 | 0.5 | 0.4 | 0.5 | 0.55 | 0.75 |
| Beach | 0.70 | 0.7 | 0.3 | 0.35 | 0.47 | 0.38 |
| Buildings | 0.75 | 0.2 | 0.4 | 0.45 | 0.56 | 0.54 |
| Buses | 0.95 | 0.8 | 0.6 | 0.65 | 0.91 | 0.97 |
| Dinosaurs | 1.00 | 0.9 | 0.96 | 0.95 | 0.94 | 0.99 |
| Elephants | 0.80 | 0.6 | 0.3 | 0.3 | 0.49 | 0.66 |
| Flowers | 0.95 | 1.00 | 0.6 | 0.75 | 0.85 | 0.92 |
| Horses | 0.90 | 0.8 | 0.6 | 0.7 | 0.52 | 0.87 |
| Mountains | 0.75 | 0.5 | 0.25 | 0.3 | 0.37 | 0.59 |
| Food | 0.75 | 0.6 | 0.45 | 0.6 | 0.55 | 0.62 |
| Mean | 0.820 | 0.661 | 0.486 | 0.555 | 0.621 | 0.729 |
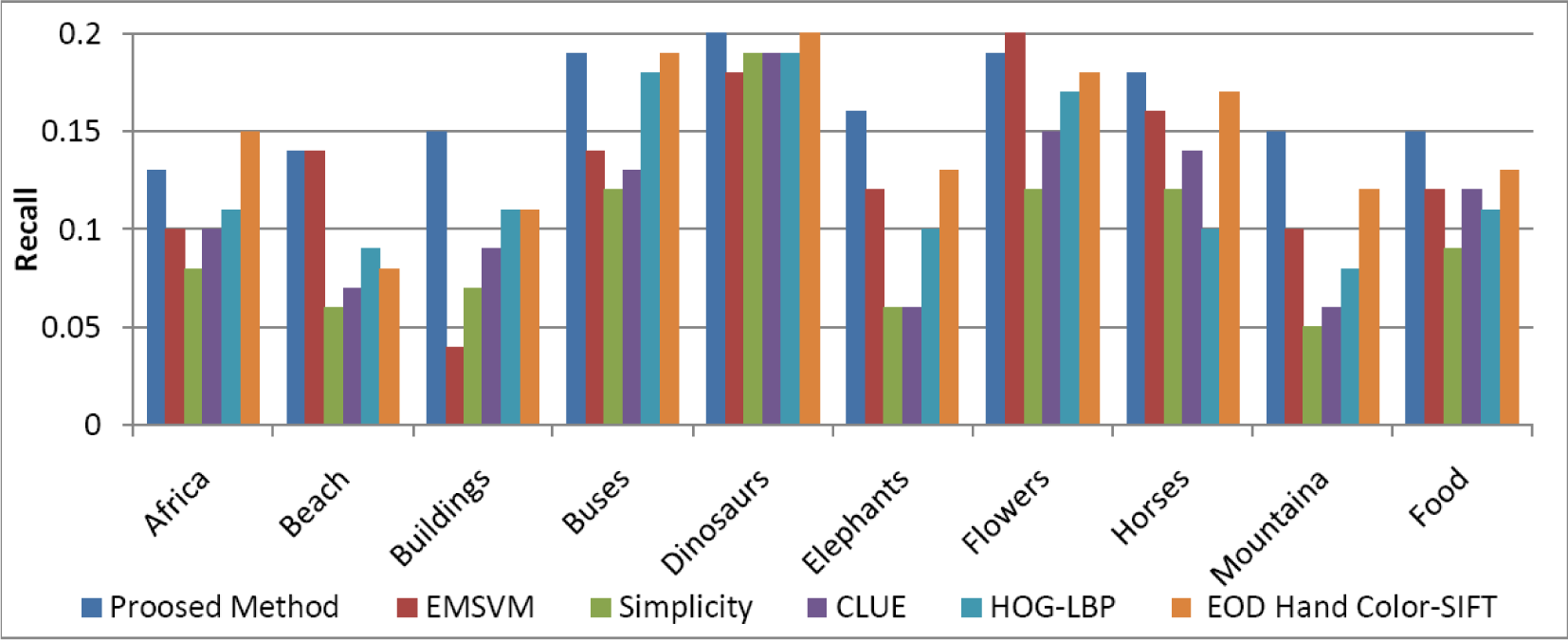
| Class | Proposed Method | EMSVM [51] | Simplicity [22] | CLUE [23] | HOG-LBP [52] | SIFT [53] |
|---|---|---|---|---|---|---|
| Africa | 0.13 | 0.1 | 0.08 | 0.1 | 0.11 | 0.15 |
| Beach | 0.14 | 0.14 | 0.06 | 0.07 | 0.09 | 0.08 |
| Buildings | 0.15 | 0.04 | 0.07 | 0.09 | 0.11 | 0.11 |
| Buses | 0.19 | 0.14 | 0.12 | 0.13 | 0.18 | 0.19 |
| Dinasours | 0.20 | 0.18 | 0.19 | 0.19 | 0.1 | 0.13 |
| Elephants | 0.16 | 0.12 | 0.06 | 0.06 | 0.1 | 0.13 |
| Flowers | 0.19 | 0.2 | 0.12 | 0.15 | 0.17 | 0.18 |
| Horses | 0.18 | 0.16 | 0.12 | 0.14 | 0.1 | 0.17 |
| Mountains | 0.15 | 0.1 | 0.05 | 0.06 | 0.08 | 0.12 |
| Food | 0.15 | 0.12 | 0.09 | 0.12 | 0.11 | 0.13 |
| Mean | 0.164 | 0.130 | 0.096 | 0.111 | 0.124 | 0.146 |
© 2015 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ashraf, R.; Bashir, K.; Irtaza, A.; Mahmood, M.T. Content Based Image Retrieval Using Embedded Neural Networks with Bandletized Regions. Entropy 2015, 17, 3552-3580. https://doi.org/10.3390/e17063552
Ashraf R, Bashir K, Irtaza A, Mahmood MT. Content Based Image Retrieval Using Embedded Neural Networks with Bandletized Regions. Entropy. 2015; 17(6):3552-3580. https://doi.org/10.3390/e17063552
Chicago/Turabian StyleAshraf, Rehan, Khalid Bashir, Aun Irtaza, and Muhammad Tariq Mahmood. 2015. "Content Based Image Retrieval Using Embedded Neural Networks with Bandletized Regions" Entropy 17, no. 6: 3552-3580. https://doi.org/10.3390/e17063552
APA StyleAshraf, R., Bashir, K., Irtaza, A., & Mahmood, M. T. (2015). Content Based Image Retrieval Using Embedded Neural Networks with Bandletized Regions. Entropy, 17(6), 3552-3580. https://doi.org/10.3390/e17063552







