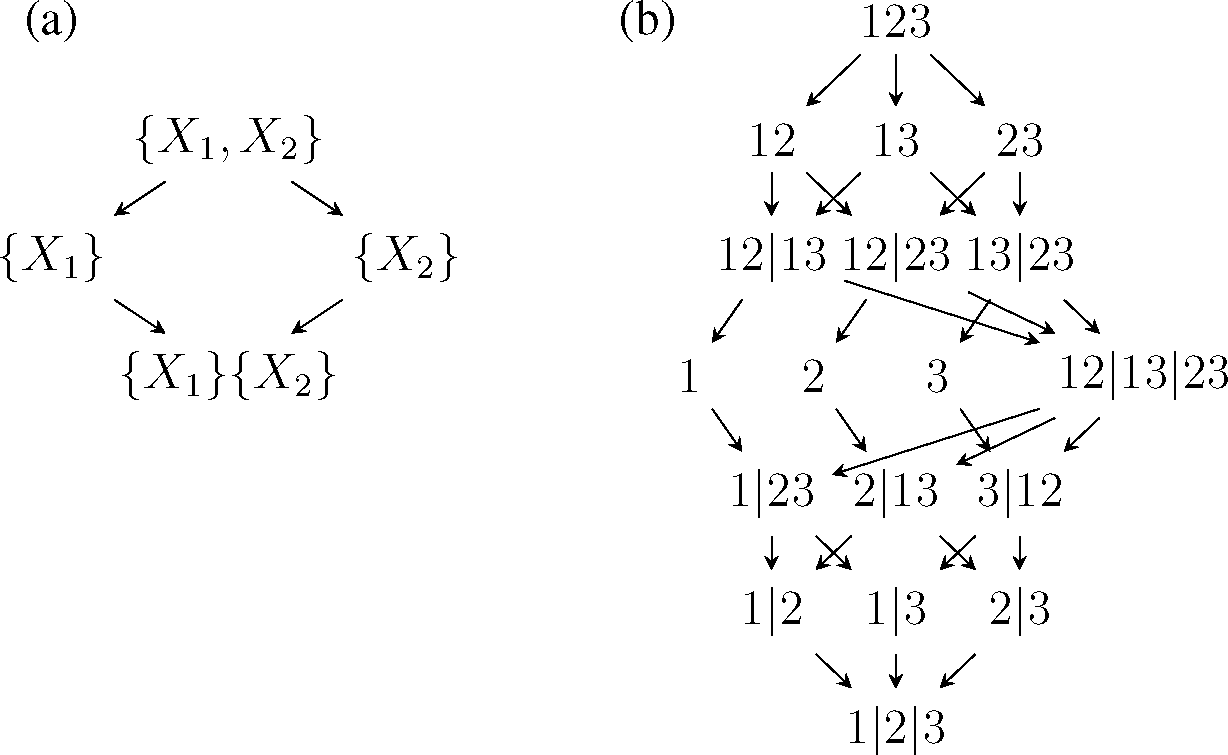For continuous random variables, there is no canonical entropy function. Instead, there is differential entropy, which is computed with respect to some reference measure d
x:
where
p now denotes the probability density of
X with respect to d
x. Taking the Lebesgue measure, the entropy of an
m-dimensional Gaussian random vector with covariance matrix Σ
X is given by:
where |Σ
X| denotes the determinant of Σ
X. This entropy is not invariant under coordinate transformations. In fact, if
A ∈ ℝ
m×m, then the covariance matrix of
AX is given by
AΣ
X At, and so the entropy of
AX is given by:
2.1. Partial Information Lattice
We want to analyze how the information that
X1, … ,
Xn have about
S is distributed among
X1, … ,
Xn. In Shannon’s theory of information, the total amount of information about
S contained in
X1, … ,
Xn is quantified by the mutual information:
We are looking for a way to write
MI(
S :
X1, … ,
Xn) as a sum of non-negative functions with a good interpretation in terms of how the information is distributed, e.g., redundantly or synergistically, among
X1, … ,
Xn. For example, as we have mentioned in the Introduction and as we will see later, several suggestions have been made to measure the total synergy of
X1, … ,
Xn in terms of a function
Synergy(
S :
X1; … ;
Xn). When starting with such a function, the idea of the information decomposition is to further decompose the difference:
as a sum of non-negative functions. The additional advantage of such a complete information decomposition would be to give a better interpretation of the difference
(2), apart from the tautological interpretation that it just measures “everything but the synergy.” Throughout the paper, we will use the following notation: the left argument of the information quantities, the target variable
S, is divided by a colon from the right arguments. The semicolon separates the different arguments on the right side, while comma-separated random variables are treated as a single vector-valued argument.
When looking for such an information decomposition, the first question is what terms to expect. In the case
n = 2, this may seem quite easy, and it seems to be common sense to expect a decomposition of the form:
into four terms corresponding to the redundant (or shared) information
SI(
S :
X1;
X2), the unique information
UI(
S :
X1 \
X2) and
UI(
S :
X2 \
X1) of
X1 and
X2, respectively, and the synergistic (or complementary) information
CI(
S :
X1;
X2).
However, when n > 2, it seems less clear in which different ways X1, … , Xn may interact with each other, combining redundant, unique and synergistic effects.
As a solution, Williams and Beer proposed the partial information framework. We explain the idea only briefly here and refer to [
4] for more detailed explanations. The basic idea is to construct such a decomposition purely in terms of a function for shared information
I∩(
S :
X1; … ;
Xn) that measures the redundant information about
S contained in
X1, … ,
Xn. Clearly, such a function should be symmetric in permutations of
X1, … ,
Xn. In a second step,
I∩ is also used to measure the redundant information
I∩(
S :
A1; … ;
Ak) about
S contained in combinations
A1, … ,
Ak of the original random variables (that is,
A1, … ,
Ak are random vectors whose components are among {
X1, … ,
Xn}). Moreover, Williams and Beer proposed that
I∩ should satisfy the following monotonicity property:
(where the inclusion
Ai ⊆
Ak+1 means that any component of
Ai is also a component of
Ak+1).
The monotonicity property shows that it suffices to consider the function
I∩ in the case where
A1, … ,
Ak form an antichain; that is,
Ai ⊈
Aj for all
i ≠
j. The set of antichains is partially ordered by the relation:
and, again by the monotonicity property,
I∩ is a monotone function with respect to this partial order. This partial order actually makes the set of antichains into a lattice.
If (
B1, … ,
Bl) ≼ (
A1, … ,
Ak), then the difference
I∩(
S :
A1;… ;
Ak) −
I∩(
S :
B1; … ;
Bl) quantifies the information contained in all
Ai, but not contained in some
Bl. The idea of Williams and Beer can be summarized by saying that all information can be classified according to within which antichains it is contained. Thus, the third step is to write:
where the function
I∂ is uniquely defined as the Möbius transform of
I∩ on the lattice of antichains.
For example, the PI lattices for
n = 2 and
n = 3 are given in
Figure 1. For
n = 2, it is easy to make the connection with
(3): The partial measures are:
and the redundancy measure satisfies:
From
(4) and the chain rule for the mutual information:
follows immediately
Even if
I∩ is non-negative (as it should be as an information quantity), it is not immediate that the function
I∂ is also non-negative. This additional requirement was called local positivity in [
5].
While the PI lattice is a beautiful framework, so far, there has been no convincing proposal of how the function
I∩ should be defined. There have been some proposals of functions
I∩(
S :
X1;
X2) with up to two arguments, so-called bivariate information decompositions [
7,
8], but so far, only two general information decompositions are known. Williams and Beer defined a function
Imin that satisfies local positivity, but, as mentioned above, it was found to give unintuitive values in many examples [
5,
6]. In [
5],
Imin was compared with the function:
which was called minimum mutual information (MMI) in [
12] (originally, it was denoted by
II in [
5]). This function has many nice mathematical properties, including local positivity. However,
Immi clearly does not have the right interpretation as measuring the shared information, since
Immi only compares the different amounts of information of
S and
Ai, without checking whether the measured information is really the “same” information [
5]. However, for Gaussian random variables,
Immi might actually lead to a reasonable information decomposition (as discussed in [
12] for the case
n = 2).
2.2. Interaction Spaces
An alternative approach to quantify synergy comes from the idea that synergy among interacting systems has to do with interactions beyond simple pair interactions. We slightly change the notation and now analyze the interaction of n + 1 random variables X0, X1, … , Xn. Later, we will put X0 = S in order to compare the setting of interaction spaces with the setting of information decompositions.
For simplicity, we restrict ourselves here to the discrete setting. Let
be the set of all subsets
A ⊆ {
X0, … ,
Xn} of cardinality |
A| = k. The exponential family of
k-th order interactions
(k) of random variables
X0,
X1, … ,
Xn consists of all distributions of the form:
where Ψ
A is a strictly positive function that only depends on those
xi with
Xi ∈
A. Taking the logarithm, this is equivalent to saying that:
where, again, each function
ψA only depends on those
xi with
Xi ∈
A. This second representation corresponds to the Gibbs–Boltzmann distribution used in statistical mechanics, and it also explains the name exponential family. Clearly,
(1) ⊆
(2) ⊆ … ⊆
(n) ⊆
(n+1).
The set
(k) is not closed (for
k > 0), in the sense that there are probability distributions outside of
(k) that can be approximated arbitrarily well by
k-th order interaction distributions. Thus, we denote by
the closure of
(k) (technically speaking, for probability spaces, there are different notions of approximation and of closure, but in the finite discrete case, they all agree; for example, one may take the induced topology by considering a probability distribution as a vector of real numbers). For example,
contains distributions that can be written as products of non-negative functions
ΨA with zeros. In particular,
consists of all possible joint distributions of
X0, … ,
Xn. However, for 1 <
k ≤ n, the closure of
(k) also contains functions that do not factorize at all (see Section 2.3 in [
13] and the references therein).
Given an arbitrary joint distribution
p of
X0, … ,
Xn, we might ask for the best approximation of
p by a
k-th order interaction distribution
q. It is customary to measure the approximation error in terms of the Kullback-Leibler divergence:
There are many relations between the KL divergence and exponential families. We need the following properties:
Proposition 1. (1).
Let be an exponential family, and let p be an arbitrary distribution. Then, there is a unique distribution p in the closure of that best approximates p, in the sense that:p is called the rI-projection of p to . (2).
If ⊆
′ are two exponential families, then: See [
9,
14] for a proof and further properties of exponential families. The second identity is also called the Pythagorean theorem for exponential families.
In the following, we will abbreviate
q(k) :=
p(k). For example,
q(n+1) =
p. For
n ≥
k > 1, there is no general formula for
q(k). For
k = 1, one can show that:
Thus,
equals the multi-information [
15] (also known as total correlation [
16]) of
X0, … ,
Xn. Applying the Pythagorean theorem
n − 1 times to the hierarchy
(1) ⊆
(
2) ⊆ … ⊆
(n), it follows that:
This equation decomposes the multi-information into terms corresponding to different interaction orders. This decomposition was introduced in [
9] and studied for several examples in [
10] or [
17] with the single terms called connected information or interaction complexities, respectively. The idea that synergy should capture everything beyond pair interactions motivates us to define:
as a measure of synergy. In this interpretation, the synergy of
X0, … ,
Xn is a part of the multi-information of
X0, … ,
Xn. The last sum shows that the hierarchy of interaction families gives a finer decomposition of
S(2) into terms that may be interpreted as “synergy of a fixed order”. In the case
n = 3 that we will study later, there is only one term, since
p = q(3) in this case. Using the maximum entropy principle behind exponential families [
14], the function
S(2) can also be expressed as:
where
denotes the set of all joint distributions r of
X0, … ,
Xn that have the same pair marginals as
p.In contrast, the partial information lattice provides a decomposition of the mutual information and not the multi-information. However, a decomposition of the mutual information
MI(
X0 :
X1, … ,
Xn) can be achieved in a similar spirit as follows. Let
be the set of all subsets
A ⊆ {
X0, … ,
Xn} of cardinality |
A| = k that contain
X0, and let
be the set of all probability distributions of the form:
where the Ψ
A are as above and where Ψ
[n] is a function that only depends on
x1, … ,
xn. As above, each
is an exponential family.
We will abbreviate
. Again, for general
k, there is no formula for
, but for
k = 1, one can show that:
Therefore,
Moreover, by the Pythagorean theorem,
Thus, we obtain a decomposition of the mutual information MI(X0 : X1, … , Xn).
Again, one can group together all terms except the last term that corresponds to the pair interactions and define:
as a measure of synergy. In this interpretation, synergy is a part of the mutual information
MI(
S :
X0, … ,
Xn). Using the maximum entropy principle behind exponential families [
14], the function
Ŝ(2) can also be expressed as:
where:
denotes the set of all joint distributions
r of
X0, … ,
Xn that have the same pair marginals as
p and for which, additionally, the marginal distribution for
X1, … ,
Xn is the same as for
p.While the exponential families (k) are symmetric in all random variables X0, … , Xn, in the definition of
, the variable X0 plays a special role. This is reminiscent of the special role of S in the information decomposition framework, when the goal is to decompose the information about S. Thus, also in Ŝ(2), the variable X0 is special.
There are some relations between the hierarchies (1) ⊆ (2) ⊆ … ⊆ (n) and
.
By definition,
and thus:
In particular,
. Moreover,
, which implies:
In particular, for n = 2, this shows S(2)(S; X; Y) = Ŝ(2)(S : X; Y).
The case
n = 2,
k = 2 is also the case that we are most interested in later for the following reasons. First, for
n = 2, the terms in the partial information lattice have an intuitively clear interpretation. Second, while there are not many examples of full information decompositions for
n > 2, there exist at least two proposals for reasonable measures of shared, unique and complementary information [
7,
8], which allow a direct comparison with measures based on the decompositions using the interaction spaces.
While the symmetric hierarchy of the families (k) is classical, to our best knowledge, the alternative hierarchy of the families
has not been studied before. We do not want to analyze this second hierarchy in detail here, but we just want to demonstrate that the framework of interaction exponential families is flexible enough to give a nice decomposition of mutual information, which can naturally be compared with the information decomposition framework. In this paper, in any case, we only consider cases where
.
It is possible to generalize the definitions of the interaction exponential families to continuous random variables, but there are some technical issues to be solved. For example, the corresponding exponential families will be infinite-dimensional. We will not do this here in detail, since we only need the following observation later: any Gaussian distribution can be described by pair-interactions. Therefore, when p is a multivariate normal distribution, then
.