Entropy Approximation in Lossy Source Coding Problem
Abstract
:1. Introduction
1.1. Motivation
1.2. Main Results
1.3. Discussion
1.4. Paper Organization
2. Entropy Calculation
2.1. Lossy Source Coding and Error-Control Families
2.2. Partition Reduction
 |
3. Entropy Approximation
3.1. Relationship with the Minimum Entropy Set Cover Problem
- choose the most probable type
- if , then assign x to , i.e., put ,
- remove from X (and from all ) the elements of ,
3.2. Greedy Approximation
 |
- For every, there exists, such that:
- For every, there exists, such that:
- To calculate the entropy, it is sufficient to consider only partitions constructed from the elements of σ-algebra generated by (see Corollary 1).
- The calculation of the entropy of an error-control family is closely related to MESC optimization problem (see Theorem 3 and Proposition 2).
4. Conclusion and Future Work
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Berger, T. Lossy source coding. IEEE Trans. Inf. Theory 1998, 44, 2693–2723. [Google Scholar]
- Gray, R.M.; Neuhoff, D.L. Quantization. IEEE Trans. Inf. Theory 1998, 44, 2325–2383. [Google Scholar]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar]
- Bottou, L.; Haffner, P.; Howard, P.G.; Simard, P.; Bengio, Y.; LeCun, Y. High quality document image compression with “DjVu”. J. Electron. Imaging 1998, 7, 410–425. [Google Scholar]
- Kieffer, J.C. A survey of the theory of source coding with a fidelity criterion. IEEE Trans. Inf. Theory 1993, 39, 1473–1490. [Google Scholar]
- Śmieja, M. Weighted approach to general entropy function. IMA J. Math. Control Inf. 2014, 32. [Google Scholar] [CrossRef]
- Śmieja, M.; Tabor, J. Entropy of the mixture of sources and entropy dimension. IEEE Trans. Inf. Theory 2012, 58, 2719–2728. [Google Scholar]
- Śmieja, M.; Tabor, J. Rényi entropy dimension of the mixture of measures. Proceedings of 2014 Science and Information Conference, London, UK, 27–29 August 2014; pp. 685–689.
- Berger, T. Rate-Distortion Theory; Wiley: Hoboken, NJ, USA, 1971. [Google Scholar]
- Ortega, A.; Ramchandran, K. Rate-distortion methods for image and video compression. IEEE Signal Process. Mag. 1998, 15, 23–50. [Google Scholar]
- Gray, R.M. Vector quantization. IEEE ASSP Mag. 1984, 1, 4–29. [Google Scholar]
- Nasrabadi, N.M.; King, R.A. Image coding using vector quantization: A review. IEEE Trans. Commun. 1998, 36, 957–971. [Google Scholar]
- Posner, E.C.; Rodemich, E.R. Epsilon entropy and data compression. Ann. Math. Stat. 1971, 42, 2079–2125. [Google Scholar]
- Posner, E.C.; Rodemich, E.R.; Rumsey, J.H. Epsilon entropy of stochastic processes. Ann. Math. Stat. 1967, 38, 1000–1020. [Google Scholar]
- Rényi, A. On the dimension and entropy of probability distributions. Acta Math. Hungar. 1959, 10, 193–215. [Google Scholar]
- Jayant, N.; Johnston, J.; Safranek, R. Signal compression based on models of human perception. Proc. IEEE 1993, 81, 1385–1422. [Google Scholar]
- Cardinal, J.; Fiorini, S.; Joret, G. Tight results on minimum entropy set cover. Algorithmica 2008, 51, 49–60. [Google Scholar]
- Halperin, E.; Karp, R.M. The minimum-entropy set cover problem. Theor. Comput. Sci. 2005, 348, 240–250. [Google Scholar]
- Kingman, J.F.C.; Taylor, S.J. Introduction to measures and probability; Cambridge University Press: Cambridge, UK, 1966. [Google Scholar]
- Bercher, J.F. Source coding with escort distributions and Rényi entropy bounds. Phys. Lett. A 2009, 373, 3235–3238. [Google Scholar]
- Czarnecki, W.M.; Tabor, J. Multithreshold entropy linear classifier: Theory and applications. Expert Syst. Appl. 2015, 42, 5591–5606. [Google Scholar]
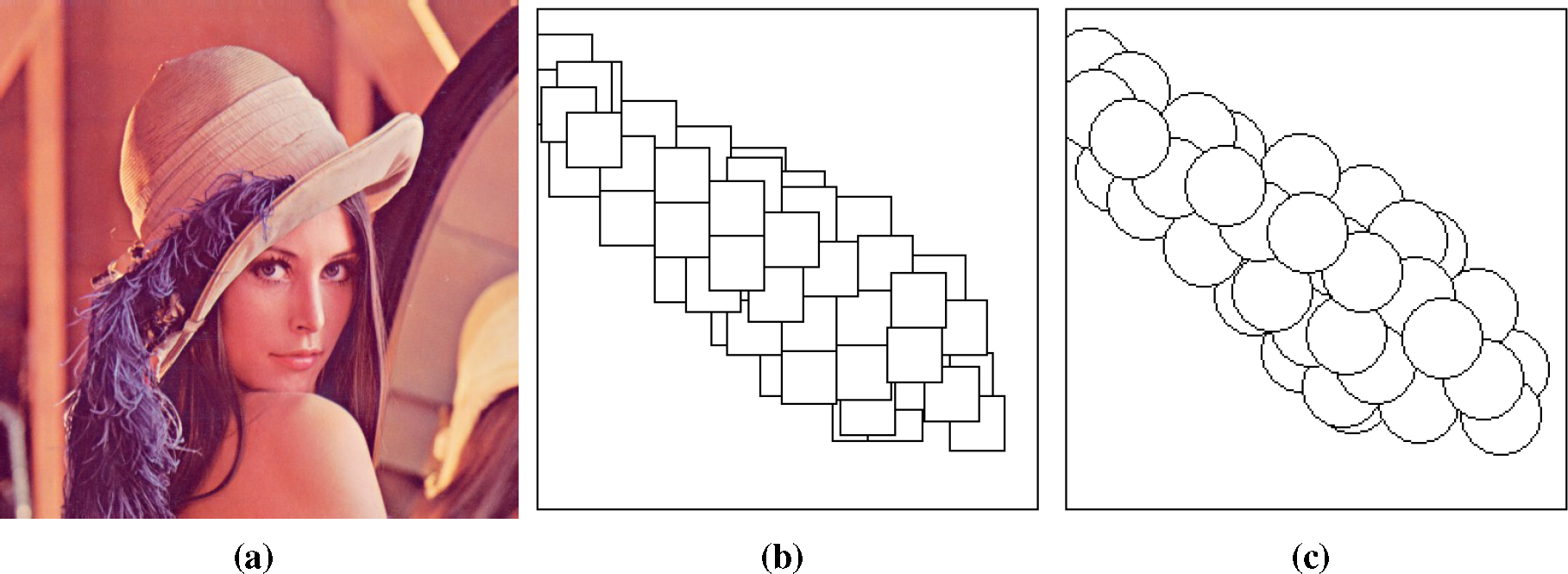
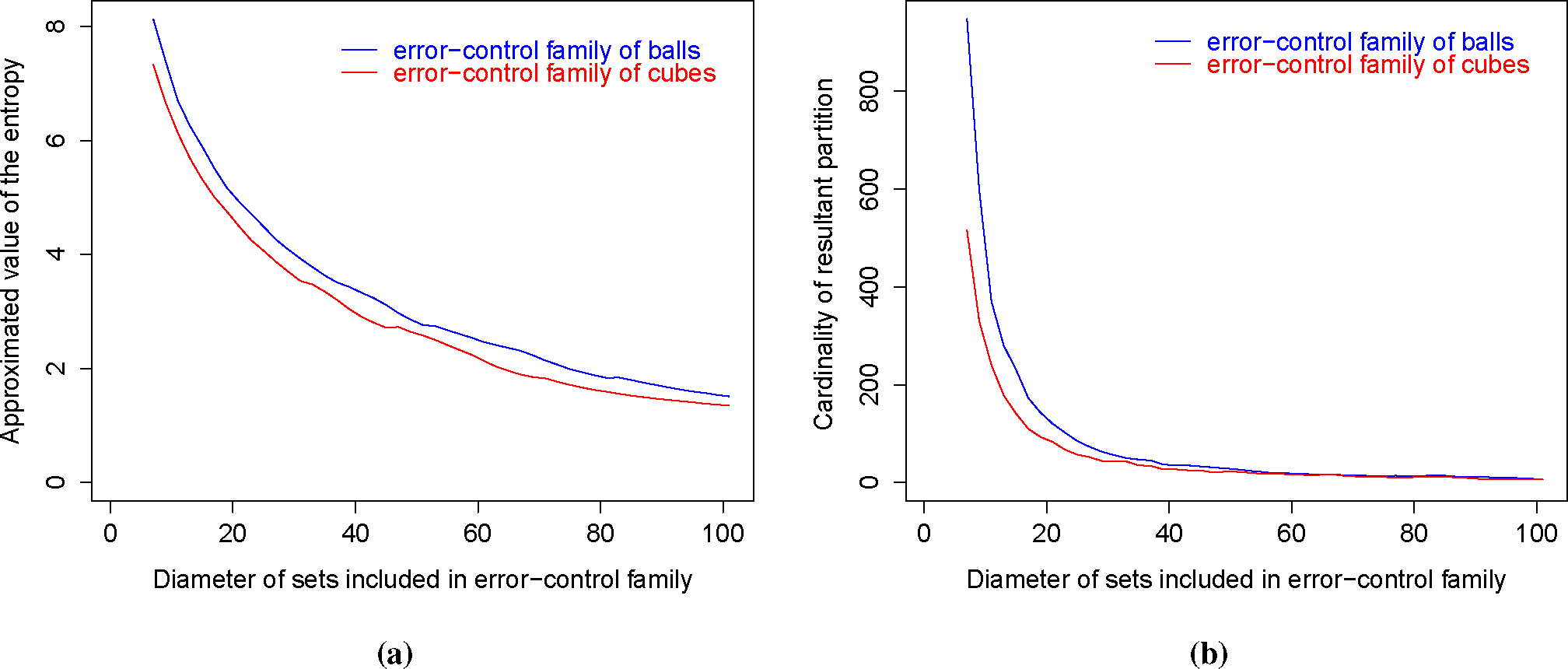
| (a)
| ||
|---|---|---|
| δ | ||
| 3 | 12.73 | 12.59 |
| 5 | 10.81 | 10.83 |
| 9 | 8.62 | 8.62 |
| 15 | 6.95 | 6.72 |
| (b)
| ||
|---|---|---|
| δ | ||
| 5 | 14.11 | 12.25 |
| 9 | 10.81 | 9.87 |
| 17 | 8.62 | 7.23 |
| 25 | 7.15 | 5.82 |
© 2015 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Śmieja, M.; Tabor, J. Entropy Approximation in Lossy Source Coding Problem. Entropy 2015, 17, 3400-3418. https://doi.org/10.3390/e17053400
Śmieja M, Tabor J. Entropy Approximation in Lossy Source Coding Problem. Entropy. 2015; 17(5):3400-3418. https://doi.org/10.3390/e17053400
Chicago/Turabian StyleŚmieja, Marek, and Jacek Tabor. 2015. "Entropy Approximation in Lossy Source Coding Problem" Entropy 17, no. 5: 3400-3418. https://doi.org/10.3390/e17053400
APA StyleŚmieja, M., & Tabor, J. (2015). Entropy Approximation in Lossy Source Coding Problem. Entropy, 17(5), 3400-3418. https://doi.org/10.3390/e17053400





