A Mean-Variance Hybrid-Entropy Model for Portfolio Selection with Fuzzy Returns
Abstract
:1. Introduction
2. Mean-Variance Hybrid-Entropy Portfolio Optimization Model
2.1. Fuzzy Returns Predicted by the Markov Method
2.1.1. The Expected Value and Variance of the Triangular Fuzzy Returns
2.1.2. Prediction of Stock Returns
- Step 1. Collect the historical trading data in a sample period (in this paper, it is one year or three years), including the opening price Rt1, closing price Rt2, ceiling price Rt3 and floor price Rt4, t = 1,2, …, N, where N is the number of sub-intervals. Then we calculate the possible average rates of returns , the highest possible rates of returns , and the lowest possible rates of returns .
- Step 2. Use the classic K-Means cluster analysis method to get the step transition matrix. We divide the range of rate of return into M intervals called state spaces and get mid-points di(i = 1,2, …, M) and probability pij(i, j = 1,2, …, M) that the return is in space j if it was in space i the last state. Then form one step transition matrix by these probabilities:
- Step 3. Develop the state transition equation. The probability of stock return in state space i can be calculated by:where x = (x1, x2, …, xM)T, x1, x2, …, xM ≥ 0, .The unique solution of the equation is x = (p1, p2, …, pM)T. Therefore the probabilities of the stock return in state space i after a long enough time are p1, p2, …, pM.
- Step 4. Compute the prediction of the stock return by function . The highest possible rate of return rth and lowest possible rate of return rtl can be calculated in the same way. That is how we get the value of the ceiling return bi and the floor return ai. Hence, the prediction of our triangular fuzzy returns turns out to be .
2.2. Hybrid Entropy
- Hh will reach its biggest value if and only if μi = 0.5 and pi = 1/n (i = 1,2,…,n);
- Hh will reach its smallest value 0 if and only if μi = 0 or 1 (i = 1,2, …, n), pi = 1 and pj = 0(j ≠ i,i,j = 1,2,…,n);
- When randomness (ambiguity) disappears, hybrid entropy should be reduced to a normal probability entropy (fuzzy entropy).
2.3. Portfolio Optimization Model
2.3.1. MVM and MEM
2.3.2. MVHEM
3. Empirical Comparisons
3.1. Sample Data
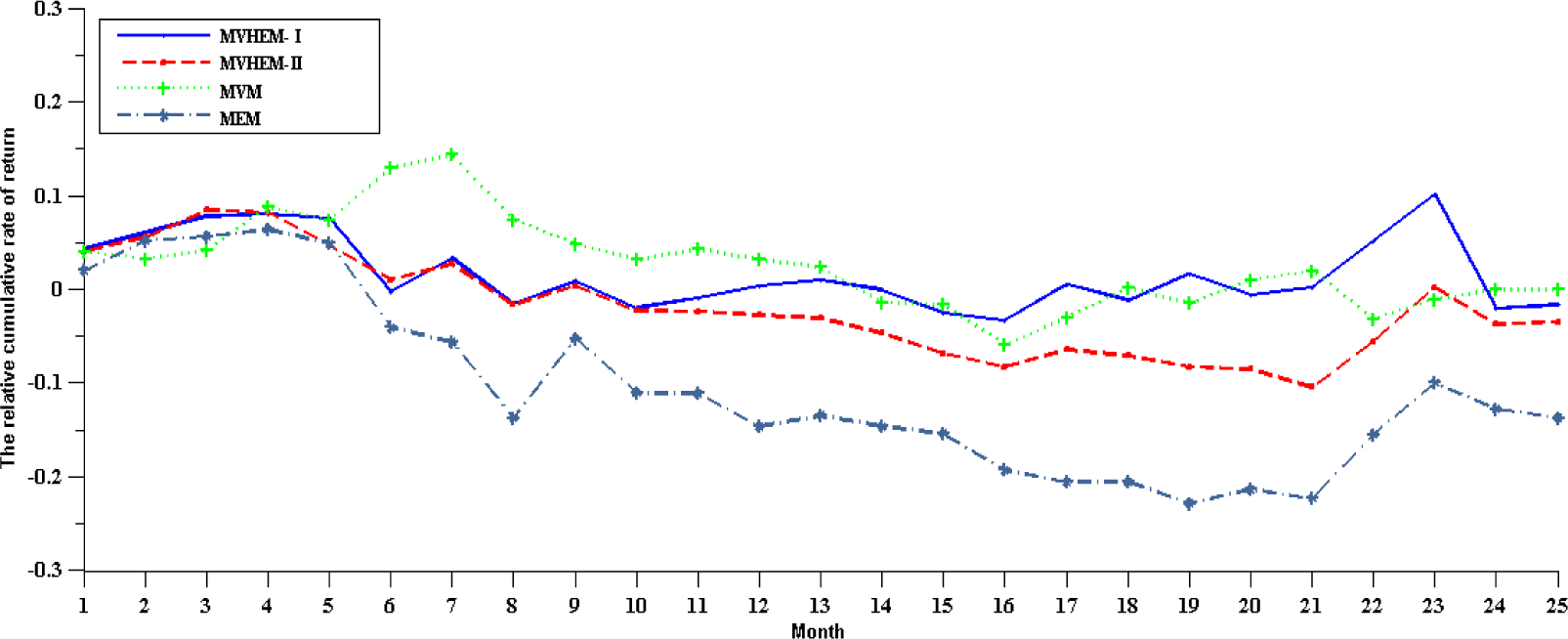
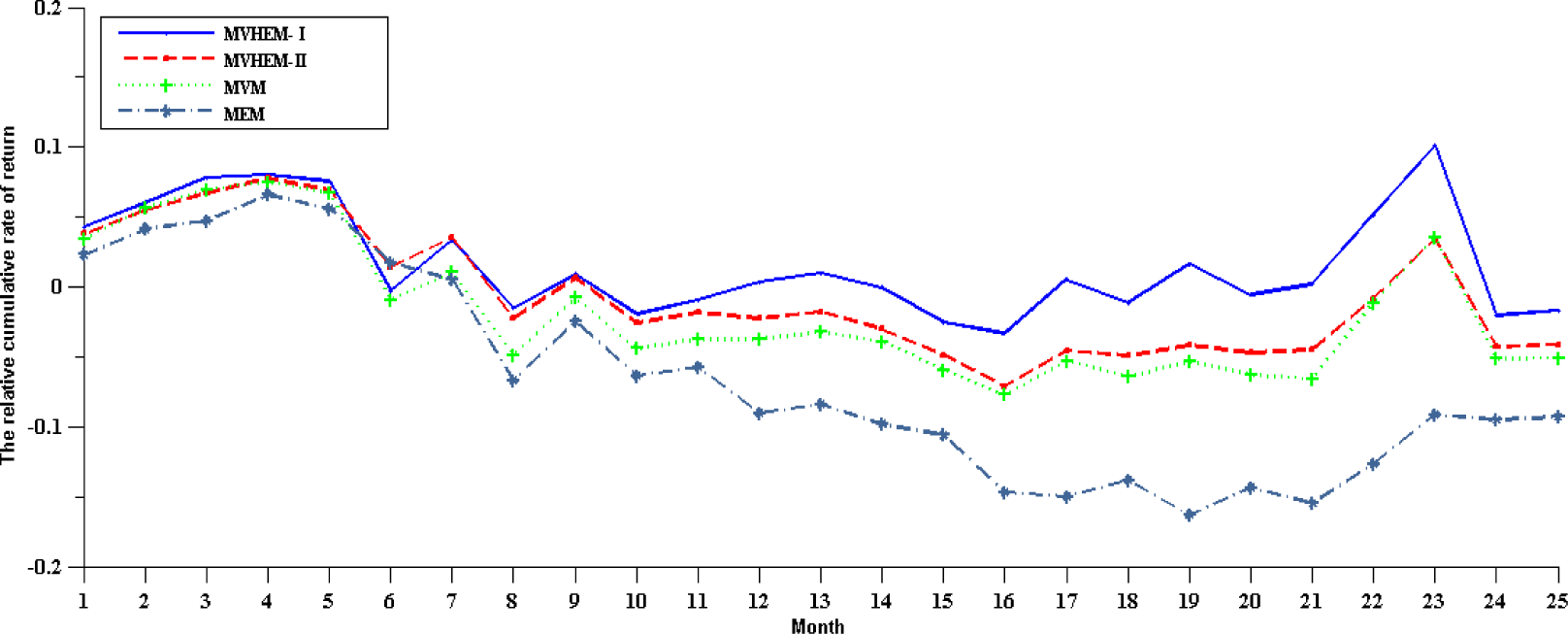
3.2. The Empirical Comparisons among MVM, MEM and MVHEM
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Markowitz, H. Portfolio selection. J. Financ. 1952, 7, 77–91. [Google Scholar]
- Watada, J. Fuzzy portfolio selection and its applications to decision making. Tatra Mt. Math. Publ. 1997, 13, 219–248. [Google Scholar]
- Ostermask, R. A fuzzy control model for dynamic portfolio management. Fuzzy Sets Syst. 1998, 78, 243–254. [Google Scholar]
- Li, X.; Qin, Z.F.; Kar, S. Mean-variance-skewness model for portfolio selection with fuzzy returns. Eur. J. Oper. Res. 2010, 202, 239–247. [Google Scholar]
- Doumpos, M.; Zopounidis, C.; Pardalos, P.M. Financial Decision Making Using Computational Intelligence. Springer Optim. Appl. 2012, 70, 253–280. [Google Scholar]
- Zhang, W.G.; Liu, Y.J.; Xu, W.J. A new fuzzy programming approach for multi-period portfolio optimization with return demand and risk control. Fuzzy Sets Syst. 2014, 246, 107–126. [Google Scholar]
- Markowitz, H. Portfolio Selection: Efficient Diversification of Investments; Wiley: New York, NY, USA, 1959. [Google Scholar]
- Konno, H.; Yamazaki, H. Mean-absolute deviation portfolio optimization model and its applications to Tokyo stock market. Manag. Sci. 1991, 37, 519–529. [Google Scholar]
- Young, M.R. A minimax portfolio selection rule with linear programming solution. Manag. Sci. 1998, 44, 673–683. [Google Scholar]
- Cai, X.Q.; Teo, K.L.; Yang, X.Q.; Zhou, X.Y. Portfolio optimization under a minimax rule. Manag. Sci. 2000, 46, 957–972. [Google Scholar]
- Bawa, V.S. Optimal rules for ordering uncertain prospects. J. Financ. Econ. 1975, 2, 95–121. [Google Scholar]
- Jana, P.; Roy, T.K.; Mazumder, S.K. Multi-objective mean-variance-skewness model for portfolio optimization. Appl. Math. Optim. 2007, 9, 181–193. [Google Scholar]
- Yu, M.; Zhou, R.X.; Wu, M. Study on the Model Selection in Portfolio Management—Models and empirical analysis based on Chinese stock market. J. Quant. Tech. Econ. 2013, 30, 98–110. [Google Scholar]
- Zhou, R.X.; Cai, R.; Tong, G.Q. Applications of Entropy in Finance: A Review. Entropy 2013, 15, 4909–4931. [Google Scholar]
- Philippatos, G.C.; Wilson, C.J. Entropy, market risk, and the selection of efficient portfolios. Appl. Econ. 1972, 4, 209–220. [Google Scholar]
- Cheng, P.; Wolverton, M.L. MPT and the downside risk framework: A comment on two recent studies. J. Real Estate Portf. Manag. 7, 125–31.
- Ou, J.S. Theory of portfolio and risk based on incremental entropy. J. Risk Financ. 2005, 6, 31–39. [Google Scholar]
- Bera, A.K.; Park, S.Y. Optimal portfolio diversification using the maximum entropy principle. Economet. Rev. 2008, 27, 484–512. [Google Scholar]
- Huang, X.X. Mean-entropy models for fuzzy portfolio selection. IEEE Trans. Fuzzy Syst. 2008, 16, 1096–1101. [Google Scholar]
- Usta, I.; Kantar, Y.M. Mean-Variance-Skewness-Entropy Measures: A Multi-Objective Approach for Portfolio Selection. Entropy 2011, 13, 117–133. [Google Scholar]
- Xu, J.P.; Zhou, X.Y.; Wu, D.D. Portfolio selection using λ mean and hybrid entropy. Ann. Oper. Res. 2011, 185, 213–229. [Google Scholar]
- Yu, J.R.; Lee, W.Y.; Chiou, W.J.P. Diversified portfolios with different entropy measures. Appl. Math. Comput. 2014, 241, 47–63. [Google Scholar]
- Zhou, R.X.; Wang, X.G.; Dong, X.F.; Zong, Z. Portfolio selection model with the measures of information entropy-incremental entropy-skewness. Adv. Inf. Sci. Serv. Sci. 2013, 5, 853–864. [Google Scholar]
- Zhang, W.G.; Liu, Y.J.; Xu, W.J. A possibilistic mean-semivariance-entropy model for multi-period portfolio selection with transaction costs. Eur. J. Oper. Res. 2012, 222, 341–349. [Google Scholar]
- Liu, B. A survey of credibility theory. Fuzzy Optim. Decision Making. 2006, 5, 387–408. [Google Scholar]
- Kalyagin, V.A.; Pardalos, P.M.; Rassias, T.M. Network Models in Economics and Finance. Springer Optim. Appl. 2014, 100, 127–146. [Google Scholar]
- De Luca, A.; Termini, S. A definition of a nonprobabilistic entropy in the setting of fuzzy sets theory. Inf. Control. 1972, 20, 301–302. [Google Scholar]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multi-objective genetic algorithm; NSGA-II. IEEE Trans. on Evolut. Comput. 2002, 6, 182–197. [Google Scholar]


| Sample Period
| One-Year Period | Three-Year Period |
|---|---|---|
| Stock Code | ||
| 600100 | (−0.0314, 0.0070, 0.0494) | (−0.0398, −0.0042, 0.0391) |
| 600270 | (−0.0411, 0.0095, 0.0583) | (−0.0365, 0.0026, 0.4238) |
| 600109 | (−0.0433, 0.0009, 0.0496) | (−0.0441, 0.0027, 0.0464) |
| 600664 | (−0.0382, 0.0008, 0.0349) | (−0.0458, −0.0078, 0.0275) |
| 600060 | (−0.0445, 0.0045, 0.0527) | (−0.0418, 0.0018, 0.0450) |
| 600714 | (−0.0392, −0.0065, 0.0399) | (−0.0511, −0.0008, 0.0512) |
| 600886 | (−0.0351, −0.0043, 0.0353) | (−0.0321, −0.0025, 0.0277) |
| 600638 | (−0.0357, 0.0057, 0.0420) | (−0.0347, 0.0030, 0.0374) |
| 600778 | (−0.0354, −0.0031, 0.0362) | (−0.0414, −0.0009, 0.0389) |
| 600081 | (−0.0409, 0.0058, 0.0527) | (−0.0008, −0.0008, 0.0462) |
| Sample Period
| One-Year Period | Three-Year Period |
|---|---|---|
| Stock Code | ||
| 002186 | (−0.0380, −0.0042, 0.0428) | (−0.0312,−0.0015,0.0313) |
| 000791 | (−0.0364, 0.0017, 0.0400) | (−0.0403, 0.0012, 0.0446) |
| 002032 | (−0.0329, 0.0031, 0.0444) | (−0.0382, −0.0026, 0.0351) |
| 000002 | (−0.0416, −0.0045, 0.0387) | (−0.0346, 0.0004, 0.0338) |
| 000768 | (−0.0357, 0.0045, 0.0513) | (−0.0347, −0.0005, 0.0414) |
| 002226 | (−0.0331, 0.0037, 0.0414) | (−0.0416, −0.0024, 0.0373) |
| 300027 | (−0.0598, 0.0284, 0.1017) | (−0.0466, 0.0055, 0.0579) |
| 000088 | (−0.0386, 0.0114, 0.0569) | (−0.0357, 0.0017, 0.0361) |
| 300005 | (−0.0531, 0.0025, 0.0549) | (−0.0488, −0.0020, 0.0464) |
| 000001 | (−0.0501, 0.0000, 0.0573) | (−0.0338, 0.0001, 0.0343) |
| Sample Period
| One-Year Period
| Three-Year Period
| ||
|---|---|---|---|---|
| Stock Code | Expected Value | Hybrid Entropy | Expected Value | Hybrid Entropy |
| 600100 | 0.0079 | 0.6303 | −0.0023 | 0.6237 |
| 600270 | 0.0091 | 0.7088 | 0.0028 | 0.5525 |
| 600109 | 0.0020 | 0.5320 | 0.0019 | 0.5852 |
| 600664 | −0.0004 | 1.0954 | −0.0085 | 1.0520 |
| 600060 | 0.0043 | 0.6288 | 0.0017 | 0.4766 |
| 600714 | −0.0031 | 0.6598 | −0.0004 | 0.6944 |
| 600886 | −0.0021 | 0.6981 | −0.0023 | 0.6944 |
| 600638 | 0.0044 | 1.1528 | 0.0022 | 0.6767 |
| 600778 | −0.0014 | 0.6217 | −0.0011 | 0.5536 |
| 600081 | 0.0058 | 0.6796 | 0.0109 | 0.3789 |
| Sample Period
| One-Year Period
| Three-Year Period
| ||
|---|---|---|---|---|
| Stock Code | Expected Value | Hybrid Entropy | Expected Value | Hybrid Entropy |
| 002186 | −0.0009 | 1.1940 | −0.0007 | 1.0360 |
| 000791 | 0.0017 | 0.6555 | 0.0017 | 0.6981 |
| 002032 | 0.0044 | 1.1211 | −0.0020 | 0.9846 |
| 000002 | −0.0029 | 0.7656 | 0.0000 | 0.5124 |
| 000768 | 0.0061 | 0.5451 | 0.0014 | 0.3668 |
| 002226 | 0.0039 | 0.5890 | −0.0023 | 1.1131 |
| 300027 | 0.0247 | 0.6167 | 0.0056 | 0.7336 |
| 000088 | 0.0103 | 1.1977 | 0.0009 | 0.7219 |
| 300005 | 0.0017 | 0.6466 | −0.0016 | 0.9808 |
| 000001 | 0.0018 | 0.7208 | 0.0002 | 0.5996 |
| Stock Code
| 600100 | 600270 | 600109 | 600664 | 600060 | 600714 | 600886 | 600638 | 600778 | 600081 |
|---|---|---|---|---|---|---|---|---|---|---|
| Model | ||||||||||
| MVHEM-I | 0.2402 | 0.1574 | 0.1222 | 0.0359 | 0.1590 | 0.0378 | 0.0529 | 0.0416 | 0.0997 | 0.0535 |
| MVHEM-II | 0.0551 | 0.1067 | 0.0452 | 0.1804 | 0.2603 | 0.0544 | 0.0654 | 0.1907 | 0.0193 | 0.0220 |
| MVM | 0.1500 | 0.7054 | 0.0189 | 0.0012 | 0.0246 | 0.0053 | 0.0004 | 0.0459 | 0.0209 | 0.0281 |
| MEM | 0.9153 | 0.0019 | 0.0779 | 0.0002 | 0.0002 | 0.0005 | 0.0017 | 0.0002 | 0.0003 | 0.0008 |
| Stock Code
| 600100 | 600270 | 600109 | 600664 | 600060 | 600714 | 600886 | 600638 | 600778 | 600081 |
|---|---|---|---|---|---|---|---|---|---|---|
| Model | ||||||||||
| MVHEM-I | 0.0102 | 0.0916 | 0.0651 | 0.0231 | 0.0457 | 0.0741 | 0.0920 | 0.0690 | 0.0626 | 0.4650 |
| MVHEM-II | 0.0022 | 0.0795 | 0.0450 | 0.0149 | 0.0372 | 0.0500 | 0.4470 | 0.0582 | 0.0553 | 0.2090 |
| MVM | 0.0015 | 0.0294 | 0.0844 | 0.0000 | 0.1065 | 0.0003 | 0.0001 | 0.0272 | 0.0002 | 0.7490 |
| MEM | 0.0069 | 0.0565 | 0.0146 | 0.0062 | 0.0412 | 0.0147 | 0.1096 | 0.0514 | 0.0306 | 0.6672 |
| Stock Code
| 002186 | 000791 | 002032 | 000002 | 000768 | 002226 | 300027 | 000088 | 300005 | 000001 |
|---|---|---|---|---|---|---|---|---|---|---|
| Model | ||||||||||
| MVHEM-I | 0.0218 | 0.0485 | 0.0369 | 0.0248 | 0.2721 | 0.2360 | 0.1991 | 0.0205 | 0.0697 | 0.0698 |
| MVHEM-II | 0.0551 | 0.1067 | 0.0452 | 0.1804 | 0.2603 | 0.0544 | 0.0654 | 0.1907 | 0.0193 | 0.0220 |
| MVM | 0.1500 | 0.7054 | 0.0189 | 0.0012 | 0.0246 | 0.0053 | 0.0004 | 0.0459 | 0.0209 | 0.0281 |
| MEM | 0.9153 | 0.0019 | 0.0779 | 0.0002 | 0.0002 | 0.0005 | 0.0017 | 0.0002 | 0.0003 | 0.0008 |
| Stock Code
| 002186 | 000791 | 002032 | 000002 | 000768 | 002226 | 300027 | 000088 | 300005 | 000001 |
|---|---|---|---|---|---|---|---|---|---|---|
| Model | ||||||||||
| MVHEM-I | 0.0002 | 0.0544 | 0.0182 | 0.0687 | 0.6542 | 0.0016 | 0.0948 | 0.0239 | 0.0231 | 0.0456 |
| MVHEM-II | 0.1518 | 0.0463 | 0.0116 | 0.0533 | 0.4074 | 0.0147 | 0.2351 | 0.0196 | 0.0203 | 0.0398 |
| MVM | 0.0153 | 0.0533 | 0.0037 | 0.0384 | 0.4796 | 0.0102 | 0.2885 | 0.0161 | 0.0183 | 0.0772 |
| MEM | 0.2690 | 0.0125 | 0.0302 | 0.0050 | 0.0138 | 0.0394 | 0.5278 | 0.0689 | 0.0008 | 0.0329 |
© 2015 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, R.; Zhan, Y.; Cai, R.; Tong, G. A Mean-Variance Hybrid-Entropy Model for Portfolio Selection with Fuzzy Returns. Entropy 2015, 17, 3319-3331. https://doi.org/10.3390/e17053319
Zhou R, Zhan Y, Cai R, Tong G. A Mean-Variance Hybrid-Entropy Model for Portfolio Selection with Fuzzy Returns. Entropy. 2015; 17(5):3319-3331. https://doi.org/10.3390/e17053319
Chicago/Turabian StyleZhou, Rongxi, Yu Zhan, Ru Cai, and Guanqun Tong. 2015. "A Mean-Variance Hybrid-Entropy Model for Portfolio Selection with Fuzzy Returns" Entropy 17, no. 5: 3319-3331. https://doi.org/10.3390/e17053319
APA StyleZhou, R., Zhan, Y., Cai, R., & Tong, G. (2015). A Mean-Variance Hybrid-Entropy Model for Portfolio Selection with Fuzzy Returns. Entropy, 17(5), 3319-3331. https://doi.org/10.3390/e17053319






