Maximum Entropy Method for Operational Loads Feedback Using Concrete Dam Displacement
Abstract
:1. Introduction
2. Interpretation Model of Concrete Dam Displacement
3. Maximum Entropy Method for the Control Loads Feedback
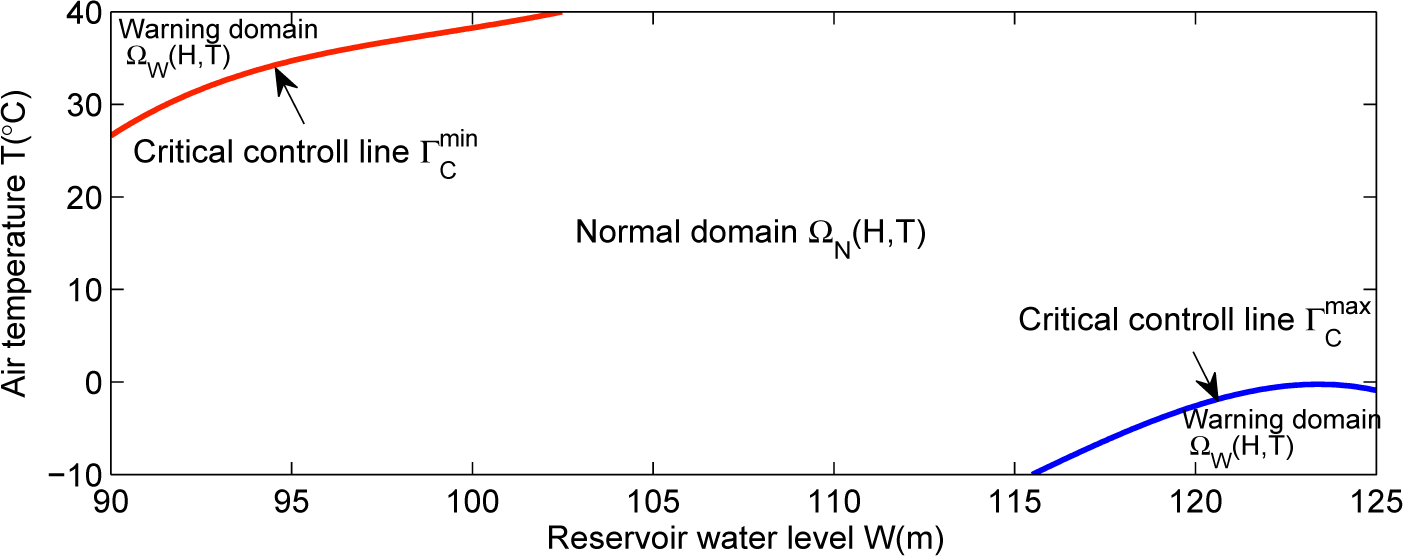
3.1. Warning Criterion for Dam Displacement
3.2. Maximum Entropy Method for the Determination of Critical Load Effect Component
3.3. Control Loads Feedback for Dam Displacement
4. Numerical Example
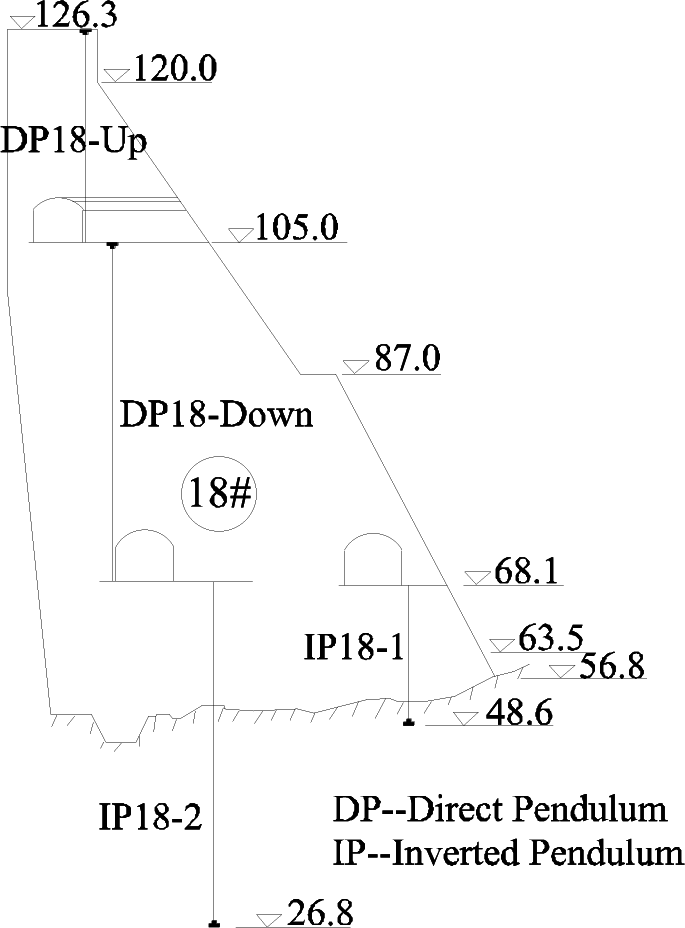
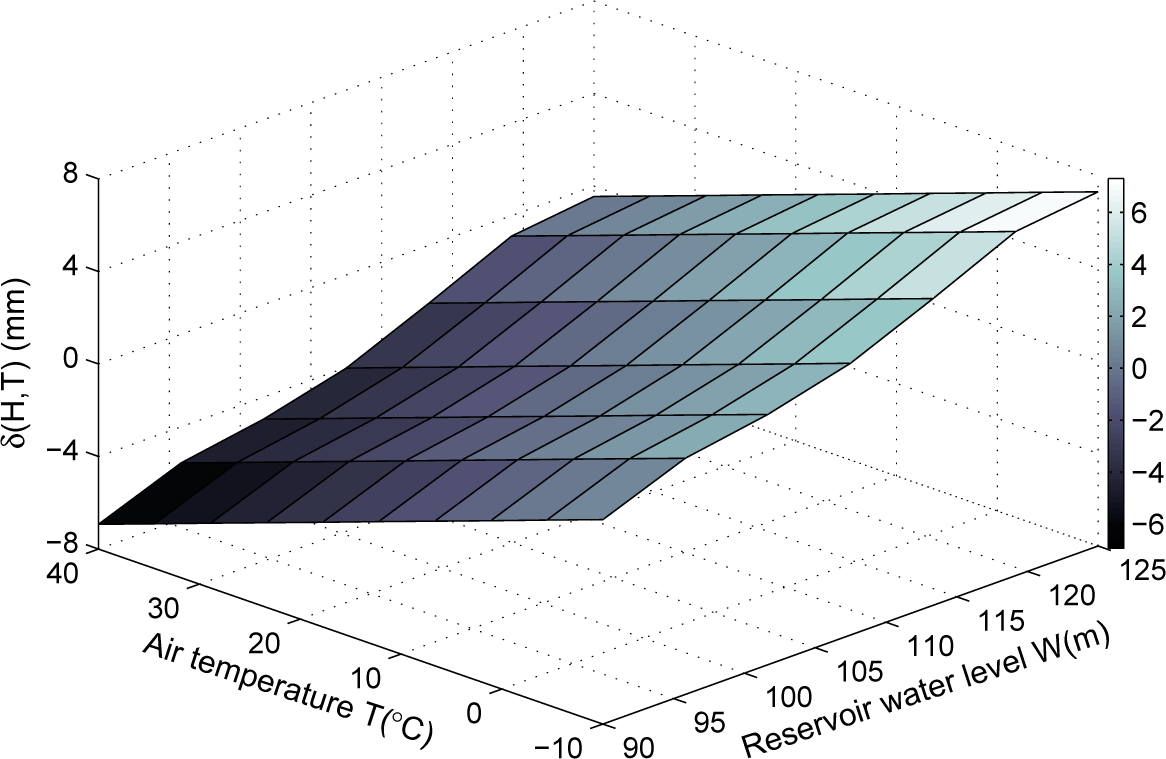
4.1. Interpretation Model of Dam Displacement
4.2. Determination of the Critical Load Effect Component by the Maximum Entropy Method
4.3. Control Loads Feedback for Dam Displacement
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- ICOLD, World Register of Dams; International Commission on Large Dams: Paris, France, 1988.
- ICOLD, Automated Observation for the Safety Control of Dams; International Commission on Large Dams: Paris, France, 1982.
- Wu, Z.R.; Gu, C.S. Safety Monitoring Theories of Hydraulic Structures and Their Application; Higher Education Process: Beijing, China, 2003; in Chinese. [Google Scholar]
- Rocha, M. A quantitative method for the interpretation of the results of the observation of dams. Proceedings of VI Congress on Large Dams, New York, NY, USA; 1958. [Google Scholar]
- Pierre, L.; Martin, L. Hydrostatic, temperature, time-displacement model for concrete dams. J. Eng. Mech 2007, 133, 267–277. [Google Scholar]
- De Sortis, A.; Paoliani, P. Statistical analysis and structural identification in concrete dam monitoring. Eng. Struct 2007, 29, 110–120. [Google Scholar]
- Mata, J.; de Castro, A.T.; da Costa, J.S. Constructing statistical models for arch dam deformation. Struct. Control Health. Monit 2014, 21, 423–437. [Google Scholar]
- Mata, J. Interpretation of concrete dam behaviour with artificial neural network and multiple linear regression models. Eng. Struct 2011, 33, 903–910. [Google Scholar]
- Gu, C.S.; Sha, Y.C. Feedback analysis method of operation and control load conditions of the dam with slot. Water Power 2002, 30–32, in Chinese. [Google Scholar]
- Li, X.H. Evolution rule and abnormality diagnosis of crack of important hydraulic concrete structure. In Ph.D. Thesis; Hohai University: Nanjing, China, 2003; in Chinese. [Google Scholar]
- Lei, P.; Xiao, F.; Su, H.Z. Analysis of control loads on concrete dam during operation. Water Resour. Hydropower Eng 2011, 42, 8–11, in Chinese. [Google Scholar]
- Jaynes, E.T. Information theory and statistical mechanics. Phys. Rev 1957, 106, 620–630. [Google Scholar]
- Jaynes, E.T. Information theory and statistical mechanics II. Phys. Rev 1957, 108, 171–190. [Google Scholar]
- Jaynes, E.T. On the rationale of maximum entropy methods. Proc. IEEE 1982, 70, 939–952. [Google Scholar]
- Zhang, G.; Zhu, W.S.; Bai, S.W. A method of maximum entropy density function calculations of approximate failure probability. Chin. J. Rock Mech. Eng 1995, 14, 119–129, in Chinese. [Google Scholar]
- Zhou, C.X.; Shen, X.D.; Wang, L.P.; Wang, H.L. The principle of maximum entropy in analysis of hydraulic construction reliability. J. Fuzhou Univ 2005, 115–118, in Chinese. [Google Scholar]
- Chen, B.; Liu, N.; Zhou, J.S. Principle of maximum entropy for back analysis in geotechnical engineering. J. Hohai Univ 2002, 30, 52–55, in Chinese. [Google Scholar]
- Deng, J.; Li, X.B. Probability distribution of rock mechanics parameters by using maximum entropy method. Chin. J. Rock Mech. Eng 2004, 23, 2177–2181, in Chinese. [Google Scholar]
- Kang, H.Y.; Kwak, B.M. Application of maximum entropy principle for reliability-based design optimization. Struct. Multidiscip. Optim 2009, 38, 331–346. [Google Scholar]
- Singh, V. Hydrologic synthesis using entropy theory: Review. J. Hydrol. Eng 2011, 16, 421–433. [Google Scholar]
- Li, C.; Wang, W.; Wang, S. Maximum-entropy method for evaluating the slope stability of earth dams. Entropy 2012, 14, 1864–1876. [Google Scholar]
- Zhou, R.; Cai, R.; Tong, G. Applications of entropy in finance: A review. Entropy 2013, 15, 4909–4931. [Google Scholar]



| Coefficient | Value | Coefficient | Value | Coefficient | Value |
|---|---|---|---|---|---|
| a0 | 0.00 | a4 | −0.0000282 | b22 | −0.365 |
| a1 | 19.6 | b11 | 0.109 | c1 | −0.0109 |
| a2 | −0.534 | b12 | 0.279E | c2 | 0.756 |
| a3 | 0.00639 | b21 | −3.07 | R | 0.964 |
| Moments | Maximum load effect component | Minimum load effect component |
|---|---|---|
| 0 | 1 | 1 |
| 1st | 3.2 | −3 |
| 2nd | 11.51 | 10.35 |
| 3rd | 44.66 | −39.41 |
| 4th | 182.93 | 160.7 |
| Lagrange multipliers | Maximum load effect component | Minimum load effect component |
|---|---|---|
| λ0 | −4.9896 | −4.3163 |
| λ1 | 2.4622 | −2.1545 |
| λ2 | 0.3847 | −0.3591 |
| λ3 | 0.000996 | 0.000986 |
| λ4 | 2.00E−08 | 2.00E−08 |
| Method | ||
|---|---|---|
| Proposed method | 5.90 | −4.85 |
| Kolmogorov–Smirnov method | 5.76 | −4.87 |
© 2015 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Gu, C. Maximum Entropy Method for Operational Loads Feedback Using Concrete Dam Displacement. Entropy 2015, 17, 2958-2972. https://doi.org/10.3390/e17052958
Zhang J, Gu C. Maximum Entropy Method for Operational Loads Feedback Using Concrete Dam Displacement. Entropy. 2015; 17(5):2958-2972. https://doi.org/10.3390/e17052958
Chicago/Turabian StyleZhang, Jingmei, and Chongshi Gu. 2015. "Maximum Entropy Method for Operational Loads Feedback Using Concrete Dam Displacement" Entropy 17, no. 5: 2958-2972. https://doi.org/10.3390/e17052958
APA StyleZhang, J., & Gu, C. (2015). Maximum Entropy Method for Operational Loads Feedback Using Concrete Dam Displacement. Entropy, 17(5), 2958-2972. https://doi.org/10.3390/e17052958





