Three-Stage Quantum Cryptography Protocol under Collective-Rotation Noise
Abstract
:1. Introduction
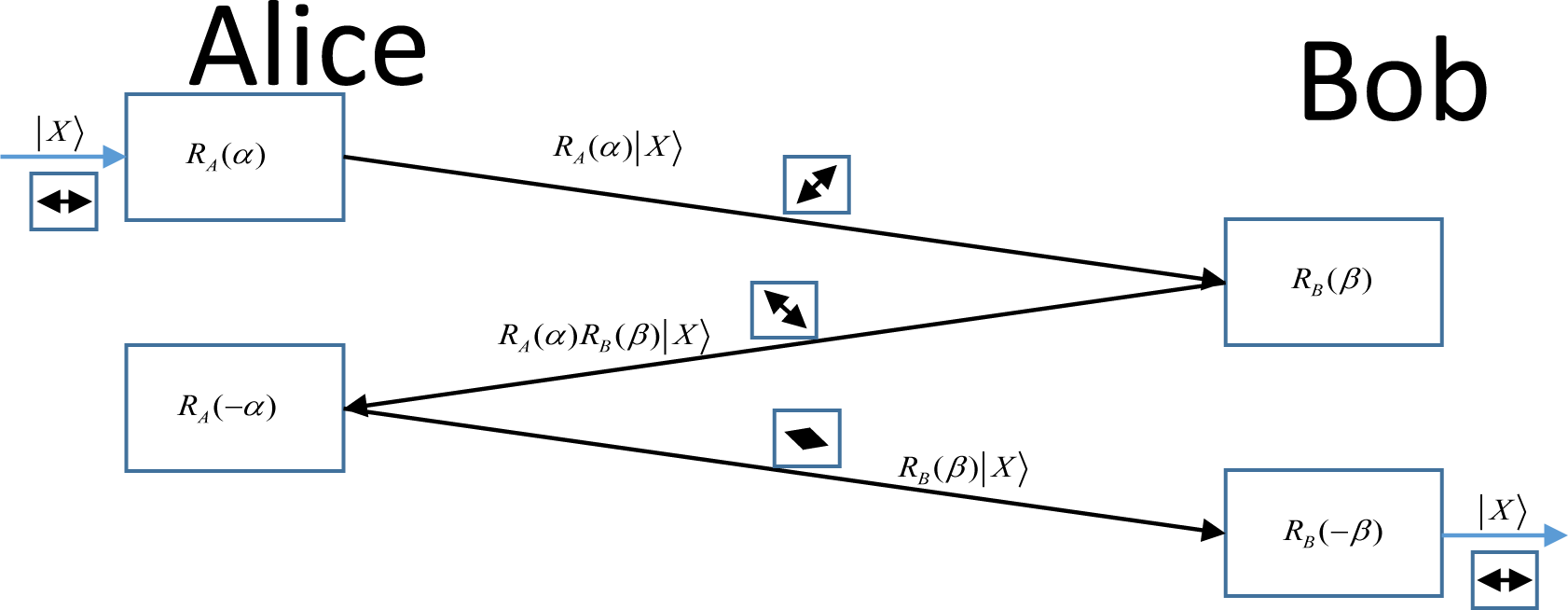
2. Three-Stage Quantum Cryptography
- Step 1: Alice applies a unitary operator RA(α) on quantum information |X〉 and sends the qubit to Bob.
- Step 2: Bob applies another unitary operator RB(β) on the received qubit state RA(α) |X〉, thereby giving RB(β) RA(α)|X〉 and sends it back to Alice. RA(α) and RB(β) should be commutative RB(β) transformations.
- Step 3: Alice applies RA(−α) (transpose of complex conjugate of RA(α)) on the received qubit state to get RA(−α)RB(β)RA(α)|X〉 = RB(β)|X〉 and sends it back to Bob.
- Step 4: Then Bob applies RB(−β) on RB(β)|X〉 to get the information |X〉.
3. Collective-Rotation Noise Analysis
3.1. Collective-Rotation Noise Model
3.2. A Single-Photon Analysis
3.3. Multi-Photon Analysis
- Case 1: N = 2k + 1, k ≥ 0
- Case 2: N = 2k + 2, k ≥ 0.
- More than k + 1 photons out of the 2k + 1 photons hit the correct photon detector (Nc ≥ k + 2). In this case, it does not matter whether the added photon hits the correct or the wrong detector. In either cases, Nw ≤ k. Therefore, Nc > Nw. The information bit is detected correctly.
- More than k + 1 photons out of the 2k + 1 photons hit the wrong photon detector (Nw ≥ k + 2). In this case, it again does not matter whether the added photon hits the correct or the wrong detector. In this case, the total number of photons reaching the correct detector Nc ≤ k. Therefore, Nw > Nc. The information bit is detected incorrectly.
- Out of 2k + 1 photons, k + 1 photons reach the correct detector and k photons reach the wrong detector. In this case, there are two possibilities. If the added photon reaches the correct detector, this will make Nc = k + 2, and Nw = k. Therefore, Nc > Nw and the information bit is detected correctly. On the other hand, if the added photon reaches the wrong detector, we have Nc = Nw = k + 1. Based on the assumption, the probability to detect a correct information bit is 1/2.
- Out of 2k + 1 photons, k photons reach the correct detector and k + 1 photons reach the wrong detector. In this case, there are also two possibilities. If the added photon reaches the wrong detector, this will make Nw = k + 2, and Nc = k. Therefore, NW > NC and the information bit is detected incorrectly. If the added photon reaches the correct detector, this will make Nc = k + 1, and Nw = k + 1 Therefore, Nc = Nw and the probability of detecting a correct information bit. Is 1/2.
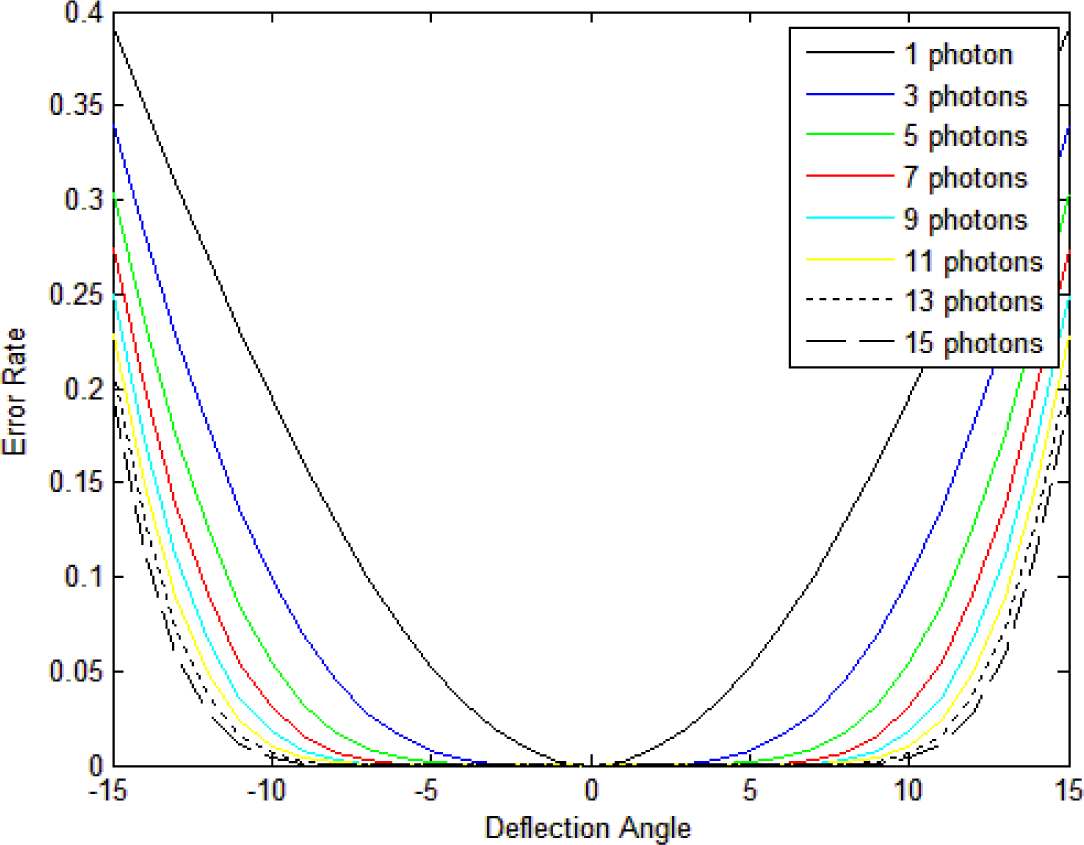
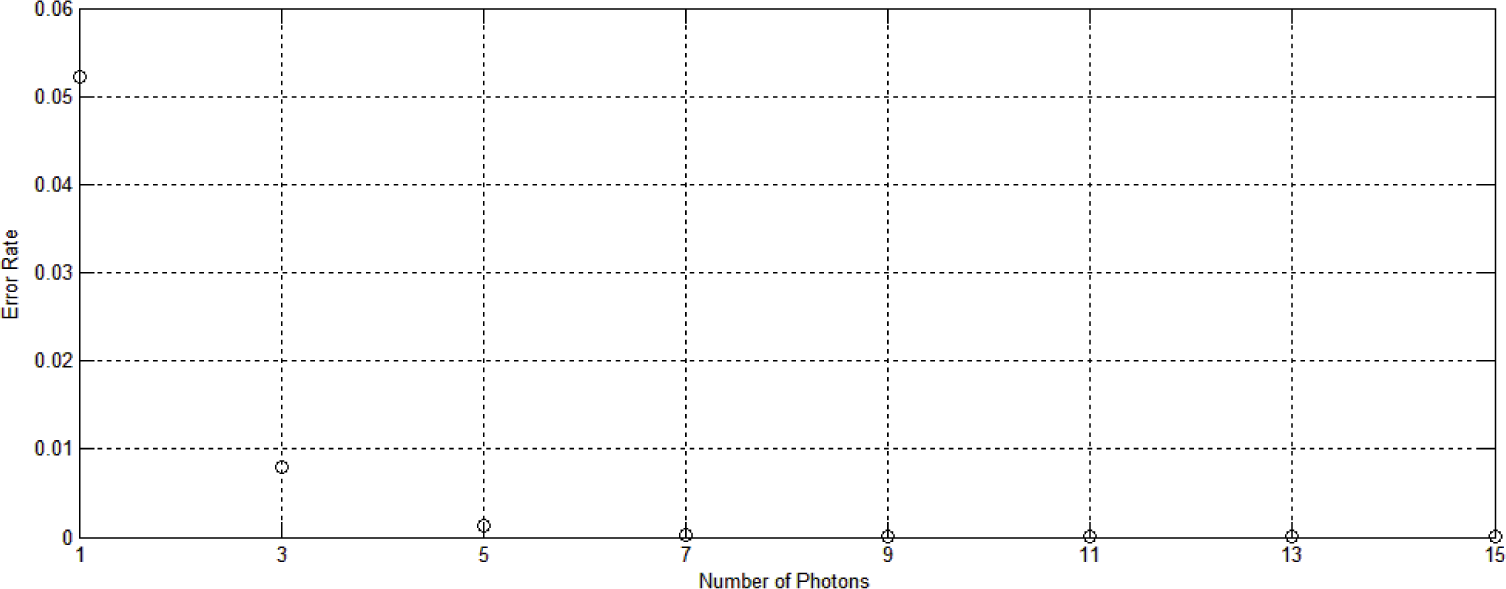
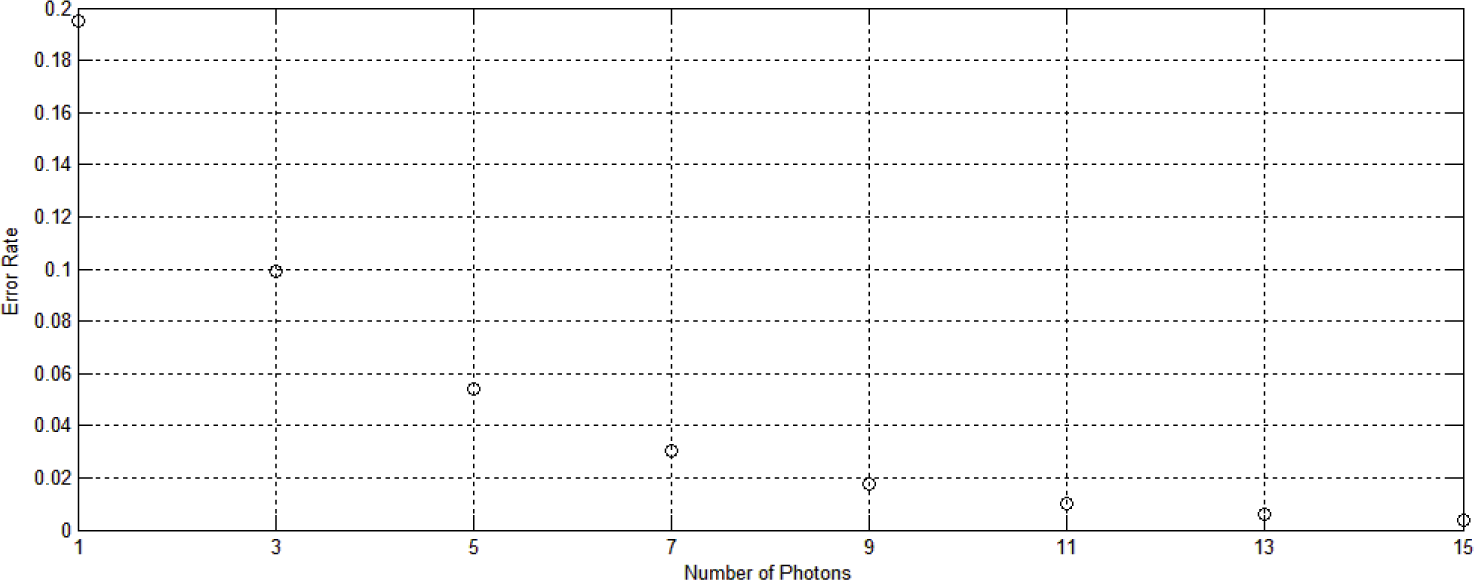
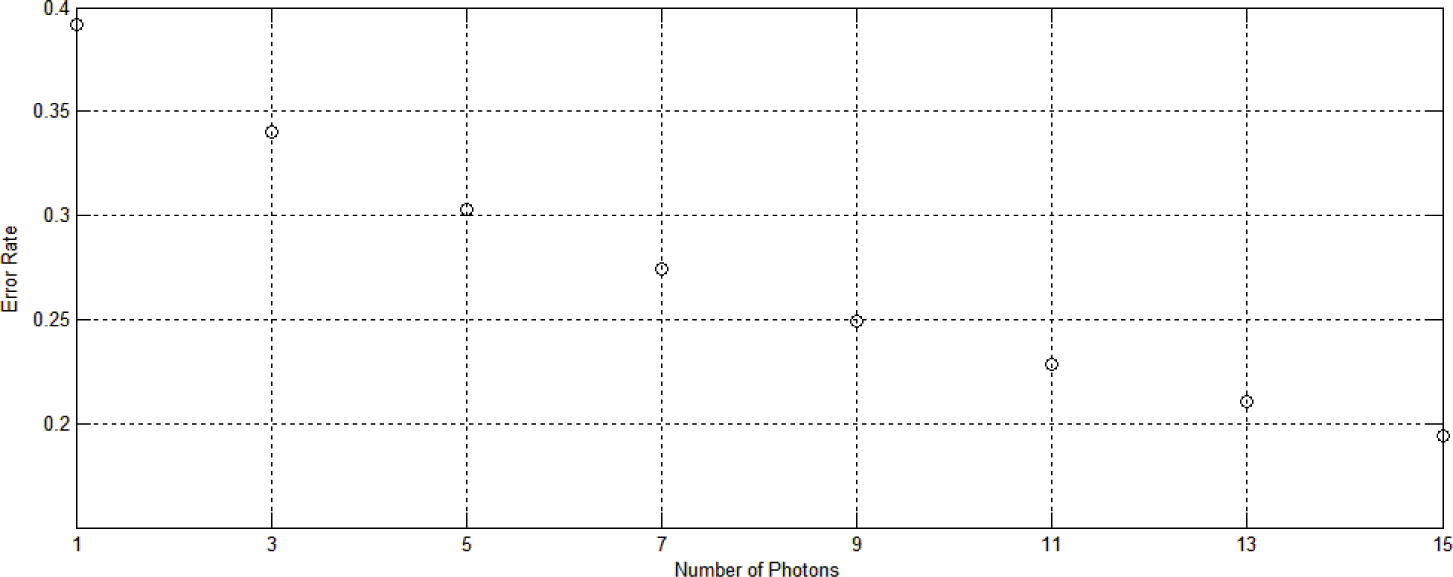
3.4. Numerical Results
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Bennett, H.C.; Brassard, G. Quantum cryptography: Public key distribution and coin tossing, Proceedings of the International Conference on Computers, Systems & Signal Processing, Bangalore, India, 10–12 December 1984; pp. 175–179.
- Ekert, K.A. Quantum cryptography based on Bell’s theorem. Phys. Rev. Lett. 1991, 67, 661–663. [Google Scholar]
- Bennett, H.C. Quantum cryptography using any two nonorthogonal states. Phys. Rev. Lett. 1992, 75, 3121–3124. [Google Scholar]
- Goldenberg, L.; Vaidman, L. Quantum Cryptography Based on Orthogonal States. Phys. Rev. Lett. 1995, 67, 1239–1243. [Google Scholar]
- Hillery, M.; Bužek, V.; Bertaiume, A. Quantum secret sharing. Phys. Rev. A 1999, 59. [Google Scholar] [CrossRef]
- Shimizu, K.; Imoto, N. Communication channels secured from eavesdropping via transmission of photonic Bell states. Phys. Rev. A 1999, 60. [Google Scholar] [CrossRef]
- Bostrom, K.; Felbinger, T. Deterministic Secure Direct Communication Using Entanglement. Phys. Rev. Lett. 2002, 89, 187902. [Google Scholar]
- Lucamarini, M.; Mancini, S. Secure Deterministic Communication without Entanglement. Phys. Rev. Lett. 2005, 94, 140501. [Google Scholar]
- Nguyen, A.B. Quantum dialogue. Phys. Lett. A 2004, 328, 6–10. [Google Scholar]
- Kak, S. A. Three-Stage Quantum Cryptography Protocol. Found. Phys. Lett. 2006, 19, 293–296. [Google Scholar]
- Mandal, S.; Macdonald, G.; El Rifai, M.; Punekar, N.; Zamani, F.; Chen, Y.; Kak, S.; Verma, P.K.; Huck, R.C.; Sluss, J. Multi-Photon Implementation of Three-Stage Quantum Cryptography Protocol, Proceedings of Information Networking (ICOIN), Bangkok, Thailand, 28–30 January 2013; pp. 6–11.
- Pirandola, S.; Braunstein, S.L.; Mancini, S.; Lloyd, S. Quantum direct communication with continuous variables. Eur. Lett. 2008, 84, 20013. [Google Scholar]
- Pirandola, S.; Braunstein, S.L.; Lloyd, S.; Mancini, S. Confidential direct communications: A quantum approach using continuous variables. IEEE J. Sel. Top. Quantum Electron. 2009, 15, 1570–1580. [Google Scholar]
- Ball, L.J.; Banaszek, K. Potential for Quantum Cryptography over Collective Noise Channels, Proceedings of AIP Conference Proceedings, Glasgow, UK, 25–29 July 2004; pp. 295–298.
- Li, X.; Deng, F.; Zhou, H. Efficient quantum key distribution over a collective noise channel. Phys. Rev. A 2008, 78, 022321. [Google Scholar]
- Niu, H.; Ren, B.; Wang, T.; Hua, M.; Deng, F. Faithful Entanglement Sharing for Quantum Communication against Collective Noise. Int. J. Theor. Phys. 2012, 51, 2346–2352. [Google Scholar]
- Li, J.; Li, L.; Jin, H.; Li, R. Security analysis of the “Ping–Pong” quantum communication protocol in the presence of collective-rotation noise. Phys. Lett. A 2013, 377, 2729–2734. [Google Scholar]
- Yang, C.; Hwang, T. Quantum dialogue protocols immune to collective noise. Quantum Inf. Process. 2013, 12, 2131–2142. [Google Scholar]
- Pirandola, S.; Braunstein, S.L.; Lloyd, S.; Mancini, S. Continuous Variable Quantum Cryptography using Two-Way Quantum Communication. Nat. Phys. 2008, 4, 726–730. [Google Scholar]
- Pirandola, S.; Mancini, S.; Lloyd, S.; Braunstein, S.L. Security of two-way quantum cryptography against asymmetric Gaussian attacks, Proceeding of the SPIE Conference “Quantum Communications and Quantum Imaging VI”, San Diego, CA, USA, 5 May 2008; 7092.
- Weedbrook, C.; Ottaviani, C.; Pirandola, S. Two-way quantum cryptography at different wavelengths. Phys. Rev. A 2014, 89, 012309. [Google Scholar]
- Nikolopoulos, M.G. Applications of single-qubit rotations in quantum public-key cryptography. Phys. Rev. A 2008, 77, 032348. [Google Scholar]

| Deflection Angle | θ | –θ |
|---|---|---|
| Probability | 1/2 | 1/2 |
| Deflection Angle | 2θ | 0 | –2θ |
|---|---|---|---|
| Probability | 1/4 | 1/2 | 1/4 |
| Deflection Angle | 3θ | θ | −θ | −3θ |
|---|---|---|---|---|
| Probability | 1/8 | 3/8 | 3/8 | 1/8 |
© 2015 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, L.; Chen, Y. Three-Stage Quantum Cryptography Protocol under Collective-Rotation Noise. Entropy 2015, 17, 2919-2931. https://doi.org/10.3390/e17052919
Wu L, Chen Y. Three-Stage Quantum Cryptography Protocol under Collective-Rotation Noise. Entropy. 2015; 17(5):2919-2931. https://doi.org/10.3390/e17052919
Chicago/Turabian StyleWu, Linsen, and Yuhua Chen. 2015. "Three-Stage Quantum Cryptography Protocol under Collective-Rotation Noise" Entropy 17, no. 5: 2919-2931. https://doi.org/10.3390/e17052919
APA StyleWu, L., & Chen, Y. (2015). Three-Stage Quantum Cryptography Protocol under Collective-Rotation Noise. Entropy, 17(5), 2919-2931. https://doi.org/10.3390/e17052919





