Stabilization Effects of Dichotomous Noise on the Lifetime of the Superconducting State in a Long Josephson Junction
Abstract
:1. Introduction
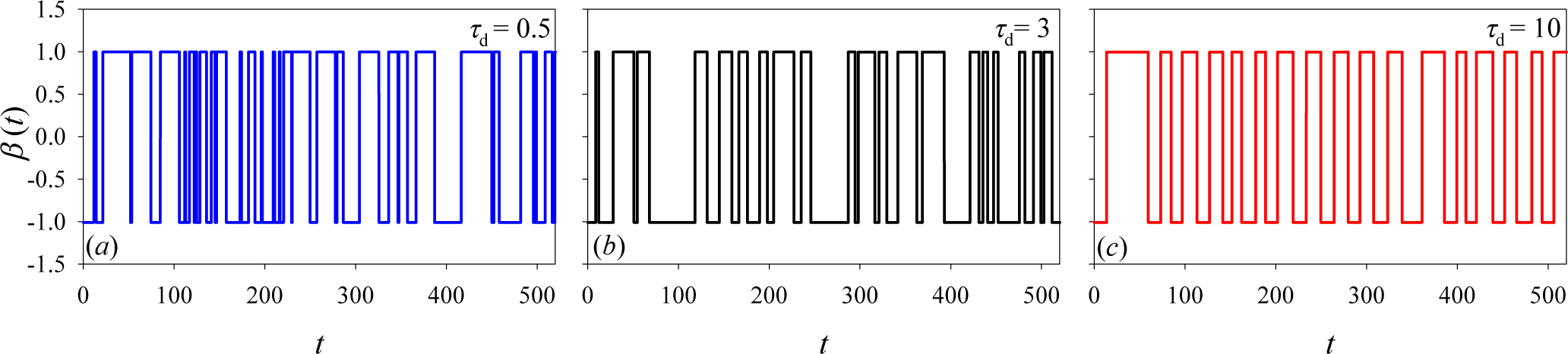
2. The Model
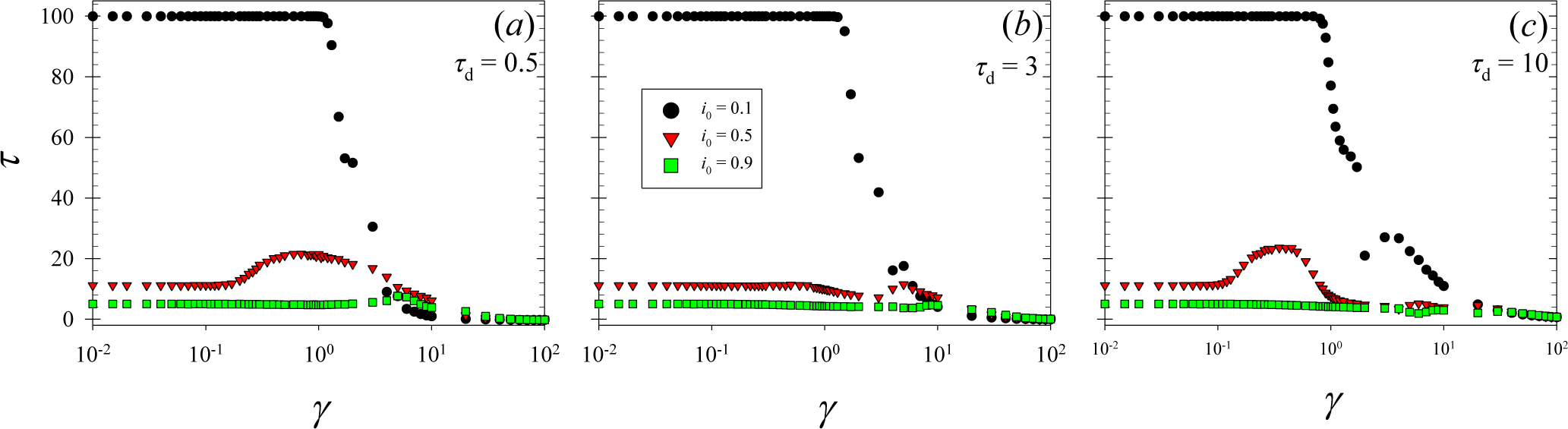
3. Results
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Kogan, S. Electronic Noise and Fluctuations in Solids; Cambridge University Press: Cambridge, UK, 1996. [Google Scholar]
- Pankratov, E.; Spagnolo, B. Optimization of impurity profile for p-n-junction in heterostructures. Eur. Phys. J. B 2005, 46, 15–19. [Google Scholar]
- Rogers, C.; Buhrman, R. Composition of 1/f Noise in Metal-Insulator-Metal Tunnel Junctions. Phys. Rev. Lett 1984, 53, 1272–1275. [Google Scholar]
- Rogers, C.; Buhrman, R. Nature of single-localized-electron states derived from tunneling measurements. Phys. Rev. Lett 1985, 55, 859–862. [Google Scholar]
- Ralls, K.; Skocpol, W.; Jackel, L.; Howard, R.; Fetter, L.; Epworth, R.; Tennant, D. Discrete Resistance Switching in Submicrometer Silicon Inversion Layers: Individual Interface Traps and Low-Frequency 1/f Noise. Phys. Rev. Lett 1984, 52, 228–231. [Google Scholar]
- Ralls, K.S.; Buhrman, R.A. Microscopic study of 1/f noise in metal nanobridges. Phys. Rev. B 1991, 44, 5800–5817. [Google Scholar]
- Wakai, R.; van Harlingen, D. Direct lifetime measurements and interactions of charged defect states in submicron Josephson junctions. Phys. Rev. Lett 1987, 58, 1687–1690. [Google Scholar]
- Parman, C.; Israeloff, N.; Kakalios, J. Random telegraph-switching noise in coplanar current measurements of amorphous silicon. Phys. Rev. B 1991, 44, 8391–8394. [Google Scholar]
- Peters, M.; Dijkhuis, J.; Molenkamp, L. Random telegraph signals and 1/f noise in a silicon quantum dot. J. Appl. Phys 1999, 86, 1523–1526. [Google Scholar]
- Gunnarsson, D.; Duty, T.; Bladh, K.; Delsing, P. Tunability of a 2e periodic single Cooper pair box. Phys. Rev. B 2004, 70, 224523. [Google Scholar]
- Eroms, J.; van Schaarenburg, L.; Driessen, E.; Plantenberg, J.; Huizinga, C.; Schouten, R.; Verbruggen, A.; Harmans, C.; Mooij, J. Low-frequency noise in Josephson junctions for superconducting qubits. Appl. Phys. Lett 2006, 89, 122516. [Google Scholar]
- Paladino, E.; Galperin, Y.; Falci, G.; Altshuler, B. 1/f noise: Implications for solid-state quantum information. Rev. Mod. Phys 2014, 86, 361–418. [Google Scholar]
- Reimann, P.; van den Broeck, C.; Linke, H.; Hänggi, P.; Rubi, J.; Pérez-Madrid, A. Giant acceleration of free diffusion by use of tilted periodic potentials. Phys. Rev. Lett 2001, 87, 010602. [Google Scholar]
- Dubkov, A.A.; Spagnolo, B. Acceleration of diffusion in randomly switching potential with supersymmetry. Phys. Rev. E 2005, 72, 041104. [Google Scholar]
- Grabert, H. Theory of a Josephson junction detector of non-Gaussian noise. Phys. Rev. B 2008, 77, 205315. [Google Scholar]
- Urban, D.; Grabert, H. Feedback and rate asymmetry of the Josephson junction noise detector. Phys. Rev. B 2009, 79, 113102. [Google Scholar]
- Filatrella, G.; Pierro, V. Detection of noise-corrupted sinusoidal signals with Josephson junctions. Phys. Rev. E 2010, 82, 046712. [Google Scholar]
- Addesso, P.; Filatrella, G.; Pierro, V. Characterization of escape times of Josephson junctions for signal detection. Phys. Rev. E 2012, 85, 016708. [Google Scholar]
- Ankerhold, J. Detecting charge noise with a Josephson junction: A problem of thermal escape in presence of non-Gaussian fluctuations. Phys. Rev. Lett 2007, 98, 036601. [Google Scholar]
- Sukhorukov, E.V.; Jordan, A.N. Stochastic dynamics of a Josephson junction threshold detector. Phys. Rev. Lett 2007, 98, 136803. [Google Scholar]
- Köpke, M.; Ankerhold, J. Linear dynamics subject to thermal fluctuations and non-Gaussian noise: From classical to quantum. New J. Phys 2013, 15, 043013. [Google Scholar]
- Oelsner, G.; Revin, L.S.; Il’Ichev, E.; Pankratov, A.L.; Meyer, H.G.; Grönberg, L.; Hassel, J.; Kuzmin, L.S. Underdamped Josephson junction as a switching current detector. Appl. Phys. Lett 2013, 14, 142605. [Google Scholar]
- Tobiska, J.; Nazarov, Y.V. Josephson junctions as threshold detectors for full counting statistics. Phys. Rev. Lett 2004, 93, 106801. [Google Scholar]
- Yu, Y.; Han, S. Resonant escape over an oscillating barrier in underdamped Josephson tunnel junctions. Phys. Rev. Lett 2003, 91, 127003. [Google Scholar]
- Sun, G.; Dong, N.; Mao, G.; Chen, J.; Xu, W.; Ji, Z.; Kang, L.; Wu, P.; Yu, Y.; Xing, D. Thermal escape from a metastable state in periodically driven Josephson junctions. Phys. Rev. E 2007, 75, 021107. [Google Scholar]
- Pan, C.; Tan, X.; Yu, Y.; Sun, G.; Kang, L.; Xu, W.; Chen, J.; Wu, P. Resonant activation through effective temperature oscillation in a Josephson tunnel junction. Phys. Rev. E 2009, 79, 030104. [Google Scholar]
- Devoret, M.H.; Martinis, J.M.; Esteve, D.; Clarke, J. Resonant activation from the zero-voltage state of a current-biased Josephson junction. Phys. Rev. Lett 1984, 53, 1260–1263. [Google Scholar]
- Devoret, M.H.; Martinis, J.M.; Clarke, J. Measurements of macroscopic quantum tunneling out of the zero-voltage state of a current-biased Josephson junction. Phys. Rev. Lett 1985, 55, 1908–1911. [Google Scholar]
- Castellano, M.; Torrioli, G.; Cosmelli, C.; Costantini, A.; Chiarello, F.; Carelli, P.; Rotoli, G.; Cirillo, M.; Kautz, R. Thermally activated escape from the zero-voltage state in long Josephson junctions. Phys. Rev. B 1996, 54, 15417–15428. [Google Scholar]
- Novotnỳ, T. Josephson junctions as threshold detectors of full counting statistics: Open issues. J. Stat. Mech. Theory Exp 2009, P01050. [Google Scholar]
- Huard, B.; Pothier, H.; Birge, N.O.; Esteve, D.; Waintal, X.; Ankerhold, J. Josephson junctions as detectors for non-Gaussian noise. Ann. Phys 2007, 16, 736–750. [Google Scholar]
- Peltonen, J.; Timofeev, A.; Meschke, M.; Heikkilä, T.; Pekola, J. Detecting non-Gaussian current fluctuations using a Josephson threshold detector. Physica E 2007, 40, 111–122. [Google Scholar]
- Montroll, E.W.; Shlesinger, M.F. Nonequilibrium Phenomena II: From Stochastics to Hydrodynamics; North-Holland: Amsterdam, 1984; pp. 1–121. [Google Scholar]
- Shlesinger, M.F.; Zaslavsky, G.M.; Frisch, U. Lévy Flights and Related Topics in Physics; Springer: Berlin/Heidelberg, Germany, 1994; Volume 450. [Google Scholar]
- Dybiec, B.; Gudowska-Nowak, E. Resonant activation in the presence of nonequilibrated baths. Phys. Rev. E 2004, 69, 016105. [Google Scholar]
- Souryal, M.R.; Larsson, E.G.; Peric, B.; Vojcic, B.R. Soft-decision metrics for coded orthogonal signaling in symmetric alpha-stable noise. IEEE Trans. Signal Process 2008, 56, 266–273. [Google Scholar]
- Fedorov, K.; Pankratov, A. Mean time of the thermal escape in a current-biased long-overlap Josephson junction. Phys. Rev. B 2007, 76, 024504. [Google Scholar]
- Fedorov, K.; Pankratov, A.L.; Spagnolo, B. Influence of length on the noise delayed switching of long Josephson junctions. Int. J. Bifurc. Chaos 2008, 18, 2857–2862. [Google Scholar]
- Augello, G.; Valenti, D.; Spagnolo, B. Effects of colored noise in short overdamped Josephson junction. Int. J. Bifurc. Chaos 2008, 6, 801–806. [Google Scholar]
- Augello, G.; Valenti, D.; Pankratov, A.L.; Spagnolo, B. Lifetime of the superconductive state in short and long Josephson junctions. Eur. Phys. J. B 2009, 70, 145–151. [Google Scholar]
- Augello, G.; Valenti, D.; Spagnolo, B. Non-Gaussian noise effects in the dynamics of a short overdamped Josephson junction. Eur. Phys. J. B 2010, 78, 225–234. [Google Scholar]
- Guarcello, C.; Valenti, D.; Augello, G.; Spagnolo, B. The Role of Non-Gaussian Sources in the Transient Dynamics of Long Josephson Junctions. Acta Phys. Pol. B 2013, 44, 997–1005. [Google Scholar]
- Valenti, D.; Guarcello, C.; Spagnolo, B. Switching times in long-overlap Josephson junctions subject to thermal fluctuations and non-Gaussian noise sources. Phys. Rev. B 2014, 89, 214510. [Google Scholar]
- Fedorov, K.G.; Pankratov, A.L. Crossover of the thermal escape problem in annular spatially distributed systems. Phys. Rev. Lett 2009, 103, 260601. [Google Scholar]
- Barone, A.; Paterno, G. Physics and Applications of the Josephson Effect; Wiley: Hoboken, NJ, USA, 1982. [Google Scholar]
- Likharev, K. Dynamics of Josephson Junctions and Circuits; Gordon & Breach: New York, NY, USA, 1986. [Google Scholar]
- Ustinov, A. Solitons in Josephson junctions. Physica D 1998, 123, 315–329. [Google Scholar]
- Büttiker, M.; Landauer, R. Nucleation theory of overdamped soliton motion. Phys. Rev. A 1981, 23, 1397–1410. [Google Scholar]
- McLaughlin, D.W.; Scott, A.C. Perturbation analysis of fluxon dynamics. Phys. Rev. A 1978, 18, 1652–1680. [Google Scholar]
- Dueholm, B.; Joergensen, E.; Levring, O.; Monaco, R.; Mygind, J.; Pedersen, N.; Samuelsen, M. An analysis of fluxons in long Josephson junctions. IEEE Trans. Magn 1983, 19, 1196–1200. [Google Scholar]
- Valenti, D.; Schimansky-Geier, L.; Sailer, X.; Spagnolo, B. Moment equations for a spatially extended system of two competing species. Eur. Phys. J. B 2006, 50, 199–203. [Google Scholar]
- Valenti, D.; Schimansky-Geier, L.; Sailer, X.; Spagnolo, B.; Iacomi, M. Moment Equations in a Lotka–Volterra Extended System with Time Correlated Noise. Acta Phys. Pol. B 2007, 38, 1961–1972. [Google Scholar]
- Valenti, D.; Spagnolo, B. Stochastic dynamics and mean field approach in a system of three interacting species. Cent. Eur. J. Phys 2009, 7, 457–471. [Google Scholar]
- Valenti, D.; Pizzolato, N.; Spagnolo, B. Mean Field Approach and Role of the Coloured Noise in the Dynamics of Three Interacting Species. Acta Phys. Pol. B 2010, 41, 1051–1071. [Google Scholar]
- Adorno, D.P.; Pizzolato, N.; Valenti, D.; Spagnolo, B. External Noise Effects in Doped Semiconductors Operating Under sub-THz Signals. Rep. Math. Phys 2012, 70, 171–179. [Google Scholar]
- Dubkov, A.A.; Agudov, N.V.; Spagnolo, B. Noise-enhanced stability in fluctuating metastable states. Phys. Rev. E 2004, 69, 061103. [Google Scholar]
- Mantegna, R.; Spagnolo, B. Noise Enhanced Stability in an Unstable System. Phys. Rev. Lett 1996, 76, 563–566. [Google Scholar]
- Agudov, N.; Spagnolo, B. Noise-enhanced stability of periodically driven metastable states. Phys. Rev. E 2001, 64, 035102. [Google Scholar]
- Agudov, N.V.; Dubkov, A.A.; Spagnolo, B. Escape from a metastable state with fluctuating barrier. Physica A 2003, 325, 144–151. [Google Scholar]
- Spagnolo, B.; Agudov, N.; Dubkov, A. Noise enhanced stability. Acta Phys. Pol. B 2004, 35, 1419–1436. [Google Scholar]
- Spagnolo, B.; Dubkov, A.; Agudov, N. Enhancement of stability in randomly switching potential with metastable state. Eur. Phys. J. B 2004, 40, 273–281. [Google Scholar]
- D’Odorico, P.; Laio, F.; Ridolfi, L. Noise-induced stability in dryland plant ecosystems. Proc. Natl. Acad. Sci. USA 2005, 102, 10819–10822. [Google Scholar]
- Fiasconaro, A.; Spagnolo, B.; Boccaletti, S. Signatures of noise-enhanced stability in metastable states. Phys. Rev. E 2005, 72, 061110. [Google Scholar]
- Hurtado, P.I.; Marro, J.; Garrido, P. Metastability, nucleation, and noise-enhanced stabilization out of equilibrium. Phys. Rev. E 2006, 74, 050101. [Google Scholar]
- Spagnolo, B.; Dubkov, A.; Pankratov, A.; Pankratova, E.; Fiasconaro, A.; Ochab-Marcinek, A. Lifetime of metastable states and suppression of noise in interdisciplinary physical models. Acta Phys. Pol. B 2007, 38, 1925–1950. [Google Scholar]
- Bonanno, G.; Valenti, D.; Spagnolo, B. Mean escape time in a system with stochastic volatility. Phys. Rev. E 2007, 75, 016106. [Google Scholar]
- Mankin, R.; Soika, E.; Sauga, A.; Ainsaar, A. Thermally enhanced stability in fluctuating bistable potentials. Phys. Rev. E 2008, 77, 051113. [Google Scholar]
- Yoshimoto, M.; Shirahama, H.; Kurosawa, S. Noise-induced order in the chaos of the Belousov–Zhabotinsky reaction. J. Chem. Phys 2008, 129, 014508. [Google Scholar]
- Valenti, D.; Augello, G.; Spagnolo, B. Dynamics of a FitzHugh-Nagumo system subjected to autocorrelated noise. Eur. Phys. J. B 2008, 65, 443–451. [Google Scholar]
- Fiasconaro, A.; Spagnolo, B. Stability measures in metastable states with Gaussian colored noise. Phys. Rev. E 2009, 80, 041110. [Google Scholar]
- Trapanese, M. Noise enhanced stability in magnetic systems. J. Appl. Phys 2009, 105, 07D313. [Google Scholar]
- Fiasconaro, A.; Mazo, J.J.; Spagnolo, B. Noise-induced enhancement of stability in a metastable system with damping. Phys. Rev. E 2010, 82, 041120. [Google Scholar]
- Li, J.h.; Łuczka, J. Thermal-inertial ratchet effects: Negative mobility, resonant activation, noise-enhanced stability, and noise-weakened stability. Phys. Rev. E 2010, 82, 041104. [Google Scholar]
- Smirnov, A.A.; Pankratov, A.L. Influence of the size of uniaxial magnetic nanoparticle on the reliability of high-speed switching. Phys. Rev. B 2010, 82, 132405. [Google Scholar]


© 2015 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guarcello, C.; Valenti, D.; Carollo, A.; Spagnolo, B. Stabilization Effects of Dichotomous Noise on the Lifetime of the Superconducting State in a Long Josephson Junction. Entropy 2015, 17, 2862-2875. https://doi.org/10.3390/e17052862
Guarcello C, Valenti D, Carollo A, Spagnolo B. Stabilization Effects of Dichotomous Noise on the Lifetime of the Superconducting State in a Long Josephson Junction. Entropy. 2015; 17(5):2862-2875. https://doi.org/10.3390/e17052862
Chicago/Turabian StyleGuarcello, Claudio, Davide Valenti, Angelo Carollo, and Bernardo Spagnolo. 2015. "Stabilization Effects of Dichotomous Noise on the Lifetime of the Superconducting State in a Long Josephson Junction" Entropy 17, no. 5: 2862-2875. https://doi.org/10.3390/e17052862
APA StyleGuarcello, C., Valenti, D., Carollo, A., & Spagnolo, B. (2015). Stabilization Effects of Dichotomous Noise on the Lifetime of the Superconducting State in a Long Josephson Junction. Entropy, 17(5), 2862-2875. https://doi.org/10.3390/e17052862







