Exergy Analysis of a Ground-Coupled Heat Pump Heating System with Different Terminals
Abstract
:1. Introduction
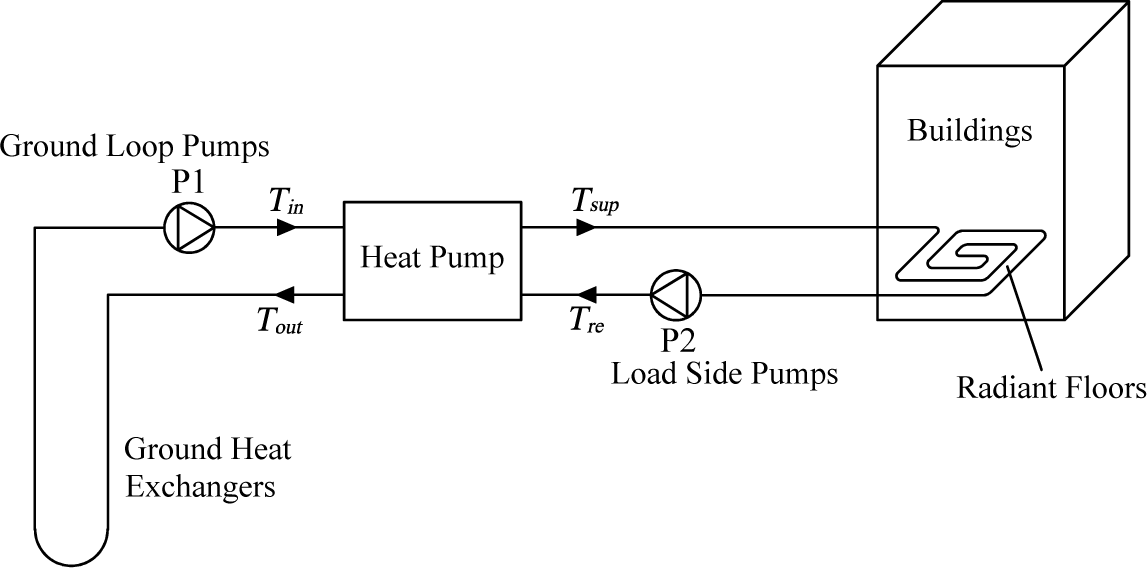
2. System Description
3. Analysis for Exergy Flow and Exergy Efficiency of Each Subsystem
3.1. Ground Heat Exchange System
3.2. Heat Pump
3.3. Heat Distribution System
3.4. Terminals
4. Results and Discussion
4.1. Test Results
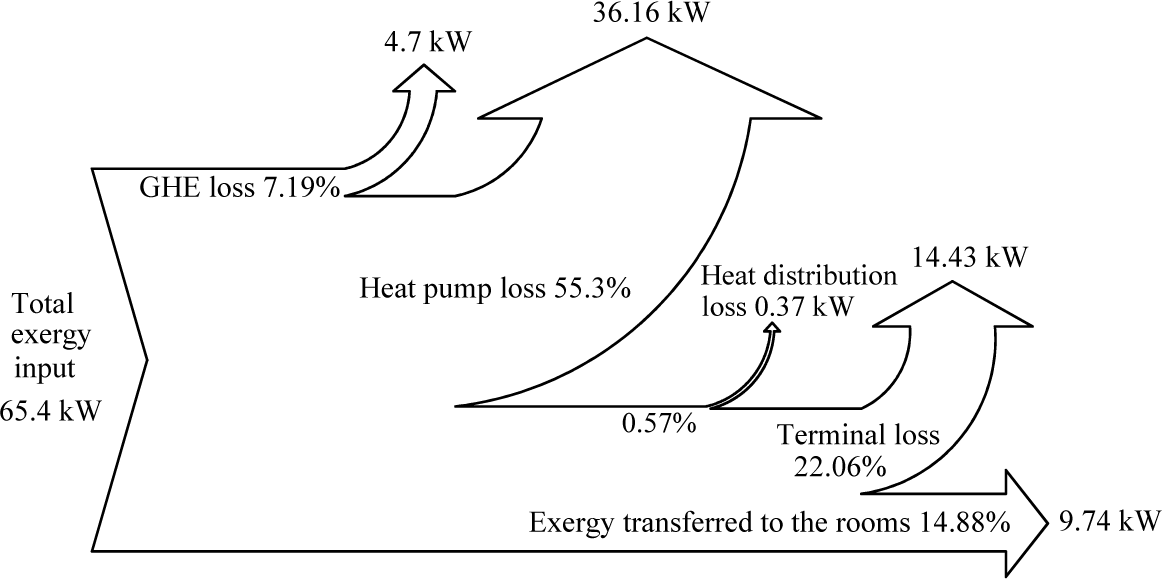
4.2. Exergy Losses and Exergy Efficiencies
4.3. Comparisons between Radiant Floors and FCU
4.3.1. Comparison of the Energy Performance
4.3.2. Comparison of the Exergetic Performance
5. Conclusions
- The heating load and exergy efficiency of the GCHP heating system with radiant floors are compared with those of the scenario system in which FCU are substituted for the radiant floors. The comparison results show that the adoption of radiant floors can result in a decrease of 12% in heating load, an increase of 3.24% in exergy efficiency of terminals and an increase of 1.18% in total exergy efficiency of system.
- The analysis results indicate that the largest exergy loss occurs in heat pump, and the second largest exergy loss occurs in terminals. The ground heat exchange system has the lowest exergy efficiency among the four subsystems. Designers of GCHP systems should pay close attention to the selection of heat pumps and terminals, especially to the design of ground heat exchange systems.
- Both load side pumping energy and source side pumping energy have obvious influence on the energy and exergetic performance of a GCHP heating system. The total exergy efficiency of a GCHP heating system will decrease with the increase of reference temperature.
Acknowledgments
Nomenclature
| Ai | area of building envelope (m2) |
| c | specific heat (kJ/kg·K) |
| E | exergy (kW) |
| I | exergy loss (kW) |
| Ki | temperature correction factors |
| m | mass flow rate (kg/s) |
| N | air exchange rate of rooms (times per hour) |
| Q | heat transfer rate (kW) |
| T | temperature (K) |
| Ui | heat transfer coefficient of building envelope (kW/m2·K) |
| V | interior volume of rooms (m3) |
| W | electric power (kW) |
| Greek Letters | |
|---|---|
| η | exergy efficiency (%) |
| ϕ | motor efficiency (%) |
| ρ | air density (kg/m3) |
| γ | heat loss ratio (%) |
| Subscripts | |
|---|---|
| a | air |
| com | screw compressor |
| FCU | fan coil units |
| g | ground |
| H | heating |
| h | hot water |
| hd | heat distribution |
| hp | heat pump |
| in | inlet of the evaporator |
| out | outlet of the evaporator |
| P1 | ground loop pumps |
| P2 | load side pumps |
| re | return water |
| rf | radiant floor |
| ro | rooms |
| sup | supply water |
| ter | terminals |
| w | water |
| 0 | reference environment condition |
Author Contributions
Conflicts of Interest
References
- American Society of Heating, Refrigerating and Air-conditioning Engineers (ASHRAE). 2011 ASHRAE Handbook-HVAC Applications; ASHRAE: Atlanta, GA, USA, 2011. [Google Scholar]
- Qiu, B.X. Situation and task of developing green and energy-efficient building in China. Proceedings of the 8th International Conference on Green and Energy-efficient Building, Beijing, China, 28–31 March 2012.
- Kotas, T.J. The Exergy Method of Thermal Plant Analysis; Paragon Publishing: Trowbridge, UK, 1995. [Google Scholar]
- Rosen, M.A.; Dincer, I. Exergy analysis of waste emissions. Int. J. Energy Res. 1999, 23, 1153–1163. [Google Scholar]
- Rosen, M.A.; Dincer, I. Thermoeconomic analysis of power plants: An application to a coal-fired electrical generating station. Energy Convers. Manag. 2003, 44, 2743–2761. [Google Scholar]
- Rosen, M.A.; Dincer, I.; Kanoglu, M. Role of exergy in increasing efficiency and sustainability and reducing environmental impact. Energy Policy 2008, 36, 128–137. [Google Scholar]
- Rosen, M.A. Using exergy to correlate energy research investments and efficiencies: Concept and case studies. Entropy 2013, 15, 262–286. [Google Scholar]
- Dincer, I.; Cengel, Y.A. Energy, entropy and exergy concepts and their roles in thermal engineering. Entropy 2001, 3, 116–149. [Google Scholar]
- Hammond, G.P. Industrial energy analysis, thermodynamics and sustainability. Appl. Energy 2007, 84, 675–700. [Google Scholar]
- Hepbasli, A.; Akdemir, O. Energy and exergy analysis of a ground source (geothermal) heat pump system. Energy Convers. Manag. 2004, 45, 737–753. [Google Scholar]
- Ozgener, O.; Hepbasli, A. A parametrical study on the energetic and exergetic assessment of a solar-assisted vertical ground-source heat pump system used for heating a greenhouse. Build. Environ. 2007, 42, 11–24. [Google Scholar]
- Esen, H.; Inalli, M.; Esen, M.; Pihtili, K. Energy and exergy analysis of a ground-coupled heat pump system with two horizontal ground heat exchangers. Build. Environ. 2007, 42, 3606–3615. [Google Scholar]
- Kuzgunkaya, E.H.; Hepbasli, A. Exergetic performance assessment of a ground-source heat pump drying system. Int. J. Energy Res. 2007, 31, 760–777. [Google Scholar]
- Bi, Y.H.; Wang, X.H.; Liu, Y. Comprehensive exergy analysis of a ground-source heat pump system for both building heating and cooling modes. Appl. Energy 2009, 86, 2560–2565. [Google Scholar]
- Akpinar, E.K.; Hepbasli, A. A comparative study on exergetic assessment of two ground-source (geothermal) heat pump systems for residential applications. Build. Environ. 2007, 42, 2004–2013. [Google Scholar]
- Balta, M.T.; Kalinci, Y.; Hepbasli, A. Evaluating a low exergy heating system from the power plant through the heat pump to the building envelope. Energy Build. 2008, 40, 1799–1804. [Google Scholar]
- Xiang, J.Y.; Zhao, J.; Qin, N. Exergetic cost analysis of a space heating system. Energy Build. 2010, 42, 1987–1994. [Google Scholar]
- China Industry Standard. Design Standard for Energy Efficiency of Residential Buildings in Hot Summer and Cold Winter Zone, JGJ 134–2010; China Architecture and Building Press: Beijing, China, 2010.
- Cengel, Y.; Boles, M.A. Thermodynamics: An Engineering Approach, 4th ed; McGraw-Hill: New York, NY, USA, 2001. [Google Scholar]
- Hernández-Román, M.Á.; Manzano-Ramírez, A.; Pineda-Piñón, J.; Ortega-Moody, J. Exergetic and thermoeconomic analyses of solar air heating processes using a parabolic trough collector. Entropy 2014, 16, 4612–4625. [Google Scholar]
- China National Standard. Design Standard for Heating Ventilation and Air Conditioning of Civil Buildings, GB 50736–2012; China Architecture and Building Press: Beijing, China, 2012.
- Carrier China Limited. Manufacturer Data of Fan Coil Units; Shanghai, China, 2011. [Google Scholar]


| Measured Parameters | Average Value |
|---|---|
| Inlet temperature of the evaporator (°C) | 9.2 |
| Outlet temperature of the evaporator (°C) | 6.1 |
| Supply water temperature of the condenser (°C) | 44.2 |
| Return water temperature of the condenser (°C) | 40 |
| Flow rate of the circulating water in GHE (m3/h) | 41.6 |
| Flow rate of the hot water (m3/h) | 40.3 |
| Electric power of the heat pump (kW) | 58.1 |
| COP (Coeffient of Performance) of the heat pump | 3.39 |
| Electric power of the ground loop pumps (kW) | 3.8 |
| Electric power of the load side pumps (kW) | 4.4 |
| Ground temperature (°C) | 16.9 |
| Average outdoor air temperature (°C) | 2.8 |
| Average indoor air temperature (°C) | 17.4 |
| Parameters | Calculated Value |
|---|---|
| Heat output of heat pump (kW) | 195.7 |
| Heat extraction rate from ground (kW) | 150 |
| COP (Coeffient of Performance) of the heat pump | 3.39 |
| Heating load of the buildings (kW) | 192.8 |
| Heat loss rate of heat distribution network (kW) | 2.9 |
| Subsystems | Exergy Efficiency (%) |
|---|---|
| Ground heat exchange system | 24.63 |
| Heat pump | 45.66 |
| Heat distribution system | 85.47 |
| Terminals (Radiant floors) | 40.31 |
© 2015 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, X.; Hao, X. Exergy Analysis of a Ground-Coupled Heat Pump Heating System with Different Terminals. Entropy 2015, 17, 2328-2340. https://doi.org/10.3390/e17042328
Chen X, Hao X. Exergy Analysis of a Ground-Coupled Heat Pump Heating System with Different Terminals. Entropy. 2015; 17(4):2328-2340. https://doi.org/10.3390/e17042328
Chicago/Turabian StyleChen, Xiao, and Xiaoli Hao. 2015. "Exergy Analysis of a Ground-Coupled Heat Pump Heating System with Different Terminals" Entropy 17, no. 4: 2328-2340. https://doi.org/10.3390/e17042328
APA StyleChen, X., & Hao, X. (2015). Exergy Analysis of a Ground-Coupled Heat Pump Heating System with Different Terminals. Entropy, 17(4), 2328-2340. https://doi.org/10.3390/e17042328






