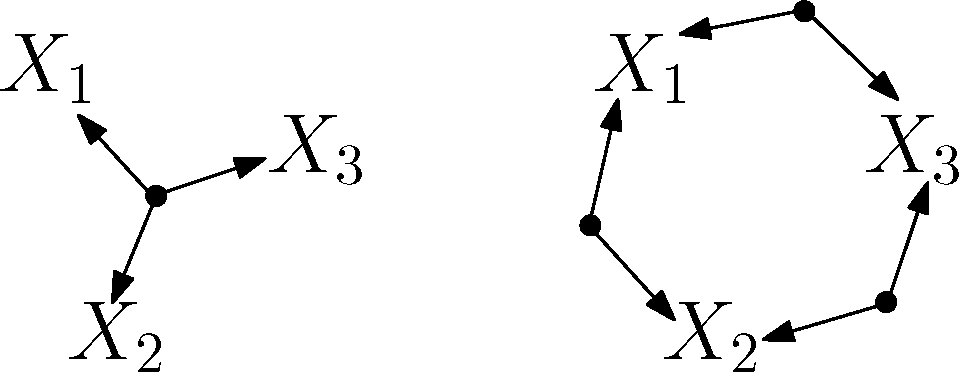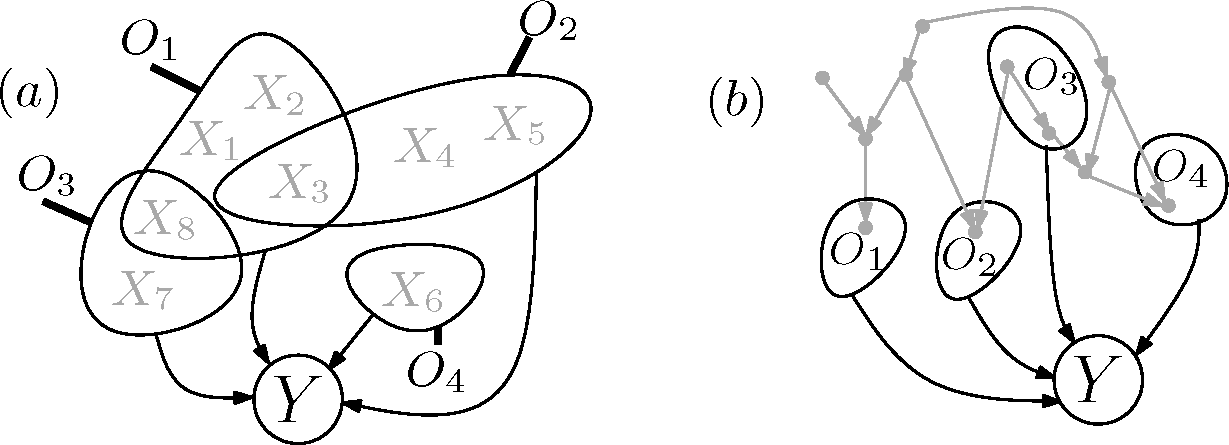1. Introduction
Causal relations among components
X1,
…, Xn of a system are commonly modeled in terms of a directed acyclic graph (DAG) in which there is an edge
Xi → Xj whenever
Xi is a direct cause of
Xj. Further, it is usually assumed that information about the causal structure can be obtained through interventions in the system. However, there are situations in which interventions are not feasible (too expensive, unethical or physically impossible) and one faces the problem of inferring causal relations from observational data only. To this end, postulates linking observations to the underlying causal structure have been employed, one of the most fundamental being the causal Markov condition [
1,
2]. It connects the underlying causal structure to conditional independencies among the observations. Explicitly, it states that every observation is independent of its non-effects given its direct causes. It formalizes the intuition that the only relevant components of a system for a given observation are its direct causes.
In terms of DAGs, the causal Markov condition states that a DAG can only be a valid causal model of a system if every node is independent of its non-descendants given its parents. The graph is then said to fulfill the local Markov condition [
3]. Consider for example the causal hypothesis
X → Y←
Z on three observations
X, Y and
Z. Assuming the causal Markov condition, the hypothesis implies that
X and
Z are independent. The violation of this independence then allows one to exclude this causal hypothesis. However, note that in general, there are many DAGs that fulfill the local Markov condition with respect to a given set of conditional independence relations. For example, all three DAGs
X → Y → Z,
X←
Y → Z and
X←
Y←
Z encode that
X is independent of
Z given
Y, and this cannot be decided from information on conditional independences alone, which is the true causal model. Nevertheless, properties that are shared by all valid DAGs (e.g., an edge between
X and
Y in the example) provide information about the underlying causal structure.
The causal Markov condition is only expected to hold for a given set of observations if all relevant components of a system have been observed, that is if there are no confounders (causes of at least two observations that have not been measured). It can then be proven by assuming a functional model of causality [
1,
4,
5]. As an example, consider the observations
X1,
…, Xn to be jointly distributed random variables. In this case, the causal Markov condition can be derived for a given DAG on
X1,
…, Xn from two assumptions: (1) every variable
Xi is a deterministic function of its parents and an independent (possibly unobserved) noise variable
Ni, and (2) the noise variables
Ni are jointly independent. However, in this paper, we assume that our observations provide only partial knowledge about a system and ask for structural properties common to all DAGs that represent the independencies of some larger set of elements.
To motivate our result, assume first that our observation consists of only two jointly-distributed random variables
X1 and
X2, which are stochastically dependent. Reichenbach [
6] postulated already in 1956 that the dependence of
X1 and
X2 needs to be explained by (at least) one of the following cases:
X1 is a cause of
X2, or
X2 is a cause of
X1, or there exists a common cause of
X1 and
X2. This link between dependence and the underlying causal structure is known as Reichenbach’s principle of common cause. It is easily seen that by assuming
X1 and
X2 to be part of some unknown larger system whose causal structure is described by a DAG
G, then the causal Markov condition for
G implies the principle of common cause. Moreover, we can subsume all three cases of the principle if we formally allow a node to be an ancestor of itself and arrive at:
The common cause principle: If two observations X1 and X2 are dependent, then they must have a common ancestor in any DAG modeling some possibly larger system.
Our main result is an information-theoretic inequality that enables us to generalize this principle to more than two variables. It leads to the:
Extended common cause principle (informal version): Consider n observations X1,…, Xn, and a number c, 1≤c≤n. If the dependence of the observations exceeds a bound that depends on c, then in any DAG modeling some possibly larger system, there exist c nodes out of X1,…, Xn that have a common ancestor.
Thus, structural information can be obtained by exploiting the degree of dependence on the subsystem, and we would like to emphasize that, in contrast to the original common cause principle, the above criterion provides a means to distinguish among cases with the same independence structure of the observed variables. This is illustrated in
Figure 1.
Above, the extended common cause principle is stated without making explicit the kind of observations we consider and how dependence is quantified. In the main case we have in mind, the observations are jointly-distributed random variables, and dependence is quantified by the mutual information [
7] function. Then the extended common cause principle (Theorem 2) relates stochastic dependence to a property of all Bayesian networks that include the observations.
However, the result holds for more general observations (such as binary strings) and for more general notions of mutual information (such as algorithmic mutual information [
8]). Therefore, we introduce an “axiomatized” version of mutual information in the following section and describe how it can be connected to a DAG. Then, in Section 3, we prove a theorem on the decomposition of information about subsets of a DAG out of which the extended common cause principle then follows as a corollary. Apart from a larger area of applicability, we think that an abstract proof based on an axiomatized notion of information better illustrates that the result is independent of the notion of “probability”. It only relies on the basic properties of (stochastic) mutual information (see Definition 1). Finally, in Section 4, we describe the result in more detail within different contexts and relate it to the notion of redundancy and synergy that was introduced in the area of neural information processing.
2. General Mutual Information and DAGs
Before introducing a general notion of mutual information, let us describe how it is connected to a DAG in the stochastic setting. Assume we are given an observation of
n discrete random variables
X1,
…, Xn in terms of their joint probability distribution
p(
X1,
…, Xn). Write [
n] =
f1,
…, ng, and for a subset
S⊆ [
n], let
XS be the random variable associated with the tuple (
Xi)
i2S. Assume further that a directed acyclic graph (DAG)
G is associated with the nodes
X1,
…, Xn that fulfill the local Markov condition [
3]: for all
i, (1 ≤
i ≤
n):
where
ndi and
pai denote the subset of indices corresponding to the non-descendants and to the parents of
Xi in
G. The tuple (
G, p(
X[n])) is called a Bayesian net [
9] and the conditional independence relations imply the factorization of the joint probability distribution
where small letters
xi stand for values of the random variables
Xi. From this factorization, it follows that the joint information measured in terms of Shannon entropy [
7] decomposes into a sum of individual conditional entropies:
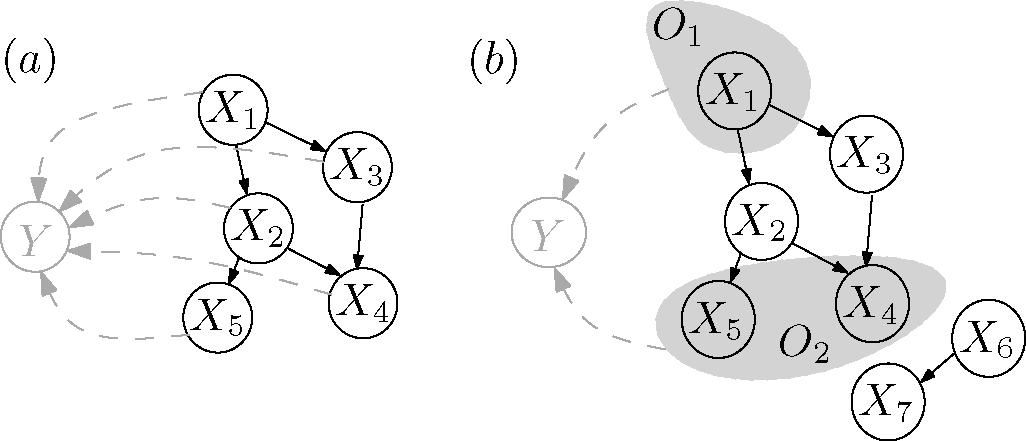
Shannon entropy can be considered as the absolute measure of information. However, in many cases, only a notion of information relative to another observation may be available. For example, in the case of continuous random variables, Shannon entropy can be negative, and hence, may not be a good measure of the information. Therefore, we would like formulate our results based on a relative measure, such as mutual information, which, moreover, induces a notion of independence in a natural way. This can be achieved by introducing a specially-designated variable
Y relative to which information will be quantified. The variable
Y can, for example, be thought of as providing a noisy measurement of the
X[n] (
Figure 2a). Then, with respect to a joint probability distribution
p(
Y, X[n]), we can transform the decomposition of entropies into a decomposition of mutual information [
7]:
For a proof and a condition for equality, see Lemma 2 below. In the case of discrete variables, Shannon entropy
H(
Xi) can be seen as mutual information of
Xi and a copy of itself:
H(
Xi) =
I(
Xi :
Xi). Therefore, we can always choose
p(
Y|X[n]), such that
Y =
X[n] and the decomposition of entropies in
(2) is recovered. We are interested in decompositions as in
(2) and
(3), since their violation allows us to exclude possible DAG structures.
However, note that the above relations are not yet very useful, since they require, through the assumption of the local Markov condition, that we have observed all relevant variables of a system. Before we relax this assumption in the next section, we introduce mutual information measures on general observations.
Definition 1 (Measure of mutual information).
Given a finite set of elements,
a measure of mutual information on is a three-argument function on the power set:such that, for disjoint sets A, B, C, D ⊆
,
it holds: We say A is independent of B given C and write (A ╨ B |C) iff I(A : B |C) = 0. Further, we will generally omit the empty set as a third argument and substitute the union by a comma, hence, we write I(A : B) instead of I(A : B |∅) and I(A : B, C) instead of I(A : B ∪ C).
Of course, mutual information of discrete, as well as of continuous random variables is included in the above definition. Further, in Section 4.2, we will discuss a recently-developed theory of causal inference [
4] based on the algorithmic mutual information of binary strings [
10]. We now state two properties of mutual information that we need later on.
Lemma 1 (Properties of mutual information).
Let I be a measure of mutual information on a set of elements.
Then:(Data processing inequality) For three disjoint sets A, B, C ⊆
:
(Increase through conditioning on independent sets) For three disjoint sets A, B, C ⊆
:
where Y is an arbitrary set Y ⊆
disjoint from the rest. Further, the difference is given by I(
A :
C |B, Y).
Proof. (i) Using the chain rule two times:
where the last inequality follows from the non-negativity of
I. To prove (ii), we again use the chain rule:
As in the stochastic setting, we can connect a DAG to the conditional independence relation that is induced by mutual information: we say that a DAG on a given set of observations fulfills the local Markov condition if every node is independent of its non-descendants given its parents. Furthermore, we show in
Appendix A that the induced independence relations are sufficiently nice, in the sense that they satisfy the semi-graphoid axioms [
11]. This is useful because it implies that a DAG that fulfills the local Markov condition is an efficient partial representation of the conditional independence structure. Namely, conditional independence relations can be read off the graph with the help of a criterion called d-separation [
1] (see
Appendix A for details).
We conclude with a general formulation of the decomposition of mutual information that we already described in the probabilistic case.
Lemma 2 (Decomposition of mutual information).
Let I be a measure of mutual information on elements O[n] = {
O1,
…, On}
and Y. Further, let G be a DAG with node set O[n] that fulfills the local Markov condition. Then:with equality if conditioning on Y does preserve the independences of the local Markov condition: that is, for all i: Proof. Assume the
Oi are ordered topologically with respect to
G. The proof is by induction on
n. The lemma is trivially true if
n = 1 with equality. Assume that it holds for
k−1 <
n. It is easy to see that the graph
Gk with nodes
O[k] that is obtained from
G by deleting all but the first
k nodes fulfills the local Markov condition with respect to
O[k]. By the chain rule,
and we are left to show that
I(
Y :
Ok |O[k−1]) ≥
I(
Y :
Ok |Opak). Since the local Markov condition holds, we have
, and the inequality follows by applying
(4). Further, by Property (ii) of the previous lemma, equality holds if for every
, which is implied by
(6).
In the next section, we derive a similar inequality in the case in which only the mutual information of Y with a subset of the nodes O[n] is known.
3. Partial Information about a System
We have shown that the information about elements of a system described by a DAG decomposes if the graph fulfills the local Markov condition. In this section, we derive a similar decomposition in cases where not all elements of a system have been observed. This decomposition will of course depend on specific properties of G and, in turn, enable us to exclude certain DAGs as models of the total system whenever we observe a violation of such a decomposition.
More precisely, we are interested in properties of the class of DAG models of a set of observations that we define as follows (see
Figure 2b).
Definition 2 (DAG model of observations). An observation of elements O[n] = {O1,…, On} with respect to a reference object Y and mutual information measure I is given by the values of I(Y : OS) for every subset S⊆ [n].
A DAG G with nodes X together with a measure of mutual information IG on is a DAG model of an observation, if the following holds:each observation Oi is a subset of the nodes of G.
G fulfills the local Markov condition with respect to IG.
IG is an extension of I, that is IG(Y : OS) = I(Y : OS) for all S⊆ [n].
Y is a leaf node (no descendants) of G.
The first three conditions state that, given the causal Markov condition, G is a valid hypothesis on the causal relations among components of some larger system, including the O[n], that is consistent with the observed mutual information values. Condition (iv) is merely a technical condition, due to the special role of Y as an observation of the O[n] external to the system.
As an example, if the Oi and Y are random variables with joint distribution p(O[n]; Y), a DAG model G with nodes
is given by the graph structure of a Bayesian net with joint distribution
, such that the marginal on O[n] and Y equals p(O[n]; Y). Moreover, if Y is a copy of O[n], then an observation in our sense is given by the values of the Shannon entropy H(OS) for every subset S⊆ [n].
The general question posed in this paper can then be formulated as follows: What can be learned from an observation given by the values I(Y : OS) about the class of DAG models?
As a first step, we present a property of mutual information about independent elements.
Lemma 3 (Submodularity of
I).
If the Oi are mutually independent, that is I(
Oi :
O[n]ni) = 0
for all i, then the function [
n] ⊇
S → −
I(
Y :
OS)
is submodular, that is, for two sets S, T⊆ [
n]:
Proof. For two subsets
S, T⊆ [
n], write
S′ =
Sn(
S ∩
T) and
T′ =
T\(
S ∩
T). Using the chain rule we, have:
where the inequality follows from Property
(4) of mutual information. □
Hence, a violation of submodularity allows one to reject mutual independence among the Oi and therefore to exclude the DAG that does not have any edges from the class of possible DAG models (the local Markov condition would imply mutual independence).
We now broaden the applicability of the above Lemma based on a result for submodular functions from [
12]: We assume that there are unknown objects
that are mutually independent and that the observed elements
will be subsets of them (see
Figure 3a).
In contrast to the previous lemma, it is not required anymore that the Oi are mutually independent themselves. It turns out that the way the information about the Oi decomposes allows for the inference of intersections among the sets Oi, namely:
Proposition 1 (Decomposition of information about sets of independent elements).
Let be mutually independent objects, that is I(
Xj :
X[r]nj) = 0
for all j. Let O[n] = {
O1,
…, On},
where each is a non-empty subset of.
For every i ∈ [
n],
let di be maximal, such that Oi has non-empty intersection with di −1
sets out of O[n] distinct from Oi. Then, the information about the O[n] can be bounded from below by: For an illustration, see
Figure 3a. Even though the proposition is actually a corollary of the following theorem, its proof is given in
Appendix B, since it is, unlike the theorem, independent of graph-theoretic notions.
As a trivial example, consider the case where
are identical subsets. Then,
d1 =
d2 = 2 and:
hence equality holds in
(7). In general, if there is an element in
Oi that is also in
k −1 different sets
Oj, then
di ≥
k, and we account for this redundancy in dividing the single information
I(
Y :
Oi) by at least
k.
Independent elements can always be modeled as root nodes of a DAG. The following theorem, which is our main result, generalizes the proposition by connecting the information about observations Oi to the intersection structure of associated ancestral sets. For a given DAG G, a set of nodes A is called ancestral, if for every edge v → w in G, such that w is in A, also v is in A. Further, for a subset of nodes S, we denote by an(S) the smallest ancestral set that contains S. Elements of an(S) will be called ancestors of S.
Theorem 1 (Decomposition of ancestral information).
Let G be a DAG model of an observation of elements O[n] = {
O1,
…, On}.
For every i, let di be the maximal number, such that the intersection of an(
Oi)
with di −1
distinct sets an is non-empty. Then, the information about all ancestors of O[n] can be bounded from below by: Furthermore, if Y only depends on whole system through the O[n],
that is:we obtain an inequality containing only known values of mutual information: The proof is given in
Appendix C, and an example is illustrated in
Figure 3b. If all quantities except the structural parameters
di are known, the inequality
(10) can be used to obtain information about the intersection structure among the
Oi that is encoded in the
di, provided that the independence assumption
(9) holds. Even if
(9) does not hold, but information on an upper bound of
I(
Y :
an(
O[n])) is available (e.g., in terms of the entropy of
Y), information about the intersection structure may be obtained from
(8). The following corollary additionally provides a bound on the minimum information about ancestral sets.
Corollary 1 (Inference of common ancestors, local version).
Given an observation of elements O[n] ={
O1,
…, On},
assume that for natural numbers c = (
c1,
…, cn)
with (1 ≤
ci ≤
n −1),
we observe: Let G be an arbitrary DAG model of the observation. For every Oi, let be the set of common ancestors in G of Oi and at least ci elements of O[n] different from Oi. Then, the joint information about all common ancestors can be bounded from below by: In particular, {or at least one index i ∊ [n], we must have; hence, there exists a common ancestor of Oi and at least ci elements of O[n] different from Oi.
The proof is given in
Appendix D. Theorem 1 and its corollary are our most general results, but due to the ease of interpretation, we illustrate them in the next section only in the special case in which all
ci are equal (Corollary 2) to obtain a lower bound on the information about all common ancestors of at least
c + 1 elements
Oi.
To conclude this section, we ask what is the maximum amount of information that one can expect to obtain about the intersection structure of ancestral sets of a DAG model of observations. The main requirement for a DAG model
G is that it fulfills the local Markov condition with respect to some larger set
X of elements. This will remain true if we add nodes and arbitrary edges in a way that
G remains acyclic. Therefore, if
G contains a common ancestor of
c elements, we can always construct a DAG model
G′ that contains a common ancestor of more than
c elements (e.g., the DAG model on the right-hand side of
Figure 1 can be transformed into the one on the left-hand side). We conclude that without adding minimality requirements for the DAG models (such as the causal faithfulness assumption [
2]), only assertions on ancestors of a minimal number of nodes can be made.
4. Structural Implications of Redundancy and Synergy
The results of the last section can be related to the notions of redundancy and synergy. In the context of neuronal information processing, it has been proposed to capture the redundancy and synergy of elements
O[n] = {
O1,
…, On} with respect to another element
Y using the function:
where
I is a measure of mutual information [
13–
15]. Thus,
r relates information that
Y has about the single elements to information about the whole set.
If the sum of information about the single Oi is larger than the information about whole set (r(Y) > 0), the O[n] are said to be redundant with respect to Y. This may be the case if Y “contains” information that is shared by multiple Oi. In general, if the Oi do not share any information, that is if they are mutually independent, then they can not be redundant with respect to any Y (this follows from Lemma 3).
On the other hand, if the information of
Y about the whole set of elements is larger than that about its single elements (
r(
Y) < 0), the
O[n] are called synergistic with respect to
Y. This may, for example, be the case if
Y is generated through a function
Y =
f(
O1,
…, On) and the function value contains little information about each argument (as is the case for the parity function; see below). If, instead,
Y is a copy of the
O[n], then
r(
Y) ≥ 0, and thus, the
O[n] are not synergistic with respect to
Y. To connect our results to the introduced notion of redundancy and synergy, we introduce the following version of
r parametrized by a parameter
c ∈ {1,
…, n}:
Intuitively, if rc(Y) > 0 for large c, then the Oi are highly redundant with respect to Y. Corollary 1 of the last section implies that high redundancy implies common ancestors of many Oi.
Corollary 2 (Redundancy explained structurally).
Let an observation of elements O[n] = {
O1,
…, On}
be given by the values of I(
Y :
OS)
for any subset S ⊆ [
n].
If rc(
Y) > 0,
then in any DAG model of the observation in which Y only depends on through O[n] [16], there exists a common ancestor of at least c + 1
elements of O[n].
In the following two subsections, we discuss this result in more detail for the cases in which the observed elements are discrete random variables and binary strings.
4.1. Common Ancestors of Discrete Random Variables
Let
X[n] = {
X1,
…, Xn} and
Y be discrete random variables with joint distribution
p(
X[n]; Y), and let
I denote the usual measure of mutual information given by the Kullback–Leibler divergence of
p from its factorized distribution [
7]. If
Y =
X[n] is a copy of the
X[n], then
I(
Y :
X[n]) =
H(
X[n]), where
H denotes the Shannon entropy. In this case, the redundancy
r1(
X[n]) is equal to the multi-information [
17] of the
X[n]. Moreover,
rc gives rise to a parametrized version of multi-information:
and from Corollary 1, we obtain
Theorem 2 (Lower bound on entropy o{ common ancestors).
Let X[n] be jointly-distributed discrete random variables. If Ic(
X[n]) > 0,
then in any Bayesian net containing
the X[n],
there exists a common ancestor of strictly more than c variables out of the X[n].
Moreover, the entropy of the set Ac+1 of all common ancestors of more than c variables is lower bounded by: We continue with a few remarks to illustrate the theorem:
Setting c = 1, the theorem states that, up to a factor 1=(n 1), the multi-information I1 is a lower bound on the entropy of common ancestors of more than two variables. In particular, if I1(X[n]) > 0, any Bayesian net containing the X[n] must have at least an edge.
Conversely, the entropy of common ancestors of all of the elements X1,…, Xn is lower bounded by (n −1)In−1(X[n]). This bound is not trivial whenever In−1(X[n]) > 0, which is, for example, the case if the Xi are only slightly disturbed copies of some not necessarily observed random variable (see the example below).
We emphasize that the inferred common ancestors can be among the elements Xi themselves. Unobserved common ancestors can only be inferred by postulating assumptions on the causal influences among the Xi. If, for example, all of the Xi were measured simultaneously, a direct causal influence among the Xi can be excluded, and any dependence or redundancy has to be attributed to unobserved common ancestors.
Finally, note that Ic > 0 is only a sufficient, but not a necessary condition for the existence of common ancestors. However, we know that the information-theoretic information provided by Ic is used in the theorem in an optimal way. By this, we mean that we can construct distributions p(X[n]), such that Ic(X[n]) = 0 for a given c, and no common ancestors of c+1 nodes have to exist.
We conclude this section with examples:
Example 1 (Three variables).
Let X1; X2 and X3 be three binary variables. Then I2(
X1; X2; X3) > 0
if and only if In this case, there must exist a common ancestor of all three variables in any Bayesian net that contains them. In particular, any Bayesian net corresponding to the DAG on the right-hand side of Figure 1 can be excluded as a model.
Example 2 (Synchrony and interaction among random variables). Let X1 = X2 = ⋯= Xn be identical random variables with non-vanishing entropy h. Then, in particular, In−1(X[n]) = (n−1)−1h > 0, and we can conclude that there has to exist a common ancestor of all n nodes in any Bayesian net that contains them.
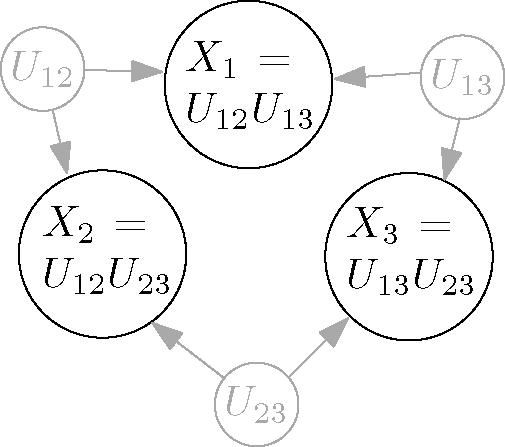
Example 3 (Interaction of maximal order).
In contrast to the synchronized case, let X1; X2,
…, Xn be binary random variables taking values in {−1,1},
and assume that the joint distribution is of pure n-interaction [18], that is for some β ≠ 0,
it has the formwhere Z is a normalization constant. It can be shown that there exists a Bayesian net including the X[n],
in which common ancestors of at most two variables exist. This is illustrated in Figure 4 for three variables and in the limiting case β = ∞
in which each Xi is uniformly distributed and X1 =
X2·
X3.
We found it somewhat surprising that, contrary to synchronization, higher order interaction among observations does not require common ancestors of many variables.
4.2. Common Ancestors in String Manipulation Processes
In some situations, it is not convenient or straightforward to summarize an observation in terms of a joint probability distribution of random variables. Consider for example cases in which the data comes from repeated observations under varying conditions (e.g., time series). A related situation is given if the number of samples is low. Janzing and Schölkopf [
4] argue that causal inference in these situations still should be possible, provided that the observations are sufficiently complex. To this end, they developed a framework for causal inference from single observations that we describe now briefly. Assume we have observed two objects
A and
B in nature (e.g., two carpets), and we encoded these observations into binary strings
a and
b. If the descriptions of the observations in terms of the strings
a and
b are sufficiently complex and sufficiently similar (e.g., the same pattern on the carpets), one would expect an explanation of this similarity in terms of a mechanism that relates these two strings in nature (are the carpets produced by the same company?). It is necessary that the descriptions are sufficiently complex, as an example of [
4] illustrates: assume the two observed strings are equal to the first hundred digits of the binary expansion of π; hence, they can be generated independently by a simple rule. If this is the case, the similarity of the two strings would not be considered as strong evidence for the existence of a causal link. To exclude such cases, the Kolmogorov complexity [
19]
K(
s) of a string
s has been used as the measure of complexity. It is defined as the length of the shortest program that prints out
s on a universal (prefix-free) Turing machine. With this definition, strings that can be generated using a simple rule, such as the constant string
s = 0⋯0 or the first
n digits of the binary expansion of π, are considered simple, whereas it can be shown that a random string of length
n is complex with high probability. Kolmogorov complexity can be transformed into a function on sets of strings by choosing a suitable concatenation function ⟨, ⟩, such that
K(
s1,
…, sn) =
K(⟨
s1, ⟨
s2,
…, ⟨
sn−1,
sn⟩
…⟩).
The algorithmic mutual information [
8] of two strings
a and
b is then equal to the sum of the lengths of the shortest programs that generate each string separately minus the length of the shortest program that generates the strings
a and
b:
where ⩲ stands for equality up to an additive constant that depends on the choice of the universal Turing machine. Analogous to Reichenbach’s principle of common cause, [
4] postulates a causal relation among
a and
b whenever
I(
a :
b) is large, which is the case if the complexities of the strings are large and both strings together can be generated by a much shorter program than the programs that describe them separately.
In formal analogy to the probabilistic case, algorithmic mutual information can be extended to a conditional version defined for sets of strings
A, B, C ⊆ {
s1,
…, sn} as:
Intuitively,
I(
A :
B |C) is the mutual information between the strings of
A and the strings of
B if the shortest program that prints the strings in
C has been provided as an additional input. Based on this notion of conditional mutual information, the causal Markov condition can be formulated in the algorithmic setting. It can be proven [
4] to hold for a directed acyclic graph
G on strings
s1,
…, sn if every
si can be computed by a simple program on a universal Turing machine from its parents and an additional string
ni, such that the
ni are mutually independent. Without going into the details, we sum up by stating that DAGs on strings can be given a causal interpretation, and it is therefore interesting to infer properties of the class of possible DAGs that represent the algorithmic conditional independence relations.
In the algorithmic setting, our result can be stated as follows:
Theorem 3 (Inference of common ancestors of strings).
Let O[n] = {
s1,
…, sn}
be a set of binary strings. If for a number c, (1≤
c ≤
n −1):
then there must exist a common ancestor of at least c+1
strings out of O[n] in any DAG model of the O[n].
(Here,
means up to an additive constant dependent only on the choice of a universal Turing machine, on c and on n.) Proof. As described, algorithmic mutual information is an information measure in our sense only up to an additive constant depending on the choice of the universal Turing machine. However, one can check that in this case, the decomposition of mutual information (Theorem 1) holds up to an additive constant that depends additionally on the number of strings n and the chosen parameter c. The result on Kolmogorov complexities follows by choosing Y = (s1,…, sn), since
.
Thus, highly-redundant strings require a common ancestor in any DAG model. Since the Kolmogorov complexity of a string
s is uncomputable, we have argued in recent work [
5] that it can be substituted by a measure of complexity in terms of the length of a compressed version of
s with respect to a chosen compression scheme (instead of a universal Turing machine), and the above result should still hold approximately.
4.3. Structural Implications from Synergy?
We saw that large redundancy implies common ancestors of many elements, and we may wonder whether structural information can be obtained from synergy in a similar way. This seems not to be possible, since synergy is related to more fine-grained information (information about the mechanisms), as the following example shows: Assume the observations
O[n] are mutually independent. Then, any DAG is a valid DAG model, since the local Markov condition will always be satisfied. We also now that
r(
Y)≤ 0, but it turns out that the amount of synergy crucially depends on the way that
Y has processed the information of the
O[n] (and therefore, not on a structural property among the
O[n] themselves). To see this, let the observations
Oi be binary random variables, which are mutual independent and distributed uniformly, such that:
Further, let Y = (Oi ⊕Oj)i<j be a function of the observations (addition is modulo two). Then, the O[n] are highly synergistic with respect to Y, that is r1(Y) = −(n−1) log 2. On the other hand, if Y = O1 ⊕⋯⊕On, then r1(Y) = −log 2 only.
Nevertheless, it is an easy observation that synergy with respect to
Y can be related to an increase of redundancy after conditioning on
Y. Since
I(·
|Y) is a measure of mutual information, as well, we define a conditioned version of
r in a canonical way as:
with respect to some observation
Z. If
I can be evaluated on non-disjoint subsets, that is if we can choose
Z =
O[n], we have the following:
Proposition 2 (Synergy from increased redundancy induced by conditioning).
Let O[n] = {
O1,
…, On}
and Y be arbitrary elements on which a mutual information function I is defined. Then:hence if conditioning on Y increases the redundancy of O[n] with respect to itself, then rc(
Y) < 0
and the O[n] are synergistic with respect to Y.
Proof. Using the chain rule, we derive
where the last equality follows because
rc(
Y|O[n]) = 0.
Continuing the example of binary random variables above, mutual independence of the
O[n] is equivalent to
r1(
O[n]) = 0 and, therefore, using the proposition
r1(
Y) =−
r1(
O[n]|Y). Thus, if
Y =
O1⊕⋯ ⊕
O[n],
as already noted above.
5. Conclusions
Based on a generalized notion of mutual information, we proved an inequality describing the decomposition of information about a whole set into the sum of information about its parts. The decomposition depended on a structural property, namely the existence of common ancestors in a DAG. We connected the result to the notions of redundancy and synergy and concluded that large redundancy implies the existence of common ancestors in any DAG model. Specialized to the case of discrete random variables, this means that large stochastic dependence in terms of multi-information needs to be explained through a common ancestor (in a Bayesian net) acting as a broadcaster of information.
Much work has been done already that examined the restrictions that are imposed on observations by graphical models that include latent variables. Pearl [
1,
20] already investigated constraints imposed by the special instrumental variable model. Furthermore, Darroch
et al. [
21] and, recently, Sullivant
et al. [
22] looked at linear Gaussian graphical models and determined constraints in terms of the entries on the covariance matrix describing the data (tetrad constraints). Further, methods of algebraic statistics were applied (e.g., [
23]) to derive constraints that are induced by latent variable models directly on the level of probabilities. In general, this does not seem to be an easy task due to the large number of variables involved. Information theory, on the other hand, provides efficient methods for comparatively easy derivations of “macroscopic” constraints, the main subject of the present article (see also [
24]).
Since the initial publication of this manuscript as a preprint [
25], subsequent progress has been made on the problem of inferring DAG models from partial observations. In [
26], the problem is treated in the wider context of inferring possible joint distributions from restrictions on marginals. There, an algorithm is presented that, even though computationally demanding, computes all Shannon-type entropic inequalities for given marginal constraints. Furthermore, it has turned out that entropic inequalities are useful in quantum physics where they restrict possible theories of data generation in more general settings than the ones using Bell inequalities (see, e.g., [
27–
30]). Moreover, we would like to mention that meanwhile, information measures for causal inference among strings based on compression length have been proposed [
31], thus extending the possible applications of inequalities like the ones presented in this article.
Initiated by the work [
32] of Williams and Beer, recent progress has been made related to the concepts of synergy and redundancy [
33–
35]. These works, however, do not address any causal interpretations. We think that the general methodology of connecting the redundancy and synergy of observations to properties of the class of possible DAG models will add new insights to this research direction.
Our generalized notion
rc of redundancy (see
(13)) has been used by Ver Steeg and Galstyan as an objective function for hierarchical representations of high-dimensional data [
36,
37], where the optimization is taken with respect to the variable
Y.
Finally, we would like to mention the works [
38] and [
39] of one of us, which were based on our present article. In the article [
38], our lower bound on the entropy of common ancestors, the inequality
(15), is interpreted as a special linear inequality of entropic terms. The solution sets of such information inequalities are studied as the basis for casual inference. The work [
39] gives a tight upper bound on our parametrized version
Ic(
X1,
…, Xn) of multi-information (see
(14)) and derives a method for discriminating between causal structures in Bayesian networks given partial observations.