Cryptographic Aspects of Quantum Reading
Abstract
:1. Introduction
2. Basic Setup for Quantum Reading
2.1. Classical Benchmark
2.2. Quantum Transmitter
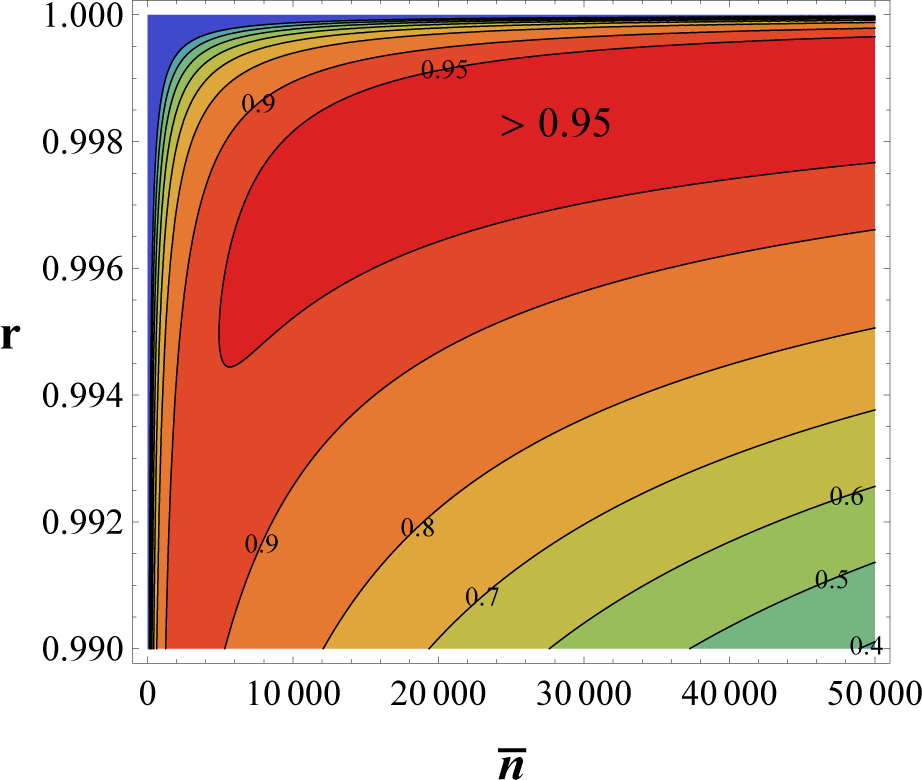
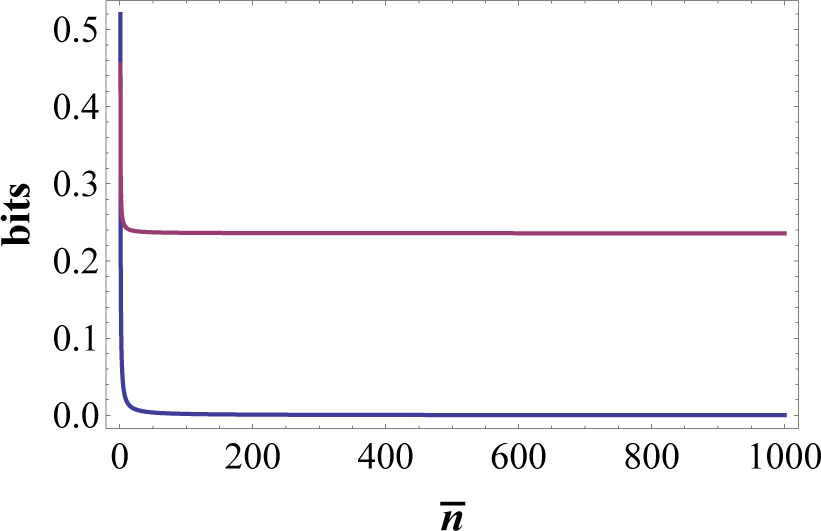
3. Data Secured by Quantum Reading
4. Conclusions
Acknowledgments
Conflicts of Interest
References
- Gisin, N.; Ribordy, G.; Tittel, W.; Zbinden, H. Quantum cryptography. Rev. Mod. Phys. 2002, 74, 145–195. [Google Scholar]
- Weedbrook, C.; Pirandola, S.; Garcia-Patron, R.; Cerf, N.J.; Ralph, T.C.; Shapiro, J.H.; Lloyd, S. Gaussian quantum information. Rev. Mod. Phys. 2012, 84, 621–669. [Google Scholar]
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Information; Cambridge University Press: Cambridge, MA, USA, 2000. [Google Scholar]
- Modi, K.; Brodutch, A.; Cable, H.; Paterek, T.; Vedral, V. The classical-quantum boundary for correlations: Discord and related measures. Rev. Mod. Phys. 2012, 84, 1655–1707. [Google Scholar]
- Pirandola, S.; Spedalieri, G.; Braunstein, S.L.; Cerf, N.J.; Lloyd, S. Optimality of Gaussian Discord. Phys. Rev. Lett. 2014, 113, 140405. [Google Scholar]
- Pirandola, S. Quantum discord as a resource for quantum cryptography. Sci. Rep. 2014, 4. [Google Scholar] [CrossRef]
- Braunstein, S.L.; Pirandola, S. Side-Channel-Free Quantum Key Distribution. Phys. Rev. Lett. 2012, 108, 130502. [Google Scholar]
- Rubenok, A.; Slater, J.A.; Chan, P.; Lucio-Martinez, I.; Tittel, W. Real-World Two-Photon Interference and Proof-of-Principle Quantum Key Distribution Immune to Detector Attacks. Phys. Rev. Lett. 2013, 111, 130501. [Google Scholar]
- Pirandola, S.; Ottaviani, C.; Spedalieri, G.; Weedbrook, C.; Braunstein, S.L.; Lloyd, S.; Gehring, T.; Jacobsen, C.S.; Andersen, U.L. High-rate quantum cryptography in untrusted networks 2013, arXiv, 1312.4104.
- Ottaviani, C.; Spedalieri, G.; Braunstein, S.L.; Pirandola, S. Continuous-variable quantum cryptography with an untrusted relay: Detailed security analysis of the symmetric configuration. Phys. Rev. A 2015, 91, 022320. [Google Scholar]
- Pirandola, S. Quantum Reading of a Classical Digital Memory. Phys. Rev. Lett. 2011, 106, 090504. [Google Scholar]
- Pirandola, S.; Lupo, C.; Giovannetti, V.; Mancini, S.; Braunstein, S.L. Quantum reading capacity. New J. Phys. 2011, 13, 113012. [Google Scholar]
- Spedalieri, G.; Lupo, C.; Mancini, S.; Braunstein, S.L.; Pirandola, S. Quantum reading under a local energy constraint. Phys. Rev. A 2012, 86, 012315. [Google Scholar]
- Lupo, C.; Pirandola, S.; Giovannetti, V.; Mancini, S. Quantum reading capacity under thermal and correlated noise. Phys. Rev. A 2013, 87, 062310. [Google Scholar]
- Hirota, O. Error Free Quantum Reading by Quasi Bell State of Entangled Coherent States 2011, arXiv, 1108.4163.
- Nair, R. Discriminating quantum-optical beam-splitter channels with number-diagonal signal states: Applications to quantum reading and target detection. Phys. Rev. A 2011, 84, 032312. [Google Scholar]
- Bisio, A.; Dall’Arno, M.; D’Ariano, G.M. Tradeoff between energy and error in the discrimination of quantum-optical devices. Phys. Rev. A 2011, 84, 012310. [Google Scholar]
- Guha, S.; Dutton, Z.; Nair, R.; Shapiro, J.; Yen, B. Information Capacity of Quantum Reading, Proceedings of Frontiers in Optics (FiO) 2011/Laser Science (LS) XXVII, San Jose, CA, USA, 16–20 October 2011.
- Dall’Arno, M.; Bisio, A.; D’Ariano, G.M.; Mikova, M.; Jezek, M.; Dusek, M. Experimental implementation of unambiguous quantum reading. Phys. Rev. A 2012, 85, 012308. [Google Scholar]
- Dall’Arno, M.; Bisio, A.; D’Ariano, G.M. Ideal Quantum Reading of Optical Memories. Int. J. Quant. Inf. 2012, 10, 1241010. [Google Scholar]
- Wilde, M.M.; Guha, S.; Tan, S.-H.; Lloyd, S. Explicit Capacity-Achieving Receivers for Optical Communication and Quantum Reading, Proceedings of the 2012 IEEE International Symposium on Information Theory (ISIT 2012), Cambridge, MA, USA, 1–6 July 2012; pp. 551–555.
- Dall’Arno, M. Optimization of Quantum Communication Protocols. Ph.D. Thesis, University of Pavia, Pavia, Italy, 2012. [Google Scholar]
- Dall’Arno, M. Gaussian Quantum Reading beyond the Standard Quantum Limit 2013, arXiv, 1302.1624.
- Einstein, A.; Podolsky, B.; Rosen, N. Can Quantum-Mechanical Description of Physical Reality Be Considered Complete? Phys. Rev. 1935, 47, 777–780. [Google Scholar]
- Lloyd, S. Enhanced Sensitivity of Photodetection via Quantum Illumination. Science 2008, 321, 1463–1465. [Google Scholar]
- Tan, S.-H.; Erkmen, B.I.; Giovannetti, V.; Guha, S.; Lloyd, S.; Maccone, L.; Pirandola, S.; Shapiro, J.H. Quantum Illumination with Gaussian States. Phys. Rev. Lett. 2008, 101, 253601. [Google Scholar]
- Guha, S.; Erkmen, B.I. Gaussian-state quantum-illumination receivers for target detection. Phys. Rev. A 2009, 80, 052310. [Google Scholar]
- Shapiro, J.H. Defeating passive eavesdropping with quantum illumination. Phys. Rev. A 2009, 80, 022320. [Google Scholar]
- Lopaeva, E.D.; Berchera, I.R.; Degiovanni, I.P.; Olivares, S.; Brida, G.; Genovese, M. Experimental Realization of Quantum Illumination. Phys. Rev. Lett. 2013, 110, 153603. [Google Scholar]
- Zhang, Z.; Tengner, M.; Zhong, T.; Wong, F.N.C.; Shapiro, J.H. Entanglement’s Benefit Survives an Entanglement-Breaking Channel. Phys. Rev. Lett. 2013, 111, 010501. [Google Scholar]
- Zhang, Z.; Mouradian, S.; Wong, F.N.C.; Shapiro, J.H. Entanglement-Enhanced Sensing in a Lossy and Noisy Environment. Phys. Rev. Lett. 2015, 114, 110506. [Google Scholar]
- Barzanjeh, S.; Guha, S.; Weedbrook, C.; Vitali, D.; Shapiro, J.H.; Pirandola, S. Microwave Quantum Illumination. Phys. Rev. Lett. 2015, 114, 080503. [Google Scholar]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory; Wiley: Hoboken, NJ, USA, 2006. [Google Scholar]
- Helstrom, C.W. Quantum Detection and Estimation Theory, Mathematics in Science and Engineering; Academic Press: New York, NY, USA, 1976; Volume 123. [Google Scholar]
- Audenaert, K.M.R.; Calsamiglia, J.; Masanes, L.; Muñoz-Tapia, R.; Acin, A.; Bagan, E.; Verstraete, F. Discriminating States: The Quantum Chernoff Bound. Phys. Rev. Lett. 2007, 98, 160501. [Google Scholar]
- Audenaert, K.M.R.; Nussbaum, M.; Szkola, A.; Verstraete, F. Asymptotic Error Rates in Quantum Hypothesis Testing. Commun. Math. Phys. 2008, 279, 251–283. [Google Scholar]
- Pirandola, S.; Lloyd, S. Computable bounds for the discrimination of Gaussian states. Phys. Rev. A 2008, 78, 012331. [Google Scholar]
- Spedalieri, G.; Braunstein, S.L. Asymmetric quantum hypothesis testing with Gaussian states. Phys. Rev. A 2014, 90, 052307. [Google Scholar]
- Spedalieri, G.; Weedbrook, C.; Pirandola, S. A limit formula for the quantum fidelity. J. Phys. A: Math. Theor. 2013, 46, 025304. [Google Scholar]
- Terhal, B.M.; DiVincenzo, D.P.; Leung, D.W. Hiding Bits in Bell States. Phys. Rev. Lett. 2001, 86, 5807–5810. [Google Scholar]
- DiVincenzo, D.P.; Leung, D.W.; Terhal, B.M. Quantum data hiding. IEEE Trans. Inf. Theory 2002, 48, 580–599. [Google Scholar]


© 2015 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Spedalieri, G. Cryptographic Aspects of Quantum Reading. Entropy 2015, 17, 2218-2227. https://doi.org/10.3390/e17042218
Spedalieri G. Cryptographic Aspects of Quantum Reading. Entropy. 2015; 17(4):2218-2227. https://doi.org/10.3390/e17042218
Chicago/Turabian StyleSpedalieri, Gaetana. 2015. "Cryptographic Aspects of Quantum Reading" Entropy 17, no. 4: 2218-2227. https://doi.org/10.3390/e17042218
APA StyleSpedalieri, G. (2015). Cryptographic Aspects of Quantum Reading. Entropy, 17(4), 2218-2227. https://doi.org/10.3390/e17042218



