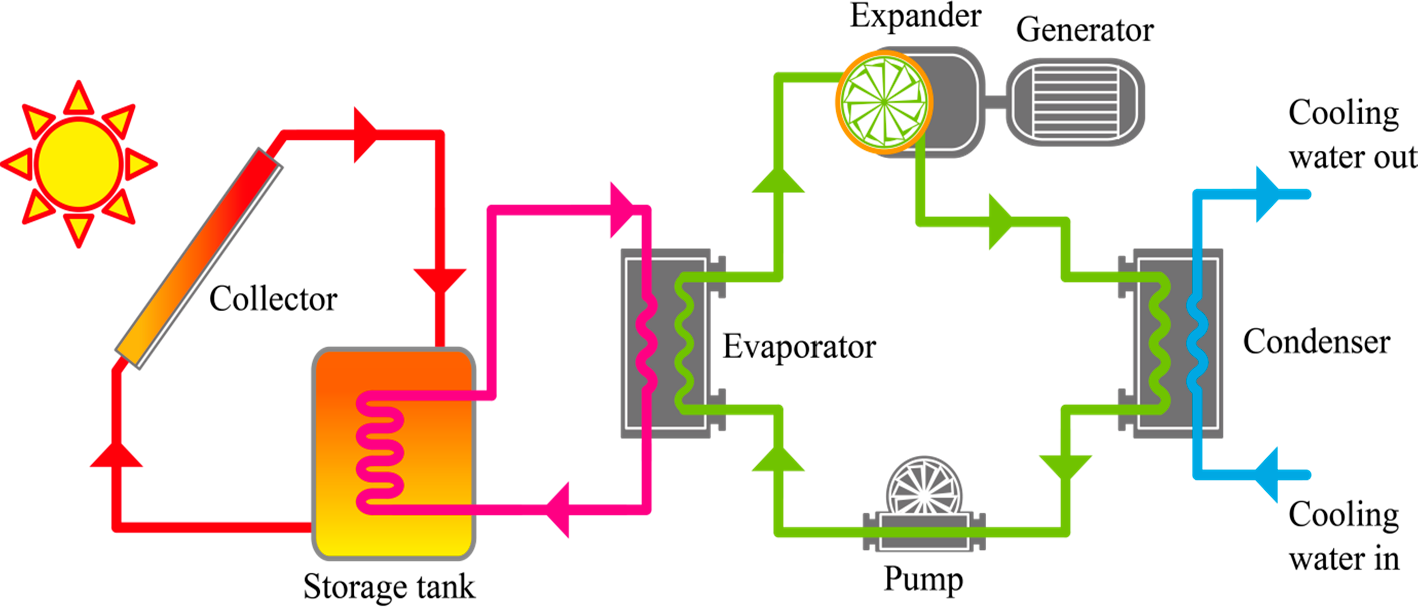
1. Introduction
Power obtained from solar energy in developing countries plays an important role in changing the living standards of people residing in remote areas. Developing countries have abundant solar energy resources and the capacity to produce and manufacture comparatively cheap solar power systems that can be harnessed. Through the proper utilization of this solar energy, the isolated rural areas of developing countries can be electrified. One of the promising technologies for powering rural areas is the solar organic Rankine (SORC) cycle system. The SORC is similar to the conventional steam Rankine cycle system but it uses renewable energy as the heat source (solar energy) and pure or mixed organic compounds as the working fluid. A small-scale SORC can be used to electrify the homes in rural communities and run small businesses. Large-scale SORC have already been commercialized, but small-scale systems are still in the development phase. The small-scale system is applied in rural areas where electricity grid connections/extensions are not economically feasible due to difficult geographic terrain. An off-grid SORC provides a sustainable and cost-effective alternative to un-eco-friendly and expensive diesel generators for electricity generation. In addition, this small-scale technology helps to replace kerosene based lamps and traditional biomass, in which 2.7 billion people around the globe depend on it for their energy requirements [
1]. An off-grid power supply can provide power for domestic uses, such as lighting, running televisions, radios, refrigerators, communications, and water pumping. Moreover, it can be used for public uses, including electrification in rural schools and health clinics. In particular, the SORC is a reliable technology for exploiting low and medium range temperature heat sources obtained from different types of collectors, such as flat plate, evacuated tube collector and parabolic type of collectors. Because the ORC system uses organic compounds as a working fluid, a poor choice of working fluid influences the solar plant performance, which could adversely affect the economics. Therefore, the working fluid properties should also be considered when designing a solar ORC system.
Several authors [
2–
7] reported R245fa to be a good candidate for a solar ORC system. This working fluid has good thermo-physical characteristics when subjected to a various range of heat source temperatures. In addition, it causes low ozone depletion, has low global warming potential, and is non-toxic and non-flammable when it is used in a solar ORC system. Several studies have discussed the SORC technology for electricity generation but few have been conducted for the purposes of rural electrification. Quoilin
et al. [
8] designed the solar ORC unit to be installed in rural clinics of Lesotho with a net target power output of 3 kW. They used a collector trough, one- or two-stage expansion device (modified commercial HVAC compressor), plate type heat exchangers, and air-cooled condenser, and reported an overall efficiency of 8%.
Mathew
et al. [
9] examined the technical and economic feasibility of the small-scale solar ORC systems comparing with photovoltaics hybridized with LPG/propane and diesel generator small plant for electricity generation in the rural areas of Africa. They showed that net cost for rural health clinic systems has a specific levelized electricity cost of 0.26–0.31 USD/kWh. Similarly, Wolpert
et al. [
10] carried out theoretical analysis of the CHP system for electricity generation using evacuated heat pipe solar collectors and reported an efficiency of 15% using the refrigerant R134a at a sink temperature of 10 °C. Similarly, Nguyen
et al. [
11] constructed and tested a small-scale solar ORC prototype that used
n-pentane and delivered 1.5 kW of electricity with a thermal efficiency of 4.3%. Kane
et al. [
12] design a mini-hybrid solar power plant integrating solar collectors, ORC cycles and bio-diesel engine to confirm the operational characteristics of this hybrid system to meet the electricity, cooling and pumping needs for rural areas. Baral
et al. [
13] tested a small-scale ORC unit with a commercial scroll expander and found that the unit has the capacity to produce 1.4 kW of electric power when the heat source was 120 °C. In a similar manner, Delgado and Lourdes [
14] conducted a parametric study of the influence of the configuration of the solar ORC system for various working fluids in a desalination process to determine the minimum aperture area required to produce mechanical power output under different operating conditions. The result showed that compound parabolic collector (CPC) and flat plate collector (FPC) require 25–26 m
2 and 22–23 m
2, respectively, to produce 1 kW power. In a different study, Gang
et al. [
15] reported an overall electrical efficiency of 8.6% using a compound parabolic trough with a solar irradiation of 750 W/m
2. Delgado [
16] studied the small-scale solar ORC system that can be used to pump water and found that they were installed mostly in Asian countries.
The main objective of this study was to determine if a small scale SORC system is a good option for electricity generation in rural areas. The findings of the present study are expected to help rural practitioners, solar ORC developers and investors to consider a small-scale solar ORC system as economically feasible for producing electricity for rural houses, health posts, schools, and even run small businesses in the un-electrified areas of developing countries. The first part of this study is on the experimental analysis of the SORC system and the second part is the thermoeconomic analysis. The experimental section includes the SORC system efficiencies, power output during months of the year, area of the solar collector required for electricity generation. The thermoeconomic analysis section contains the cost of energy per kWh through energy analysis, payback period and sensitivity analysis.
4. Thermodynamic Fundamentals
The described SORC system was analyzed from the code developed using the Engineering Equation Solver (EES). The following assumptions were made for the analyses of the overall performance, system and sub-systems:
All the thermodynamic processes and systems are in a steady state.
The working fluid feed and expansion devices are adiabatic devices.
The simple ORC system has negligible pressure losses in the heat exchanger and piping system so it is neglected.
The reference state (dead state) temperature and pressure are 25 °C and 1 bar, respectively, for the system’s performance calculations.
The energy balance is applied to each of the system components based on the first law of thermodynamics. The general energy balance equation in steady state for any components can be written as follows:
where subscripts in and out represent the inlet and outlet, respectively;
and
h represents the mass flow rate and specific enthalpy of the streams of the system working fluid, respectively, and
and
represent the heat transfer crossing the component boundaries, respectively.
The limitation of the energy assessment can be overcome using the method of exergy analysis. This analysis deals with the conversion of energy along with the second law of thermodynamics. Because energy and mass are neither consumed nor generated, exergy is consumed during the thermodynamic process due to the irreversibility of transformation and this exergy consumption is proportional to entropy generation. In this paper, exergy analysis was carried to determine the maximum energy that can be extracted from the system. This helps to reduce the existing inefficiencies caused by different heat sources. In addition, it is the maximum theoretical useful work that can be obtained when the system interacts to equilibrium with the surrounding environment. The exergy balance in the system components at the steady state can be determined using the following general equation:
where
denotes the exergy destruction rate occurring on device
k, and
and
denote the exergy rate due to work and heat transfer, respectively. The exergy rates following in and out in the system is denoted by (
). The exergy transfer due to heat and work can be expressed as
where
T0 is the reference state temperature (dead state) that describes the state at which the system is in equilibrium with the environment and
T is the boundary temperature at which heat transfer occurs.
The useful collected energy rate from the vacuum tubular single collector is defined as
where
Cp is the specific heat capacity,
is the mass flow rate in the collector and
To and
Ti are the outlet and inlet temperature of solar collector, respectively.
The area of the solar collector was calculated using the collector energy balance equation as follows:
where
,
and
are the collector efficiency, area of collector and global radiation on the surface, respectively.
The net solar ORC efficiency of the system is given by the following equation:
where
is the thermal efficiency of the ORC system.
The exergy from the sun (exergy input), which is also a function of the sun’s outer surface temperature (
is given by the following equation:
The net electrical exergy efficiency is a defined as follows:
The irreversibility ratio of a component
k is defined as
The improvement potential in the exergy destruction of a component
k is defined as
5. Results and Discussion: Solar ORC System Performance
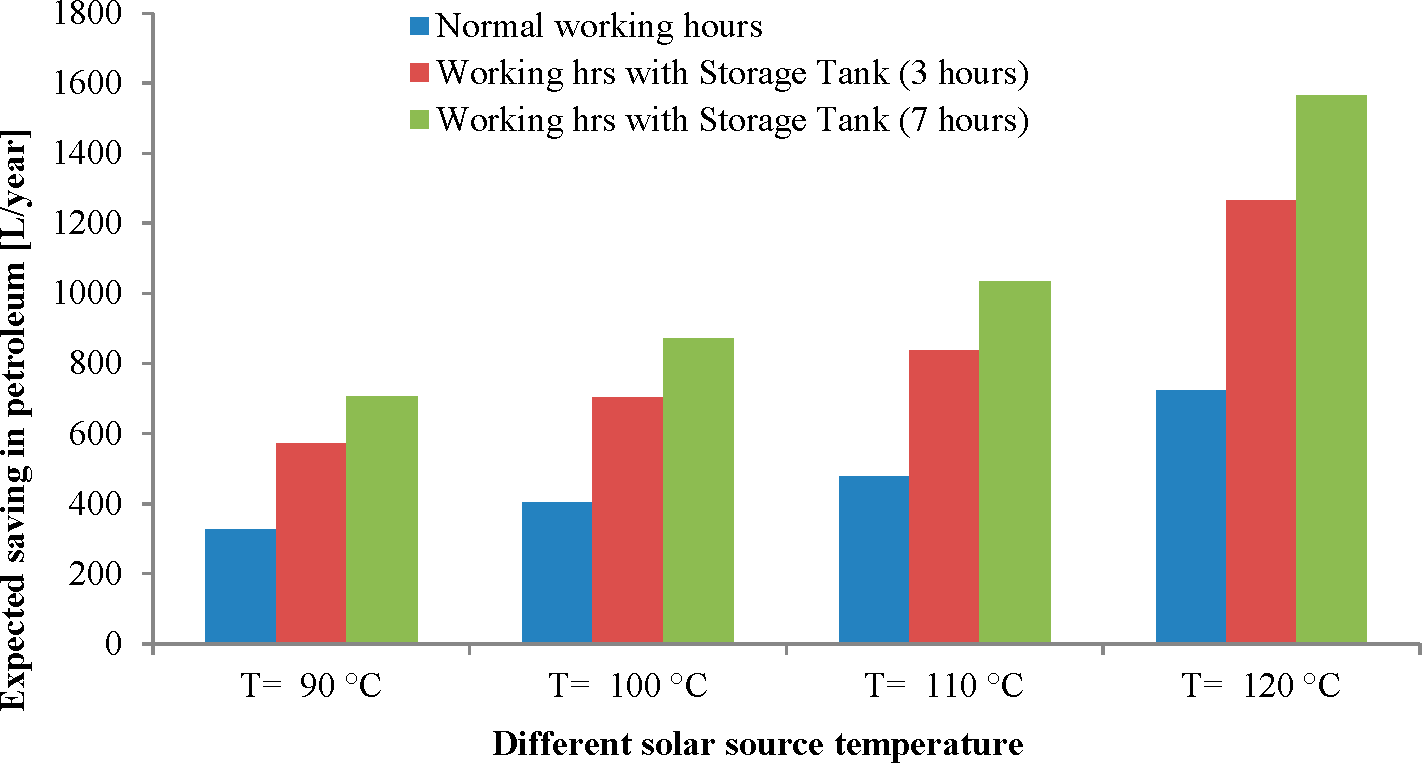
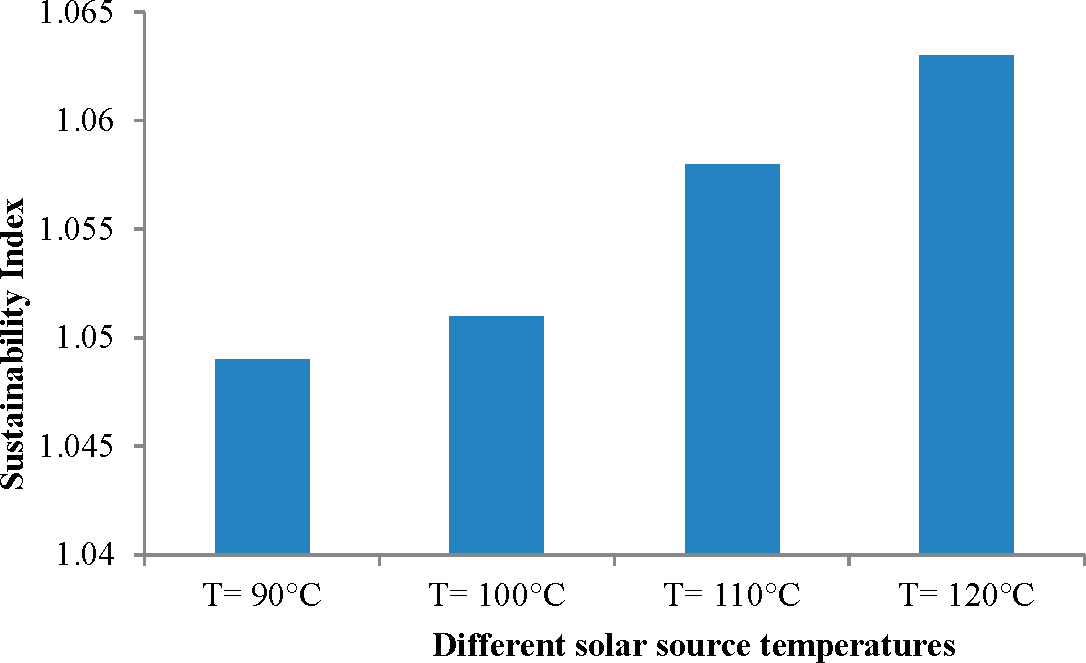
In designing a solar ORC system, the main parameter to examine is the heat input required to produce the power output at different heat source temperatures. From the experimental results, the heat input and solar collector area needed to produce solar ORC power output was determined, as shown in
Table 2. For solar sources of 90 °C, 100 °C, 110 °C, and 120 °C, the heat required was 11.05 kW, 12.3 kW, 12.6 kW, and 17 kW, respectively. This experimental data showed that a 7.1 bar, 9.9 bar, 10.2 bar, and 13 bar evaporator inlet pressure is needed to produce a power of 0.63 kW, 0.77 kW, 0.87 kW, and 1.38 kW, respectively, at corresponding different solar source temperatures. The ORC unit was operated at 3600 RPM, which is the maximum rotational speed of the expander. The maximum inlet pressure of the scroll expander is limited,
i.e., maximum operating pressure is 13.5 bar. The commercial expander is designed for utilization of a low temperature heat source. The corresponding expander inlet temperatures were 79.9 °C, 90.49 °C, 99.41 °C, and 113 °C, respectively. The experimental analysis shows that the scroll expander has a maximum isentropic efficiency of 70% when the unit working is with a heat source temperature of 120 °C and inlet pressure of 13 bar.
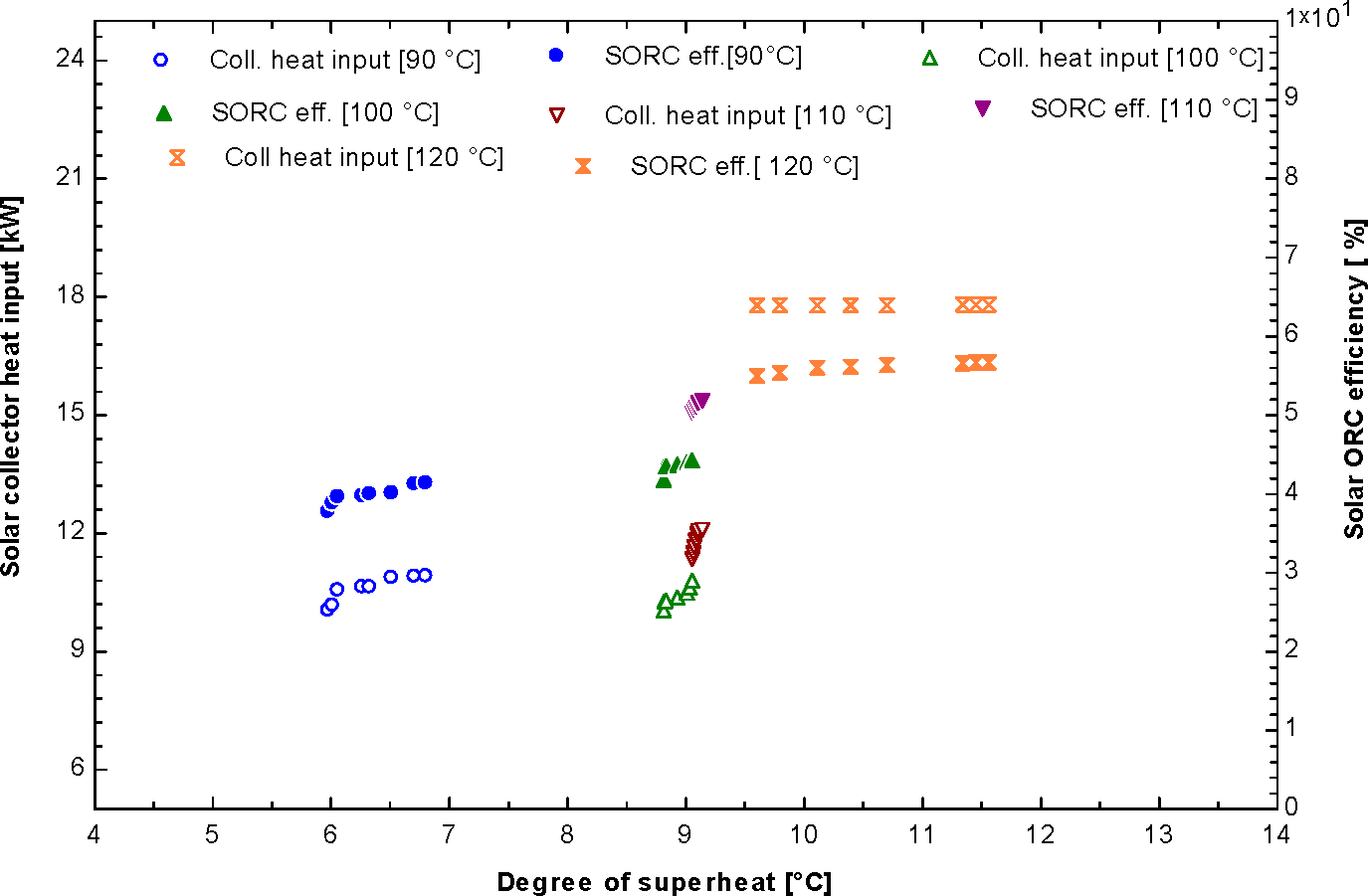
The pump isentropic efficiency was assumed to be around same as the expander. In the experiment, the refrigerant, R245fa, was superheated. This superheat temperature of the working fluid increases the solar ORC efficiency slightly. The efficiency of the solar ORC system was calculated based on the thermal efficiency and collector efficiency obtained from the scale-small prototype unit.
Figure 3 shows the variation of the collector heat input and solar ORC efficiency when the degree of superheat changes. The maximum solar ORC efficiency was 4.14%, 4.42%, 5.18%, and 5.66% when the degree of the superheat temperature are 7.9 °C, 8.8 °C, 9.09 °C, and 11.69 °C, respectively.
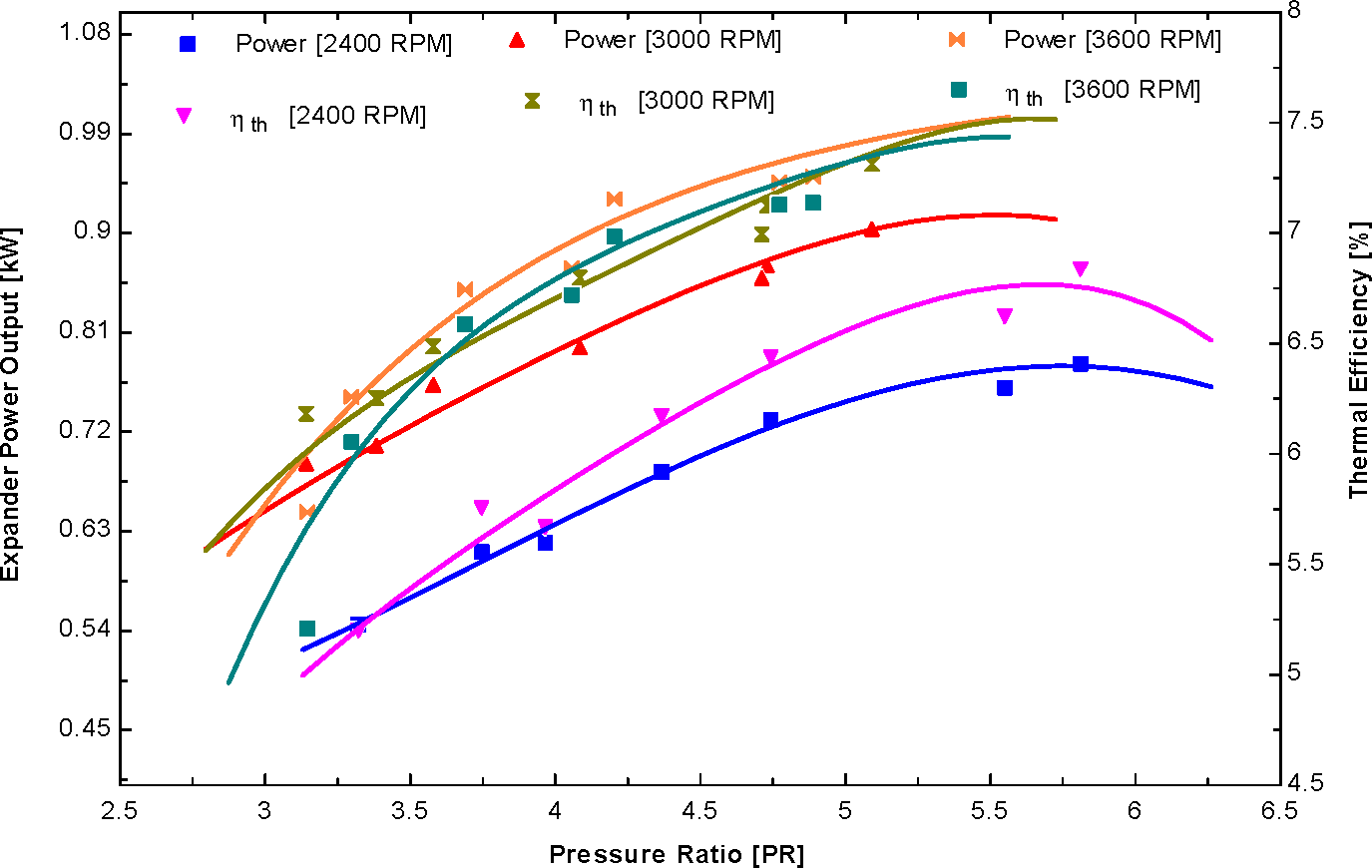
Different temperatures and pressures in the ORC system will cause the scroll expander to be operated at off-design conditions. The power output in the commercial expander can be controlled by changing the rotational speed of expander and can be illustrated from the
Figure 4. When the temperature and pressure change, the ORC system is operated at low RPM. From the experimental results, it is seen that power output decreases from 0.98 kW to 0.63 kW when the rotational speed of the expander changes from 3600 RPM to 2400 RPM. Thermal efficiency decreases from 7.5% to 6.3% during the change in rotational speed of the expander.
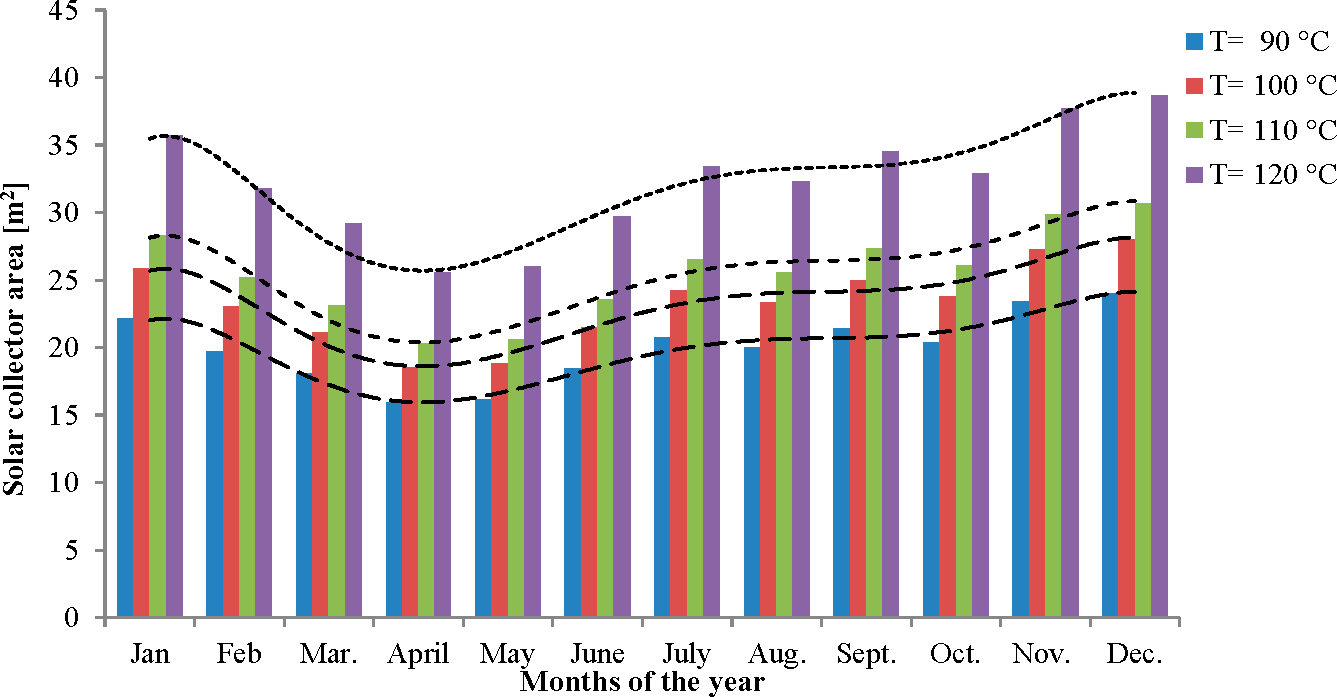
The variation of the solar irradiation on the solar ORC system plays an important role in producing power output.
Figure 5 shows the solar collector area needed to produce a power output at different source temperatures during different months of the year. The maximum area of the collector needed depends on the solar irradiation during the month. In this case, it was 23 m
2 in December and 15 m
2 in April for a 90 °C solar source. Similarly, 37 m
2 and 25 m
2 collector areas were needed to achieve a 120 °C solar source temperature in December and April, respectively. The utilization of solar energy is subjected to change according to the seasons, weather and location. Therefore, the efficiency of the collector changes with the varying solar irradiation. The working conditions of a solar ORC system are instantaneous. Therefore, to analyze the monthly performance of a SORC system, it is essential to consider the efficiency of the collector. According to the manufacturer’s catalog, the prototype collector efficiency could be up to 70%. In this framework, the monthly solar ORC power output was calculated.
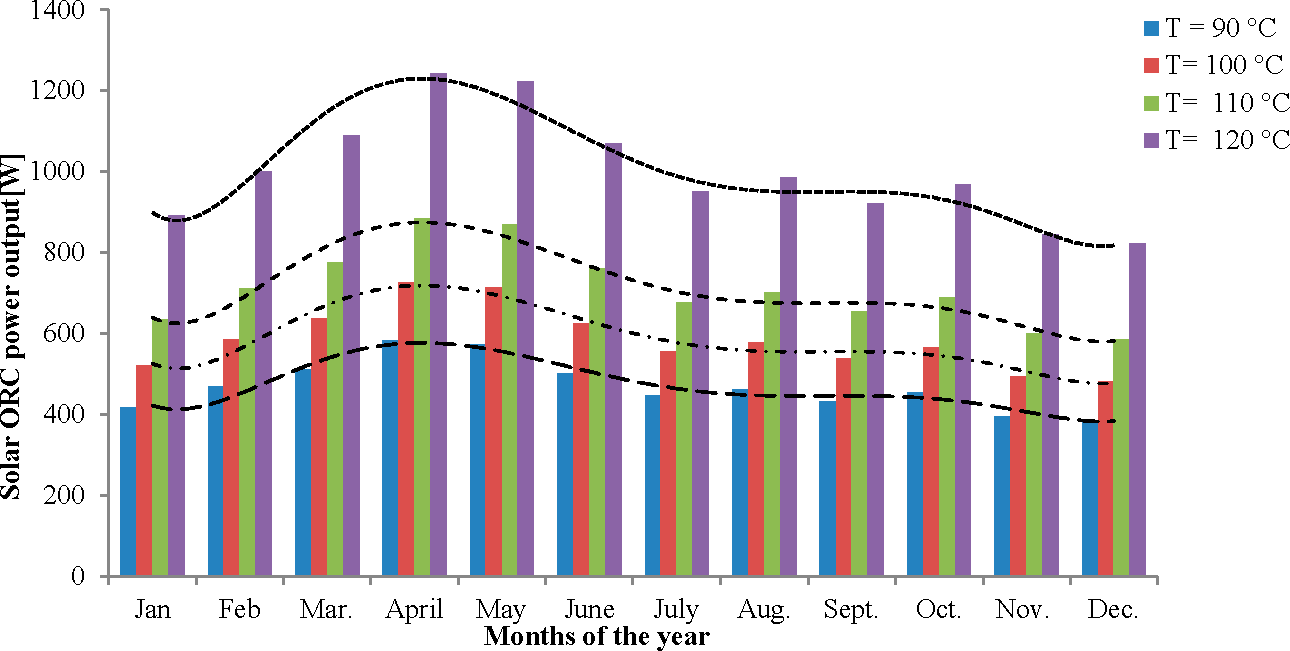
Figure 6 shows the monthly solar ORC power output for different temperatures according to the meteorological conditions of Busan City (South Korea).
The maximum solar power output can be obtained when there is high solar irradiance. In April and May, the maximum power was obtained (1.2 kW and 1.19 kW, respectively), whereas in December, the output power obtained was 0.9 kW for a solar source temperature of 120 °C. The lowest power obtained from the solar ORC system during December was 0.4 kW, 0.53 kW and 0.61 kW for T = 90 °C, T = 100 °C and T = 110 °C, respectively. The solar irradiance varied from 2.68 kWh/m2/day to 5.57 kWh/m2/day during the year in Busan.
In order to see if the solar ORC system can be operated at different loads at different times of the year, an electricity demand load in the particular location should be known. For this, a case study conducted by Beck and Cecilia [
18] in Dhading district, Nepal has been taken as a reference for estimating electricity demand in the Rayal village, which has 70 households. The electricity demand of Rayal was estimated based on observations of the daily life in the village. It was observed that electricity demand of 8.6 kWh/day was needed to fulfill the basic human needs (lighting). For this, four LED lamps (5 W each) and one wall socket for recharging cellphones (5 W) per household was needed. The time for electricity demand was from 6–8 a.m. and 7–11 p.m. Based on the case study, electricity demand per month has been estimated in order to observe the performance change in different months of the year when optimal solar ORC configuration is suggested. The monthly electricity demand is estimated to be 224.25 kWh.
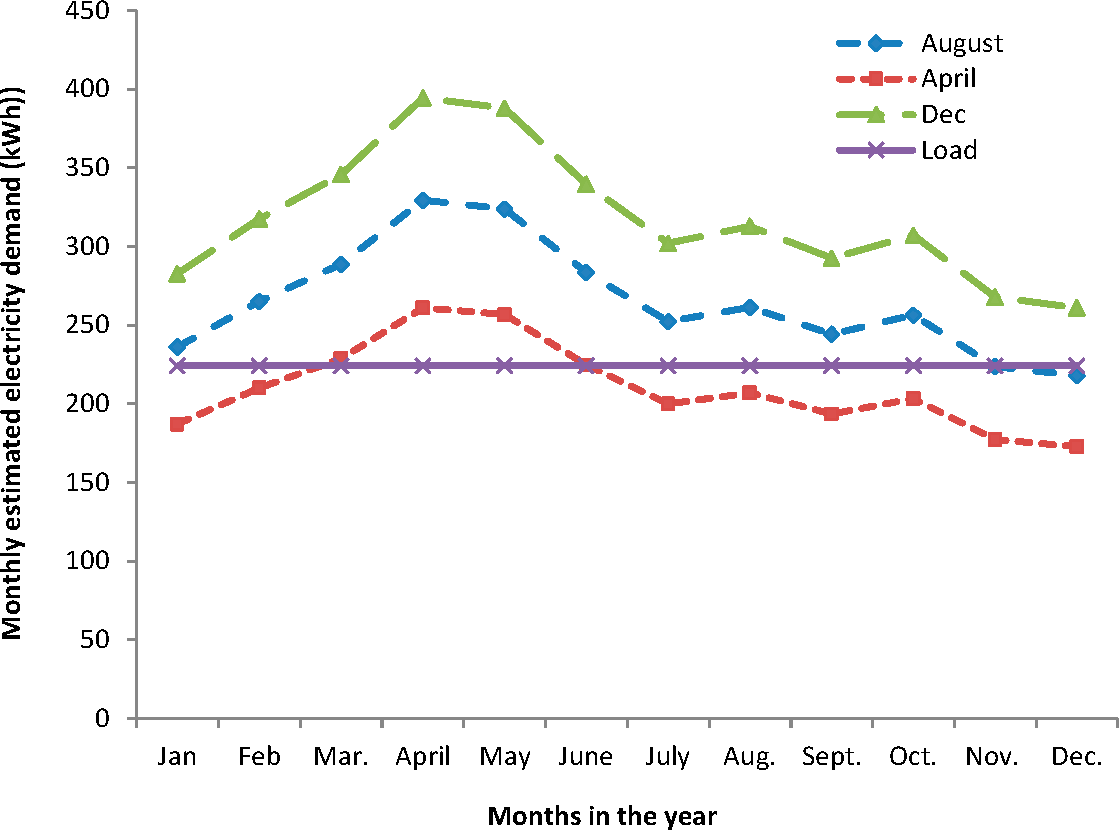
Figure 7 shows that the electricity demand can be met easily by the solar ORC system of collector area 37 m
2 (December) but there is an excess production of energy in the month of April if it is design to operate through the year. Another design configuration selected is the collector area 25 m
2 (April). Here, the electricity demand is only met during the summer season so designing the solar ORC based on April is also not favorable. The most suitable solar ORC configuration is to design the system based on the collector area needed in August (32.3 m
2). In this case, the electricity demand is met almost throughout the year, but the energy is excessive during the summer season. This excessive energy can be utilized in production of hot water for domestic purposes. The maximum power output obtained is 394 kWh during the month of April if the collector area is designed based on the month of December.
Detailed exergy analysis was conducted for different solar source temperatures through an exergetic assessment of the solar ORC system components. The main parameters for consideration of the exergetic assessment included the exergy destruction rate, exergetic improvement potential and relative irreversibility.
Table 3 lists the calculated parameters. The parameters were estimated under the following baseline conditions: solar insolation, G
b = 800 W/m
2 and power output (0.65 kW, 0.75 kW, 0.88 kW, and 1.38 kW) for 90 °C, 100 °C, 110 °C, and 120 °C, respectively. As shown in
Table 3, the main source of exergy destruction is the solar collector, which are 14 kW, 15.3 kW, 16.9 kW, and 21.3 kW for 90 °C, 100 °C, 110 °C, and 120 °C, respectively. The key reasons for this large exergy destruction in the solar collectors were incomplete absorption of the incident radiation coming from the sun, heat dispersed to the environment, and the large temperature difference between the sun, the absorber plate and fluid.
Similarly, other sources of exergy destruction are the evaporator followed by the scroll expander, condenser and pump. The exergy destruction in the evaporator is due mainly to the following reasons: heat transfer between the hot water and working fluid are not uniform, pressure losses due to fluid friction, and dissipation of energy to the environment. The trends are the same for all different heat source temperatures. The exergy destruction in the system components can be improved by careful design of the system components from an exergetic point of view. As observed from
Table 3, the largest proportion of exergy destruction is the solar collector, so it requires careful design to improve its performance. For a solar ORC system that uses the working fluid R245fa, the total exergy destroyed were 14.71 kW, 16.16 kW, 17.88, and 22.60 kW, respectively, whereas the improvement potential were 13.97 kW, 15.35 kW, 16.81 kW, and 21.02 kW for 90 °C, 100 °C, 110 °C, and 120 °C, respectively. This means that approximately 94% of the destroyed exergy can be avoided with careful design of the solar collector. An improvement in designing a higher optical efficiency of the collector should be taken into consideration while other improvements include minimizing the heat losses from the collector receiver. Further improvements can be obtained by careful design of the evaporator that requires a larger heat exchange surface area. Another important exergetic parameter that identifies the ratio of the exergy destroyed to the total exergy destroyed in a system is the relative irreversibility. As shown in
Table 3, 94%–95% is the destroyed exergy in the solar collectors and 3% is in the evaporator.
7. Conclusions
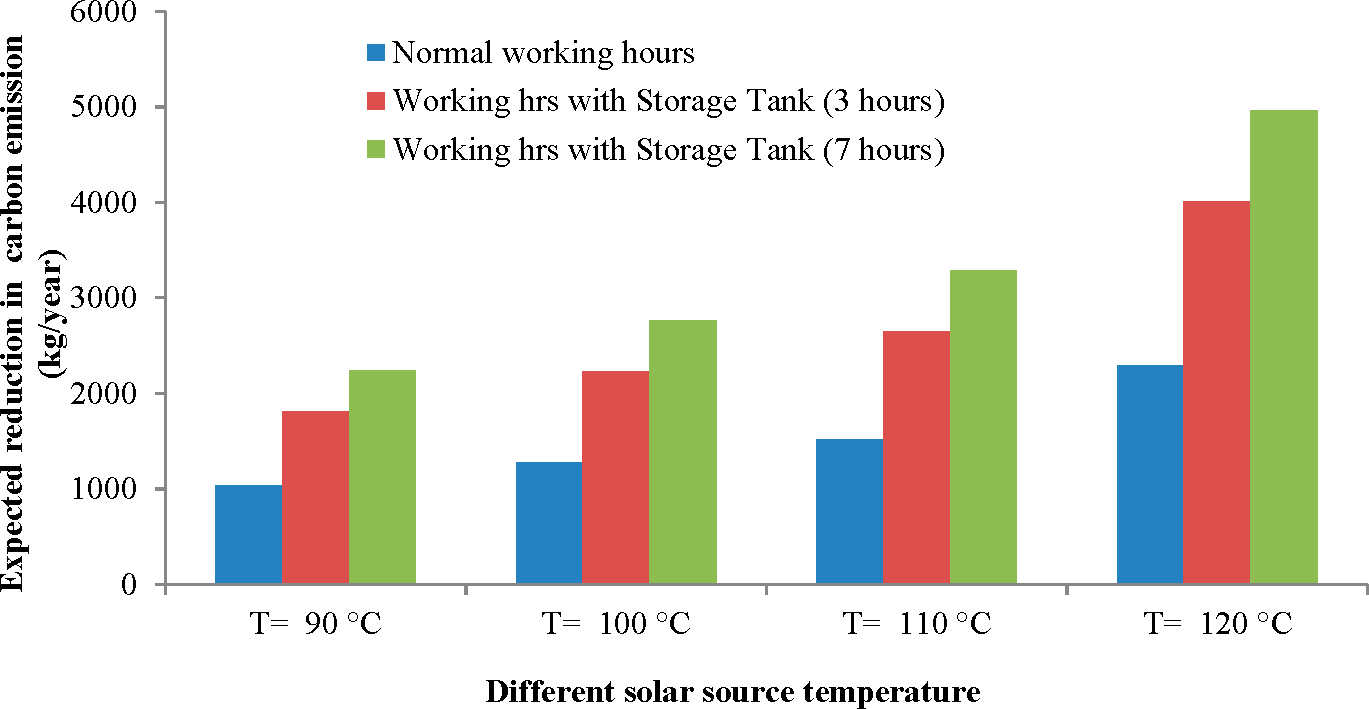
This paper reported the experimental results and thermoeconomic analysis of small-scale solar ORC system for electricity generation suitable for remote rural un-electrified areas in developing countries. The experiment conducted in the laboratory revealed acceptable performance characteristics that could be suitable for installation in rural areas. The maximum solar ORC efficiency was found to be approximately 6% for a 120 °C solar source temperature. To confirm the robustness of the unit, a magnetically-coupled commercial scroll expander was adopted and showed no leakage during the experiment. The seasonal variation of the solar ORC power output was also calculated. The maximum and minimum power outputs were obtained during April and December, respectively. The different solar source temperatures produce different power outputs. Therefore, the system was sized based on the weather conditions of Busan for all different months of the year. The collector area was determined based on the meteorological data of Busan City. In addition, the detailed exergy results showed the maximum exergy destruction in the solar collector followed by the evaporator, expander, condenser, and pump. The improvement potential percentage was 94%.
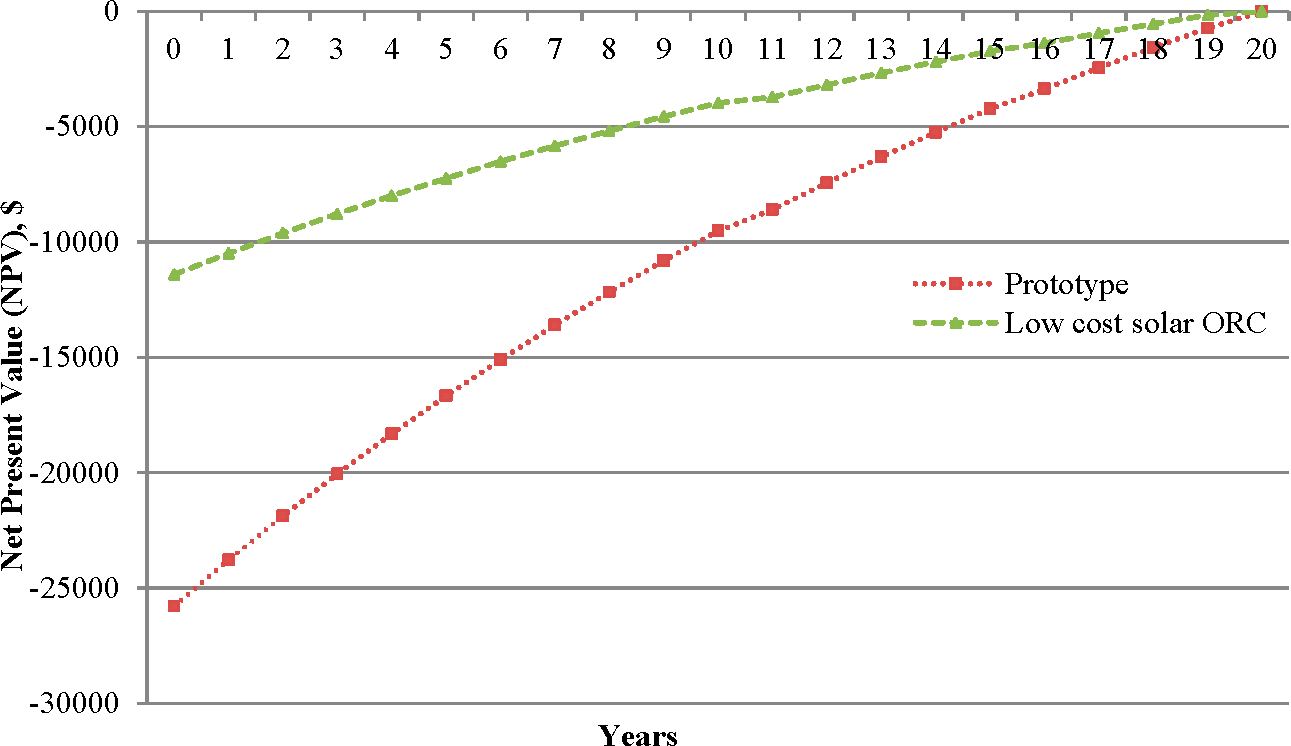
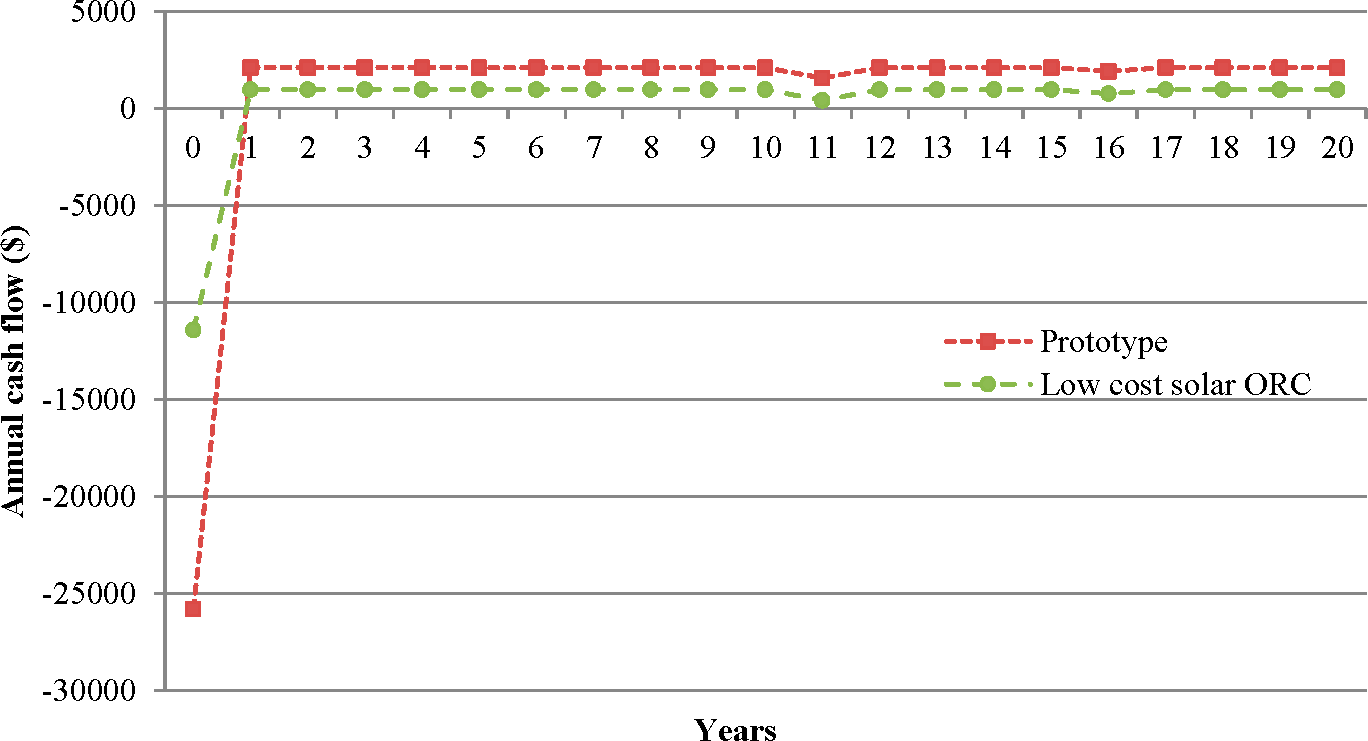
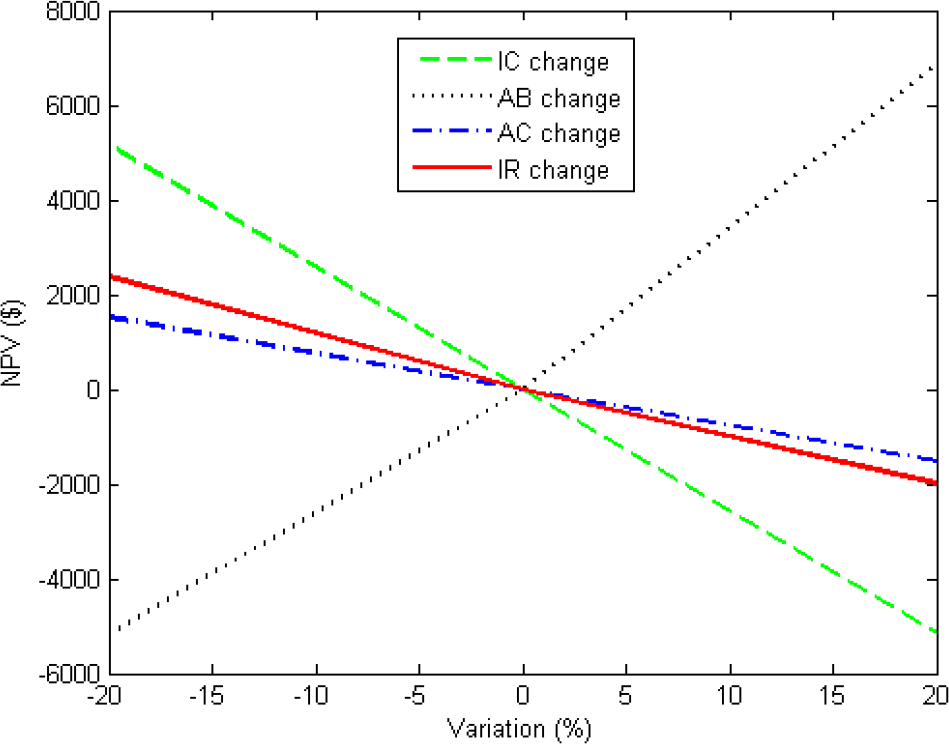
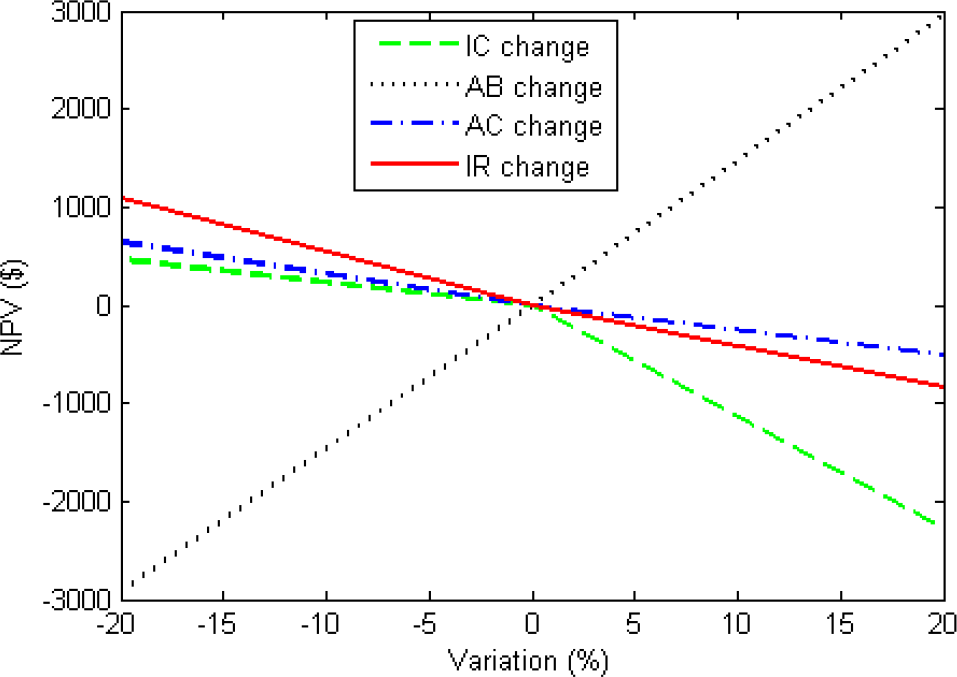
In the second part of the study, economics and thermoeconomic analyses were conducted to estimate the selling price of produced electricity. The selling price of electricity (for prototype) is 0.68 $/kWh, whereas for low cost solar ORC is 0.39 $/kWh. The payback period for the solar ORC system is 19 years, which is almost equal to life cycle of the system. Since the payback period is very high, this technology is only used in rural areas of developing countries, which lack electricity for lighting homes. The sensitivity analysis was carried out to observe the influence in the NPV of SORC. It is concluded that the reduction in investment and annual costs result in lowering the cost of energy per kWh. Special care should be taken in the estimation of the interest rate together with a realistic estimation of the total cost and the annual cash flow rates for economic analysis because the interest rate has strong influence on the specific cost of the developed system. The prototype cost of the system is very high, so if subsidies are not given the SORC market cannot grow exponentially. The small-scale solar ORC is currently expensive as compared to medium and large scale but if it could be successfully scaled down, the low cost solar ORC could see improved competitive with PV in short term. The mass production of the SORC components can play an important role in reducing the total investment cost of the system. The SORC system, which utilizes solar energy, helps develop sustainability and can serve to sustain the lives of millions of underprivileged people in developing countries.