Assessing Coupling Dynamics from an Ensemble of Time Series
Abstract
:1. Introduction
2. Entropy Combinations
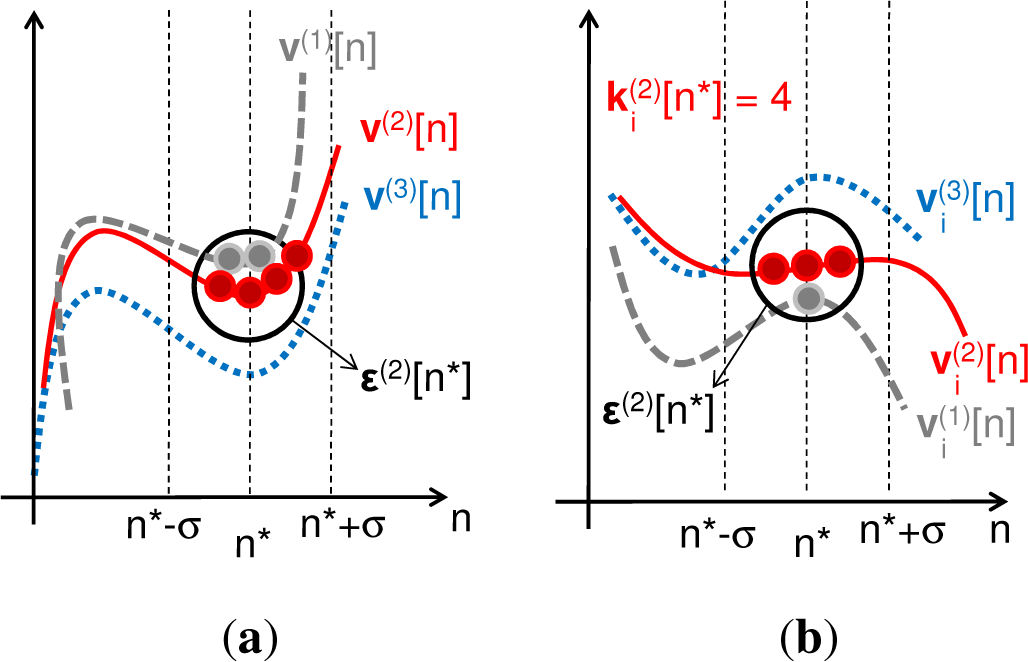
3. Ensemble Estimators for Entropy Combinations
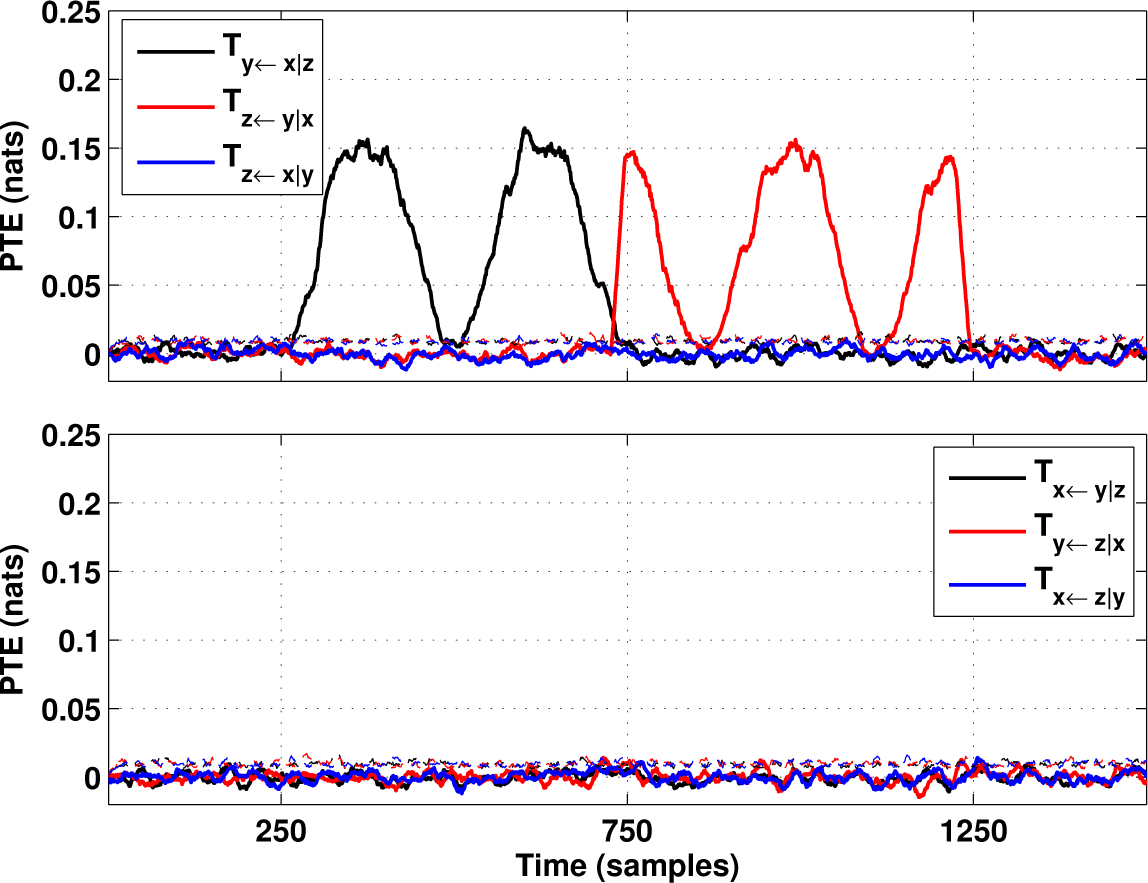
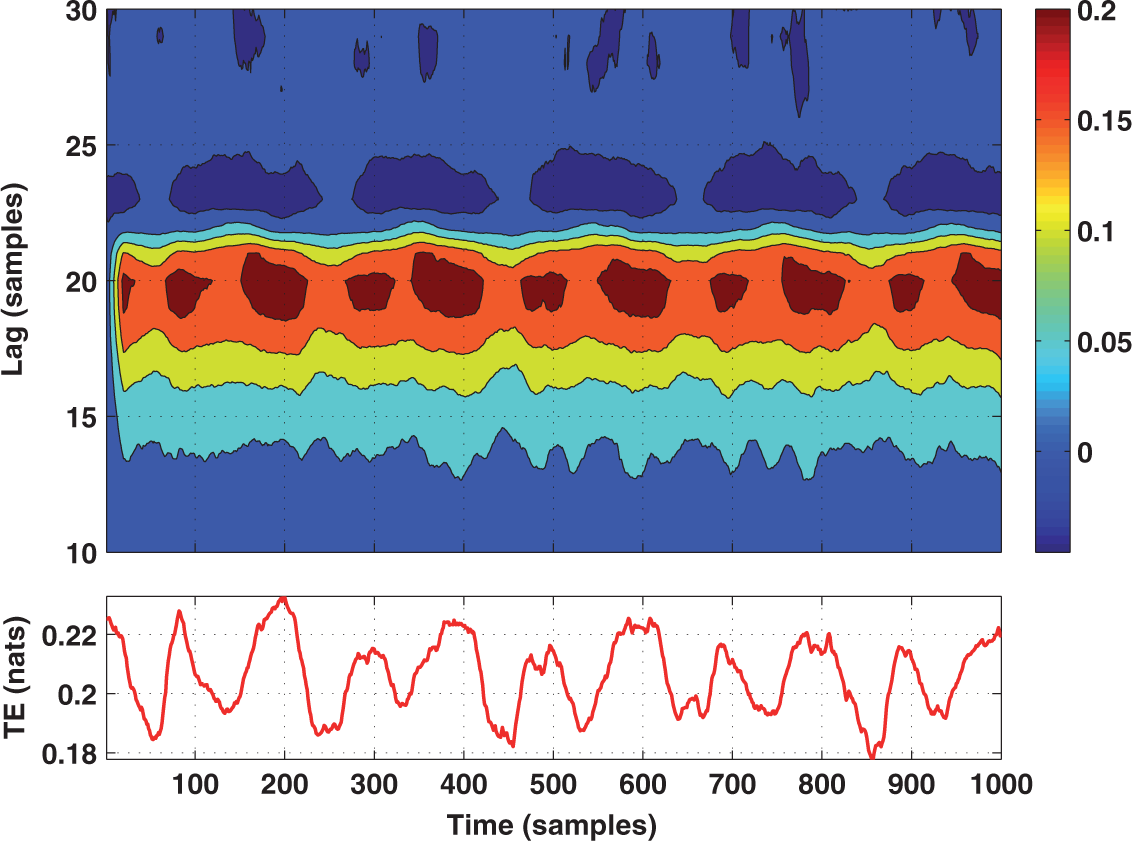
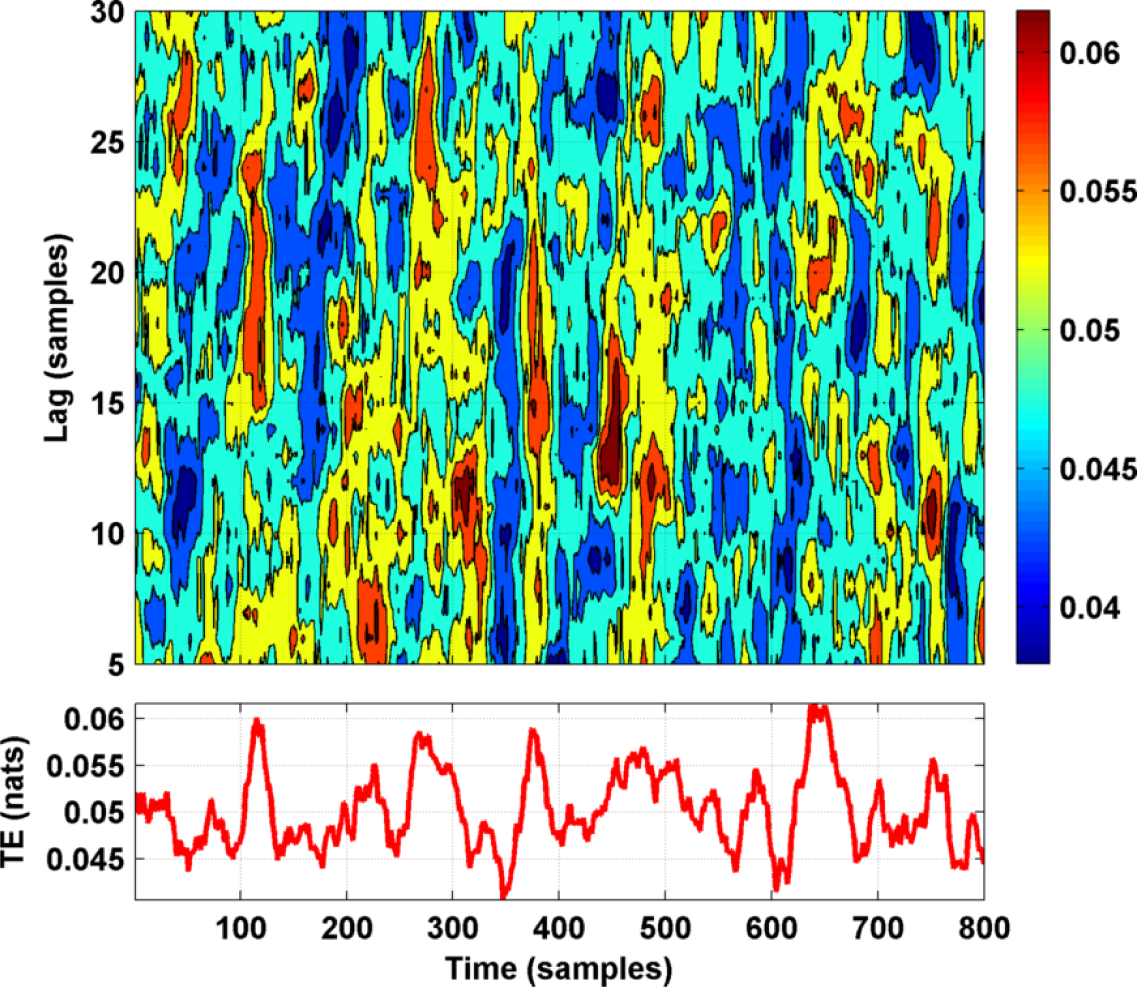
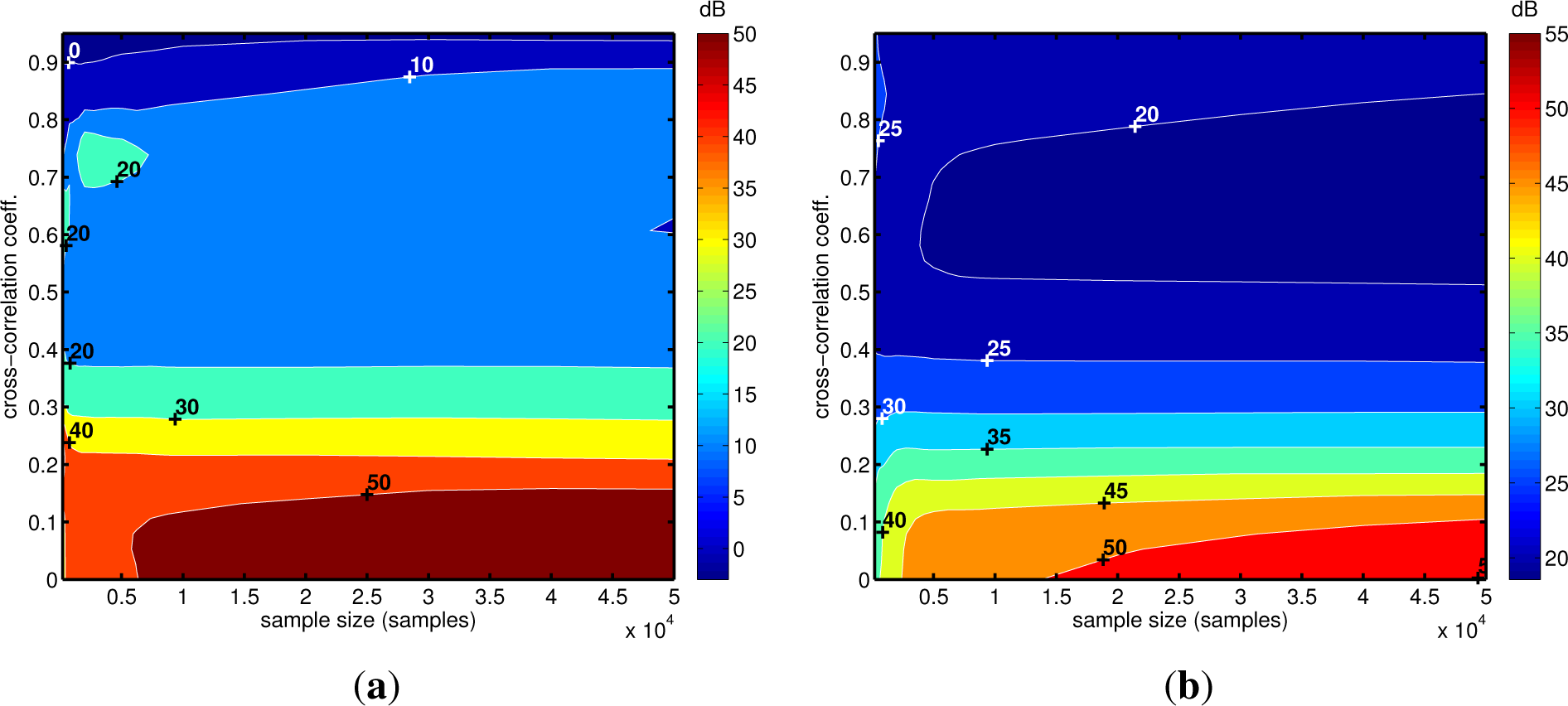
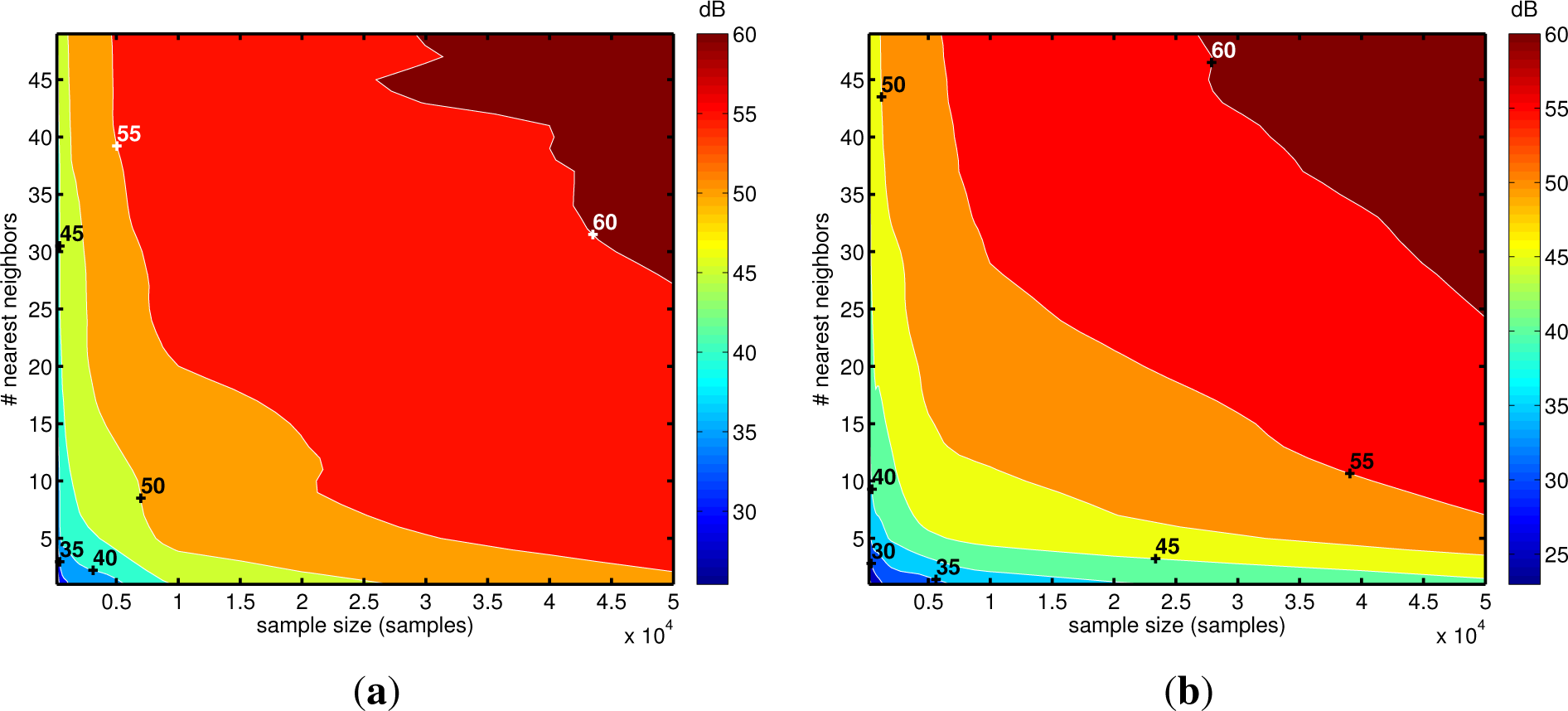
4. Tests on Simulated and Experimental Data
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Gray, C.; Konig, P.; Engel, A.; Singer, W. Oscillatory responses in cat visual cortex exhibit inter-columnar synchronization which reflects global stimulus properties. Nature 1989, 338, 334. [Google Scholar]
- Bjornstad, O.; Grenfell, B. Noisy clockwork: Time series analysis of population fluctuations in animals. Science 2001, 293, 638. [Google Scholar]
- Granger, C.; Hatanaka, M. Spectral Analysis of Economic Time Series; Princeton University Press: Princeton, NJ, USA, 1964. [Google Scholar]
- Valdes-Sosa, P.A.; Roebroeck, A.; Daunizeau, J.; Friston, K. Effective connectivity: Influence, causality and biophysical modeling. Neuroimage 2011, 58, 339. [Google Scholar]
- Granger, C. Investigating causal relations by econometric models and cross-spectral methods. Econometrica 1969, 37, 424. [Google Scholar]
- Pereda, E.; Quian Quiroga, R.; Bhattacharya, J. Nonlinear multivariate analysis of neurophysiological signals. Prog. Neurobio. 2005, 77, 1. [Google Scholar]
- Cover, T.; Thomas, J. Elements of Information Theory; Wiley: Hoboken, NY, USA, 2006. [Google Scholar]
- Wiener, N. The theory of prediction. In Modern Mathematics for Engineers; McGraw-Hill: New York NY, USA, 1956. [Google Scholar]
- Schreiber, T. Measuring information transfer. Phys. Rev. Lett 2000, 85, 461. [Google Scholar]
- Chicharro, D.; Ledberg, A. When two become one: the limits of causality analysis of brain dynamics. PLoS One 2012, 7, e32466. [Google Scholar]
- Wibral, M.; Vicente, R.; Lizier, J.T. Directed Information Measures in Neuroscience; Springer: Berlin, Germany, 2014. [Google Scholar]
- Wibral, M.; Vicente, R.; Lindner, M. Transfer entropy in Neuroscience. In Directed Information Measures in Neuroscience; Wibral, M., Vicente, R., Lizier, J.T., Eds.; Springer: Berlin, Germany, 2014. [Google Scholar]
- Lizier, J.T. The Local Information Dynamics of Distributed Computation in Complex Systems; Springer: Berlin, Germany, 2013. [Google Scholar]
- Kantz, H.; Schreiber, T. Nonlinear Time Series Analysis, 2nd ed; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Wyner, A.D. A Definition of Conditional Mutual Information for Arbitrary Ensembles. Inf. Control 1978, 38, 51. [Google Scholar]
- Frenzel, S.; Pompe, B. Partial mutual information for coupling analysis of multivariate time series. Phys. Rev. Lett 2007, 99, 204101. [Google Scholar]
- Verdes, P.F. Assessing causality from multivariate time series. Phys. Rev. E 2005, 72, 026222. [Google Scholar]
- Gómez-Herrero, G. Ph.D. thesis, Department of Signal Processing, Tampere University of Technology, Finland, 2010.
- Ragwitz, M.; Kantz, H. Markov models from data by simple nonlinear time series predictors in delay embedding spaces. Phys. Rev. E 2002, 65, 056201. [Google Scholar]
- Victor, J.D. Binless strategies for estimation of information from neural data. Phys. Rev. E 2002, 66, 051903. [Google Scholar]
- Vicente, R.; Wibral, M. Efficient estimation of information transfer. In Directed Information Measures in Neuroscience; Wibral, M., Vicente, R., Lizier, J.T., Eds.; Springer: Berlin, Germany, 2014. [Google Scholar]
- Kozachenko, L.; Leonenko, N. Sample Estimate of the Entropy of a Random Vector. Problemy Peredachi Informatsii 1987, 23, 9. [Google Scholar]
- Kraskov, A.; Stögbauer, H.; Grassberger, P. Estimating mutual information. Phys. Rev. E 2004, 69, 066138. [Google Scholar]
- Kramer, M.A.; Edwards, E.; Soltani, M.; Berger, M.S.; Knight, R.T.; Szeri, A.J. Synchronization measures of bursting data: application to the electrocorticogram of an auditory event-related experiment. Phys. Rev. E 2004, 70, 011914. [Google Scholar]
- Cao, L. Practical method for determining the minimum embedding dimension of a scalar time series. Physica D 1997, 110, 43. [Google Scholar]
- Wibral, M.; Pampu, N.; Priesemann, V.; Siebenhuhner; Seiwert; Lindner; Lizier; Vicente, R. Measuring information-transfer delays. PLoS One 2013, 8, e55809. [Google Scholar]
- Wollstadt, P.; Martinez-Zarzuela, M.; Vicente, R.; Diaz-Pernas, F.J.; Wibral, M. Efficient transfer entropy analysis of non-stationary neural time series. PLoS One 2014, 9, e102833. [Google Scholar]
- Pesarin, F. Multivariate Permutation Tests; John Wiley and Sons: Hoboken, NJ, USA, 2001. [Google Scholar]
- Kaiser, A.; Schreiber, T. Information transfer in continuous processes. Physica D 2002, 166, 43. [Google Scholar]
- Kantz, H.; Ragwitz, M. Phase space reconstruction and nonlinear predictions for stationary and nonstationary Markovian processes. Int. J. Bifurc. Chaos 2004, 14, 1935. [Google Scholar]
- Rutanen, K. TIM 1.2.0. Available online: http://www.tut.fi/tim accessed on 2 April 2015.
- Lindner, M.; Vicente, R.; Priesemann, V.; Wibral, M. TRENTOOL: A Matlab open source toolbox to analyse information flow in time series data with transfer entropy. BMC Neurosci. 2011, 12, 119. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Gómez-Herrero, G.; Wu, W.; Rutanen, K.; Soriano, M.C.; Pipa, G.; Vicente, R. Assessing Coupling Dynamics from an Ensemble of Time Series. Entropy 2015, 17, 1958-1970. https://doi.org/10.3390/e17041958
Gómez-Herrero G, Wu W, Rutanen K, Soriano MC, Pipa G, Vicente R. Assessing Coupling Dynamics from an Ensemble of Time Series. Entropy. 2015; 17(4):1958-1970. https://doi.org/10.3390/e17041958
Chicago/Turabian StyleGómez-Herrero, Germán, Wei Wu, Kalle Rutanen, Miguel C. Soriano, Gordon Pipa, and Raul Vicente. 2015. "Assessing Coupling Dynamics from an Ensemble of Time Series" Entropy 17, no. 4: 1958-1970. https://doi.org/10.3390/e17041958
APA StyleGómez-Herrero, G., Wu, W., Rutanen, K., Soriano, M. C., Pipa, G., & Vicente, R. (2015). Assessing Coupling Dynamics from an Ensemble of Time Series. Entropy, 17(4), 1958-1970. https://doi.org/10.3390/e17041958





