Kinetic Theory Modeling and Efficient Numerical Simulation of Gene Regulatory Networks Based on Qualitative Descriptions
Abstract
:1. Introduction
2. Methodologies
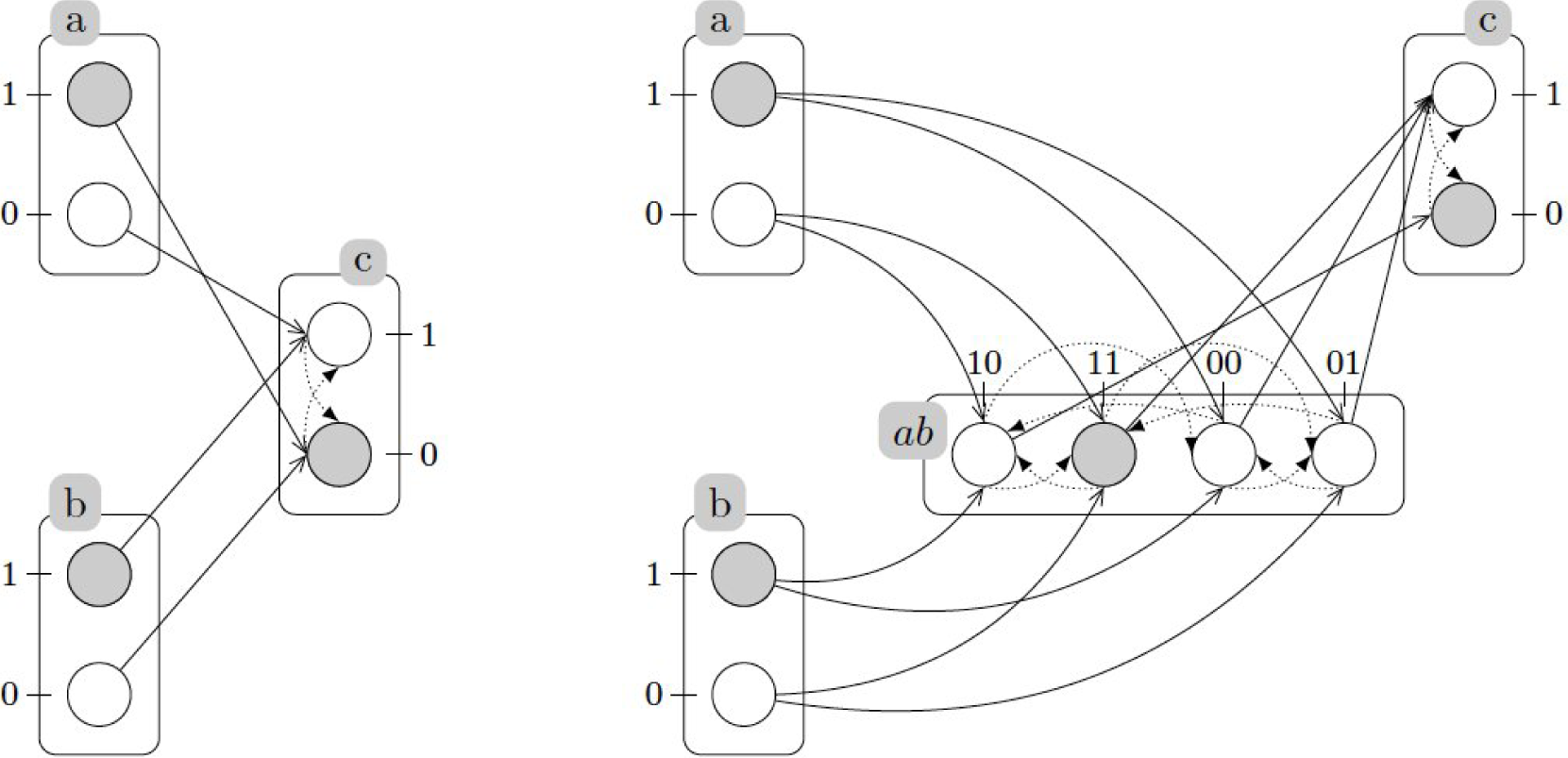
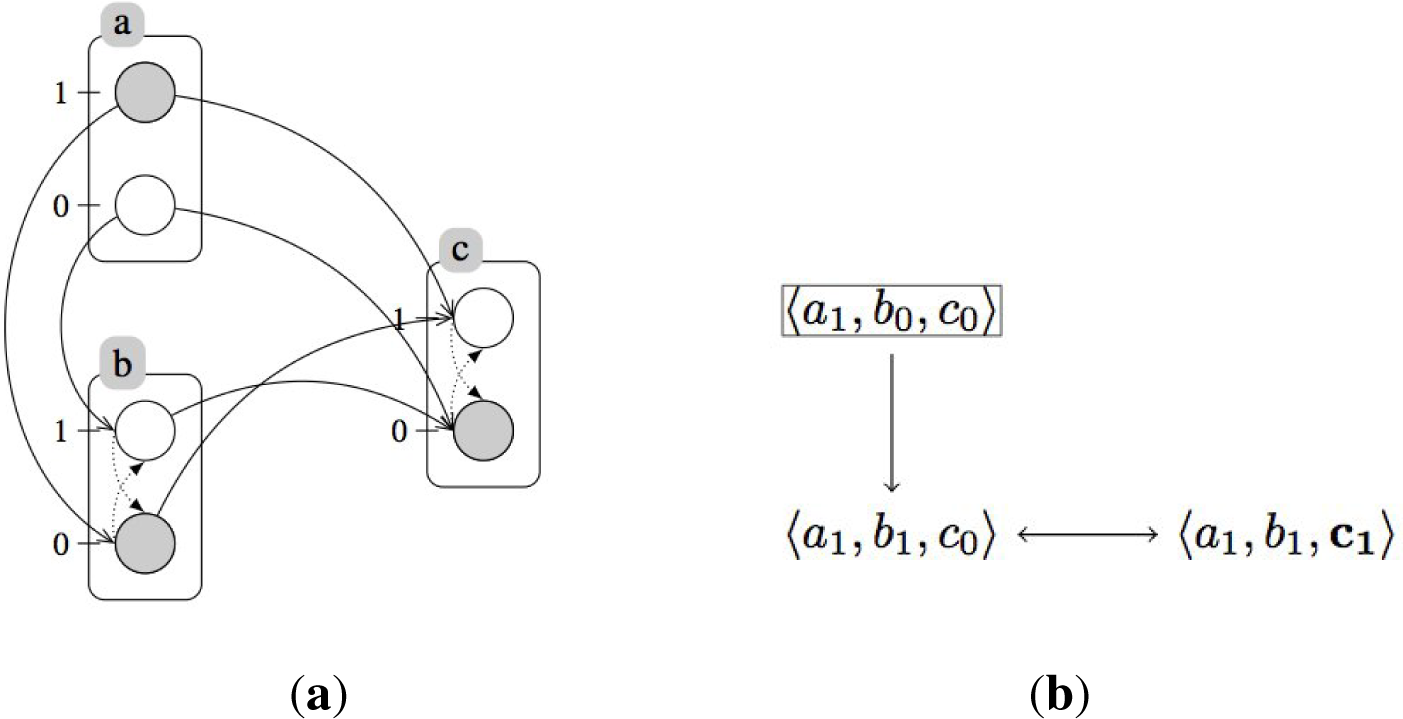
2.1. Qualitative Modeling: Process Hitting
2.2. Treating Qualitative Systems with Numerical Techniques
3. Application to a Biological Network
3.1. Treating Qualitative Systems with Numerical Techniques
3.2. Incorporation of Unknown Parameters
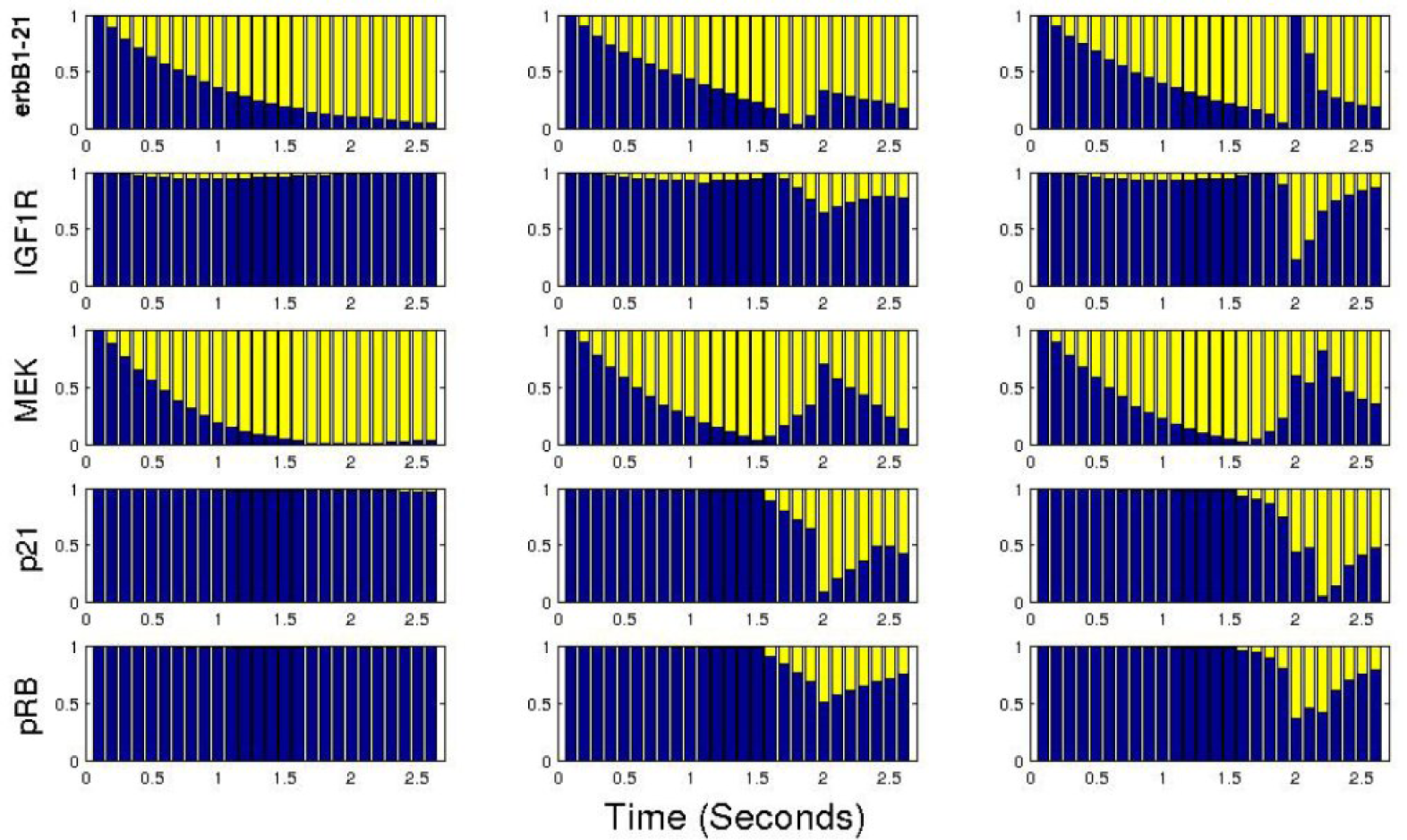
4. Evaluation and Analysis
5. Conclusions
Appendix
A. Qualitative Modeling: Process Hitting
A.1. Generalized Dynamics
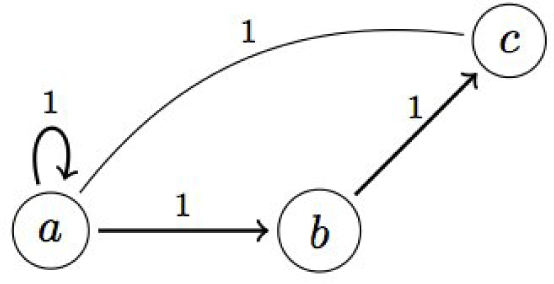
A.2. Example: Generalized Dynamics of the Incoherent Feed-Forward Loop
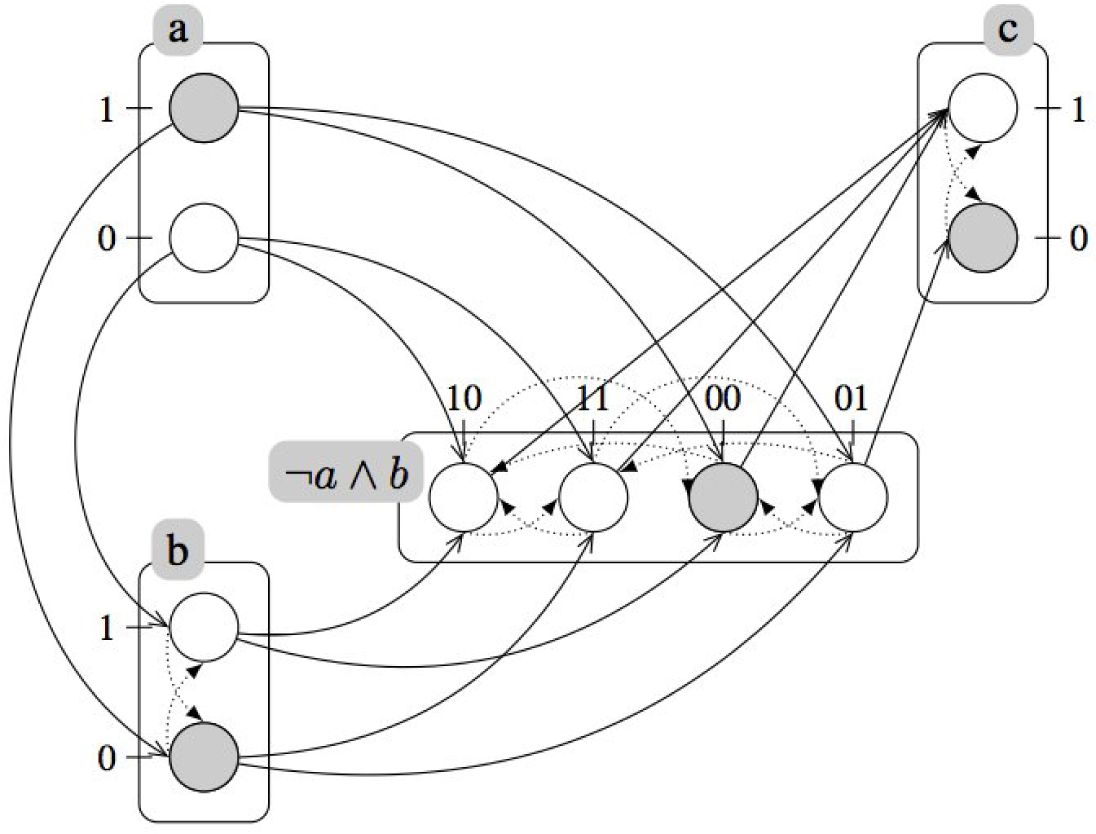
A.3. Refining Dynamics with Cooperativity
A.4. Example (Continued): Refined Dynamics of the Incoherent Feed-Forward Loop
B. PGD Constructor
B.1. Calculation of Functions
B.2. Calculation of Function
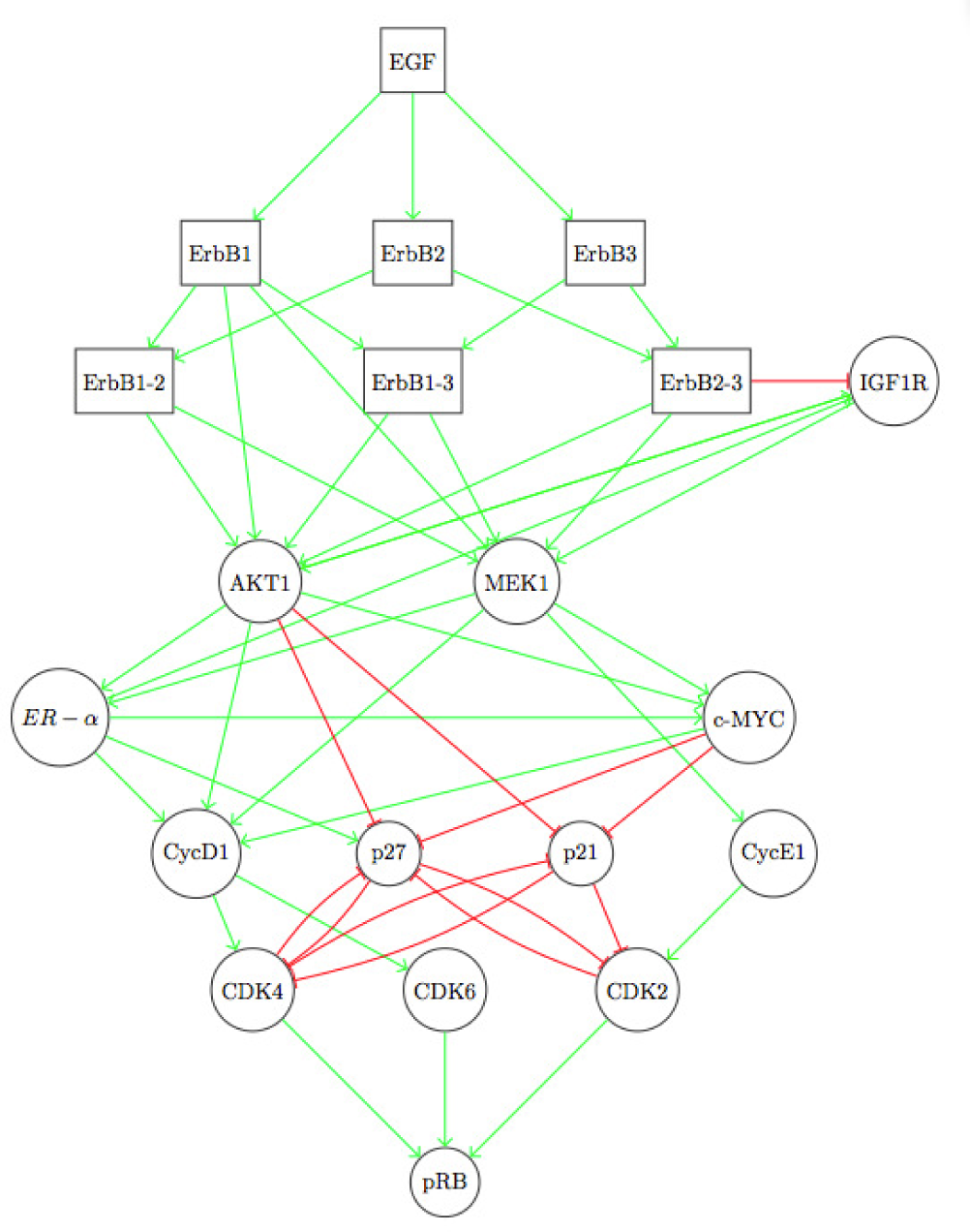
C. The ErbB Signaling Pathway
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Gillespie, D.T. Exact stochastic simulation of coupled chemical reactions. J. Phys. Chem. 1977, 81, 2340–2361. [Google Scholar]
- Gillespie, D.T. Approximate accelerated stochastic simulation of chemically reacting systems. J. Chem. Phys. 2001, 115, 1716–1733. [Google Scholar]
- Hegland, M.; Burden, C.; Santoso, L.; MacNamara, S.; Boothm, H. A solver for the stochastic master equation applied to gene regulatory networks. J. Comput. Appl. Math. 2007, 205, 708–724. [Google Scholar]
- Hasty, J.; McMillen, D.; Isaacs, F.; Collins, J.J. Computational studies of gene regulatory networks: in numero molecular Biology. Nature Rev. Genet 2001, 2, 268–279. [Google Scholar]
- Munsky, B.; Khammash, M. The finite state projection algorithm for the solution of the chemical master equation. J. Chem. Phys. 2006, 124/4, 044104. [Google Scholar]
- Sasai, M.; Wolynes, P.G. Stochastic gene expression as a many-body problem. Proc. Natl. Acad. Sci. 2003, 100, 2374–2379. [Google Scholar]
- Sreenath, S.N.; Cho, K.H.; Wellstead, P. Modeling the dynamics of signalling pathways. Essays Biochem. 2008, 45, 1–28. [Google Scholar]
- Kim, K.Y.; Wang, J. Potential energy landscape and robustness of a gene regulatory network: toggle switch. PLoS Comput. Biol. 2007, 3, 0565–0577. [Google Scholar]
- Priami, C.; Regev, A.; Shapiro, E.; Silverman, W. Application of a stochastic name-passing calculus to representation and simulation of molecular processes. Inf. Process. Lett. 2001, 80, 25–31. [Google Scholar]
- Ammar, A.; Cueto, E.; Chinesta, F. Reduction of the Chemical Master Equation for Gene Regulatory Networks Using Proper Generalized Decompositions. Int. J. Numer. Methods Biomed. Eng. 2012, 28, 960–973. [Google Scholar]
- Andreychenko, A.; Mikeev, L.; Wolf, V. Reconstruction of multimodal distributions for hybrid moment-based chemical kinetics. J. Coupled Syst. Multiscale Dyn. 2014, arXiv, 1410.3267. [Google Scholar]
- Kauffman, S.A. Metabolic stability and epigenesis in randomly constructed genetic nets. J. Theor. Biol. 1969, 22, 437–467. [Google Scholar]
- Thomas, R. Regulatory networks seen as asynchronous automata: a logical description. J. Theor. Biol. 1991, 153, 1–23. [Google Scholar]
- Pauleve, L.; Magnin, M.; Roux, O. Tuning temporal features within the stochastic π-calculus. IEEE Trans. Softw. Eng. 2011, 37, 858–871. [Google Scholar]
- Folschette, M.; Pauleve, L.; Magnin, M.; Roux, O. Under-approximation of reachability in multivalued asynchronous networks. Elect. Notes Theor. Comput. Sci. 2013, 299, 33–51. [Google Scholar]
- Pauleve, L.; Magnin, M.; Roux, O. Refining dynamics of gene regulatory networks in a stochastic π-calculus Framework. In Transactions on Computational Systems Biology XIII; Springer: Berlin/Heidelberg, Germany, 2011; pp. 171–191. [Google Scholar]
- Ammar, A.; Mokdad, B.; Chinesta, F.; Keunings, R. A new family of solvers for some classes of multidimensional partial differential equations encountered in kinetic theory modeling of complex fluids. J. Non-Newtonian Fluid Mech. 2006, 139, 153–176. [Google Scholar]
- Ammar, A.; Mokdad, B.; Chinesta, F.; Keunings, R. A new family of solvers for some classes of multidimensional partial differential equations encountered in kinetic theory modeling of complex fluids. Part II: transient simulation using space-time separated representations. J. Non-Newton. Fluid Mech. 2007, 144, 98–121. [Google Scholar]
- Chinesta, F.; Ammar, A.; Falco, A.; Laso, M. On the reduction of stochastic kinetic theory models of complex fluids. Model. Simul. Mater. Sci. Eng. 2007, 15, 639–652. [Google Scholar]
- Chinesta, F.; Ammar, A.; Joyot, P. The nanometric and micrometric scales of the structure and mechanics of materials revisited: An introduction to the challenges of fully deterministic numerical descriptions. International. J. Multiscale Comput. Eng. 2008, 6, 191–213. [Google Scholar]
- Kazeev, V.; Khammash, M.; Nip, M.; Schwab, C. Direct Solution of the Chemical Master Equation Using Quantized Tensor Trains. PLoS Comput. Biol. 2014, 10/3, e1003359. [Google Scholar] [CrossRef]
- Ammar, A.; Chinesta, F.; Diez, P.; Huerta, A. An error estimator for separated representations of highly multidimensional models. Comput. Methods Appl. Mech. Eng. 2010, 199, 1872–1880. [Google Scholar]
- Chinesta, F.; Ammar, A.; Leygue, A.; Keunings, R. An overview of the proper generalized decomposition with applications in computational rheology. J. Non-Newton. Fluid Mech. 2011, 166/11, 578–592. [Google Scholar]
- Chinesta, F.; Keunings, R.; Leygue, A. The Proper Generalized Decomposition for advanced numerical simulations. A primer. In Springer Briefs in Applied Sciences and Technology; Springer: Heidelberg, Germany, New York, NY, USA, Dordrecht, The Netherlands, London, UK, 2014. [Google Scholar]
- Chinesta, F.; Ammar, A.; Cueto, E. Recent advances and new challenges in the use of the proper generalized decomposition for solving multidimensional models. Arch. Comput. Methods Eng. 2010, 17, 327–350. [Google Scholar]
- Chinesta, F.; Ladeveze, P.; Cueto, E. A short review on model order reduction based on proper generalized decomposition. Arch. Comput. Methods Eng. 2011, 18, 395–404. [Google Scholar]
- Sahin, O.; Frohlich, H.; Lobke, C.; Korf, U.; Burmester, S.; Majety, M.; Mattern, J.; Schupp, I.; Chaouiya, C.; Thierry, D.; Poustka, A.; Wiemann, S.; Beissbarth, T.; D. Arlt, D. Modeling erbb receptor-regulated g1/s transition to find novel targets for de novo trastuzumab resistance. BMC Syst. Biol. 2009, 3. [Google Scholar] [CrossRef]
- Folschette, M.; Pauleve, L.; Inoue, K.; Magnin, M.; Roux, O. Concretizing the process hitting into biological regulatory networks. In Computational Methods in Systems Biology; Gilbert, D., Heiner, M., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2012; pp. 166–186. [Google Scholar]
- Chinesta, F.; Leygue, A.; Bordeu, F.; Aguado, J.V.; Cueto, E.; Gonzalez, D.; Alfaro, I.; Ammar, A.; Huerta, A. PGD-based computational vademecum for efficient design, optimization and control. Arch. Comput. Methods Eng. 2013, 20/1, 31–59. [Google Scholar]
- Mangan, S.; Alon, U. Structure and function of the feed-forward loop network motif. PNAS 2003, 21, 11980–11985. [Google Scholar]

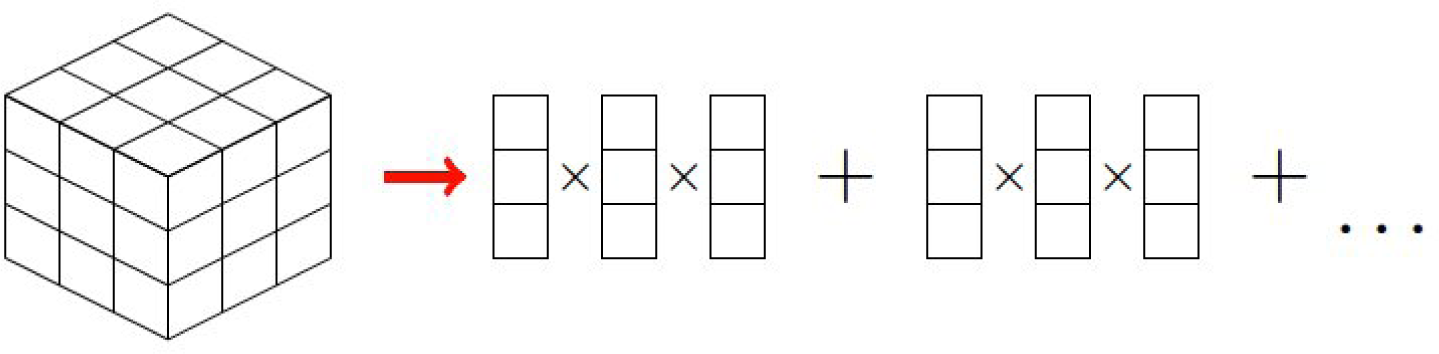


| Model | Fixed points | EGF absent | EGF present |
|---|---|---|---|
| Gen. Dynam. | 0 | Fail | Pass |
| Refined | 3 | Pass | Pass |
© 2015 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chinesta, F.; Magnin, M.; Roux, O.; Ammar, A.; Cueto, E. Kinetic Theory Modeling and Efficient Numerical Simulation of Gene Regulatory Networks Based on Qualitative Descriptions. Entropy 2015, 17, 1896-1915. https://doi.org/10.3390/e17041896
Chinesta F, Magnin M, Roux O, Ammar A, Cueto E. Kinetic Theory Modeling and Efficient Numerical Simulation of Gene Regulatory Networks Based on Qualitative Descriptions. Entropy. 2015; 17(4):1896-1915. https://doi.org/10.3390/e17041896
Chicago/Turabian StyleChinesta, Francisco, Morgan Magnin, Olivier Roux, Amine Ammar, and Elias Cueto. 2015. "Kinetic Theory Modeling and Efficient Numerical Simulation of Gene Regulatory Networks Based on Qualitative Descriptions" Entropy 17, no. 4: 1896-1915. https://doi.org/10.3390/e17041896
APA StyleChinesta, F., Magnin, M., Roux, O., Ammar, A., & Cueto, E. (2015). Kinetic Theory Modeling and Efficient Numerical Simulation of Gene Regulatory Networks Based on Qualitative Descriptions. Entropy, 17(4), 1896-1915. https://doi.org/10.3390/e17041896







