Preclinical Diagnosis of Magnetic Resonance (MR) Brain Images via Discrete Wavelet Packet Transform with Tsallis Entropy and Generalized Eigenvalue Proximal Support Vector Machine (GEPSVM)
Abstract
:Background
Methods
Results
Conclusions
1. Introduction
2. Materials and Methods
2.1. Benchmark Dataset
- Changing the class distribution: resampling, instance reweighting, metacost;
- Boost methods: AdaBoost/Adacost, cost boosting, asymmetric boosting;
- Modifying the learning algorithms: modifying the decision tree, modifying neural networks, modifying SVMs, modifying naive Bayes classifier;
- Direct cost-sensitive learning: Laplace correction, smoothing, curtailment, Platt calibration, and Isotonic regression;
- Other methods: Cost-sensitive CBR, Cost-sensitive specification, Cost-sensitive genetic programming.
2.2. CV Setting
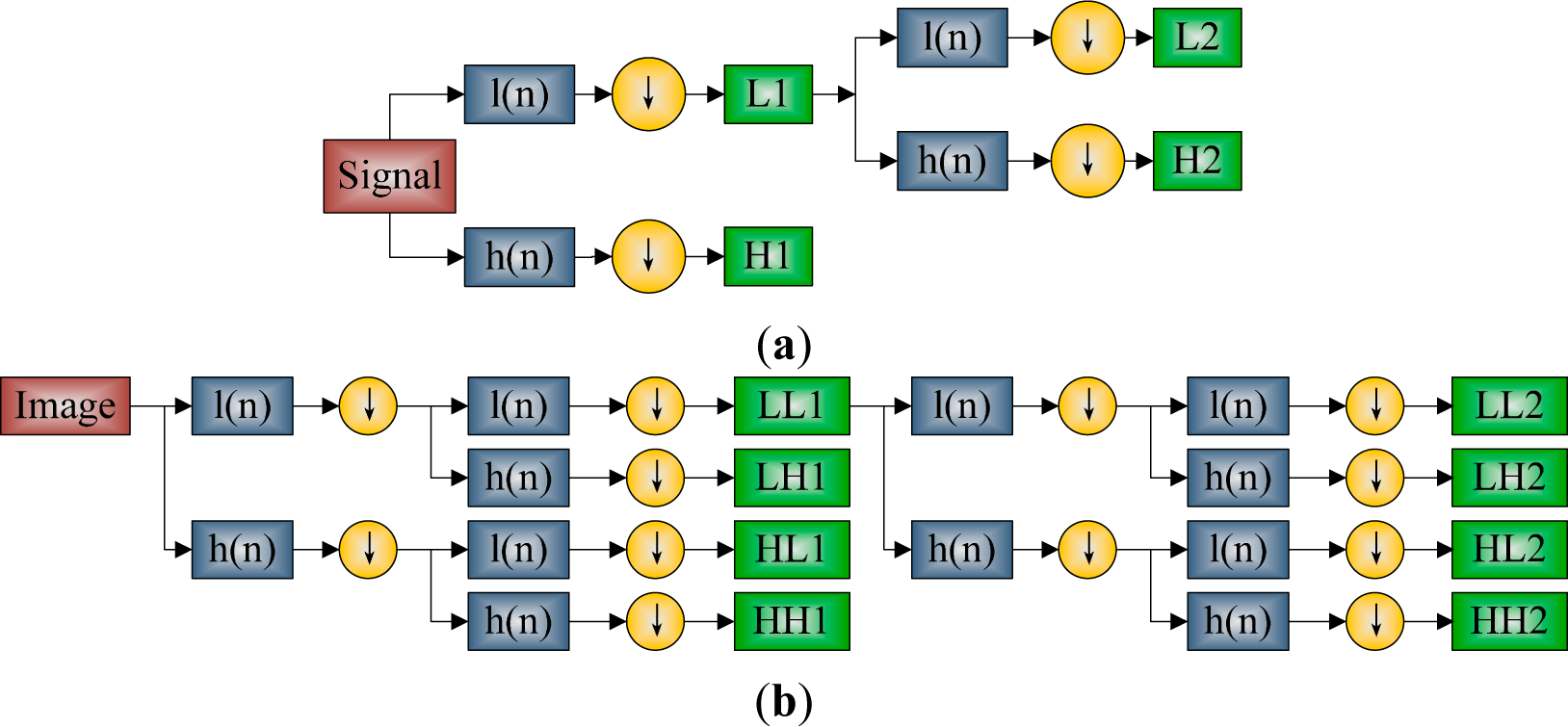
2.3. Discrete Wavelet Transform
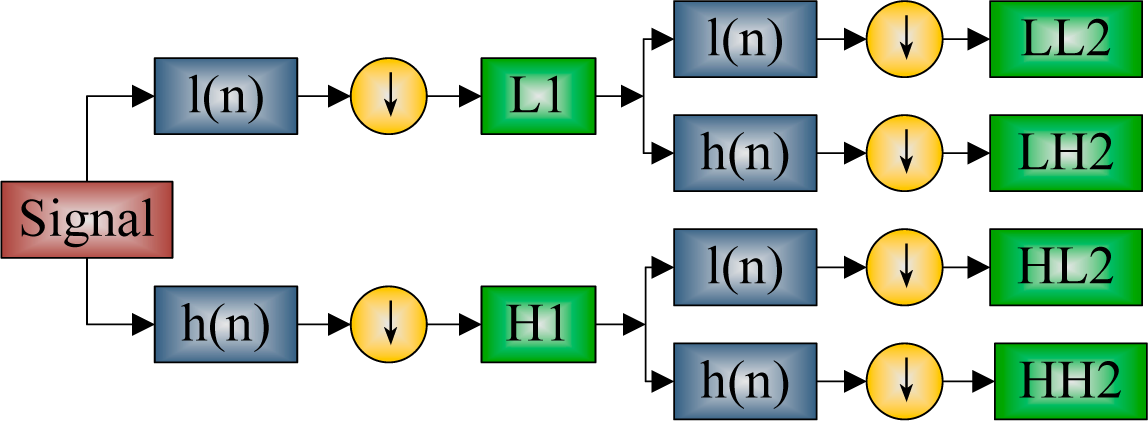
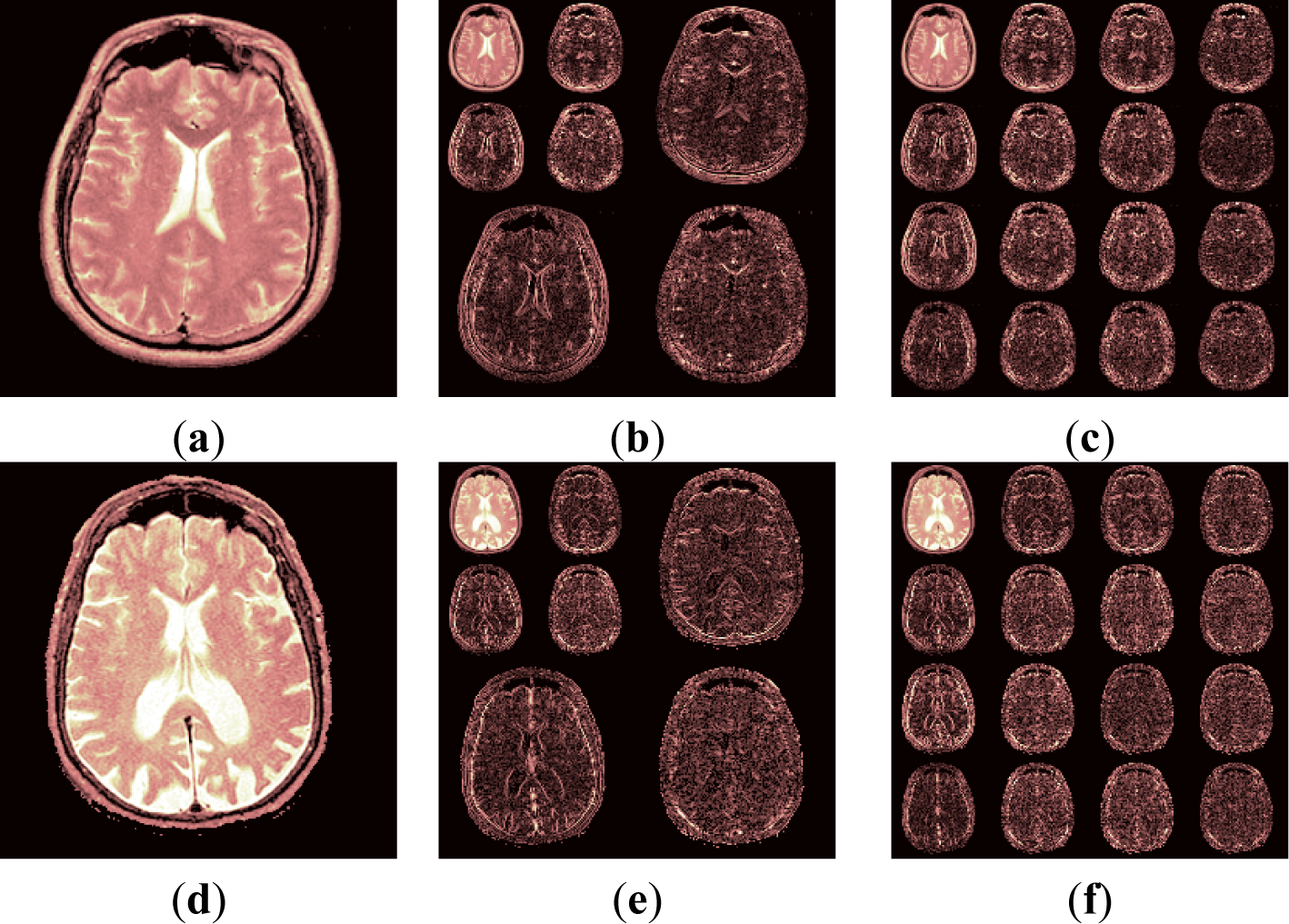
2.4. Discrete Wavelet Packet Transform
2.5. Shannon and Tsallis Entropy
2.6. Feature Extraction
| Step 1 Import MR image. |
| Step 2 Carry out 2-level DWPT decomposition. |
| Step 3 Calculate the entropy of each subband. |
| Step 4 Output 16-element entropy vector. |
2.7. Generalized Eigenvalue Proximal SVM
2.8. Kernel Technique
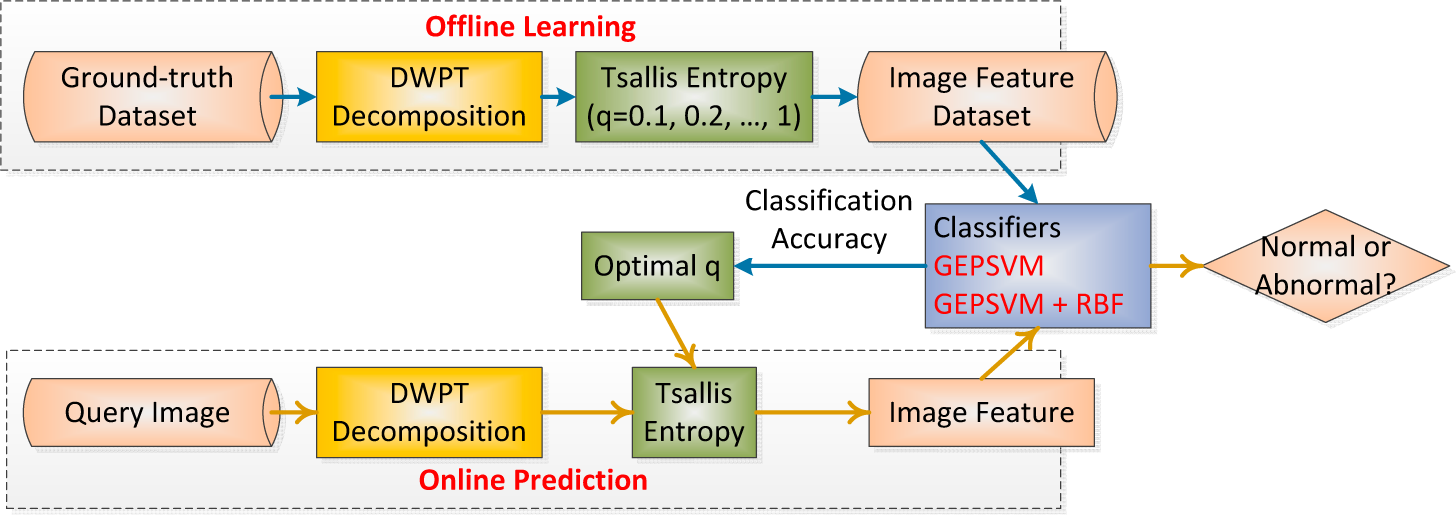
2.9. Implementation of the Proposed Method
| Phase I: Offline learning (users are scientists) | |
|---|---|
| Step 1. | Feature Extraction: Users decompose images by DWPT, and extract Tsallis entropies from all subbands |
| Step 2. | Classifier Training: The set of features along with the corresponding labels, were used to train the classifier. 10 repetition of K-fold stratified CV was employed for get the out-of-sample evaluation |
| Step 3. | Evaluation: Report the classification performance. |
| Step 3. | Parameter Selection: Above three steps iterated with q varies from 0.1 to 1 with increment of 0.1. Select the optimal q that corresponds to the highest classification accuracy. |
| Phase II: Online prediction (users are doctors and radiologists) | |
| Step 1. | Feature Extraction: Users presented to the system the query image to be classified. Its feature was obtained as in the offline learning phase. |
| Step 2. | Predict: Input the features of the query image to previously trained classifier. The classifier labeled the input query image as normal or abnormal. |
2.10. Evaluation
- (i) DWPT + SE + GEPSVM;
- (ii) DWPT + TE + GEPSVM;
- (iii) DWPT + SE + GEPSVM + RBF;
- (iv) DWPT + TE + GEPSVM + RBF;
3. Experimental Results
3.1. DWPT Result
3.2. Classification Comparison
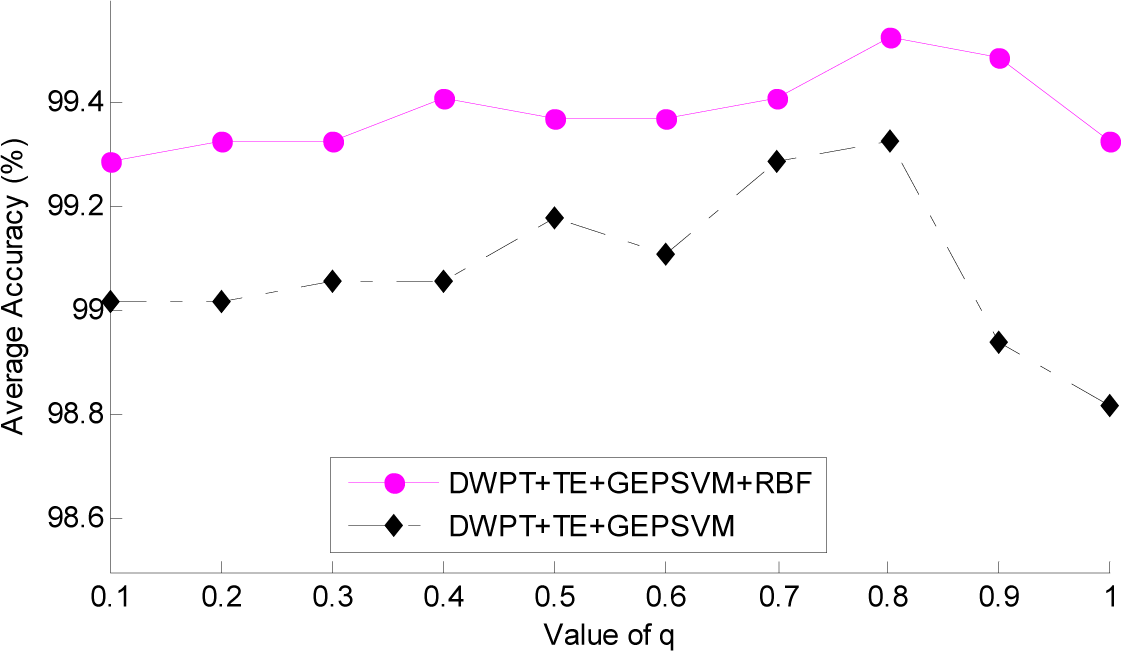
3.3. Setting of Parameter q
3.4. Computational Burden Analysis
3.5. Discussion
3.5.1. Discussion of Results
3.5.2. Discussion on the Proposed Method
4. Conclusions and Future Research
Nomenclature
| t | Time |
| x | 1D signal |
| I | 2D image |
| ψ | Wavelet function |
| fs | scale factor |
| ft | translation factor |
| C | Coefficients of wavelet decomposition |
| w | weight |
| b | bias |
| z | Combination of weight and bias |
| N | Sample number |
| n | Index of sample |
| p | Attribute number |
| X | Sample matrix |
| X1 | Sample matrix belonging to class 1 |
| X2 | Sample matrix belonging to class 2 |
| y | Class label (y = 1 for class 1 |
| y | = −1 for class 2) |
| e | Vector of ones (dimension varies) |
| δ | Tikhonov factor |
| λ | eigenvalue |
| K | Folds of CV |
| q | Entropic parameter of TE |
Acknowledgments
Author Contributions
Conflict of Interest
References
- Goh, S.; Dong, Z.; Zhang, Y.; DiMauro, S.; Peterson, B.S. Mitochondrial dysfunction as a neurobiological subtype of autism spectrum disorder: Evidence from brain imaging. JAMA Psychiatry 2014, 71, 665–671. [Google Scholar]
- Zhang, Y.; Wang, S.; Ji, G.; Dong, Z. Exponential wavelet iterative shrinkage thresholding algorithm with random shift for compressed sensing magnetic resonance imaging. IEEJ Trans. Electr. Electron. Eng. 2015, 10, 116–117. [Google Scholar]
- Zhang, Y.D.; Dong, Z.C.; Ji, G.L.; Wang, S.H. An improved reconstruction method for CS-MRI based on exponential wavelet transform and iterative shrinkage/thresholding algorithm. J. Electromagn. Waves Appl 2014, 28, 2327–2338. [Google Scholar]
- Levman, J.E.D.; Warner, E.; Causer, P.; Martel, A.L. A Vector machine formulation with application to the computer-aided diagnosis of breast cancer from DCE-MRI screening examinations. J. Digit. Imaging 2014, 27, 145–151. [Google Scholar]
- Chaplot, S.; Patnaik, L.M.; Jagannathan, N.R. Classification of magnetic resonance brain images using wavelets as input to support vector machine and neural network. Biomed. Signal Process. Control 2006, 1, 86–92. [Google Scholar]
- Maitra, M.; Chatterjee, A. A Slantlet transform based intelligent system for magnetic resonance brain image classification. Biomed. Signal Process. Control 2006, 1, 299–306. [Google Scholar]
- El-Dahshan, E.S.A.; Hosny, T.; Salem, A.B.M. Hybrid intelligent techniques for MRI brain images classification. Digit. Signal Process 2010, 20, 433–441. [Google Scholar]
- Zhang, Y.; Wu, L.; Wang, S. Magnetic resonance brain image classification by an improved artificial bee colony algorithm. Progress Electromagn. Res. 2011, 116, 65–79. [Google Scholar]
- Zhang, Y.; Dong, Z.; Wu, L.; Wang, S. A hybrid method for MRI brain image classification. Expert Syst. Appl 2011, 38, 10049–10053. [Google Scholar]
- Ramasamy, R.; Anandhakumar, P. Brain tissue classification of MR images using fast Fourier transform based expectation-maximization Gaussian mixture model. In Advances in Computing and Information Technology; Springer: Berlin/Heidelberg, Germany, 2011; pp. 387–398. [Google Scholar]
- Zhang, Y.; Wu, L. An MR brain images classifier via principal component analysis and Kernel support vector machine. Progress Electromagn. Res. 2012, 130, 369–388. [Google Scholar]
- Saritha, M.; Paul Joseph, K.; Mathew, A.T. Classification of MRI brain images using combined wavelet entropy based spider web plots and probabilistic neural network. Pattern Recognit. Lett. 2013, 34, 2151–2156. [Google Scholar]
- Das, S.; Chowdhury, M.; Kundu, M.K. Brain MR image classification using multiscale geometric analysis of ripplet. Progress Electromagn. Res. 2013, 137, 1–17. [Google Scholar]
- Kalbkhani, H.; Shayesteh, M.G.; Zali-Vargahan, B. Robust algorithm for brain magnetic resonance image (MRI) classification based on GARCH variances series. Biomed. Signal Process. Control 2013, 8, 909–919. [Google Scholar]
- Zhang, Y.; Wang, S.; Dong, Z. Classification of Alzheimer disease based on structural Magnetic resonance imaging by Kernel support vector machine decision tree. Progress Electromagn. Res. 2014, 144, 171–184. [Google Scholar]
- Qin, Z.X.; Zhang, C.Q.; Wang, T.; Zhang, S.C. Cost sensitive classification in data mining. Adv. Data Min. Appl 2010, Pt I 2010, 6440, 1–11. [Google Scholar]
- Zhang, Y.; Wang, S.; Phillips, P.; Ji, G. Binary PSO with mutation operator for feature selection using decision tree applied to spam detection. Knowl.-Based Syst. 2014, 64, 22–31. [Google Scholar]
- Kong, Y.H.; Zhang, S.M.; Cheng, P.Y. Super-resolution reconstruction face recognition based on multi-level FFD registration. Optik 2013, 124, 6926–6931. [Google Scholar]
- Liao, S.; Shen, D.G.; Chung, A.C.S. A Markov random field groupwise registration framework for face recognition. IEEE Trans. Pattern Anal. Mach. Intell. 2014, 36, 657–669. [Google Scholar]
- Shi, J.G.; Qi, C. From local geometry to global structure: Learning latent subspace for low-resolution face image recognition. IEEE Signal Process. Lett. 2015, 22, 554–558. [Google Scholar]
- Fan, Z.Z.; Ni, M.; Zhu, Q.; Liu, E. Weighted sparse representation for face recognition. Neurocomputing 2015, 151, 304–309. [Google Scholar]
- Ribbens, A.; Hermans, J.; Maes, F.; Vandermeulen, D.; Suetens, P.; Alzheimers Dis, N. Unsupervised segmentation, clustering, and groupwise registration of heterogeneous populations of brain MR images. IEEE Trans. Med. Imaging 2014, 33, 201–224. [Google Scholar]
- Schwarz, D.; Kasparek, T. Brain morphometry of MR images for automated classification of first-episode schizophrenia. Inf. Fusion 2014, 19, 97–102. [Google Scholar]
- Fang, L.; Wu, L.; Zhang, Y. A novel demodulation system based on continuous wavelet transform. Math. Probl. Eng. 2015, 2015. [Google Scholar] [CrossRef]
- Zhou, R.; Bao, W.; Li, N.; Huang, X.; Yu, D. Mechanical equipment fault diagnosis based on redundant second generation wavelet packet transform. Digit. Signal Process 2010, 20, 276–288. [Google Scholar]
- Campos, D. Real and spurious contributions for the Shannon, Rényi and Tsallis entropies. Physica A 2010, 389, 3761–3768. [Google Scholar]
- Tsallis, C. Nonadditive entropy: The concept and its use. Eur. Phys. J. A. 2009, 40, 257–266. [Google Scholar]
- Zhang, Y.; Wu, L. Optimal multi-level thresholding based on maximum Tsallis entropy via an artificial bee colony approach. Entropy 2011, 13, 841–859. [Google Scholar]
- Tsallis, C. The nonadditive entropy S-q and its applications in physics and elsewhere: Some remarks. Entropy 2011, 13, 1765–1804. [Google Scholar]
- Amaral-Silva, H.; Wichert-Ana, L.; Murta, L.O.; Romualdo-Suzuki, L.; Itikawa, E.; Bussato, G.F.; Azevedo-Marques, P. The superiority of Tsallis entropy over traditional cost functions for brain MRI and SPECT registration. Entropy 2014, 16, 1632–1651. [Google Scholar]
- Venkatesan, A.S.; Parthiban, L. A Novel nature inspired fuzzy Tsallis entropy segmentation of magnetic resonance images. Neuroquantology 2014, 12, 221–229. [Google Scholar]
- Khader, M.; Ben Hamza, A. Nonrigid image registration using an entropic similarity. IEEE Trans. Inf. Technol. Biomed. 2011, 15, 681–690. [Google Scholar]
- Hussain, M. Mammogram enhancement using lifting dyadic wavelet transform and normalized Tsallis entropy. J. Comput. Sci. Technol 2014, 29, 1048–1057. [Google Scholar]
- Liu, Z.G.; Hu, Q.L.; Cui, Y.; Zhang, Q.G. A new detection approach of transient disturbances combining wavelet packet and Tsallis entropy. Neurocomputing 2014, 142, 393–407. [Google Scholar]
- Chen, J.K.; Li, G.Q. Tsallis wavelet entropy and its application in power signal analysis. Entropy 2014, 16, 3009–3025. [Google Scholar]
- Mangasarian, O.L.; Wild, E.W. Multisurface proximal support vector machine classification via generalized eigenvalues. IEEE Trans. Pattern Anal. Mach. Intell 2006, 28, 69–74. [Google Scholar]
- Tsallis, C. An introduction to nonadditive entropies and a thermostatistical approach to inanimate and living matter. Contemp. Phys. 2014, 55, 179–197. [Google Scholar]
- Sturzbecher, M.J.; Tedeschi, W.; Cabella, B.C.T.; Baffa, O.; Neves, U.P.C.; de Araujo, D.B. Non-extensive entropy and the extraction of BOLD spatial information in event-related functional MRI. Phys. Med. Biol 2009, 54, 161–174. [Google Scholar]
- Cabella, B.C.T.; Sturzbecher, M.J.; de Araujo, D.B.; Neves, U.P.C. Generalized relative entropy in functional magnetic resonance imaging. Physica A 2009, 388, 41–50. [Google Scholar]
- Diniz, P.R.B.; Murta, L.O.; Brum, D.G.; de Araujo, D.B.; Santos, A.C. Brain tissue segmentation using q-entropy in multiple sclerosis magnetic resonance images. Braz. J. Med. Biol. Res. 2010, 43, 77–84. [Google Scholar]
- Dong, Z.; Zhang, Y.; Liu, F.; Duan, Y.; Kangarlu, A.; Peterson, B.S. Improving the spectral resolution and spectral fitting of 1H MRSI data from human calf muscle by the SPREAD technique. NMR Biomed. 2014, 27, 1325–1332. [Google Scholar]
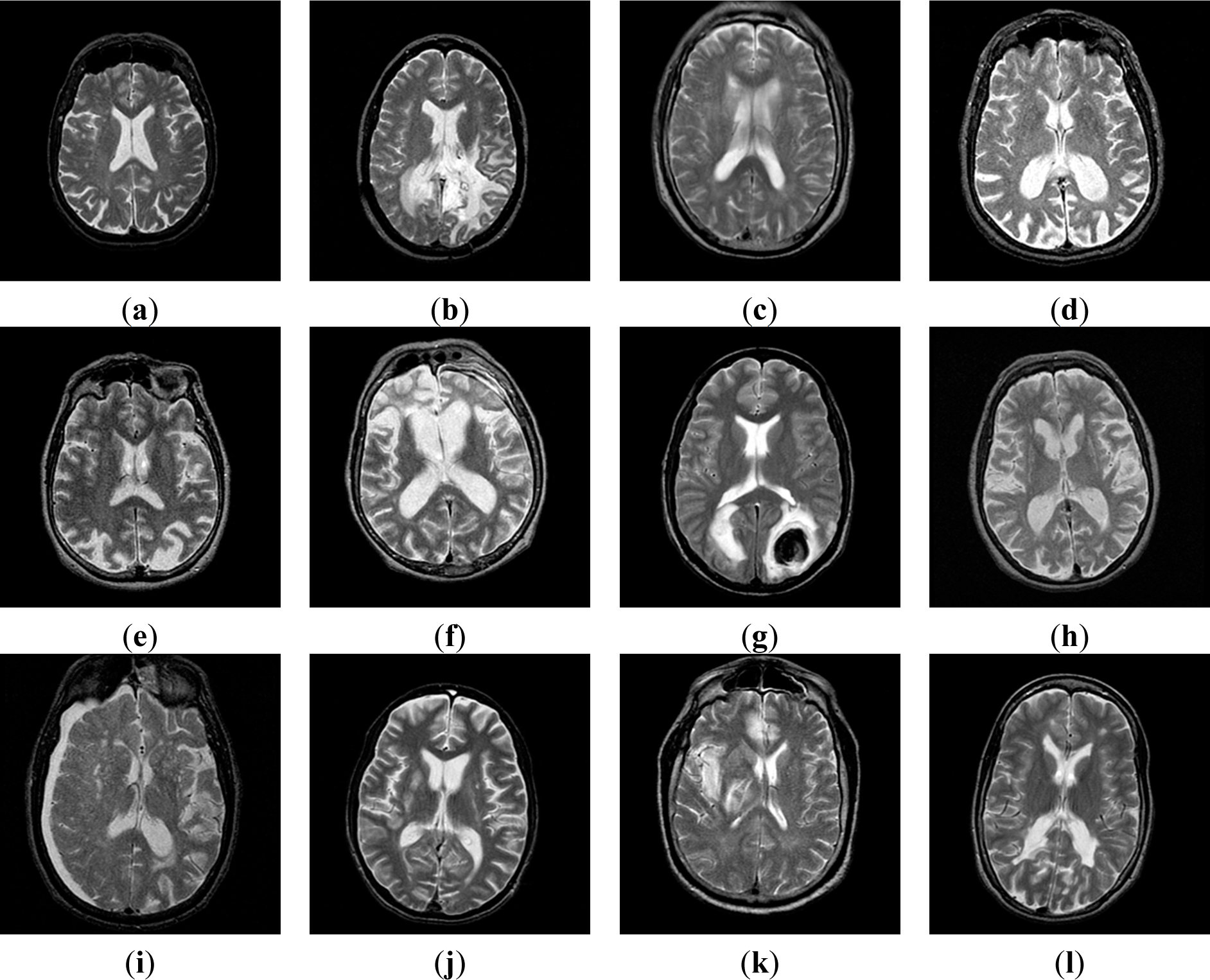
| Dataset | Total
| Training
| Validation
| K-Fold
| |||
|---|---|---|---|---|---|---|---|
| Normal | Abnormal | Normal | Abnormal | Normal | Abnormal | ||
| Dataset-66 | 18 | 48 | 15 | 40 | 3 | 8 | 6- |
| Dataset-160 | 20 | 140 | 16 | 112 | 4 | 28 | 5- |
| Dataset-255 | 35 | 220 | 28 | 177 | 7 | 43 | 5- |
| Dataset-66 | Dataset-160 | Dataset-255 | ||
|---|---|---|---|---|
| Existing Approaches [13] (5 Repetitions) | DWT+SOM [5] | 94.00 | 93.17 | 91.65 |
| DWT+SVM [5] | 96.15 | 95.38 | 94.05 | |
| DWT + SVM + POLY [5] | 98.00 | 97.15 | 96.37 | |
| DWT + SVM + RBF [5] | 98.00 | 97.33 | 96.18 | |
| DWT + PCA + FP-ANN [7] | 97.00 | 96.98 | 95.29 | |
| DWT + PCA + KNN [7] | 98.00 | 97.54 | 96.79 | |
| DWT + PCA + SVM [11] | 96.01 | 95.00 | 94.29 | |
| DWT + PCA + SVM + HPOL [11] | 98.34 | 96.88 | 95.61 | |
| DWT + PCA + SVM + IPOL [11] | 100.00 | 98.12 | 97.73 | |
| DWT + PCA + SVM + GRB [11] | 100.00 | 99.38 | 98.82 | |
| DWT + SE + SWP + PNN [12] | 100.00 | 99.88 | 98.90 | |
| RT + PCA + LS-SVM [13] | 100.00 | 100.00 | 99.39 | |
| Proposed approaches (10 repetitions) | DWPT + SE + GEPSVM | 99.85 | 99.62 | 98.78 |
| DWPT + TE + GEPSVM | 100.00 | 100.00 | 99.33 | |
| DWPT + SE + GEPSVM + RBF | 100.00 | 99.88 | 99.33 | |
| DWPT + TE + GEPSVM + RBF | 100.00 | 100.00 | 99.53 |
| Dataset | Sensitivity | Specificity | Precision | Accuracy |
|---|---|---|---|---|
| Dataset-66 | 100.00 | 100.00 | 100.00 | 100.00 |
| Dataset-160 | 100.00 | 100.00 | 100.00 | 100.00 |
| Dataset-255 | 100.00 | 97.14 | 99.55 | 99.61 |
| Method | q = 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | 1 |
|---|---|---|---|---|---|---|---|---|---|---|
| DWPT + TE + GEPSVM | 99.02 | 99.02 | 99.06 | 99.06 | 99.18 | 99.11 | 99.29 | 99.33 | 98.94 | 98.82 |
| DWPT + TE + GEPSVM + RBF | 99.29 | 99.33 | 99.33 | 99.41 | 99.37 | 99.37 | 99.41 | 99.53 | 99.49 | 99.33 |
| Step | Time (s) | |
|---|---|---|
| Offline Learning | DWPT decomposition | 4.0565 |
| Entropy calculation | 3.4961 | |
| Classifier training | 0.8904 | |
| Online Prediction | DWPT decomposition | 0.0817 |
| Entropy calculation | 0.0213 | |
| Brain classification | 0.0029 |
© 2015 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Dong, Z.; Wang, S.; Ji, G.; Yang, J. Preclinical Diagnosis of Magnetic Resonance (MR) Brain Images via Discrete Wavelet Packet Transform with Tsallis Entropy and Generalized Eigenvalue Proximal Support Vector Machine (GEPSVM). Entropy 2015, 17, 1795-1813. https://doi.org/10.3390/e17041795
Zhang Y, Dong Z, Wang S, Ji G, Yang J. Preclinical Diagnosis of Magnetic Resonance (MR) Brain Images via Discrete Wavelet Packet Transform with Tsallis Entropy and Generalized Eigenvalue Proximal Support Vector Machine (GEPSVM). Entropy. 2015; 17(4):1795-1813. https://doi.org/10.3390/e17041795
Chicago/Turabian StyleZhang, Yudong, Zhengchao Dong, Shuihua Wang, Genlin Ji, and Jiquan Yang. 2015. "Preclinical Diagnosis of Magnetic Resonance (MR) Brain Images via Discrete Wavelet Packet Transform with Tsallis Entropy and Generalized Eigenvalue Proximal Support Vector Machine (GEPSVM)" Entropy 17, no. 4: 1795-1813. https://doi.org/10.3390/e17041795
APA StyleZhang, Y., Dong, Z., Wang, S., Ji, G., & Yang, J. (2015). Preclinical Diagnosis of Magnetic Resonance (MR) Brain Images via Discrete Wavelet Packet Transform with Tsallis Entropy and Generalized Eigenvalue Proximal Support Vector Machine (GEPSVM). Entropy, 17(4), 1795-1813. https://doi.org/10.3390/e17041795







