Distributed Vector Quantization Based on Kullback-Leibler Divergence
Abstract
:1. Introduction
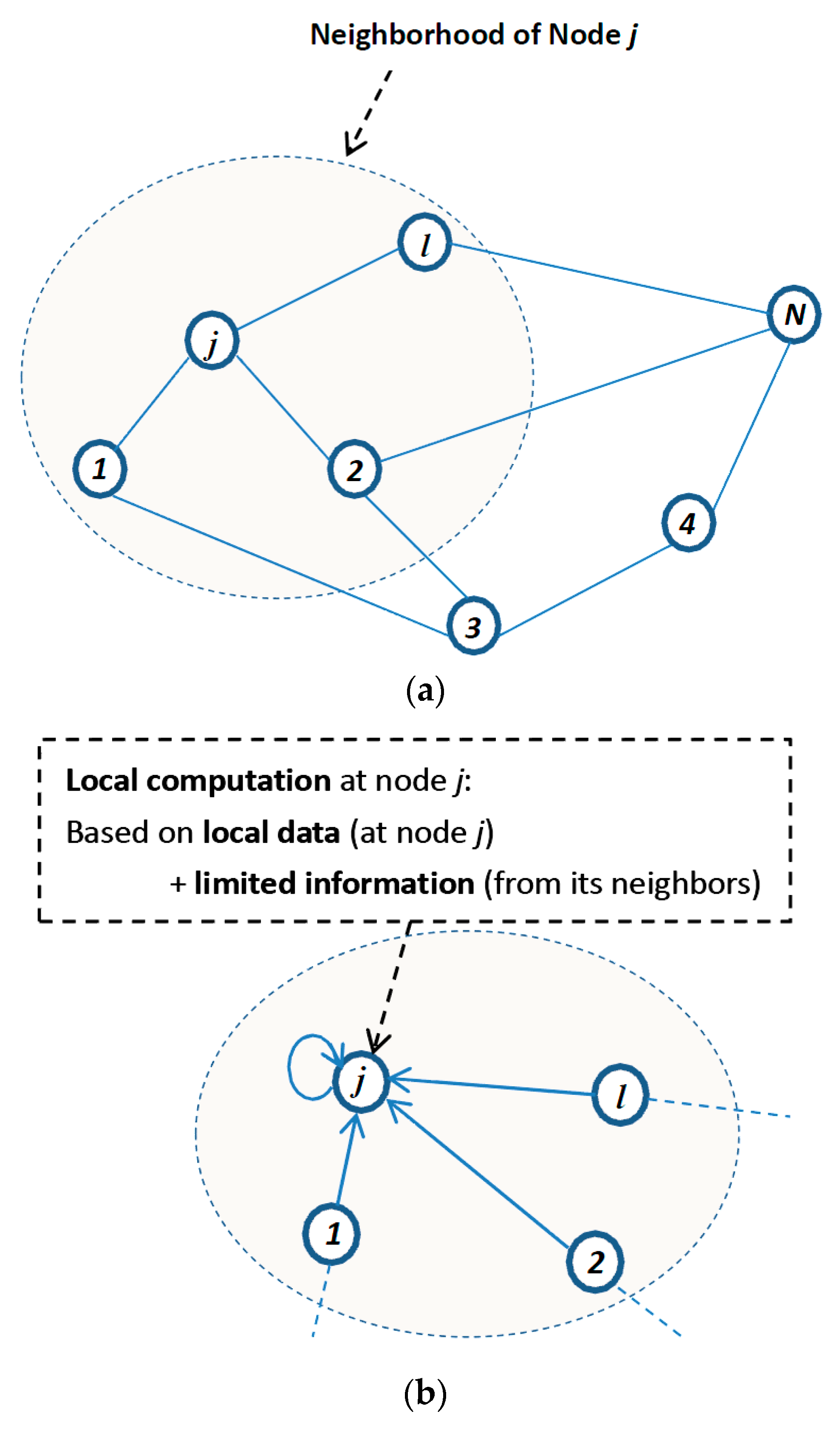
2. Distributed Vector Quantization Algorithm Using K-L Divergence
2.1. Starting from the Centralized Case
2.2. Extended to Distributed Cases
- Use parts of the node’s local input vectors to iteratively update the estimates via Equation (7).
- Transmit the local estimation results to neighbors.
- Fuse the results from the neighbors to obtain fused estimates of the reproduction vectors via Equation (8).
2.3. Communication Complexity Analysis
3. Numerical Experiments
3.1. Data Generation and Evaluation Indexes
3.2. Results
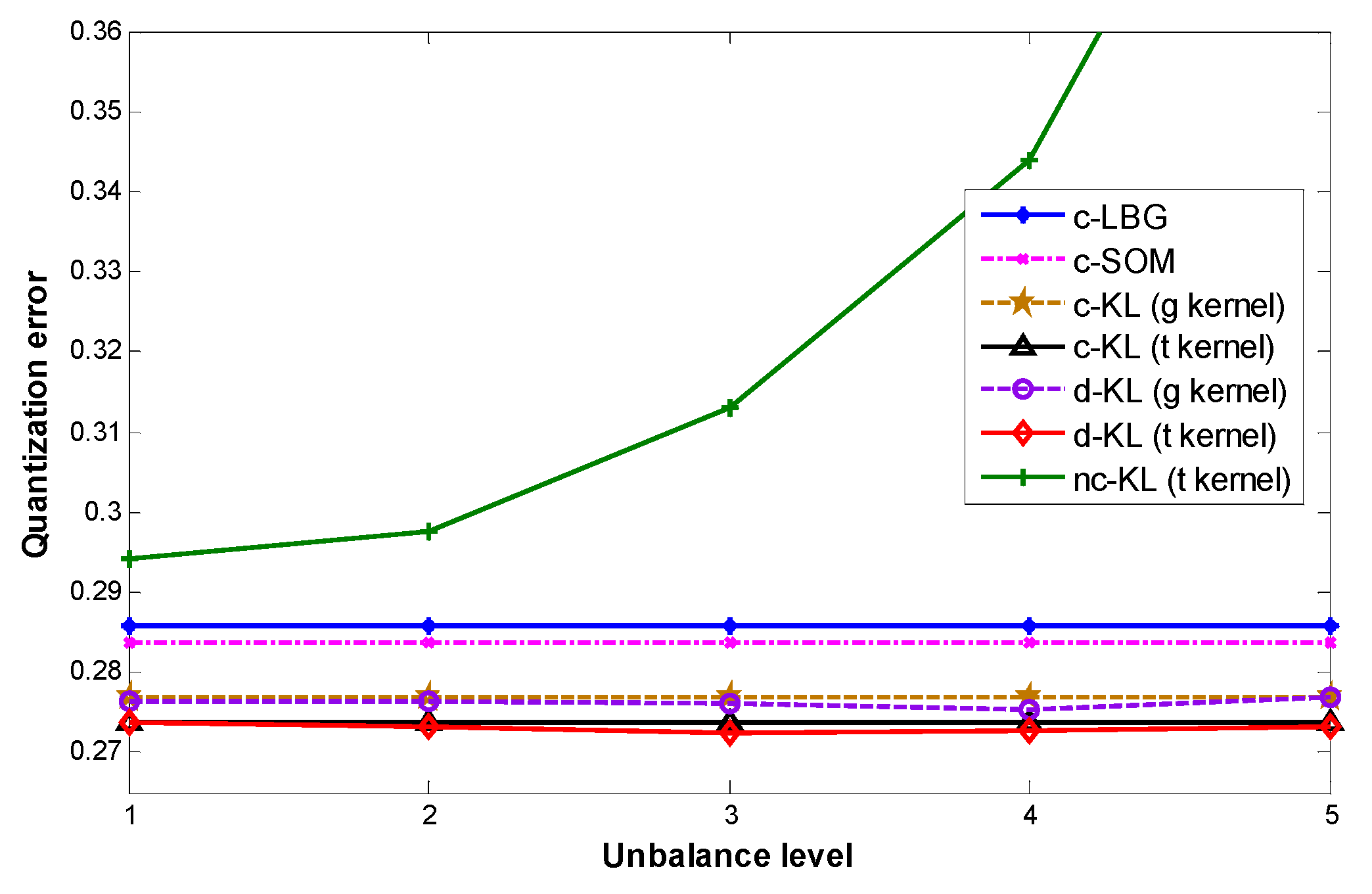
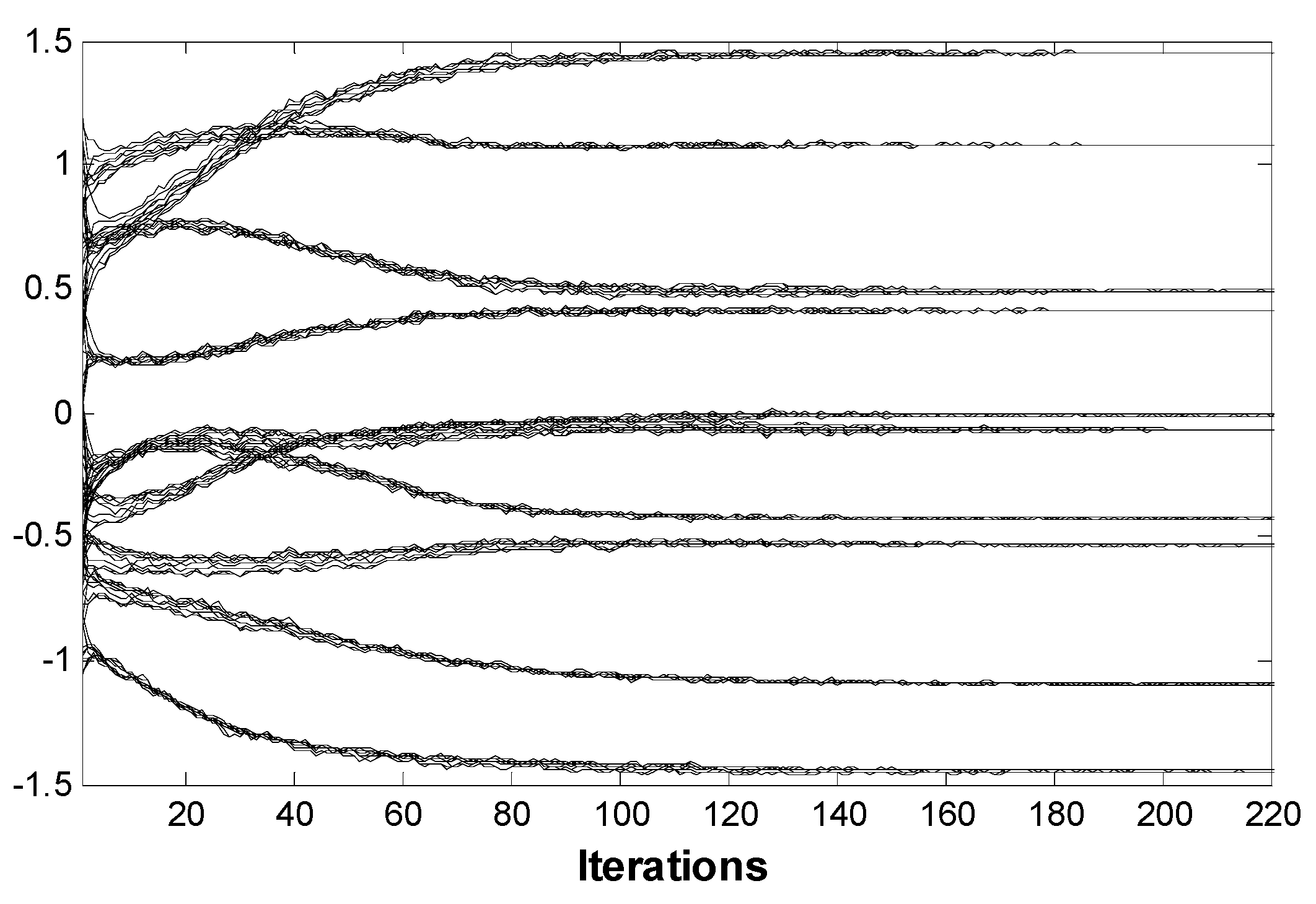
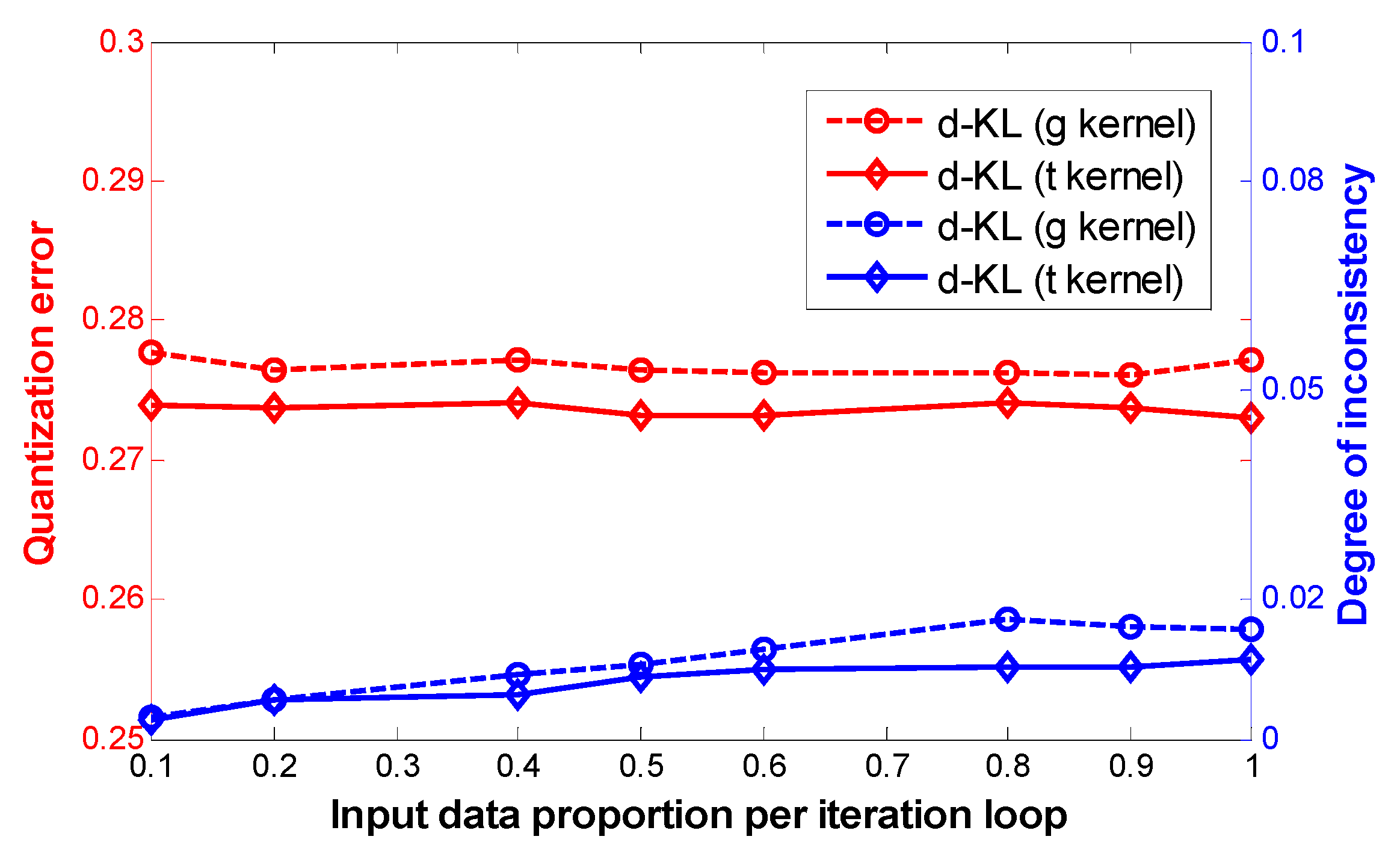
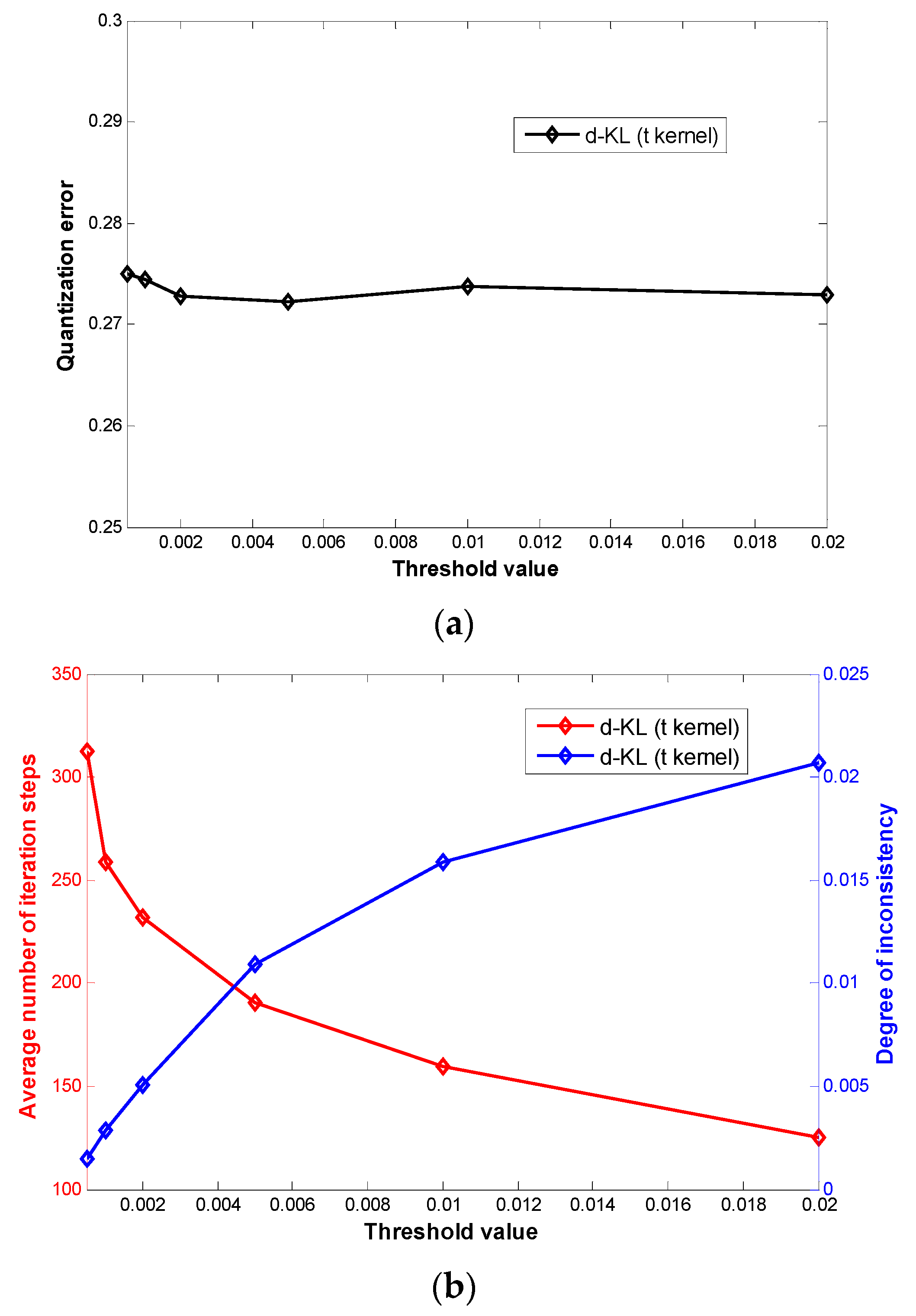

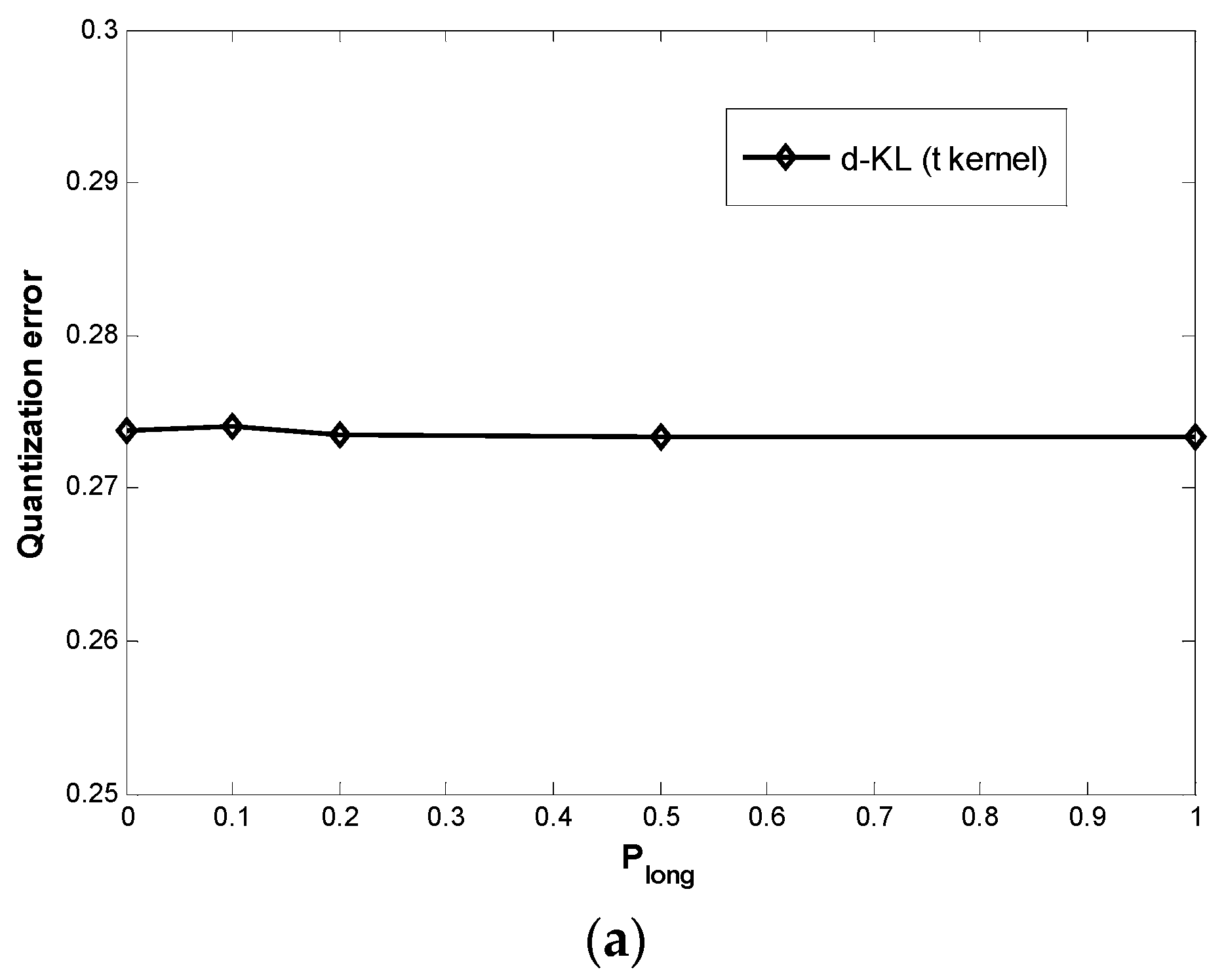
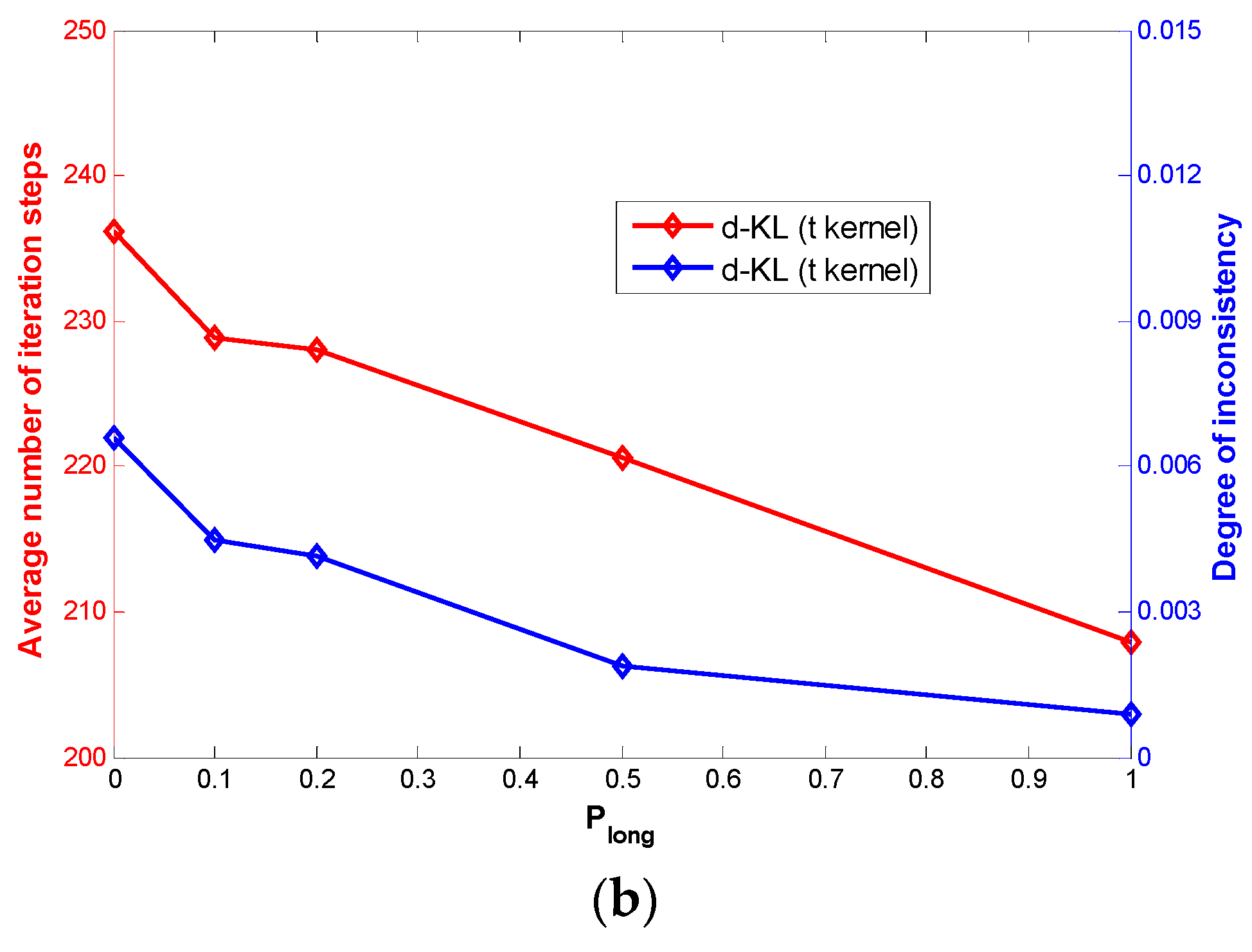
| Quantization Error | Average NoIS | Inconsistency Degree | |
|---|---|---|---|
| WS | 0.273 | 227 | 8.23 × 10−3 |
| ER | 0.273 | 225 | 4.43 × 10−3 |
| BA | 0.273 | 232 | 7.93 × 10−3 |
| RG | 0.274 | 236 | 1.22 × 10−2 |
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Gray, R.M. Vector quantization. IEEE ASSP Mag. 1984, 1, 4–29. [Google Scholar] [CrossRef]
- Gray, R.M.; Neuhoff, D.L. Quantization. IEEE Trans. Inf. Theory 1998, 44, 2325–2383. [Google Scholar] [CrossRef]
- Linde, Y.; Buzo, A.; Gray, R.M. An algorithm for vector quantizer design. IEEE Trans. Commun. 1980, 28, 84–95. [Google Scholar] [CrossRef]
- Lloyd, S. Least squares quantization in PCM. IEEE Trans. Inf. Theory 1982, 28, 129–137. [Google Scholar] [CrossRef]
- Kohonen, T. The self-organizing map. Proc. IEEE 1990, 78, 1464–1480. [Google Scholar] [CrossRef]
- Nasrabadi, N.M.; Feng, Y. Vector quantization of images based upon the Kohonen self-organizing feature maps. In Proceedings of the 1988 IEEE International Conference on Neural Networks, San Diego, CA, USA, 24–27 July 1988; pp. 101–108.
- Vesanto, J.; Alhoniemi, E. Clustering of the self-organizing map. IEEE Trans. Neural Netw. 2000, 11, 586–600. [Google Scholar] [CrossRef] [PubMed]
- Lehn-Schiøler, T.; Hegde, A.; Erdogmus, D.; Principe, J.C. Vector quantization using information theoretic concepts. Nat. Comput. 2005, 4, 39–51. [Google Scholar] [CrossRef]
- Hegde, A.; Erdogmus, D.; Lehn-Schioler, T.; Rao, Y.N.; Principe, J.C. Vector-Quantization by density matching in the minimum Kullback-Leibler divergence sense. In Proceedings of the IEEE International Joint Conference on Neural Networks, Budapest, Hungary, 25–29 July 2004; Volume 1, pp. 105–109.
- Sayed, A.H. Adaptive Networks. Proc. IEEE 2014, 102, 460–497. [Google Scholar] [CrossRef]
- Lopes, C.G.; Sayed, A.H. Diffusion Least-Mean Squares Over Adaptive Networks: Formulation and Performance Analysis. IEEE Trans. Signal Process. 2008, 56, 3122–3136. [Google Scholar] [CrossRef]
- Cattivelli, F.S.; Lopes, C.G.; Sayed, A.H. Diffusion recursive least-squares for distributed estimation over adaptive networks. IEEE Trans. Signal Process. 2008, 56, 1865–1877. [Google Scholar] [CrossRef]
- Schizas, I.D.; Mateos, G.; Giannakis, G.B. Distributed LMS for consensus-based in-network adaptive processing. IEEE Trans. Signal Process. 2009, 57, 2365–2382. [Google Scholar] [CrossRef]
- Mateos, G.; Schizas, I.D.; Giannakis, G.B. Distributed recursive least-squares for consensus-based in-network adaptive estimation. IEEE Trans. Signal Process. 2009, 57, 4583–4599. [Google Scholar] [CrossRef]
- Liu, Y.; Li, C.; Tang, W.K.; Zhang, Z. Distributed estimation over complex networks. Inf. Sci. 2012, 197, 91–104. [Google Scholar] [CrossRef]
- Liu, Y.; Yang, C.; Tang, W.K.; Li, C. Optimal topological design for distributed estimation over sensor networks. Inf. Sci. 2014, 254, 83–97. [Google Scholar] [CrossRef]
- Kar, S.; Moura, J.M.F. Convergence rate analysis of distributed gossip (linear parameter) estimation: Fundamental limits and tradeoffs. IEEE J. Sel. Top. Signal Process. 2011, 5, 674–690. [Google Scholar] [CrossRef]
- Kar, S.; Moura, J.M.F.; Ramanan, K. Distributed parameter estimation in sensor networks: Nonlinear observation models and imperfect communication. IEEE Trans. Inf. Theory 2012, 58, 3575–3605. [Google Scholar] [CrossRef]
- Liu, Y.; Li, C.; Zhang, Z. Diffusion sparse least-mean squares over networks. IEEE Trans. Signal Process. 2012, 60, 4480–4485. [Google Scholar] [CrossRef]
- Liu, Z.; Liu, Y.; Li, C. Distributed Sparse Recursive Least-Squares over Networks. IEEE Trans. Signal Process. 2014, 62, 1386–1395. [Google Scholar] [CrossRef]
- Olfati-Saber, R. Distributed Kalman filter with embedded consensus filters. In Proceedings of the Joint IEEE Conference Decision Control/European Control Conference, Seville, Spain, 6–9 December 2005; pp. 8179–8184.
- Carli, R.; Chiuso, A.; Schenato, L.; Zampieri, S. Distributed Kalman filtering using consensus strategies. IEEE J. Sel. Areas Commun. 2008, 26, 622–633. [Google Scholar] [CrossRef]
- Aldosari, S.A.; Moura, J.M. Topology of sensor networks in distributed detection. In Proceedings of the 2006 IEEE International Conference on Acoustics, Speech and Signal Processing, Toulouse, France, 14–19 May 2006; pp. 1061–1064.
- Aldosari, S.A.; Moura, J.M. Distributed detection in sensor networks: Connectivity graph and small world networks. In Proceedings of the Thirty-Ninth Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 30 October–2 November 2005; pp. 230–234.
- Forero, P.A.; Cano, A.; Giannakis, G.B. Distributed clustering using wireless sensor networks. IEEE J. Sel. Top. Signal Process. 2011, 5, 707–724. [Google Scholar] [CrossRef]
- Datta, S.; Giannella, C.R.; Kargupta, H. Approximate distributed k-means clustering over a peer-to-peer network. IEEE Trans. Knowl. Data Eng. 2009, 21, 1372–1388. [Google Scholar] [CrossRef]
- Li, C.; Shen, P.; Liu, Y.; Zhang, Z. Diffusion Information Theoretic Learning for Distributed Estimation over Network. IEEE Trans. Signal Process. 2013, 61, 4011–4024. [Google Scholar] [CrossRef]
- Shen, P.; Li, C. Distributed Information Theoretic Clustering. IEEE Trans. Signal Process. 2014, 62, 3442–3453. [Google Scholar] [CrossRef]
- Li, C.; Luo, Y. Distributed Vector Quantization over Sensor Network. Int. J. Distrib. Sensor Netw. 2014, 2014. [Google Scholar] [CrossRef]
- Robbins, H.; Monro, S. A stochastic approximation method. Ann. Math. Stat. 1951, 22, 400–407. [Google Scholar] [CrossRef]
- Yin, H.; Allinson, N.M. Self-organizing mixture networks for probability density estimation. IEEE Trans. Neural Netw. 2001, 12, 405–411. [Google Scholar] [CrossRef] [PubMed]
- Cichocki, A.; Amari, S.-I. Families of alpha- beta- and gamma- divergences: Flexible and robust measures of similarities. Entropy 2010, 12, 1532–1568. [Google Scholar] [CrossRef]
- Peel, D.; McLachlan, G.J. Robust mixture modeling using the t distributions. Stat. Comput. 2000, 10, 335–344. [Google Scholar] [CrossRef]
- Wei, X.; Li, C. The infinite Student’s t-mixture for robust modeling. Signal Process. 2012, 92, 224–234. [Google Scholar] [CrossRef]
- Bianchi, P.; Fort, G.; Hachem, W.; Jakubowicz, J. Performance of a distributed Robbins-Monro algorithm for sensor networks. In Proceedings of the 19th EUSIPCO, Barcelona, Spain, 29 August–2 September 2011; pp. 1030–1034.
- Bianchi, P.; Fort, G.; Hachem, W.; Jakubowicz, J. Convergence of a distributed parameter estimator for sensor networks with local averaging of the estimates. In Proceedings of the 2011 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Praha, Czech Republic, 22–27 May 2011; pp. 3764–3767.
- Xiao, L.; Boyd, S. Fast linear iterations for distributed averaging. Syst. Control Lett. 2004, 53, 65–78. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, P.; Li, C.; Luo, Y. Distributed Vector Quantization Based on Kullback-Leibler Divergence. Entropy 2015, 17, 7875-7887. https://doi.org/10.3390/e17127851
Shen P, Li C, Luo Y. Distributed Vector Quantization Based on Kullback-Leibler Divergence. Entropy. 2015; 17(12):7875-7887. https://doi.org/10.3390/e17127851
Chicago/Turabian StyleShen, Pengcheng, Chunguang Li, and Yiliang Luo. 2015. "Distributed Vector Quantization Based on Kullback-Leibler Divergence" Entropy 17, no. 12: 7875-7887. https://doi.org/10.3390/e17127851
APA StyleShen, P., Li, C., & Luo, Y. (2015). Distributed Vector Quantization Based on Kullback-Leibler Divergence. Entropy, 17(12), 7875-7887. https://doi.org/10.3390/e17127851






